清华大学材料力学习题详解范钦珊6章
清华大学材料力学范钦珊主讲---第六章--弹性杆件位移分析

约束对位移的影响
连续光滑曲线;铰支座对位移的限念
约束对位移的影响
连续光滑曲线;固定端对位移的限制
第6 章
弹性杆件位移分析
确定梁位移 的积分方法
第6章
弹性杆件位移分析
确定梁位移的积分方法
对于拉伸(压缩)、扭转位移定积分 对于梁的位移不定积分
弹性曲线的小挠度微分方程 弯矩方程的两种写法及其利弊
第6 章
弹性杆件位移分析
奇异函数的应用
梁挠度方程的 奇异函数形式 (2)挠度微分方程
w M ( x) 3 F x F x l EI d P 4 4 P dx
2 2
1
(3)微分方程的积分
2 F 3 d w EI dx EI 8 FP x P 2 3 F 3 l P EIw 1 F x x 6 4 8 P
F P1
M1
q1
F P2
q2
M2
F P3
第6章
弹性杆件位移分析
奇异函数的应用
集 中 力 偶 作 用 的 情 形
弯矩方程的奇异函数表示
M ( M i ) M i x ai
0
第6章
弹性杆件位移分析
奇异函数的应用
弯矩方程的奇异函数表示
集 中 力 作 用 的 情 形
j
M ( FP j ) FP j x b j
xa
n
0
( x a)
( x a)
n
( x a)
第6章
弹性杆件位移分析
奇异函数的应用
奇 异 函 数 图 形
第6章
弹性杆件位移分析
奇异函数的应用
清华出版社工程力学答案-第6章 拉压杆件的应力变形分析与强度设计

∑ Fx = 0 , FNAC cos 45D + FNAD = 0
解得 AD 杆轴力大小为: FNAD = 15kN(拉)
2. 强度条件
拉杆:
AAD
=
FNAD [σ ]+
=
15 ×103 120 ×10−6
= 125mm2
压杆:
AAC
=
2. 钢杆的伸长量:
ΔlBC
=
FPlBC Es As
=
60×103 × 2.1 200×109 × π ×152 ×10−6
= 3.565mm
4
3. 钢杆 C 端向下移动的距离: uC = ΔlAB + ΔlBC = 0.935 + 3.565 = 4.50 mm
6-3 螺旋压紧装置如图所示。现已知工件所受的压紧力为 F=4 kN。装置中旋紧螺栓
10
习题 6-10 图
解:1.活塞杆 受到的轴力为:
FN
=
pA
=
p
⎡π ⎢ ⎣
(
D
2− 4
d2)⎤ ⎥ ⎦
=
⎡π 2.5⎢
⎣
(5602 − 4
1002
)
⎤ ⎥ ⎦
=
596.12kN
活塞杆的正应力: σ = FN = 596.12 ×103 = 75.9MPa A杆 π ×1002 / 4
工作安全系数: n = σ s = 300 = 3.95 σ 75.9
弹性模量E和泊松比ν 。
l0
b
解:1.计算弹性模量E
h 习题 6-11 图
11
εx
=
材料力学_范钦珊_习题参考解答
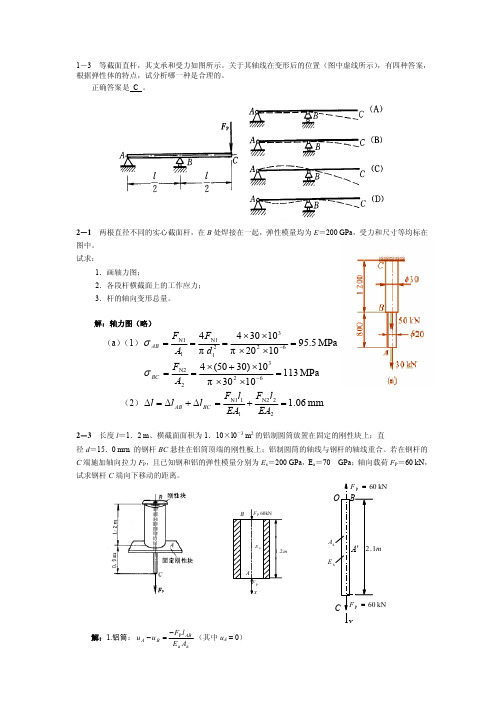
2-11 图示组合柱由钢和铸铁制成,组合柱横截面为边长为 2b 的正方形,钢和铸铁各占横截面的一 半(b×2b)。载荷 FP,通过刚性板沿铅垂方向加在组合柱上。已知钢和铸铁的弹性模量分别为 Es=196 GPa, Ei=98.0 GPa。今欲使刚性板保持水平位置,试求加力点的位置 x=?
解: ∑ M 0
( ) ( ) τmax
AB
= M xAB WPAB
= M xAB πd13
= π×
2936 70 ×10-3
3
= 43.6 MPa
16
16
BC 段:
M xBC = M e1 = 1171 N ⋅ m
( ) ( ) τmax
BC
=
M xBC WP 2
= M xBC
πd
3 2
= π×
1171 50 ×10−3
解:1. τ1max
=
Mx WP
=T WP
=T πd 3
= 3 ×103 ×16 = 70.7 MPa π× 0.063
16
∫ ∫ 2.
Mr =
ρ ⋅τdA =
A1
r
ρ
⋅
M
x
ρ ⋅ 2πρdρ
=
2πM x
⋅
r4
0 Ip
Ip
4
M r = 2πr 4 = 2πr 4 = 16r 4 = 16 × (15 )4 = 1 = 6.25%
Mx
4Ip
4 ⋅ πd 4
d4
60 16
32
3.
τ 2 max
=
Mx Wp
=
T
=75.4MPa
πd 3 ⎜⎛1 − ( 1 )4 ⎟⎞
高教范钦珊材料力学习题集_【有答案】

习题1-1图 习题1-2图习题1-3图习题1-4图习题1-5图习题1-6图 材料力学习题集第1章 引 论1-1 图示矩形截面直杆,右端固定,左端在杆的对称平面内作用有集中力偶,数值为M 。
关于固定端处横截面A -A 上的内力分布,有四种答案,根据弹性体的特点,试分析哪一种答案比较合理。
正确答案是 C 。
1-2 图示带缺口的直杆在两端承受拉力F P 作用。
关于A -A 截面上的内力分布,有四种答案,根据弹性体的特点,试判断哪一种答案是合理的。
正确答案是 D 。
1-3 图示直杆ACB 在两端A 、B 处固定。
关于其两端的约束力有四种答案。
试分析哪一种答案最合理。
正确答案是 D 。
1-4 等截面直杆在两端承受沿杆轴线的拉力F P 。
关于杆中点处截面A -A 在杆变形后的位置(图中虚线所示),有四种答案,根据弹性体的特点,试判断哪一种答案是正确的。
正确答案是 D 。
1-5 图示等截面直杆在两端作用有力偶,数值为M ,力偶作用面与杆的对称面一致。
关于杆中点处截面A -A 在杆变形后的位置(对于左端,由A A '→;对于右端,由A A ''→),有四种答案,试判断哪一种答案是正确的。
正确答案是 C 。
1-6 等截面直杆,其支承和受力如图所示。
关于其轴线在变形后的位置(图中虚线所示),有四种答案,根据弹性体的特点,试分析哪一种是合理的。
正确答案是 C 。
习题2-1图习题2-2图习题2-3图习题2-4图ABABC)(ql 2lM QF QF 454141第2章 杆件的内力分析2-1 平衡微分方程中的正负号由哪些因素所确定?简支梁受力及Ox 坐标取向如图所示。
试分析下列平衡微分方程中哪一个是正确的。
(A ))(d d Q x q x F =;Q d d F x M=; (B ))(d d Q x q x F -=,Q d d F x M-=; (C ))(d d Q x q x F -=,Q d d F x M=; (D ))(d d Q x q x F =,Q d d F xM-=。
工程力学习题答案

球的尺寸忽略不计。
TA
TB
A
ϕ1 ϕ2
B
FNA
FNB 2N
1N
习题 1-12 图
解:
∩
AB
=
0.2m
, ϕ1
+ϕ2
=
2×
360° 2π
= 114°35′
图(a):A 平衡: ∑ Fy = 0 , TA = 1⋅ sin ϕ1
AG = 2CD (图(a)) 在图(a)中: 设 OF = d,则
d = 4 cot θ (d + 3sin θ ) = AG = 2CD
(1)
CD = CE sin θ = (4.5 − d )sin θ 2
(2)
即 (d + 3)sin θ = 2(4.5 − d )sin θ 2
d +3=9−d
1 一 5 试画出图示结构中各杆的受力图。
习 题 1-5 图
B FB
FC
C
C
FC'
FD'
D
FAx
A
FAy
(a-1)
D FD
F
E
FE'
(a-2)
FE
E
(a-3)
T
FCx C FCy
W
(b-1)
FAx
A
C FC' x
FAy
FC' y
(b-3)
FE E
B
FB
(b-2)
FB'
B
FB'
FC'
材料力学高教第二版范钦珊第6章习题答案要点

材料力学_高教第二版_范钦珊_第6章习题答案第6章杆件横截面的位移分析6-1 直径d = 36mm的钢杆ABC与铜杆CD在C处连接,杆受力如图所示。
若不考虑杆的自重,试: 1.求C、D二截面的铅垂位移;Fl2.令FP1 = 0,设AC段长度为l1,杆全长为l,杆的总伸长,写出E的表达式。
EA习题6-1图(a) (F)l(F)l解:(1)πdπdEsEs2332(FN)CDlCDπdEc4(2)EAEsAEcAEEsEclEcEs令FP6-2 承受自重和集中载荷作用的柱如图所示,其横截面积沿高度方向按材料的比重。
试作下列量的变化曲线: 1.轴力FNx(x); 2.应力; 3.位移u(x)。
解:(1),(FN变化,其中为FPFN(x)-FPx习题6-2图(a)FPFPA0FP(2)A(x)A0eFPFP— 89 —(3)A0,当。
∴,则EA0EA0EA06-3 图示连接件由两片宽20mm、厚6mm的铜片与一片同样宽厚的钢片在B处连接而成。
已知钢与铜的弹性模量分别为Es = 200GPa,Ec =105GPa,钢片与铜片之间的摩擦忽略不计。
试求E和B处的位移。
F习题6-3图解:6-4 长为1.2m、横截面面积为的铝制筒放置在固定刚块上,直径为15.0mm的钢杆BC悬挂在铝筒顶端的刚性板上,若二者轴线重合、载荷作用线与轴线一致,且已知钢和铝的弹性模量分别为kNEs = 200Gpa,Ea = 70GPa,FP = 60kN。
试求钢杆上C处位移。
Am EkN(a) 习题6-4图 (b)解:(其中uA = 0) EaAa ∴钢杆6-5 变截面圆锥杆下端B处固定,上端A处承受外力偶矩T作用,如图所示,试证明A端扭转角表达式为解:Mx = T习题6-5图6-6 试比较图示二梁的受力、内力(弯矩)、变形和位移,总结从中所得到的结论。
(a) 解:(b) wmaxFPl3 48EIFlEI— 90 —两者弯矩相同,挠曲线曲率相同,但(b)梁的最大挠度比(a)梁要大,即不相等。
清华大学材料力学-第6章

z
x S平面
一点处应力状态描述及其分类
y
1
FQy
TSINGHUA UNIVERSITY
1
4 2
3
Mz
4
x
z
Mx
3
第6章 应力状态分析
TSINGHUA UNIVERSITY
返回总目录
平面应力状态任意 方向面上的应力
返回
平面应力状态任意方向面上的应力
TSINGHUA UNIVERSITY
x'
xP
x'
yP
yp
xp
x-y坐标系
x´-y´坐标 系
xp-yp坐标系
第6章 应力状态分析
TSINGHUA UNIVERSITY
返回总目录
主应力、主方向与 面内最大切应力
返回
主应力、主方向与面内最大切应力
TSINGHUA UNIVERSITY
主平面、主应力与主方向 平面应力状态的三个主应力 用主应力表示的应力状态 面内最大切应力
x'
平面应力状态任意方向面上的应力
微元的局部平衡
TSINGHUA UNIVERSITY
最后,得到以下四个方程:
x x cos2q ysin 2q xysinq cosq yxsinq cosq
y xsin 2q y cos2q xysinq cosq yxsinq cosq
第6章 应力状态分析
TSINGHUA UNIVERSITY
2、应力的三个重要概念
应力的点的概念; 应力的面的概念; 应力状态的概念.
第6章 应力状态分析
工程力学(静力学+材料力学) 范钦珊
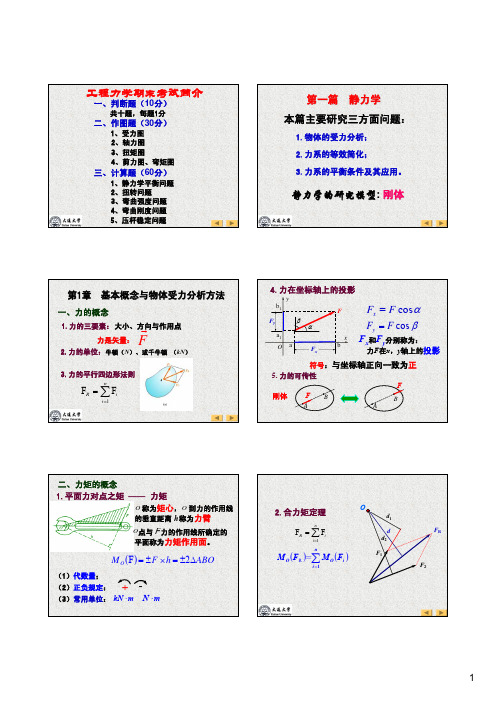
[ ] 等直杆: σ max
=
FN max A
≤
σ
三类强度计算问题:(1)强度校核;
(2)截面设计; (3)计算许可荷载
九、拉伸与压缩时材料的力学性能
1. 低碳钢拉伸时的力学性能 ( (12) )四 四个 个阶 强段 度指标σ
极限强度σb
局部变形阶段
屈服强度σs 弹性极限σe
2.力偶矩
M = ±F ⋅d
A
F Dd
B
C
F'
(1)代数量;
(2)正负号规定:表示力偶的转向;
+
(3)单位:力偶矩的单位与力矩相同。
-
3.力偶的性质
(1)力偶对任意点取矩都等于力偶矩,不因矩心的 改变而改变.
(2)力偶在任意坐标轴上的投影等于零.
(3)力偶没有合力,本身又不平衡,力偶只能由 力偶来平衡.
σ(MPa)
600
压缩 400 300
抗压强度>>抗拉强度
拉伸 0.05
0.10 ε
第6章 圆轴扭转
一、扭转的概念 Me
Me
主要发生扭转变形的杆
ϕ BA
轴
本章主要介绍
A
l
B
圆轴(实心或空心)扭转
二、外加扭转力偶矩与功率、转速之间的关系
Me
=
9549
P n
[N ⋅ m]
其中P为功率,单位为千瓦 (kW);n为轴的转速,单 位为转/分(r/min)。
Bh AF
F'
B M A
M = MB (F) = Fh
4
三、平面一般力系的简化结果
y F1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
—2—
第 6 章 梁的弯曲问题(2)截面的几何性质
6-1 图示的三角形中 b、h。试用积分法求 Iz、Iy、Iyz 。 解:1、计算 Iy 取微面积如图 b 所示:
(a)
(b)
(c)
习题 6-1 图
dA = b ( z) dz, b ( z) = b z
h
∫ ∫ I y = z2dA = A
将组合图形分解为 1、2、3 三个矩形。根据反对称性,矩形 1 的形心 C1 即为组合图形 的形心。
2、建立初始坐标系,确定组合图形对于初始坐标系的惯性矩与惯性积
以 C1 为坐标原点,奖励 C1zy 坐标系,利用叠加的方法,求组合图形对于 z、y 轴的惯 性矩与惯性积
I y = I y (1) + I y (2) + I y (3)
6-4 图中所示组合截面为两根 No.20a 的普通热轧槽 形钢所组成的截面,今欲使 Ix = Iy,试求 b =?(提示:计算 所需要数据均可由型钢表中查得。)
解:由型钢表查到 No.20a 普通热轧槽钢 Iy1 = 1780.4 cm4,Iz1 = 128 cm4 yO = 2.01cm,A = 28.83cm2
×
π × 402 4
⎞ ⎟ ⎠
= (5.0 + 0.1674)×106 − (0.1256 + 0.8044 )×106
= 4.239×106 mm4
6-3 几何图形尺寸如图所示(单位为 mm)。试: 1、 确定形心主轴与水平方向的夹角; 2、 确定形心主惯性矩。
(a)
(b)
习题 6-3 图
解:1、确定形心位置
h z2 ( b z)dz = bh3
0h
4
2、计算 Iz 取微面积如图 b 所示:
dA
=
−h(
y)dy
=
−h
⎛⎜⎝1 −
y b
⎞ ⎟⎠
dy
∫ I z
=
−
−b 0
y2h ⎛⎜⎝1−
y b
⎞ ⎟⎠
dy
=
hb3 12
3、计算 Iyz 由图 b,
∫ ∫ I yz =
yzdA =
A
yzb( z )dz
A
b(z) = b z h
=
Iy
+ 2
Iz
−
1 2
I y − I z 2 + 4 I yz 2
=
⎡ ⎢⎣
3.674
+ 2
15.17
−
1 2
(3.674
−15.17
)2
+
4
(
−5.88)2
⎤ ⎥⎦
×106
= (9.422 − 8.223)×106 = 1.199×106 mm4 = 1.199×10−6 m4
( ) ( ) Iz0 =
范钦珊教育教学工作室
FAN Qin-Shan’s Education & Teaching Studio
eBook
材料力学习题详细解答
教师用书
(第 6 章)
2006-01-18
—1—
习题 6-1 习题 6-2 习题 6-3 习题 6-4 习题 6-5 习题 6-6 习题 6-7 习题 6-8 习题 6-9 习题 6-10
( ) =
120 ×103 12
+
2
⎡ 70 × 203
⎥ ⎦
( ) = 1×104 + 2 57.2×104 +126×104 = 3.674×106 mm4
—5—
Iz = Iz (1) + Iz (2) + Iz (3)
( ) =
10 ×1203 12
+
2
⎡ 20 × 703
⎢ ⎣
12
+
702 × 20× 30
⎤ ⎥ ⎦
( ) = 1.44×106 + 2 4.667 ×104 + 6.86×106 = 15.17 ×106 mm4
I yz = I yz (1) + I yz (2) + I yz (3) = 0 + 2I yz (2) = 0 + 2 ⎡⎣0 − (20× 70× 70× 30)⎤⎦
×105
+
⎝
a2
×
π642 8
⎞ ⎟ ⎠
a = 40 − 2× 64 = 26.4 mm 3π
Iz
=
100 ×803 12
−
2
⎛ ⎜1.15
×105
+
⎝
26.42
×
π642 8
⎞ ⎟ ⎠
= 1.792×106
mm4
(b)题: 先求图形心位置:z 轴为对称轴,所以形心必在 z 轴上。 yC = 0
—4—
Iy
+ 2
Iz
+
1 2
2
2
I y − Iz + 4 I yz
( ) ( ) Iy0
=
Iy
+ 2
Iz
−
1 2
I y − Iz 2 + 4 I yz 2
=
⎡ ⎢⎣
3.674
+ 2
15.17
+
1 2
(3.674
− 15.17 )2
+
4
( −5.88)2
⎤ ⎥⎦
×106
= (9.422 + 8.223)×106 = 1.765×107 mm4 = 1.765×10−5 m4
y = − b(z) = − b z 2 2h
—3—
∫ ∫ I yz =
A
yzb( z )dz
=
h 0
⎛ ⎜⎝
−
b 2h
z
⎞ ⎟⎠
z
⎛ ⎜⎝
b h
z
⎞ ⎟⎠
dz
=
−
b2h2 8
6-2 试确定图中所示图形的形心主轴和形心主惯性矩。 解:(a)题:
(a)
(b)
图中 y、z 即为形心主轴
习题 6-2 图
Iy
=
80 ×1003 12
−
π644 64
= 5.84×106
mm4
半圆对于自身形心轴的惯性矩:
I z′
=
π 644 128
−
⎛ ⎜⎝
2
× 64 3π
⎞2 ⎟⎠
×
π642 8
= 1.15×105
mm4
组合图形对于 z 轴的惯性矩:
其中 代入上式后,算得
Iz
=
100 ×803 12
−
2
⎛ ⎜1.15
( ) = 2× −49.6×104 = −5.88×106 mm4
3、确定形心主轴与 z 轴的夹角
tanα0
=
2I yz Iy − Iz
=
−2× 5.88×106
(3.674 −15.17)×106
= 1.023
α0 = arctan (1.023) = 45.65D
3、确定形心主惯性矩
( ) ( ) Iy0
100× 60× (−20) − 0
zC = 100× 60 − π × 402 = 25.3 mm 4
Iz
= 100 × 603 12
− π × 404 64
= 1.674×106
mm4
Iy
=
⎛ ⎜ ⎝
60 ×1003 12
+ 5.32
×100 ×
60
⎞ ⎟
−
⎛ ⎜
⎠⎝
π × 404 64
+ 25.32
Iy= 2Iy1
Iz
=
2
⎡ ⎢⎣
I
z1
+
( y0
+
b )2 2
A⎤⎥⎦
—6—
习题 6-4 图
若 Iy = Iz,则
I y1
=
I z1
+
(
y0
+
b )2 2
A
⎛ b = 2⎜⎜⎝
I y1
− Iz1 A
−
y0
⎞ ⎟⎟⎠
=
⎛ 2 ⎜⎜⎝
1780.4 −128 28.83
