苏科版四(下)奥数教案第3讲~多人多次相遇与追及
苏科版四(下)奥数教案第3讲~多人多次相遇与追及

四(下)奥数第3讲~多人多次相遇与追及【知识精讲】在之前的课程中,我们已经学过了如何处理两个对象之间的相遇与追及问题,本讲我们进一步学习过程更为复杂的三个对象之间的行程问题。
本讲中画线段图非常重要。
第一部分:复习基本相遇问题:速度和×相遇时间=路程和路程和÷速度和=相遇时间路程和÷相遇时间=速度和1:甲、乙两车从相距1500千米的两地同时出发,相向而行。
甲车每小时行40千米,乙车每小时行60千米,请问:出发多少小时后两车相遇?2:一辆巴士和一辆小轿车同时从A、B两地出发,相向而行。
巴士每小时行50千米,小轿车每小时行60千米,3小时后两车相遇,请问:A、B两地相距多少千米?3:A、B两艘船同时从相距150千米的两个码头出发,相向而行,3小时相遇,A船每小时航行25千米,请问:B船每小时航行多少千米?基本追及问题:速度差×追及时间=路程差路程差÷速度差=追及时间路程差÷追及时间=速度差1:圆圆、乐乐两人分别从相距30千米的两地同时向南行驶,圆圆骑自行车每小时行14千米,乐乐步行每小时走4千米,请问:多少小时后圆圆可以追上乐乐?2:蚂蚁在蜘蛛前面几百米处,同时出发同向而行,蜘蛛每分钟跑55米,蚂蚁每分钟爬1米,10分钟后蜘蛛追上了蚂蚁,请问:开始时蚂蚁距蜘蛛多少米?第二部分:多人相遇例1: 有A、B、C三个人,A每分钟走20米,B每分钟走40米,C每分钟走30米。
甲、乙两地相距3000米。
A从甲地,B、C从乙地同时出发相向而行。
请问:A在与B相遇之后多少分钟又与C相遇?练1:有圆圆、乐乐、静静三人,圆圆每秒钟走2米,乐乐每秒钟走4米,静静每秒钟走6米。
A、B 两地相距4800米。
圆圆从A地,乐乐、静静从B地同时出发相向而行,请问:圆圆与静静相遇后多少秒又与乐乐相遇?例2:有A、B、C三人,A每分钟走30米,B每分钟走70米,C每分钟走20米。
小学奥数讲义4年级-20-多人多次相遇与追及-难版

本讲在以前学习相遇追及的基础上进行综合拓展,难度较大,教师要把握好节奏。
多人相遇追及问题,即在同一直线上,3个或3个以上的对象之间的相遇追及问题。
所有行程问题都是围绕“=⨯路程速度时间”这一条基本关系式展开的,比如我们遇到的两大典型行程题相遇问题和追及问题的本质也是这三个量之间的关系转化.由此还可以得到如下两条关系式:=⨯路程和速度和相遇时间;=⨯路程差速度差追及时间;多人相遇与追及问题虽然较复杂,但只要抓住这两条公式,逐步表征题目中所涉及的数量,问题即可迎刃而解.【例1】★甲、乙两名同学在周长为300米圆形跑道上从同一地点同时背向练习跑步,甲每秒钟跑3.5米,乙每秒钟跑4米,问:他们第十次相遇时,甲还需跑多少米才能回到出发点?【解析】从开始到两人第十次相遇的这段时间内,甲、乙两人共跑的路程是操场周长的10倍,为300103000⨯=米,因为甲的速度为每秒钟跑3.5米,乙的速度为每秒钟跑4米,所以这段时间内甲共行了 3.5300014003.54⨯=+米,也就是甲最后一次离开出发点继续行了200米,可知甲还需行300200100-=米才能回到出发点.【小试牛刀】甲乙两人在相距90米的直路上来回跑步,甲的速度是每秒3米,乙的速度是每秒2米.如果他们同时分别从直路两端出发,10分钟内共相遇几次?【解析】17典型例题知识梳理【例2】★★上午8点8分,小明骑自行车从家里出发,8分钟后,爸爸骑摩托车去追他,在离家4千米的地方追上了他.然后爸爸立即回家,到家后又立刻回头去追小明,再追上小明的时候,离家恰好是8千米,这时是几点几分?【解析】画一张简单的示意图:图上可以看出,从爸爸第一次追上到第二次追上,小明走了8-4=4(千米).而爸爸骑的距离是 4+ 8= 12(千米).这就知道,爸爸骑摩托车的速度是小明骑自行车速度的 12÷4=3(倍).按照这个倍数计算,小明骑8千米,爸爸可以骑行8×3=24(千米).但事实上,爸爸少用了8分钟,骑行了4+12=16(千米).少骑行24-16=8(千米).摩托车的速度是8÷8=1(千米/分),爸爸骑行16千米需要16分钟. 8+8+16=32.所以这时是8点32分。
四年级奥数第3讲:追及问题-教案
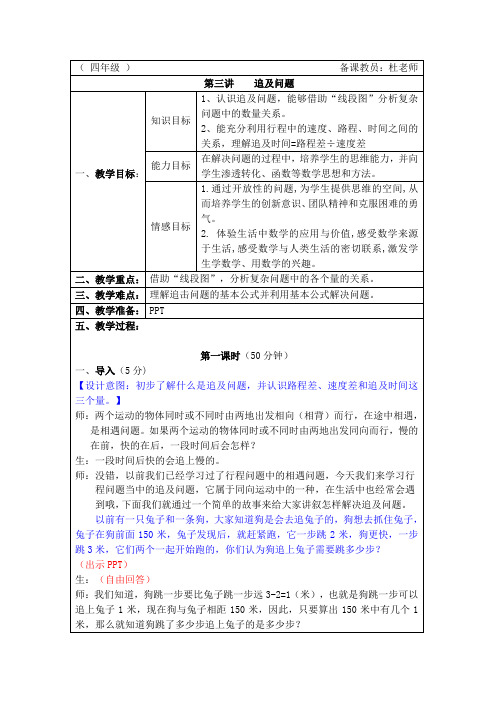
300米,卡尔每分钟跑200米。
两人从起跑线同方向出发,经过多长时间米德第一次追上卡尔?讲解重点:理解环形追及问题第一次追上,路程差就是一圈的长度。
师:仔细读题,你得到了什么信息?生:他们是围绕着一条长400米的环形跑道练习长跑。
米德每分钟跑300米,卡尔每分钟跑200米。
两人从起跑线同方向出发。
师:条件中我们看到米德跑的比卡尔快,怎么才能够追上卡尔呢?生:只要米德比卡尔多跑了1圈才可以追上。
师:没错,很聪明,这样的问题我们把它们叫做环形跑道的追及问题。
米德比卡尔多跑了1圈,就是多跑多少米?生:1圈就是400米,说明米德比卡尔多跑400米。
师:我们知道是一个追及问题,问题是经过多长时间米德第一次追上卡尔?要求的是追及问题的什么?生:追及时间。
师:要求追及时间就必须知道什么?生:路程差和速度差。
师:米德比卡尔多跑400米。
就是追及问题中的什么?生:路程差。
师:知道了路程差,速度差怎么求呢?生:根据两人跑步的速度,可知速度差为:300-200=100(米/分钟)。
师:追及时间怎么求?生:由追及时间=路程差÷速度差,求得追及时间为400÷(300-200)=4(分钟)。
板书:400÷(300-200)=4(分钟)答:经过4分钟米德第一次追上卡尔。
练习3:(5分)在200米的环形跑道上,欧拉在阿派后面40米处,两人同时同方向出发,欧拉的速度是6米/秒,阿派的速度为8米/秒,问多少秒后阿派第一次追上欧拉?分析:从条件中可以看出阿派的速度比欧拉快,而要我们求经过多长时间阿派第一次追上欧拉,因为欧拉在阿派后面40米同时同方向出发,说明阿派比欧拉多跑了(200-40)米才可以追上,即:(200-40)米就是路程差,再根据两人跑步的速度,可知速度差为:8-6=2(米/秒),再由追及时间=路程差÷速度差,求得追及时间。
板书:(200-40)÷(8-6)=80(秒)答:80秒后阿派第一次追上欧拉。
第2讲:多人多次的相遇与追及(教学设计)-2023-2024学年四年级下册数学人教版

第2讲:多人多次的相遇与追及(教学设计)-2023-2024学年四年级下册数学人教版一、课程基本信息1. 课程名称:第2讲:多人多次的相遇与追及2. 教学年级和班级:2023-2024学年四年级下册数学3. 授课时间:2023年3月15日星期三下午第一节课4. 教学时数:45分钟课程目标:1. 让学生理解多人多次相遇与追及的概念,掌握计算方法。
2. 培养学生运用数学知识解决实际问题的能力。
3. 提高学生的思维能力和团队合作能力。
教学内容:1. 多人多次相遇2. 多人多次追及3. 相遇与追及的计算方法教学过程:1. 导入(5分钟)教师通过实际生活中的例子,引发学生对多人多次相遇与追及的兴趣,引导学生思考如何用数学知识解决此类问题。
2. 讲解多人多次相遇(10分钟)教师通过讲解和示例,让学生理解多人多次相遇的概念,并掌握计算方法。
3. 讲解多人多次追及(10分钟)教师通过讲解和示例,让学生理解多人多次追及的概念,并掌握计算方法。
4. 小组合作(15分钟)学生分成小组,共同完成一个多人多次相遇与追及的实际问题,培养学生的团队合作能力。
5. 总结与作业(5分钟)教师对本节课的内容进行总结,布置相关的作业,帮助学生巩固所学知识。
教学资源:1. 教材:四年级下册数学人教版2. 教具:黑板、粉笔、PPT等3. 学具:练习本、铅笔、橡皮等教学评价:1. 学生能理解多人多次相遇与追及的概念,掌握计算方法。
2. 学生能运用数学知识解决实际问题。
3. 学生能积极参与小组合作,提高团队合作能力。
二、核心素养目标三、学习者分析1. 学生已经掌握了哪些相关知识:学生在之前的学习中已经了解了简单的相遇与追及问题,能够运用基本的速度和时间关系来解决一些简单的相遇与追及问题。
2. 学生的学习兴趣、能力和学习风格:四年级的学生对生活中的数学问题通常比较感兴趣,他们喜欢通过实际操作和游戏来学习。
在学习风格上,他们喜欢合作学习,能够通过小组讨论来解决问题。
奥数——行程、多次相遇和追及问题

一、由简单行程问题拓展出的多次相遇问题所有行程问题都是围绕“=⨯路程速度时间”这一条基本关系式展开的,多人相遇与追及问题虽然较复杂,但只要抓住这个公式,逐步表征题目中所涉及的数量,问题即可迎刃而解.二、多次相遇与全程的关系1. 两地相向出发:第1次相遇,共走1个全程;第2次相遇,共走3个全程;第3次相遇,共走5个全程;…………, ………………;第N 次相遇,共走2N-1个全程;注意:除了第1次,剩下的次与次之间都是2个全程。
即甲第1次如果走了N 米,以后每次都走2N 米。
2. 同地同向出发:第1次相遇,共走2个全程;第2次相遇,共走4个全程;第3次相遇,共走6个全程;…………, ………………;第N 次相遇,共走2N 个全程;3、多人多次相遇追及的解题关键多次相遇追及的解题关键 几个全程多人相遇追及的解题关键 路程差三、解多次相遇问题的工具——柳卡柳卡图,不用基本公式解决,快速的解法是直接画时间-距离图,再画上密密麻麻的交叉线,按要求数交点个数即可完成。
折线示意图往往能够清晰的体现运动过程中“相遇的次数”,“相遇的地点”,以及“由相遇的地点求出全程”,使用折线示意图法一般需要我们知道每个物体走完一个全程时所用的时间是多少。
如果不画图,单凭想象似乎对于像我这样的一般人儿来说不容易。
知识框架 多次相遇与追及问题例题精讲【例 1】甲、乙两名同学在周长为300米圆形跑道上从同一地点同时背向练习跑步,甲每秒钟跑3.5米,乙每秒钟跑4米,问:他们第十次相遇时,甲还需跑多少米才能回到出发点?【巩固】甲乙两人在相距90米的直路上来回跑步,甲的速度是每秒3米,乙的速度是每秒2米.如果他们同时分别从直路两端出发,10分钟内共相遇几次?【例 2】甲、乙两车同时从A地出发,不停的往返行驶于A,B两地之间。
已知甲车的速度比乙车快,并且两车出发后第一次和第二次相遇都在途中C地。
问:甲车的速度是乙车的多少倍?【巩固】甲、乙二人从相距 60千米的两地同时相向而行,6时后相遇。
奥数——行程、多次相遇和追及问题

精心整理但只1.第2第3第N2.第2第3…………,………………;第N 次相遇,共走2N 个全程;3、多人多次相遇追及的解题关键多次相遇追及的解题关键几个全程多人相遇追及的解题关键路程差三、解多次相遇问题的工具——柳卡柳卡图,不用基本公式解决,快速的解法是直接画时间-距离图,再画上密密麻麻的交叉线,按要求数交点个数即可完成。
折线示意图往往能够清晰的体现运动过程中“相遇的次数”,“相遇的地点”,以及“由相遇的地点求出多次相遇与追及问题全程”,使用折线示意图法一般需要我们知道每个物体走完一个全程时所用的时间是多少。
如果不画图,单凭想象似乎对于像我这样的一般人儿来说不容易。
【例 1】甲、乙两名同学在周长为300米圆形跑道上从同一地点同时背向练习跑步,甲每秒钟跑3.5米,乙每秒钟跑4米,问:他们第十次相遇时,甲还需跑多少米才能回到出发点?【巩固】 甲乙两人在相距90米的直路上来回跑步,甲的速度是每秒3米,乙的速度是每秒2米.如果他们同时分别【例 2】【巩固】【例 3】【巩固】【例 4】【巩固】.【例 5】.【巩固】【例 6】2001次相遇地点之间的距离.【巩固】 甲、乙二人以均匀的速度分别从A 、B 两地同时出发,相向而行,他们第一次相遇地点离A 地7千米,相遇后二人继续前进,走到对方出发点后立即返回,在距B 地3千米处第二次相遇,求第三次相遇时共走了多少千米.【例 7】A 、B 两地相距2400米,甲从A 地、乙从B 地同时出发,在A 、B 间往返长跑。
甲每分钟跑300米,乙每分钟跑240米,在30分钟后停止运动。
甲、乙两人在第几次相遇时A 地最近?最近距离是多少米?【巩固】 A 、B 两地相距950米。
甲、乙两人同时由A 地出发往返锻炼半小时。
甲步行,每分钟走40米;乙跑步,每分钟行150米。
则甲、乙二人第_____次迎面相遇时距B 地最近。
例题精讲【例 8】甲、乙两车分别从A ,B 两地出发,并在A ,B 两地间不断往返行驶。
四年级下第3讲《多人多次相遇与追及》教学课件

极限挑战
mathematics
例题5:A、B两城相距48千米,甲、乙、丙三人分别以每小时4千米、2千米、2千米的速度 行走;甲、乙两人从A城,丙从B城同时出发,相向而行;请问:出发多长时间后,甲正好 在乙和丙的中点? 分析:速度分别是4、2、2,那么我们可以把三人的路程分别设为几份呢?请试着画出线
例题4:甲、乙、丙三人走路,甲每分钟走60米,乙每分钟走50米,丙每分钟走40米;如 果甲从A地,乙和丙从B地同时出发相向而行,甲和乙相遇后,过了15分钟又与丙相遇;求 A、B两地间的距离为多少米? 分析:请自己画出详细的线段图,好好分析一下,还能像前面两个例题那样一段一段计
算吗?如果不能,该怎么办呢?
分析,看看哪个过程是可以计算的?
A地 叮叮
咚咚
B地 铛铛
例题讲解
mathematics
练习2:小春、小秋两人从A地出发,小夏则从B地同时出发,相向而行;小春的速度为每小 时60千米,小夏的速度为每小时40千米,出发3小时后,小春与小夏相遇,又过了1小时, 小秋也与小夏相遇,请问:小秋的速度是多少?
例题讲解
mathematics
练习4:刘备、关羽、张飞三人,刘备每分钟走40米,关羽每分钟走60米,张飞每分钟走50 米;如果刘备从A地,关羽和张飞从B地同时出发相向而行,刘备和关羽相遇后,过了10分 钟又与张飞相遇,求A、B两地间的距离为多少米?
例题讲解
mathematics
上面几道例题的运动过程是一样的,在这样的运动过程里面,会有两次相遇运动和 一次追及运动;在这个运动过程中有一段路程既是路程和又是路程差,需要同学们 格外注意. 接下来我们来看一下和速度倍数相关的行程问题,大家想象一下,如果甲、乙两人 的同时出发同向前进,甲的速度是乙的3倍,那么5分钟后,甲的路程是乙的几倍? 30分钟后,甲的路程又是乙的几倍?2个小时后,甲的路程又是乙的几倍?其实上述 问题的答案都是3倍,不管时间过了多久,只要甲、乙两人的时间相同,他们路程的 倍数关系就等于速度的倍数关系.
奥数-行程多次相遇和追问题

一、由简单行程问题拓展出的多次相遇问题所有行程问题都是围绕“=⨯路程速度时间”这一条基本关系式展开的,多人相遇与追及问题虽然较复杂,但只要抓住这个公式,逐步表征题目中所涉及的数量,问题即可迎刃而解.二、多次相遇与全程的关系1. 两地相向出发:第1次相遇,共走1个全程;第2次相遇,共走3个全程; 第3次相遇,共走5个全程; …………, ………………; 第N 次相遇,共走2N-1个全程;注意:除了第1次,剩下的次与次之间都是2个全程。
即甲第1次如果走了N 米,以后每次都走2N 米。
2. 同地同向出发:第1次相遇,共走2个全程;第2次相遇,共走4个全程; 第3次相遇,共走6个全程; …………, ………………; 第N 次相遇,共走2N 个全程; 3、多人多次相遇追及的解题关键多次相遇追及的解题关键 几个全程 多人相遇追及的解题关键 路程差三、解多次相遇问题的工具——柳卡知识框架多次相遇与追及问题柳卡图,不用基本公式解决,快速的解法是直接画时间-距离图,再画上密密麻麻的交叉线,按要求数交点个数即可完成。
折线示意图往往能够清晰的体现运动过程中“相遇的次数”,“相遇的地点”,以及“由相遇的地点求出全程”,使用折线示意图法一般需要我们知道每个物体走完一个全程时所用的时间是多少。
如果不画图,单凭想象似乎对于像我这样的一般人儿来说不容易。
【例 1】甲、乙两名同学在周长为300米圆形跑道上从同一地点同时背向练习跑步,甲每秒钟跑3.5米,乙每秒钟跑4米,问:他们第十次相遇时,甲还需跑多少米才能回到出发点?【巩固】 甲乙两人在相距90米的直路上来回跑步,甲的速度是每秒3米,乙的速度是每秒2米.如果他们同时分别从直路两端出发,10分钟内共相遇几次?【例 2】甲、乙两车同时从A 地出发,不停的往返行驶于A ,B 两地之间。
已知甲车的速度比乙车快,并且两车出发后第一次和第二次相遇都在途中C 地。
问:甲车的速度是乙车的多少倍?例题精讲【巩固】甲、乙二人从相距 60千米的两地同时相向而行,6时后相遇。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四(下)奥数第3讲~多人多次相遇与追及
【知识精讲】
在之前的课程中,我们已经学过了如何处理两个对象之间的相遇与追及问题,本讲我们进一步学习过程更为复杂的三个对象之间的行程问题。
本讲中画线段图非常重要。
第一部分:复习
基本相遇问题:
速度和×相遇时间=路程和
路程和÷速度和=相遇时间
路程和÷相遇时间=速度和
1:甲、乙两车从相距1500千米的两地同时出发,相向而行。
甲车每小时行40千米,乙车每小时行60千米,请问:出发多少小时后两车相遇?
2:一辆巴士和一辆小轿车同时从A、B两地出发,相向而行。
巴士每小时行50千米,小轿车每小时行60千米,3小时后两车相遇,请问:A、B两地相距多少千米?
3:A、B两艘船同时从相距150千米的两个码头出发,相向而行,3小时相遇,A船每小时航行25千米,请问:B船每小时航行多少千米?
基本追及问题:
速度差×追及时间=路程差
路程差÷速度差=追及时间
路程差÷追及时间=速度差
1:圆圆、乐乐两人分别从相距30千米的两地同时向南行驶,圆圆骑自行车每小时行14千米,乐乐步行每小时走4千米,请问:多少小时后圆圆可以追上乐乐?
2:蚂蚁在蜘蛛前面几百米处,同时出发同向而行,蜘蛛每分钟跑55米,蚂蚁每分钟爬1米,10分钟后蜘蛛追上了蚂蚁,请问:开始时蚂蚁距蜘蛛多少米?
第二部分:多人相遇
例1: 有A、B、C三个人,A每分钟走20米,B每分钟走40米,C每分钟走30米。
甲、乙两地相距3000米。
A从甲地,B、C从乙地同时出发相向而行。
请问:A在与B相遇之后多少分钟又与C相遇?
练1:有圆圆、乐乐、静静三人,圆圆每秒钟走2米,乐乐每秒钟走4米,静静每秒钟走6米。
A、B 两地相距4800米。
圆圆从A地,乐乐、静静从B地同时出发相向而行,请问:圆圆与静静相遇后多少秒又与乐乐相遇?
例2:有A、B、C三人,A每分钟走30米,B每分钟走70米,C每分钟走20米。
A从甲地,B、C从乙地同时出发相向而行,A和B经过10分钟相遇。
请问:A和C要经过多长时间才能相遇?
练2:有小水、小雨、小雪三个人,小水每秒钟走2米,小雨每秒钟走3米、小雪每秒钟走5米,小雨从A地,小雪、小水从B地同时出发相向而行,小雨和小雪经过100秒相遇了,请问:小雨和小水要经过多长时间才能相遇?
例3:小丁、小冬两人开车从甲地,小当则从乙地同时出发,相向而行。
小丁的速度为每小时60千米,小当的速度为每小时40千米,出发4小时后,小丁与小当相遇。
又过了1小时,小冬也与小当相遇。
请问:小冬的车速是多少?
练3:小风,小霜两人从A地,小雨则从B地同时出发,相向而行。
小风的速度为每小时50千米,小雨的速度为每小时70千米。
出发3小时后,小风与小雨相遇。
又过了1小时,小霜也与小雨相遇。
请问:小霜的速度是多少?
第三部分:多人相遇与追及
例4:大、小两辆汽车的速度分别为每小时60千米和每小时40千米,两车同时从A地出发到B地去,出发5小时后,大车遇到一辆从B地同时出发的卡车。
又过了1小时,小车也遇到了这辆卡车。
请问:这辆卡车的速度是多少?
练4:快、慢两辆汽车的速度分别为75千米/小时和30千米/小时,两车同时从A地出发到B地去,出发2小时后,快车遇到一辆从B地同时出发的公共汽车,又过了1小时,,慢车也遇到了这辆公共汽车。
请问:这辆公共汽车的速度是多少?
自我挑战:
1:有熊熊、大大、小二三人,熊熊每分钟走50米,大大每分钟走30米,小二每分钟走50米。
A、B 两地相距7200米。
大大、小二从B地,熊熊从A地同时出发相向而行,请问:熊熊与小二相遇后多少分钟又与大大相遇?
2:有东、西两城,小花从东向西走,每小时走13千米;小二从西向东走,每小时走12千米;小辉骑自行车从东向西行,每小时行38千米,三人同时出发,1小时后小二遇到小辉,请问:小二和小花要经过多长时间才能相遇?
3:有快、中、慢三辆车,快车从甲地出发,中、慢车从乙地出发相向而行。
快车的速度是每小时24千米,中车的速度是每小时20千米,出发12小时后快、中车相遇。
又过了4小时,快、慢车也相遇了,请问慢车速度?
4:A、B两地,甲、乙、丙三人,甲的速度是2米每秒,乙的速度是1米每秒。
甲乙在A地,丙在B 地。
同时出发相向而行。
甲丙100秒后相遇,又过25秒乙丙相遇。
问丙车的速度是多少?
温故而知新!
1:有甲、乙、丙三人,甲每分钟走35米,乙每分钟走45米,丙每分钟走25米。
A、B两地相距8000米。
甲从A地,乙、丙从B地同时出发相向而行。
那么从出发到甲、乙相遇,丙走了多少?
2:有甲、乙、丙三人,甲每分钟走40米,乙每分钟走50米,丙每分钟走30米。
A、B两地相距6300米。
甲从A地,乙、丙从B地同时出发相向而行。
那么甲与乙相遇之后多少分钟又与丙相遇?
3:有甲、乙、丙三人,甲每分钟走55米,乙每分钟走45米,丙每分钟走35米。
甲从A地,乙、丙从B地同时出发相向而行,甲和乙经过了9分钟相遇了。
那么甲和丙要经过多少分钟才能相遇?
4:多多、甜甜、明明三人周末一起出门逛街,多多每分钟走50米,甜甜每分钟走30米,明明每分钟走20米。
多多从A地,甜甜、明明从B地同时出发相向而行,多多和甜甜经过了14分钟相遇了。
那么多多和明明经过多少分钟才能相遇?
5:小竹、小松两人从A地,小梅则从B地同时出发,相向而行。
小竹的速度为每小时55千米,小梅的速度为每小时45千米。
出发4小时后,小竹与小梅相遇。
又过了1小时,小松也与小梅相遇。
小松每小时走多少千米?
6:甲、乙两辆汽车的速度分别为每小时80千米和每小时65千米,两车同时从A地出发到B地去,出发8小时后,甲车遇到一辆从B地同时出发的卡车。
又过了1小时,乙车也遇到这辆卡车。
那么这辆卡车每小时多少千米?。
