费根鲍姆常数4669…上
数学之旅测试题

1爱因斯坦创立广义相对论时用到了下列什么重要的数学工具?黎曼几何2下面这个方程有没有整数解?方程有没有整数解?有3下列哪个是孪生素数对?(17,19)4圆与椭圆在下列哪个数学分支中可看作一样?拓扑5具有同样周长的下列图形哪个面积更大?圆6以下汉字哪一个可以一笔不重复地写出?日7偶数与正整数哪个多?一样多8数列极限趋于0的直观定义的弱点是下面哪一点?缺乏可操作性9课程中费曼的故事告诉我们懂得一件事情最重要的是下面列出的哪一条?找到感觉10超弦理论中蜷缩的空间可以用下面那个空间来描述?Calabi-Yau空间11下面哪一位人物用穷竭法证明了圆的面积与其直径平方成正比?欧多克索斯12以下什么成果是阿基米德首先得到的?抛物线弓形的面积13阿基米德求几何级数的和用的是什么方法?几何的方法14欧多克索斯、阿基米德和刘徽等人对微积分的贡献主要体现在什么方面?定积分15《一种发展连续不可分量的新几何学的方法》是下列哪位数学家的著作?卡瓦列里16现在我们一直在用的“函数(function)”这个词是谁引进的?莱布尼兹17本课程提到的最美的风景点是指?牛顿-莱布尼兹公式18一直沿用至今的ε-δ语言是哪位数学家引入的?魏尔斯特拉斯19康托尔所创立的什么理论是实数以至整个微积分理论体系的基础?集合论20下面关于黎曼可积和勒贝格可积的论述那一项是正确的?黎曼可积函数类是不完备的,勒贝格可积函数类是完备的21试用阿基米德的方法求下面几何级数的和。
22计算加百列号的表面积与体积,并解释为何在这个号角里面灌满油漆,油漆的体积是有限的,但它却能够涂满无限的表面积?23举例说明黎曼积分中积分号和极限号有时不可交换,并给出可交换时需要的条件。
24下列四个定义中,哪个不能作为Rn中的度量(距离)?25度量的三个基本属性中不包括下列哪一个?连续性(三角不等式,正定型,对称性)26下列关于度量和范数的说法中正确的是?由范数可以定义距离,但由距离不可以定义范数27下列说法中不正确的是?对,若为的范数,则下列说法中不正确的是?若为实数,则有28以下现象可以用什么原理来解释?在三维空间中,波的传播有清晰的前后阵面,但是在二维空间中却没有?惠更斯原理29下列选项中正确的是?以下向量组中哪个不能构成的基向量?(0,1,1),(2,1,1),(1,0,0)30下列哪个选项是正确的?若向量a=(1,0,5,2),b=(3,-2,3,-4),c=(-1,1,t,3)线性相关,那么t的值为?1 31下列选项正确的是?向量和的夹角为?32下列说法哪一个是正确的?向量组线性无关的充分必要条件是?齐次线性方程组只有零解33下列哪个属性不是内积所具有的?三角不等式(对称性,对第一个变元的线性性,正定性)34给定一个集合,试验证下面两个集族是否构成集合M上的拓扑?1).2).35随着网络的迅速发展,人们越来越多的使用e-mail联系和交流。
费根鲍姆常数4.669…9(上)

程 ( 称 离散 动力 系统 ) 亦 .
对 于满 足 =( ) f 的 叫做 f ) ( 在
[ , ] 的一 个不 动点 . n b上 又若 =f ( )且 当 1 <n时 , , ≤ ≠I ( )则 称 为 f ) [ , ] 的一 厂 X , ( 在 n b上
图8
() 2
口=3 8 5时 , 3周 期解 或 有 3 定 常解 .3 有 个
图7
换言 之 , 人们 首先 发 现 : 对于不 同 的 a而 言 , 同一 初 始 点 出 发 从
进 行迭 代 , 敛 情 况 ( 方 程 迭 代 结 果 ) 很 收 或 有
大差 异 .
口=34 .7时 , 有周期 4解
至此 , 迭代 结果 已产 生 很 大 的差 异 , 言 换 之, 迭代 在 a=4附 近 出现 了 问 题 . 同时 也 看 到: a的取 值 不 同, 映射 稳定 不 动 点 、 定周 期 稳 点 的周期数 ( 定常点的个 数) 会有 明显差异 .
a=27时 , 稳 定 不 动 点 . 有
迭
3
代
次
l 0 1 78 6 0 .4 3 9 0 1 78 44 9 9 .4 2 4 0.4 1 1 1 78 25 82
数
n
5 06 4 2 .3
9 44 2 0 0 63 22 l5 . 6 4 5
O 6 87 5 0 46 . 5 5 9
显 然 , 可 视 为 形 如 Y= ( 一X 的 函 它 1 )
数进 行数 值 计 算 时 的某 种 迭 代 模 式 ( 其 不 求
动点 ) 人们称 之 为 Lg t , oi i sc映射 . 当然它 也 是一 元二 次方 程 似 + +c=
费根鲍姆常数是新近发现的

(→∞)(αα())(αห้องสมุดไป่ตู้)α)……
费根鲍姆常数是新近发现地、且在学术界认定地一个普适常数,这个常数与“混沌现象”有关.其大小δ≈ .....
吸引子地图
发现历史
某些数学映射用一个单独地线性参数来展示表象随机地行为,即混沌(),这个参数地值在一定范围之内,参数值在被增大地过程中,其映射会在参数地一些特定值处形成分岔(),最初是一个稳定点,随后分岔表现为在两个值之间摆动,然后分岔表现为在四个值之间摆动,以此类推.b5E2R。
变换地图
年,费根鲍姆用计算器计算后得出,这种周期倍增分岔( )发生时地参数之间地差率是一个常数,他为此提供了数学证明.他进一步揭示了同样地现象、同样地常数适用于广泛地数学函数领域,这个普适地结论使数学家们能够在对表象不可捉摸地混沌系统地解密道路上迈出了第一步.这个“极限率”( )现在通称为费根鲍姆常数.年他发表了关于映射地研究地重要论文 《一个非线性变换类型地量子普适性》,其中特别谈到了对于混沌理论有直接意义地映射.p1Ean。
初中物理基本物理量单位公式常数汇总用
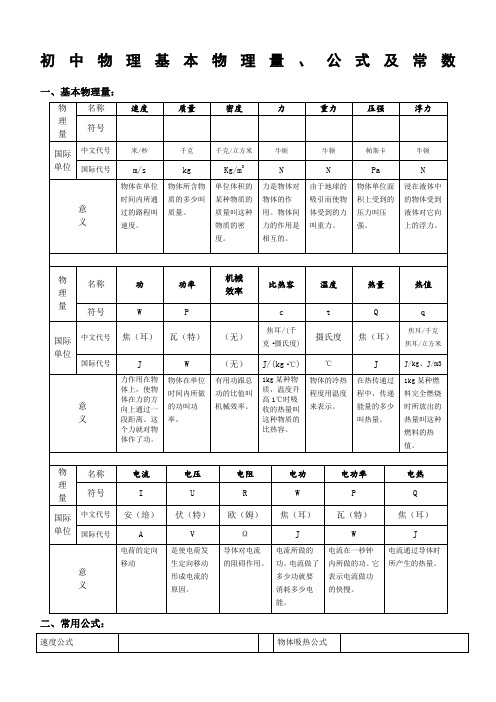
初中物理基本物理量、公式及常数一、基本物理量:
二、常用公式:
三、常用数据:
四、初中物理单位换算:
五、课本重点实验:
复习内容:实验名称、实验器材、实验原理、实验步骤、实验现象、物理量及数据记录表格、结论。
八年级:(1)同种物质的质量与体积的关系;
(2)测量盐水和形状不规则塑料块(不吸水)的密度;
(3)阻力对物体运动的影响(牛顿第一运动定律);
(4)二力平衡的条件;
(5)重力的大小跟什么因素有关
(6)滑动摩擦力的大小与什么因素有关?
(7)杠杆的平衡条件;
(8)比较定滑轮和动滑轮的特点;
(9)压力的作用效果跟什么因素有关?
(10)液体内部压强规律;
(11)流体压强与流速的关系;
(12)浮力的大小等于什么(阿基米德原理)
(13)斜面的机械效率;
(14)光的反射规律;
(15)探究凸透镜成像的规律;
(16)固体熔化室温度的变化规律;
(17)水的沸腾;
(18)动能大小的影响因素
(19)重力势能大小的影响因素
九年级:
(1)比较不同物质的吸热能力
(2)串联电路中各点的电流规律;
(3)并联电路中干路电流与各支路电流有什么关系;
(4)串联电路各点间电压的关系;
(5)并联电路电压的关系;
(6)怎样用变阻器改变灯泡的亮度;
(7)电阻上的电流跟两端电压的关系;
(8)测量小灯泡的电阻;
(9)测量小灯泡的电功率;
(10)探究通电螺线管的磁场是什么样的?
(11)研究电磁铁;
(12)什么情况下磁能生点;。
全国高中学生化学竞赛试题及答案

评分通则1.凡要求计算或推导的,必须示出计算或推导过程。
没有计算或推导过程,即使结果正确也不得分。
2.有效数字错误,扣0.5分,但每一大题只扣1次。
3.单位不写或表达错误,扣0.5分,但每一大题只扣1次。
4.只要求1个答案、而给出多个答案,其中有错误的,不得分。
5.方程式(不是反应式!)不配平不得分。
6.用铅笔解答(包括作图)无效。
7.使用涂改液涂改的解答无效。
8.不包括在标准答案的0.5分的题,可由省、市、自治区评分组讨论决定是否给分。
9.答案中红色字为标准答案,而蓝字体(加下划线)为注释语不属于答案。
气体常数R =8.31447 J K -1 mol -1 法拉第常数F =96485 C mol -1 阿佛加德罗常数N A =6.022142×1023 mol -1第1题 (15分)1-1 2009年10月合成了第117号元素,从此填满了周期表第七周期所有空格,是元素周期系发展的一个里程碑。
117号元素是用249Bk 轰击48Ca 靶合成的,总共得到6个117号元素的原子,其中1个原子经p 次α衰变得到270Db 后发生裂变;5个原子则经q 次α衰变得到281Rg 后发生裂变。
用元素周期表上的117号元素符号,写出得到117号元素的核反应方程式(在元素符号的左上角每式1分,画箭头也得 1分。
两式合并为 23n +Uns 5+Uns =Bk 6+Ca 629397294117249974820也得满分。
(2分)(3分)1-3 一氯一溴二(氨基乙酸根)合钴(III)酸根离子有多种异构体,其中之一可用如第2题(5 分)最近我国有人报道,将0.1 mol L-1的硫化钠溶液装进一只掏空洗净的鸡蛋壳里,将蛋壳开口朝上,部分浸入盛有0.1 mol L-1的氯化铜溶液的烧杯中,在静置一周的过程中,蛋壳外表面逐渐出现金属铜,同时烧杯中的溶液渐渐褪色,并变得混浊。
2-1设此装置中发生的是铜离子和硫离子直接相遇的反应,已知φӨ(Cu2+/Cu)和φӨ(S/S2-)分别为0.345 V和-0.476 V,nFEӨ=RT ln K,EӨ表示反应的标准电动势,n为该反应得失电子数。
基本物理常数
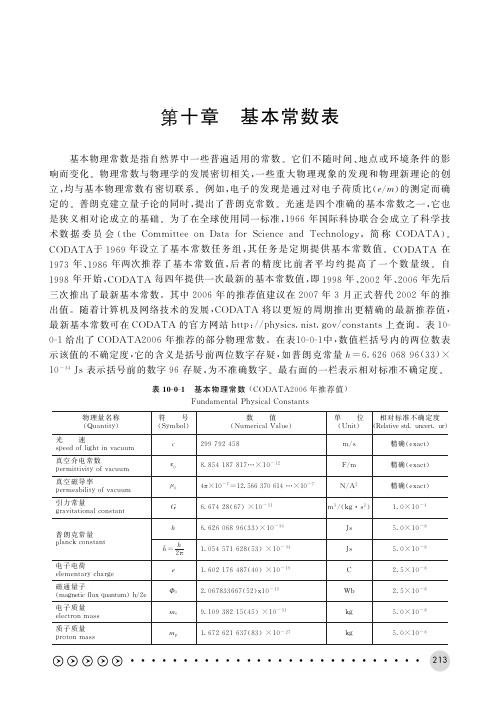
标准大气压 (standardatmosphere)
101325
原子质量单位 (atomicmassunit)m(12C)/12
amu
1灡660538782(83)x10-27
单暋暋位 相对标准不确定度 (Unit) (Relativestd灡uncert灡ur) 6灡8暳10-10
m-1
6灡6暳10-12
物暋暋质 密度(kg/m3) 物质
密 度 (kg/m3)
铝
2灡669暳103
水
1灡000暳103
铜
8灡96暳103
水银
13灡55暳103
铁
7灡874暳103 无水甘油 1灡260暳103
银
10灡5暳103 无水乙醇 0灡7894暳103
金
19灡32暳103 蓖麻油 0灡957暳103
钨
19灡30暳103 钟表油 0灡981暳103
10-10牛顿,则此时的电流为1 安培
热力学温度
Thermodynamic tempera灢
T
ture
开 [尔 文 ] Kelvin
K
暋1 开尔文是水三相点热力学温度的1/273灡16
214
续上表
物理量名称
物质的量 Amountofsubstance
表示符号 单位名称 单位符号 v 或n 摩[尔]mole mol
N/A2
精 确 (exact)
G
6灡67428(67)暳10-11
m3/(kg·s2)
1灡0暳10-4
普朗克常量 planckconstant
电子电荷 elementarycharge 磁通量子 (magneticfluxquantum)h/2e 电子质量 electron mass
e有时被称为自然常数

e有时被称为自然常数(Natural constant),是一个约等于2.71828182845904523536……的无理数。
以e为底的对数称为自然对数(Natural logarithm),数学中使用自然(Natural)这个词的还有自然数(Natural number)。
这里的“自然”并不是现代人所习惯的“大自然”,而是有点儿“天然存在,非人为”的意思。
就像我们把食品分为天然食品和加工食品,天然食品就是未经人为处理的食品。
但这样解读“自然”这个词太浅薄了!为了还原全貌,必须穿越到2500多年前的古希腊时代。
(你也知道,穿越剧都很长(>﹏<),不喜欢长篇大论的,可直接跳到后面看结论。
)“自然”的发明我们知道,人类历史上曾出现过很多辉煌的文明,例如大家熟知的四大文明:古巴比伦、古埃及、古印度河以及古代中国。
但是要说谁对现代文明的影响最大?对不起,四大文明谁都排不上!真正对现代文明影响最大的是古希腊文明,特别是古希腊的哲学、科学思想,是整个现代文明的源头和基石。
这里并不是要贬低四大文明,现代文明也从各文明继承了大量的文化遗产,只是相比古希腊要少很多。
现代人的基础教育,无论是什么国家、什么社会制度、什么民族,在教科书里除了介绍自己的古代成就外(如四大发明),还会大篇幅的介绍古希腊的科学、哲学思想,来启蒙学生的心智,这是跨越国界的共同做法。
大家都这样做的原因,就是因为古希腊哲学家发明了科学的思维方法和“自然”(Natural)这个词,在理论中用自然来取代具体的神灵,这是人类文明史上划时代的发明。
如果没有这个发明,现代文明可能还会晚出现数千年,所以这是至关重要的进步。
在古希腊文明之外的古文明里,人们解释世间万物的运行时,总是要引入神灵等超自然、拟人化的因素。
例如,得病了就认为鬼神附体,洪水泛滥就认为天神发怒,石人一出天下就可以造反了,总有一个超自然的神灵在操纵万物的运行。
人们偏爱形象而戏剧化的解释,拟人化的神灵恰恰具有形象、戏剧化的特点,最易于接受和传播。
费根鲍姆常数的计算

m=m+1 x=abs(x2-0.5) w rite(i,*)r,m,x w rite(*,*)r,m,x e nd if i f(y1==x2) e xit e nd do e n d do p ause e nd p rogram fgbma
计算结果: 3.55464005470276
3.56667017936707
数据处理后得: = 4.651105651105840
的计算程序:
p rogram fgbmr i mplicit n one r eal*8::x1,x2,y1,y2,r1,r2,ran,x,lamda,s i nteger*4::x0,i,j,k,time x0=time() o pen(1,file='output1.txt') o pen(2,file='output2.txt') d o r1=3.4,3.7,0.00001 s=0 d o i=0,5 x1=ran(x0) d o j=0,10000 x2=r1*x1*(1-x1) x1=x2 x=x2 e nd do y1=x1 d o k=0,100000 y2=r1*y1*(1-y1) lamda=abs(r1-2*r1*y2) s=s+dlog(lamda) y1=y2 i f((abs(y2-0.5)<0.00001).and.(s<=0))then w rite(1,*)r1,k,y2 w rite(2,*)r1,s w rite(*,*)r1,k,y2 e nd if
1 1
4.597438023040301E-002 1.833155892373406E-002
处理后得: = 2.507936200171143 结论:计算结果还是比较理想的,和文献参上的参考值 ( =4.669
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
罗辑斯蒂 (Logistic) 方程
在生态学研究中 ,人们建立了个数为 N 的生物群体随时间 t 进化 (或繁衍) 的数学模 型 (微分方程形式) :
dN dt
=
rN ( k -
N)
-
mN ,
这里 r 、m 表示该物种出生 、死亡常数 , k 表示
环境负载能力. 人们称它为 Logistic 方程.
x0 出发反复迭代 ,可有
x1 = f ( x0 ) , x2 = f ( x1 ) = f ( f ( x0 ) ) = f 2 ( x0 ) ,
x3 = f ( x2 ) = f ( f ( x1 ) ) = f ( f ( f ( x0 ) ) ) = f 3 ( x0 ) ,
……
xn +1 = f ( xn) = f ( f ( xn - 1) ) = … = f ( f ( …f ( x0 ) …) ) .
011
011 + 10 - 8
011 + 2 ×10 - 8
1
0136
01360 000 003 2 01360 000 006 4
2
01921 6
迭
3 01289 013 76
代
⁝
…
次
10 01147 836 559 9
数
⁝
…
n 52 01634 955 924 4
⁝
…
01921 600 035 8 0t +1 = Nt
1+ r
1-
Nt k
.
显然 ,它可视为形如 y = kx (1 - x) 的函
数进行数值计算时的某种迭代模式 (求其不
动点) ,人们称之为 Logistic 映射.
当然它也是一元二次方程 ax2 + bx + c =
0 用数值算法计算其根时的迭代模式.
一般地 ,若 [ a , b ] 上的函数 y = f ( x) 从
α= 3147 时 ,有周期 4 解 图 10
α= 31999 时 ,产生混沌 图 11
特别是图 11 给出以无穷为周期的解的 情形 ,称之为混沌 (以前曾撰文介绍过[5] ) .
如此可看到 :α的不同取值对于迭代定常 点的个数 (或周期解的周期数) 不一 ,见表 2.
表 2
α取值 < 3 (3 ,1 + 6) (1 + 6 ,31544) … > 31569 945 673 …
n + 1个
其中 , xn + 1 = f ( xn ) 在数学上称为差分方 程 (亦称离散动力系统) .
对于满足 x 3 = f ( x 3 ) 的 x 3 叫做 f ( x) 在 [ a , b ]上的一个不动点.
又若 x 3 = f n ( x 3 ) ,且当 1 ≤k < n 时 , x 3 ≠f k ( x 3 ) ,则称 x 3 为 f ( x) 在 [ a , b ] 上的一 个 n 周期点.
2002 年第 3 期
25
●数海拾贝 ●
费根鲍姆常数 41669 …(上)
吴振奎
(天津商学院 ,300122)
在数学中 ,除了象π、e 、01618 等已为人们 熟知的常数外 ,现代数学研究又使人们陆续 发现了一些新的常数 ,比如费根鲍姆常数 (Feigenbaum)δ= 41669 201 609 …就是其中一 例.
图1
图2
如此下去 ,最终可收敛到一个定态点 x 3
(它有两个不动点 ,一个是 0 ,一个是 1 - α1 ) .
26
图3
图4
迭代 19 次
迭代 70 次
图5
图6
但由于 α取值不同 ,有时也可以得到一
些周期解 (此时原来的不动点已失稳 ,而周期
解稳定 ,我们称它为定常解) .
中等数学
表 1
初始点 x0
我们考察一下简单的 Logistic 方程 xn + 1 =αxn (1 - xn ) 的不动点的计算 (α> 0) .
几何上讲 ,这是在笛卡儿坐标系中求直 线
y = x (第一象限角分线) 与抛物线
y =αx (1 - x) (因 α> 0 ,开口向下) 的交点.
假设从某个初始点 x0 出发 (见图 1 ,图 1 中 R 的横坐标即为 x0 ) 作 xn 轴的垂线与抛物 线交于点 A ;再自 A 作 AB ⊥AR 交 y = x 于 B ; 自 B 作 BC ⊥AB 交抛物线于 C , …如此下去 可有下面诸图形 (以下诸图摘自文[ 3 ]) .
定常点个数 1
2
4
…
混沌
(未完待续)
α= 217 时 ,有稳定不动点 图8
α= 314 时 ,有周期 2 解 图9
α= 31835 时 ,有 3 周期解或有 3 个定常解 图7
换言之 ,人们首先发现 : 对于不同的 α而言 ,从同一初始点出发 进行迭代 ,收敛情况 (或方程迭代结果) 有很 大差异. 此外 ,人们在迭代中还发现了下面一个 令人不解的现象 : 对某些 α来讲 ,初始点的小小差异 (一般 来讲它对于迭代的收敛的影响不会很大) ,会 使迭代结果相去甚远. 表 1 给出 α= 4 时从相 差甚微的不同初始点出发迭代一些步骤后的 数据
… 01147 824 449 9
… 01066 342 251 5
…
01921 600 071 7 01289 013 518 2
… 01147 812 518 2
… 01658 755 094 6
…
至此 ,迭代结果已产生很大的差异. 换言 之 ,迭代在 α= 4 附近出现了问题. 同时也看 到 :α的取值不同 ,映射稳定不动点、稳定周期 点的周期数(定常点的个数) 会有明显差异.
