第五章 位置的确定评价试题
北师大版八上《第五章位置的确定》word同步测试

北师大版广东省南山一中2011年八年级数学上册第五章位置的确定测试题一、选择题1、在平面内,确定一个点的位置一般需要的数据个数是( )A .1B .2C .3D .42、点M 在x 轴的上侧,距离x 轴5个单位长度,距离y 轴3个单位长度,则M 点的坐标为( )A. (5,3)B. (-5,3)或(5,3)C. (3,5)D. (-3,5)或(3,5)3、若0=xy ,则点P (x,y )的位置是( ) A. 在数轴上 B. 在去掉原点的横轴上C. 在纵轴上D. 在去掉原点的纵轴上4、点P (13++m m ,)在直角坐标系的x 轴上,则点P 的坐标为( )A .(0,-2)B .(2,0)C .(4,0)D .(0,-4)5、点P (-1,3)关于原点对称的点的坐标是 ( )A .(-1,-3)B .(1,-3)C .(1,3)D .(-3,1)6、如果直线AB 平行于y 轴,则点A 、B 的坐标之间的关系是( )A .横坐标相等B .纵坐标相等C .横坐标的绝对值相等D .纵坐标的绝对值相等7、A (-3,2)关于原点的对称点是B ,B 关于x 轴的对称点是C ,则点C 的坐标是( )A .(3,2)B .(-3,2)C .(3,-2)D .(-2,3)8、直角坐标系中,一个图案上各个点的横坐标和纵坐标分别乘以正数a (a >1),那么所得的图案与原来图案相比( )A. 形状不变,大小扩大到原来的a 2倍B. 图案向右平移了a 个单位C. 图案向上平移了a 个单位D. 图案沿纵向拉长为a 倍9、平面直角坐标系内有一点A (a ,b ),若ab =0,则点A 的位置在( )A .原点B .x 轴上C .y 轴上D .坐标轴上10、一个平行四边形三个顶点的坐标分别是(0,0)、(2,0)、(1,2),第四个顶点在x 轴下方,则第四个顶点的坐标为( )A .(-1,-2)B .(1,-2)C .(3,2)D .(-1,2)11、图是深圳市南山区地图的一角,用刻度尺、量角器测量可知,深圳大学( ) 大约在南山区政府(★)的什么方向上A .南偏东80°B .南偏东10°C .北偏西80°D .北偏西10°12、矩形ABCD 中的顶点A 、B 、C 、D 按顺时针方向排列,若在平面直角坐标系内,B、D 两点对应的坐标分别是(2, 0), (0, 0),且 A、C两点关于x轴对称.则C 点对应的坐标是(A)(1, -2)(B) (-1, 1) (C) (1, 1) (D) (2, -2)二、填空题13、已知点A(a-1,a+1)在x轴上,则a等于______.14、已知P(-3,2),P′点是P点关于原点O的对称点,则P′点的坐标为______.15、已知点 P(-4,5),点A与点P关于y轴对称,则点A的坐标是 .16、以点(4,0)为圆心,以5为半径的圆与y轴交点的坐标为______.17、已知小岛A在灯塔B的北偏东30°的方向上,则灯塔B在小岛A的________ 的方向上。
苏教版数学六年级下册第五单元《位置确定》测试卷及答案

第五单元位置确定知识点:1.实际上,在野外或图上确定位置时,常把东北方向叫做北偏东,西北方向叫做北偏西。
2.在填方向时,不仅要填出北或南、偏东或偏西,还要填出偏东或偏西多少度。
3.比例尺表示图上距离与实际距离的比。
1:100的含义是图上1厘米的线段表示实际100厘米。
一、填空题1.地图中“北”可以用字母()表示,“南”可以用字母()表示,()可以用字母E 表示,“西”可以用字母()表示。
2.东北方面可以叫做(),西北方面可以叫做()。
3.测量地面上相隔较远的两点间的距离,一般先要通过这两点测定一条(),然后沿着这条直线进行测量。
4.实际测量时,一般要用到()、()、()等测量工具。
二、选择1.天天面向南站立。
他向左旋转28°后所面对的方向是()①南偏东28°②南偏西28°③南偏东62°④南偏西62°2.在图纸上箭头指向N,表示()方向。
①正北②正南③正东④正西三、解决问题1.根据下面的描述,在平面图上表示出位置。
(1)电影院在文化广场北偏东45°方向1千米处。
(2)电视台在文化广场南偏西60°方向1500米处。
(3)市政府在文化广场南偏东30°方向2千米处。
(4)少年宫在文化广场北偏东40°方向500米处。
苏教版数学六年级下册第五单元试卷及答案2.学校组织学生从学校去电影院看《我的长征》。
根据下面的路线图,写出学生们去电影院和返回学校时所走的方向和路程,完成下表。
方向路程学校至新华书店新华书店至电影院电影院至新华书店新华书店至学校3.在解放军的一次军事演习中,海军舰队派出4架直升机担任预警任务。
雷达屏幕上,每相邻圆之间的距离是10千米。
以舰队雷达为观测点,请你在图中用点表示出各架直升机的位置。
(1)直升机A在南偏西60°方向30千米处;(2)直升机B在南偏东30°方向50千米处;(3)直升机C在北偏东45°方向70千米处;(4)直升机D在南偏西60°方向40千米处。
《位置的确定》评估卷
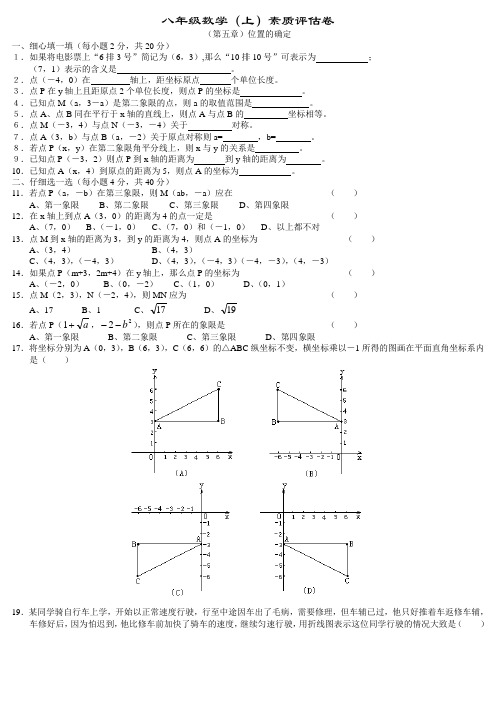
八年级数学(上)素质评估卷(第五章)位置的确定一、细心填一填(每小题2分,共20分)1.如果将电影票上“6排3号”简记为(6,3),那么“10排10号”可表示为 ;(7,1)表示的含义是 。
2.点(-4,0)在 轴上,距坐标原点 个单位长度。
3.点P 在y 轴上且距原点2个单位长度,则点P 的坐标是 。
4.已知点M (a ,3-a )是第二象限的点,则a 的取值范围是 。
5.点A 、点B 同在平行于x 轴的直线上,则点A 与点B 的 坐标相等。
6.点M (-3,4)与点N (-3,-4)关于 对称。
7.点A (3,b )与点B (a ,-2)关于原点对称则a= ,b= 。
8.若点P (x ,y )在第二象限角平分线上,则x 与y 的关系是 。
9.已知点P (-3,2)则点P 到x 轴的距离为 到y 轴的距离为 。
10.已知点A (x ,4)到原点的距离为5,则点A 的坐标为 。
二、仔细选一选(每小题4分,共40分)11.若点P (a ,-b )在第三象限,则M (ab ,-a )应在 ( )A 、第一象限B 、第二象限C 、第三象限D 、第四象限12.在x 轴上到点A (3,0)的距离为4的点一定是 ( )A 、(7,0)B 、(-1,0)C 、(7,0)和(-1,0)D 、以上都不对13.点M 到x 轴的距离为3,到y 的距离为4,则点A 的坐标为 ( )A 、(3,4)B 、(4,3)C 、(4,3),(-4,3)D 、(4,3),(-4,3)(-4,-3),(4,-3)14.如果点P (m+3,2m+4)在y 轴上,那么点P 的坐标为 ( )A 、(-2,0)B 、(0,-2)C 、(1,0)D 、(0,1)15.点M (2,3),N (-2,4),则MN 应为 ( )A 、17B 、1C 、17D 、19 16.若点P (a +1,22b --),则点P 所在的象限是 ( )A 、第一象限B 、第二象限C 、第三象限D 、第四象限17.将坐标分别为A (0,3),B (6,3),C (6,6)的△ABC 纵坐标不变,横坐标乘以-1所得的图画在平面直角坐标系内是( )19.某同学骑自行车上学,开始以正常速度行驶,行至中途因车出了毛病,需要修理,但车辅已过,他只好推着车返修车辅,车修好后,因为怕迟到,他比修车前加快了骑车的速度,继续匀速行驶,用折线图表示这位同学行驶的情况大致是( )20.若点P (-1-2a ,2a -4)关于原点的对称点是第一象限内的点,则a 的整数解有( )A 、1个B 、2个C 、3个D 、4个三、用心做一做(每小题8分,共40分)21.如图所示,OA=8,OB=6,∠XOA=45°,∠XOB=120°,求A 、B 的坐标。
初二数学第五章位置的确定-初中二年级数学试题练习、期中期末试卷-初中数学试卷

初二数学第五章位置的确定-初中二年级数学试题练习、期中期末试卷、测验题、复习资料-初中数学试卷-试卷下载初二数学第五章位置的确定一、填空题(每空4分,共33分)1.生活中,确定物体的平面位置需要_____________数据。
2.电影院里6排4号可用(6,4)来表示,则5排1号可表示为___________,(7,3)表示的含义是__________________。
3.对于平面内任意一点P,过点P分别向x轴、y轴做垂线,垂足分别是A,B,若P点坐标是(6,8),则PB=_____________.4.如图,从观测点O观察到A点位置,如图所示,试用两种方式表示A点位置__________。
第4题第5题5.写出图中各点坐标:A_________,B________,C__________.6.点A在x轴上,位于原点右侧,距离原点5个单位长度;点B在y 轴上,距离原点3个点为长度,则A点的坐标是____________,B点的坐标是_____________.7.将点P(-4,+3)沿x轴负方向平移一个单位,得到点P’_________,再将点P’沿y轴负方向平移两个单位得到P”_______________.8.在平面直角坐标系中,点A(3,a)在x轴上,点B(b,4)在y轴上,则a=___________,b=__________,=_________.9.如图,在直角坐标系中,是等边三角形,若B点坐标是(2,0),则A点坐标是_______________.第9题10.在直角坐标系中,点p和p’关于y轴对称,点p与点p’’关于x轴对称,若点p的坐标是(3,1),那么点p’的坐标是__________,点p’’的坐标是__________。
11.A(-a,b)和点B(a,b)关于________成轴对称;点P(-1,2)关于原点的对称点是________;已知点Q(-8,6),它到x轴的距离是__________,它到y轴的距离是_________,它到原点点的距离是________;当x=0,y是任意实数时,点A(x,y)在__________上;如果点(-1,3)和(b,-3)关于x轴对称,则b=_______.12.已知点A在x轴上,且距原点的距离为4个单位长度,则A点的坐标为__________;一个点在y轴上,位于原点下方,距离原点3个单位长度,这个点是__________.13.(a,b)位于x轴上方,y轴左侧,则a_____0,b_______0。
位置的确定总结以及练习

第五章 位置的确定 一位置的确定复习 1.在生活中,确定物体的位置有____种方法:一种是____例如:_______;另一种是______,例如: __________ . 2.某市区有3个加油站,位置如图所示,若加油站1的位置表示为(B,2),则加油站2的位置可表示为________,加油站3的位置可表示为________.3.一家超市在学校的北偏东60°方向,距离学校600米,则学校在这家超市的 ____________.4.小虫在小方格的线路上爬行,它的起始位置是A(2,2),先爬到B(2,4),再爬到C(5,4),最后爬到D(5,6),则小虫共爬了( ).单位A .7个B .5个C .4个D .3个 练习1.如图5-1-3所示,如果点A 的位置记为(1,1),点B 的位置记为(1,3),那么点C 的位置记为( ; ) ,点E 的位置记为( , ) ,点G 的位置记为( , ) (5,4)表示的点是 ,在图上标出表示(2,4)的点H .2.如图图书馆在大门北偏东_____方向距离____处;操场在大门北偏西____方向距离______处;车站在大门的_____方向距离____处.3.如图5-1-5,点A 表示3街与5大道的十字路口,点B 表示5街与3大道的十字路口,如果用(3,5)→(4,5)→ (5,5)→ (5,4)→ (5,3)表示由A 到B 的一条路径,那么你能用同样的方式写出由A 到B4.如下表所示,是某高新技术开发区规划示意图,其中将“开发区管理中(1)说出“基因工程研究所”、“生化制药厂”、“电子元件厂”、“计算机组装厂”所在的区域.(2)计划在A4区建一个“新材料研发公司”在C3区建一个“软件开发园”,请在图上相应区内标上该企业名称. 二 平面直角坐标系(1)复习 1.在平面内两条 且有 的数轴组成平面直角坐标系.2.平面直角坐标系中,两条数轴分别置于 位置和 位置,取向 或 的方向分别为两条数轴的正方向.3.水平的数轴叫做 或 铅直的数轴叫做 或 ,x 轴或y 轴统称 它们的公共原点O 称为直角坐标系的 .4.已知点P 在第二象限,且到x 轴的距离是3,到y 轴上的距离是2,则点P 坐标为 .5.已知点P 在第三象限,它的横坐标与纵坐标的绝对值都为5,则点P 的坐标为 . 练习1.点P(3,-4)关于x 轴的对称点的坐标是( , ) 关于y 轴的对称点的坐标是( , ) ,关于原点的对称点的坐标是( , ) .2.点M(-5,-8)到x 轴的距离是 到y 轴的距离是 到原点O 的距离是 .3.若点A 和点B 的横坐标相同,则线段AB 一定平行于 轴,垂直于 轴.4.平面内一点P ,过点P 作x 轴的垂线,垂足在x 轴上对应的数为a ,过点P 作y 轴的垂线,垂足在y 轴上对应的数为b ,则数a 叫做点P 的 数b 叫做点P 的 点P 的坐标记为( , ) .5.在直角坐标系中,O 为坐标原点,已知点A(1,1),在x 轴上确定点P ,使△AOP 为等腰三角形,则符合条件的点P 的个数共有A .4 B .3 C .2 D .1 6.点(,2)P a a -在第四象限,则a 的取值范围是( ) A .—2<a <0 B .0<a <2 C .a >0 D .a <0 7.如图5-2-1,求边长为2的正六边形的各顶点坐标.8.点(4,12)A m m --在第三象限,求m 的取值范围. 9.矩形ABCD 中,A 、B 、C 三点的坐标分别是(0,0),(6,0),(6,3),则点D 的坐标是 . 10.如图ABCD 为平行四边形,AD=4,AB=5,点A(0,-2),图34图5街2街1街 O求点B、C、11的坐标是三、平面直角坐标系(2)复习1.平面直角坐标系中,两坐标轴把平面分成部分,右上部分叫做其它部分按逆时针方向依次叫做、和坐标轴上的点任何象限内.2.已知点P到x轴和y轴的距离分别是3,4,则点P在第二象限内的坐标为.3.点P(m,1)在第二象限,则点Q(-m,0)在()A.x轴正半轴上B.x轴负半轴上C.y轴正半轴上D.y轴负半轴上4.如果P(m+3,2m+4)在y轴上,那么点P的坐标是()A.(-2,0) B.(0,-2) C.(1,0) D.(0,1)练习12.34A坐标轴上的点的坐标至少有一个是0 、B横轴上的点的横坐标为0C.纵轴上的点的纵坐标为0 D.以上说法都不正确5.点M(3,-4),N(5,a)之间的距离是2,则a的值是()A.(B.3)-C.(-D.(3,92(3)0b+=,则点(,)M a b-在()A.第一象限B.第二象限C.第三象限D.第四象限10.过点(且平行于y轴的直线上的点()A..横标是D.纵标是11.已知点A(0,2),点B(0,-3),点C在x轴上,如果△ABC的面积为20,求点C的坐标.四、平面直角坐标系(3)复习y轴上,则点P的坐标为( , )x轴的距离是,到y轴O的距离是.y轴的对称点是B(-3,y),则x= ,x轴对称点的坐标是.A位于y轴左侧,距y轴5个单x轴3个单位长度,则点A坐A坐标是(3,6),将该点向左平移2个3个单位得到点( , )P(x,y)满足5x=216y=则点P的坐标2.点)2,2(-P到x轴的距离是,到y轴的距离是,到原点O的距离是.3.点A(3,-2)关于y轴的对称点是( , ) 关于原点O的对称点是( , 4(1)写出图中△(2)求△ABC5.点P(2m-1,3)在第二象限,则m 的取值范围是( )A .12m >B .12m ≥C .21<m D .12m ≤ 6.点M(-3,4)关于原点的对称点为N ,则MN= 7已知A(m,3)和B(4,n)两点根据下列条件求出m 、n 的值. (1)A 、B 两点关于y 轴对称; (2)A 、B 两点关于x 轴对称; (3)A 、B 两点关于原点O 对称; (4)AB ∥y 轴; (5)A 、B 两点在第一、三象限两条坐标轴夹角的平分线上.8试求:910是(0,0)A 11 125-4-3PAB ,△PBC ,△PCD ,△PDA P 点有几个?写出它们的坐标). B(-a+2,5b-6)在第___象限. 2.若一个正方形面积是另一个正方形面积的4倍,则它的边长是另一个正方形边长的 倍.3.若224(3)0x y -+-=,那么点(5,1)P x y +-的坐标是A .(7,2)B .(5,2)C .(7,3)D .不能确定 4.将点(3,5)P 向右平移2个单位,得到的点1P 的坐标是1P ( , ) 将点(3,5)P 向左平移2个单位,得到的点2P 的坐标是2P ( ,)将点(3,5)P 向上平移2个单位,得到的点3P 的坐标是3P( , )将点(3,5)P 向下平移2个单位,得到的点4P 的坐标是4P ( , )平移,横坐标减平移,纵坐标减 )b -,4(,)P a b --,则:3P 关于 对称;4P关于 对称. 1P (3,4),那么点P 关 .(5,2) D .(3,4) (0,0),,(0,0),就得到一3,再将所得的点用CD 的顶点坐标分别为A(1,1),B(3,1),C(3,3),D(1,3). (1)在同一直角坐标系中,将正方形向左平移2个单位,画出你相应的图形,并写出各点的坐标.(2)将正方形向下平移2个单位,画出相应的图形,并写出各点的坐标.(3)在(1)(2)中,你发现各点的横、纵坐标发生了哪些变化?5.以点P(4,0)为圆心,以5为半径的圆与y 轴交点的坐标为6.下列关于A,B 两点的说法中,正确的个数是( )①如果点A 与点B 关于y 轴对称,那么它们的纵坐标相同 ②如果点A 与点B 的纵坐标相同,那么它们关于y 轴对称 ③如果点A 与点B 的横坐标相同,那么它们关于x 轴对称 ④如果点A 与点B 关于x 轴对称,那么它们的横坐标相同 A .1个 B .2个 C .3个 D .4个7如果△点A′8限.六、变化的“鱼”(2)复习1.点M(3,-4)到原点的距离是 .2A 关于原点O 的对称点的坐标B(6,-8)则点A 的坐标是 .4.A(-3,2)关于原点O 的对称点是B ,B 关于x 轴的对称,则点C 的坐标是( )B .(-3,2)C .(3,-2)D .(-2,3) 平面直角坐标系中的图形将会发生怎样的变3倍,图形将 2倍,图形将 1,图形将 ;纵坐标分别加2,图形将 ; -1,图形将 ; 5个单位长度,需将 坐 个单位长度;4倍需将此图形的横、纵坐标分别 ;(8)若想要此图形向右平移3个单位长度,需将 坐标分别 个单位长度. 练习1.把点A(-3,4)的横坐标不变,纵坐标乘以-1(即纵坐标取相反数),得到的点B 的坐标为 ;这个点B 和点A 关于 对称.2.把点A(-3,4)的纵坐标不变,横坐标乘以-1(即横坐标取相反数),得到的点C 的坐标为 ;这个点C 和点A 关于 对称.3.点M(a,-3)和点N(2,b)关于x 轴对称,则ba = . 4.点A(3,-4)关于y 轴的对称点是点B ,则线段AB 的长是 个单位,点A(3,-4)关于原点的对称点是点C ,则线段AC 的长是 个单位.(,3)P m m -m 的取值范围 x 轴3个单位长度,且位于y 则M 点的坐标为 .(0,1)B ,(0,3)C ,求点D 的坐P 是x 轴上的一点,求:PA PB +的最小值.9.设m 是实数,那么平面上的点2(352,1)P m m m -+-不可能在第几象限?第五章位置的确定单元测试A卷一、选择题(每题3分,共24分)1.点P(-2,1)关于xA.(2,1) B.(-2,-1) C.(2,-1)2.下列数据不能确定物体位置的是(A.北纬58°36′,东经108°11′ BC.中山路128号D.地王大厦253.点(2,1)P x x++在x轴上,则点PA.(0,-1) B.(1,0) C.(4,0)4.若点Q(m,n)x轴的距离为2,则点Q的坐标为(A.(2,2) B.(-2,-2) C.(2,2)或或(-2,2)5.已知点M(a,b)在x轴下方,且0ab<()A.第一象限B.第二象限C四象限6.A.关于x轴对称B.关于y轴对称C.关于原点对称D.沿y轴向下平移1个单位长度7.与平面直角坐标系内的点对应的坐标是()A.一对实数B一对有序实数C一对有理数D.一对有序有理数8.点P在第二象限内,点P到x轴的距离是4,到y轴的距离是3,那么点P的坐标为()A.(-4,3) B.(4,-3) C.(-3,4) D.(3,-4)二、填空题(每题4分,共20分)17.如图所示,Rt ABO∆的直角顶点在原点,OA=6,AB=10,AO与x轴正半轴的夹角为30°,求A,B两点的坐标.(10分)16题图四边ABNM 都是什么样的四边形吗?(9分) 第五章 位置的确定单元测试B 卷 一、选择题(每题3分,共24分)1.在平面内,确定一个点的位置一般需要的数据个数是( )A .1B .2C .3D .42.在平面直角坐标系中,点(3,-4)所在的象限是( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限3.将点P(-2,2)沿x 轴的正方向平移4个单位得到的点P ′的坐标为A .(-2,6) B .(-6,2) C .(2,2) D .(2,-2)4.点(,)P x y 满足2(3)10x y -++=,则点P 的坐标为( ) A.(-3,-1) B .(3,1) C .(-3,1) D .(3,-1)5.已知点P(-2,3)关于y 轴的对称点为Q(a,b),则a+b 的值是( )A .1B .-1C .5D .-56.一个平行四边形三个顶点的坐标分别是(0,0),(2,0),(1,2),第四个顶点在x 轴下方,则第四个顶点的坐标为( )A .(-1,-2)B .(1,-2)C .(3,2)D .(-1,2) 7.平面直角坐标系中,将平行四边形向上平移3个单位后,得到的平行四边形各顶点与原来平行四边形各顶点的坐标相比( ) A .横坐标不变,纵坐标加3 B .纵坐标不变,横坐标加3C .横坐标不变,纵坐标乘3D .纵坐标不变,横坐标乘38.如图所示,小明从家到达学校要穿过一个居民小区,小区的道路均是正南或正东方向,小明走下面哪条线路不能到达学校( ) A .(0,4)→(0,0)→(4,0) C .(0,4)→(1,4)→(1,1)→(4,1)→(4,0) D .(0,4)→(3,4)→(4,2)→(4,0) 二、填空题(每空2分,共22分)9.点A 在y 轴上,距离原点4个单位长度,则点A 标是 10.如图,△AOB 是边长为5的等边三角形,则A 、两点的坐标分别是A ,B11.如图,正方形OABC 的各顶点在坐标系中的位置如图,则点A 、B 、C 分别关于x 轴,y 轴,原点对称的点的坐标是 , , .12.已知点A(a-1,a+1)在x 轴上,则a = . 13.点P(-5,3)到x 轴的距离为 ,到y 轴的距离为 .14以(3,0)为圆心以2为半径画圆则圆与x 轴的交点坐标为 .15在矩形ABCD A(4,1),B(0,1),C(0,3),则点D 的坐标为 16.分)17 18.C(5,0) 19.在直角坐标系中,依次连接点(1,0),(1,3),(7,3),(7,0),(1,0)和点(0,3),(8,3),(4,5),(0,3),两组图形共同组成了一个什么图形? (1)如果将上面各点的横坐标都加1,纵坐标不变,那么用同样方式连接相应各点所得的图形发生了哪些变化?(4分)(2)若把图中各点的横坐标都乘以-1,纵坐标都乘以-1,所得的图案与原图案有何关系?(3分)8题图 10题图 11题图(探究题)已知平面直角坐标系上有六个点,请将上述的六个点按下列要求分成两类,并写出同类点具有而另一类点不具有的一个特征(请将答案按要求写在横线上,特征不能用否定形式表述...........,点用字母表示).⑴甲类含两个点,乙类含其余四个点.甲类:点____,____是同一类点,其特征是______;乙类:点____,____是同一类点,其特征是______;⑵甲类含三个点,乙类含其余三个点.甲类:点___,___,____是同一类点,其特征是___;乙类:点___,___,____是同一类点,其特征是___.。
八年级(上)数学形第五章位置的确定测试题

]八年级(上)数学形成性评价(六)(第五章 位置的确定)学校 班级 姓名 学号 分数一、选择题(每小题3分,满分24分) 1.下列数据不能确定物体位置的是( ){A .4楼8号B .北偏东30°C .希望路25号D .东经118°、北纬40°2.点P 在第二象限,若该点到x 轴的距离为3,到y 轴的距离为1,则点P 的坐标 是( ) A .(-1,3)B .(-3,1)C .(3,-1)D .(1,3)3.如图1所示的是某学校的平面示意图,在10×10的正方形网格中(每个小方格都是边长为1的正方形),如果分别用(1,2),(1,6)表示图中校门和图书馆的位置,那么花坛的位置应表示为( ) A .(6,0) B .(6,-1) C .(6,2)D .(-1,6){4.小明住在平安小区3单元4幢501室,现把他家的位置记为(3,4,501),那么小琴住在平安小区6单元3幢206室可记为( ) A .(6,3)B .(6,206,3)C .(6,3,206)D .(3,6,206)5.已知ABC ∆的顶点坐标分别是(0,0),(4,0),(0,4)A B C -,现将,,A B C 三个顶点的横、纵坐标都变为原来的12,那么新三角形的面积为( )A .8B .4C .2D .16.若点(,1)P m 在第二象限内,则点Q (,0m -)在( ) A .x 轴正半轴上B .x 轴负半轴上—C .y 轴正半轴上D .y 轴负半轴上7.在一次科学探测活动中,探测人员发现一目标在如图2所 示的阴影区域内,则目标坐标可能是( ) A .(-3,300)B .(7,-500)C .(9,600)D .(-2,-800)8.如图3所示,已知点(1,0)A -和点(1,2)B ,在坐标轴上确定点P , 使得ABP ∆为直角三角形,则满足这样条件的点P 共有( ) A .2个 B . 4个 C . 6个D . 7个。
初二上册数学第五章位置的确定测试题(附答案)

初二上册数学第五章位置的确定测试题(附答案)5.1 确定位置填空题1.在生活中,确定物体的位置有________种方法,一种是______________________,例如:____________________________;另一种是________________ _________________,例如:_________________________ _______________.2. 下图是把一个树干和一幅扇子在方格纸上摆出的图案.如果用(0,0)表示M的位置,用(2,1)表示N的位置,那么图1 图2(1)图1中A、B、C、D、E的位置分别为_____________________________________.(2)图2中A、B、C、D、E、F、G的位置A____ _ ______ __________________________.(3)在图1和图2中分别找出(4,11)和(8,10)的位置.3.张坚在某市动物园大门口看到这个动物园的平面示意图(如图3),试借助刻度尺、量角器解决如下问题:(注:A代表驼鸟峰,B代表猴山,C代表百鸟园,D 代表熊猫馆,E代表大门)(1)熊猫馆D位于园门E的北偏东度的方向上,到园门的图上距离为________厘米,实际距离为________千米.(2)百鸟园在大门的北偏东度方向上,驼鸟峰在大门的南偏东________ 度方向上,到大门的距离约为_ _______厘米,实际距离为________千米.4.如图4,小王家在1街与2大道的十字路口,如果用(2,2)→(2,3)→(2,4)→(3,4)→(4,4)→(5,4) 表示小王从家到工厂上班的一条路径,那么你能用同样的方式写出由家到工厂小王走的路径吗?图3图4试一试:___________________________________________________________ _____________________ 参考答案一、1.2,用两个有序实数表示电影院中座位的确定一个方位角数字在海上行船时,船与某岛的位置 2.(1)A(10,8) ,B(7,10),C(5,9),D(3,8),E(9,1)(2)A(7,0),B(0,3),C(2,6),D(4,7),E(10,7),F(12,6),G(14,3)(3)略X|k |b| 1 . c|o |m3.略4.(2,1)→(3,1)→(4,1)→(5,1)→(5,2)→(5,3)→(5,4)或(2,1)→(3,2)→(4,3)→(5,4)5.2 平面直角坐标系(1)当你进礼堂看电影时,你通过几个数据确定你座位的位置?(2)张坚在某市动物园大门口看到这个动物园的平面示意图(如上图),试借助刻度尺、量角器解决如下问题:①以大门为坐标原点建立互相垂直的两条数轴,分别取向右和向上为正方向.你能表示猴山、驼峰、百鸟园的大概位置吗?②填空:百鸟园大约在大门的北偏东______度方向上,熊猫馆在大门的北偏东______度的方向上,到大门的距离约为______厘米. 测验评价等级:A B C,我对测验结果(满意、一般、不满意)参考答案(1)通过两个数据,排数和列数.(2)略注:坐标建立的不同,结果也不一样.5.2平面直角坐标系班级:________ 姓名:________一、填空题1.____________________________ _________________________组成平面直角坐标系.2.(1)图1中多边形ABCDEF各顶点坐标为___________________________________________________________ ___________________________________________________________ ___________________ ___________.(2)A与B和E与D的横坐标有什么关系___ __________ ___________________________________________________________ ___________________________.(3)B与D、C与F坐标的特点是________________________________________________.(4)线段AB 与ED所在直线的位置关系是___________________________________________________________ _______________________________________ __. 图1 图23.图2是画在方格纸上的某行政区简图,(1)则地点B,E,H,R的坐标分别为:___________________________________________________________ __________.(2)(2,4),(5,3),( 7,7),(11,4)所代表的地点分别为___________________________________________________________ ________________________________________.4.已知:如图3等腰△ABC的腰长为2 ,底边BC=4,以BC所在的直线为x轴,BC 的垂直平分线为y轴建立如图所示的直角坐标系,则B( )、C( )、A( ). 图3 图45.如图4草房的地基AB长15米,房檐CD的长为20米,门宽为6米,CD到地面的距离为18米,请你建立适当的直角坐标系并写出A、B、C、D、E、F的坐标.(1)以_________为x 轴,以_____________为y轴建立平面直角坐标系,则A________,B________C________,D________,E________,F________.二、建立一个直角坐标系,并在坐标系中,把以下各组点描出来,并观察图形像什么?(1)(0,4),(0,2),(3,5),(4,6),(0,-2),(-3,5),(-4,6),(6,0),(-6,0)(2)(0,-4),(3,-5),(-3,-5),(6,0),(-6,0)测验评价结果:_____________;对自己想说的一句话是:______________________. 参考答案一、1 .有公共原点且互相垂直的两条数轴2.(1)A(-4,3),B(-4,0),C(0,-2),D(5,0),E(5,3),F(0,5)(2)相同(3)均有个坐标为0,B、D纵坐标为0,C、F横坐标为0 (4)平行3.(1)B(4,8),E(11,4),H(10,4),R(6,1) (2)M,I,C,E4.(-2,0),(2,0),A(0,2)5.注:草房所在的平面图是轴对称图形二、略参考练习1.下图是一种活动门的示意图,平时不用的时候推到一边去,晚上要用的时候拉过来锁上,不占地方,非常方便,它是由一个个菱形组成的,图中菱形的一个角是60°,请用适当的方式表示菱形各顶点的位置. 2.下图是正六边形ABCDEF,它的边长为2,请你建立适当的直角坐标系,把各顶点的坐标写出来. 答案:略二、创新思维探索1.设m是实数,那么平面上的点P(3m2-5m+2,1-m)不可能在第_______ __象限?分析:要判断点P不经过第几象限,需讨论点P的横纵坐标符号的可能性.解:∵3m2-5m+2=(m-1) (3m-2)∴当m≤时,3m2-5m+2≥0此时1-m>0,点P在第一象限或y轴上.当<m<1时,3m2-5m+2<0.此时1-m>0,点P在第二象限.当m≥1时,3m2-5m+2≥0.此时1-m<0,点P在第四象限.综观以上结论,可知点P不可能在第三象限 2.如果点A(-3,2m+1)关于原点对称的点在第四象限,求m的取值范围.分析:由于第四象限关于原点对称的点在第二象限,反之第二象限的点关于原点对称的点在第四象限,所以A(-3,2m+1)应在第二象限,由第二象限的符号特征解之.解:∵A(-3,2m+1)关于原点对称的点在第四象限.∴A(-3,2m+1)在第二象限.∴A点的纵坐标2m+1>0. ∴m>-.3.如果B(m+1,3m-5)到x 轴的距离与它到y轴的距离相等,求m.分析:坐标平面内的点到两轴的距离实际上就是该点两坐标的绝对值.解:∵B(m+1,3m-5)到x轴、y轴的距离相等.∴|m+1|=|3m-5|.∴m+1=3m-5或m+1=5-3m.∴m=3或m=1.平面直角坐标系一、填空题、选择题:1.确定平面内某一点的位置一般需要_______个数据.2.点A的横坐标是4,纵坐标是-3,点A的坐标记作_______.3.点A(3,-4)到y轴的距离为_______,到x轴的距离为_____,到原点距离为_____.4.与点A(3,4)关于x轴对称的点的坐标为_______,关于y轴对称的点的坐标为_______,关于原点对称的点的坐标为_____.5.已知点A(a,-2)与点B(3,-2)关于y轴对称,则a=_______,点C的坐标为(4,-3),若将点C向上平移3个单位,则平移后的点C坐标为________.6.点A (–3,4)和点B(3,4)的关于___________轴对称;7.如果点P1 ( ,)和P2 (1,)关于轴对称,则= ;8.点关于轴对称的点的坐标是()A B C D 9.若A(a,b)在第四象限,则在()A 第一象限B第二象限C第三象限D第四象限10.下列关于A、B两点的说法中,(1)如果点A与点B关于y轴对称,则它们的纵坐标相同;(2)如果点A与点B的纵坐标相同,则它们关于y 轴对称;(3)如果点A与点B的横坐标相同,则它们关于x轴对称;(4)如果点A与点B关于x轴对称,则它们的横坐标相同.正确的个数是()A.1个 B.2个 C.3个 D.4个二、解答题:11.在直角坐标系中描出下列各组点,并将各组内的点用线段依次连接起来:(1)(2,6),(4,6),(4,8),(2,8);(2)(3,3),(3,6);(3)(3,5),(1,6);(4)(3,5),(5,6);(5)(3,3),(2,0);(6)(3,3),(4,0).观察所得的图形,你觉得它象什么?12.在直角坐标系中描出下列各组点,并组各组的点用线段依次连结起来.(1)(1,0),(6,0),(6,1),(5,0),(6,-1),(6,0); (2)(2,0),(5,3),(4,0); (3)(2,0),(5,-3),(4,0). 观察所得到的图形像什么?如果要将此图形向上平移到x轴上方, 那么至少要向上平移几个单位长度.13、建立一个直角坐标系,并在坐标系中,把以下各组点描出来,并观察图形像什么?(1)(0,4),(0,2),(3,5),(4,6),(0,-2),(-3,5),(-4,6),(6,0),(-6,0)(2)(0,-4),(3,-5),(-3,-5),(6,0),(-6,0)参考答案:一、1.2 2.(4,-3) 3.3,4,5 4.(3,-4),(-3,4),(-3,-4) 5.-3,(4,0)6、y 7、3 8、B 9、B 10、B二解答题:11.如图,所得的图形象机器人.12.图略至少要向上平移3个以单位长度13、略5.3 变化的“鱼”下面的三角形ABC,三顶点的坐标分别为A(0,0),B(4,-2),C(5 ,3)下面将三角形三顶点的坐标做如下变化(1)横坐标不变,纵坐标变为原来的2倍,此时所得三角形与原三角形相比有什么变化?(2)横、纵坐标均乘以-1,所得新三角形与原三角形相比有什么变化?(3)在(2)的条件下,横坐标减去2,纵坐标加上2,所得图形与原三角形有什么变化?测验评价等级:A B C,我对测验结果(满意、一般、不满意)参考答案(1)横坐标保持不变,纵坐标变为原来的2倍,所得各顶点的坐标依次是A(0,0),B(4,-4 ),C(5,6),连结OB、OC 、BC,整个三角形纵向拉长原来的2倍.(2)横纵坐标均乘以-1,所得各顶点坐标依次为A(0 ,0),B(-4,2),C (-5,-3),连结OB、OC、BC,整个三角形绕原点旋转180 °.(3)横坐标减去2,坐标加上2,得各顶点坐标为A(-2,2),B (-6,4),C(-7,-1),连结AB、BC、CA,所得三角形向左平移2个单位,再向上平移2个单位.(图略)5.3. 变化的“鱼”班级:________ 姓名:________一、填空题1.点P(-2,5)关于原点的对称点的坐标是________.2.点A在x轴上,且与原点的距离为5,则点A的坐标是________.3.如图1正方形的边长为2 ,则正方形的顶点坐标为:________________________________ __________________.4.点A(x1,-5),B(2,y2),若(1)A,B关于x 轴对称,则x1=________,y2=________ 图1 (2)A,B 关于y轴对称,则x1=________,y2=________ (3) A,B关于原点对称,则x1=________,y2=________.二、如图2,如果将图中各点纵、横坐标分别乘以-1,那么所得图案将发生什么变化?三、图3中的不明飞行物是将坐标(0,0),(1,0),(3,0),(2,1),(3,4),(5,3),(5,2),(3,2)的点用线段依次连接而成的. 图2图3下面将以上各点做如下变化:(1)横坐标保持不变,纵坐标分别乘以-1,所得图案与原图案有什么变化?(2)横坐标和纵坐标都乘以-1,所得图案与原图案相比有什么变化?(3)横坐标加1,纵坐标加2,所得图案与原图案相比有什么变化?测验评价结果:_____________;对自己想说的一句话是:_________________ _____.参考答案一、1.(2,-5)2.(5,0)或(-5,0)3.A(0,0),B( ,),C(0,2 ),D(-,)4.(1)2 5 (2)-2 -5 (3)-2 5二、所得图案是将原图案绕原点旋转180°而得到三、(1)所得图案与原图形成轴对称图形,关于x轴对称(2)所得图案与原图形成中心对称图形,所得图案与原图形关于原点对称图形(3)所得图形向右平移一个单位再向上平移两个单位.数学小步训练——变化的鱼一、温故知新1、的相反数是,的相反数是,=________;3、点M(-3,4)到x轴的距离是______;到y轴的距离是______;到原点的距离是;4、若点A关于x轴对称的点是(2,3),则A点坐标为__ ____;若点A关于y轴对称的点是(2,3),则A点坐标为_ _____;若点A关于原点对称的点是(2, 3),则A点坐标为______ ;5、点A()和点B()关于轴对称,则。
第五章《位置的确定》专题复习(含答案)

第五章《位置的确定》专项练习专题一:确定位置例1.如图1,已知棋子“车”的坐标为(-2,3),棋子“马”的坐标为(1,3),则棋子“炮”的坐标为A .(3,2)B .(3,1)C .(2,2)D .(-2,2)例2.如图2是某市市区四个旅游景点示意图(图中每个小正方形的边长为1个单位长度),请以某景点为原点, 建立平面直角坐标系(保留坐标系的痕迹),并用坐标表示下列景 点的位置。
①动物园 , ②烈士陵园 。
专练一:1、已知外婆家在小明家的正东方,学校在外婆家的北偏西40,外婆家到学校与小明家到学校的距离相等,则学校在小明家的( ) A.南偏东50B.南偏东40C.北偏东50D.北偏东402、张老师住在学校的正东200米外,从张老师家出发向北走150米就到李老师家,若选取李老师家为原点,分别以正东、正北方向为x 轴,y 轴正方向建立平面直角坐标系,则学校的坐标是( )A 、(-200,-150)B 、(200,150)C 、(-150,-200)D 、(150,200) 3、小明从家里出发向正北方向走200m 就到了学校,如果以小明家为原点,学校的位置为 ,如果以学校为原点,他家的位置为 .4、某地震多发地区有互相垂直的两条交通主干线,以这两条主干线为轴建立直角坐标系,长度单位为100km ,地震监测部门预报该地区将有一次地震发生,震中位置为(12)-,,影响范围的半径为300km ,则下列主干线沿线的6个城市在地震影响范围内有 个.主干线沿线的6个城市为:(01)A -,,(02.5)B ,,(1.240)C ,,(0.50)D -,,(1.20)E ,,( 3.220)F -,图2图1 O5、如图3,是小英所在学校的平面示意图,小英应该如何描述她所住的宿舍位置呢?专题二:平面直角坐标系例1.若点M (1,12-a )在第四象限内,则a 例2.点(12)A -,关于x 轴对称的点的坐标是 ;点是 .例3.点P 在第二象限内,P 到x 轴的距离是4,到y ( ).A.()4,3-B.()3,4--C.()3,4-D.()3,4-专练二:1、下列各点中,在第一象限的点是( )A .(23),B .(23)-,C .(23)-,D .(23)--,6、在一次科学探测活动中,探测人员发现一目标在如图10能是( )A.(3300)-, B.(7500)-,C.(9600), D.(2800)--,8、点(a ,)b 关于y 轴的对称点的坐标是 ( ) A.(a -,)b -B.(a ,)b -C.(a ,)bD.(a -,)b9、若点(P m ,)n 在第二象限,则点(Q m ,)n -在第 象限.15、 已知点P 坐标为(2a -,36)a +,且点P 到两坐标轴距离相等,求P 点坐标.专题三:变化的鱼图10例1.已知,如图13,在平面直角坐标系中,O 为坐标原点,四边形OABC 是矩形,点A 、C 的坐标分别 为A (10,0)、C (0,4),点D 是OA 的中点,点P 在BC 边上运动,当△ODP 是腰长为5的等腰三角形时, 点P 的坐标为 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学大教育科技(北京)有限公司 Beijing XueDa Century Education Technology
第五章(位置的确定)评价试题
一、选择题(共5小题,每小题4分,共20分.在四个选项中,只有一项是符合题目要求的,请把符合要求一项的字母代号填在题后括号内.)
1.在平面内,确定一个点的位置一般需要的数据个数是( )
A.1
B.2
C.3
D.4
2.如图,已知校门的坐标是(1,1),那么下列对于实验楼位置的叙述正确的个数为( )
(1)实验楼的坐标是3
(2)实验楼的坐标是(3,3)
(3)实验楼的坐标为(4,4)
(4)实验楼在校门的东北方向上,距校门200米
A.1个
B.2个
C.3个
D.4个
3.已知点M到x轴的距离为3,到y轴的距离为2,则M点的坐标为( )
A.(3,2)
B.(-3,-2)
C.(3,-2)
D.(2,3),(2,-3),(-2,3),(-2,-3)
4.点P(-1,3)关于原点对称的点的坐标是( )
A.(-1,-3)
B.(1,3)
C.(1,-3)
D.(-3,1)
5.平面直角坐标系内有一点A(a,b),若ab=0,则点A的位置在( )
A.坐标轴上
B.x轴上
C.y轴上
D.原点
二、填空题(共6小题,每小题5分,共30分.把答案填在题中的横线上.)
6.点A(-2,1)在第_______象限.
7.在直角坐标系内, 将点A(-2.3)向右平移3个单位到B点, 则点B的坐标是_______.
8.已知点 P(-3,2),点A与点P关于y轴对称,则点A的坐标是_______.
9.在矩形ABCD中,A点的坐标为(1,3),B点坐标为(1,-2),C点坐标为(-4,-2),则D点的坐标是_______.
10.一正三角形ABC, A(0,0),B(-4,0),C(-2,),将三角形ABC绕原点顺时针旋转120°得到的三角形的三个顶点坐标分别是_______.
11.如图,一个机器人从O点出发,向正东方向走3米到达A1点,再向正北方向走6
米到
达A2点,再向正西方向走9米到达A3点,再向正南方向走12米到达A4点,再向正东方向走
15米到达A5点.按如此规律走下去,当机器人走到A6点时,离O点的距离是_______米.
三、解答题(共5小题,每小题10分,共50分.解答应写出文字说明,证明过程或演算步骤.)
12.根据图填表:
13.在直角坐标系中,描出下列各点:
(1)(2,1),(-2,1);
(2)(-3,4),(3, 4);
(3)(5,-4),(-5,-4).
你能发现上述各对点的位置有何特点吗?它们的坐标有何异同?你能总结出一般的规律吗?
14.某地为了城市发展,在现有的四个城市A、B、C、D附近新建机场E.试建立适当的直角坐标系,写出点A、B、C、D、E的坐标.
15.对于边长为6的正三角形ABC,建立适当的直角坐标系,写出各个顶点的坐标.
16.在直角坐标系中,描出点(1,0),(1,2),(2,1),(1,1),并用线
段依次连接起来.
(1)纵坐标不变,横坐标分别加上2,所得图案与原图相比有什么变化?
(2)横坐标不变,纵坐标分别乘以-1呢?
(3)横坐标,纵坐标都变成原来的2倍呢?
附加题(10分,不计入总分)
国际象棋、中国象棋和围棋号称世界三大棋种. 国际象棋中的“皇后”的威力可比中国象棋中的“车”大得多:“皇后”不仅能控制她所在的行与列中的每一个小方格,而且还能控制“斜”方向的两条直线上的每一个小方格.如图甲是一个4×4的小方格棋盘,图中的“皇后Q”能控制图中虚线所经过的每一个小方格.
(1)在如图乙的小方格棋盘中有一“皇后Q”,她所在的位置可用“(2,3)”来表示,请用这种表示法分别写出棋盘中不能被该“皇后Q”所控制的四个位置.
(2)如图丙也是一个4×4的小方格棋盘,请在这个棋盘中放入四个“皇后Q”,使这四个“皇后Q”之间互不受对方控制(在图丙中的某四个小方格中标出字母Q即可).
3)
每个坐标1分,每两个象限1分,坐标轴各1分,共10分.
13.
每对点的位置关于关于y轴对称;它们的纵坐标相同,横坐标互为相反数;在直角坐标系中,关于y轴对称的点,纵坐标相同,横坐标互为相反数.
每画一个点1分,共6分;总结规律4分;共10分.
14.
答:A(0,0),B(8,2),C(8,7),D(5,6).E(1,8).
解法不唯一,建立坐标系5分,写出每点坐标各1分,共10分.
15.
建立坐标系4分,写出每点坐标各2分,共10分.
16.答:(1)所得图案与原图相比,整个图案向右平移两个单位.……6分
(含画坐标系2分,描点2分)
(2)所得图案与原图相比,关于x轴对称.……8分
(3)所得图案与原图相比,形状不变,长度和高度都扩大2倍.……10分
附加题
(1)答: 不能被该“皇后Q”所控制的四个位置是
(1,1),(3,1),(4,2),(4,4).……4分
(2)如图:……10分。
