矛盾方程组的最小二乘解
最小二乘法

最小二乘法最小二乘法起源于以测量和观测为基础的天文学。
Gauss 在1794年利用最小二乘法解决了多余观测问题,当时他只有十七岁。
可以用下面的简单例子描述这类问题。
假定通过观测或实验得到如下一组数据(即列表函数):我们的目的是一简单的式子表出这些数据间的关系。
从分析数据看出,这些点差不多分布在一条直线上,因此我们自然想到用线性式b ax y +=表示它们之间的关系。
这就须定出参数a 和b 的值来。
这实际上是多余观测问题,用插值法不能确定出a 和b 的值。
代定参数的确定归结为矛盾方程组的求解问题。
假定有某方法可以定出a 和b ,则按bx a y +=,给出一个x 便可以算出一个y 。
我们记).8,,1( =+=k bxa y kk y 称为k y 的估计值,显然它们不会是完全相同的,它们之间的差(通常称为残差))8,,1( =-=k y y kk k ε无疑是衡量被确定的参数a 和b (也就是近似多项式b ax y +=)好坏的重要标志。
可以规定许多原则来确定参数b a ,。
例如(1) 参数的确定,将使残差绝对值中最大的一个达到最小,即kkT εmax =为最小;(2) 参数的确定,将使残差绝对值之和达到最小,即∑kk ε为最小;(3) 参数的确定,将使残差的平方和达到最小,即∑2k ε为最小。
(1) 和(2)两个原则是很直观的,也很理想,但很不好用;而原则(3)既直观又很好用。
按原则(3)确定待定参数,从而得到近似多项式的方法,就是通常所说的最小二乘法。
这一方法的理论根据是,概率理论已证明,只有这样的原则才能使得观测或实验的偶然误差对于所作的近似多项式有最小的影响。
回到所提出的问题上来,即用最小二乘法确定参数b a ,。
按最小二乘法,应使∑=+-=si i i b a y b a S 12))((),(取最小值。
因此,应有.0))((2,0))((28181=+-=∂∂=+-=∂∂∑∑==i i i i i i i x b a y b Sb a y a S由此,得到如下线性方程组:.,81812818181810∑∑∑∑∑∑=======+=+i i i i i i i i i i i i y x x b x a y x b i a经过简单计算,这个方程组成为⎩⎨⎧=+=+.3.4714028,2.12288b a b a 解之可得,110.0,142.1==b a 从而得近似多项式.110.0142.1)(1x x p +=现在转入讨论更为一般的情形。
最小二乘问题

1 1
例
已知A 1
1
,求A的广义逆A。
1 1
解:A是列满秩的矩阵,可以求它的左逆
A
( AT A)1 AT
14 8 -4
2 2
2 2
验算有A A
I2 , 但AA
I
。
3
10
数值分析
数值分析
4 A Rmn是行满秩矩阵(m n, r( A) m),则
A=A(T AAT)1,且AA Im (但一般不成立A A In );
4
数值分析
数值分析
定理1 : x Rn是矛盾方程组Ax b的最小二乘解的 充分必要条件是 : x是方程组AT Ax AT b的解.
证明: 设有x, y Rn ,且x y,则 r( y) 2 b Ay 2 (b Ax) ( Ax Ay) 2
r( x) ( Ax Ay) 2 r( x) 2 2(r( x), Ax Ay) ( Ax Ay) 2
(2)最小二乘解不唯一;
(3)x=A+b最小二乘解中欧氏范数最小的解;
(4)A列满秩时,最小二乘解唯一。
22
数值分析
数值分析
第四节 列满秩线性最小二乘问题 的数值解法
列满秩线性最小二乘问题存在唯一解x=A+b 有四种解法: 1. 直接解法方程 ATAx=ATb 2. 正交分解法 A=QR 3. 奇异值分解法 A=U∑VT 4. 迭代法
数值分析
数值分析
1 0 B 1 0,
0 1
1 0
BT
B
1 0
1 0
0 1
1 0
0 1
2 0
0 1
B
(BT B)1 BT
1 / 2
62第二节 超定方程组的解

2x1 4x2 11.0478 3x1 5x2 2.9119
x1 2x2 5.5239
b1 b2 b3
解得最小二乘解为
x1 x2
3.0403 1.2418
2x1 x2 7.3224 b4
m
n
m
故误差平方和为 I r 2 2
数学学院 信息与计算科学系
nm
m
即有 ( aij aik )xk aij bi ( j 1,2,..., n)
k 1 i1
i 1
此线性方程组写成矩阵形式就是
AT Ax AT b
故x*是 ATAx=ATb 的解.
定理得证.
这里 ATAx=ATb 是关于x1,x2, …,xn的线性 方程组,称为正规方程组或法方程组.
数学学院 信息与计算科学系
解的存在唯一性
由于ATA是n 阶方阵,且是对称阵,当R(A)=n 时, 对任意 y≠0,有Ay≠0 ,所以
yT ( AT A) y ( Ay, Ay) Ay 2 0 2
可见ATA是正定矩阵,必有det(ATA)>0。故法方程
AT Ax AT b
的解存在且唯一.
2 2 yT AT (b Ax* )
2
Ay
2 2
b Ax*
2
Ay 2
b Ax*
2
2
2
2
所以x*是Ax=b 的最小二乘解.
数学学院 信息与计算科学系
必要性 误差向量r=b-Ax 的第 i 个分量为
n
ri bi aik xk (i 1,2,..., m),
应用数值分析【研究生课程】课后习题答案04章

应用数值分析【研究生课程】课后习题答案04章第四章习题解答1、 求下列矩阵的满秩分解。
121002123011,04111002514211A A ⎡⎤-⎡⎤⎢⎥-⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦-⎣⎦解:因为1A 的秩为2,可求出满秩分解为11110011001001121A B C ⎡⎤⎢⎥⎡⎤⎢⎥==⎢⎥⎢⎥-⎣⎦⎢⎥⎣⎦又因为2A 的秩为2,可求出满秩分解为22210212301041111A B C ⎡⎤-⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦2、 根据定义求下列矩阵的广义逆A +。
1210012011,24100211A A ⎡⎤⎢⎥-⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦⎢⎥-⎣⎦解:(1)先求出1A 的一个满秩分解。
因为1A 的秩为1,可求出满秩分解为[]1111122A B C ⎡⎤==⎢⎥⎣⎦于是有[]11111111111()12511()52T T T T B B B B C C C C +-+-==⎡⎤==⎢⎥⎣⎦最后得1111212524A C B +++⎡⎤==⎢⎥⎣⎦(2)先求出2A 的一个满秩分解。
因为2A 的秩为2,可求出满秩分解为22210011001001121A B C ⎡⎤⎢⎥⎡⎤⎢⎥==⎢⎥⎢⎥-⎣⎦⎢⎥⎣⎦于是有1222212222111114444()5131144441011()052102T TT T B B B B C C C C +-+-⎡⎤-⎢⎥==⎢⎥⎢⎥--⎢⎥⎣⎦⎡⎤⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦最后得222111144441311888813118888A C B +++⎡⎤-⎢⎥⎢⎥⎢⎥==--⎢⎥⎢⎥⎢⎥--⎢⎥⎣⎦3、 证明下述广义逆矩阵的性质,设,m nn m A R A R ⨯+⨯∈∈。
(1)()AA ++=;(2)2()AA AA ++=;(3)2()AA A A ++=。
证明:(1)因为由定义可得,,(),()T T A AA A AA A A A A A A AA AA ++++++++====故由广义逆的定义可知()A A ++=。
最小二乘法拟合原理

最小二乘拟合在物理实验中经常要观测两个有函数关系的物理量。
根据两个量的许多组观测数据来确定它们的函数曲线,这就是实验数据处理中的曲线拟合问题。
这类问题通常有两种情况:一种是两个观测量x 与y 之间的函数形式已知,但一些参数未知,需要确定未知参数的最佳估计值;另一种是x 与y 之间的函数形式还不知道,需要找出它们之间的经验公式。
后一种情况常假设x 与y 之间的关系是一个待定的多项式,多项式系数就是待定的未知参数,从而可采用类似于前一种情况的处理方法。
一、最小二乘法原理在两个观测量中,往往总有一个量精度比另一个高得多,为简单起见把精度较高的观测量看作没有误差,并把这个观测量选作x ,而把所有的误差只认为是y 的误差。
设x 和y 的函数关系由理论公式y =f (x ;c 1,c 2,……c m ) (0-0-1)给出,其中c 1,c 2,……c m 是m 个要通过实验确定的参数。
对于每组观测数据(x i ,y i )i =1,2,……,N 。
都对应于xy 平面上一个点。
若不存在测量误差,则这些数据点都准确落在理论曲线上。
只要选取m 组测量值代入式(0-0-1),便得到方程组y i =f (x ;c 1,c 2,……c m ) (0-0-2) 式中i =1,2,……,m.求m 个方程的联立解即得m 个参数的数值。
显然N<m 时,参数不能确定。
在N>m 的情况下,式(0-0-2)成为矛盾方程组,不能直接用解方程的方法求得m 个参数值,只能用曲线拟合的方法来处理。
设测量中不存在着系统误差,或者说已经修正,则y 的观测值y i 围绕着期望值 <f (x ;c 1,c 2,……c m )> 摆动,其分布为正态分布,则y i 的概率密度为()()[]⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧--=22212,......,,;exp 21i m i i i i c c c x f y y p σσπ,式中i σ是分布的标准误差。
线性回归之最小二乘法
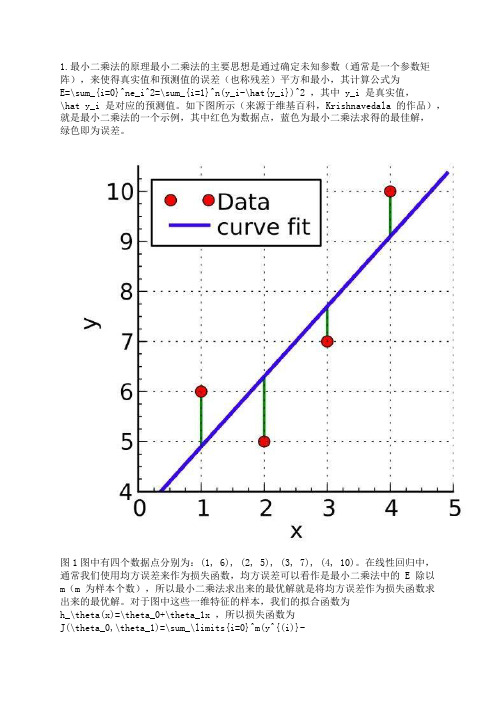
1.最小二乘法的原理最小二乘法的主要思想是通过确定未知参数(通常是一个参数矩阵),来使得真实值和预测值的误差(也称残差)平方和最小,其计算公式为E=\sum_{i=0}^ne_i^2=\sum_{i=1}^n(y_i-\hat{y_i})^2 ,其中 y_i 是真实值,\hat y_i 是对应的预测值。
如下图所示(来源于维基百科,Krishnavedala 的作品),就是最小二乘法的一个示例,其中红色为数据点,蓝色为最小二乘法求得的最佳解,绿色即为误差。
图1图中有四个数据点分别为:(1, 6), (2, 5), (3, 7), (4, 10)。
在线性回归中,通常我们使用均方误差来作为损失函数,均方误差可以看作是最小二乘法中的 E 除以m(m 为样本个数),所以最小二乘法求出来的最优解就是将均方误差作为损失函数求出来的最优解。
对于图中这些一维特征的样本,我们的拟合函数为h_\theta(x)=\theta_0+\theta_1x ,所以损失函数为J(\theta_0,\theta_1)=\sum_\limits{i=0}^m(y^{(i)}-h_\theta(x^{(i)}))^2=\sum_\limits{i=0}^m(y^{(i)}-\theta_0-\theta_1x^{(i)})^2 (这里损失函数使用最小二乘法,并非均方误差),其中上标(i)表示第 i 个样本。
2.最小二乘法求解要使损失函数最小,可以将损失函数当作多元函数来处理,采用多元函数求偏导的方法来计算函数的极小值。
例如对于一维特征的最小二乘法, J(\theta_0,\theta_1) 分别对 \theta_0 , \theta_1 求偏导,令偏导等于 0 ,得:\frac{\partial J(\theta_0,\theta_1)}{\partial\theta_0}=-2\sum_\limits{i=1}^{m}(y^{(i)}-\theta_0-\theta_1x^{(i)}) =0\tag{2.1}\frac{\partial J(\theta_0,\theta_1)}{\partial\theta_1}=-2\sum_\limits{i=1}^{m}(y^{(i)}-\theta_0-\theta_1x^{(i)})x^{(i)} = 0\tag{2.2}联立两式,求解可得:\theta_0=\frac{\sum_\limits{i=1}^m(x^{(i)})^2\sum_\limits{i=1}^my^{(i)}-\sum_\limits{i=1}^mx^{(i)}\sum_\limits{i=1}^mx^{(i)}y^{(i)}}{m\sum_\limits{i=1}^m(x^{(i)})^2-(\sum_\limits{i=1}^mx^{(i)})^2} \tag{2.3}\theta_1=\frac{m\sum_\limits{i=1}^mx^{(i)}y^{(i)}-\sum_\limits{i=1}^mx^{(i)}\sum_\limits{i=1}^my^{(i)}}{m\sum_\limits{i=1}^m(x^{(i)})^2-(\sum_\limits{i=1}^mx^{(i)})^2} \tag{2.4}对于图 1 中的例子,代入公式进行计算,得: \theta_0 = 3.5, \theta_1=1.4,J(\theta) = 4.2 。
最小二乘法在解决实际问题中的应用

最小二乘法在解决实际问题中的应用摘要最小二乘法是从拟合方面入手,多用于参数估计系统检测等多个地方。
然而,最小二乘法通常由于其抽象而无法准确理解。
在本文中,讨论了最小二乘法的基本原理及其各种拟合方法,这其中有:一元线性的最小二乘法拟合,多元的线性拟合,多项式的拟合,非线性的拟合和可转化成为线性拟合的非线性拟合。
关键词:数据拟合;数学工具;分析应用;误差项;层次分析法AbstractThe least squares method is used to estimate or identify the regression model from the perspective of error fitting. It is widely used in many fields such as parameter estimation, system identification and forecasting and forecasting. However, the least squares method is usually not easily understood due to its abstraction. In this paper, the basic principle of least squares method and its various fitting methods are discussed. There are one linear linear least squares fitting, multiple linear fitting, polynomial fitting, nonlinear fitting and Can be transformed into linear fitting of linear fitting, and the application of least squares method in practice is shown by examples. On this basis, the design principle of several least squares procedures is given.Keywords: Least square method; Weighted least square method; Linear fitting; Curve fitting ;Application example目录TOC \o "1-3" \h \z \u 摘要IAbstract II目录III1引言11.1研究意义与现状:11.2最小二乘法的定义:21.3主要性质和定理21.4最小二乘法的优点和缺点22运用22.1 曲线性拟合22.1.1一元线性拟合22.1.2多元线性拟合52.1.3指数函数拟合52.1.4 非线性最小二乘法拟合62.1.5 可化为线性拟合的非线性拟合 72.2 加权最小二乘法82.2.1加权最小二乘法定义82.2.2加权最小二乘法原理82.3一元线性拟合实例92.4用最小二乘法分析国民经济的增长趋势112.4.1.问题背景112.4.2大致数据112.4.3问题求解112.5武器装备批量生产成本费用研究12总结14参考文献16谢辞181引言最小二乘法第一次出现的时间是1805年,天文学家勒让德是出书的人,而且附录里边是计算彗星的轨道的新方法,并且它作为计算方法,它也处于应用数学的初级阶段。
计算方法

计算方法(09秋模拟试题1)一、 单项选择题(每小题5分,共15分)1.通过点),(00y x ,),(11y x 的拉格朗日插值基函数)(00x l ,)(11x l满足性质( ).A .1)(00=x l ,1)(11=x l B. 0)(00=x l ,0)(11=x lC .0)(00=x l ,1)(11=x l D. 0)(00=x l ,0)(11=x l2.若T X )3,0,4(-=,则=2X ( ).A. 4B. 5C. 7D. 93. 求积公式:)32(43)0(41d )(10f f x x f +=⎰的代数精度为( ). A. 0 B. 1 C. 2 D. 3二、填空题(每小题5分,共15分)1.近似值21003012.0⨯的准确位数是 .2. 用辛卜生公式计算积分≈⎰21xdx . 3.求实对称矩阵全部特征值和特征向量的变换方法是 .三、计算题(每小题15分 ,共60分)1. 用紧凑格式解方程组⎪⎩⎪⎨⎧=+-=+-=--1322123121321x x x x x x x . 2. 用高斯—塞德尔迭代法解方程组⎪⎩⎪⎨⎧=++=++=++45725245321321321x x x x x x x x x取初始值T X )0,0,0()0(=,求出)1(X3.用切线法求方程0253=+-x x 的最小正根.(求出1x 即可)4.用预估-校正法求初值问题:⎩⎨⎧=='1)0(2y y y ,在2.0)1.0(0=x 处的数值解.四、证明题(本题10分)设),,1,0()(n k x l k =为n 次插值基函数,证明 )5(,)(505≥=∑=n x x x l nk kk 计算方法(09秋模拟试题1)参考答案一、单项选择题(每小题5分,共15分)1.A 2. B 3. C二、填空题(每小题5分,共15分)1. 310-2. 3625 3.雅可比法 三、计算题(每题15分,共60分)1.解:方程组的系数矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=301021112A ,对系数矩阵直接分解得: ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡---⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=372123112131211211301021112A 8分 解方程b LY = 即解⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡---121131211211321y y y ,得 T Y )37,25,1(= 再解方程Y RX = 即解⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡---37251372123112321x x x ,得T X )1,2,2(= 15分 2.解:因为系数矩阵A 为严格对角占优矩阵,所以高斯-塞德尔迭代法收敛。
