CDI相干衍射成像综述报告 PPT
被散射介质遮挡目标的相干衍射成像实验

第32卷第5期大学物理实验Vol.32No.52019年10月PHYSICALEXPERIMENTOFCOLLEGEOct.2019收稿日期:2019 ̄05 ̄02文章编号:1007 ̄2934(2019)05 ̄0024 ̄05被散射介质遮挡目标的相干衍射成像实验李英威ꎬ唐武盛ꎬ周奇功ꎬ史皓太ꎬ李修建(国防科技大学ꎬ湖南长沙㊀410000)摘要:激光照明条件下ꎬ可以利用相干衍射成像方法重建被照明物体的清晰图像ꎮ按照传统方法ꎬ若物体被散射介质遮挡ꎬ则需要提前标定或者引入全息实验中使用的参考光才能重建清晰的图像ꎮ我们提出了一种线性模型ꎬ即使存在散射层的干扰ꎬ仍旧能够通过实验获得的功率谱重建被遮挡物体ꎬ而无需预先标定ꎮ实验结果表明ꎬ该方法利用傅立叶变换的精确功率谱图像可以快速收敛至唯一正确的重构解ꎬ重建隐藏物体的清晰图像ꎮ关键词:散射介质ꎻ相干衍射ꎻ光学成像ꎻ功率谱图像中图分类号:O312.2文献标志码:ADOI:10.14139/j.cnki.cn22 ̄1228.2019.05.007透过散射介质直接获取目标物体的形状和结构信息一直是光学成像领域重要的研究课题ꎬ比如光学相干断层扫描技术㊁纳米成像技术和水下成像技术[1 ̄3]ꎮ诸如生物组织等不透明的强散射介质ꎬ位于其后面的目标物体由于介质的不规则扩散而失去重要的空间信息ꎮ虽然最近的研究已经成功实现了被隐藏物体的非侵入式成像ꎬ但这些方法需要角度扫描ꎬ依赖精确的电流镜控制技术[4]ꎬ或者需要额外的参考光以及旋转的磨砂玻璃[5]ꎬ这无疑增加了实际操作的复杂性ꎮ在非相干光照明条件下ꎬ被遮挡物体可以通过单次散斑实验进行图像重建ꎬ但缺失的空间信息会造成重构解的不唯一ꎬ降低成像的分辨率ꎮ为了改善这种情况ꎬ往往需要额外的标定步骤[6]ꎮ相干衍射成像(CDI)是一种新型的无透镜成像技术ꎬ已成功应用于光学测量㊁显微成像和自适应光学[7]ꎮ它克服了传统光学成像的一些缺点ꎬ例如高质量镜头一般成本较高ꎬ系统衍射极限造成的低分辨率等问题ꎮ相干衍射成像的优点主要在于简洁的实验光路和计算成像的成本优势ꎬ利用该成像方法实现隐藏物体的图像重建是一个值得尝试的思路ꎮ我们借助相干衍射实验平台ꎬ仅使用一幅被散射介质所遮挡物体的功率谱图像ꎬ去重建物体的形状和结构信息ꎮ国内对于散射成像的研究处于起步阶段[8]ꎬ将散射成像与相干衍射相结合的研究也只处于理论与仿真阶段ꎬ这个实验尝试非常有意义ꎮ本文在傅立叶光学成像光路中加入磨砂玻璃当作遮挡物体的散射介质ꎬ通过相干衍射成像实验得到频谱图ꎬ利用该频谱图重建分辨率板上的数字目标ꎮ1㊀实验原理如图1(a)所示的设置ꎬ我们搭建了相干衍射成像实验光路ꎮ氦氖激光器(波长λ=632.8nm)经过准直放大(C ̄E器件)后照亮物体(USAF1951负分辨率板上的数字 4 )ꎮ在离物体d=15mm的距离处放置不透明的散射层(DG10 ̄220 ̄MDThorlabs)ꎮ然后我们按顺序放置标准傅立叶变换镜头(焦距f=250mm)和CCD传感器(480ˑ480像素ꎬMantaG ̄033BASGꎬAlliedVision)ꎬ物体和传感器分别置于镜头的前后焦平面上ꎮ如果探测器直接拍摄被隐藏的物体ꎬ如图1(b)所示ꎬ并不能获得物体的空间信息ꎬ因此物体的形状和结构信息无法直接识别观察ꎮ为了获得隐藏在不透明散射层后面的物体的形状和结构信息ꎬ我们可以建立以下模型[9](仅考虑二维重建)ꎮ在线性空间不变系统中ꎬ由于散射层对物体的扩散ꎬ物体在磨砂玻璃后平面上的散斑图案显示ꎬ相当于磨砂玻璃可以被视为没有吸收的相位调制器ꎬ它引入了一个额外的空间随机相位ꎮ图1 相干衍射成像实验光路我们假设来自物体的光束ꎬ即物体光束ꎬ在磨砂玻璃的前平面上表示为u(xꎬy)ꎬ随机相位是φ(xꎬy)ꎮ当物体光束通过磨砂玻璃传输时ꎬ磨砂玻璃后平面上的光场ud(xꎬy)由(1)式表达:ud(xꎬy)=u(xꎬy)exp[iφ(xꎬy)](1)当傅立叶变换透镜放置在磨砂玻璃后时ꎬ放置在傅立叶透镜焦面上的CCD传感器将以强度的形式采集被遮挡物体的夫琅禾费衍射图ꎬ可以表示为uf(uꎬv)=expjk1-l/f()u2+v2()/2f[]jλfˑ∬ud(xꎬy)P(xꎬy)exp[-j2πλf(xu+yv)]dxdy(2)光瞳函数P在此处已包含在光学成像系统的点扩散函数(PSF)h中ꎮ对于磨砂玻璃位于傅立叶透镜前焦平面的情况ꎬ公式(2)可以改写为:uf(uꎬv)=1jλfˑ∬ud(xꎬy)h(u-xꎬv-y)dxdy(3)一般来说ꎬCCD传感器收集光场的强度分布ꎬ即物体经过傅立叶变换后的功率谱ꎮ通过将公式(1)和公式(3)相结合ꎬ我们可以用公式(4)表示收集到的功率谱:I(uꎬv)=Cᶄ∬∬u(x1ꎬy1)u∗(x2ꎬy2)exp[iφ(x1ꎬy1)]exp[-iφ(x2ꎬy2)]ˑh(u-x1ꎬv-y1)h∗(u-x2ꎬv-y2)dx1dy1dx2dy2(4)其中ꎬC 是常数系数ꎮ由于傅立叶变换透镜的孔径远远大于物体尺寸ꎬ因此可以忽略衍射有限成像透镜的增益损失ꎬ从而保证了CCD传感器可以主要采集功率谱ꎮ根据OriKatz等人理论研究成果[2]ꎬ在这里多像素CCD传感器捕获的单射图像可以看作是光强的时间平均ꎬ如公式(5) ̄(7)所示:I(uꎬv)=TʏT/2-T/2∬∬u(x1ꎬy1)u∗(x2ꎬy2)exp[iφ(x1ꎬy1ꎬt)]exp[-iφ(x2ꎬy2ꎬt)]ˑh(u-x1ꎬv-y1)h∗(u-x2ꎬv-y2)dx1dy1dx2dy2dt(5)I(uꎬv)=Cᶄ∬∬u(x1ꎬy1)u∗(x2ꎬy2)ˑh(u-x1ꎬv-y1)h∗(u-x2ꎬv-y2)ˑ1TʏT/2-T/2exp[iφ(x1ꎬy1ꎬt)]exp[-iφ(x2ꎬy2ꎬt)]dt{}dx1dy1dx2dy2(6)I(uꎬv)=Cᶄ∬∬u(x1ꎬy1)u∗(x2ꎬy2)ˑh(u-x1ꎬv-y1)h∗(u-x2ꎬv-y2)ˑexp[iφ(x1ꎬy1ꎬt)]exp[-iφ(x2ꎬy2ꎬt)]dx1dy1dx2dy2(7)52被散射介质遮挡目标的相干衍射成像实验由于散射介质粒子(即磨砂玻璃上颗粒)的平均直径ꎬ比物体尺寸小得多ꎬ因此在实验中可认为不透明散射介质层统计均匀ꎬ这将有助于简化图像重建过程ꎮ记忆效应表明ꎬ通过散射介质的小角度改变的入射光不会改变产生的散斑图案ꎬ即在平面波照明下ꎬ记忆效果意味着物体上相近的点发出的光通过扩散介质散射后会产在相机上发生偏移且高度相关的随机散斑图案ꎮ这里物体的大小大约是几毫米ꎬ磨砂玻璃的平均自由传输路径很小ꎬ这将满足记忆效应要求的数值范围ꎮ基于此事实ꎬ我们认为拍摄一幅频谱图相当于多次拍摄的空间平均:exp[iφ(x1ꎬy1ꎬt)]exp[-iφ(x2ꎬy2ꎬt)]=δ(x1-x2ꎬy1-y2)(8)因此ꎬ根据公式(7)和公式(8)ꎬ我们设置了x=x1=x2和y=y1=y2ꎬ通过以下方式得到CCD捕获的功率谱图像的强度:I(uꎬv)=Cᶄ∬|u(xꎬy)|2ˑ|h(u-xꎬv-y)|2dxdy(9)根据自相关定理ꎬ我们可以得到F(I)=CᶄF[|u|2]F[|h|2](10)在实验中ꎬ物体尺寸足够小ꎮ在相干平面波照射下ꎬh的自相关结果是一种δ函数ꎬ因此h的傅里叶变换是常数ꎬ结合傅立叶变换的唯一可逆性ꎬ我们可以得到理想功率谱与实际功率谱之间的线性关系:I=Cᵡ|F[o]|2(11)根据这个线性模型ꎬ传感器收集模糊物体的功率谱强度ꎬ作为相干衍射成像算法所需的原始数据可直接用于重建ꎮ算法结束的标志是测量和计算的傅里叶模数之间的差异收敛到指定的误差ꎬ这意味着通过重建获得的物体强度和相位分布已经非常接近真实物体ꎮ2㊀实验过程和结果传感器收集的结果如图2(b)所示ꎬ实验过程中我们还收集了没有放置散射层时的衍射强度图ꎬ如图2(a)所示ꎮ可以看出ꎬ尽管散射层的引入导致了功率谱中随机斑点分布的增加ꎬ但表征物体细节特征的衍射尖峰仍然很明显ꎬ只不过背景存在更多的随机班点ꎬ这证明了我们的线性模型是正确的ꎮ为了提高显示的清晰度ꎬ我们延长了曝光时间ꎬ而实际用于重建的图像曝光时间要短得多ꎮ图2 传感器收集的实验结果基于测量强度ꎬ我们在普通笔记本电脑(华硕N75s㊁英特尔(R)酷睿I7 ̄2670qmcpu㊁16Gram)上使用Matlab(MATLABr2014a)程序执行重建过程ꎮ重建结果如图3所示ꎮ图3(a)显示了遮挡前直接拍摄的物体的图像ꎮ如果我们直接使用单反相机拍摄遮挡物体ꎬ其空间信息是完全无法获知的ꎬ如图3(b)所示ꎮ62被散射介质遮挡目标的相干衍射成像实验图3㊀重建图像与隐藏物体的比较图3(c)显示了用相干衍射成像方法将隐藏在不透明散射层后面的物体的重建结果ꎮ该过程中使用的唯一测量数据来自图2(b)ꎬ即单幅功率谱图像ꎮ在进行算法重构的时候ꎬ我们应用了一次简单的中值滤波ꎬ这极大地增强了频谱的应用效率ꎮ我们重建的数字 4 已经可以体现分辨率板上的数字的字体和细节特征ꎮ可以看出ꎬ相干衍射成像方法可以直接获取隐藏在不透明散射层后面的物体的形状和结构信息ꎮ图4㊀传感器收集的实验功率谱模式在重建过程中ꎬ算法会迅速收敛到唯一正确的解ꎮ实验结果显示了唯一清晰的重建物体ꎬ并未出现相干衍射成像算法中经常出现的孪生像等解模糊等现象ꎮ如果我们不使用标准的傅立叶变换频谱图ꎬ例如使用非标准傅立叶透镜(图4(a))或将CCD放在非焦点平面上(图4(b))ꎬ重建结果(数字 5 )72被散射介质遮挡目标的相干衍射成像实验82被散射介质遮挡目标的相干衍射成像实验将会出现严重的解模糊现象ꎬ如图4(c)和图4(d)所示ꎮ对比之下ꎬ利用标准傅立叶透镜ꎬ可以直接重建清晰的物体图像ꎮ需要注意的是ꎬ在重建算法中ꎬ我们对原始数据进行了简单的预处理ꎬ以减少背景噪声ꎬ这也有助于保证物体重构解的唯一性ꎮ3㊀结㊀论通过使用简洁的光学设置和CDI算法ꎬ我们在实验上实现了在相干光照明条件下隐藏在不透明散射层后面的目标物体重建ꎮ利用标准傅立叶变换透镜和单幅功率谱图ꎬ可以获得完全模糊物体的相关信息ꎬ并且重建出唯一的清晰的物体图像ꎮ这对于人体组织的病理检查和不适合直接观察的物体检测具有重要的意义ꎮ参考文献:[1]㊀RamachandranꎬH.ꎬImagingthroughturbidmediaꎬCurrentenceꎬ1999ꎬ76(10):1334 ̄1340.[2]㊀KatzꎬO.ꎬHeidmannꎬP.ꎬFinkꎬM.andGiganꎬS.ꎬNon ̄invasivesingle ̄shotimagingthroughscatteringlayersandaroundcor ̄nersviaspecklecorrelationsꎬNat.Photonicsꎬ2014ꎬ8(10):784 ̄790.[3]㊀NagarꎬH.ꎬDekelꎬE.ꎬKasimovꎬD.andRoichmanY.ꎬNon ̄diffractingbeamsforlabel ̄freeimagingthroughturbidmediaꎬOpt.Lettꎬ2018ꎬ43(2):190.[4]㊀BertolottiꎬJ.ꎬPuttenꎬE.G.V.ꎬBlumꎬC.ꎬLagendijkꎬA.ꎬVosꎬW.L.andMoskꎬA.P.ꎬNon ̄invasiveimagingthroughopaquescatteringlayersꎬNatureꎬ2012ꎬ491(7423):232.[5]㊀SinghꎬA.K.ꎬNaikꎬD.N.ꎬPedriniꎬG.ꎬTakedaꎬM.andOstenW.ꎬLookingthroughadiffuserandaroundanopaquesurface:aholographicapproachꎬOpt.Expressꎬ2014ꎬ22(7):7694 ̄701.[6]㊀MildenhallꎬB.ꎬBostanꎬE.ꎬKuoꎬG.ꎬAntipaꎬN.ꎬHeckelꎬR.andWallerL.ꎬDiffuserCam:lenslesssingle ̄exposure3DimagingꎬOpticaꎬ2018ꎬ5(1):1 ̄9.[7]㊀SzameitꎬA.ꎬShechtmanꎬY.ꎬOsherovichꎬE.ꎬBulkichꎬE.ꎬandSidorenkoꎬP.ꎬDanaꎬH.ꎬSteinerꎬS.ꎬKleyꎬE.B.ꎬGazitꎬS.ꎬCo ̄hen ̄HyamsꎬT.ShohamꎬS.ꎬZibulevskyꎬM.ꎬYavnehꎬI.ꎬEldarꎬY.C.ꎬCohenꎬO.andSegevꎬM.ꎬSparsity ̄basedsingle ̄shotsubwavelengthcoherentdiffractiveimagingꎬNat.Materꎬ2012ꎬ11(5):455.[8]㊀吴腾飞.基于光学记忆效应的非侵入式散射成像方法研究ꎬ西安电子科技大学ꎬ博士论文ꎬ2018.[9]㊀WushengTangꎬJiankunYangꎬWenjunYiꎬQianwenNieꎬJuboZhuꎬMengjunZhuꎬYanfangGuoꎬMengzhuLiꎬXiujianLiꎬandWeiWangꎬ Single ̄shotcoherentpower ̄spectrumimagingofobjectshiddenbyopaquescatteringmedia ꎬAppliedOpticsꎬ2019ꎬ58(4):1033 ̄1039.ExperimentalCoherentDiffractiveImagingofObjectsHiddenbyScatteringMediumLIYingweiꎬTANGWushengꎬZHOUQigongꎬSHIHaotaiꎬLIXiujian(NationalUniversityofDefenseandTechnologyꎬChangsha410000ꎬChina)Abstract:Undertheconditionoflaserilluminationꎬtheclearimageofilluminatedobjectcanbereconstructedbycoherentdiffractionimagingmethod.Accordingtothetraditionalmethodꎬifanobjectisobscuredbyascat ̄teringmediumꎬthereferencelightusedintheholographicexperimentneedstobecalibratedorintroducedinadvancetoreconstructtheclearimage.Weproposealinearmodelthatꎬevenwiththeinterferenceofthescat ̄teringlayerꎬcanstillreconstructtheoccludedobjectbythepowerspectrumobtainedexperimentallyꎬwithouttheneedforpre ̄calibration.ExperimentalresultsshowthatthismethodcanquicklyconvergetotheonlycorrectreconstructionsolutionbyusingtheprecisepowerspectrumimageofFouriertransformꎬandreconstructtheclearimageofthehiddenobject.Keywords:scatteringmediumꎻcoherentdiffractionꎻopticalimagingꎻpowerspectrumimage。
光的衍射现象PPT课件

(1)n1
An (P0 )]
1 2
Ak1(P0 )
(1)n1 An (P0 )
故,无论k是奇是偶,中心总是亮的
半波带法解释了圆孔、圆屏衍射的一些主要特征
第27页/共79页
3、 矢量图解法
若圆孔内包含的不是整数个半波带,则需要对每个半波 带进一步细化分。
对于第一个半波带
Nm M1
N2
N1
o
b
P0
第39页/共79页
它们是振幅相等的次波源,向多个方向发出次波。由于
接收屏位于L2的像方焦面上,角度 相同的衍射线会
聚于同一点 P
设入射光与光轴平行,则在波面AB上无位相差,单 缝上下边缘A、B到 P 的衍射线间的光程差为
L BN
设缝宽为a,则
L asin
如何求振动的合成?
第40页/共79页
(1)矢量图解法:
f (n ) 0,从而An 0
A(P0 )
1 2
A1 ( P0
)
自由传播时整个波前在 P0 产生的振幅是第一个半波带的效果之半
第25页/共79页
2)圆孔衍射: 当孔的大小刚好等于第一个半波带时, A(P0 ) A1(P0 ),即中心是亮点 若孔中包含两个半波带时, A(P0 ) A1(P0 ) A2 (P0 ) 0,即中心是暗点
由A点作一系列等长的 小矢量首尾相接,逐个 转过一个相同的角度, 最后到达B点。
C
R
B
R
A
共转过的角度为:
A
2 L 2 a sin
A 单缝衍射的矢量图解
A0
A:波前S对P处振动的贡献,取S 0,则小矢量 A连成的
折线化为圆弧,弧中心为C点,半径为R,圆心角为2
大学物理光的衍射ppt
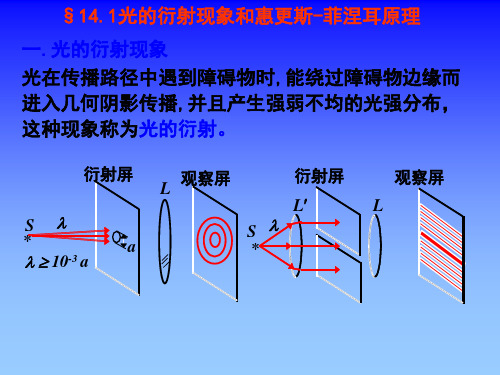
=90°→ kmax
a b
E
于是 kmax=d /l=10
p
缺级:
k d k 4k 4,8 a
o 屏上实际呈现: 0,±1,±2,±3,±5,±6, ±7,±9共8级,15条亮纹(±10在 无穷远处,看不见)。
f
例:一光栅的光栅常数d=2.1×10-6m,透光缝宽a=0.7×10-6, 用波长l=5000Å的光、以i=30°的入射角照射,求能看见几级、 几条谱线。
§14.1光的衍射现象和惠更斯-菲涅耳原理
一.光的衍射现象 光在传播路径中遇到障碍物时,能绕过障碍物边缘而 进入几何阴影传播,并且产生强弱不均的光强分布, 这种现象称为光的衍射。
衍射屏
Sl
*
a
l10-3 a
观察屏 L
衍射屏
L
Sl
*
观察屏 L
二.惠更斯-菲涅耳原理
惠更斯原理:媒质中波所传到的各点都可看作是发射子波的波
例:(1)b=a, d=a+b=2a,则 k=2k =±2,4,6,…级缺。
(2)b=2a, d=a+b=3a, 则 k=3k =±3,6,9,…级缺。
讨论d和l 对衍射图样的影响
d sin kl (k 0,1,2,)
k 1,
s in k 1
sink
l
d
光栅常数越小,明纹越窄,明纹间相隔越远.
2
a sinθ (2k 1) l 亮纹 (k=1,2,3,…)
2
θ 0 零级(中央)亮纹
波带数
S
*
A
a
C B
p
注意:
1.k=1...
2.明暗…
o
3. ...
4.波带数
CDI相干衍射成像综述报告 PPT
针对成像时间长的问题。2013年刘诚提出用光栅分光法实现PIE的单次曝光 PIE方法。基本思路是通过一个正交光栅将入射光分为衍射方向不同的子光 束照明样品,并用CCD同时记录多个衍射光斑。
成像误差函数
经过800次迭代后 误差变为0.007
标准ptychography是分段扫描,在获取数据之前,需要样品移动完成并且 固定在指定位子。这个分段扫描花费的时间步进电机每个像素100ms,压电 马达每个像素20ms,最终整个数据获取会积累成一个很大的数字。
飞扫(Fly-scan ptychography)
扫描轨迹:
为了解决以上问题,2004年Rodenburg提出了可扩展成像范围的相位恢复技术—— PIE技术(Ptychographical Iterative Engine)。
PIE是一种结合横向扫描的数据记录和重建方法。该方法对待测物体用相干照明光 进行阵列扫描,同时记录各个位置的衍射光斑,保证相邻位置直接有一定的重叠 部分,重叠部分的数据含有干涉效应的应用,所以收敛速度和成像质量都得到质 的提高。
对CCD探测衍射强度的反傅里叶变换为样品电子密度的自相关函数。所 得
结果尺寸为样品各维度的2倍。
过采样理论
相位恢复
迭代算法
G-S迭代算法 HIO算法 GHIO算法 ER算法
a:Nyquist频率取样的衍射图样 b:对应a图的实空间样品 c:4倍Nyquist频率取样的衍射图样 d:对应C图的实空间样品
成像系统中由于使用了直射光遮光板,会导致中心数据丢失,需要使用 STXM的成像结果来补充
平面波CDI成像:原理简 单,对设备稳定性要求 较低。样品必须处于光 束范围内,限制了样品 尺寸
菲涅尔CDI成像:光路系 统中不需要直射光遮光器, 相位恢复和重建收敛速度 快,样品尺寸不受限制。 对设备稳定性要求高,对 震动敏感。
光的衍射ppt

02
光的衍射理论
惠更斯-菲涅尔原理
波前相干叠加
惠更斯-菲涅尔原理是波动光学中的一个重要原理,它基于波前的相干叠加, 即波前的每一点都可以视为一个独立的子波源,这些子波源发出的子波在空 间某点处相互叠加,形成该点的总波幅。
波前干涉
当两个或多个波源的波前在空间某点相遇时,它们会相互叠加并产生干涉现 象。干涉现象表现为波前的加强或减弱,从而形成明暗相间的条纹。
衍射的分类
菲涅尔衍射
当光通过一个具有有限大小的孔或狭缝时,会发生菲涅尔衍射。菲涅尔衍射的明 暗条纹是交替出现的,且条纹间距与孔径大小有关。
夫琅禾费衍射
当光通过一个具有无限小的孔或狭缝时,会发生夫琅禾费衍射。夫琅禾费衍射的 明暗条纹是连续分布的,且条纹间距与波长和孔径大小有关。
影响衍射的因素
孔径大小
03
光的衍射实验
实验目的
探究光的波动性质
通过观察和实验,了解光的衍射现象和特点,验证光的波动性。
学习基本实验技能
通过实验操作,掌握基本的光学实验技能,如调节光学系统、观察和记录实验现象等。
了解现象背后的原理
探究光的衍射现象的原理,了解光的波动光学的基本理论。
实验原理01衍射现象 Nhomakorabea当光通过具有与波长相当的空间时,光会出现散射和传播方向的改变
光的衍射现象举例
阳光照射到树叶缝隙时,产生的衍射现象形成光斑。 在全息照相中,利用光的衍射现象可以记录并再现物体的三维图像。
光的衍射的物理意义
衍射现象是光的波 动性的表现之一。
光的衍射现象在光 学仪器、信息处理 和通信等领域有广 泛应用。
光的衍射现象说明 光具有波动性和粒 子性,是物理学中 基本概念之一。
衍射及成像原理-图文

(4) 滑移面: b: (xj, yj, zj) –> (-xj, 1/2+yj, -zj),对于(hk0),k = 2n
衍射及成像原理_图文.ppt
2. 单原子散射
与时间无关的薛定谔方程
E1、 = Ekin + V总能量。解是粒子的状态。 对于平面波(点光源的波阵面(等相位面)为球面形,距离远,近 似为平面波,V = 常数)的单原子散射,其解为: = A exp(2pik.r) ,其中 r为wavefront上的一点,k是波矢(波矢空间或倒易空间,IkI = 1/l = (2m0e(E-V)/h2 ) 1/2 = (2m0eEkin/h2 ) 1/2 )
S – S0
k q
k0
S0
k – k0 = K
q
S (hkl)
3.5 单胞散射
单胞内所有原子散射波的总和,振幅正比于
F(q) = Sfj(q) exp[-2pi(k – k0).rj],结构因子
k – k0 = K
k
k0
q
ra
3.6 完整晶体散射
fg=S Fn exp[-2piK.rn],其中Fn是第n个单胞的散射因子 ,rn =n1a+n2b+n3c是第n个单胞的位置,K是倒易矢量 当K.rn=m时产生衍射,即K 为倒易点阵结点位置 = g = h a* + k b* + l c*
同理,三维情形:
a (cos a – cosa0) = h.l, 等效于: a (H2A1 – A2H1) = h.l
= a (S – S0),S、S0为单位矢量。 LAUE方程
光的衍射课件PPT课件课件

C.衍射条纹的疏密程度与狭缝宽度有关 D.衍射条纹的间距与光的波【长A有CD关】
第14页,此课件共38页哦
练习3:观察实验回答下列问题
1.在观察光的衍射现象的实验中,通过紧
靠眼睛的卡尺测脚形成的狭缝,观看远处
的日光灯管或线状白炽灯丝(灯管或灯丝
都要平行于狭缝),可以看到
A.黑白相间的直条纹 B.黑白相间的弧形条纹
5 、关于衍射下列说法正确的是
ABD
A.衍射现象中衍射花样有亮暗条纹的出现是光的叠加
的结果
B.双缝干涉中也存在着光的衍射现象
C.影的存在是一个与衍射现象相矛盾的客观事实
D.一切波都可以产生衍射
第33页,此课件共38页哦
6 、用点燃的蜡烛照亮一个带有圆孔的遮光板,当圆孔的直
径由数厘米逐渐减小为零的过程中,位于遮光板后面的屏上将依
关于光的衍射课件PPT课件
第1页,此课件共38页哦
复习提问
问题1.什么是波的衍射现象?
问题2.发生明显衍பைடு நூலகம்的条件是什么?
障碍物或孔的尺寸跟波长差不多或比波长小。
第2页,此课件共38页哦
光的衍射
光的干涉现象反映了光的波动性,而波动性的 另一特征是波的衍射现象,光是否具有衍射现象 呢?如果有衍射现象,为什么在日常生活中我们 没有观察到光的衍射现象呢?
中央亮纹越宽
第10页,此课件共38页哦
光的衍射
一、单缝衍射
1 衍射图样:明暗相间且不等距条纹 2
1)波长一定时,单缝越窄,中央条纹越宽,各条纹间距越大.
2)单缝不变时,波长大的中央亮纹越宽,条纹间隔越大
3)白光的单缝衍射条纹为中央亮,两侧为彩色条纹,
且外侧呈红色,靠近光源的内侧为紫色.
相干衍射成像--高次谐波的应用讲解

毕业论文题目:衍射成像——高次谐波的应用学院:物理与电子工程学院专业:物理学毕业年限:2015年学生姓名:杜宁学号:201172010307指导教师:王国利目录摘要 (1)一、引言 (2)二、高次谐波的发射 (3)2.1高次谐波的发射机制 (3)2.2高次谐波的特点及应用 (4)三、实验机制 (5)四、结果与讨论 (6)4.1光源的产生 (6)4.2光源的空间相干性 (7)4.3衍射图像的采集 (8)五、图像分析 (9)六、总结 (11)七、展望 (11)参考文献 (13)致谢 (15)衍射成像——高次谐波的应用摘要:高次谐波是强激光与原子分子等介质相互作用而产生的一种相干辐射波,其具有从可见光到真空紫外甚至软X 射线光辐射的宽频区域,可以用作一种非常便捷的相干光源。
本文介绍了一个高次谐波在衍射成像中的应用实验。
在相干衍射成像中,用高次谐波作为空间相干光源照射要研究的样品,而被电荷耦合元件CCD (Charge coupled device)照相机所记录的衍射图像通过迭代相位恢复法来重构目标物体。
利用13.5 nm的谐波进行相干衍射成像,其空间分辨率可以达到200 nm。
关键字:高次谐波辐射,迭代相位恢复法,相干衍射成像Diffractive Imaging Using High Order Harmonic Generation Abstract: High order harmonic, which occurs in the interacion between an intense laser pulse and an atomic or molecuar medium, is a coherent radiation wave. High order harmonic can be used as a very convenient coherent light source because it has a broadband range from visible light to vacuum ultraviolet even a soft X-ray soure. In this article, we will introduce an experiment about high order harmonic apply in diffractive imaging. The sample to be investigated is illuminated with high order harmonic and the object is reconstructed from the diffraction pattern recorded on a CCD camera by means of iterative phase retrieval algorithms.A spatial resolution of ~200nm can be achieved if one use harmonic around 13.5nm to proceed the coherent diffractive imaging.Keyword: high order harmonic generation;iterative phase retrieval algorithms;coherent diffractive imaging一、引言相干衍射成像(Coherent diffractive imaging,CDI)是一种不需要光学元件(比如透镜组)来获得放大图像的成像技术[1-6]。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
扫描CDI成像:图像重建 的收敛速度更快,重建结 果更好,样品尺寸不受限 制。对设备稳定性要求较 高,样品的震动对成像结 果影响明显。
BraggCDI成像:主要用 于研究纳米晶体。
大家应该也有点累了,稍作休息
大家有疑问的,可以询问和交流
对于CDI成像,根据夫琅禾费近似条件,样品远场处的衍射图样为其电子密 度的傅里叶变换。 而探测器记录的衍射图样只是其强度信息,根据
重叠部分的区域起到了全息成像中参考光的作用,可以确定不同区域之间 的相对相位。
使用上述方法对物体进行成像在技术上有5个问题需要解决。
进行机械扫描时,由于机构的迟滞效应或者回程误差,实际扫描位置难以精确 知晓。
照明光P(r)的强度和相位分布需要精确预知,这对许多实验来说很难实现。
物体的透射光等于照明光和物体透过函数的乘积,前提是物体是一个可以忽略 厚度的二维样品,然而样品都是有厚度的,厚样品更是无法计算。
针对成像时间长的问题。2013年刘诚提出用光栅分光法实现PIE的单次曝光 PIE方法。基本思路是通过一个正交光栅将入射光分为衍射方向不同的子光 束照明样品,并用CCD同时记录多个衍射光斑。
成像误差函数
经过800次迭代后 误差变为0.007
标准ptychography是分段扫描,在获取数据之前,需要样品移动完成并且 固定在指定位子。这个分段扫描花费的时间步进电机每个像素100ms,压电 马达每个像素20ms,最终整个数据获取会积累成一个很大的数字。
为了解决以上问题,2004年Rodenburg提出了可扩展成像范围的相位恢复技术—— PIE技术(Ptychographical Iterative Engine)。
PIE是一种结合横向扫描的数据记录和重建方法。该方法对待测物体用相干照明光 进行阵列扫描,同时记录各个位置的衍射光斑,保证相邻位置直接有一定的重叠 部分,重叠部分的数据含有干涉效应的应用,所以收敛速度和成像质量都得到质 的提高。
飞扫(Fly-scan ptychography)
扫描轨迹:
成像系统中由于使用了直射光遮光板,会导致中心数据丢失,需要使用 STXM的成像结果来补充
平面波CDI成像:原理简 单,对设备稳定性要求 较低。样品必须处于光 束范围内,限制了样品 尺寸
菲涅尔CDI成像:光路系 统中不需要直射光遮光器, 相位恢复和重建收敛速度 快,样品尺寸不受限制。 对设备稳定性要求高,对 震动敏感。
GerchbergSaxton算法
ER和HIO算法都在G-S迭代算法基础上发展而来,区别只是在实空间引入的限定条件不同,二 者引入的是有限尺寸和正密度约束条件
二者的限定条件分别为:
Ptychography/scanning CDI
江琦 6-28
CDI概念在1970左右被提出,相位还原问题是CDI的核心问题,从最早的G-S算法, 到Fineup改进的ER和HIO算法。但是ER和HIO算法都容易陷入局部最优解的陷阱, 且传统CDI视场小,限制了样品尺寸。
对CCD探测衍射强度的反傅里叶变换为样品电子密度的自相关函数。所 得
结果尺寸为样品各维度的2倍。
过采样理论
相位恢复
迭代算法
G-S迭代算法 HIO算法 GHIO算法 ER算法
a:Nyquist频率取样的衍射图样 b:对应a图的实空间样品 c:4倍Nyquist频率取样的衍射图样 d:对应C图的实空间样品
1980年,sayre指出非周期性独立样品的相干衍射图样是连续的,不受 bragg衍射斑的限制,可以获得足够的信息,X射线晶体学的衍射理论同样 适用于解析非周期性独立样品的结构。
1999年,miao首次在实验上实现相干衍射成像。高亮度的相干衍射光源是 CDI实验的保证。
目前,CDI在物理学,生物学,材料学方面得到广泛利用。
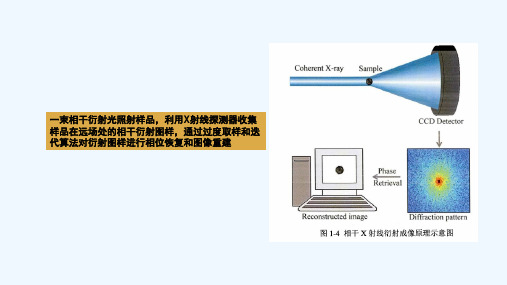
一束相干衍射光照射样品,利用X射线探测器收集 样品在远场处的相干衍射图样,通过过度取样和迭 代算法对衍射图样进行相位恢复和图像重建
相干X射线衍射成像在X射线晶体学的基础上发展而来。
1952年,sayre在shannon晶体采样理论的基础上提出,如果可以记录晶体 bragg衍射斑之间的信号强度,也许会有足够的信息来直接解析晶体的衍射 图样。
对于器材的稳定性和样本的稳定性提出很高要求
飞扫原理:样品沿着快速扫描方向连续的移动,探测器与样本同步移动相 同的距离,运用动态成像ptychography的方法进行处理可以重建样品结构。
飞扫(Fly-scan ptychography)
远场衍射强度是由单色和相干光源照射在静止的样品上,j代表位置,则有: 若是部分相干光源,则把光源看做互相不相干的相干光源的叠加,则有: 若是飞扫模式中,衍射强度来自于一个连续移动的样品,则有:
CDI成像过程不使用任何X射线聚焦元件,摆脱了X射线聚焦元件对于成像分 辨率的限制。
X射线与样品的作用是X射线样品电子的作用,记录的样品衍射图样反映了 样品的电子密度。使得对样品成分的定量分析成为可能。
CDI可以同时提供样品的强度和相位衬度图像,在自然状态下实现高衬度定 量成像。
CDI可以与多种X射线相结合,如X射线近边吸收,X射线荧光技术等,在获 得高分辨图像的同时也可以实现元素的特异性成像。
照明光P(r)入射到分布为O(r)的样品上,r为 待测物体面的坐标。 PIE的成功的关键在相邻扫描位置之间有一定的重 叠,重叠区域起到了参考光的作用,可以对不同 位置之间的相位关系进行锁定。
No Image
Ptyቤተ መጻሕፍቲ ባይዱho来自希腊语“πτυξ”,意思是重叠,所有ptychography又称为重叠关 联成像。
和传统的CDI样品一样,PIE要求光源为完全相干光源,对于X射线和电子束来 说,这个要求很难达到。
PIE算法需要照明光对物体进行阵列扫描,数据记录时间长,因此对光源稳定 性和样品稳定性都有较高要求。如何提高采集速度,甚至实现单次测量是PIE 的研究方向。
(1)针对弱散射样品,pan等人提出一种改进办法,相对位置不再由平移台 控制软件读出,而是在记录光斑分布的同时读出相应的移动距离。缺点是仅 适用于弱散射样品,且对CCD靶面尺寸要求较高。
(2)照明光自动重建。PIE要求照明光P(r)分布精确预知,但是实际使用 中,光学元件和环境扰动导致的波前畸变无法精确预知。
对于有厚度的样品,有人提出3PIE算法,可以解决厚样品的重建问题。
光源相干性的影响及处理。PIE要求光源完全相干,但实验中却发现有时用 相干性不理想的电子束可以得到不错的重构像。
