经验分布函数与直方图共43页

合集下载

经验分布和分布函数

经验分布和分布函数在统计学中，经验分布和分布函数是两个重要的概念。

经验分布是指根据一组观测数据得到的概率分布函数的估计，而分布函数则是用于描述一个随机变量的概率分布的函数。

经验分布是通过对观测数据进行统计分析来估计真实概率分布的方法之一。

在实际应用中，我们通常无法获得全部的数据，而只能通过抽样得到一部分数据。

因此，我们需要通过对抽样数据进行分析来得到总体的概率分布。

经验分布的计算方法很简单，只需要统计抽样数据中每个取值出现的频率即可。

然后将这些频率按照大小顺序累加，就得到了经验分布。

经验分布是对真实分布的一种估计，它可以用来描述抽样数据的分布特征。

分布函数是用来描述一个随机变量的概率分布的函数。

它定义为随机变量小于等于某个特定值的概率。

分布函数通常用大写字母F表示，其数学表达式为F(x) = P(X ≤ x)，其中X表示随机变量，x表示一个实数。

分布函数是概率论中最基本的概念之一，它能够完整地描述一个随机变量的概率分布。

分布函数具有以下性质：1) F(x)是一个非减函数；2) F(x)的取值范围在0到1之间；3) F(x)在x趋于负无穷时趋于0，x趋于正无穷时趋于1。

经验分布和分布函数在统计学中有着广泛的应用。

它们可以用来描述随机变量的分布特征，从而对随机变量进行概率推断和统计推断。

例如，在假设检验中，我们可以通过计算经验分布和分布函数来判断某个假设的可行性。

另外，在参数估计中，我们也可以利用经验分布和分布函数来估计未知参数的值。

此外，经验分布和分布函数还可以用来进行模型拟合和预测，从而对未来的观测数据进行预测和分析。

经验分布和分布函数是统计学中两个重要的概念。

它们可以用来描述随机变量的分布特征，进行参数估计和假设检验。

在实际应用中，我们可以通过对观测数据进行统计分析来计算经验分布和分布函数，从而对随机变量的概率分布进行估计和推断。

经验分布和分布函数的应用范围广泛，对于统计学的研究和实践都具有重要的意义。

1.3 顺序统计量

求 F ( u, v ) ．对于任意 u, v ，有
PX (1) u, X ( n ) v Pu X 1 v,, u X n v Pu X 1 v Pu X n v [ F ( v ) F ( u)]n , 若u v， 0 , 若u v ； F ( u, v ) PX (1 ) u, X ( n ) v PX ( n ) v PX (1 ) u, X ( n ) v [ F (v )]n [ F (v ) F ( u )]n , 若u v， n ，若 u v． [ F (v )]
1.3 顺序统计量
§1.3
顺序统计量、经验分布函数和直方图
一、顺序统计量另一类常见的统计量是顺序统计量. 定义 1 设 X 1 , X 2 ,, X n 是取自总体 X 的样本, X ( i ) 称为该样本的第 i 个顺序统计量，它的取值是将样本观测值由小到大排列后得到的第 i 个观测值。x(1) x( 2 ) x( n ) ，X ( i ) 的值是 x ( i ) 。其中 X (1) minX 1 , X 2 ,, X n 称为该样本的最小顺序统计量，称 X ( n ) maxX 1 , X 2 ,, X n 为该样本的最大顺序统计量。我们知道，在一个样本中， X 1 , X 2 ,, X n 是独立同分布的，而次序统计量 X (1) , X ( 2) ,, X ( n) 则既不独立，分布也不相同，看下例。
假设总体 X 在区间[0,2]上服从均匀分布； Fn ( x )
是总体 X 的经验分布函数，基于来自 X 的容量为 n 的简单随机样本，求 Fn ( x ) 的概率分布，数学期望和方差．解总体 X 的分布函数为

§6.2 经验分布函数和频率直方图PPT课件

河北 8362
浙江 14655
山西 5460
安徽 5221
内蒙古 6463
福建 12362
辽宁 12041
江西 5221
吉林 7640
山东 10465
黑龙江 9349
河南 5924
湖北湖南广东广西海南重庆四川贵州 7813 6054 13730 4668 7135 5654 5250 2895
P
fn (x)
p(x)
1
2
E fn (x)
p(x)2
2 2
E fn (x) Efn (x)2 Efn (x) p(x)2
(1)
由于Rn(a,b)~B(n,pk)，其中
pk P
X [tk , tk 1)
tk1 p( y)dy Kh
tk
所以当n
时，E
fn (x)
Efn (x)2
用事件{X<x)发生的频率作为其估计即可。这就引出了下面所谓经验分布函数的概念。
一、经验分布函数设X1,…,Xn是抽自总体X的一个样本，观察值为x1,…,xn，次序观测值x(1)≤ …≤x(n)，则总体X的经验分布函数定义为
Fn
(x)
样本中小于x的观测值的个数 n
，x
R.
即
0,
Fn
(x)
k
0.032258 0.00000516
频率直方图如下图所示：
初步判断数据是来自什么样的总体？这个例子中数据量相对来说比较少，一般情况下数据量最好大于100，分组的个数根据数据量来确定，一般介于[n/10,n/5]之间，最多不能超过20组。
定理6.2.2 密度函数p(x)在点x[t0,tm)处连续，样本容量为n，且

人教版七年级数学下册《利用频数分布直方图描述数据：直方图》PPT

条形图与直方图的异同：
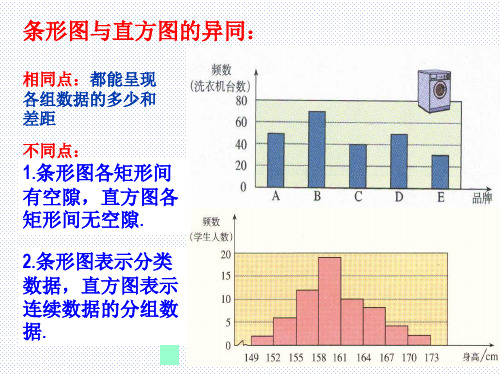
相同点：都能呈现各组数据的多少和差距
不同点：
1.条形图各矩形间有空隙，直方图各矩形间无空隙.
2.条形图表示分类数据，直方图表示连续数据的分组数据.
用表格整理数据
身高 149 151 153 154 155 156 157 158 159 160 161
人数 1 1 3 3 2 5 5 8 7 4 2
要挑出身高相差不多的40名同学参加比赛，我们该怎样挑选呢？
学习目标
了解组距、组数的概念画直方图的步骤学会对数据进行合理的分组处理,通过学习用简单频
数分布直方图描述数据的方法,进一步体会统计图表在描述数据中的作用. 会画简单的频数分布直方图,并利用频数分布直方图解释数据中蕴含的信息。
（不含合1计64 cm）的学生中选队员．
63
4、绘制频数分布直方图
频数（学生人数）
横轴表示身高纵轴表示频数
身高/cm
4、绘制频数分布直方图
频数（学生人数）
20
横轴表示身高纵轴表示频数ຫໍສະໝຸດ 151050
149 152 155 158 161 164 167 170 173
身高/cm
4、绘制频数分布直方图
学生人数
60
理得到如图所示的频数分布 50
直方图，请回答下列问题： 40
（1）此次抽样调查的样本容量是_____
30
28
20 15
10 10 5
0
28 14
0~35 36~47 48~59 60~71 72~83 84~95 96~107 108~120
分数
2003年中考结束后，某市从参加中考的12000名学生中抽

应用数理统计课件(配庄楚强版教材)第二章

（ξ1,ξ2,..,ξn), 则（ξ1,ξ2,…,ξn)的联合分布函
数为： F ( x1 , x2 ,L , xn )
= P { ξ1 < x1 , ξ 2 < x2 , ..., ξ n < xn }
= P { ξ1 < x1}P{ ξ 2 < x2 } ⋅ ... ⋅ P{ ξ n < xn }
（2）χ2 分布（Chi-square distribution）
χ 2 ～χ 2 (n)
{ } p分位点：χ p2 (n ) 满足P
χ
2
<
χ
2 p
(n)
=p
p53（9 347）表 4
χ
2 0.95
(9
)
=
16.91（9
p540)
表p 4 χ2 分布分位数表
n
p
8
9
0 ．90 13．362 14．684
又如：α = 0.1，uα = u0.1 = ? (表中没有)
u0.1 = −u1−0.1 = −u0.9 = −1.282
对称性(symmetricy)：
0.1
uα = −u1−α
α = 0.1
u0.1
u1− 0.1
习题或附表中α通常是指分位点之外的概率（面积）
单侧分位点：α放在分位点u1−α的一侧双侧分位点: α分割放在正负对称的
2 +L +
)
m
1
9
二. t 分布 (t distribution)
Definition: 若ξ～N(0,1), η～χ2(n)且相互独立,
则有
t=
ξ η
～ t (n )

冀教版八年级数学下册《频数分布表与直方图》PPT课件(3篇)

2.在水平射线上，适当分配条形的位置，确定直条的宽度和间隔。
3.在与水平射线垂直的射线上，根据数据的大小情况，确定单位长度的多少，再照根据大小，画出长短不同的直条并注名数量
条形图直方图的区别
1：条形图各矩形间有空隙，直方图各矩形间无空隙
2.直方图的横轴数据是连续的小组的位置是固定的
而条形图不是
全班 40人呦
D小沈 6
频数：每个小组内数据的个数频率﹦ 频数÷总数
某班一次数学测验成绩如下：
63，84，91，53，69，81，61，69，91，78，75，81，80， 67，76，81，79，94，61，69，89，70，70，87，81，86， 90，88，85，67，71，82，87，75，87，95，53，65，74， 77．
你认为原因是什么？
2
15 25 35 45 55 65 75 年龄（岁）
心系灾区
去年6月份以后我国南方强降雨范围继续扩大，雨量增强，部分县市区降雨量达100毫米以上，造成严重洪涝灾害。
（1）降雨量在100毫米以上的有几个县市？36 （2）最需要救助的县市有几个？ 4个
频数
20 16 12 8 4
1、计算最大值与最小值. 在上面的数据中:最小值是149，最大值是172。它们的差是23.说明身高总的变化范围是23.
2、决定组距和组数. 把所有数据分成若干组,每个小组的两个端点之间的
19 男 164 83 89 优
20 女 161 75 77 良
21 男 162 86 97 优
22 男 164 91 91 优
23 女 163 87 82 优
24 男 154 82 88 优
25 男 172 68 70 中

《频数分布表与直方图》PPT课件

直方图是为了把表中的结果直观地表示出来，它
们是频数分布的“数”与“形”的两种不同形式，
互相补充．
（来自《点拨》）
知2－练
1 某学校八年级共有你n名男生. 现测量他们的身高 (单位：cm. 结果精确到1 cm)，依据数据绘制的频数分布直方图如图所示(为了避免有些数据落在分组的界限上，对作为分点的数保留一位小数).
的学生为正常，试求身高正常的学生的百分比．
知2－讲
导引知：先识确点定最大值与最小值的差为180－140＝40(cm)，故可
将数据按组距为5进行分组，可分40÷5＝8(组)．解：(1)计算这组数据的最大值与最小值的差为180－140＝
40(cm)．确定组数与组距，将数据按组距为5进行分组，可分为40÷5＝8(组)，即每个小组的范围分别是140≤x＜ 145，145≤x＜150，150≤x＜155，155≤x＜160，160≤ x＜165，165≤x＜170，170≤x＜175，175≤x≤180. 其中x为学生身高．
C．8组
D．10组
导引：因为这组数据的最大值是187，最小值是140，最大值与最小值的差是47，且 47 7 5 ，所以应 66 分为8组. 答案：C
总结
知1－讲
确定组数的方法：若最大值与最小值的差除以组距所得的商是整数，则这个商即为组数；若最大值与最小值的差除以组距所得的商是小数，则这个商的整数部分＋1即为组数．
知2－讲
知2－讲
例2 某中学部分同学参加全国初中数学竞赛，取得了优异的成
绩，指导老师统计了所有参赛同学的成绩(成绩都是整数，试题满分120分)，并且绘制了如图所示的频数分布直方图 (每组中含最低分数，但不含最高分数)，请回答： (1)该中学参加本次数学竞

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

▪
27、只有把抱怨环境的心情，化为上进的力量，才是成功的保证。——罗曼·罗兰
▪
28、知之者不如好之者，好之者不如乐之者的决心能够抵得上武器的精良。——达·芬奇
▪
30、意志是一个强壮的盲人，倚靠在明眼的跛子肩上。——叔本华
谢谢！
43
经验分布函数与直方图
21、静念园林好，人间良可辞。 22、步步寻往迹，有处特依依。 23、望云惭高鸟，临木愧游鱼。 24、结庐在人境，而无车马喧；问君何能尔？心远地自偏。 25、人生归有道，衣食固其端。
▪
26、要使整个人生都过得舒适、愉快，这是不可能的，因为人类必须具备一种能应付逆境的态度。——卢梭