塑性理论应力应变关系例题
塑性应力应变关系

2 加载条件
单轴情况
f 0, 且 f 0, 且 f 0, 且
多轴情况
f d ij 0时,加载 ij f d ij 0时,中性变载 ij f d《0时,卸载 ij ij
对理想塑性材料,则为
f f 0, and d ij 0 ij f f 0, and d ij 0 ij
5 塑性应力应变关系的推导
有
0
p ii
(塑性体积应变为零)
令
f f n / σ σ
(屈服面外法向单位向量)
f f f f f : σ σ σ ij ij
n :n 1
f d nij σ
p ij
(流动法则)
作为塑性变形的度量,引进等效塑性变形及其增量
加载或中性变载
卸载
f<0 and f>0是什么?
3 强化模型
各向同性强化:假设屈服面均匀膨胀,没有崎 变和移动,此时屈服面可表达为
f ( ij , k ) f ( ij ) k ( ) 0
强化模型实际上表示后继屈服面的变化规律, 即如何随硬化参数而变。强化参数可以取累积 塑性变形。
e d ij
1 1 d ij dsij d kk ij dsij 2G 9K 对刚塑性材料,不计弹性部分,为 d ij dsij 此为Levy Mises方程
d的确定 理想塑性
对理想塑性J 2材料,有 2 2 2 sij sij e2 y (1) 3 3 两边求导,有 2 sij dsij 0 (2) 偏应变增量可写为 1 dsij dsij (3) 2G 上式两边同乘以sij并求和有 deij sij deij 1 sij dsij dsij sij dsij sij 2G ( 4)
塑性理论课件-塑性变形时的应力应变关系

3、如果從初始狀態先加純剪應力通過 屈服點B到達D點,這時的應力和應變見表 5.1的第3行。
4、如同樣經後繼屈服軌跡裏面的任意 路線變載到F點,則應力應變見表5.1第4行。
5、如果從初始狀態沿真線OF`F到達F 點,則應力和應變見表5.1第5行,這時主軸 重合。
下一頁 返回
上述的第1、3、5種加載路線就是簡單加載。 由表中可看出,同樣的一種應力狀態σf、τf,由於 加載路線不同,就有好幾種應變狀態(如C、D點 應變);同樣,一種應變狀態(如εc),也可有 幾種應力狀態(如C、F點應力),而且應力應變 主軸不一定重合。從上述簡單的例子中,我們可 以看到,離開加載路線來建立應力與全量塑性應 變之間的普遍關係是不可能的。因此,一般情況 下只能建立起應力和應變增量之間的關係爭然後 根據具體的加載路線,具休分析。另一方面,我 們從上述例子中也看到,在簡單加載的條件下, 應力和應變的主軸重合,而且它們之間有對應關 係,因此可以建立全量理論。
下一頁 返回
另一方面,從工程角度來看,對於一 些繁雜的問題,那怕是能給出定性結果也 很可貴,具體的定量問題可以從實驗中進 一步探索(由於如摩擦條件等數學模型還 未給出,要精確計算也很難辦到)。鑒於 壓力加工理論中關於成形規律闡述上存在 的一些問題,吸取了增量理論及全量理論 的共同點,提出了應力應變順序對應規律, 並使該規律的闡述逐漸簡明和便於應用。 現簡述如下:
返回
5.2增量理論(流動理論) 一、列維-密席斯方程 二、普朗特-勞斯方程
返回
一、列維-密席斯方程
列維-密席斯方程適用條件:
(1)材料是理想剛塑性材料,即彈性應變增 量為零,塑性應變增量就是總應變增量;
(2)材料符合密席斯屈服準則,即 s
(完整版)弹塑性力学作业(含答案)(1)

第二章 应力理论和应变理论2—3.试求图示单元体斜截面上的σ30°和τ30°(应力单位为MPa )并说明使用材料力学求斜截面应力为公式应用于弹性力学的应力计算时,其符号及正负值应作何修正。
解:在右图示单元体上建立xoy 坐标,则知 σx = -10 σy = -4 τxy = -2 (以上应力符号均按材力的规定)代入材力有关公式得: 代入弹性力学的有关公式得: 己知 σx = -10 σy= -4 τxy = +2由以上计算知,材力与弹力在计算某一斜截面上的应力时,所使用的公式是不同的,所得结果剪应力的正负值不同,但都反映了同一客观实事。
2—6. 悬挂的等直杆在自重W 作用下(如图所示)。
材料比重为γ弹性模量为 E ,横截面面积为A 。
试求离固定端z 处一点C 的应变εz 与杆的总伸长量Δl 。
解:据题意选点如图所示坐标系xoz ,在距下端(原点)为z 处的c 点取一截面考虑下半段杆的平衡得:c 截面的内力:N z =γ·A ·z ;c 截面上的应力:z z N A zz A Aγσγ⋅⋅===⋅;所以离下端为z 处的任意一点c 的线应变εz 为:z z z E Eσγε==;则距下端(原点)为z 的一段杆件在自重作用下,其伸长量为:()22z z z z z z z z y zz l d l d d zd EEEγγγε=⎰⋅∆=⎰⋅=⎰=⎰=ooooV ;显然该杆件的总的伸长量为(也即下端面的位移):()2222ll A l lW ll d l EEAEAγγ⋅⋅⋅⋅⋅=⎰∆===oV ;(W=γAl ) 2—9.己知物体内一点的应力张量为:σij =50030080030003008003001100-⎡⎤⎢⎥+-⎢⎥⎢⎥--⎣⎦应力单位为kg /cm 2 。
试确定外法线为n i(也即三个方向余弦都相等)的微分斜截面上的总应力n P v、正应力σn 及剪应力τn 。
《弹塑性力学》第四章 应力应变关系(本构方程)-精品文档42页

28.09.2019
2
第四章 应力应变关系(本构方程)
共9个方程,但需确定的未知函数共15个:
ui,ij=ji, ij=ji,
还需要根据材料的物理性质来建立应力与 应变间的关系:
ij = ji = fij ( kl )
Wijij
——W为
的函数。
ij
28.09.2019
11
§4-1 应变能、应变能密度与弹性材料的
本构关系
因为W只取决于弹性体的初始应变状态和最 终应变状态,与变形过程(加载路线)无关,
所以W 为它的全微分
W
W
ij
ij
28.09.2019
12
§4-1 应变能、应变能密度与弹性材料的
时刻达到 t +t:位移有增量 uuiei
应变增量 ijeiej 外力功增量:A Vfu d V S F u d S
28.09.2019
8
§4-1 应变能、应变能密度与弹性材料的
A 本构f关u 系d VF u d :函S 数增量
则 [C] 为对称矩阵 [C]= [C]T。
28.09.2019
19
§4-2 线弹性体的本构关系
2.1 各向异性材料 Eijkl 的独立系数为21个——材料为各向
异性线弹性材料。
*对各向异性材料的本构关系可见,剪应 变引起正应力,正应变也产生剪应力。 弹性材料性质一般都具有某些对称性, 利用对称可进一步简化 [C] 中系数。
V
S
Vfiuid V sF iuid SU V Wd
应变能增量A 中有体积分和面积分,利用
弹性与塑性力学基础-第五章屈服准则与塑性应力应变关系

0
m
0 0 m
Uv
1 3 ( m m m m m m ) m m 2 2 1 m ( 1 2 3 ) 3
1 m ( 1 2 3 ) 3
弹性与塑性 力 学 基 础
第五章 屈服准则与塑性应力应变关系
积之和的一半(主坐标系中)
U
1 ( 1 1 2 2 3 3 ) 2
1 0 ij T 0 2 0 0
0 0 3
1 0 ij T 0 2 0 0
0 0 3
弹性与塑性 力 学 基 础
第五章 屈服准则与塑性应力应变关系
§5-2 米塞斯屈服准则
5.2.1 米塞斯屈服准的物理意义 米塞斯屈服准则 5.2.2
由广义虎克定律
1
1 2 [ 2 ( 1 3 )] E 1 3 [ 3 ( 1 2 )] E
式中, 为波桑系数,于是可得
弹性与塑性 力 学 基 础
第五章 屈服准则与塑性应力应变关系
§5-2 米塞斯屈服准则
5.2.1 米塞斯屈服准的物理意义 米塞斯屈服准则 5.2.2
单位体积变化位能Uv确定
取应力球张量及应变球张量
m T0
由此得
0
m
0 0 m
m T0
§5-10 全量理论
5.10.1 问题的背景及引出 5.10.2 亨盖理论(1924年) 5.10.3 那达依理论(1937年) 5.10.4 伊留申理论(1943年) 5.10.5 全量理论的问题与发展
弹性与塑性 力 学 基 础
塑性力学复习题
塑性力学复习题一、填空题1.塑性变形不仅与当前的应力状态有关,还和()有关。
2.对一般金属,体积应变完全是()的,静水压力不产生()。
它对屈服极限的影响()。
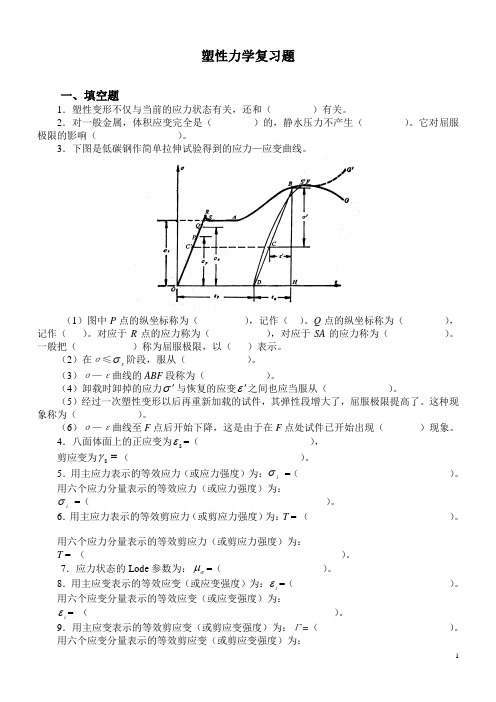
3.下图是低碳钢作简单拉伸试验得到的应力—应变曲线。
(1)图中P点的纵坐标称为(),记作()。
Q点的纵坐标称为(),记作()。
对应于R点的应力称为(),对应于SA的应力称为()。
一般把()称为屈服极限,以()表示。
σ阶段,服从()。
(2)在σ≤s(3)σ—ε曲线的ABF段称为()。
(4)卸载时卸掉的应力σ'与恢复的应变ε'之间也应当服从()。
(5)经过一次塑性变形以后再重新加载的试件,其弹性段增大了,屈服极限提高了。
这种现象称为()。
(6)σ—ε曲线至F点后开始下降,这是由于在F点处试件已开始出现()现象。
ε=(),4.八面体面上的正应变为8γ()。
剪应变为=8σ=()。
5.用主应力表示的等效应力(或应力强度)为:i用六个应力分量表示的等效应力(或应力强度)为:σ=()。
i6.用主应力表示的等效剪应力(或剪应力强度)为:T = ()。
用六个应力分量表示的等效剪应力(或剪应力强度)为:T = ()。
μ=()。
7.应力状态的Lode参数为:σε=()。
8.用主应变表示的等效应变(或应变强度)为:i用六个应变分量表示的等效应变(或应变强度)为:ε= ()。
i9.用主应变表示的等效剪应变(或剪应变强度)为:Γ=()。
用六个应变分量表示的等效剪应变(或剪应变强度)为:Γ=( )。
10.表示应变状态特征的Lode 参数为:εμ=( )。
11.第一应力不变量为:1I =( )=( )。
第二应力不变量为:2I =( )=( )。
第三应力不变量为:3I =( )=( )。
12.第一应变不变量为:1I '=( )=( )。
第二应变不变量为:2I '=( )=( )。
第三应变不变量为:='3I ( )=( )。
13.应力偏张量的第一不变量为:=1J ( )。
第五节塑性成形时应力应变关系-2013年编辑

21
由于加载路线不同,同一种应力状态可以对
应不同的应变状态; 而且应力与应变主轴不一定重合。
同一种应变状态,也可以对应几种应力状态,
因此,一般情况下只能建立起应力和应变增 量之间的关系,仅在简单加载的条件下,应力主
轴与应变主轴重合,才可以建立全量关系。
22
τ D B I
初始屈服轨迹
F ( f , f )
及
x y y z z x xy yz zx 1 x y y z z x xy yz zx 2G
应 力 应 变 关 系
上式表明:应变莫尔圆与应力莫尔圆几何相似,且成 正比。
13
弹性变形时的应力应变关系的特点
20
清是哪条路径下的σ-ε关系。
加载路线A→C,应力为σc ,而应变为ε1=εc , ε2=ε3 = -εc/2。 若卸载至E点,由于塑性变形不可逆,E点应变仍然为C 点应变,再施加切应力E→F,此时应力为σF、τF,而F 点应变仍然为C点应变,因此,F点C点应变状态相同(即 ε1=εc,ε2=ε3=-εc/2。),而应力不同,不一一对应。
§应力与应变完全成线性关系。 §应力主轴与全量应变主轴重合
§弹性变形是可逆的,与应变历史 (加载过程无关),应力与应变 之间存在统一的单值关系.
§弹性变形时,应力张量使物体产 生体积变化,泊松比小于0.5.
1 2 m m 0,即: 1 2 0, 0.5 E
14
5.2
同理
'
y
1 ' y 2G
' ij
'
z
1 ' z 2G
第十七章 塑性应力应变关系(本构关系)

• 广义胡克定律的比例式:
x y y z z x xy yz zx 1 x y y z z x xy yz zx 2G
弹性应力应变关系的特点
• 应力与应变完全呈线性关系,应力主轴与应变主 轴重合。 • 弹性变形是可逆的,应力与应变单值对应。 • 弹性变形时,应力球张量使物体产生体积变化, 泊松比υ<0.5
' y
z
' z
xy
xy
yz
yz
zx
zx
d
d 3 2
x y
z x d x y y z z x 1 2 2 3 3 1 d 1 2 2 3 3 1
• 流动理论是描述材料处于塑性状态时,应 力与应变增量或应变速率之间关系的理论。 该理论针对是加载过程的任一瞬间,认为 应力状态确定的不是全量应变,而是该瞬 时的应变增量,从而撇开了加载路线和加 载历史的影响。
Levy—Mises方程
' ' ij ij d
x
' x
y
第五节 塑性应力应变关系(本构关系)
• 一、弹性应力应变关系———Hooke’s Law 对于各向同性材料,有广义虎克定律:
1 1 x y z ; xy xy E 2G 1 1 y y x z ; yz yz E 2G 1 1 z z x y ; zx zx E 2G
• 弹塑性
塑性应变
