重庆市巴蜀中学204-205学年七年级(下)期末数学试卷(解析版)
重庆市巴蜀中学2020-2021年人教版七年级下期末数学试卷含答案解析
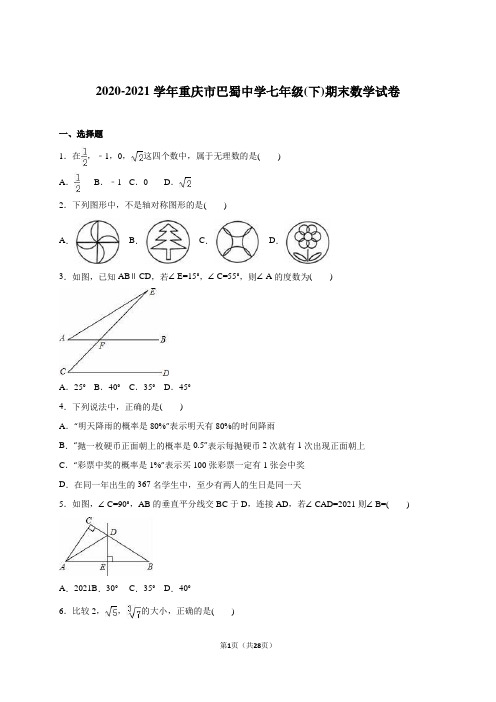
2020-2021学年重庆市巴蜀中学七年级(下)期末数学试卷一、选择题1.在,﹣1,0,这四个数中,属于无理数的是()A.B.﹣1 C.0 D.2.下列图形中,不是轴对称图形的是()A.B.C.D.3.如图,已知AB∥CD,若∠E=15°,∠C=55°,则∠A的度数为()A.25°B.40°C.35°D.45°4.下列说法中,正确的是()A.“明天降雨的概率是80%”表示明天有80%的时间降雨B.“抛一枚硬币正面朝上的概率是0.5”表示每抛硬币2次就有1次出现正面朝上C.“彩票中奖的概率是1%”表示买100张彩票一定有1张会中奖D.在同一年出生的367名学生中,至少有两人的生日是同一天5.如图,∠C=90°,AB的垂直平分线交BC于D,连接AD,若∠CAD=2021则∠B=()A.2021B.30°C.35°D.40°6.比较2,,的大小,正确的是()A.B.2C.2D.<27.如果的解也是2x+3y=6的解,那么k的值是()A.B.C.﹣D.﹣8.如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→D→C→B→A,设P 点经过的路程为x,以点A、P、D为顶点的三角形的面积是y,则下列图象能大致反映y与x的函数关系的是()A. B.C.D.9.如图,在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是()A.B.C.D.10.如图,△ABC内角∠ABC和外角∠ACD的平分线交于点E,BE交AC于点F,过点E作EG∥BD 交AB于点G,交AC于点H,连接AE,有以下结论;①BG=EG;②△HEF≌△CBF;③∠AEB+∠ACE=90°;④BG﹣CH=GH;⑤∠AEC+∠ABE=90°其中正确的结论是()A.1个B.2个C.3个D.4个二、填空题包11.的算术平方根是.12.将一副三角板如图放置,使点A在DE上,∠B=45°,∠E=30°,BC∥DE,则∠EFB的度数为.13.如图,AD,AE分别是△ABC的角平分线和高线,且∠B=50°,∠C=70°,则∠EAD=.14.已知鞋子的“码”与“厘米”之间的对应关系如表所示:码34 35 36 37 38厘米22 22.5 23 23.5 24设鞋子的“码”为x(码),“厘米”为y(厘米),则y与x之间的函数关系式是.15.在一个不透明的布袋中,红色、黑色、白色的乒乓球共有2021除颜色外,形状、大小、质地等完全相同.小明通过多次摸球实验后发现其中投到红色、黑色球的频率稳定在5%和15%,则口袋中白色球的个数很可能是个.16.已知关于x,y的二元一次方程组的解互为相反数,则k的值是.17.若5﹣的小数部分为a,若2+的小数部分为b,则a+b=.18.一个装有进水管和出水管的容器,从某一时刻起只打开进水管进水,经过一段时间,再打开出水管放水,至12分钟时,关停进水管.在打开进水管到关停进水管这段时间内,容器内的水量y(单位:升)与时间x(单位:分钟)之间的函数关系如图所示,关停进水管后,经过分钟,容器中的水恰好放完.19.已知实数m满足+=,则m=.2021图,△ABC中,∠ACB=90°,AC=8cm,BC=15cm,点M从A点出发沿A→C→B路径向终点运动,终点为B点,点N从B点出发沿B→C→A路径向终点运动,终点为A点,点M和N分别以每秒2m和3cm的运动速度同时开始运动,两点都要到达相应的终点时才能停止运动,分别过M 和N作ME⊥l于E,NF⊥l于F.设运动时间为t秒,要使以点M,E,C为顶点的三角形与以点N,F,C为顶点的三角形全等,则t的值为.三、解答题21.计算:(1)(2)(20).22.解方程组:(1)(2).23.已知:如图,∠B=∠D,∠DAB=∠EAC,AB=AD.求证:BC=DE.24.端午节至,甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程S(米)与时间t(分钟)之间的函数关系图象如图所示,请你根据图象,回答下列问题:(1)这次龙舟赛的全程是米,队先到达终点;(2)求乙与甲相遇时乙的速度;(3)求出在乙队与甲相遇之前,他们何时相距100米?25.列方程组解应用题:某服装店购进一批甲、乙两种款式时尚T恤衫,用142021恰好购进100件,已知甲种款型T恤进价为130元/件,且甲种款型的每件进价比乙种款型每件进价少30元.(1)求甲、乙两种款型的T恤各购进多少件?(2)商店按进价提高60%标价销售,销售一段时间后,甲款全部售完,乙款剩余一半,商店决定对乙款型按标价的五折降价销售,很快全部售完,求售完这批T恤商店共获得多少元?26.如图,在△ABC中,∠BAC=90°,过点B作BC的垂线交∠ACB的角平分线于点D,CD与AB 边交于点E,过D作DF⊥AB于点F.(1)若△BDE是边长为2的等边三角形,求AE的长;(2)求证:AE=BF.27.已知△ABC和△DEC都是等腰直角三角形,C为它们的公共直角顶点,D、E分别在BC、AC 边上.(1)如图1,F是线段AD上的一点,连接CF,若AF=CF;①求证:点F是AD的中点;②判断BE与CF的数量关系和位置关系,并说明理由;(2)如图2,把△DEC绕点C顺时针旋转α角(0<α<90°),点F是AD的中点,其他条件不变,判断BE与CF的关系是否不变?若不变,请说明理由;若要变,请求出相应的正确结论.2020-2021学年重庆市巴蜀中学七年级(下)期末数学试卷参考答案与试题解析一、选择题1.在,﹣1,0,这四个数中,属于无理数的是()A.B.﹣1 C.0 D.【考点】无理数.【分析】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.【解答】解:是分数,是有理数;﹣1和0是整数,是有理数;是无理数.故选D.【点评】此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.2.下列图形中,不是轴对称图形的是()A.B.C.D.【考点】轴对称图形.【分析】根据轴对称图形的概念对各选项分析判断后利用排除法求解.【解答】解:A、不是轴对称图形,故本选项正确;B、是轴对称图形,故本选项错误;C、是轴对称图形,故本选项错误;D、是轴对称图形,故本选项错误.故选A.【点评】本题考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.3.如图,已知AB∥CD,若∠E=15°,∠C=55°,则∠A的度数为()A.25°B.40°C.35°D.45°【考点】平行线的性质;三角形的外角性质.【分析】根据两直线平行,同位角相等可得∠1=∠C,再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.【解答】解:如图,∵AB∥CD,∴∠1=∠C=55°,∴∠A=∠1﹣∠E=55°﹣15°=40°.故选B.【点评】本题考查了平行线的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质是解题的关键.4.下列说法中,正确的是()A.“明天降雨的概率是80%”表示明天有80%的时间降雨B.“抛一枚硬币正面朝上的概率是0.5”表示每抛硬币2次就有1次出现正面朝上C.“彩票中奖的概率是1%”表示买100张彩票一定有1张会中奖D.在同一年出生的367名学生中,至少有两人的生日是同一天【分析】根据概率的意义分析各个选项,找到正确选项即可.【解答】解:A、“明天降雨的概率是80%”表示明天有降雨的可能性,故错误;B、“抛一枚硬币正面朝上的概率是0.5”表示抛一枚硬币正面朝上与反面朝上的机会是一样的,故错误;C、“彩票中奖的概率是1%”表示在设计彩票时,有1%的机会中奖,但不一定买100张彩票一定有1张会中奖,故错误;D、在同一年出生的367名学生,而一年中至多有366天,因而至少有两人的生日是同一天.故选:D.【点评】本题解决的关键是理解概率只是反映事件发生机会的大小.5.如图,∠C=90°,AB的垂直平分线交BC于D,连接AD,若∠CAD=2021则∠B=()A.2021B.30°C.35°D.40°【考点】线段垂直平分线的性质;三角形内角和定理;等腰三角形的判定与性质.【分析】由已知条件,根据线段垂直平分线的性质得到线段及角相等,再利用直角三角形两锐角互余得到∠B=(180°﹣∠ADB)÷2答案可得.【解答】解:∵DE垂直平分AB,∴AD=DB∴∠B=∠DAB∵∠C=90°,∠CAD=2021∴∠B=(180°﹣∠C﹣∠CAD)÷2=35°故选C【点评】本题考查了线段垂直平分线的性质、等腰三角形的判定与性质及三角形内角和定理;解决本题的关键是利用线段的垂直平分线性质得到相应的角相等,然后根据三角形的内角和求解.6.比较2,,的大小,正确的是()A.B.2C.2D.<2【分析】首先根据2=,可得2;然后根据,可得,据此判断出2,,的大小关系即可.【解答】解:∵2=,∴2;∵,∴,∴<.故选:A.【点评】此题主要考查了实数大小比较的方法,要熟练掌握,解答此题的关键是判断出2和的大小关系.7.如果的解也是2x+3y=6的解,那么k的值是()A.B.C.﹣D.﹣【考点】解二元一次方程组;二元一次方程的解.【分析】求出方程组的解x=7k,y=﹣2k,代入2x+3y=6得出关于k的方程,求出方程的解即可.【解答】解:,①+②得:2x=14k,x=7k,①﹣②得:2y=﹣4k,y=﹣2k,把x=7k和y=﹣2k代入2x+3y=6得:14k﹣6k=6,k=,故选A.【点评】本题考查了解二元一次方程组的应用,关键是得出关于k的方程.8.如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→D→C→B→A,设P 点经过的路程为x,以点A、P、D为顶点的三角形的面积是y,则下列图象能大致反映y与x的函数关系的是()A. B.C.D.【考点】动点问题的函数图象.【分析】根据动点从点A出发,首先向点D运动,此时y不随x的增加而增大,当点P在DC上运动时,y随着x的增大而增大,当点P在CB上运动时,y不变,据此作出选择即可.【解答】解:当点P由点A向点D运动,即0≤x≤4时,y的值为0;当点P在DC上运动,即4<x≤8时,y随着x的增大而增大;当点P在CB上运动,即8<x≤12时,y不变;当点P在BA上运动,即12<x≤16时,y随x的增大而减小.故选B.【点评】本题考查了动点问题的函数图象,解决动点问题的函数图象问题关键是发现y随x的变化而变化的趋势.9.如图,在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是()A.B.C.D.【考点】概率公式;轴对称图形.【分析】由随机选择标有序号①②③④⑤中的一个小正方形涂黑,共有5种等可能的结果,使与图中阴影部分构成轴对称图形的有3种情况,直接利用概率公式求解即可求得答案.【解答】解:∵在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,共有5种等可能的结果,使与图中阴影部分构成轴对称图形的有②④⑤,3种情况,∴使与图中阴影部分构成轴对称图形的概率是:3÷5=.故选C.【点评】此题考查了概率公式的应用.注意用到的知识点为:概率=所求情况数与总情况数之比.也考查了轴对称图形的定义.10.如图,△ABC内角∠ABC和外角∠ACD的平分线交于点E,BE交AC于点F,过点E作EG∥BD 交AB于点G,交AC于点H,连接AE,有以下结论;①BG=EG;②△HEF≌△CBF;③∠AEB+∠ACE=90°;④BG﹣CH=GH;⑤∠AEC+∠ABE=90°其中正确的结论是()A.1个B.2个C.3个D.4个【考点】全等三角形的判定与性质;等腰三角形的判定与性质.【分析】①根据角平分线定义得出∠ABE=∠CBE,根据平行线性质得出∠CBE=∠BEG,从而得出∠ABE=∠BEG,由等腰三角形的判定定理即可得到结论;②根据相似三角形的判定定理得到两个三角形相似,不能得出全等;③由于E是两条角平分线的交点,根据角平分线的性质可得出点E到BA、AC、BC和距离相等,从而得出AE为∠BAC外角平分线这个重要结论,再利用三角形内角和性质与外角性质进行角度的推导即可轻松得出结论.④根据∠AEC=180﹣x﹣z,于是得到∠AEC=180﹣(y+90°),推出y+∠AEC=90°,即可得到结论;⑤由BG=GE,CH=EH,于是得到BG﹣CH=GE﹣EH=GH.即可得到结论.【解答】解:①∵BE平分∠ABC,π∴∠ABE=∠CBE,∵GE∥BC,∴∠CBE=∠GEB,∴∠ABE=∠GEB,∴BG=GE,故①正确.同理CH=HE.②△HEF与△CBF只有两个角是相等的,能得出相似,但不含相等的边,所有不能得出全等的结论,故②错误.③过点E作EN⊥AC于N,ED⊥BC于D,EM⊥BA于M,如图,∵BE平分∠ABC,∴EM=ED,∵CE平分∠ACD,∴EN=ED,∴EN=EM,∴AE平分∠CAM,设∠ACE=∠DCE=x,∠ABE=∠CBE=y,∠MAE=∠CAE=z,如图,则∠BAC=180°﹣2z,∠ACB=180﹣2x,∵∠ABC+∠ACB+∠BAC=180°,∴2y+180°﹣2z+180°﹣2x=180°,∴x+z=y+90°,∵z=y+∠AEB,∴x+y+∠AEB=y+90°,∴x+∠AEB=90°,即∠ACE+∠AEB=90°,故③正确.④∵∠AEC=180﹣x﹣z,∴∠AEC=180﹣(y+90°),∴y+∠AEC=90°,即∠ABE+∠AEC=90°,故④正确.⑤∵BG=GE,CH=EH,∴BG﹣CH=GE﹣EH=GH.故⑤正确.综上,①③④⑤正确,共4个.故选D.【点评】本题考查了平行线的性质,角平分线的定义,角平分线的性质与判定,等腰三角形的判定,三角形内角和定理、三角形外角性质等多个知识点,难度中等.判断出AE是∠BAC外角平分线是关键,事实上,点E就是△ABC的旁心.二、填空题包11.的算术平方根是2.【考点】算术平方根.【专题】计算题.【分析】首先根据算术平方根的定义求出的值,然后再利用算术平方根的定义即可求出结果.【解答】解:∵=4,∴的算术平方根是=2.故答案为:2.【点评】此题主要考查了算术平方根的定义,注意要首先计算=4.12.将一副三角板如图放置,使点A在DE上,∠B=45°,∠E=30°,BC∥DE,则∠EFB的度数为75°.【考点】平行线的性质.【分析】由平行线的性质得出内错角相等∠BCF=∠E=30°,再由三角形的外角性质得出∠EFB=∠B+∠BCF,即可得出结果.【解答】解:∵BC∥DE,∴∠BCF=∠E=30°,∴∠EFB=∠B+∠BCF=45°+30°=75°,故答案为75°.【点评】本题考查了平行线的性质、三角形的外角性质;熟练掌握平行线的性质,并能进行推理计算是解决问题的关键.13.如图,AD,AE分别是△ABC的角平分线和高线,且∠B=50°,∠C=70°,则∠EAD=10°.【考点】三角形内角和定理.【分析】根据三角形的内角和等于180°求出∠BAC,再根据角平分线的定义求出∠BAD,根据直角三角形两锐角互余求出∠BAE,然后根据∠EAD=∠BAE﹣∠BAD代入数据进行计算即可得解.【解答】解:∵∠B=50°,∠C=70°,∴∠BAC=180°﹣∠B﹣∠C=180°﹣50°﹣70°=60°,∵AD是△ABC的角平分线,∴∠BAD=∠BAC=×60°=30°,∵AE是△ABC的高线,∴∠BAE=90°﹣∠B=90°﹣50°=40°,∴∠EAD=∠BAE﹣∠BAD=40°﹣30°=10°.故答案为:10°.【点评】本题考查了三角形的内角和定理,三角形的角平分线、高线的定义,是基础题,准确识图找出各角度之间的关系是解题的关键.14.已知鞋子的“码”与“厘米”之间的对应关系如表所示:码34 35 36 37 38厘米22 22.5 23 23.5 24设鞋子的“码”为x(码),“厘米”为y(厘米),则y与x之间的函数关系式是y=0.5x+5.【考点】根据实际问题列一次函数关系式.【分析】设鞋长用x表示,鞋码用y表示,利用待定系数法即可求解.【解答】解:设鞋子的“码”为x(码),“厘米”为y(厘米),则y与x之间的函数关系式是:y=kx+b,∴,解得:,∴y与x之间的函数关系式是:y=0.5x+5.故答案为:y=0.5x+5.【点评】本题考查了一次函数的应用,利用一次函数解决鞋的长度与鞋码之间的关系是解题关键.15.在一个不透明的布袋中,红色、黑色、白色的乒乓球共有2021除颜色外,形状、大小、质地等完全相同.小明通过多次摸球实验后发现其中投到红色、黑色球的频率稳定在5%和15%,则口袋中白色球的个数很可能是16个.【考点】利用频率估计概率.【专题】计算题.【分析】在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,可以从比例关系入手,先求得白球的频率,再乘以总球数求解.【解答】解:白色球的个数是:20211﹣5%﹣15%)=20210%=16,故答案为:16,【点评】此题主要考查了利用频率估计概率,解答此题的关键是要计算出口袋中白色球所占的比例,再计算其个数.16.已知关于x,y的二元一次方程组的解互为相反数,则k的值是﹣1.【考点】二元一次方程组的解.【分析】将方程组用k表示出x,y,根据方程组的解互为相反数,得到关于k的方程,即可求出k 的值.【解答】解:解方程组得:,因为关于x,y的二元一次方程组的解互为相反数,可得:2k+3﹣2﹣k=0,解得:k=﹣1.故答案为:﹣1.【点评】此题考查方程组的解,关键是用k表示出x,y的值.17.若5﹣的小数部分为a,若2+的小数部分为b,则a+b=1.【考点】估算无理数的大小.【分析】先估算出的大小,再求出a、b的值即可.【解答】解:∵4<6<9,∴2<<3,∴2<5﹣<3,∴a=5﹣﹣2=3﹣.同理,b=﹣2.∴a+b=3﹣+﹣2=1.故答案是:1.【点评】本题主要考查了无理数的估算,解题关键是确定无理数的小数部分即可解决问题.18.一个装有进水管和出水管的容器,从某一时刻起只打开进水管进水,经过一段时间,再打开出水管放水,至12分钟时,关停进水管.在打开进水管到关停进水管这段时间内,容器内的水量y(单位:升)与时间x(单位:分钟)之间的函数关系如图所示,关停进水管后,经过8分钟,容器中的水恰好放完.【考点】函数的图象;一次函数的应用.【分析】由0﹣4分钟的函数图象可知进水管的速度,根据4﹣12分钟的函数图象求出水管的速度,再求关停进水管后,出水经过的时间.【解答】解:进水管的速度为:2021=5(升/分),出水管的速度为:5﹣(30﹣2021(12﹣4)=3.75(升/分),∴关停进水管后,出水经过的时间为:30÷3.75=8分钟.故答案为:8.【点评】本题考查利用函数的图象解决实际问题.正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决.19.已知实数m满足+=,则m=7.【考点】二次根式的性质与化简;二次根式有意义的条件.【分析】根据二次根式的性质和化简解答即可.【解答】解:因为实数m满足+=,可得:m﹣2+=m,可得:m﹣3=4,解得:m=7,故答案为:7【点评】此题考查二次根式问题,关键是根据二次根式的性质和化简分析.2021图,△ABC中,∠ACB=90°,AC=8cm,BC=15cm,点M从A点出发沿A→C→B路径向终点运动,终点为B点,点N从B点出发沿B→C→A路径向终点运动,终点为A点,点M和N分别以每秒2m和3cm的运动速度同时开始运动,两点都要到达相应的终点时才能停止运动,分别过M和N作ME⊥l于E,NF⊥l于F.设运动时间为t秒,要使以点M,E,C为顶点的三角形与以点N,F,C为顶点的三角形全等,则t的值为或7或8.【考点】全等三角形的判定.【专题】动点型.【分析】易证∠MEC=∠CFN,∠MCE=∠CNF.只需MC=NC,就可得到△MEC与△CFN全等,然后只需根据点M和点N不同位置进行分类讨论即可解决问题.【解答】解:①当0≤t<4时,点M在AC上,点N在BC上,如图①,此时有AM=2t,BN=3t,AC=8,BC=15.当MC=NC即8﹣2t=15﹣3t,解得t=7,不合题意舍去;②当4≤t<5时,点M在BC上,点N也在BC上,如图②,若MC=NC,则点M与点N重合,即2t﹣8=15﹣3t,解得t=;③当5≤t<时,点M在BC上,点N在AC上,如图③,当MC=NC即2t﹣8=3t﹣15,解得t=7;④当≤t<时,点N停在点A处,点M在BC上,如图④,当MC=NC即2t﹣8=8,解得t=8;综上所述:当t等于或7或8秒时,以点M,E,C为顶点的三角形与以点N,F,C为顶点的三角形全等.故答案为:或7或8.【点评】本题主要考查了全等三角形的判定以及分类讨论的思想,可能会因考虑不全面而出错,是一道易错题.三、解答题21.计算:(1)(2)(20).【考点】二次根式的混合运算.【专题】计算题.【分析】(1)先把各二次根式化为最简二次根式,然后合并即可;(2)先把各二次根式化为最简二次根式,然后把括号内合并后进行二次根式的除法运算.【解答】解:(1)原式=2﹣3+6﹣10=﹣5;(2)原式=(60﹣16﹣6)÷2=38÷2=19.【点评】本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.22.解方程组:(1)(2).【考点】解二元一次方程组.【专题】计算题.【分析】(1)方程组利用代入消元法求出解即可;(2)方程组整理后,利用加减消元法求出解即可.【解答】解:(1),把①代入②得:10y﹣42+3y=23,即y=5,把y=5代入①得:x=2,则方程组的解为;(2)方程组整理得:,①+②得:7x=14,即x=2,把x=2代入②得:y=﹣1,则方程组的解为.【点评】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.23.已知:如图,∠B=∠D,∠DAB=∠EAC,AB=AD.求证:BC=DE.【考点】全等三角形的判定与性质.【专题】证明题.【分析】因为∠DAB=∠EAC,从图上可以看出∠DAB+∠BAE=∠EAC+∠BAE,即∠DAE=∠BAC,又因为,∠B=∠D,AB=AD,所以很容易证明△DAE≌△BAC,从而得出结论.【解答】证明:∵∠DAB=∠EAC,∴∠DAB+∠BAE=∠EAC+∠BAE,即∠DAE=∠BAC,在△DAE和△BAC中,∴△DAE≌△BAC(ASA)∴BC=DE.【点评】本题考查全等三角形的判定定理,根据ASA可证明三角形全等,从而可得出结论.24.端午节至,甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程S(米)与时间t(分钟)之间的函数关系图象如图所示,请你根据图象,回答下列问题:(1)这次龙舟赛的全程是1000米,乙队先到达终点;(2)求乙与甲相遇时乙的速度;(3)求出在乙队与甲相遇之前,他们何时相距100米?【考点】函数的图象.【分析】(1)根据函数图象的纵坐标,可得比赛的路程,根据函数图象的横坐标,可得比赛的结果;(2)根据乙加速后行驶的路程除以加速后的时间,可得答案;(3)分类讨论,乙加速前,乙加速后,根据甲的路程减去乙的路程,可得关于t的方程,根据解方程,可得答案.【解答】解:(1)由纵坐标看出,这次龙舟赛的全程是1000米,由横坐标看出,乙队先到达终点,故答案为:1000,乙;(2)由图象看出,相遇是在乙加速后,加速后的路程是1000﹣400=600米,加速后的时间时3.8﹣2.2=1.6分钟,乙与甲相遇时乙的速度600÷1.6=375米/分钟;(3)①乙加速前,设行驶x秒时,甲乙相距100米,x﹣x=100.解得x=2;②乙加速后,设行驶x秒时,甲乙相距100米,∵×2.2=550,∴x﹣x=550﹣400﹣100.解得x=0.4,∴行驶了2.2+00.4=2.6,答:在乙队与甲相遇之前,他们行驶2或2.6分钟时相距100米.【点评】本题考查了函数图象,分类讨论是解题关键,乙加速前的速度,乙加速后的速度,注意相遇时的速度是加速后的速度.25.列方程组解应用题:某服装店购进一批甲、乙两种款式时尚T恤衫,用142021恰好购进100件,已知甲种款型T恤进价为130元/件,且甲种款型的每件进价比乙种款型每件进价少30元.(1)求甲、乙两种款型的T恤各购进多少件?(2)商店按进价提高60%标价销售,销售一段时间后,甲款全部售完,乙款剩余一半,商店决定对乙款型按标价的五折降价销售,很快全部售完,求售完这批T恤商店共获得多少元?【考点】二元一次方程组的应用.【分析】(1)可设甲种款型的T恤衫购进x件,则甲种款型的T恤衫购进y件,根据用142021恰好购进100件,甲种款型每件的进价比乙种款型每件的进价少30元,列出方程组即可求解;(2)先求出甲款型的利润,乙款型前面销售一半的利润,后面销售一半的亏损,再相加即可求解.【解答】解:(1)设甲种款型的T恤衫购进x件,则乙种款型的T恤衫购进y件,由题意得解得答:甲种款型的T恤衫购进60件,乙种款型的T恤衫购进40件.(2)130×60%×60+160×60%×(40÷2)﹣160×[1﹣(1+60%)×0.5]×(40÷2)=4680+19202140=5960(元).答:售完这批T恤衫商店共获利5960元.【点评】此题考查二元一次方程组的实际运用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.26.如图,在△ABC中,∠BAC=90°,过点B作BC的垂线交∠ACB的角平分线于点D,CD与AB 边交于点E,过D作DF⊥AB于点F.(1)若△BDE是边长为2的等边三角形,求AE的长;(2)求证:AE=BF.【考点】全等三角形的判定与性质.【分析】(1)由BD⊥BC,得到∠DBC=90°,由于△BDE是边长为2的等边三角形,于是得到∠DBA=∠BDE=60°,求得∠ABC=∠DCB=30°,得到CD=2BD=4,根据直角三角形的性质即可得到结果;(2)根据已知条件证得△BDF≌△ACE,即可得到AE=BF.【解答】解:(1)∵BD⊥BC,∴∠DBC=90°,∵△BDE是边长为2的等边三角形,∴∠DBA=∠BDE=60°,∴∠ABC=∠DCB=30°,∴CD=2BD=4,∴CE=2,∵∠A=90°∠AEC=∠DEB=60°,∴∠ACE=30°,∴AE=CE=1;(2)在△BDF与△ACE中,,∴△BDF≌△ACE,∴AE=BF.【点评】本题考查了全等三角形的判定和性质,直角三角形的性质,等边三角形的性质,熟练掌握各性质是解题的关键.27.已知△ABC和△DEC都是等腰直角三角形,C为它们的公共直角顶点,D、E分别在BC、AC 边上.(1)如图1,F是线段AD上的一点,连接CF,若AF=CF;①求证:点F是AD的中点;②判断BE与CF的数量关系和位置关系,并说明理由;(2)如图2,把△DEC绕点C顺时针旋转α角(0<α<90°),点F是AD的中点,其他条件不变,判断BE与CF的关系是否不变?若不变,请说明理由;若要变,请求出相应的正确结论.【考点】旋转的性质;全等三角形的判定与性质;等腰直角三角形.【专题】探究型.【分析】(1)①如图1,由AF=CF得到∠1=∠2,则利用等角的余角相等可得∠3=∠ADC,然后根据等腰三角形的判定定理得FD=FC,易得AF=FD;②先利用等腰直角三角形的性质得CA=CB,CD=CE,则可证明△ADC≌△BEC得到AD=BE,∠1=∠CBE,由于AD=2CF,∠1=∠2,则BE=2CF,再证明∠CBE+∠3=90°,于是可判断CF⊥BE;(2)延长CF到G使FG=CF,连结AG、DG,如图2,易得四边形ACDG为平行四边形,则AG=CD,AG∥CD,于是根据平行线的性质得∠GAC=180°﹣∠ACD,所以CD=CE=AG,再根据旋转的性质得∠BCD=α,所以∠BCE=∠DCE+∠BCD=90°+α=90°+90°﹣∠ACD=180°﹣∠ACD,得到∠GAC=∠ECB,接着可证明△AGC≌△CEB,得到CG=BE,∠2=∠1,所以BE=2CF,和前面一样可证得CF⊥BE.【解答】(1)①证明:如图1,∵AF=CF,∴∠1=∠2,∵∠1+∠ADC=90°,∠2+∠3=90°,∴∠3=∠ADC,∴FD=FC,∴AF=FD,即点F是AD的中点;②BE=2CF,BE⊥CF.理由如下:∵△ABC和△DEC都是等腰直角三角形,∴CA=CB,CD=CE,在△ADC和△BEC中,∴△ADC≌△BEC,∴AD=BE,∠1=∠CBE,而AD=2CF,∠1=∠2,∴BE=2CF,而∠2+∠3=90°,∴∠CBE+∠3=90°,∴CF⊥BE;(2)仍然有BE=2CF,BE⊥CF.理由如下:延长CF到G使FG=CF,连结AG、DG,如图2,∵AF=DF,FG=FC,∴四边形ACDG为平行四边形,∴AG=CD,AG∥CD,∴∠GAC+∠ACD=180°,即∠GAC=180°﹣∠ACD,∴CD=CE=AG,∵△DEC绕点C顺时针旋转α角(0<α<90°),∴∠BCD=α,∴∠BCE=∠DCE+∠BCD=90°+α=90°+90°﹣∠ACD=180°﹣∠ACD,∴∠GAC=∠ECB,在△AGC和△CEB中,∴△AGC≌△CEB,∴CG=BE,∠2=∠1,∴BE=2CF,而∠2+∠BCF=90°,∴∠BCF+∠1=90°,∴CF⊥BE.【点评】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了全等三角形的判定与性质和等腰直角三角形的性质.。
重庆巴蜀中学人教版七年级下册数学全册单元期末试卷及答案-百度文库

(探究 2):如图 2,已知 O 是外角∠DBC 与外角∠ECB 的平分线 BO 和 CO 的交点,则
∠BOC 与∠A 有怎样的关系?请说明理由.
(应用):如图 3,在 RtΔAOB 中,∠AOB=90º,已知 AB 不平行与 CD,AC、BD 分别是
∠BAO 和∠ABO 的角平分线,又 CE、DE 分别是∠ACD 和∠BDC 的角平分线,则
D. 8
)
A.90°
B.100°
C.105°
D.110°
二、填空题
x1
11.若 y 4 是二元一次方程 3x+ay=5 的一组解,则 a= ______ .
12.若(3x+2y)2=(3x﹣2y)2+A,则代数式 A 为______. 13.已知 a+b=5,ab=3,求: (1)a2b+ab2; (2)a2+b2. 14.分解因式:x2﹣4x=__.
3.4)
B.
x y 500 3%x 4%y
3.4%
C.
x (1
y 500 3%)x
(1
4%)
y
500(1 3.4%)
D.
x y 4%x
500 3%y
500 3.4%
9.若多项式 a2 kab 4b2 是完全平方式,则 k 的值为( )
A.4
B. 2
C. 4
10.将一副三角板如图放置,作 CF//AB,则∠ EFC 的度数是(
(3)如图 3 所示,点 M 在线段 EF 上,点 N 在直线 CD 的下方,点 P 是直线 AB 上一点 (在 E 的左侧),连接 MP, PN, NF ,若 MPN 2MPB,NFH 2HFD ,则请直接 写出 PMH 与 N 之间的数量
重庆巴蜀中学七年级下册数学期末试卷测试卷(含答案解析)

重庆巴蜀中学七年级下册数学期末试卷测试卷(含答案解析)一、解答题1.已知,AB ∥DE ,点C 在AB 上方,连接BC 、CD . (1)如图1,求证:∠BCD +∠CDE =∠ABC ;(2)如图2,过点C 作CF ⊥BC 交ED 的延长线于点F ,探究∠ABC 和∠F 之间的数量关系;(3)如图3,在(2)的条件下,∠CFD 的平分线交CD 于点G ,连接GB 并延长至点H ,若BH 平分∠ABC ,求∠BGD ﹣∠CGF 的值.2.如图,//MN GH ,点A 、B 分别在直线MN 、GH 上,点O 在直线MN 、GH 之间,若116NAO ∠=︒,144OBH ∠=︒.(1)AOB ∠= ︒;(2)如图2,点C 、D 是NAO ∠、GBO ∠角平分线上的两点,且35CDB ∠=︒,求ACD ∠ 的度数;(3)如图3,点F 是平面上的一点,连结FA 、FB ,E 是射线FA 上的一点,若MAE ∠=n OAE ∠,HBF n OBF ∠=∠,且60AFB ∠=︒,求n 的值.3.问题情境:(1)如图1,//AB CD ,128PAB ∠=︒,119PCD ∠=︒.求APC ∠度数.小颖同学的解题思路是:如图2,过点P 作//PE AB ,请你接着完成解答. 问题迁移:(2)如图3,//AD BC ,点P 在射线OM 上运动,当点P 在A 、B 两点之间运动时,ADP α∠=∠,PCE β∠=∠.试判断CPD ∠、α∠、β∠之间有何数量关系?(提示:过点P 作//PF AD ),请说明理由;(3)在(2)的条件下,如果点P 在A 、B 两点外侧运动时(点P 与点A 、B 、O 三点不重合),请你猜想CPD ∠、α∠、β∠之间的数量关系并证明.4.如图,//MN PQ ,直线AD 与MN 、PQ 分别交于点A 、D ,点B 在直线PQ 上,过点B 作BG AD ⊥,垂足为点G .(1)如图1,求证:90MAG PBG ∠+∠=︒;(2)若点C 在线段AD 上(不与A 、D 、G 重合),连接BC ,MAG ∠和PBC ∠的平分线交于点H 请在图2中补全图形,猜想并证明CBG ∠与AHB ∠的数量关系;5.如图,已知直线//AB 射线CD ,100CEB ∠=︒.P 是射线EB 上一动点,过点P 作PQ //EC 交射线CD 于点Q ,连接CP .作PCF PCQ ∠=∠,交直线AB 于点F ,CG 平分ECF ∠.(1)若点P ,F ,G 都在点E 的右侧,求PCG ∠的度数;(2)若点P ,F ,G 都在点E 的右侧,30EGC ECG ∠-∠=︒,求CPQ ∠的度数; (3)在点P 的运动过程中,是否存在这样的情形,使:4:3EGC EFC ∠∠=?若存在,求出CPQ ∠的度数;若不存在,请说明理由.二、解答题6.已知//a b ,直角ABC 的边与直线a 分别相交于O 、G 两点,与直线b 分别交于E ,F 点,且90ACB ∠=︒.(1)将直角ABC 如图1位置摆放,如果56AOG ∠=︒,则CEF ∠=________; (2)将直角ABC 如图2位置摆放,N 为AC 上一点,180NEF CEF ∠+∠=︒,请写出NEF ∠与AOG ∠之间的等量关系,并说明理由;(3)将直角ABC 如图3位置摆放,若135GOC ∠=︒,延长AC 交直线b 于点Q ,点P 是射线GF 上一动点,探究,POQ OPQ ∠∠与PQF ∠的数量关系,请直接写出结论.7.(1)光线从空气中射入水中会产生折射现象,同时光线从水中射入空气中也会产生折射现象,如图1,光线a 从空气中射入水中,再从水中射入空气中,形成光线b ,根据光学知识有12,34∠=∠∠=∠,请判断光线a 与光线b 是否平行,并说明理由.(2)光线照射到镜面会产生反射现象,由光学知识,入射光线与镜面的夹角与反射光线与镜面的夹角相等,如图2有一口井,已知入射光线α与水平线OC 的夹角为40︒,问如何放置平面镜MN ,可使反射光线b 正好垂直照射到井底?(即求MN 与水平线的夹角) (3)如图3,直线EF 上有两点A 、C ,分别引两条射线AB 、CD .105BAF ∠=︒,65DCF ∠=︒,射线AB 、CD 分别绕A 点,C 点以1度/秒和3度/秒的速度同时顺时针转动,设时间为t ,在射线CD 转动一周的时间内,是否存在某时刻,使得CD 与AB 平行?若存在,求出所有满足条件的时间t .8.如图1,//AB CD ,E 是AB 、CD 之间的一点.(1)判定BAE ∠,CDE ∠与AED ∠之间的数量关系,并证明你的结论;(2)如图2,若BAE ∠、CDE ∠的两条平分线交于点F .直接写出AFD ∠与AED ∠之间的数量关系;(3)将图2中的射线DC 沿DE 翻折交AF 于点G 得图3,若AGD ∠的余角等于2E ∠的补角,求BAE ∠的大小.9.已知射线//AB 射线CD ,P 为一动点,AE 平分PAB ∠,CE 平分PCD ∠,且AE 与CE 相交于点E .(注意:此题不允许使用三角形,四边形内角和进行解答)(1)在图1中,当点P 运动到线段AC 上时,180APC ∠=︒.直接写出AEC ∠的度数; (2)当点P 运动到图2的位置时,猜想AEC ∠与APC ∠之间的关系,并加以说明; (3)当点P 运动到图3的位置时,(2)中的结论是否还成立?若成立,请说明理由:若不成立,请写出AEC ∠与APC ∠之间的关系,并加以证明.10.长江汛期即将来临,防汛指挥部在一危险地带两岸各安置了一探照灯,便于夜间查看江水及两岸河堤的情况,如图,灯A 射线自AM 顺时针旋转至AN 便立即回转,灯B 射线自BP 顺时针旋转至BQ 便立即回转,两灯不停交叉照射巡视,若灯A 转动的速度是a °/秒,灯B 转动的速度是b °/秒,且a 、b 满足()2450a b a b -++-=.假定这一带长江两岸河堤是平行的,即//PQ MN ,且60BAN ∠=︒(1)求a 、b 的值;(2)若灯B 射线先转动45秒,灯A 射线才开始转动,当灯B 射线第一次到达BQ 时运动停止,问A 灯转动几秒,两灯的光束互相平行?(3)如图,两灯同时转动,在灯A 射线到达AN 之前.若射出的光束交于点C ,过C 作CD AC ⊥交PQ 于点D ,则在转动过程中,BAC ∠与BCD ∠的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请求出其取值范围.三、解答题11.小明在学习过程中,对教材中的一个有趣问题做如下探究:(习题回顾)已知:如图1,在ABC 中,90ACB ∠=︒,AE 是角平分线,CD 是高,AE 、CD 相交于点F .求证:CFE CEF ∠=∠;(变式思考)如图2,在ABC 中,90ACB ∠=︒,CD 是AB 边上的高,若ABC 的外角BAG ∠的平分线交CD 的延长线于点F ,其反向延长线与BC 边的延长线交于点E ,则CFE ∠与CEF ∠还相等吗?说明理由;(探究延伸)如图3,在ABC 中,AB 上存在一点D ,使得ACD B ∠=∠,BAC ∠的平分线AE 交CD 于点F .ABC 的外角BAG ∠的平分线所在直线MN 与BC 的延长线交于点M .直接写出M ∠与CFE ∠的数量关系.12.如图所示,已知射线//,//,100CB OA AB OC C OAB ︒∠=∠=.点E 、F 在射线CB 上,且满足FOB AOB ∠=∠,OE 平分COF ∠ (1)求EOB ∠的度数;(2)若平行移动AB ,那么:OBC OFC ∠∠的值是否随之发生变化?如果变化,找出变化规律.若不变,求出这个比值;(3)在平行移动AB 的过程中,是否存在某种情况,使OEC OBA ∠=∠?若存在,求出其度数.若不存在,请说明理由.13.(1)如图1所示,△ABC 中,∠ACB 的角平分线CF 与∠EAC 的角平分线AD 的反向延长线交于点F ;①若∠B =90°则∠F = ;②若∠B =a ,求∠F 的度数(用a 表示);(2)如图2所示,若点G 是CB 延长线上任意一动点,连接AG ,∠AGB 与∠GAB 的角平分线交于点H ,随着点G 的运动,∠F +∠H 的值是否变化?若变化,请说明理由;若不变,请求出其值.14.【问题探究】如图1,DF ∥CE ,∠PCE=∠α,∠PDF=∠β,猜想∠DPC 与α、β之间有何数量关系?并说明理由; 【问题迁移】如图2,DF ∥CE ,点P 在三角板AB 边上滑动,∠PCE=∠α,∠PDF=∠β. (1)当点P 在E 、F 两点之间运动时,如果α=30°,β=40°,则∠DPC= °.(2)如果点P 在E 、F 两点外侧运动时(点P 与点A 、B 、E 、F 四点不重合),写出∠DPC 与α、β之间的数量关系,并说明理由.(图1) (图2)15.在ABC 中,100BAC ∠=︒,A ABC CB =∠∠,点D 在直线BC 上运动(不与点B 、C 重合),点E 在射线AC 上运动,且ADE AED ∠=∠,设DAC n ∠=︒.(1)如图①,当点D 在边BC 上,且40n =︒时,则BAD ∠=__________︒,CDE ∠=__________︒;(2)如图②,当点D 运动到点B 的左侧时,其他条件不变,请猜想BAD ∠和CDE ∠的数量关系,并说明理由;(3)当点D 运动到点C 的右侧时,其他条件不变,BAD ∠和CDE ∠还满足(2)中的数量关系吗?请在图③中画出图形,并给予证明.(画图痕迹用黑色签字笔加粗加黑)【参考答案】一、解答题1.(1)证明见解析;(2);(3). 【分析】(1)过点作,先根据平行线的性质可得,再根据平行公理推论可得,然后根据平行线的性质可得,由此即可得证;(2)过点作,同(1)的方法,先根据平行线的性质解析:(1)证明见解析;(2)90ABC F ∠-∠=︒;(3)45︒. 【分析】(1)过点C 作CF AB ∥,先根据平行线的性质可得180ABC BCF ∠+∠=︒,再根据平行公理推论可得CF DE ,然后根据平行线的性质可得180CDE BCF BCD ∠+∠+∠=︒,由此即可得证;(2)过点C 作CG AB ∥,同(1)的方法,先根据平行线的性质得出180ABC BCG ∠+∠=︒,180F BCG BCF ∠+∠+∠=︒,从而可得ABC F BCF ∠-∠=∠,再根据垂直的定义可得90BCF ∠=︒,由此即可得出结论;(3)过点G 作GM AB ,延长FG 至点N ,先根据平行线的性质可得ABH MGH ∠=∠,MGN DFG ∠=∠,从而可得MGH MGN ABH DFG ∠-∠=∠-∠,再根据角平分线的定义、结合(2)的结论可得45MGH MGN ∠=-∠︒,然后根据角的和差、对顶角相等可得BGD CG MGH MGN F ∠-∠=∠-∠,由此即可得出答案.【详解】证明:(1)如图,过点C 作CF AB ∥,180ABC BCF ∴∠+∠=︒,AB DE , CFDE ∴,180CDE DCF ∴∠+∠=︒,即180CDE BCF BCD ∠+∠+∠=︒,CDE BCF BCD ABC BCF ∴∠+∠+∠=∠+∠, BCD CDE ABC ∴∠+∠=∠;(2)如图,过点C 作CG AB ∥,180ABC BCG ∴∠+∠=︒,AB DE , CG DE ∴,180F FCG ∴∠+∠=︒,即180F BCG BCF ∠+∠+∠=︒, F BCG BCF ABC BCG ∴∠+∠+∠=∠+∠, ABC F BCF ∴∠-∠=∠, CF BC ⊥,90BCF ∴∠=︒,90ABC F ∴∠-∠=︒;(3)如图,过点G 作GM AB ,延长FG 至点N ,ABH MGH ∴∠=∠,AB DE , GM DE ∴,MGN DFG ∴∠=∠,BH 平分ABC ∠,FN 平分CFD ∠, 11,22ABH AB D C CF DFG ∴∠=∠∠∠=,由(2)可知,90ABC CFD ∠-∠=︒,411225MGH MGN ABH DFG CF B D A C ∠-∠=∠-∠∠∠-==∴︒,又BGD MGH MGDCGF DGN MGN MGD∠=∠+∠⎧⎨∠=∠=∠+∠⎩,45MGH BGD GF MGN C ∠-∠∴-==∠∠︒.【点睛】本题考查了平行线的性质、对顶角相等、角平分线的定义等知识点,熟练掌握平行线的性质是解题关键.2.(1)100;(2)75°;(3)n=3. 【分析】(1)如图:过O 作OP//MN ,由MN//OP//GH 得∠NAO+∠POA=180°,∠POB+∠OBH=180°,即∠NAO+∠AOB+∠OB解析:(1)100;(2)75°;(3)n =3. 【分析】(1)如图:过O 作OP //MN ,由MN //OP //GH 得∠NAO +∠POA =180°,∠POB +∠OBH =180°,即∠NAO +∠AOB +∠OBH =360°,即可求出∠AOB ;(2)如图:分别延长AC 、CD 交GH 于点E 、F ,先根据角平分线求得58NAC ∠=︒,再根据平行线的性质得到58CEF ∠=︒;进一步求得18DBF ∠=︒,17DFB ∠=︒,然后根据三角形外角的性质解答即可;(3)设BF 交MN 于K ,由∠NAO =116°,得∠MAO =64°,故∠MAE =641nn ︒⨯+,同理∠OBH =144°,∠HBF =n ∠OBF ,得∠FBH =1441n n ︒⨯+,从而=n BKA FBH n ∠∠=⨯︒+1441,又∠FKN =∠F +∠FAK ,得144606411n nn n ︒︒︒⨯=+⨯++,即可求n . 【详解】解:(1)如图:过O 作OP //MN , ∵MN //GHl ∴MN //OP //GH∴∠NAO +∠POA =180°,∠POB +∠OBH =180° ∴∠NAO +∠AOB +∠OBH =360° ∵∠NAO =116°,∠OBH =144° ∴∠AOB =360°-116°-144°=100°;(2)分别延长AC 、CD 交GH 于点E 、F ,∵AC 平分NAO ∠且116NAO ∠=︒, ∴58NAC ∠=︒,又∵MN //GH , ∴58CEF ∠=︒;∵144OBH ∠=︒,36OBG ∠=︒ ∵BD 平分OBG ∠, ∴18DBF ∠=︒, 又∵,CDB ∠=︒35∴351817DFB CDB DBF ∠=∠-∠=-=︒; ∴175875ACD DFB AEF ∠=∠+∠=︒+︒=︒; (3)设FB 交MN 于K ,∵116NAO ∠=︒,则MAO ∠=︒64; ∴641nMAE n ∠=⨯︒+ ∵144OBH ∠=︒, ∴+1n FBH n ∠=⨯︒144,=n BKA FBH n ∠∠=⨯︒+1441, 在△FAK 中,64601nBKA FKA F n ∠=∠+∠=⨯︒+︒+, ∴144646011n n n n ⨯︒=⨯︒+︒++, ∴3n =.经检验:3n =是原方程的根,且符合题意. 【点睛】本题主要考查平行线的性质及应用,正确作出辅助线、构造平行线、再利用平行线性质进行求解是解答本题的关键.3.(1)见解析;(2),理由见解析;(3)①当在延长线时(点不与点重合),;②当在之间时(点不与点,重合),.理由见解析 【分析】(1)过P 作PE ∥AB ,构造同旁内角,利用平行线性质,可得∠APC=解析:(1)见解析;(2)180CPD αβ∠=∠+︒-∠,理由见解析;(3)①当P 在BA 延长线时(点P 不与点A 重合),180CPD βα∠=︒-∠-∠;②当P 在BO 之间时(点P 不与点B ,O 重合),180CPD αβ∠=∠-︒+∠.理由见解析 【分析】(1)过P 作PE ∥AB ,构造同旁内角,利用平行线性质,可得∠APC =113°; (2)过过P 作//PF AD 交CD 于F ,,推出////AD PF BC ,根据平行线的性质得出180BCP ,即可得出答案;(3)画出图形(分两种情况:①点P 在BA 的延长线上,②当P 在BO 之间时(点P 不与点B ,O 重合)),根据平行线的性质即可得出答案.【详解】解:(1)过P 作//PE AB ,//AB CD ,////PE AB CD ∴,=180APE PAB ,180CPE PCD ∠+∠=︒,128PAB ∠=︒,119PCD ∠=︒52APE ∴∠=︒,61CPE ∠=︒,5261113APC ∴∠=︒+︒=︒;(2)180CPD αβ∠=∠+︒-∠,理由如下:如图3,过P 作//PF AD 交CD 于F ,//AD BC ,////AD PF BC ∴,ADP DPF ∴∠=∠,BCP CPF ∠=∠,180BCP PCE ∠+∠=︒,PCE β∠=∠,180BCP β∴∠=︒-∠又ADP α∠=∠=180CPD DPF CPF ;(3)①当P 在BA 延长线时(点P 不与点A 重合),180CPD βα∠=︒-∠-∠; 理由:如图4,过P 作//PF AD 交CD 于F ,//AD BC ,////AD PF BC ∴,ADP DPF ∴∠=∠,BCP CPF ∠=∠,180BCP PCE ∠+∠=︒,PCE β∠=∠,180BCP β∴∠=︒-∠,又ADP α∠=∠,180CPD CPF DPF αβ∴∠=∠-∠=︒-∠-∠;②当P 在BO 之间时(点P 不与点B ,O 重合),180CPD αβ∠=∠-︒+∠.理由:如图5,过P 作//PF AD 交CD 于F ,//AD BC ,////AD PF BC ∴,ADP DPF ∴∠=∠,BCP CPF ∠=∠,180BCP PCE ∠+∠=︒,PCE β∠=∠,180BCP β∴∠=︒-∠,又ADP α∠=∠180CPD DPF CPF αβ∴∠=∠-∠=∠+∠-︒.【点睛】本题考查了平行线的性质的应用,主要考查学生的推理能力,解决问题的关键是作辅助线构造内错角以及同旁内角.4.(1)证明见解析;(2)补图见解析;当点在上时,;当点在上时,.【分析】(1)过点作,根据平行线的性质即可求解;(2)分两种情况:当点在上,当点在上,再过点作即可求解.【详解】(1)证明:解析:(1)证明见解析;(2)补图见解析;当点C 在AG 上时,290AHB CBG ∠-∠=︒;当点C 在DG 上时,290AHB CBG ∠+∠=︒.【分析】(1)过点G 作//GE MN ,根据平行线的性质即可求解;(2)分两种情况:当点C 在AG 上,当点C 在DG 上,再过点H 作//HF MN 即可求解.【详解】(1)证明:如图,过点G 作//GE MN ,∴MAG AGE ∠=∠,∵//MN PQ ,∴//GE PQ .∴PBG BGE ∠=∠.∵BG AD ⊥,∴90AGB ∠=︒,∴90MAG PBG AGE BGE AGB ∠+∠=∠+∠=∠=︒.(2)补全图形如图2、图3,猜想:290AHB CBG ∠-∠=︒或290AHB CBG ∠+∠=︒.证明:过点H 作//HF MN .∴1AHF ∠=∠.∵//MN PQ ,∴//HF PQ∴2BHF ∠=∠,∴12AHB AHF BHF ∠=∠+∠=∠+∠.∵AH 平分MAG ∠,∴21MAG ∠=∠.如图3,当点C 在AG 上时,∵BH 平分PBC ∠,∴22PBC PBG CBG ∠=∠+∠=∠,∵//MN PQ ,∴MAG GDB ∠=∠,2212290AHB MAG PBG CBGGDB PBG CBG CBG∴∠=∠+∠=∠+∠+∠=∠+∠+∠=︒+∠即290AHB CBG ∠-∠=︒.如图2,当点C 在DG 上时,∵BH 平分PBC ∠,∴22PBC PBG CBG ∠=∠-∠=∠.∴2212290AHB MAG PBG CBG CBG ∠=∠+∠=∠+∠-∠=︒-∠.即290AHB CBG ∠+∠=︒.【点睛】本题考查了平行线的基本性质、角平分线的基本性质及角的运算,解题的关键是准确作出平行线,找出角与角之间的数量关系.5.(1)40°;(2)65°;(3)存在,56°或20°【分析】(1)依据平行线的性质以及角平分线的定义,即可得到∠PCG 的度数; (2)依据平行线的性质以及角平分线的定义,即可得到∠ECG=∠G解析:(1)40°;(2)65°;(3)存在,56°或20°【分析】(1)依据平行线的性质以及角平分线的定义,即可得到∠PCG 的度数;(2)依据平行线的性质以及角平分线的定义,即可得到∠ECG =∠GCF =25°,再根据PQ ∥CE ,即可得出∠CPQ =∠ECP =65°;(3)设∠EGC =4x ,∠EFC =3x ,则∠GCF =4x -3x =x ,分两种情况讨论:①当点G 、F 在点E 的右侧时,②当点G 、F 在点E 的左侧时,依据等量关系列方程求解即可.【详解】解:(1)∵∠CEB =100°,AB ∥CD ,∴∠ECQ =80°,∵∠PCF =∠PCQ ,CG 平分∠ECF ,∴∠PCG =∠PCF +∠FCG =12∠QCF +12∠FCE =12∠ECQ =40°;(2)∵AB ∥CD∴∠QCG =∠EGC ,∠QCG +∠ECG =∠ECQ =80°,∴∠EGC +∠ECG =80°,又∵∠EGC -∠ECG =30°,∴∠EGC =55°,∠ECG =25°,∴∠ECG =∠GCF =25°,∠PCF =∠PCQ =12(80°-50°)=15°,∵PQ ∥CE ,∴∠CPQ =∠ECP =65°;(3)设∠EGC =4x ,∠EFC =3x ,则∠GCF=∠FCD =4x -3x =x ,①当点G 、F 在点E 的右侧时,则∠ECG=x,∠PCF=∠PCD=32 x,∵∠ECD=80°,∴x+x+32x+32x=80°,解得x=16°,∴∠CPQ=∠ECP=x+x+32x=56°;②当点G、F在点E的左侧时,则∠ECG=∠GCF=x,∵∠CGF=180°-4x,∠GCQ=80°+x,∴180°-4x=80°+x,解得x=20°,∴∠FCQ=∠ECF+∠ECQ=40°+80°=120°,∴∠PCQ=12∠FCQ=60°,∴∠CPQ=∠ECP=80°-60°=20°.【点睛】本题主要考查了平行线的性质,解题时注意:两直线平行,同旁内角互补;两直线平行,内错角相等.二、解答题6.(1)146°;(2)∠AOG+∠NEF=90°;(3)见解析【分析】(1)作CP//a,则CP//a//b,根据平行线的性质求解.(2)作CP//a,由平行线的性质及等量代换得∠AOG+∠N解析:(1)146°;(2)∠AOG+∠NEF=90°;(3)见解析【分析】(1)作CP//a,则CP//a//b,根据平行线的性质求解.(2)作CP//a,由平行线的性质及等量代换得∠AOG+∠NEF=∠ACP+∠PCB=90°.(3)分类讨论点P在线段GF上或线段GF延长线上两种情况,过点P作a,b的平行线求解.【详解】解:(1)如图,作CP//a,∵a//b,CP//a,∴CP//a//b,∴∠AOG=∠ACP=56°,∠BCP+∠CEF=180°,∴∠BCP=180°-∠CEF,∵∠ACP+∠BCP=90°,∴∠AOG+180°-∠CEF=90°,∴∠CEF=180°-90°+∠AOG=146°.(2)∠AOG+∠NEF=90°.理由如下:如图,作CP//a,则CP//a//b,∴∠AOG=∠ACP,∠BCP+∠CEF=180°,∵∠NEF+∠CEF=180°,∴∠BCP=∠NEF,∵∠ACP+∠BCP=90°,∴∠AOG+∠NEF=90°.(3)如图,当点P在GF上时,作PN//a,连接PQ,OP,则PN//a//b,∴∠GOP=∠OPN,∠PQF=∠NPQ,∴∠OPQ=∠OPN+∠NPQ=∠GOP+∠PQF,∵∠GOC=∠GOP+∠POQ=135°,∴∠GOP=135°-∠POQ,∴∠OPQ=135°-∠POQ+∠PQF.如图,当点P在GF延长线上时,作PN//a,连接PQ,OP,则PN//a//b,∴∠GOP=∠OPN,∠PQF=∠NPQ,∵∠OPN=∠OPQ+∠QPN,∴∠GOP=∠OPQ+∠PQF,∴135°-∠POQ=∠OPQ+∠PQF.【点睛】本题考查平行线的性质的应用,解题关键是熟练掌握平行线的性质,通过添加辅助线及分类讨论的方法求解.7.(1)平行,理由见解析;(2)65°;(3)5秒或95秒【分析】(1)根据等角的补角相等求出∠3与∠4的补角相等,再根据内错角相等,两直线平行即可判定a∥b;(2)根据入射光线与镜面的夹角与反解析:(1)平行,理由见解析;(2)65°;(3)5秒或95秒【分析】(1)根据等角的补角相等求出∠3与∠4的补角相等,再根据内错角相等,两直线平行即可判定a∥b;(2)根据入射光线与镜面的夹角与反射光线与镜面的夹角相等可得∠1=∠2,然后根据平角等于180°求出∠1的度数,再加上40°即可得解;(3)分①AB与CD在EF的两侧,分别表示出∠ACD与∠BAC,然后根据两直线平行,内错角相等列式计算即可得解;②CD旋转到与AB都在EF的右侧,分别表示出∠DCF与∠BAC,然后根据两直线平行,同位角相等列式计算即可得解;③CD旋转到与AB都在EF 的左侧,分别表示出∠DCF与∠BAC,然后根据两直线平行,同位角相等列式计算即可得解.【详解】解:(1)平行.理由如下:如图1,∵∠3=∠4,∴∠5=∠6,∵∠1=∠2,∴∠1+∠5=∠2+∠6,∴a∥b(内错角相等,两直线平行);(2)如图2:∵入射光线与镜面的夹角与反射光线与镜面的夹角相等,∴∠1=∠2,∵入射光线a与水平线OC的夹角为40°,b垂直照射到井底,∴∠1+∠2=180°-40°-90°=50°,∴∠1=1×50°=25°,2∴MN与水平线的夹角为:25°+40°=65°,即MN与水平线的夹角为65°,可使反射光线b正好垂直照射到井底;(3)存在.如图①,AB与CD在EF的两侧时,∵∠BAF=105°,∠DCF=65°,∴∠ACD=180°-65°-3t°=115°-3t°,∠BAC=105°-t°,要使AB∥CD,则∠ACD=∠BAC,即115-3t=105-t,解得t=5;如图②,CD旋转到与AB都在EF的右侧时,∵∠BAF=105°,∠DCF=65°,∴∠DCF=360°-3t°-65°=295°-3t°,∠BAC=105°-t°,要使AB∥CD,则∠DCF=∠BAC,即295-3t=105-t,解得t=95;如图③,CD旋转到与AB都在EF的左侧时,∵∠BAF=105°,∠DCF=65°,∴∠DCF=3t°-(180°-65°+180°)=3t°-295°,∠BAC=t°-105°,要使AB∥CD,则∠DCF=∠BAC,即3t-295=t-105,解得t=95,此时t>105,∴此情况不存在.综上所述,t为5秒或95秒时,CD与AB平行.【点睛】本题考查了平行线的判定与性质,光学原理,读懂题意并熟练掌握平行线的判定方法与性质是解题的关键,(3)要注意分情况讨论.8.(1),见解析;(2);(3)60°【分析】(1)作EF//AB ,如图1,则EF//CD ,利用平行线的性质得∠1=∠BAE ,∠2=∠CDE ,从而得到∠BAE +∠CDE =∠AED ;(2)如图2,解析:(1)BAE CDE AED ∠+∠=∠,见解析;(2)12AFD AED ∠=∠;(3)60° 【分析】(1)作EF //AB ,如图1,则EF //CD ,利用平行线的性质得∠1=∠BAE ,∠2=∠CDE ,从而得到∠BAE +∠CDE =∠AED ;(2)如图2,由(1)的结论得∠AFD =∠BAF +∠CDF ,根据角平分线的定义得到∠BAF =12∠BAE ,∠CDF =12∠CDE ,则∠AFD =12(∠BAE +∠CDE ),加上(1)的结论得到∠AFD =12∠AED ;(3)由(1)的结论得∠AGD =∠BAF +∠CDG ,利用折叠性质得∠CDG =4∠CDF ,再利用等量代换得到∠AGD =2∠AED -32∠BAE ,加上90°-∠AGD =180°-2∠AED ,从而可计算出∠BAE 的度数.【详解】解:(1)BAE CDE AED ∠+∠=∠理由如下:作//EF AB ,如图1,//AB CD ,//EF CD ∴.1BAE ∴∠=∠,2CDE ∠=∠,BAE CDE AED ∴∠+∠=∠;(2)如图2,由(1)的结论得AFD BAF CDF ∠=∠+∠,BAE ∠、CDE ∠的两条平分线交于点F ,12BAF BAE ∴∠=∠,12CDF CDE ∠=∠, 1()2AFD BAE CDE ∴∠=∠+∠,BAE CDE AED ∠+∠=∠,12AFD AED ∴∠=∠; (3)由(1)的结论得AGD BAF CDG ∠=∠+∠,而射线DC 沿DE 翻折交AF 于点G ,4CDG CDF ∴∠=∠,11422()22AGD BAF CDF BAE CDE BAE AED BAE ∴∠=∠+∠=∠+∠=∠+∠-∠= 322AED BAE ∠-∠, 901802AGD AED ︒-∠=︒-∠,390218022AED BAE AED ∴︒-∠+∠=︒-∠, 60BAE ∴∠=︒.【点睛】本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.9.(1);(2),证明见解析;(3),证明见解析.【分析】(1)过点作,先根据平行线的性质、平行公理推论可得,从而可得,再根据平行线的性质可得,然后根据角平分线的定义可得,最后根据角的和差即可得; 解析:(1)90︒;(2)2APC AEC ∠=∠,证明见解析;(3)2360APC AEC ∠+∠=︒,证明见解析.【分析】(1)过点E 作//EF AB ,先根据平行线的性质、平行公理推论可得,AEF BAE CEF DCE ∠=∠∠=∠,从而可得AEC BAE DCE ∠=∠+∠,再根据平行线的性质可得180PAB PCD ∠+∠=︒,然后根据角平分线的定义可得11,22BAE PAB DCE PCD ∠=∠∠=∠,最后根据角的和差即可得; (2)过点E 作//EF AB ,过点P 作//PQ AB ,先根据(1)可得1()2AEC BAE DCE PAB PCD ∠=∠+∠=∠+∠,再根据(1)同样的方法可得APC PAB PCD ∠=∠+∠,由此即可得出结论;(3)过点E 作//EF AB ,过点P 作//PQ AB ,先根据(1)可得2PAB PCD AEC ∠+∠=∠,再根据平行线的性质、平行公理推论可得180,180APQ PAB CPQ PCD ∠=︒-∠∠=︒-∠,然后根据角的和差、等量代换即可得出结论.【详解】解:(1)如图,过点E 作//EF AB ,AEF BAE ∴∠=∠,//AB CD ,//EF CD ∴,CEF DCE ∴∠=∠,AEC AEF CEF BAE DCE ∴∠=∠+∠=∠+∠,又//AB CD ,且点P 运动到线段AC 上,180PAB PCD ∴∠+∠=︒,AE ∵平分PAB ∠,CE 平分PCD ∠, 11,22BAE PAB DCE PCD ∴∠=∠∠=∠, 111()90222AEC PAB PCD PAB PCD ∴∠=∠+∠=∠+∠=︒; (2)猜想2APC AEC ∠=∠,证明如下:如图,过点E 作//EF AB ,过点P 作//PQ AB ,由(1)已得:1()2AEC BAE DCE PAB PCD ∠=∠+∠=∠+∠, 同理可得:APC PAB PCD ∠=∠+∠,2APC AEC ∴∠=∠;(3)2360APC AEC ∠+∠=︒,证明如下:如图,过点E 作//EF AB ,过点P 作//PQ AB ,由(1)已得:1()2AEC BAE DCE PAB PCD ∠=∠+∠=∠+∠, 即2PAB PCD AEC ∠+∠=∠,//PQ AB ,180APQ PAB ∴∠+∠=︒,即180APQ PAB ∠=︒-∠,//AB CD ,//PQ CD ∴,180CPQ PCD ∴∠+∠=︒,即180CPQ PCD ∠=︒-∠,APC APQ CPQ ∴∠=∠+∠,180180PAB PCD =︒-∠+︒-∠,()360PAB PCD =︒-∠+∠,3602AEC =︒-∠,即2360APC AEC ∠+∠=︒.【点睛】本题考查了平行线的性质、平行公理推论、角平分线的定义等知识点,熟练掌握平行线的性质是解题关键.10.(1),;(2)15秒或63秒;(3)不发生变化,【分析】(1)利用非负数的性质解决问题即可.(2)分三种情形,利用平行线的性质构建方程即可解决问题.(3)由参数表示,即可判断.【详解】解析:(1)4a =,1b =;(2)15秒或63秒;(3)不发生变化,34BAC BCD ∠=∠【分析】(1)利用非负数的性质解决问题即可.(2)分三种情形,利用平行线的性质构建方程即可解决问题.(3)由参数t 表示BAC ∠,BCD ∠即可判断.【详解】解:(1)∵()2450a b a b -++-=, ∴4050a b a b -=⎧⎨+-=⎩, 4a ∴=,1b =;(2)设A 灯转动t 秒,两灯的光束互相平行,①当045t <<时,4(45)1t t =+⨯,解得15t =;②当4590t <<时,()418018045t t -=-+,解得63t =;③当90135t <<时,436045t t -=+,解得135t =,(不合题意)综上所述,当t =15秒或63秒时,两灯的光束互相平行;(3)设A 灯转动时间为t 秒,1804CAN t ∠=︒-,60(1804)4120BAC t t ∴∠=︒-︒-=-︒,又//PQ MN ,18041803BCA CBD CAN t t t ∴∠=∠+∠=+︒-=︒-,而90ACD ∠=︒,9090(1803)390BCD BCA t t ∴∠=︒-∠=︒-︒-=-︒,:4:3BAC BCD ∴∠∠=,即34BAC BCD ∠=∠.【点睛】本题考查平行线的性质和判定,非负数的性质等知识,解题的关键是理解题意,学会利用参数构建方程解决问题,属于中考常考题型.三、解答题11.[习题回顾]证明见解析;[变式思考] 相等,证明见解析;[探究延伸] ∠M+∠CFE=90°,证明见解析.【分析】[习题回顾]根据同角的余角相等可证明∠B=∠ACD ,再根据三角形的外角的性质即可解析:[习题回顾]证明见解析;[变式思考] 相等,证明见解析;[探究延伸]∠M+∠CFE=90°,证明见解析.【分析】[习题回顾]根据同角的余角相等可证明∠B=∠ACD ,再根据三角形的外角的性质即可证明;[变式思考]根据角平分线的定义和对顶角相等可得∠CAE=∠DAF 、再根据直角三角形的性质和等角的余角相等即可得出CFE ∠=CEF ∠;[探究延伸]根据角平分线的定义可得∠EAN=90°,根据直角三角形两锐角互余可得∠M+∠CEF=90°,再根据三角形外角的性质可得∠CEF=∠CFE ,由此可证∠M+∠CFE=90°.【详解】[习题回顾]证明:∵∠ACB=90°,CD 是高,∴∠B+∠CAB=90°,∠ACD+∠CAB=90°,∴∠B=∠ACD ,∵AE 是角平分线,∴∠CAF=∠DAF ,∵∠CFE=∠CAF+∠ACD ,∠CEF=∠DAF+∠B ,∴∠CEF=∠CFE ;[变式思考]相等,理由如下:证明:∵AF 为∠BAG 的角平分线,∴∠GAF=∠DAF ,∵∠CAE=∠GAF ,∴∠CAE=∠DAF ,∵CD 为AB 边上的高,∠ACB=90°,∴∠ADC=90°,∴∠ADF=∠ACE=90°,∴∠DAF+∠F=90°,∠E+∠CAE=90°,∴∠CEF=∠CFE ;[探究延伸]∠M+∠CFE=90°,证明:∵C 、A 、G 三点共线 AE 、AN 为角平分线,∴∠EAN=90°,又∵∠GAN=∠CAM ,∴∠M+∠CEF=90°,∵∠CEF=∠EAB+∠B ,∠CFE=∠EAC+∠ACD ,∠ACD=∠B ,∴∠CEF=∠CFE ,∴∠M+∠CFE=90°.【点睛】本题考查三角形的外角的性质,直角三角形两锐角互余,角平分线的有关证明,等角或同角的余角相等.在本题中用的比较多的是利用等角或同角的余角相等证明角相等和三角形一个外角等于与它不相邻的两个内角之和,理解并掌握是解决此题的关键.12.(1)40°;(2)的值不变,比值为;(3)∠OEC=∠OBA=60°.【分析】(1)根据OB 平分∠AOF ,OE 平分∠COF ,即可得出∠EOB=∠EOF+∠FOB=∠COA ,从而得出答案;(2解析:(1)40°;(2):OBC OFC ∠∠的值不变,比值为12;(3)∠OEC=∠OBA=60°.【分析】(1)根据OB 平分∠AOF ,OE 平分∠COF ,即可得出∠EOB=∠EOF+∠FOB=12∠COA ,从而得出答案;(2)根据平行线的性质,即可得出∠OBC=∠BOA ,∠OFC=∠FOA ,再根据∠FOA=∠FOB+∠AOB=2∠AOB ,即可得出∠OBC :∠OFC 的值为1:2.(3)设∠AOB=x ,根据两直线平行,内错角相等表示出∠CBO=∠AOB=x ,再根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠OEC ,然后利用三角形的内角和等于180°列式表示出∠OBA ,然后列出方程求解即可.【详解】(1)∵CB ∥OA∴∠C+∠COA=180°∵∠C=100°∴∠COA=180°-∠C=80°∵∠FOB=∠AOB ,OE 平分∠COF∴∠FOB+∠EOF=12(∠AOF+∠COF)=12∠COA=40°;∴∠EOB=40°;(2)∠OBC:∠OFC的值不发生变化∵CB∥OA∴∠OBC=∠BOA,∠OFC=∠FOA∵∠FOB=∠AOB∴∠FOA=2∠BOA∴∠OFC=2∠OBC∴∠OBC:∠OFC=1:2(3)当平行移动AB至∠OBA=60°时,∠OEC=∠OBA.设∠AOB=x,∵CB∥AO,∴∠CBO=∠AOB=x,∵CB∥OA,AB∥OC,∴∠OAB+∠ABC=180°,∠C+∠ABC=180°∴∠OAB=∠C=100°.∵∠OEC=∠CBO+∠EOB=x+40°,∠OBA=180°-∠OAB-∠AOB=180°-100°-x=80°-x,∴x+40°=80°-x,∴x=20°,∴∠OEC=∠OBA=80°-20°=60°.【点睛】本题主要考查了平行线、角平分线的性质以及三角形内角和定理,熟记各性质并准确识图理清图中各角度之间的关系是解题的关键.13.(1)①45°;②∠F=a;(2)∠F+∠H的值不变,是定值180°.【分析】(1)①②依据AD平分∠CAE,CF平分∠ACB,可得∠CAD=∠CAE,∠ACF=∠ACB,依据∠CAE是△ABC解析:(1)①45°;②∠F=12a;(2)∠F+∠H的值不变,是定值180°.【分析】(1)①②依据AD平分∠CAE,CF平分∠ACB,可得∠CAD=12∠CAE,∠ACF=12∠ACB,依据∠CAE是△ABC的外角,可得∠B=∠CAE-∠ACB,再根据∠CAD是△ACF的外角,即可得到∠F=∠CAD-∠ACF=12∠CAE-12∠ACB=12(∠CAE-∠ACB)=12∠B;(2)由(1)可得,∠F=12∠ABC,根据角平分线的定义以及三角形内角和定理,即可得到∠H=90°+12∠ABG,进而得到∠F+∠H=90°+12∠CBG=180°.解:(1)①∵AD平分∠CAE,CF平分∠ACB,∴∠CAD=12∠CAE,∠ACF=12∠ACB,∵∠CAE是△ABC的外角,∴∠B=∠CAE﹣∠ACB,∵∠CAD是△ACF的外角,∴∠F=∠CAD﹣∠ACF=12∠CAE﹣12∠ACB=12(∠CAE﹣∠ACB)=12∠B=45°,故答案为45°;②∵AD平分∠CAE,CF平分∠ACB,∴∠CAD=12∠CAE,∠ACF=12∠ACB,∵∠CAE是△ABC的外角,∴∠B=∠CAE﹣∠ACB,∵∠CAD是△ACF的外角,∴∠F=∠CAD﹣∠ACF=12∠CAE﹣12∠ACB=12(∠CAE﹣∠ACB)=12∠B=12a;(2)由(1)可得,∠F=12∠ABC,∵∠AGB与∠GAB的角平分线交于点H,∴∠AGH=12∠AGB,∠GAH=12∠GAB,∴∠H=180°﹣(∠AGH+∠GAH)=180°﹣12(∠AGB+∠GAB)=180°﹣12(180°﹣∠ABG)=90°+12∠ABG,∴∠F+∠H=12∠ABC+90°+12∠ABG=90°+12∠CBG=180°,∴∠F+∠H的值不变,是定值180°.【点睛】本题主要考查了三角形内角和定理、三角形外角性质的综合运用,熟练运用定理是解题的关键.14.∠DPC=α+β,理由见解析;(1)70 ;(2) ∠DPC=α –β,理由见解析.【解析】(1)过P作PE∥AD交CD于E,推出AD∥PE∥BC,根据平行线的性质得出∠α=∠DPE,∠β=∠C解析:∠DPC=α+β,理由见解析;(1)70 ;(2) ∠DPC=α –β,理由见解析.【解析】(1)过P作PE∥AD交CD于E,推出AD∥PE∥BC,根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出答案;(2)化成图形,根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出答案.【问题探究】解:∠DPC=α+β过P作PH∥DF∵DF∥CE,∴∠PCE=∠1=α,∠PDF=∠2∵∠DPC=∠2+∠1=α+β【问题迁移】(1)70(图1)(图2)(2) 如图1,∠DPC=β -α∵DF∥CE,∴∠PCE=∠1=β,∵∠DPC=∠1-∠FDP=∠1-α.∴∠DPC=β -α如图2,∠DPC= α -β∵DF∥CE,∴∠PDF=∠1=α∵∠DPC=∠1-∠ACE=∠1-β.∴∠DPC=α - β15.(1)60,30;(2)∠BAD=2∠CDE,证明见解析;(3)成立,∠BAD=2∠CDE,证明见解析【分析】(1)如图①,将∠BAC=100°,∠DAC=40°代入∠BAD=∠BAC-∠DAC解析:(1)60,30;(2)∠BAD=2∠CDE,证明见解析;(3)成立,∠BAD=2∠CDE,证明见解析【分析】(1)如图①,将∠BAC=100°,∠DAC=40°代入∠BAD=∠BAC-∠DAC,求出∠BAD.在△ABC 中利用三角形内角和定理求出∠ABC=∠ACB=40°,根据三角形外角的性质得出∠ADC=∠ABC+∠BAD=100°,在△ADE中利用三角形内角和定理求出∠ADE=∠AED=70°,那么∠CDE=∠ADC-∠ADE=30°;(2)如图②,在△ABC和△ADE中利用三角形内角和定理求出∠ABC=∠ACB=40°,∠ADE=∠AED=1802n︒-.根据三角形外角的性质得出∠CDE=∠ACB-∠AED=1002n-︒,再由∠BAD=∠DAC-∠BAC得到∠BAD=n-100°,从而得出结论∠BAD=2∠CDE;(3)如图③,在△ABC和△ADE中利用三角形内角和定理求出∠ABC=∠ACB=40°,∠ADE=∠AED=1802n︒-.根据三角形外角的性质得出∠CDE=∠ACD-∠AED=1002n︒+,再由∠BAD=∠BAC+∠DAC得到∠BAD=100°+n,从而得出结论∠BAD=2∠CDE.【详解】解:(1)∠BAD=∠BAC-∠DAC=100°-40°=60°.∵在△ABC中,∠BAC=100°,∠ABC=∠ACB,∴∠ABC=∠ACB=40°,∴∠ADC=∠ABC+∠BAD=40°+60°=100°.∵∠DAC=40°,∠ADE=∠AED,∴∠ADE=∠AED=70°,∴∠CDE=∠ADC-∠ADE=100°-70°=30°.故答案为60,30.(2)∠BAD=2∠CDE,理由如下:如图②,在△ABC中,∠BAC=100°,∴∠ABC=∠ACB=40°.在△ADE中,∠DAC=n,∴∠ADE=∠AED=1802n︒-,∵∠ACB=∠CDE+∠AED,∴∠CDE=∠ACB-∠AED=40°-1802n︒-=1002n-︒,∵∠BAC=100°,∠DAC=n,∴∠BAD=n-100°,∴∠BAD=2∠CDE.(3)成立,∠BAD=2∠CDE,理由如下:如图③,在△ABC中,∠BAC=100°,∴∠ABC=∠ACB=40°,∴∠ACD=140°.在△ADE中,∠DAC=n,∴∠ADE=∠AED=1802n︒-,∵∠ACD=∠CDE+∠AED,∴∠CDE=∠ACD-∠AED=140°-1802n︒-=1002n︒+,∵∠BAC=100°,∠DAC=n,∴∠BAD=100°+n,∴∠BAD=2∠CDE.【点睛】本题考查了三角形内角和定理,三角形外角的性质,从图形中得出相关角度之间的关系是解题的关键.。
2021-2022学年重庆市渝中区巴蜀中学初一数学第二学期期末试卷及解析

2021-2022学年重庆市渝中区巴蜀中学初一数学第二学期期末试卷A 卷一、选择题:(本大题12个小题,每小题4分,共48分) 1.下列四个图形中,是轴对称图形的是( )A .B .C .D .2.在实数:3.142,4,227,π中,无理数是( ) A .3.142B .4C .227D .π3.下列调查中,适宜采用全面调查(普查)方式的是( ) A .对全国七年级学生视力情况的调查B .调查重庆市民对中央电视台2022年春节联欢晚会的满意度C .疫情期间,对进入重医附一院的人士“渝康码”的检查D .对重庆市各大药房口罩销售情况的调查 4.估算262-的值是在( ) A .2到3之间B .3到4之间C .4到5之间D .5到6之间5.下列生活中的实例利用到三角形的稳定性的是( ) A .自行车的三角车架 B .用两颗钉子把木条固定在墙上 C .学校大门口的伸缩门 D .四条腿的方桌6.已知点(23,1)A m --在第四象限,则m 的取值范围是( ) A .32m <B .32m >-C .32m <-D .32m >7.如图,在ABC ∆和ABD ∆中,ABC ABD ∠=∠,则添加以下条件,不能判定ABC ABD ∆≅∆的是( )A .BC BD =B .CAB DAB ∠=∠C .CD ∠=∠ D .AC AD =8.下列对ABC ∆的判断,错误的是( )A .若AB AC =,60B ∠=︒,则ABC ∆是等边三角形 B .若::2:3:5A B C ∠∠∠=,则ABC ∆是直角三角形 C .若20A ∠=︒,80B ∠=︒,则ABC ∆是等腰三角形D .若AB BC =,40C ∠=︒,则40B ∠=︒ 9.下列叙述正确的是( ) A .若a b >,则33a b +>+ B .若a b >,则22a b ->-C .若a b >,则22a b >D .若a b <,则35a b > 10.如图,ABC ∆中,2CE BE =,点D 为AC 中点,连接DE 、AE ,取DE 的中点F ,连接AF ,若AEF ∆的面积是1,则ABC ∆的面积是( )A .2B .4C .6D .811.如图,在ABC ∆的边BC 上有两点D 、E ,连接AD ,AE ,若AB BE =,CA CD =,且100BAC ∠=︒,那么DAE ∠的度数为( )A .80︒B .40︒C .30︒D .100︒12.若关于x 的不等式组6511462x a x x -⎧⎪-⎨-<⎪⎩恰好有3个整数解,且关于y 的方程11a y +=-的解是非负数,则符合条件的所有整数a 的个数是( ) A .2个B .3个C .4个D .5个二、填空题:(本大题6个小题,每小题4分,共24分) 13.64的算术平方根是 .14.已知(3,4)P -,则P 点到x 轴的距离为 .15.一个凸n 边形的内角和是540︒,则n = .16.若关于x 、y 的等式2|3|0x y -++=成立,则x y += .17.如图,将长方形纸片ABCD 折叠,使点D 与点B 重合,点C 落在点C 处,折痕为EF ,若40ABE ∠=︒,那么EFC '∠的度数为 .18.如图,在ABC ∆中,D 为边AC 上一点,且BD 平分ABC ∠,过A 作AE BD ⊥于E .若52ABC ∠=︒,32C ∠=︒, 5.2AB =,9.8BC =,则AE = .三、解答题:(本大题5个小题,共36分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上. 19.计算:228(2)(5)+-+. 20.解不等式:41132x x -+>,并在数轴上表示其解集.21.某学校物理组教师为了激发八年级学生学习物理的学起,举办了一场《物理向未来》的综艺直播秀.分别演示了《倔强的尺子》、《发电很容易》、《人工撒花机》、《神奇的摆动》四个实验,学生们被奇妙的实验深深吸引,每个实验都那么的不可思议,为了了解学生心中“最不可思议的实验”的情况,随机抽取了部分学生(每人只选择一个实验)进行调查,如表和图是根据调查结果绘制的统计图表的一部分和扇形统计图.实验名称 频数(人)频率 A .《倔强的尺子》 12 0.15B .《发电很容易》 16mC.《人工撒花机》n0.3D.《神奇的摆动》28根据以上信息,回答下列问题:(1)本次调查的样本容量为,m=;(2)扇形统计图中认为“最不可思议的实验”是D扇形的圆心角度;(3)若该八年级校共有600名学生,请根据调查结果,估计认为“最不可思议的实验”是B的学生人数.22.在每个小正方形的边长都为1的网格中,有一个格点ABC∆(即三角形的顶点都在格点上),建立如图所示的直角坐标系.(1)作出ABC∆关于x轴对称的图形△A B C;111(2)将ABC∆向右平移5个单位得△A B C;222(3)则ABC∆的面积为.23.尺规作图并完成证明.如图,点D、点F在ABCAF BC,ABD CAF∠=∠,∆外,连接AF、AD、BD,且//=.BD AC(1)用尺规完成以下基本作图:作ABC∠的平分线BE交AF于点E,连接CE(保留作图痕迹,不写作法);(2)根据(1)中作图,求证:AD CE=;请完善下面的证明过程.证明:BE 平分ABC ∠, CBE ∴∠= . //AF BC . CBE ∴∠= .ABE AEB ∴∠=∠.∴ .在ACE 和BDA ∆中, AE AB ABD CAF AC BD =⎧⎪∠=∠⎨⎪=⎩. ACE BDA ∴∆≅∆. AD CE ∴=.B 卷四、填空题:(本大题4个小题,每小题3分.共12分)请将每小题的答案填在答题卡中对应的横线上. 24.若有理数a 、b 满足26946(0)a b a +=+>.则a b -的值为 . 25.等腰ABC ∆两腰上的高所在直线夹角为45︒,则顶角A ∠的度数为 .26.如图,等腰直角ABC 中,90ACB ∠=︒,45ABC ∠=︒,CH AB ⊥于点H ,AD 垂直平分BE ,交BC 于点F ,交CH 于点G ,则下列结论中正确的有 . ①EBC CAF ∠=∠; ②AG DE =; ③BC CG AB +=; ④ACG BFGHS S∆=.27.“鲁巴好少年,一起向未来”,重庆市鲁能巴蜀中学校春季运动会在4月27日如期举行.各班同学积极参与,热情高涨;运动员挥洒汗水,激昂赛场;场下观众文明观赛,有序加油.后勤团队也不甘示弱,积极为同学们做好各种后勤保障,其中,采购小组的同学们就为全班同学准备了百事可乐,红牛和脉动三种饮料.已知百事可乐、红牛和脉动的单价之和为14元,计划购买百事可乐,红牛和脉动的数量总共不超过160瓶,其中脉动的单价为每瓶5元,计划购买20瓶,百事可乐的数量不多于红牛数量的一半,但至少购买40瓶,结果,在做预算时,将百事可乐和红牛的单价弄反了,结果在实际购买时,总费用比预算多了150元.若百事可乐、红牛和脉动的单价均为整数,则实际购买百事可乐、红牛和脉动的总费用最多需要花费.五、解答题:(本大题3个小题,每小题10分,共30分)28.吃粽子是端午节的习俗,某糕点店推出的“海鸭蛋蛋黄粽”和“红豆鲜肉粽”深受顾客喜欢.“海鸭蛋蛋黄粽“每个售价是“红豆鲜肉粽”的53倍,去年端午节期间,“海鸭蛋蛋黄粽”销量为3500个,“红豆鲜肉粽”销量为2500个,两款粽子销售额共为50000元.(1)求“海鸭蛋蛋黄粽”和“红豆鲜肉粽”的售价各是多少元?(2)糕点店在今年端午节前夕,“海鸭蛋蛋黄粽”和“红豆鲜肉粽”的进货量均为去年端午节期间两种粽子销售量的两倍,计划利用店庆活动让利于新老顾客,对两种粽子都开展降价的促销活动;其中,“海鸭蛋蛋黄粽”每个让利0.5a元销售(a为整数),“红豆鲜肉粽”则按原售价打(5)a+折出售,并且降价后的“海鸭蛋蛋黄粽”售价不低于“红豆鲜肉粽”售价的2倍,最终两种粽子全部都销售了出去,且总销售额不超过84000元,求出a的值.29.一个四位正整数A满足百位上的数字比千位上的数字小2.个位上的数字比十位上的数字小2,百位上的数字与个位上的数字不相等且各个数位上的数字均不为零,则称A为“比翼双飞数”,将“比翼双飞数“A的千位和十位数字组成的两位数与百位和个位数字组成的两位数的和记为F(A),将“比翼双飞数“A的千位和百位数字组成的两位数与十位和个位数字组成的两位数的差记为f(A).例如:四位正整数9764,972-=,642-=且74≠,9764∴是“比翼双飞数”,此时,F(A)9674170=+=,f(A)976433=-=.(1)判断:8631,5322是否是“比翼双飞数”,并说明理由;(2)若“比翼双飞数”A能被2整除,且满足F(A)f-(A)能被4整除,求F(A)的值.30.在Rt ABC∆中,AB BC=,在Rt CEH∆中,45CEH∠=︒,90ECH∠=︒,连接AE.(1)如图1,若点E在CB延长线上,连接AH,且6AH=,求AE的长;(2)如图2,若点E在AC上,F为AE的中点,连接BF、BH,当2BH BF=,1452EHB HBF∠+∠=︒时,求证:AE CE=;(3)如图3,若点E在线段AC上运动,取AE的中点F,作//FH BC'交AB于H,连接BE并延长到D,使得BE DE=,连接AD、CD;在线段BC上取一点G,使得CG AF=,并连接EG;若点E在线段AC 上运动的过程中,当ACD的周长取得最小值时,AED∆的面积为25,请直接写出GE BH+'的最小值.答案与解析A卷一、选择题:(本大题12个小题,每小题4分,共48分)1.解:A.不是轴对称图形,故此选项不合题意;B.不是轴对称图形,故此选项不合题意;C.是轴对称图形,故此选项符合题意;D.不是轴对称图形,故此选项不合题意;故选:C.2.解:A、3.142是有限小数,属于有理数,故本选项不合题意;B2,2是整数,属于有理数,故本选项不合题意;C、227是分数,属于有理数,故本选项不合题意;D、π是无理数,故本选项符合题意.故选:D.3.解:A.对全国七年级学生视力情况的调查,适合使用抽样调查,因此选项A不符合题意;B.调查重庆市民对中央电视台2022年春节联欢晚会的满意度,适合使用抽样调查,因此选项B不符合题意;C.疫情期间,对进入重医附一院的人士“渝康码”的检查,适合使用全面调查,因此选项C符合题意;D.对重庆市各大药房口罩销售情况的调查,适合使用抽样调查,因此选项D不符合题意;故选:C.4.解:5266<<,∴减2得:324<<,2的值在3到4之间,故选:B.5.解:A、自行车的三角车架是利用了三角形的稳定性,符合题意;B、用两颗钉子把木条固定在墙上是利用了两点确定一条直线,不符合题意;C、学校大门口的伸缩门利用了四边形的不稳定性,不符合题意;D、四条腿的方桌不是利用了三角形的稳定性,不符合题意.故选:A.6.解:点(23,1)A m --在第四象限, 230m ∴->,则32m >, 故选:D .7.解:A .AB AB =,ABC ABD ∠=∠,BC BD =,符合全等三角形的判定定理SAS ,能推出ABC ABD ∆≅∆,故本选项不符合题意;B .CAB DAB ∠=∠,AB AB =,ABC ABD ∠=∠,符合全等三角形的判定定理ASA ,能推出ABC ABD ∆≅∆,故本选项不符合题意;C .CD ∠=∠,ABC ABD ∠=∠,AB AB =,符合全等三角形的判定定理AAS ,能推出ABC ABD ∆≅∆,故本选项不符合题意;D .AB AB =,AC AD =,ABC ABD ∠=∠,不符合全等三角形的判定定理,不能推出ABC ABD ∆≅∆,故本选项符合题意; 故选:D . 8.解:A .AB AC =,60B ∠=︒,ABC ∴∆是等边三角形(有一个角是60︒的等腰三角形是等边三角形),故本选项不符合题意; B .::2:3:5A B C ∠∠∠=,180A B C ∠+∠+∠=︒,∴最大角C ∠的度数是518090235︒⨯=︒++,ABC ∴∆是直角三角形,故本选项不符合题意; C .20A ∠=︒,80B ∠=︒, 18080C A B ∴∠=︒-∠-∠=︒, B C ∴∠=∠,ABC ∴∆是等腰三角形,故本选项不符合题意;D .AB BC =,C A ∴∠=∠, 40C ∠=︒, 40A ∴∠=︒,180100B A C ∴∠=︒-∠-∠=︒,故本选项符合题意;故选:D . 9.解:a b >, 33a b ∴+>+,∴选项A 符合题意;a b >, 22a b ∴-<-,∴选项B 不符合题意;a b >时,22a b >不一定成立,例如:24>-,但是222(4)<-,∴选项C 不符合题意;a b <时,35a b>不一定成立, 例如:35<,但是3535=,∴选项D 不符合题意.故选:A .10.解:ABC ∆中,2CE BE =, 2AEC ABE S S ∆∆∴=,3ABC ABE S S ∆∆=,F 为DE 的中点,1AEF AFD S S ∆∆∴==, 2AED S ∆∴=,点D 为AC 中点, 2224AEC AED S S ∆∆∴==⨯=, 2ABE S ∆∴=, 236ABC S ∆∴=⨯=,ABC ∴∆的面积是6.故选:C . 11.解:AB BE =,BAE BEA ∴∠=∠,1802B BAE ∴∠=︒-∠,① CD CA =, CAD CDA ∴∠=∠,1802C CAD ∴∠=︒-∠,②①+②得:3602()B C BAE CAD ∠+∠=︒-∠+∠,1803602[()()]BAC BAD DAE DAE CAE ∴︒-∠=︒-∠+∠+∠+∠,1802[()]BAC BAD DAE CAE DAE ∴-∠=︒-∠+∠+∠+∠,1802()BAC BAC DAE ∴-∠=︒-∠+∠,2180DAE BAC ∴∠=︒-∠,100BAC ∠=︒,218010080DAE ∴∠=︒-︒=︒,40DAE ∴∠=︒.故选:B .12.解:6511462x a x x -⎧⎪⎨--<⎪⎩①②,解不等式①得:56a x +, 解不等式②得:4x <,∴原不等式组的解集为:546a x +<, 不等式组恰好有3个整数解,5016a +∴<, 51a ∴-<,11a y +=-,解得:2y a =+,方程的解是非负数, 20a ∴+,2a ∴-, 综上所述,21a -,∴符合条件的所有整数a 的值为:2-,1-,0,1,∴符合条件的所有整数a 的个数为4,故选:C .二、填空题:(本大题6个小题,每小题4分,共24分)请将每小题的答案直接填在答题卡中对应的横线上.13.解:2864=∴8=.故答案为:8.14.解:(3,4)P -,则P 点到x 轴的距离为:4.故答案为:4.15.解:根据题意得,(2)180540n -⋅︒=︒,解得5n =,故答案为:5.16.解:|3|0y +=,20x ∴-=,30y +=,2x ∴=,3y =-,231x y ∴+=-=-.故答案为:1-.17.解:Rt ABE ∆中,40ABE ∠=︒,50AEB ∴∠=︒,由折叠的性质知:BEF DEF ∠=∠,而180130BED AEB ∠=︒-∠=︒,65DEF ∴∠=︒,//AD BC ,180EFC DEF ∴∠+∠=︒,180115EFC DEF ∴∠=︒-∠=︒,由折叠的性质得,115EFC EFC '∠=∠=︒,故答案为:115︒.18.解:延长AE 交BC 于F , BD 平分ABC ∠,ABE FBE ∴∠=∠,在ABE ∆和FBE ∆中,90AEB FEB BE BEABE FBE ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩, ()ABE FBE ASA ∴∆≅∆,AE EF ∴=, 5.2AB BF ==, 1(18052)642BAF BFA ∴∠=∠=⨯︒-︒=︒, 32C ∠=︒,32CAF AFB C ∴∠=∠-∠=︒,CAF C ∴∠=∠,AF CF ∴=,9.8BC =,4.6CF BC BF ∴=-=,4.6AF ∴=,2.3AE ∴=,故答案为:2.3.三、解答题:(本大题5个小题,共36分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上.19.解:228(2)(5)-825=++15=.20.解:41132x x -+>, 去分母,得2(41)3(1)x x ->+,移项,得8332x x ->+,合并同类项,得55x >,化系数为1,得1x >.所以在数轴上表示为:.21.解:(1)本次调查的样本容量为:120.1580÷=,16800.2m=÷=,故答案为:80,0.2;(2)扇形统计图中认为“最不可思议的实验”是D扇形的圆心角为:28 36012680︒⨯=︒,故答案为:126;(3)6000.2120⨯=(人),答:估计认为“最不可思议的实验”是B的学生人数为120人.22.解:(1)如图所示,△111A B C即为所求.(2)如图所示,△222A B C即为所求.(3)ABC∆的面积为11111 342314132222⨯-⨯⨯-⨯⨯-⨯⨯=,故答案为:112.23.(1)解:图形如图所示:(2)证明:BE平分ABC∠,CBE ABE ∴∠=∠,//AF BC ,CBE AEB ∴∠=∠,ABE AEB ∴∠=∠,AE AB ∴=,在ACE 和BDA ∆中,AE AB ABD CAF AC BD =⎧⎪∠=∠⎨⎪=⎩,()ACE BDA SAS ∴∆≅∆,AD CE ∴=.故答案为:ABE ∠,AEB ∠,AE AB =.B 卷四、填空题:(本大题4个小题,每小题3分.共12分)请将每小题的答案填在答题卡中对应的横线上.24.解:由a ,b 为有理数,满足26946(0)a b a +=+>,可得29a =,4b =,0a >,3a ∴=,341a b ∴-=-=-.故答案为:1-.25.解:如图,当BAC ∠是钝角时,由题意:AB AC =,90AEH ADH ∠=∠=︒,45EHD ∠=︒,360909045135BAC EAD ∴∠=∠=︒-︒-︒-︒=︒;如图,当A ∠是锐角时,由题意:AB AC =,90CDA BEA ∠=∠=︒,45CHE ∠=︒,180135DHE CHE ∴∠=︒-∠=︒,360909013545A ∴∠=︒-︒-︒-︒=︒,故答案为:135︒或45︒.26.解:ABC ∆是等腰直角三角形,90ACB ∠=︒,AC BC ∴=,AD BE ⊥,90ADE ACB BCE ∴∠=∠=∠=︒,90E EBC E CAF ∴∠+∠=︒=∠+∠,EBC CAF ∴∠=∠,故①正确;在BCE ∆和ACF ∆中,EBC CAF AC BCACF BCE ∠=∠⎧⎪=⎨⎪∠=∠⎩, ()BCE ACF ASA ∴∆≅∆,EC CF ∴=, AD 垂直平分BE ,AB AE ∴=,AD BE ⊥,BD DE =,BAD CAD ∴∠=∠,CH AB ⊥,90CHA ACB ∴∠=︒=∠,90BAD AGH CAD CFA ∴∠+∠=︒=∠+∠,CFA AGH CGF ∴∠=∠=∠,CG CF CE ∴==,CG BC CE AC AE AB ∴+=+==,故③正确;故答案为:①③.27.解:设购买x 瓶百事可乐,y 瓶红牛,百事可乐的单价为m 元,则红牛的单价为145(9)m m --=-元, 依题意得:(9)[(9)]150xm y m x m ym +---+=, 整理得:15092y x m -=-, 12x y ,40x , 20160x y ∴++,140x y ∴+,又x ,y ,m 均为正整数,12x y , y x ∴-是正整数,4.5m <,927m ∴-=(舍去)或925m -=或923m -=或921m -=,2m ∴=或3m =或4m =,当2m =时,97m -=,30y x -=,∴4030140x x x ⎧⎨++⎩, 解得:4055x ,此时实际购买这三种物品的总费用为:5202710027(30)9310x y x x x ⨯++=+++=+,∴当x 取最大值55时,总费用最大为955310805⨯+=(元)(不合题意舍去); 当3m =时,96m -=,50y x -=,4050140x x x ⎧⎨++⎩, 解得4045y ,∴此时实际购买这三种物品的总费用为:52036(50)9400x x x ⨯+++=+,∴当x 取最大值45时,总费用最大为945400805⨯+=(元);当4m =时,95m -=,150y x -=,∴40150140x x x ⎧⎨++⎩, 此时不等式组无解.综上所述,实际购买百事可乐、红牛和脉动的总费用最多需要花费805元. 故答案为:805元.五、解答题:(本大题3个小题,每小题10分,共30分)28.解:(1)设“红豆鲜肉粽”的售价是x 元,则“海鸭蛋蛋黄粽”的售价是53x 元, 依题意得:535002500500003x x ⨯+=, 解得:6x =, ∴5561033x =⨯=. 答:“海鸭蛋蛋黄粽”的售价为10元,“红豆鲜肉粽”的售价是6元.(2)依题意得:5100.52610535002(100.5)2500268400010a a a a +⎧-⨯⨯⎪⎪⎨+⎪⨯⨯-+⨯⨯⨯⎪⎩, 解得:40217a , 又a 为整数,2a ∴=.答:a 的值为2.29.解:(1)8631是“比翼双飞数”,5322不是“比翼双飞数”.理由如下: 862-=,312-=且61≠,8631∴是“比翼双飞数”, 532-=,但2202-=≠,5322∴不是“比翼双飞数”; (2)设“比翼双飞数” (2)(2)(A a a b b a b =++≠,a 、b 为整数,17a ,17)b , “比翼双飞数” A 能被2整除,∴1000(2)10010(2)5505101022a ab b b a b +++++=+++为整数, b ∴为偶数,2b ∴=或4或6,F (A )10(2)21020222a b a b a b =+++++=++,f (A )[10(2)][10(2)]1111a a b b a b =++-++=-,F ∴(A )f -(A )91322a b =++, F (A )f -(A )能被4整除, ∴91322223544a b a b a b ++++=+++为整数, ∴24a b ++为整数, 4a ∴=,2b =或2a =,4b =或6a =,4b =或4a =,6b =, 6442A ∴=或4264或8664或6486F ∴(A )6442=+或4624+或8664+或6846+,即F (A )106=或70或150或114.30.(1)解:在Rt ABC ∆中,AB BC =,45BAC ACB ∴∠=∠=︒,90ECH ∠=︒,45ACH ∴∠=︒,ACE ACH ∴∠=∠,在Rt CEH ∆中,45CEH ∠=︒,45CHE ∴∠=︒,CE CH ∴=,AC AC =,()ACE ACH SAS ∴∆≅∆,6AE AH ∴==;(2)证明:如图1,连接BE ,设BH 与AC 交于点G ,1452EHB HBF ∠+∠=︒,90ABC ∠=︒, 1452ABF HBF ∴∠+∠=︒, BCH ABG ∴∠=∠,AB AC =,45A ACB ∠=∠=︒,()ABF CBG ASA ∴∆≅∆,BG BF ∴=,2BH BF =,2BH BG ∴=,45HEG BCG ∠=∠=︒,EGH CGB ∠=∠,()EGH CGB AAS ∴∆≅∆,EG CG ∴=,∴四边形EBCH 是平行四边形,//BE CH ∴,90BEG ECH ∴∠=∠=︒,AE CE ∴=;(3)解:如图2,作//DN AC 作点A 的对称点A ',连接AC 交DN 于D ',连接BD ',交AC 与E ', 则当点D 在D '处,点E 在点E '处时,ACD ∆的周长最小,此时ACD ∆为等腰直角三角形, 21252ADE S AE ∆='=, 52AE ∴'=2102AC AE ∴='=210AB BC AC ∴===, 15222AF AE ==第21页(共21页)52H F AH AF ∴'='==, 5151022BH ∴'=-=, 作GR CE ⊥'于R ,在Rt CGR ∆中,12CG AF ==45BAC ∠=︒,52222GR CR ∴===⨯=, 在Rt GRE ∆'中,52E R E C CR '='-=,E G '==152GE BH ∴+'=+.。
巴蜀初一下期末数学试卷

一、选择题(每题5分,共20分)1. 下列各数中,正数是()A. -2B. 0C. 1.5D. -0.52. 下列各数中,有理数是()A. √2B. πC. -√3D. 3/43. 已知a、b是实数,且a+b=0,则下列说法正确的是()A. a=0,b≠0B. b=0,a≠0C. a、b同时为0D. 无法确定4. 下列各式中,等式成立的是()A. (x+1)^2 = x^2 + 2x + 1B. (x-1)^2 = x^2 - 2x + 1C. (x+1)^2 = x^2 - 2x + 1D. (x-1)^2 = x^2 + 2x - 15. 下列各式中,最简二次根式是()A. √18B. √25C. √49D. √100二、填空题(每题5分,共25分)6. 计算:(-3)^2 + 4×(-2) + 1 = _______7. 计算:(-2)^3 ÷ (-2)^2 = _______8. 已知x+3=5,求x的值:x = _______9. 等腰三角形的底边长为8,腰长为10,则三角形的周长为 _______10. 已知一个数的平方根是2,求这个数的值:这个数 = _______三、解答题(共50分)11. (10分)已知a、b是实数,且a^2 + b^2 = 1,求a+b的最大值。
12. (10分)已知x是实数,且x^2 - 4x + 3 = 0,求x的值。
13. (10分)已知一个长方体的长、宽、高分别为a、b、c,求长方体的体积V。
14. (10分)已知一个等腰三角形的底边长为6,腰长为8,求三角形的面积。
15. (10分)已知一个数的平方根是-3,求这个数的值。
四、附加题(10分)16. (10分)已知a、b是实数,且a^2 + b^2 = 1,求a-b的最小值。
答案:一、选择题:1. C2. D3. C4. B5. C二、填空题:6. -37. -28. 29. 2410. 9三、解答题:11. a+b的最大值为1。
重庆巴蜀中学数学七年级下学期期末数学试题

18.如图,将△ABE向右平移2cm得到△DCF,如果△ABE的周长是16cm,那么四边形ABFD的周长是_____.
19.一个容量为 的样本的最大值为 ,最小值为 ,若取组距为 ,则应该分的组数是为_______.
20.已知一个多边形的每一个外角都等于 ,则这个多边形的边数是.
4.下列各式中,不能用平方差公式计算的是()
A.xyxyB.-x-y-xyC.x-y-x-yD.xy-xy
5.x2•x3=( )
A.x5B.x6C.x8D.x9
6.下列各式从左到右的变形中,是因式分解的为( )
A.ab+ac+d=a(b+c)+dB.(x+2)(x﹣2)=x2﹣4
C.6ab=2a⋅3bD.x2﹣8x+16=(x﹣4)2
∴∠PDC+∠PCD= (∠BCD+∠CDE)=270°- α,
∴∠P=180°-(270°- α)= α-90°.
故选:A.
【点睛】
此题考查多边形的内角和公式,角平分线的定义,熟记公式是解题的关键.注意整体思想的运用.
3.B
解析:B
【解析】
试题分析:A、2+2=4,不能构成三角形,故本选项错误;
B、3、4、5,满足任意两边之和大于第三边,能构成三角形,故本选项正确;
7.下列运算正确的是( )
A.a2+a2=a4B.(﹣b2)3=﹣b6
C.2x•2x2=2x3D.(m﹣n)2=m2﹣n2
8.已知a、b、c是△ABC的三条边长,化简|a+b-c|-|c-a-b|的结果为( )
A.2a+2b-2cB.2a+2bC.2cD.0
巴蜀期末考初一下数学试卷
一、选择题(每题3分,共30分)1. 下列数中,是负数的是()A. -3.5B. 0C. 1.5D. -52. 若a > 0,b < 0,则下列不等式中正确的是()A. a + b > 0B. a - b < 0C. -a + b > 0D. -a - b < 03. 下列图形中,是轴对称图形的是()A. 长方形B. 等腰三角形C. 正方形D. 梯形4. 若a² = 9,则a的值为()A. ±3B. ±4C. ±5D. ±65. 下列代数式中,同类项的是()A. 2x² - 3yB. 5a²b - 2ab²C. 4m³ - 7mD. 3x + 2x²6. 若一个等腰三角形的底边长为8cm,腰长为10cm,则该三角形的周长为()A. 24cmB. 26cmC. 28cmD. 30cm7. 下列关于圆的命题中,正确的是()A. 圆的直径是圆的半径的两倍B. 圆的半径是圆的直径的一半C. 圆的直径等于圆的半径D. 圆的半径是圆的直径的两倍8. 下列分数中,最简分数是()A. 3/9B. 5/10C. 7/21D. 11/139. 下列数中,能被3整除的是()A. 14B. 21C. 28D. 3310. 若一个数的平方根是4,则该数是()A. 16B. 32C. 64D. 128二、填空题(每题3分,共30分)11. 5的平方根是_________。
12. 下列数中,绝对值最小的是_________。
13. 下列数中,是质数的是_________。
14. 下列图形中,是平行四边形的是_________。
15. 一个长方形的长是8cm,宽是5cm,则它的周长是_________。
16. 一个等边三角形的边长是6cm,则它的面积是_________。
17. 下列数中,能被4整除的是_________。
巴蜀七年级下期末数学试卷
一、选择题(每题3分,共30分)1. 已知函数y=2x+1,当x=3时,y的值为()A. 5B. 6C. 7D. 82. 若a+b=5,ab=6,则a^2+b^2的值为()A. 11B. 13C. 15D. 173. 在直角坐标系中,点P(2,3)关于x轴的对称点坐标为()A. (2,-3)B. (-2,3)C. (-2,-3)D. (2,-3)4. 下列分式方程中,解为x=2的是()A. x+1/x=3B. x-1/x=3C. x+1/x=2D. x-1/x=25. 下列各数中,属于正数的是()A. -2.5B. 0C. 3.14D. -36. 下列各式中,计算正确的是()A. 2.5×4.5=11.25B. 2.5×4.5=12.25C. 2.5×4.5=10.25D.2.5×4.5=9.257. 在一次函数y=kx+b中,k和b的值分别为()A. k=2,b=1B. k=3,b=2C. k=4,b=3D. k=5,b=48. 下列各数中,能被3整除的是()A. 9B. 10C. 11D. 129. 下列图形中,是平行四边形的是()A. 正方形B. 矩形C. 等腰梯形D. 等边三角形10. 下列关于圆的定理中,正确的是()A. 圆的直径是圆的最长弦B. 圆的半径是圆的最长弦C. 圆的直径是圆的最短弦D. 圆的半径是圆的最短弦二、填空题(每题3分,共30分)1. 若a+b=7,ab=12,则a^2+b^2的值为______。
2. 在直角坐标系中,点A(2,3)关于y轴的对称点坐标为______。
3. 下列分式方程中,解为x=3的是______。
4. 下列各数中,属于负数的是______。
5. 下列各式中,计算正确的是______。
6. 在一次函数y=kx+b中,k和b的值分别为______。
7. 下列各数中,能被5整除的是______。
8. 下列图形中,是矩形的是______。
重庆市巴蜀中学七年级下学期期末考试数学试题
重庆市巴蜀中学20XX-20XX 学年度第二学期期末考试初20XX 级(一下)数学试题卷命题人:薛运朋一、选择题:(此题共12个小题,每题4分,共48分) 1、以下图形中,不是轴对称图形的是()• •洪遂牌工2、以下事件为必然事件的是()A 、 小王参加本次数学考试,成绩是150分B 、 某射击运发动射靶一次.正中靶心C 、 打工电视机,CCTV 第一套节目正在播放新闻D 、 口袋中装有2个红球和1个白球,从中摸出2个球.其中必有红球 r = |3、 厂- 是方程3x-uy = 6的一个解,那么。
=()A 、-3B 、3C 、-2D 、24、 如图,点A 、D 、C 、F 在同一条直线上,AB = DE. BC=EF ,要使MBC 三^DEF , 还宥要添加一个条件是( )5、将一副直角三角尺如图放置,己知AE//BC.那么ZAFD 的度数是<)6、 如图.点E 在正方形ABCD 内.满足NA 欢=90"《=6,8弥=8.那么阴影局部的面 积是(〉A 、4«B 、60C 、76D 、807、 在一个不透明的盘子里.装有4个黑球和假设干个白球,它们除颜色外没有任何其他区别. 摇匀后从中随机摸出一个球记下颜色,再把它放回盒子中.不断至夏,共摸球40次,其中 10次摸到黑球,那么估计盒子中大约有白球()A 、12 个B 、16 个C 、20 个D 、30 个A 、45°B 、50°C 、60°D 、75°(4题A 、ZBCA = ZFB 、D 、2A = YEDFio 建由/8、把一张矩形纸片(矩形人BCD,按如图方式折登,使顶点B和。
点重合,折痕为EF °II 、如图,P 为MBC 的边AB 、AC 的中垂线的交点.A 、104° C 、38。
12、如图,A48C 中,ZABC = 451 CD 1 AB 2] D. BE 平分匕ABC,HUELACTE.与CD 相交于点F.H 是BC 边的中点,连接DH 与 BE 相交于点G,以下结论正确的有()个①HF = AC:②CE =、BF ;③△DGF 是等腰三角形:2假设AB = 3s. BC = 5顷.那么重登局部MDEF 的面积是<A 、7.5cnrB 、5. \cm 2C 、5.2cm 2D 、7.2cm z9、万州某运输公司的一艘轮船在长江上航行,往返于万州、朝天门两地”假设轮船在静水 中的速度不变,长江的水流速度不变,该轮船从万州出发,逆水航行到朝天门,停留一段时 间(卸货,装货、加燃料等),又顺水航行返回力州。
2022-2023学年重庆市渝中区巴蜀中学七年级(下)期末数学试卷及答案解析
2022-2023学年重庆市渝中区巴蜀中学七年级(下)期末数学试卷一、选择题:(本大题10个小题,每小题4分,共40分)1.(4分)在实数﹣3、0、﹣、3中,最小的实数是()A.﹣3B.0C.﹣D.32.(4分)下列调查中,最适宜采用抽样调查方式的是()A.检查神舟飞船各个零部件的情况B.调查市场上奶制品的质量情况C.了解某班学生的身体健康状况D.调查和某新冠肺炎感染者密切接触人群3.(4分)估算﹣3的结果在两个整数之间正确的是()A.3和4之间B.4和5之间C.5和6之间D.6和7之间4.(4分)一个多边形的每个内角均为108°,则这个多边形是()A.七边形B.六边形C.五边形D.四边形5.(4分)在平面直角坐标系中,已知点A(2,m)和点B(n,﹣3)关于x轴对称,则m+n的值是()A.﹣1B.1C.5D.﹣56.(4分)下列命题中正确的有()个.①三个内角对应相等的两个三角形全等;②三条边对应相等的两个三角形全等;③等腰三角形的角平分线、高线、中线互相重合;④等底等高的两个三角形全等.A.1B.2C.3D.47.(4分)如图,在△ABC中,AB=AC,∠A=42°,AB的垂直平分线MN交AC于D点,连接BD,则∠DBC的度数是()A.22°B.27°C.32°D.40°8.(4分)巴广高速公路在5月10日正式通车,从巴中到广元全长约为126km.一辆小汽车,一辆货车同时从巴中,广元两地相向开出,经过45分钟相遇,相遇时小汽车比货车多行6km,设小汽车和货车的速度分别为xkm/h,ykm/h,则下列方程组正确的是()A.B.C.D.9.(4分)在平面直角坐标系中,已知A(0,3),B(3,0),若点C在坐标轴上,且△ABC 为等腰三角形,则满足条件的点C的个数是()A.3B.4C.6D.710.(4分)如图,△ABC是等边三角形,点D、E分别在边AB、BC上,CD、AE交于点F,∠AFD=60°.FG为△AFC的角平分线,点H在FG的延长线上,连接HA、HC.∠AHC+∠AFC=180°,①BD=CE;②AF+CF=FH;③FC=CG;④S△CBD=S△CGH;其中说法正确的有()A.1个B.2个C.3个D.4个二、填空题:(本大题8个小题,每小题4分,共32分)11.(4分)100的算术平方根是.12.(4分)已知a,b,c是△ABC的三边长,满足a=7,b=2,c为奇数,则△ABC的周长为.13.(4分)在平面直角坐标系中,若点P(2x+6,5x)在第四象限,则x的取值范围是.14.(4分)如图,△ABC中,点D为AC边上一点,满足AD=3DC,连接BD,点E为BD中点,连接AE,若△AED的面积是3,则△ABC的面积是.15.(4分)如图,在Rt△ABC中,∠ACB=90°,AC=9,BC=12,AB=15,AD是∠BAC 的平分线,若点P、Q分别是AD和AC上的动点,则PC+PQ的最小值是.16.(4分)如图,△ABC中,BD⊥AC于点D,E为AC边上一点,连接BE并延长BE至F,BF=BC,∠CBF=∠FAC,若AC=7.4,AF=5.2,则AD的长度为.17.(4分)若关于x的不等式组有且只有2个整数解,且关于y的方程5+ay=2y﹣7的解是负整数,则符合条件的所有整数a的和是.18.(4分)材料:如果一个四位自然数N各个数位的数字都不为0,把它前两位数字组成的两位数记为x,后两位数字组成的两位数记为y,规定F(N)=,G(N)=2x ﹣y,当F(N)为整数时,称这个四位数为“齐心协力数”.则F(1126)﹣G(1126)=.若“齐心协力数”S=1020a+100b+c+5,(1≤a≤4,1≤b≤6,0≤c≤4,a,b,c为整数),且G(S)除以7余数为2,则S=.三、解答题:(本大题共8个小题,共78分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上. 19.(8分)计算:(1);(2)解不等式组,并把解集在数轴上表示出来.20.(10分)如图,在平面直角坐标系中,点A的坐标为(﹣3,2).请按要求分别完成下列各小题:(1)把△ABC向下平移6个单位得到△A1B1C1,画出△A1B1C1;(2)画出A1B1C1关于y轴对称的△A2B2C2;(3)在y轴上找一点P,使得它到点A和点B的距离和最小(不要求写作法).21.(10分)如图,点C在线段AB上,AD∥BE,AC=BE,AD=BC,DE交AB于点G.(1)尺规作图:过点A作线段DE的垂线交DE于点F.(基本作图,保留作图痕迹,不写作法,不下结论)(2)求证:DF=FG(请补全证明过程).证明:∵AD∥BE,∴∠DAC=.在△ACD和△BEC中,∴△ACD≌△BEC(SAS).∴∠ADC=∠BCE,CD=,∴∠CDE=∠CED.∴∠ADC+∠CDE=∠BCE+∠CED,∴∠ADG=∠AGD,∴.∵AF⊥,∴DF=FG.22.(10分)如图,在△ABC中,AC=BC,∠ACB=100°,D是AB边上一点(不与A,B重合),以CD为边作等腰△CDE,CD=CE,且∠DCE=100°,CB与DE交于点F,连接BE.(1)求证:△ACD≌△BCE;(2)当AD=BF时,求∠BFE.23.(10分)重庆市2023年体育中考已经结束,现从某校初三年级随机抽取部分学生的成绩进行统计分析(成绩得分用x表示,共分成4个等级.A:30≤x<35,B:35≤x<40,C:40≤x<45,D:45≤x≤50),绘制了如下的统计图,请根据统计图信息解答下列问题.(1)本次共调查了名学生;(2)请补全条形统计图;(3)在扇形统计图中,m的值是;B对应的扇形圆心角的度数是;(4)若该校初三年级共有2000名学生,估计此次测试成绩优秀(40≤x≤50)的学生共有多少人?24.(10分)某工厂采购A,B两种原料共花费1380万元.A原料采购了300吨,B原料采购了240吨.两种原料的单价之和是5万元.(1)求A,B两种原料单价各为多少万元/吨?(2)现计划安排甲,乙两种不同规格的货车共50辆运输这批原料,每辆甲货车可装7吨A原料和3吨B原料,每辆乙货车可装5吨A原料和7吨B原料,问共有哪几种运输方案?25.(10分)在平面直角坐标系中,已知A(﹣2,0),B(0,4),C(1,2)(1)如图1,将线段AB平移至EF,点A与点E对应,点B与点F对应,若F点的坐标为(5,1),求△CEF的面积;(2)如图2,以AB为腰做等腰直角△ABB',点B'′在第二象限,且∠BAB'=90°,如果在平面直角坐标系内有一点P(a,3),使得△AB′P的面积是△ABO面积的2倍,求a的值.26.(10分)如图,△ABC中,以AB,AC为边,分别在各自的上方作等边三角形△ABD,等腰三角形△ACE,AE=CE,∠AEC=120°,连接DE,BC.(1)如图1,若AB∥CE,AB=AC=12,求△ABC的面积;(2)如图2,点F为BC中点,求证:DE=2EF;(3)如图3,DE=AB,∠ADE=32°,点N为直线BC上的动点,连接DN,作△ACE 关于DN所在直线的对称图形,记作△A′C′E′,连接AE′,BE′,当△ABE′为直角三角形时,请直接写出∠ADN的度数.2022-2023学年重庆市渝中区巴蜀中学七年级(下)期末数学试卷参考答案与试题解析一、选择题:(本大题10个小题,每小题4分,共40分)1.【分析】先估算出﹣的大小,然后再比较即可.【解答】解:∵1<2<4,∴1<<2.∴﹣1>﹣>﹣2.∵3>2,∴﹣3<﹣2.∴﹣3<﹣2<﹣<0<3.∴其中最小的实数是﹣3.故选:A.【点评】本题主要考查的是比较实数的大小,估算出﹣的大小是解题的关键.2.【分析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.【解答】解:A.检查神舟飞船各个零部件的情况,适合全面调查,故本选项不符合题意;B.调查市场上奶制品的质量情况,适合抽样调查,故本选项符合题意;C.了解某班学生的身体健康状况,适合全面调查,故本选项不合题意;D.调查和某新冠肺炎感染者密切接触人群,适合全面调查,故本选项不合题意.故选:B.【点评】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.3.【分析】先求出的范围,再两边都减去3,即可得出选项.【解答】解:∵7<<8,∴7﹣3<﹣3<8﹣3,∴4<﹣3<5,故选:B.【点评】本题考查了估算无理数的大小的应用,解此题的关键是估算出的范围.4.【分析】首先求得外角的度数,然后利用360除以外角的度数即可求解.【解答】解:外角的度数是:180﹣108=72°,则这个多边形的边数是:360÷72=5.故选:C.【点评】本题考查根据多边形的外角和求多边形的边数,解答时要会根据公式进行正确运算、变形和数据处理5.【分析】根据关于x轴对称的点的横坐标相同,纵坐标互为相反数,可得m、n的值,根据有理数的加法,可得答案.【解答】解:由点A(2,m)和点B(n,﹣3)关于x轴对称,得n=2,m=3.则m+n=2+3=5.故选:C.【点评】本题考查了关于x轴对称的点的横坐标相同,纵坐标互为相反数得出m、n的值是解题关键.6.【分析】根据全等三角形的判定与等腰三角形的性质逐项判断.【解答】解:三个内角对应相等的两个三角形不一定全等,故①错误;三条边对应相等的两个三角形全等,故②正确;等腰三角形顶角的角平分线、底边上的高线、底边上的中线互相重合,故③错误;等底等高的两个三角形不一定全等,故④错误;∴正确的有1个,故选:A.【点评】本题考查命题与定理,解题的关键是掌握全等三角形的判定与等腰三角形的性质.7.【分析】根据等腰三角形两底角相等求出∠ABC的度数,再根据线段垂直平分线上的点到线段两端点的距离相等可得AD=BD,根据等边对等角的性质可得∠ABD=∠A,然后求解即可.【解答】解:∵AB=AC,∠A=42°,∴∠ABC=(180°﹣∠A)=(180°﹣42°)=69°,∵MN垂直平分线AB,∴AD=BD,∴∠ABD=∠A=42°,∴∠DBC=∠ABC﹣∠ABD=69°﹣42°=27°.故选:B.【点评】本题主要考查了线段垂直平分线上的点到线段两端点的距离相等的性质,等腰三角形两底角相等的性质,等边对等角的性质,是基础题,熟记性质是解题的关键.8.【分析】此题考查的是相遇问题,根据题意列二元一次方程组即可.【解答】解:设小汽车的速度为xkm/h,则45分钟小汽车行进的路程为xkm;设货车的速度为ykm/h,则45分钟货车行进的路程为ykm.由两车起初相距126km,则可得出;又由相遇时小汽车比货车多行6km,则可得出.∴可得出方程组.故选:D.【点评】学生在分析解答此题时需注意弄清题意,明白所要考查的要点.另外,还需注意单位的换算,避免粗心造成失误.9.【分析】分为AB=AC、BC=BA,CB=CA三种情况画图判断即可.【解答】解:如图所示:当AB=AC时,符合条件的点有3个;当BA=BC时,符合条件的点有3个;当点C在AB的垂直平分线上时,符合条件的点有一个.故符合条件的点C共有7个.故选:D.【点评】本题主要考查的是等腰三角形的定义、线段垂直平分线的性质,熟练掌握线段垂直平分线的性质是解题的关键.10.【分析】①由∠AFD=60°可证明△CAE≌△BCD,从而可判断①正确;②作CM⊥AE交AE的延长线于M,作CN⊥HF于N,可证明△ECM≌△GCN(AAS)得CE=CG,EM=GN,∠ECM=∠GCN,即可证明△AMC≌△HNC(SAS),有∠ACM =∠HCN,AC=HC,从而得△ACH是等边三角形,故②正确;③由∠CFH=∠AFH=60°,若FC=CG,可得∠FCG=60°,即可判定③不正确;④根据△ECM≌△GCN,△AMC≌△HNC,△CAE≌△BCD,可判定④正确.【解答】解:①∵△ABC是等边三角形,∴∠B=∠ACE=60°,BC=AC,∵∠AFD=∠CAE+∠ACD=60°,∠BCD+∠ACD=∠ACB=60°,∴∠BCD=∠CAE,在△BCD和△CAE中,,∴△BCD≌△CAE(ASA),∴BD=CE,故①正确;②作CM⊥AE交AE的延长线于M,作CN⊥HF于N,如图:∵∠EFC=∠AFD=60°,∴∠AFC=120°,∵FG为△AFC的角平分线,∴∠CFH=∠AFH=60°,∴∠CFH=∠CFE=60°,∵CM⊥AE,CN⊥HF,∴CM=CN,∵∠CEM=∠ACE+∠CAE=60°+∠CAE,∠CGN=∠AFH+∠CAE=60°+∠CAE,∴∠CEM=∠CGN,在△ECM和△GCN中,,∴△ECM≌△GCN(AAS),∴CE=CG,EM=GN,∠ECM=∠GCN,∴∠MCN=∠ECG=60°,由①知△CAE≌△BCD,∴AE=CD,∵HG=CD,∴AE=HG,∴AE+EM=HG+GN,即AM=HN,在△AMC和△HNC中,,∴△AMC≌△HNC(SAS),∴∠ACM=∠HCN,AC=HC,∴∠ACM﹣∠ECM=∠HCN﹣∠GCN,即∠ACE=∠HCG=60°,∴△ACH是等边三角形,∴∠AHC=60°,故②正确;③由②知∠CFH=∠AFH=60°,若FC=CG,则∠CGF=60°,从而∠FCG=60°,这与∠ACB=60°矛盾,故③不正确;④∵△ECM≌△GCN,△AMC≌△HNC,﹣S△ECM=S△HNC﹣S△GCN,即S△ACE=S△CGH,∴S△AMC∵△CAE≌△BCD,=S△ACE=S△CGH,故④正确,∴S△BCD∴正确的有:①②④,故选:C.【点评】本题考查等边三角形的性质及判定,全等三角形的性质及判定,涉及三角形面积等知识,解题的关键是作辅助线,构造全等三角形.二、填空题:(本大题8个小题,每小题4分,共32分)11.【分析】根据算术平方根的定义即可求解.【解答】解:∵102=100,∴=10.故填10.【点评】此题在于考查了算术平方根的概念,比较简单.12.【分析】根据三角形的三边关系和三角形周长公式即可得到结论.【解答】解:由三角形三边关系定理得:7﹣2<c<7+2,即5<c<9,又∵c为奇数,∴c=7,∴△ABC的周长为7+2+7=16.故答案为:16.【点评】本题考查了三角形三边关系,此题实际上就是根据三角形三边关系定理列出不等式,然后解不等式即可.13.【分析】根据第四象限点的特征,列出不等式组即可解决问题.【解答】解:∵点P(2x+6,5x)在第四象限,∴,解得﹣3<x<0,故答案为:﹣3<x<0【点评】本题考查点的坐标、一元一次不等式组等知识,解题的关键是学会用转化的思想思考问题,属于中考常考题型.14.【分析】根据E为BD的中点得△ABE和△AED等底同高,则面积相等,进而得S△ABD=2,据此可求出△=6,再根据△BAD和△BCD同高得,进而得S△CBDABC的面积.【解答】解:∵点E为BD的中点,∴BE=ED,∴△ABE和△AED等底同高,=S△AED=3,∴S△ABE=6,∴S△ABD又∵△BAD和△BCD同高,∴,∵AD=3DC,∴,∴,∴,=S△ABD+S△CBD=8.∴S△ABC故答案为:8.【点评】此题主要考查了三角形的面积,解答此题的关键是理解同底(等底)同高(等高)的两个三角形的面积相等,同高(或等高)的两个三角形的面积之比等于底边的比.15.【分析】过点D作DE⊥AB于点E,过点E作EQ⊥AC于点Q,EQ交AD于点P,连接CP,此时PC+PQ=EQ取最小值,根据三角形全等得出∠AFC=∠AQE=90°,EQ =CF,利用三角形面积公式得出EQ=CF=,此题得解.【解答】解:过点D作DE⊥AB于点E,过点E作EQ⊥AC于点Q,EQ交AD于点P,连接CP,此时PC+PQ=EQ取最小值,如图所示.在Rt△ABC中,∠ACB=90°,AC=9,BC=12,AB=15.∵AD是∠BAC的平分线,DC⊥AC,DE⊥AB,∴CD=ED,在Rt△ACD和Rt△AED中,,∴Rt△ACD≌Rt△AED(HL),∴AE=AC=9.在△ACP和△AEP中,,∴△ACP和△AEP(SAS),∴∠ACP=∠AEQ,延长CP,交AB于F,在△ACF和△AEQ中,,∴△ACF≌△AEQ(ASA),∴∠AFC=∠AQE=90°,EQ=CF,∴AB•CF=AC•BC,∴CF===∴EQ=CF=.∴PC+PQ的最小值是,故答案为.【点评】本题考查了轴对称﹣最短路线问题以及三角形全等的判定和性质,三角形面积公式的应用,找出点P、Q的位置是解题的关键.16.【分析】过点B作BG⊥FA交FA的延长线于点G,利用AAS证明△BCD≌BFG,得到BD=BG,再利用HL证明Rt△BAD≌Rt△BAG,得到AD=AG,利用线段的和差求解即可.【解答】解:如图,过点B作BG⊥FA交FA的延长线于点G,∵∠CBF=∠FAC,∠BEC=∠AEF,∴∠C=∠F,∴BD⊥AC,BG⊥FA,∴∠BDC=∠BGF=90°,在△BCD和△BFG中,,∴△BCD≌△BFG(AAS),∴CD=FG,BD=BG,在Rt△BAD和Rt△BAG中,,∴Rt△BAD≌Rt△BAG(HL),∴AD=AG,∴CD=FG,∴CD=AF+AG=AF+AD,∴AC+AF=2CD,CD==6.3,∴AD=AC﹣CD=7.4﹣6.3=1.1.故答案为:1.1.【点评】本题考查了全等三角形的判定与性质,线段的和差,正确作辅助线是解题的关键.17.【分析】根据不等式组的解集以及整数解的个数,确定a的取值范围,再根据分式方程的根和增根进一步确定a的取值范围,再求出符合条件的整式的和即可.【解答】解:解关于x的不等式组可得,由于这个不等式组的解集中有且只有2个整数解,∴4≤<5,解得8≤a<16,又关于y的方程5+ay=2y﹣7的解为y=,∵8≤a<16,为负整数,∴符合条件的所有整数a的值有8,14,∴8+14=22.故答案为:22.【点评】本题考查一元一次不等式组的整数解、解一元一次方程,解答本题的关键是求出a的取值范围.18.【分析】根据定义分别求出F(1126)=9,G(1126)=﹣4,再求F(1126)﹣G(1126)=13;根据所给的条件结合定义可得F(S)=,G(S)=2b﹣c﹣5,由题意可得2b﹣c能被7整除,则b=1,c=2或b=2,c=4或b=4,c=1或b=5,c=3,再分情况讨论即可.【解答】解:∵F(1126)==9,G(1126)=2×11﹣26=﹣4,∴F(1126)﹣G(1126)=9+4=13;∵S=1020a+100b+c+5,1≤a≤4,1≤b≤6,0≤c≤4,∴x=10a+b,y=20a+c+5,∴F(S)==,G(S)=2(10+b)﹣(20a+c+5)=2b﹣c﹣5,∵G(S)除以7余数为2,∴2b﹣c﹣7能被7整除,∴2b﹣c能被7整除,∵1≤b≤6,0≤c≤4,∴﹣1≤2b﹣c≤12,∴2b﹣c=0或2b﹣c=7,∴b=1,c=2或b=2,c=4或b=4,c=1或b=5,c=3,当b=1,c=2时,F(S)=,∵1≤a≤4,∴F(S)不是整数,∴此时不符合题意;当b=2,c=4时,F(S)=,当a=1时,F(S)是整数,符合题意;∴S=1229;当b=5,c=3时,F(S)=,∵1≤a≤4,∴F(S)不是整数,∴此时不符合题意;综上所述:S为1229,故答案为:13,1229.【点评】本题考查因式分解的应用,能够理解新定义内容,再根据数的特点分类讨论是解题的关键.三、解答题:(本大题共8个小题,共78分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上. 19.【分析】(1)原式利用乘方的意义,二次根式性质,以及绝对值的意义计算即可求出值;(2)分别求出不等式组中两不等式的解集,找出两解集的公共部分确定出不等式组的解集,表示在数轴上即可.【解答】解:(1)原式=﹣1+2+2﹣=3﹣;(2)由①得:x≤2,由②得:x>﹣3,则不等式组的解集为﹣3<x≤2,【点评】此题考查了解一元一次不等式组,以及实数的运算,熟练掌握运算法则是解本题的关键.20.【分析】(1)依据平移的方向和距离,即可得到△A1B1C1,即可得出点A1的坐标;(2)依据轴对称的性质,即可得到△A2B2C2,进而得出点C2的坐标;(3)作点A关于y轴的对称点A',连接A'B,与y轴交点即为点P,依据两点之间,线段最短,即可得到点P到点A和点B的距离和最小.【解答】解:(1)如图所示,△A1B1C1即为所求;(2)如图所示,△A2B2C2即为所求;(3)如图所示,点P即为所求,点P到点A和点B的距离和最小.【点评】此题主要考查了平移变换以及轴对称变换,正确得出对应点位置是解题的关键.凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合轴对称变换来解决,多数情况要作点关于某直线的对称点.21.【分析】(1)利用基本作图,过A点作DE的垂线即可;(2)先证明△ACD≌△BEC得到∠ADC=∠BCE,CD=CE,则∠CDE=∠CED,再证明∠ADG=∠AGD,所以AD=AG,然后根据等腰三角形的性质得到DF=FG.【解答】解:(1)如图,AF为所作;(2)在△ACD和△BEC中,,∴△ACD≌△BEC(SAS),∴∠ADC=∠BCE,CD=CE,∴∠ADC+∠CDE=∠BCE+∠CED,∴∠ADG=∠AGD,∴AD=AG,∵AF⊥DG,∴DF=FG.故答案为:∠CBE,DC=EC,AD=AG,DG.【点评】本题考查了作图﹣复杂作图、全等三角形的判定与性质,解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.22.【分析】(1)由AC=BC,∠ACD=∠BCE=100°﹣∠DCB,CD=CE,根据全等三角形的判定定理“SAS”证明△ACD≌△BCE;(2)由△ACD≌△BCE,得AD=BE,∠A=∠CBE=40°,而AD=BF,则BE=BF,所以∠BFE=∠BEF=70°.【解答】(1)证明:∵AC=BC,∠ACB=100°,∴∠A=∠CBA=×(180°﹣100°)=40°,∵∠DCE=100°,∴∠ACD=∠BCE=100°﹣∠DCB,在△ACD和△BCE中,,∴△ACD≌△BCE(SAS).(2)解:∵△ACD≌△BCE,∴AD=BE,∠A=∠CBE=40°,∵AD=BF,∴BE=BF,∴∠BFE=∠BEF,∵∠BFE+∠BEF+∠CBE=180°,∴2∠BFE+40°=180°,【点评】此题重点考查等腰三角形的性质、全等三角形的判定与性质、三角形内角和定理等知识,证明∠ACD=∠BCE进而证明△ACD≌△BCE是解题的关键.23.【分析】(1)从两个统计图可知,样本中成绩在“D等级”的有20人,占调查人数的40%,由频率=即可求出调查人数;(2)求出样本中成绩在“C等级”的学生人数,即可补全条形统计图;(3)根据频率=可求出成绩在“C等级”、“B等级”的所占的百分比,进而确定m的值和相应的圆心角度数;(4)求出样本中成绩在“D等级”,即优秀等级所占的百分比,估计总体中,优秀所占的百分比,由频率=进行计算即可.【解答】解:(1)20÷40%=50(名),故答案为:50;(2)成绩在“C等级”的学生人数为:50﹣10﹣15﹣20=5(名),补全条形统计图如下:(3)成绩在“C等级”所占的百分比为:5÷50×100%=10%,即m=10,成绩在“B等级”的所对应的圆心角度数为:360°×=108°,故答案为:10,108°;(4)2000×=800(名),答:该校初三年级2000名学生中测试成绩优秀(40≤x≤50)的学生大约有800人.【点评】本题考查条形统计图、扇形统计图,理解两个统计图中数量之间的关系是解决问题的前提,掌握频率=是正确解答的关键.24.【分析】(1)设A原料单价为x万元/吨,B原料单价为y万元/吨,根据“两种原料的单价之和是5万元;A原料采购了300吨,B原料采购了240吨,共花费1380万元”,可列出关于x,y的二元一次方程组,解之即可得出结论;(2)设安排m辆甲货车,则安排(50﹣m)辆乙货车,根据安排的两种货车一次可运输A原料不少于300吨、B原料不少于240吨,可列出关于m的一元一次不等式组,解之可得出m的取值范围,再结合m为正整数,即可得出各运输方案.【解答】解:(1)设A原料单价为x万元/吨,B原料单价为y万元/吨,根据题意得:,解得:.答:A原料单价为3万元/吨,B原料单价为2万元/吨;(2)设安排m辆甲货车,则安排(50﹣m)辆乙货车,根据题意得:,解得:25≤m≤,又∵m为正整数,∴m可以为25,26,27,∴共有3种运输方案,方案1:安排25辆甲货车,25辆乙货车;方案2:安排26辆甲货车,24辆乙货车;方案3:安排27辆甲货车,23辆乙货车.【点评】本题考查了二元一次方程组的应用以及一元一次不等式组的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式组.25.【分析】(1)根据平移坐标的变化规律得出点E的坐标,将点的坐标转化为线段的长,利用面积之间的和差关系进行计算即可;(2)根据全等三角形的性质得出AG,B′Q的长,确定直线AB′的关系式,进而求出点M的坐标,由三角形面积之间的和差关系分两种情况列方程求解即可.【解答】解:(1)如图1,∵B(0,4),平移后点B的对应点F的坐标为(5,1),∴将点B先向右平移5个单位,再向下平移3个单位,∵A(﹣2,0),∴点A平移后的对应点E(3,﹣3),∴CH=2+3=5,CD=5﹣1=4,DF=2﹣1=1,FG=2+3=4,HE=EG=2,=S矩形CDGH﹣S△CHE﹣S△EFG﹣S△CDF∴S△CEF=5×4﹣﹣﹣=20﹣5﹣4﹣2=9;(2)如图2,点P在平行于x轴,且到x轴的距离为3的直线y=3上,延长AB′交直线y=3于点M,过点B′作y轴的平行线分别交x轴、直线y=3于点Q、N,∵△ABB′是等腰直角三角形,∴∠B′AQ+∠BAO=180°﹣90°=90°,∵∠BAO+∠ABO=90°,∴∠B′AQ=∠ABO,∵∠B′QA=∠AOB=90°,∴△ABO≌△B′AQ(AAS),∴AQ=OB=4,B′Q=OA=2,∴点B′(﹣6,2),设直线AB′的关系式为y=kx+b,由于点A(﹣2,0),点B′(﹣6,2),∴,解得,∴直线AB′的关系式为y=﹣x﹣1,当y=3时,即﹣x﹣1=3,解得x=﹣8,∴点M(﹣8,3),设点P(a,3),当点P在点M的右侧时,有△AB′P1的面积=△AMP1的面积﹣△B′MP1的面积=2S=2×4=8,△AOB∴(a+8)×3﹣(a+8)×1=8,解得a=0,当点P在点M的左侧时,有△AB′P2的面积=△AMP2的面积﹣△B′MP2的面积=2S=2×4=8,△AOB∴(﹣8﹣a)×3﹣(﹣8﹣a)×1=8,解得a=﹣16,综上所述,a的值为0或﹣16.【点评】本题考查坐标与图形变化,全等三角形的判定和性质,掌握平移坐标变化规律是正确解答的前提,确定点M坐标以及三角形面积的和差关系是正确解答的关键.26.【分析】(1)作CF⊥BA交BA的延长线于点F,求出∠CAF=∠ECA=30°,利用含30°角的直角三角形的性质及三角形的面积公式即可求解;(2)延长EF至点M,使FM=EF,延长CE交BD于点N,连接DM,BM,根据条件判定△MFB≌△EFC,△DAE≌△DBM,推出△DEM是等边三角形,据此即可证明结论成立;(3)由题意得点E'在以D为圆心,DE为半径的圆上,分四种情况讨论,分别画出图形,利用轴对称的性质即可求解.【解答】(1)解:如图1,作CF⊥BA交BA的延长线于点F,∵AE=CE,∠AEC=120°,∴∠EAC=∠ECA=30°,∵AB∥CE,∴∠CAF=∠ECA=30°,∵AB=AC=12,∴CF=AC=6,∴△ABC的面积=AB•CF=36;(2)证明:延长EF至点M,使FM=EF,延长CE交BD于点N,连接DM,BM,在△MFB和△EFC中,,∴△MFB≌△EFC(SAS),∴CE=BM,∠FCE=∠FBM,∴CE∥BM,∴∠DNE=∠DBM,∵∠AEC=120°,∴∠AEN=60°,∵∠NDA+∠DNE=∠NEA+∠DAE,即60°+∠DNE=60°+∠DAE,∴∠DAE=∠DNE,∴∠DAE=∠DBM,在△DAE和△DBM中,,∴△DAE≌△DBM(SAS),∴DE=DM,∠AED=∠BDM,∵∠EDM=∠EDA+∠ADM=∠BDM+∠ADM=∠ADB=60°,∴△DEM是等边三角形,∵FM=EF,∴∠EDF=∠EDM=30°,∴DE=2EF;(3)解:分四种情况讨论,由题意得点E'在以D为圆心,DE为半径的圆上,①当∠E'BA=90°时,∠ADN=(∠E'DA+∠ADE)﹣∠ADE=(120°+32°)﹣32°=44°;②当∠E'AB=90°时,∠ADN=(60°﹣32°)+32°=46°;③当∠AE'B=90°时,∠ADN=(60°+32°)﹣32°=14°;④当∠AE'B=90°时,∠ADN=×32°=16°;综上,∠ADN的度数为44°或46°或14°或16°.【点评】本题是几何变换综合题,主要考查轴对称的性质,等边三角形的判定和性质,等腰三角形的性质,直角三角形的性质,全等三角形的判定与性质,深入理解题意是解决问题的关键。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014-2015学年重庆市巴蜀中学七年级(下)期末数学试卷一、选择题1.在,﹣1,0,这四个数中,属于无理数的是()A.B.﹣1 C.0 D.2.下列图形中,不是轴对称图形的是()A.B.C.D.3.如图,已知AB∥CD,若∠E=15°,∠C=55°,则∠A的度数为()A.25°B.40°C.35°D.45°4.下列说法中,正确的是()A.“明天降雨的概率是80%”表示明天有80%的时间降雨B.“抛一枚硬币正面朝上的概率是0.5”表示每抛硬币2次就有1次出现正面朝上C.“彩票中奖的概率是1%”表示买100张彩票一定有1张会中奖D.在同一年出生的367名学生中,至少有两人的生日是同一天5.如图,∠C=90°,AB的垂直平分线交BC于D,连接AD,若∠CAD=20°,则∠B=()A.20°B.30°C.35°D.40°6.比较2,,的大小,正确的是()A.B.2 C.2 D.<27.如果的解也是2x+3y=6的解,那么k的值是()A.B.C.﹣D.﹣8.如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→D→C→B→A,设P 点经过的路程为x,以点A、P、D为顶点的三角形的面积是y,则下列图象能大致反映y与x的函数关系的是()A. B.C.D.9.如图,在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是()A.B.C.D.10.如图,△ABC内角∠ABC和外角∠ACD的平分线交于点E,BE交AC于点F,过点E作EG∥BD 交AB于点G,交AC于点H,连接AE,有以下结论;①BG=EG;②△HEF≌△CBF;③∠AEB+∠ACE=90°;④BG﹣CH=GH;⑤∠AEC+∠ABE=90°其中正确的结论是()A.1个B.2个C.3个D.4个二、填空题包11.的算术平方根是.12.将一副三角板如图放置,使点A在DE上,∠B=45°,∠E=30°,BC∥DE,则∠EFB的度数为.13.如图,AD,AE分别是△ABC的角平分线和高线,且∠B=50°,∠C=70°,则∠EAD=.14.已知鞋子的“码”与“厘米”之间的对应关系如表所示:设鞋子的“码”为x(码),“厘米”为y(厘米),则y与x之间的函数关系式是.15.在一个不透明的布袋中,红色、黑色、白色的乒乓球共有20个,除颜色外,形状、大小、质地等完全相同.小明通过多次摸球实验后发现其中投到红色、黑色球的频率稳定在5%和15%,则口袋中白色球的个数很可能是个.16.已知关于x,y的二元一次方程组的解互为相反数,则k的值是.17.若5﹣的小数部分为a,若2+的小数部分为b,则a+b=.18.一个装有进水管和出水管的容器,从某一时刻起只打开进水管进水,经过一段时间,再打开出水管放水,至12分钟时,关停进水管.在打开进水管到关停进水管这段时间内,容器内的水量y(单位:升)与时间x(单位:分钟)之间的函数关系如图所示,关停进水管后,经过分钟,容器中的水恰好放完.19.已知实数m满足+=,则m=.20.如图,△ABC中,∠ACB=90°,AC=8cm,BC=15cm,点M从A点出发沿A→C→B路径向终点运动,终点为B点,点N从B点出发沿B→C→A路径向终点运动,终点为A点,点M和N分别以每秒2m和3cm的运动速度同时开始运动,两点都要到达相应的终点时才能停止运动,分别过M和N作ME⊥l于E,NF⊥l于F.设运动时间为t秒,要使以点M,E,C为顶点的三角形与以点N,F,C为顶点的三角形全等,则t的值为.三、解答题21.计算:(1)(2)(20).22.解方程组:(1)(2).23.已知:如图,∠B=∠D,∠DAB=∠EAC,AB=AD.求证:BC=DE.24.端午节至,甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程S(米)与时间t(分钟)之间的函数关系图象如图所示,请你根据图象,回答下列问题:(1)这次龙舟赛的全程是米,队先到达终点;(2)求乙与甲相遇时乙的速度;(3)求出在乙队与甲相遇之前,他们何时相距100米?25.列方程组解应用题:某服装店购进一批甲、乙两种款式时尚T恤衫,用14200元恰好购进100件,已知甲种款型T恤进价为130元/件,且甲种款型的每件进价比乙种款型每件进价少30元.(1)求甲、乙两种款型的T恤各购进多少件?(2)商店按进价提高60%标价销售,销售一段时间后,甲款全部售完,乙款剩余一半,商店决定对乙款型按标价的五折降价销售,很快全部售完,求售完这批T恤商店共获得多少元?26.如图,在△ABC中,∠BAC=90°,过点B作BC的垂线交∠ACB的角平分线于点D,CD与AB 边交于点E,过D作DF⊥AB于点F.(1)若△BDE是边长为2的等边三角形,求AE的长;(2)求证:AE=BF.27.已知△ABC和△DEC都是等腰直角三角形,C为它们的公共直角顶点,D、E分别在BC、AC 边上.(1)如图1,F是线段AD上的一点,连接CF,若AF=CF;①求证:点F是AD的中点;②判断BE与CF的数量关系和位置关系,并说明理由;(2)如图2,把△DEC绕点C顺时针旋转α角(0<α<90°),点F是AD的中点,其他条件不变,判断BE与CF的关系是否不变?若不变,请说明理由;若要变,请求出相应的正确结论.2014-2015学年重庆市巴蜀中学七年级(下)期末数学试卷参考答案与试题解析一、选择题1.在,﹣1,0,这四个数中,属于无理数的是()A.B.﹣1 C.0 D.【考点】无理数.【分析】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.【解答】解:是分数,是有理数;﹣1和0是整数,是有理数;是无理数.故选D.【点评】此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.2.下列图形中,不是轴对称图形的是()A.B.C.D.【考点】轴对称图形.【分析】根据轴对称图形的概念对各选项分析判断后利用排除法求解.【解答】解:A、不是轴对称图形,故本选项正确;B、是轴对称图形,故本选项错误;C、是轴对称图形,故本选项错误;D、是轴对称图形,故本选项错误.故选A.【点评】本题考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.3.如图,已知AB∥CD,若∠E=15°,∠C=55°,则∠A的度数为()A.25°B.40°C.35°D.45°【考点】平行线的性质;三角形的外角性质.【分析】根据两直线平行,同位角相等可得∠1=∠C,再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.【解答】解:如图,∵AB∥CD,∴∠1=∠C=55°,∴∠A=∠1﹣∠E=55°﹣15°=40°.故选B.【点评】本题考查了平行线的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质是解题的关键.4.下列说法中,正确的是()A.“明天降雨的概率是80%”表示明天有80%的时间降雨B.“抛一枚硬币正面朝上的概率是0.5”表示每抛硬币2次就有1次出现正面朝上C.“彩票中奖的概率是1%”表示买100张彩票一定有1张会中奖D.在同一年出生的367名学生中,至少有两人的生日是同一天【考点】概率的意义.【分析】根据概率的意义分析各个选项,找到正确选项即可.【解答】解:A、“明天降雨的概率是80%”表示明天有降雨的可能性,故错误;B、“抛一枚硬币正面朝上的概率是0.5”表示抛一枚硬币正面朝上与反面朝上的机会是一样的,故错误;C、“彩票中奖的概率是1%”表示在设计彩票时,有1%的机会中奖,但不一定买100张彩票一定有1张会中奖,故错误;D、在同一年出生的367名学生,而一年中至多有366天,因而至少有两人的生日是同一天.故选:D.【点评】本题解决的关键是理解概率只是反映事件发生机会的大小.5.如图,∠C=90°,AB的垂直平分线交BC于D,连接AD,若∠CAD=20°,则∠B=()A.20°B.30°C.35°D.40°【考点】线段垂直平分线的性质;三角形内角和定理;等腰三角形的判定与性质.【分析】由已知条件,根据线段垂直平分线的性质得到线段及角相等,再利用直角三角形两锐角互余得到∠B=(180°﹣∠ADB)÷2答案可得.【解答】解:∵DE垂直平分AB,∴AD=DB∴∠B=∠DAB∵∠C=90°,∠CAD=20°∴∠B=(180°﹣∠C﹣∠CAD)÷2=35°故选C【点评】本题考查了线段垂直平分线的性质、等腰三角形的判定与性质及三角形内角和定理;解决本题的关键是利用线段的垂直平分线性质得到相应的角相等,然后根据三角形的内角和求解.6.比较2,,的大小,正确的是()A.B.2 C.2 D.<2【考点】实数大小比较.【分析】首先根据2=,可得2;然后根据,可得,据此判断出2,,的大小关系即可.【解答】解:∵2=,∴2;∵,∴,∴<.故选:A.【点评】此题主要考查了实数大小比较的方法,要熟练掌握,解答此题的关键是判断出2和的大小关系.7.如果的解也是2x+3y=6的解,那么k的值是()A.B.C.﹣D.﹣【考点】解二元一次方程组;二元一次方程的解.【分析】求出方程组的解x=7k,y=﹣2k,代入2x+3y=6得出关于k的方程,求出方程的解即可.【解答】解:,①+②得:2x=14k,x=7k,①﹣②得:2y=﹣4k,y=﹣2k,把x=7k和y=﹣2k代入2x+3y=6得:14k﹣6k=6,k=,故选A.【点评】本题考查了解二元一次方程组的应用,关键是得出关于k的方程.8.如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→D→C→B→A,设P 点经过的路程为x,以点A、P、D为顶点的三角形的面积是y,则下列图象能大致反映y与x的函数关系的是()A. B.C.D.【考点】动点问题的函数图象.【分析】根据动点从点A出发,首先向点D运动,此时y不随x的增加而增大,当点P在DC上运动时,y随着x的增大而增大,当点P在CB上运动时,y不变,据此作出选择即可.【解答】解:当点P由点A向点D运动,即0≤x≤4时,y的值为0;当点P在DC上运动,即4<x≤8时,y随着x的增大而增大;当点P在CB上运动,即8<x≤12时,y不变;当点P在BA上运动,即12<x≤16时,y随x的增大而减小.故选B.【点评】本题考查了动点问题的函数图象,解决动点问题的函数图象问题关键是发现y随x的变化而变化的趋势.9.如图,在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是()A.B.C.D.【考点】概率公式;轴对称图形.【分析】由随机选择标有序号①②③④⑤中的一个小正方形涂黑,共有5种等可能的结果,使与图中阴影部分构成轴对称图形的有3种情况,直接利用概率公式求解即可求得答案.【解答】解:∵在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,共有5种等可能的结果,使与图中阴影部分构成轴对称图形的有②④⑤,3种情况,∴使与图中阴影部分构成轴对称图形的概率是:3÷5=.故选C.【点评】此题考查了概率公式的应用.注意用到的知识点为:概率=所求情况数与总情况数之比.也考查了轴对称图形的定义.10.如图,△ABC内角∠ABC和外角∠ACD的平分线交于点E,BE交AC于点F,过点E作EG∥BD 交AB于点G,交AC于点H,连接AE,有以下结论;①BG=EG;②△HEF≌△CBF;③∠AEB+∠ACE=90°;④BG﹣CH=GH;⑤∠AEC+∠ABE=90°其中正确的结论是()A.1个B.2个C.3个D.4个【考点】全等三角形的判定与性质;等腰三角形的判定与性质.【分析】①根据角平分线定义得出∠ABE=∠CBE,根据平行线性质得出∠CBE=∠BEG,从而得出∠ABE=∠BEG,由等腰三角形的判定定理即可得到结论;②根据相似三角形的判定定理得到两个三角形相似,不能得出全等;③由于E是两条角平分线的交点,根据角平分线的性质可得出点E到BA、AC、BC和距离相等,从而得出AE为∠BAC外角平分线这个重要结论,再利用三角形内角和性质与外角性质进行角度的推导即可轻松得出结论.④根据∠AEC=180﹣x﹣z,于是得到∠AEC=180﹣(y+90°),推出y+∠AEC=90°,即可得到结论;⑤由BG=GE,CH=EH,于是得到BG﹣CH=GE﹣EH=GH.即可得到结论.【解答】解:①∵BE平分∠ABC,π∴∠ABE=∠CBE,∵GE∥BC,∴∠CBE=∠GEB,∴∠ABE=∠GEB,∴BG=GE,故①正确.同理CH=HE.②△HEF与△CBF只有两个角是相等的,能得出相似,但不含相等的边,所有不能得出全等的结论,故②错误.③过点E作EN⊥AC于N,ED⊥BC于D,EM⊥BA于M,如图,∵BE平分∠ABC,∴EM=ED,∵CE平分∠ACD,∴EN=ED,∴EN=EM,∴AE平分∠CAM,设∠ACE=∠DCE=x,∠ABE=∠CBE=y,∠MAE=∠CAE=z,如图,则∠BAC=180°﹣2z,∠ACB=180﹣2x,∵∠ABC+∠ACB+∠BAC=180°,∴2y+180°﹣2z+180°﹣2x=180°,∴x+z=y+90°,∵z=y+∠AEB,∴x+y+∠AEB=y+90°,∴x+∠AEB=90°,即∠ACE+∠AEB=90°,故③正确.④∵∠AEC=180﹣x﹣z,∴∠AEC=180﹣(y+90°),∴y+∠AEC=90°,即∠ABE+∠AEC=90°,故④正确.⑤∵BG=GE,CH=EH,∴BG﹣CH=GE﹣EH=GH.故⑤正确.综上,①③④⑤正确,共4个.故选D.【点评】本题考查了平行线的性质,角平分线的定义,角平分线的性质与判定,等腰三角形的判定,三角形内角和定理、三角形外角性质等多个知识点,难度中等.判断出AE是∠BAC外角平分线是关键,事实上,点E就是△ABC的旁心.二、填空题包11.的算术平方根是2.【考点】算术平方根.【专题】计算题.【分析】首先根据算术平方根的定义求出的值,然后再利用算术平方根的定义即可求出结果.【解答】解:∵=4,∴的算术平方根是=2.故答案为:2.【点评】此题主要考查了算术平方根的定义,注意要首先计算=4.12.将一副三角板如图放置,使点A在DE上,∠B=45°,∠E=30°,BC∥DE,则∠EFB的度数为75°.【考点】平行线的性质.【分析】由平行线的性质得出内错角相等∠BCF=∠E=30°,再由三角形的外角性质得出∠EFB=∠B+∠BCF,即可得出结果.【解答】解:∵BC∥DE,∴∠BCF=∠E=30°,∴∠EFB=∠B+∠BCF=45°+30°=75°,故答案为75°.【点评】本题考查了平行线的性质、三角形的外角性质;熟练掌握平行线的性质,并能进行推理计算是解决问题的关键.13.如图,AD,AE分别是△ABC的角平分线和高线,且∠B=50°,∠C=70°,则∠EAD=10°.【考点】三角形内角和定理.【分析】根据三角形的内角和等于180°求出∠BAC,再根据角平分线的定义求出∠BAD,根据直角三角形两锐角互余求出∠BAE,然后根据∠EAD=∠BAE﹣∠BAD代入数据进行计算即可得解.【解答】解:∵∠B=50°,∠C=70°,∴∠BAC=180°﹣∠B﹣∠C=180°﹣50°﹣70°=60°,∵AD是△ABC的角平分线,∴∠BAD=∠BAC=×60°=30°,∵AE是△ABC的高线,∴∠BAE=90°﹣∠B=90°﹣50°=40°,∴∠EAD=∠BAE﹣∠BAD=40°﹣30°=10°.故答案为:10°.【点评】本题考查了三角形的内角和定理,三角形的角平分线、高线的定义,是基础题,准确识图找出各角度之间的关系是解题的关键.14.已知鞋子的“码”与“厘米”之间的对应关系如表所示:设鞋子的“码”为x(码),“厘米”为y(厘米),则y与x之间的函数关系式是y=0.5x+5.【考点】根据实际问题列一次函数关系式.【分析】设鞋长用x表示,鞋码用y表示,利用待定系数法即可求解.【解答】解:设鞋子的“码”为x(码),“厘米”为y(厘米),则y与x之间的函数关系式是:y=kx+b,∴,解得:,∴y与x之间的函数关系式是:y=0.5x+5.故答案为:y=0.5x+5.【点评】本题考查了一次函数的应用,利用一次函数解决鞋的长度与鞋码之间的关系是解题关键.15.在一个不透明的布袋中,红色、黑色、白色的乒乓球共有20个,除颜色外,形状、大小、质地等完全相同.小明通过多次摸球实验后发现其中投到红色、黑色球的频率稳定在5%和15%,则口袋中白色球的个数很可能是16个.【考点】利用频率估计概率.【专题】计算题.【分析】在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,可以从比例关系入手,先求得白球的频率,再乘以总球数求解.【解答】解:白色球的个数是:20×(1﹣5%﹣15%)=20×80%=16,故答案为:16,【点评】此题主要考查了利用频率估计概率,解答此题的关键是要计算出口袋中白色球所占的比例,再计算其个数.16.已知关于x,y的二元一次方程组的解互为相反数,则k的值是﹣1.【考点】二元一次方程组的解.【分析】将方程组用k表示出x,y,根据方程组的解互为相反数,得到关于k的方程,即可求出k 的值.【解答】解:解方程组得:,因为关于x,y的二元一次方程组的解互为相反数,可得:2k+3﹣2﹣k=0,解得:k=﹣1.故答案为:﹣1.【点评】此题考查方程组的解,关键是用k表示出x,y的值.17.若5﹣的小数部分为a,若2+的小数部分为b,则a+b=1.【考点】估算无理数的大小.【分析】先估算出的大小,再求出a、b的值即可.【解答】解:∵4<6<9,∴2<<3,∴2<5﹣<3,∴a=5﹣﹣2=3﹣.同理,b=﹣2.∴a+b=3﹣+﹣2=1.故答案是:1.【点评】本题主要考查了无理数的估算,解题关键是确定无理数的小数部分即可解决问题.18.一个装有进水管和出水管的容器,从某一时刻起只打开进水管进水,经过一段时间,再打开出水管放水,至12分钟时,关停进水管.在打开进水管到关停进水管这段时间内,容器内的水量y(单位:升)与时间x(单位:分钟)之间的函数关系如图所示,关停进水管后,经过8分钟,容器中的水恰好放完.【考点】函数的图象;一次函数的应用.【分析】由0﹣4分钟的函数图象可知进水管的速度,根据4﹣12分钟的函数图象求出水管的速度,再求关停进水管后,出水经过的时间.【解答】解:进水管的速度为:20÷4=5(升/分),出水管的速度为:5﹣(30﹣20)÷(12﹣4)=3.75(升/分),∴关停进水管后,出水经过的时间为:30÷3.75=8分钟.故答案为:8.【点评】本题考查利用函数的图象解决实际问题.正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决.19.已知实数m满足+=,则m=7.【考点】二次根式的性质与化简;二次根式有意义的条件.【分析】根据二次根式的性质和化简解答即可.【解答】解:因为实数m满足+=,可得:m﹣2+=m,可得:m﹣3=4,解得:m=7,故答案为:7【点评】此题考查二次根式问题,关键是根据二次根式的性质和化简分析.20.如图,△ABC中,∠ACB=90°,AC=8cm,BC=15cm,点M从A点出发沿A→C→B路径向终点运动,终点为B点,点N从B点出发沿B→C→A路径向终点运动,终点为A点,点M和N分别以每秒2m和3cm的运动速度同时开始运动,两点都要到达相应的终点时才能停止运动,分别过M和N作ME⊥l于E,NF⊥l于F.设运动时间为t秒,要使以点M,E,C为顶点的三角形与以点N,F,C为顶点的三角形全等,则t的值为或7或8.【考点】全等三角形的判定.【专题】动点型.【分析】易证∠MEC=∠CFN,∠MCE=∠CNF.只需MC=NC,就可得到△MEC与△CFN全等,然后只需根据点M和点N不同位置进行分类讨论即可解决问题.【解答】解:①当0≤t<4时,点M在AC上,点N在BC上,如图①,此时有AM=2t,BN=3t,AC=8,BC=15.当MC=NC即8﹣2t=15﹣3t,解得t=7,不合题意舍去;②当4≤t<5时,点M在BC上,点N也在BC上,如图②,若MC=NC,则点M与点N重合,即2t﹣8=15﹣3t,解得t=;③当5≤t<时,点M在BC上,点N在AC上,如图③,当MC=NC即2t﹣8=3t﹣15,解得t=7;④当≤t<时,点N停在点A处,点M在BC上,如图④,当MC=NC即2t﹣8=8,解得t=8;综上所述:当t等于或7或8秒时,以点M,E,C为顶点的三角形与以点N,F,C为顶点的三角形全等.故答案为:或7或8.【点评】本题主要考查了全等三角形的判定以及分类讨论的思想,可能会因考虑不全面而出错,是一道易错题.三、解答题21.计算:(1)(2)(20).【考点】二次根式的混合运算.【专题】计算题.【分析】(1)先把各二次根式化为最简二次根式,然后合并即可;(2)先把各二次根式化为最简二次根式,然后把括号内合并后进行二次根式的除法运算.【解答】解:(1)原式=2﹣3+6﹣10=﹣5;(2)原式=(60﹣16﹣6)÷2=38÷2=19.【点评】本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.22.解方程组:(1)(2).【考点】解二元一次方程组.【专题】计算题.【分析】(1)方程组利用代入消元法求出解即可;(2)方程组整理后,利用加减消元法求出解即可.【解答】解:(1),把①代入②得:10y﹣42+3y=23,即y=5,把y=5代入①得:x=2,则方程组的解为;(2)方程组整理得:,①+②得:7x=14,即x=2,把x=2代入②得:y=﹣1,则方程组的解为.【点评】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.23.已知:如图,∠B=∠D,∠DAB=∠EAC,AB=AD.求证:BC=DE.【考点】全等三角形的判定与性质.【专题】证明题.【分析】因为∠DAB=∠EAC,从图上可以看出∠DAB+∠BAE=∠EAC+∠BAE,即∠DAE=∠BAC,又因为,∠B=∠D,AB=AD,所以很容易证明△DAE≌△BAC,从而得出结论.【解答】证明:∵∠DAB=∠EAC,∴∠DAB+∠BAE=∠EAC+∠BAE,即∠DAE=∠BAC,在△DAE和△BAC中,∴△DAE≌△BAC(ASA)∴BC=DE.【点评】本题考查全等三角形的判定定理,根据ASA可证明三角形全等,从而可得出结论.24.端午节至,甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程S(米)与时间t(分钟)之间的函数关系图象如图所示,请你根据图象,回答下列问题:(1)这次龙舟赛的全程是1000米,乙队先到达终点;(2)求乙与甲相遇时乙的速度;(3)求出在乙队与甲相遇之前,他们何时相距100米?【考点】函数的图象.【分析】(1)根据函数图象的纵坐标,可得比赛的路程,根据函数图象的横坐标,可得比赛的结果;(2)根据乙加速后行驶的路程除以加速后的时间,可得答案;(3)分类讨论,乙加速前,乙加速后,根据甲的路程减去乙的路程,可得关于t的方程,根据解方程,可得答案.【解答】解:(1)由纵坐标看出,这次龙舟赛的全程是1000米,由横坐标看出,乙队先到达终点,故答案为:1000,乙;(2)由图象看出,相遇是在乙加速后,加速后的路程是1000﹣400=600米,加速后的时间时3.8﹣2.2=1.6分钟,乙与甲相遇时乙的速度600÷1.6=375米/分钟;(3)①乙加速前,设行驶x秒时,甲乙相距100米,x﹣x=100.解得x=2;②乙加速后,设行驶x秒时,甲乙相距100米,∵×2.2=550,∴x﹣x=550﹣400﹣100.解得x=0.4,∴行驶了2.2+00.4=2.6,答:在乙队与甲相遇之前,他们行驶2或2.6分钟时相距100米.【点评】本题考查了函数图象,分类讨论是解题关键,乙加速前的速度,乙加速后的速度,注意相遇时的速度是加速后的速度.25.列方程组解应用题:某服装店购进一批甲、乙两种款式时尚T恤衫,用14200元恰好购进100件,已知甲种款型T恤进价为130元/件,且甲种款型的每件进价比乙种款型每件进价少30元.(1)求甲、乙两种款型的T恤各购进多少件?(2)商店按进价提高60%标价销售,销售一段时间后,甲款全部售完,乙款剩余一半,商店决定对乙款型按标价的五折降价销售,很快全部售完,求售完这批T恤商店共获得多少元?【考点】二元一次方程组的应用.【分析】(1)可设甲种款型的T恤衫购进x件,则甲种款型的T恤衫购进y件,根据用14200元恰好购进100件,甲种款型每件的进价比乙种款型每件的进价少30元,列出方程组即可求解;(2)先求出甲款型的利润,乙款型前面销售一半的利润,后面销售一半的亏损,再相加即可求解.【解答】解:(1)设甲种款型的T恤衫购进x件,则乙种款型的T恤衫购进y件,由题意得解得答:甲种款型的T恤衫购进60件,乙种款型的T恤衫购进40件.(2)130×60%×60+160×60%×(40÷2)﹣160×[1﹣(1+60%)×0.5]×(40÷2)=4680+1920﹣640=5960(元).答:售完这批T恤衫商店共获利5960元.【点评】此题考查二元一次方程组的实际运用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.26.如图,在△ABC中,∠BAC=90°,过点B作BC的垂线交∠ACB的角平分线于点D,CD与AB 边交于点E,过D作DF⊥AB于点F.(1)若△BDE是边长为2的等边三角形,求AE的长;(2)求证:AE=BF.【考点】全等三角形的判定与性质.【分析】(1)由BD⊥BC,得到∠DBC=90°,由于△BDE是边长为2的等边三角形,于是得到∠DBA=∠BDE=60°,求得∠ABC=∠DCB=30°,得到CD=2BD=4,根据直角三角形的性质即可得到结果;(2)根据已知条件证得△BDF≌△ACE,即可得到AE=BF.【解答】解:(1)∵BD⊥BC,∴∠DBC=90°,∵△BDE是边长为2的等边三角形,∴∠DBA=∠BDE=60°,∴∠ABC=∠DCB=30°,∴CD=2BD=4,∴CE=2,∵∠A=90°∠AEC=∠DEB=60°,∴∠ACE=30°,∴AE=CE=1;(2)在△BDF与△ACE中,,∴△BDF≌△ACE,∴AE=BF.【点评】本题考查了全等三角形的判定和性质,直角三角形的性质,等边三角形的性质,熟练掌握各性质是解题的关键.27.已知△ABC和△DEC都是等腰直角三角形,C为它们的公共直角顶点,D、E分别在BC、AC 边上.(1)如图1,F是线段AD上的一点,连接CF,若AF=CF;①求证:点F是AD的中点;②判断BE与CF的数量关系和位置关系,并说明理由;(2)如图2,把△DEC绕点C顺时针旋转α角(0<α<90°),点F是AD的中点,其他条件不变,判断BE与CF的关系是否不变?若不变,请说明理由;若要变,请求出相应的正确结论.【考点】旋转的性质;全等三角形的判定与性质;等腰直角三角形.【专题】探究型.【分析】(1)①如图1,由AF=CF得到∠1=∠2,则利用等角的余角相等可得∠3=∠ADC,然后根据等腰三角形的判定定理得FD=FC,易得AF=FD;②先利用等腰直角三角形的性质得CA=CB,CD=CE,则可证明△ADC≌△BEC得到AD=BE,∠1=∠CBE,由于AD=2CF,∠1=∠2,则BE=2CF,再证明∠CBE+∠3=90°,于是可判断CF⊥BE;(2)延长CF到G使FG=CF,连结AG、DG,如图2,易得四边形ACDG为平行四边形,则AG=CD,AG∥CD,于是根据平行线的性质得∠GAC=180°﹣∠ACD,所以CD=CE=AG,再根据旋转的性质得∠BCD=α,所以∠BCE=∠DCE+∠BCD=90°+α=90°+90°﹣∠ACD=180°﹣∠ACD,得到∠GAC=∠ECB,接着可证明△AGC≌△CEB,得到CG=BE,∠2=∠1,所以BE=2CF,和前面一样可证得CF⊥BE.【解答】(1)①证明:如图1,∵AF=CF,∴∠1=∠2,∵∠1+∠ADC=90°,∠2+∠3=90°,∴∠3=∠ADC,∴FD=FC,∴AF=FD,即点F是AD的中点;②BE=2CF,BE⊥CF.理由如下:∵△ABC和△DEC都是等腰直角三角形,∴CA=CB,CD=CE,在△ADC和△BEC中,∴△ADC≌△BEC,∴AD=BE,∠1=∠CBE,而AD=2CF,∠1=∠2,∴BE=2CF,而∠2+∠3=90°,∴∠CBE+∠3=90°,∴CF⊥BE;(2)仍然有BE=2CF,BE⊥CF.理由如下:延长CF到G使FG=CF,连结AG、DG,如图2,∵AF=DF,FG=FC,∴四边形ACDG为平行四边形,∴AG=CD,AG∥CD,∴∠GAC+∠ACD=180°,即∠GAC=180°﹣∠ACD,∴CD=CE=AG,∵△DEC绕点C顺时针旋转α角(0<α<90°),∴∠BCD=α,∴∠BCE=∠DCE+∠BCD=90°+α=90°+90°﹣∠ACD=180°﹣∠ACD,∴∠GAC=∠ECB,在△AGC和△CEB中,∴△AGC≌△CEB,∴CG=BE,∠2=∠1,∴BE=2CF,而∠2+∠BCF=90°,∴∠BCF+∠1=90°,∴CF⊥BE.【点评】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了全等三角形的判定与性质和等腰直角三角形的性质.。
