1.1变化率与导数-教学设计-教案
变化率与导数(教学设计)

3.1变化率与导数(教学设计)(2)3.1.2导数的概念教学目标:1、知识与技能:通过对课本实例的分析,经历由平均变化率过渡到瞬时变化率的过程,了解导数概念的实际背景,让学生知道瞬时变化率就是导数。
2、过程与方法:①通过动手计算(作图)培养学生观察、分析、比较和归纳能力,并结合物理学中的知识进行对比。
②通过问题的探究体会逼近、类比、以已知探求未知、从特殊到一般的数学思想方法。
3、情感、态度与价值观:通过运动的观点体会导数的内涵,使学生掌握导数的概念不再困难,从而激发学生学习数学的兴趣. 教学重点、难点重点:导数概念的形成,导数内涵的理解,由瞬时变化率过度到导数的概念难点:在平均变化率的基础上去探求瞬时变化率,深刻理解导数的内涵,通过逼近的方法,引导学生观察来突破难点教学过程:一、创设情景,引入新课:1、回顾上节课留下的思考题:在高台跳水运动中,运动员相对水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系h(t)=-4.9t 2+6.5t+10.计算运动员在6549t≤≤这段时间里的平均速度,并思考下面的问题:(1)运动员在这段时间里是静止的吗?(2)你认为用平均速度描述运动员的运动状态有什么问题吗?在学生相互讨论,交流结果的基础上,提出:大家得到运动员在这段时间内的平均速度为“0”,但我们知道运动员在这段时间内并没有“静止”。
为什么会产生这样的情况呢?二、师生互动、新课讲解:问题一:请大家思考如何求运动员的瞬时速度,如t=2时刻的瞬时速度?问题二:请大家继续思考,当Δt取不同值时,尝试计算(2)(2)h t ht+∆-=∆v的值?学生对概念的认知需要借助大量的直观数据,所以我让学生利用计算器,分组完成问题二,问题三:当Δt 趋于0时,平均速度有怎样的变化趋势?让学生分组讨论,板演,展示计算结果,同时口答:在t=2时刻,Δt 趋于0时,平均速度趋于一个确定的值-13.1,即瞬时速度,体会逼近思想;另一方面借助动画多渠道地引导学生观察、分析、比较、归纳,通过逼近思想,为了表述方便,数学中用简洁的符号来表示,即0(2)(2)lim 13.1t h t h t∆→+∆-=-∆问题四:运动员在某个时刻0t 的瞬时速度如何表示呢?运动员在某个时刻0t 的瞬时速度如何表示? 学生意识到将0t 代替2,可类比得到000()()lim t h t t h t t∆→+∆-∆(1)气球在体积v 0时的瞬时膨胀率如何表示呢?类比之前学习的瞬时速度问题,引导学生得到瞬时膨胀率的表示000()()limv r v v r v v∆→+∆-∆(2)如果将这两个变化率问题中的函数用()f x 来表示,那么函数()f x 在0x x =处的瞬时变化率如何呢?导数的概念:从函数y =f (x )在x =x 0处的瞬时变化率是:0000()()limlim x x f x x f x fx x∆→∆→+∆-∆=∆∆ 我们称它为函数()y f x =在0x x =出的导数,记作'0()f x 或0'|x x y =,即0000()()()limx f x x f x f x x∆→+∆-'=∆说明:(1)导数即为函数y =f (x )在x =x 0处的瞬时变化率(2)0x x x ∆=-,当0x ∆→时,0x x →,所以000()()()lim x f x f x f x x x ∆→-'=-例1:求函数y =3x 2在x =1处的导数.分析:先求Δf =Δy =f (1+Δx )-f (1)=6Δx +(Δx )2再求6f x x∆=+∆∆再求0lim 6x f x ∆→∆=∆解:222211113313(1)|limlim lim3(1)611x x x x x x y x x x =→→→-⋅-'===+=-- 例2:求函数f (x )=x x +-2在1x =-附近的平均变化率,并求出在该点处的导数.解:x xx x x y ∆-=∆-∆+-+∆+--=∆∆32)1()1(2 200(1)(1)2(1)lim lim(3)3x x y x x f x x x∆→∆→∆--+∆+-+∆-'-===-∆=∆∆例3(课本P75例1):将原油精炼为汽油、柴油、塑料等不同产品,需要对原油进行冷却和加热。
1.1变化率与导数第3课时优秀教学设计

1.1变化率与导数【课题】:1.1.2导数的概念(2)【教学目标】:(1)知识目标:使学生熟悉导数定义,进一步理解导数内涵。
(2)情感目标:让学生充分体会到生活中处处有数学。
(3)能力目标:提高学生学习能力与探究能力、理解表达能力。
【教学重点】:熟悉导数定义,进一步理解导数内涵【教学难点】:熟悉导数定义,进一步理解导数内涵【课前准备】:powerpoint【教学过程设计】:教学环节教学活动设计意图一、复习回顾(1)速度的平均变化率:tt vtt v∆-∆+)()((2)瞬时加速度:当无限趋近于0 时,t∆无限趋近于一个常数,这个常数称为t=t0tt vtt v∆-∆+)()(时的瞬时加速度注:瞬时加速度是速度对于时间的瞬时变化率(3)函数的增量;)()(xfxxfy-∆+=∆(4)求平均变化率;xxfxxfxy∆-∆+=∆∆)()((5)取极限,得导数.xyxfx∆∆='→∆0lim)(导数的概念函数在处的瞬时变化率()f xx x=即在处的导数,记0000()()lim limx xf x x f x fx x∆→∆→+∆-∆=∆∆()y f x=x x=作或,即()'f xx x='y00()()()limxf x x f xf xx∆→+∆-'=∆(6)思想方法:“以已知探求未知”、逼近、类比、从特殊到一般让学生自己回顾、梳理已经学过的知识点有利于自行构建知识体系,理清知识脉络,养成良好的学习习惯。
加深学生对导数概念的理解二、实践新知例1:将原油精炼为汽油、柴油、塑料等不同产品,需要对原油进行冷却和加热。
如果在第x h时候,原油温度(单位:)为.计算第2h和第6hc︒2()715(08)f x x x x=-+≤≤时,原油温度的瞬时变化率,并说明它的意义。
①启发学生根据导数定义,分别求出和(2)f'(6)f'②既然我们得到了第2h和第6h的原油温度的瞬时变化率分别为-3与5,大家能说明它的含义吗?师生共同归纳得到,导数即瞬时变化率,可反映物体变○3化的快慢发展学生的应用意识,是高中数学课程标准所倡导的重要理念之一。
1.1.1和1.1.2变化率问题、导数的概念课件人教新课标1

【解析】(1)自变量x从1变到2时,函数f(x)=2x+1的函数值的
增量为Δy=5-3=2,故增量之比是2.
答案:2
(2)函数f(x)=x2在x=1处的瞬时变化率是 lim f (1 x) f (1)
x0
x
lim (1 x)2 12 lim (2 x) 2.
x0
x
x0
答案:2
(3)函数y=f(x)= 1 在x=-1处的导数可表示为f′(-1)或
【微思考】
(1)函数f(x)在区间[x1,x2]上的平均变化率的大小与曲线 y=f(x)在区间[x1,x2]上的“峻峭”程度有什么关系? 提示:平均变化率的绝对值越大,曲线y=f(x)在区间[x1,x2]
上越“峻峭”,反之亦然. (2)平均变化率可以是零吗? 举例说明. 提示:可以是零,如函数f(x)=a(a为常数).
Δx趋于0的距离要多近有多近,即|Δx-0|可以小于给定的任
意小的正数,且始终Δx≠0.
3.对导数概念的两点说明
(若1)当xy 的Δ极x≠限0不时存,在比,值则xyf的 (x极)在限点存x在0处,不则可f导(x或)在无点导x数0处.可导;
(2)在点x=x0处的导数的定义可变形为f′(x0)=
lim f (x0 x) f (x0 )
取定值,x1取不同的数值时,函数的平均变化率也是不同的.
特别地,当函数f(x)为常数函数时,Δy=0,则 y =0.
x
2.对平均变化率的三点说明 (1)y=f(x)在区间[x1,x2]上的平均变化率是曲线y=f(x)在 区间[x1,x2]上峻峭程度的“数量化”,曲线峻峭程度是平 均变化率的“视觉化”. (2)平均变化率的几何意义就是函数y=f(x)图象上两点P1(x1,
2019高中数学 第一章1.1 变化率与导数 1.1.1 变化率问题 1.1.2 导数的概念学案 新人教A版选修2-2

1.1 变化率与导数1.1.1 变化率问题 1.1.2 导数的概念学习目标:1.通过对大量实例的分析,经历由平均变化率过渡到瞬时变化率的过程,了解导数概念的实际背景.2.会求函数在某一点附近的平均变化率.(重点)3.会利用导数的定义求函数在某点处的导数.(重点、难点)4.理解函数的平均变化率,瞬时变化率及导数的概念.(易混点)[自 主 预 习·探 新 知]1.函数的平均变化率(1)函数y =f (x )从x 1到x 2的平均变化率为Δy Δx=fx 2-f x 1x 2-x 1,其中Δx =x 2-x 1是相对于x 1的一个“增量”,Δy =f (x 2)-f (x 1)=f (x 1+Δx )-f (x 1)是相对于f (x 1)的一个“增量”.(2)平均变化率的几何意义设A (x 1,f (x 1)),B (x 2,f (x 2))是曲线y =f (x )上任意不同的两点,函数y =f (x )的平均变化率Δy Δx=f x 2-f x 1x 2-x 1=f x 1+Δx -f x 1Δx为割线AB 的斜率,如图111所示.图111思考:Δx ,Δy 的值一定是正值吗?平均变化率是否一定为正值?[提示] Δx ,Δy 可正可负,Δy 也可以为零,但Δx 不能为零.平均变化率ΔyΔx 可正、可负、可为零.2.瞬时速度与瞬时变化率(1)物体在某一时刻的速度称为瞬时速度.(2)函数f (x )在x =x 0处的瞬时变化率是函数f (x )从x 0到x 0+Δx 的平均变化率在Δx →0时的极限即lim Δx →0Δy Δx=lim Δx →0f x 0+Δx -f x 0Δx.3.导数的概念函数y =f (x )在x =x 0处的导数就是函数y =f (x )在x =x 0处的瞬时变化率,记作f ′(x 0)或y ′| x =x 0,即f ′(x 0)=lim Δx →0f x 0+Δx -f x 0Δx.[基础自测]1.思考辨析(1)函数y=f(x)在x=x0处的导数值与Δx值的正、负无关.( )(2)瞬时变化率是刻画某函数值在区间[x1,x2]上变化快慢的物理量.( )(3)在导数的定义中,Δx,Δy都不可能为零.( )提示:(1)由导数的定义知,函数在x=x0处的导数只与x0有关,故正确.(2)瞬时变化率是刻画某一时刻变化快慢的物理量,故错误.(3)在导数的定义中,Δy可以为零,故错误.[答案] (1)√(2)×(3)×2.函数y=f(x),自变量x由x0改变到x0+Δx时,函数的改变量Δy为( )【导学号:31062000】A.f(x0+Δx) B.f(x0)+ΔxC.f(x0)·Δx D.f(x0+Δx)-f(x0)D[Δy=f(x0+Δx)-f(x0),故选D.]3.若一质点按规律s=8+t2运动,则在一小段时间[2,2.1]内的平均速度是( ) A.4 B.4.1C.0.41 D.-1.1B[v=ΔsΔt=s-s2.1-2=2.12-220.1=4.1,故选B.]4.函数f(x)=x2在x=1处的瞬时变化率是________.[解析]∵f(x)=x2.∴在x=1处的瞬时变化率是lim Δx→0ΔyΔx=limΔx→0f+Δx-fΔx=limΔx→0+Δx2-12Δx=limΔx→0(2+Δx)=2.[答案] 25.函数f(x)=2在x=6处的导数等于________.[解析]f′(6)=limΔx→0f+Δx-fΔx=limΔx→02-2Δx=0.[答案] 0[合作探究·攻重难](1)从0.1到0.2的平均变化率;(2)在区间[x 0,x 0+Δx ]上的平均变化率.【导学号:31062001】[解] (1)因为f (x )=3x 2+5, 所以从0.1到0.2的平均变化率为 3×0.22+5-3×0.12-50.2-0.1=0.9.(2)f (x 0+Δx )-f (x 0)=3(x 0+Δx )2+5-(3x 20+5) =3x 20+6x 0Δx +3(Δx )2+5-3x 20-5=6x 0Δx +3(Δx )2. 函数f (x )在区间[x 0,x 0+Δx ]上的平均变化率为6x 0Δx +Δx2Δx =6x 0+3Δx .[规律方法] 1.求函数平均变化率的三个步骤第一步,求自变量的增量Δx =x 2-x 1; 第二步,求函数值的增量Δy =f x 2-f x 1;第三步,求平均变化率Δy Δx=fx 2-f x 1x 2-x 12.求平均变化率的一个关注点求点x 0附近的平均变化率,可用f x 0+Δx -f x 0Δx的形式.[跟踪训练]1.如图112,函数y =f (x )在A ,B 两点间的平均变化率等于( )图112A .1B .-1C .2D .-2B [平均变化率为1-33-1=-1.故选B.]2.已知函数y =f (x )=2x 2的图象上点P (1,2)及邻近点Q (1+Δx,2+Δy ),则Δy Δx 的值为( )【导学号:31062002】A .4B .4xC .4+2Δx 2D .4+2ΔxD [Δy Δx =+Δx 2-2×12Δx=4+2Δx .故选D.][探究问题]1.物体的路程s 与时间t 的关系是s (t )=5t 2,如何计算物体在[1,1+Δt ]这段时间内的平均速度?提示:Δs =5(1+Δt )2-5=10Δt +5(Δt )2,v =Δs Δt=10+5Δt .2.当Δt 趋近于0时,探究1中的平均速度趋近于多少?怎样理解这一速度? 提示:当Δt 趋近于0时,ΔsΔt趋近于10,这时的平均速度即为当t =1时的瞬时速度.某物体的运动路程s (单位:m)与时间t (单位:s)的关系可用函数s (t )=t 2+t+1表示,求物体在t =1 s 时的瞬时速度.[思路探究] 计算物体在[1,1+Δt ]内的平均速度Δs Δt ――→令Δt →0计算lim Δt →0ΔsΔt―→得t =1 s 时的瞬时速度[解] ∵Δs Δt =s+Δt -sΔt=+Δt2++Δt +1-2+1+Δt=3+Δt ,∴lim Δt →0ΔsΔt=lim Δt →0(3+Δt )=3.∴物体在t =1处的瞬时变化率为3. 即物体在t =1 s 时的瞬时速度为3 m/s.母题探究:1.(变结论)在本例条件不变的前提下,试求物体的初速度. [解] 求物体的初速度,即求物体在t =0时的瞬时速度. ∵Δs Δt =s +Δt -sΔt=+Δt2++Δt +1-1Δt=1+Δt ,∴lim Δt →0(1+Δt )=1.∴物体在t =0时的瞬时变化率为1,即物体的初速度为1 m/s.2.(变结论)在本例条件不变的前提下,试问物体在哪一时刻的瞬时速度为9 m/s. [解] 设物体在t 0时刻的瞬时速度为9 m/s.又Δs Δt =s t 0+Δt -s t 0Δt=(2t 0+1)+Δt .lim Δt →0ΔsΔt=lim Δt →0(2t 0+1+Δt )=2t 0+1. 则2t 0+1=9, ∴t 0=4.则物体在4 s 时的瞬时速度为9 m/s.[规律方法] 求运动物体瞬时速度的三个步骤求时间改变量Δt 和位移改变量Δs =s t 0+Δt -s t 0求平均速度v =Δs Δt求瞬时速度,当Δt 无限趋近于0时,\f(Δs,Δt )无限趋近于常数v ,即为瞬时速度.(1)设函数y =f (x )在x =x 0处可导,且lim Δx →00x 0Δx=1,则f ′(x 0)等于( )A .1B .-1C .-13D .13(2)求函数f (x )=x -1x在x =1处的导数.[思路探究] (1)类比f ′(x 0)=lim Δx →0f x 0+Δx -f x 0Δx求解.(2)先求Δy ―→再求Δy Δx ―→计算lim Δx →0ΔyΔx(1)C [∵lim Δx →0f x 0-3Δx -f x 0Δx=lim Δx →0⎣⎢⎡⎦⎥⎤f x 0-3Δx -f x 0-3Δx -=-3f ′(x 0)=1,∴f ′(x 0)=-13,故选C.](2)∵Δy =(1+Δx )-11+Δx -⎝ ⎛⎭⎪⎫1-11 =Δx +1-11+Δx =Δx +Δx1+Δx, ∴Δy Δx =Δx +Δx 1+Δx Δx =1+11+Δx , ∴f ′(1)=lim Δx →0Δy Δx =lim Δx →0⎝ ⎛⎭⎪⎫1+11+Δx =2.[规律方法] 求函数y =f (x )在点x 0处的导数的三个步骤简称:一差、二比、三极限. [跟踪训练]3.已知f ′(1)=-2,则lim Δx →0f-2Δx -fΔx=________.【导学号:31062003】[解析] ∵f ′(1)=-2, ∴limΔx →0f-2Δx -fΔx=lim Δx →0f-2Δx -f ⎝ ⎛⎭⎪⎫-12-2Δx=-2lim Δx →0f-2Δx -f -2Δx=-2f ′(1)=-2×(-2)=4.[答案] 44.求函数y =3x 2在x =1处的导数.[解] ∵Δy =f (1+Δx )-f (1)=3(1+Δx )2-3=6Δx +3(Δx )2,∴Δy Δx =6+3Δx ,∴f ′(1)=lim Δx →0ΔyΔx=lim Δx →0(6+3Δx )=6.[当 堂 达 标·固 双 基]1.一物体的运动方程是s =3+2t ,则在[2,2.1]这段时间内的平均速度是( )A .0.4B .2C .0.3D .0.2B [v =s-s 2.1-2=4.2-40.1=2.]2.物体自由落体的运动方程为s (t )=12gt 2,g =9.8 m/s 2,若v =lim Δt →0=s 1+Δt -s 1Δt=9.8 m/s ,那么下列说法中正确的是( )【导学号:31062004】A .9.8 m/s 是物体从0 s 到1 s 这段时间内的速率B .9.8 m/s 是1 s 到(1+Δt )s 这段时间内的速率C .9.8 m/s 是物体在t =1 s 这一时刻的速率D .9.8 m/s 是物体从1 s 到(1+Δt )s 这段时间内的平均速率 C [结合平均变化率与瞬时变化率可知选项C 正确.] 3.函数f (x )=x 在x =1处的导数为________. [解析] ∵Δy =f (1+Δx )-f (1)=1+Δx -1, ∴Δy Δx =1+Δx -1Δx =11+Δx +1, ∴f ′(1)=lim Δx →0Δy Δx =lim Δx →011+Δx +1=12.[答案] 124.设f (x )在x 0处可导,若lim Δx →0f x 0+3Δx -f x 0Δx=A ,则f ′(x 0)=________.[解析] lim Δx →0f x 0+3Δx -f x 0Δx=3lim 3Δx →0f x 0+3Δx -f x 03Δx=3f ′(x 0)=A .故f ′(x 0)=13A .[答案] A35.在曲线y =f (x )=x 2+3上取一点P (1,4)及附近一点(1+Δx,4+Δy ),求:(1)Δy Δx ;(2)f ′(1).【导学号:31062005】[解] (1)Δy Δx =f+Δx -fΔx=+Δx2+3-2+Δx=2+Δx .(2)f ′(1)=lim Δx →0f+Δx -fΔx=lim Δx →0(2+Δx )=2.。
人教版数学高二变化率问题 精品教学设计

本章内容的兴趣。
2.形成概念问题1:甲用5年时间挣到10万元, 乙用5个月时间挣到2万元, 如何比较和评价甲、乙两人的经营成果?设计意图:使学生了解生活中的变化率问题,为归纳函数平均变化率提供更多的实际背景。
师生活动:稍加点拨,继续引导学生举出生活中的变化率问题。
问题2:大家可能都有过吹气球的回忆。
在吹气球的过程中,可以发现,随着气球内空气容量的增加,气球的半径增加越来越慢.从数学角度,如何描述这种现象呢?设计意图:通过熟悉的生活体验,提炼出数学模型,从而为归纳函数平均变化率概念提供具体背景。
师生活动:由球的体积公式推导半径关于体积的函数解析式,然后通过计算,用数据来回答问题,解释上述现象。
思考:当空气容量从增加到时,气球的平均膨胀率是多少?设计意图:把问题2中的具体数据运算提升到一般的字母表示,体现从特殊到一般的数学思想。
为归纳函数平均变化率概念作铺垫。
师生活动:教师播放多媒体,学生可以直接回答问题,教师板书其正确答案。
问题3:在高台跳水运动中, 运动员相对于水面的高度(单位:m)与起跳后的时间(单位:s) 存在函数关系,如果用运动员在某段时间内的平均速度描述其运动状态, 那么:(1):(1)在这段时间里,运动员的平均速度为多少?(2)在在这段时间里, 运动员的平均速度为多少?设计意图:高台跳水展示了生活中最常见的一种变化率——运动速度,而运动速度是学生非常熟悉的物理知识,这样可以减少因为背景的复杂而可能引起的对数学知识学习的干扰。
通过计算为归纳函数平均变化率概念提供又一重要背景。
师生活动:教师播放多媒体,学生通过计算回答问题。
对第(2)小题的答案说明其物理意义。
探究:计算运动员在在6549t≤≤这段时间里的平均速度,并思考下面的问题:(1) 运动员在这段时间里是静止的吗?(2) 你认为用平均速度描述运动员的运动状态有什么问题吗?设计意图:通过计算得出平均速度只能粗略地描述运动状态,从而为瞬时速度的提出埋下伏笔即为导数的概念作了铺垫,利用图像解释的过程体现了数形结合的数学思想方法。
高中数学选修2-2教学设计8:1.1.1 变化率问题教案
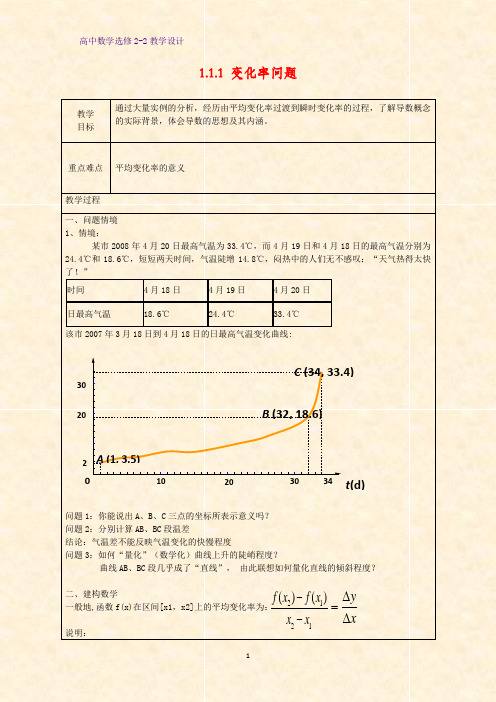
1.1.1 变化率问题教学目标 通过大量实例的分析,经历由平均变化率过渡到瞬时变化率的过程,了解导数概念的实际背景,体会导数的思想及其内涵。
重点难点 平均变化率的意义教学过程一、问题情境1、情境:某市2008年4月20日最高气温为33.4℃,而4月19日和4月18日的最高气温分别为24.4℃和18.6℃,短短两天时间,气温陡增14.8℃,闷热中的人们无不感叹:“天气热得太快了!”时间4月18日 4月19日 4月20日 日最高气温 18.6℃ 24.4℃ 33.4℃该市2007年3月18日到4月18日的日最高气温变化曲线:问题1:你能说出A 、B 、C 三点的坐标所表示意义吗?问题2:分别计算AB 、BC 段温差结论:气温差不能反映气温变化的快慢程度问题3:如何“量化”(数学化)曲线上升的陡峭程度?曲线AB 、BC 段几乎成了“直线”, 由此联想如何量化直线的倾斜程度?二、建构数学一般地,函数f(x)在区间[x1,x2]上的平均变化率为: 说明: t (d)20 30 34 210 20 30A (1, 3.5)B (32, 18.6)0 C (34, 33.4) T (℃)2 10 2121()()f x f x x x--x y ∆∆=(1)平均变化率是曲线陡峭程度的“数量化”,曲线的陡峭程度是平均变化率的“视觉化” (2)用平均变化率量化一段曲线的陡峭程度是“粗糙不精确的”,但应注意当x2—x1很小时,这种量化便由“粗糙”逼近“精确”。
例1、某婴儿从出生到第12个月的体重变化如图所示,试分别计算从出生到第3个月与第6个月到第12个月该婴儿体重的平均变化率;由此你能得到什么结论?(1)1kg/月(2)0.4kg/月结论:该婴儿从出生到第3个月体重增加的速度比第6个月到第12个月体重增加的速度要快。
例2、水经过虹吸管从容器甲中流向容器乙,t s 后容器甲中水的体积 (单位: )计算第一个10s 内V 的平均变化率。
1-1 3.1变化率与导数学案
§3.1 变化率与导数学案§3.1.1 变化率问题学习目标:1.理解平均变化率的概念;2.了解平均变化率的几何意义;3.会求函数在某点处附近的平均变化率.教学过程:一、学习背景为了描述现实世界中运动、过程等变化着的现象,在数学中引入了函数,随着对函数的研究,产生了微积分,微积分的创立以自然科学中四类问题的处理直接相关:1、已知物体运动的路程作为时间的函数,求物体在任意时刻的速度与加速度等;2、求曲线的切线;3、求已知函数的最大值与最小值;4、求长度、面积、体积和重心等.导数是微积分的核心概念之一,它是研究函数增减、变化快慢、最大(小)值等问题最一般、最有效的工具.导数研究的问题即变化率问题:研究某个变量相对于另一个变量变化的快慢程度.二、新课学习(一)问题提出问题1 气球膨胀率我们都吹过气球回忆一下吹气球的过程,可以发现,随着气球内空气容量的增加,气球的半径增加越来越慢.从数学角度,如何描述这种现象呢?分析: (1)当V从0增加到1时,气球半径增加了Array气球的平均膨胀率为(2)当V从1增加到2时,气球半径增加了气球的平均膨胀率为可以看出:思考: 当空气容量从V1增加到V2时,气球的平均膨胀率是多少?问题2 高台跳水在高台跳水运动中,运动员相对于水面的高度h (单位:m )与起跳后的时间t (单位:s )存在函数关系105.69.4)(2++-=t t t h .如何用运动员在某些时间段内的平均速v 度粗略地描述其运动状态? 思考计算: 5.00≤≤t 和21≤≤t 的平均速度v探究: 计算运动员在49650≤≤t 这段时间里的平均速度,并思考以下问题:(1)运动员在这段时间内使静止的吗?(2)你认为用平均速度描述运动员的运动状态有什么问题吗?(二)平均变化率概念 1.上述问题中的变化率可用式子1212)()(x x x f x f --表示,称为函数)(x f 从1x 到2x 的平均变化率.2.若设12x x x -=∆, )()(12x f x f f -=∆(这里x ∆看作是对于1x 的一个“增量”可用x x ∆+1代替2x ,同样)()(12x f x f y f -=∆=∆) 则平均变化率为=∆∆=∆∆x fx y xx f x x f x x x f x f ∆-∆+=--)()()()(111212 思考: 观察函数)(x f 的图象平均变化率=∆∆x f 1212)()(x x x f x f --表示什么?三、典例分析例 1 已知函数x x x f +-=2)(的图象上的一点)2,1(--A 及临近一点)2,1(y x B ∆+-∆+-,则=∆∆xy. 解:例2 求2x y =在0x x =附近的平均变化率. 解:四、课堂练习1.质点运动规律为32+=t s ,则在时间)3,3(t ∆+中相应的平均速度为 .2.物体按照43)(2++=t t t s 的规律作直线运动,求在s 4附近的平均变化率.3.过曲线3)(x x f y ==上两点)1,1(P 和)1,1(y x Q ∆+∆+作曲线的割线, 求出当1.0=∆x 时割线的斜率.五、课堂反馈1. 设函数()x f y =,当自变量x 由0x 改变到x x ∆+0时,函数的改变量y ∆为( ) A ()x x f ∆+0 B ()x x f ∆+0 C ()x x f ∆⋅0 D ()()00x f x x f -∆+ 2. 一质点运动的方程为221t s -=,则在一段时间[]2,1内的平均速度为( )A -4B -8C 6D -63. 将半径为R 的球加热,若球的半径增加R ∆,则球的表面积增加S ∆等于( ) A R R ∆π8 B ()248R R R ∆+∆ππ C ()244R R R ∆+∆ππ D ()24R ∆π4. 在曲线12+=x y 的图象上取一点(1,2)及附近一点()y x ∆+∆+2,1,则xy∆∆为( ) A 21+∆+∆x x B 21-∆-∆x x C 2+∆x D xx ∆-∆+12 5.函数()x f y =的平均变化率的物理意义是指把()x f y =看成物体运动方程时,在区间[]21,t t 内的6.函数()x f y =的平均变化率的几何意义是指函数()x f y =图象上两点()()111,x f x P 、()()222,x f x P 连线的7.函数8232--=x x y 在31=x 处有增量5.0=∆x ,则()x f 在1x 到x x ∆+1上的平均变化率是 8.正弦函数x y sin =在区间⎥⎦⎤⎢⎣⎡6,0π和⎥⎦⎤⎢⎣⎡2,3ππ的平均变化率哪一个较大? 9.在受到制动后的t 秒内一个飞轮上一点P 旋转过的角度(单位:孤度)由函数()23.04t t t -=ϕ(单位:秒)给出(1)求t =2秒时,P 点转过的角度(2)求在t t ∆+≤≤22时间段内P 点转过的平均角速度,其中①1=∆t ,②1.0=∆t ③01.0=∆t§3.1.2 导数的概念学习目标:1.了解瞬时速度、瞬时变化率的概念;2.理解导数的概念,知道瞬时变化率就是导数,体会导数的思想及其内涵;3.会求函数在某点的导数. 学习过程: 一、创设情景 (一)平均变化率: (二)探究探究: 计算运动员在49650≤≤t 这段时间里的平均速度,(1)运动员在这段时间内使静止的吗?(2)你认为用平均速度描述运动员的运动状态有什么问题吗?探究过程:二、学习新知 1.瞬时速度我们把物体在某一时刻的速度称为瞬时速度.运动员的平均速度不能反映他在某一时刻的瞬时速度,那么,如何求运动员的瞬时速度呢?比如,2t =时的瞬时速度是多少?考察2t =附近的情况:思考: 当t ∆趋近于0时,平均速度v 有什么样的变化趋势? 结论: 小结:2.导数的概念从函数)(x f y =在0x x =处的瞬时变化率是:0000()()limlim x x f x x f x fxx ∆→∆→+∆-∆=∆∆我们称它为函数()y f x =在0x x =出的导数,记作'0()f x 或0'|x x y =即0000()()()limx f x x f x f x x∆→+∆-'=∆说明: (1)导数即为函数)(x f y =在0x x =处的瞬时变化率; (2)0x x x ∆=-,当0x ∆→时,0x x →,所以000()()()lim x f x f x f x x x ∆→-'=-.三、典例分析例1 (1)求函数23x y =在1=x 处的导数.(2)求函数x x x f +-=2)(在1x =-附近的平均变化率,并求出该点处的导数. 分析: 先求)()(00x f x x f y f -∆+=∆=∆,再求xy ∆∆,最后求x y x ∆∆→∆0lim .解: (1)(2)例2 将原油精炼为汽油、柴油、塑胶等各种不同产品,需要对原油进行冷却和加热,如果第xh 时,原油的温度(单位:C)为2()715(08)f x x x x =-+≤≤,计算第2h 时和第6h 时,原油温度的瞬时变化率,并说明它们的意义. 解:注: 一般地,'0()f x 反映了原油温度在时刻0x 附近的变化情况.四、课堂练习1.质点运动规律为32+=t s ,求质点在3t =的瞬时速度为.2.求曲线3)(x x f y ==在1x =时的导数.3.例2中,计算第3h 时和第5h 时,原油温度的瞬时变化率,并说明它们的意义.五、课堂反馈1.自变量由0x 变到1x 时,函数值的增量与相应自变量的增量之比是函数( )A 在区间],[10x x 上的平均变化率B 在0x 处的变化率C 在1x 处的变化率D 在区间],[10x x 上的导数2.下列各式中正确的是( )A xx f x x f y x x x ∆-∆-=→∆=)()(|000'limB xx f x x f x f x ∆∆-∆-=→∆)()()(000'lim C xx f x x f y x x x ∆+∆+=→∆=)()(|000'limD xx x f x f x f x ∆∆--=→∆)()()(0000'lim 3.设4)(+=ax x f ,若2)1('=f ,则a 的值( )A 2B . -2C 3D -34.任一做直线运动的物体,其位移s 与时间t 的关系是23t t s -=,则物体的初速度是( ) A 0B 3C -2D t 23-5.函数xx y 1+=, 在1=x 处的导数是6.13-=x y ,当2=x 时 ,=∆∆→∆xyx lim7.设圆的面积为A ,半径为r ,求面积A 关于半径r 的变化率。
高中数学 第二章 变化率与导数及导数的应用 计算导数教案 北师大版选修1-1
计算导数教学过程:一、复习1、导数的定义;2、导数的几何意义;3、导函数的定义;4、求函数的导数的流程图。
(1)求函数的改变量)()(x f x x f y -∆+=∆(2)求平均变化率xx f x x f x y ∆-∆+=∆∆)()( (3)取极限,得导数/y =()f x '=x y x ∆∆→∆0lim 本节课我们将学习常见函数的导数。
首先我们来求下面几个函数的导数。
(1)、y=x (2)、y=x 2 (3)、y=x 3问题1:1-=x y ,2-=x y ,3-=x y 呢? 问题2:从对上面几个幂函数求导,我们能发现有什么规律吗?二、新授1、基本初等函数的求导公式:⑴ ()kx b k '+= (k,b 为常数) ⑵ 0)(='C (C 为常数)⑶ ()1x '= ⑷ 2()2x x '=⑸ 32()3x x '= ⑹ 211()x x '=-⑺'=由⑶~⑹你能发现什么规律? ⑻ 1()x xααα-'= (α为常数) ⑼ ()ln (01)x x a a a a a '=>≠, ⑽ a a 11(log x)log e (01)x xlnaa a '==>≠,且 ⑾ x x e )(e =' ⑿ x 1)(lnx =' ⒀ cosx )(sinx =' ⒁ sinx )(cosx -=' 从上面这一组公式来看,我们只要掌握幂函数、指对数函数、正余弦函数的求导就可以了。
例1、求下列函数导数。
(1)5-=x y (2)x y 4= (3)x x x y =(4)x y 3log = (5)y=sin(2π+x) (6) y=sin 3π (7)y=cos(2π-x) (8)y=(1)f '例2:已知点P 在函数y=cosx 上,(0≤x≤2π),在P 处的切线斜率大于0,求点P 的横坐标的取值范围。
1.1变化率与导数(4课时)
作业:
P10习题1.1A组:2,3,4.
1.1
1.1.3
变化率与导数
导数的几何意义
问题提出
1.函数f(x)在x=x0处的导数的含义是 什么?
Vy f (x 0 + Vx ) - f (x 0 ) f¢ (x 0 ) = lim = lim Vx 0 Vx Vx 0 Vx
2.求函数f(x)在x=x0处的导数有哪 几个基本步骤?
若给定函数f(x)和x0的值,那么f′(x0) 是变量还是定值?
f¢ (x 0 ) = lim
思考3:如何求函数f(x)=x2在x=1处的 导数?一般地,求函数f(x)在x=x0处的 导数有哪几个基本步骤? 第一步,求函数值增量:
Vy Vx ® 0 Vx
△y=f(x+△x)-f(x0); 第二步,求平均变化率:
思考2:如果将半径r表示为体积V的函数, 则该函数的解析式是什么?
r (V ) =
3
3V 4p
思考3:当空气容量V从0增加到1时,气 球的半径增加了多少?可以用哪个数据 来刻画气球的平均膨胀率?
r(1)-r(0)≈0.62(dm),
r (1) - r (0) » 0.62(dm / L ) 1- 0
探究(一):气球的膨胀率 【背景材料】在吹气球的过程中,随着 气球内空气容量的增加,气球的半径增 加的速度越来越慢.设气球的体积为V (单位:L),某一时刻的半径为r(单 位:dm). 思考1:气球的体积V与半径r的函数关系 是什么? 4 3 V (r ) = p r 3
4 3 pr 3
V (r ) =
3.函数的平均变化率与自变量的初始 值及其增量有关,它能刻画函数在某个 区间内函数值的平均取值情况,但不能 反映函数在区间内各点的函数值.
变化率与导数教学设计(共7篇)
变化率与导数教学设计(共7篇)第1篇:1.1变化率与导数教学设计教案教学准备1. 教学目标知道了物体的运动规律,用极限来定义物体的瞬时速度,学会求物体的瞬时速度掌握导数的定义.2. 教学重点/难点【教学重点】:理解掌握物体的瞬时速度的意义和导数的定义.【教学难点】:理解掌握物体的瞬时速度的意义和导数的定义.3. 教学用具多媒体4. 标签变化率与导数教学过程课堂小结课后习题第2篇:1.1变化率与导数教学设计教案教学准备1. 教学目标(1)理解平均变化率的概念.(2)了解瞬时速度、瞬时变化率、的概念.(3)理解导数的概念(4)会求函数在某点的导数或瞬时变化率.2. 教学重点/难点教学重点:瞬时速度、瞬时变化率的概念及导数概念的形成和理解教学难点:会求简单函数y=f(x)在x=x0处的导数3. 教学用具多媒体、板书4. 标签教学过程一、创设情景、引入课题【师】十七世纪,在欧洲资本主义发展初期,由于工场的手工业向机器生产过渡,提高了生产力,促进了科学技术的快速发展,其中突出的成就就是数学研究中取得了丰硕的成果―――微积分的产生。
【板演/PPT】【师】人们发现在高台跳水运动中,运动员相对于水面的高度h(单位:米)与起跳后的时间t(单位:秒)存在函数关系h(t)=-4.9t2+6.5t+10.如何用运动员在某些时间段内的平均速度粗略地描述其运动状态? 【板演/PPT】让学生自由发言,教师不急于下结论,而是继续引导学生:欲知结论怎样,让我们一起来观察、研探。
【设计意图】自然进入课题内容。
二、新知探究 [1]变化率问题【合作探究】探究1 气球膨胀率【师】很多人都吹过气球,回忆一下吹气球的过程,可以发现,随着气球内空气容量的增加,气球的半径增加越来越慢.从数学角度,如何描述这种现象呢? 气球的体积V(单位:L)与半径r(单位:dm)之间的函数关系是如果将半径r表示为体积V的函数,那么【板演/PPT】【活动】【分析】当V从0增加到1时,气球半径增加了气球的平均膨胀率为(1)当V从1增加到2时,气球半径增加了气球的平均膨胀率为0.62>0.16 可以看出,随着气球体积逐渐增大,它的平均膨胀率逐渐变小了.【思考】当空气容量从V1增加到V2时,气球的平均膨胀率是多少? 解析:探究2 高台跳水【师】在高台跳水运动中,运动员相对于水面的高度h(单位:米)与起跳后的时间t(单位:秒)存在函数关系 h(t)=-4.9t2+6.5t+10.如何用运动员在某些时间段内的平均速度粗略地描述其运动状态? (请计算)【板演/PPT】【生】学生举手回答【活动】学生觉得问题有价值,具有挑战性,迫切想知道解决问题的方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.1变化率与导数-教学设计-教案I教学准备1.教学目标(1)理解平均变化率的概念(2)了解瞬时速度、瞬时变化率、的概念•(3)理解导数的概念(4)会求函数在某点的导数或瞬时变化率•2.教学重点/难点教学重点:瞬时速度、瞬时变化率的概念及导数概念的形成和理解教学难点:会求简单函数y = f (x )在x = x0 处的导数3.教学用具多媒体、板书4.标签教学过程一、创设情景、弓I入课题【师】十七世纪,在欧洲资本主义发展初期,由于工场的手工业向机器生产过渡,提高了生产力,促进了科学技术的快速发展,其中突出的成就就是数学研究中取得了丰硕的成果------------------------- 微积分的产生。
【板演/PPT】【师】人们发现在高台跳水运动中,运动员相对于水面的高度h(单位:米)与起跳后的时间t (单位:秒)存在函数关系h(t)=-4.9t 2+6.5t+10.如何用运动员在某些时间段内的平均速度粗略地描述其运动状态?【板演/PPT】让学生自由发言,教师不急于下结论,而是继续引导学生:欲知结论怎样,让我们一起来观察、研探。
【设计意图】自然进入课题内容。
二、新知探究[1]变化率问题【合作探究】探究1气球膨胀率【师】很多人都吹过气球,回忆一下吹气球的过程,可以发现,随着气球内空气容量的增加,气球的半径增加越来越慢•从数学角度,如何描述这种现象呢?气球的体积V(单位:L)与半径r(单位:dm)之间的函数关系是■如果将半径r表示为体积V的函数,那么【板演/PPT】【活动】【分析】仍=瞪当V从0增加到1时,气球半径增加了XT.9AT—13.1气球的平均膨胀率为芝严^0.62(亦2)(1)当V从1增加到2时,气球半径增加了气球的平均膨胀率为号护如°0.62>0.16可以看出,随着气球体积逐渐增大,它的平均膨胀率逐渐变小了.【思考】当空气容量从V1增加到V2时,气球的平均膨胀率是多少?r(V)-r(V):解析:探究2高台跳水【师】在高台跳水运动中,运动员相对于水面的高度h(单位:米)与起跳后的时间t (单位:秒)存在函数关系h(t)=-4.9t 2+6.5t+10.如何用运动员在某些时间段内的平均速度粗略地描述其运动状态?(请计算)f •沖U二二-时®屮环朿度【生】学生举手回答【活动】学生觉得问题有价值,具有挑战性, 迫切想知道解决问题的方法。
【师】解析:h(t)=-4.9t在时阿昱【设计意图】两个问题由易到难,让学生一步一个台阶。
为引入变化率的概念以及加深对变化率概念的理解服=-8J2(M I S)【板演/PPT】拭纣一*⑴务。
探究3计算运动员在。
兰“宁这段时间里的平均速度,并思考下面的问题:轨鑰=拭0)=10 »=孚=0(1)运动员在这段时间里是静止的吗?(2)你认为用平均速度描述运动员的运动状态有什么问题吗?【板演/PPT】【生】学生举手回答【师】在高台跳水运动中,平均速度不能准确反映他在这段时间里运动状态.【活动】师生共同归纳出结论平均变化率:上述两个问题中的函数关系用y = f (x)表示, 那么问题中的变化率可用式子心)-心表示.可—旳我们把这个式子称为函数y=f(x)从x1到x2的平均变化率.习惯上用△ x=%x1, △ y=f(%f(x1)这里Ax看作是对于x1的一个增量”可用x1+Ax 代替x2同样△ y=f(x)-f(x),于是,平均变化率可以表示为:【几何意义】观察函数f (x)的图象,平均变化率驚先护的几何意义是什么?【提示】:直线AB的斜率【生】学生结合图象思考问题【设计意图】问题的目的是:①让学生加深对平均变化率的理解;②为下节课学习导数的几何意义作辅垫;③③培养学生数形结合的能力。
[2]导数的概念探究1何为瞬时速度【板演/PPT】在高台跳水运动中,平均速度不能反映他在这段时间里运动状态,需要用瞬时速度描述运动状态。
我们把物体在某一时刻的速度称为瞬时速度•平均变化率近似地刻画了曲线在某一区间上的变化趋势•【师】如何精确地刻画曲线在一点处的变化趋势呢?ft(f)= _4.9f3 +6.5r + 10求:从2s到(2+4)s这段时间内平均速度解:v =—探究2当△趋近于0时,平均速度有什么变化趋势?从2s到(2+凸:方这段时间内平均速度当厶t 趋近于0时,即无论t 从小于2的一边, 还是从大于2的一边趋近于2时,平均速度都趋 近与一个确定的值 -3.1.从物理的角度看,时间间隔|无限变小时, 平均速度就无限趋近于t = 2时的瞬时速度.因 此,运动员在t = 2时的瞬时速度是 -3.1 m/s.表示 当t =2, △趋近于0时,平均速度 趋近于确定值T3.1 ”.【瞬时速度】表示当t=2, △趋近于0时,平均速度趋于确 定值-13.1 ”.局部以匀速代替变速,以平均速度代替瞬时速 度,然后通过取极限,从瞬时速度的近似值过渡 到瞬时速度的精确值。
那么,运动员在某一时 刻的瞬时速度?为了表述方便,我们用血吃+凶)-也)=g z Af我们用/i(2+2V)-;:(2)Af= -13.1【设计意图】让学生体会由平均速度到瞬时速度的逼近思想:△越小,V越接近于t = 2秒时的瞬时速度探究3:(1).运动员在某一时刻t0的瞬时速度怎样表示?(2).函数f(x)在x = X。
处的瞬时变化率怎样表示?盘TO &_伽7・9(&):-(9■號-6①&扛TO &=Lim (7・9 AT —43" * 6.5)=一9-8" +6*5导数的概念:一般地,函数y = f (x)在x = x o处的瞬时变化率是血叟二沁空亡土竺L.0七Bx业* A x称为函数y = f(x)在x = x0处的导数,记作爪。
)或门3或亀务孑哼李【总结提升】1F(心百心的值有关.不祠的比其导数值一也不相同血2f(叫百&的具休取值无关*3購时妾化率与导数是同一概念的两个名称,由导数的定义可知,求函数y = f (x)的导数的,般方法:2. 求平均变化率生/E+am 叫Av Av3. 求值八切弓轆字[3 ]例题讲解例题1将原油精炼为汽油、柴油、塑胶等各 种不同产品,需要对原油进行冷却和加热.如果 第x h 时,原油的温度(单位:)为y=f (x)= x 2刁x+15 ( 0< x <)8.计算第2h 与第6h 时,原油 温度的瞬时变化率,并说明它们的意义•解:在第2h 和第6h 时,原油温度的瞬时变化 率就是广⑵和八&)IQ + 一7(2+山)+15 —(牙—了灼+1 匀 A 厲-------- =O¥ —3 所乩f ⑵巳戛兰巳呷A —主同理可得广(6)二5在第2h 和第6h 时,原油温度的瞬时变化率分 别为43和5.它说明在第2h 附近,原油温度大约 以3 /h 的速率下降;在第6h 附近,原油温度大 约以5 /h 的速率上升.[4]本节课知识总结1. 函数的平均变化率根据导数的定义^-/(2+AY)-/(2) AvA JC2.求函数的平均变化率的步骤(1)求函数的增量△ y=f(x)-f(xj(2)计算平均变化率3、求物体运动的瞬时速度:(1)求位移增量△ s=s(t+ Adk(t)(2)求平均速度(3)求极限1 理知蝕竺严•4、由导数的定义可得求导数的一般步骤:(1)求函数的增量△ y=f(x+A t-f(x0)(2))平均变化率若(3)求极限.三、复习总结和作业布置[1]课堂练习1■函数y = f(x)的自变量x由x0改变到x0+Ax 时,函数值的改变量Ay% ()A. f(x0+ Ax)B. f(x o) +AxC.f(x0)・AxD.f(x0 + A x” f(x0)2•若一质点按规律s= 8 +12运动,则在时间段2〜2.1中,平均速度是()C . 0.41D1.13.求y=x 2在x=x o附近的平均速度。
4■过曲线 y=f(x)=x 3上两点 P (1, 1) 和 Q(1+ △ x,1+ 作曲线的割线,求出当 △ x=0.1时割 线的斜率.5求函麴=咅也处的导数 课堂练习【参考答案】1. D解析:分别写出x = X 0和x = x o+Ax 对应的函 数值f(x o )和f(x 0+ Ax)两式相减,就得到了函数 值的改变量 △尸f(x o + Ax — f(x o ),故应选D. 2. B-=^=(^2.^-(S ^>=2^=41 At 2.1-2 0.1 ' 4. 解析:^^pr^+3^^^3+3x0-1+0-^3-31解析:3.解析: A YA X4 _ J_ ________ 4 ________葺解析十+2*-Ar+Ar3玄巳Ax Av Ar4^:-4^ -8x・&一4“->^-8A<iv-4Av;+2x Ar +Ar')At + 2x Av+AxJ&v—Sx-^£ —4Zix/ —8x—4Av(x1 + 2x- Ax' + Av;) M 疋{/ + 2A_-Av +Av')-肛o 心4课后习题1、复习本节课所讲内容2、预习下一节课内容3、课本P.10 习题1.1A 组123,4.。
