运筹学第9章 目标规划
管理运筹学作业 韩伯棠第3版高等教育出版社课后答案

课程:管理运筹学管理运筹学作业第二章线性规划的图解法P23:Q2:(1)-(6);Q3:(2)Q2:用图解法求解下列线性规划问题,并指出哪个问题具有唯一最优解,无穷多最优解,无界解或无可行解。
(1)Min f=6X1+4X2约束条件:2X1+X2>=1,3X1+4X2>=3X1, X2>=0解题如下:如图1Min f=3.6X1=0.2, X2=0.6本题具有唯一最优解。
图1(2)Max z=4X1+8X2约束条件:2X1+2X2<=10-X1+X2>=8X1,X2>=0解题如下:如图2:Max Z 无可行解。
图2(3) Max z =X1+X2 约束条件 8X1+6X2>=24 4X1+6X2>=-12 2X2>=4 X1,X2>=0 解题如下:如图3: Max Z=有无界解。
图3(4) Max Z =3X1-2X2 约束条件:X1+X2<=1 2X1+2X2>=4 X1,X2>=0 解题如下:如图4: Max Z 无可行解。
图4(5)Max Z=3X1+9X2 约束条件:X1+3X2<=22-X1+X2<=4X2<=62X1-5X2<=0X1,X2>=0解题如下:如图5:Max Z =66;X1=4 X2=6本题有唯一最优解。
图5(6)Max Z=3X1+4X2 约束条件:-X1+2X2<=8X1+2X2<=122X1+X2<=162X1-5X2<=0X1,X2>=0解题如下:如图6Max Z =30.669X1=6.667 X2=2.667本题有唯一最优解。
图6Q3:将线性规划问题转化为标准形式(2)min f=4X1+6X2约束条件:3X1-2X2>=6X1+2X2>=107X1-6X2=4X1,X2>=0解题如下:1)目标函数求最小值化为求最大值:目标函数等式左边min改为max,等式右边各项均改变正负号。
规划数学(运筹学)第三版课后习题答案 习 题 2
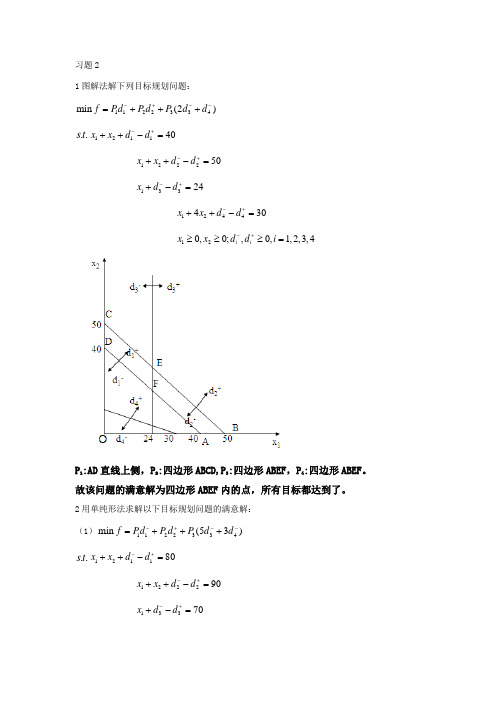
习题21图解法解下列目标规划问题:1122334min (2)f Pd P d P d d -+--=+++..s t 121140x x d d -+++-=122250x x d d -+++-=13324x d d -++-=1244430x x d d -+++-=120,0;,0,1,2,3,4i i x x d d i -+≥≥≥=P 1:AD 直线上侧,P 2:四边形ABCD,P 3:四边形ABEF ,P 4:四边形ABEF 。
故该问题的满意解为四边形ABEF 内的点,所有目标都达到了。
2用单纯形法求解以下目标规划问题的满意解:(1)1122334min (53)f Pd P d P d d -+--=+++..s t 121180x x d d -+++-=122290x x d d -+++-=13370x d d -++-=24445x d d -++-=120,0;,0,1,2,3,4i i x x d d i -+≥≥≥=(2)1122234min ()f P d d P d P d -+--=+++..s t 12114580x x d d -+++-=12224248x x d d -+++-=123381080x x d d -+++-=1445x d d -++-=120,0;,0,1,2,3,4i i x x d d i -+≥≥≥=5案例练习(1)某厂生产甲、乙两种产品,每件利润分别为20、30元。
这两种产品都要在A 、B 、C 、D 四种设备上加工,每件甲产品需,而这4种设备正常生产能力依次为每天12、8、16、12机时。
此外,A 、B 两种设备每天还可加班运行。
试拟订一个满足下列目标的生产计划: 1P :两种产品每天总利润不低于120元;2P :两种产品的产量尽可能均衡;3P :A 、B 设备都应不超负荷,其中A 设备能力还应充分利用(A 比B 重要3倍)。
运筹学线性规划模型及目标规划模型

问题一:建立一个资源利用的规划模型,需加入时间资源、资金资源。
1、问题的提出1.1基本情况某公司现在新购一生产线,生产电脑配件B1、B2、B3。
已知生产单位产品的利润与所需的劳动力时间、设备台时及单位产品的资金投入,公司的资金拥有量和工作时间拥有量如表1-1所示:表1T项目B1配件种类资源限制B2B3资金(百元)412200劳动力/工时643360设备台时(小323210时)产品利润(元/754件)1.2提出问题1、假设每种配件的市场都是供不应求,不用考虑市场及原材料的供应问题那么在现有的条件下应该如何分配者三种配件的生产才能获得最大利润。
2、模型的建立2.1确定决策变量因为获得最大利润的核心目标,要确定各种配件的生产数量从而去求得所能获得的最大利润。
因此可以设尤,x ,x来表示B1,B2, B3的产量。
1 2 32.2确定目标函数该问题归结为求效益最大化的问题。
这里所追求的利润s应是最大(简写为max)max S = 7 x + 5 x + 4 x1 2 32.3确定约束条件考虑到资金限制和劳动力总工时以及设备台时的要求,会有一定的约束条件用不等式表示参考表1_1数值有'4x + x + 2x < 200<6x + 4x + 3x < 360I3x + 2x + 3x < 210侦1 2 32.4建立模型综合前述各步及变量非负的条件建立起线性规划模型如下。
求变量气(i = 1,2,3)使得目标函数:max S = 7 x + 5 x + 4 x1 2 3取得最大值,并满足如下的约束条件的要求:4x + x + 2x < 2001 2 36x + 4x + 3 x < 360s.t. < 1 2 3|3x i+ 2x2 + 3x3 < 210I x , x , x > 0v 1 2 33、模型的求解分析上述线性规划模型是非标准的线性规划模型,用常规方法将其变为标准型的线性规划模型,然后利用单纯形法进行求解。
运筹学钱颂迪答案

运筹学钱颂迪答案【篇一: 803 运筹学】class=txt>运筹学考试大纲一、考试性质运筹学是我校航空运输管理学院硕士生入学考试的综合考试科目之一,它是我校为招收交通运输规划与管理学科硕士研究生而实施的水平考试,其评价标准是普通高等院校优秀本科毕业生能够达到的及格以上水平,以保证被录取者较好地掌握了必备的专业基础知识。
本门课程主要考试内容包括:线性规划及其对偶理论、运输问题、目标规划、整数规划、动态规划、图与网络分析,注重考察考生是否已经掌握运筹学最基本的理论知识与方法。
二、考试形式与试卷结构1.答卷方式:闭卷、笔试2.答卷时间: 180 分钟3.题型比例:满分 150 分,基本概念 20% ,计算及证明题 80%三、考查要点1.线性规划及对偶理论:单纯形法,改进单纯形法。
线性规划的对偶理论,对偶单纯形法,灵敏度分析;2.运输问题:运输问题的数学模型;用表上作业法求解运输问题;产销不平衡的运输问题及其求解方法;3.目标规划:目标规划的数学模型,目标规划的图解法与单纯形法;4.整数规划:0-1 型整数规划,分支定界解法,割平面解法,指派问题;5.动态规划:动态规划的基本概念和基本方法,动态规划的最优性原理与最优性定理,动态规划与静态规划的关系,动态规划的应用;6.图与网络分析:图与树的基本概念,最短路问题,网络最大流问题,最小费用最大流问题,中国邮路问题,网络计划。
四、主要参考书目1、郭耀煌,李军 .运筹学原理与方法. 成都:西南交通大学出版社,2004 ;2 、钱颂迪主编. 运筹学(修订版). 北京:清华大学出版社,1991 。
【篇二:运筹学大纲(13 、 14 级使用)2014.9 】(理论课程)开课系(部):数理教研部课程编号:380020 、 381703课程类型:专业必修课或学科必修课总学时: 48 或 32学分:3或2适用专业:信息管理与信息系统、投资学、工业工程、工程管理、经济统计学、物流管理开课学期: 3 或 4 或 5先修课程:高等数学、线性代数一、课程简述本课程是以经济活动方面的问题以及解决这类问题的原理和方法作为研究的对象,把经济活动中的问题归结为对应的某种数学模型,运用数学知识等工具求得最合理的工作方案。
运筹学答案 第 9 章 目标规划

−d3
d3
−
0
⎪
2.5x1
−
0.5x2
0.3x3
−d4
d4
20
⎪
1
−
0
⎪
0
0
−
⎩
得:
x1,x2,x3,di
,di
≥0,i1,2,3,4
−
−
−
x1
9.474,x2
20,x3
−
2.105,d
1
0,d
1
0,d
2
8.387,d
2
0,d
3
0,d
3
7.368,
d
4
14.316,d
4
0,
所以食品厂商为了依次达到4个活动目标,需在电视上发布广告9.474次,报纸
纸产生的工业废水的处理费用为40元。
该纸张制造厂近期目标如下:
目标1:纸张利润不少于15万;
目标2:工业废水的处理费用不超过1万元。
a.设目标1的优先权为P1,目标2的优先权为P2,P1>P2,建立目标规划模型
并用图解法求解。
b.若目标2的优先权为P1,目标1的优先权为P2,建立目标规划模型并求解。
品分别预测了在销售良好和销售较差时的预期利润。这两种产品都经过甲、乙两
台设备加工。已知产品A和B分别在甲和乙设备上的单位加工时间,甲、乙设备
的可用加工时间以及预期利润如下表所示,要求首先是保证在销售较差时,预期
利润不少于5千元,其次是要求销售良好时,预期利润尽量达到1万元。试建立
多目标规划模型并求解。
(150,120)。
4、解:设该汽车装配厂为达到目标要求生产产品Ax1件,生产产品Bx2件。
运筹学与目标规划

例;
(3) C和D为贵重设备,严格禁止超时使用;
(4) 设备B必要时可以加班,但加班时间要控制;设备A即要求
充分利用,又尽可能不加班。
要考虑上述多方面的目标,需要借助目标规划的方法。
线性规划模型存在的局限性:
明确问题,列出 目标的优先级和 权系数
构造目标规 划模型
求出满意解
N
满意否?
分析各项目标 完成情况
Y
据此制定出决策方案
2.目标规划的图解法
适用两个变量的目标规划问题,但其操作简单, 原理一目了然。同时,也有助于理解一般目标规划 的求解原理和过程。 图解法解题步骤:
1. 将所有约束条件(包括目标约束和绝对约束,暂不考虑正负偏差变量)的直 线方程分别标示于坐标平面上。 2. 确定系统约束的可行域。 3. 在目标约束所代表的边界线上,用箭头标出正、负偏差变量值增大的方向。 4. 求满足最高优先等级目标的解 5. 转到下一个优先等级的目标,再不破坏所有较高优先等级目标的前提下,求 出该优先等级目标的解 6. 重复5,直到所有优先等级的目标都已审查完毕为止 7. 确定最优解和满意解。
目标规划数学模型的一般形式
min Z j1 n j1 xj d k
n
L
l 1
P l ( lk d k lk d k )
k 1
K
达成函数
c kj x j d k d k g k ( k 1 .2 K ) a ij x 0
Chapter9 目标规划
( Goal programming )
兰州大学运筹学——目标规划 课后习题题解

B3
`供应量
A1
4
7
5
12
A2
6
4
8
5
A3
3
6
10
6
A4
5
4
8
11
需求量
12
16
18
经营决策中要求所有产地的产量都必须全部运出,希望达到目标以及优先等级如下: பைடு நூலகம்1------销地 B1、B2 至少得到它需求量的 50%。 P2------必须满足销地 B3 全部需求量。 P3------由于客观原因,要尽量减少 A4 到 B2 的货运量。 P4------若期望运费 132 元,并尽可能减少运输费用。
4 xl ≤680
4x2 ≤600 2 xl+3x2-d1+ +d1-=12
xl-x2-d2++d2-=0 d1-=第一级的最优结果 xl,x2,d1+,d1-,d2+,d2-≥0
S.T.
min d3-+ d3+
4 xl ≤680
4x2 ≤600 2 xl+3x2-d1+ +d1-=12
xl-x2-d2++d2-=0 2 xl+2x2-d3++d3-=12
d1-=0 d2-=0
xi≥0 (i=1,2,3) di+ 、di- ≥0 (i=1,2,3)
得最优解:(334,0,0) 最优值:d1-=0,d2-=0,d3-=70
第四级:
min d4-+d4++d5-+d5++d6-+d6+ S.T. 450xl+550x2+700x3-d1+ +d1-=150000
韩伯棠管理运筹学(第三版)_第九章_目标规划

• step • • • • • • • • • • • • •
3 目标函数值为 : 1100 变量 解 相差值 --------------------x1 166.667 0 x2 250 0 d10 0 d1+ 36666.667 0 d233.333 0 d2+ 0 15.167 d30 26 d3+ 0 26 d41100 0 d4+ 0 2
练习:某厂生产Ⅰ、Ⅱ 两种产品,有关数据如 表所示。试求获利最大 的生产方案?
Ⅰ 原材料 设备(台时) 2 1
Ⅱ 1 2
拥有量 11 10
单件利润
8
10
在此基础上考虑: 1、产品Ⅱ的产量不低于产品Ⅰ的产量; 2、充分利用设备有效台时,不加班; 3、利润不小于 56 元。 解: 分析 第一目标:P1d1 即产品Ⅰ的产量不大于Ⅱ的产量。 第二目标: P2 ( d2 d2 )
运筹学
运筹谋划
一石多鸟
第九章 目标规划
1
第七章
目标规划
• §1 目标规划问题举例 • §2 目标规划的图解法
• §3 复杂情况下的目标规划
• §4.加权目标规划
2
§1 目标规划问题举例
例1.企业生产 • 不同企业的生产目标是不同的。多数企业 追求最大的经济效益。但随着环境问题的 日益突出,可持续发展已经成为全社会所 必须考虑的问题。因此,企业生产就不能 再如以往那样只考虑企业利润,必须承担 起社会责任,要考虑环境污染、社会效益、 公众形象等多个方面。兼顾好这几者关系, 企业才可能过引入目标值和偏差变量,可 以将目标函数转化为目标约束。 目标值:是指预先给定的某个目标的一个 期望值。 实现值或决策值:是指当决策变量xj 选定 以后,目标函数的对应值。 偏差变量(事先无法确定的未知数):是 指实现值和目标值之间的差异,记为 d 。 正偏差变量:表示实现值超过目标值的部 分,记为 d+。 负偏差变量:表示实现值未达到目标值的 部分,记为 d-。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
17
使用运筹学软件求解可得: x1=250;x2=60;d1+=0;d1-=0;d2+=80;d2-=0;d3+=0;d3-=0; d4+=50;d4-=0;d5+=0;d5-=60,目标函数d4-+2d5- =120。 可见,目标1、目标3和目标4达到了,但目标2、目标5都有
一些偏差。
课号 1 2 3 4 5 6 7 8 9 课名 微积分 线性代数 最优化方法 数据结构 应用统计 计算机模拟 计算机编程 预测理论 数学实验
也不能超过680工时;
对应P2有一个目标:每周的利润超过70000元;
对应P3有两个目标:每周产品A和B的产量分别不低于200和
120件。
管
理
运
筹
学
16
采用简化模式,最终得到目标线性规划如下: Min P1(d1+)+ P1(d2-)+P2(d3-)+ P3(d4-)+ P3(2d5-)
s.t.
2x1+3x2-d1++d1-=680 对应第1个目标
第九章
目标规划
管
理
运
筹
学
1
§1 目标规划问题举例
例1.企业生产 • 不同企业的生产目标是不同的。多数企业追求最大的经济效益。 但随着环境问题的日益突出,可持续发展已经成为全社会所必须 考虑的问题。因此,企业生产就不能再如以往那样只考虑企业利 润,必须承担起社会责任,要考虑环境污染、社会效益、公众形 象等多个方面。兼顾好这几者关系,企业才可能保持长期的发展。 例2.商务活动 • 企业在进行盈亏平衡预算时,不能只集中在一种产品上,因为某 一种产品的投入和产出仅仅是企业所有投入和产出的一部分。因 此,需要用多产品的盈亏分析来解决具有多个盈亏平衡点的决策 问题(多产品的盈亏平衡点往往是不一致的)。
i 1
两目标(多目标)规划
• 以课程最少为目标, 不管学分多少。 • 以学分最多为目标, 不管课程多少。
管 理 运
Min { Z , W }
多目标优化的处理方法:化成单目标优化。
最优解如上,6门课 程,总学分21 。 最优解显然是选修所 有9门课程 。
筹 学
23
多目标规划
• 在课程最少的前提下 以学分最多为目标。
决策变量
xi=1 ~选修课号i 的 课程(xi=0 ~不选)
管
理
运
筹
学
22
讨论:选修课程最少,学分尽量多,应学习哪些课程?
课程最少
Min Z
学分最多
Max
9
xi
W 5 x1 4 x 2 4 x 3 3 x 4 4 x 5 3 x 6 2 x 7 2 x8 3 x9
Min d2s.t. 20x1+50x2≤90000 0.5x1 +0.2x2-d1++d1-=700
3x1+4x2-d2++d2-=10000
d1+=0 x1,x2,d1+,d1-,d2+,d2-≥0
管 理 运 筹 学
11
x2
4000
3000 0.5x1 +0.2x2=700 3x1+4x2=10000
管
理
运
筹
学
18
§4 加权目标规划
• 加权目标规划是另一种解决多目标决策问题的方法,其基 本方法是通过量化的方法分配给每个目标的偏离的严重程 度一个罚数权重,然后建立总的目标函数,该目标函数表 示的目标是要使每个目标函数与各自目标的加权偏差之和 最小,假设所有单个的目标函数及约束条件都符合线性规 划的要求,那么,整个问题都可以描述为一个线性规划的 问题。 • 如果在例7中我们对每周总耗费的人力资源超过680工时或 低于600工时的每工时罚数权重定为7;每周利润低于70000 元时,每元的罚数权重为5;每周产品A产量低于200件时每 件罚数权重为2,而每周产品B产量低于120件时每件罚数权 重为4。
200和120件,因为B产品比A产品更重要,不妨假设B完成最低产
量120件的重要性是A完成200件的重要性的1倍。 试求如何安排生产?
管 理 运 筹 学
15
解: 本问题中有3个不同优先权的目标,不妨用P1 、P2 、P3 表示 从高至低的优先权。 对应P1有两个目标:每周总耗费人力资源不能低于600工时,
目标是满足风险不超过700。分配给第一个目标较高的优先权P1,
分配给第二个目标较低的优先权P2。 针对每一个优先权,应当建立一个单一目标的线性规划模型。 首先建立具有最高优先权的目标的线性规划模型,求解;然后再 按照优先权逐渐降低的顺序分别建立单一目标的线性规划模型,
方法是在原来模型的基础上修改目标函数,并把原来模型求解所
x1,x2,d1+,d1-,d2+,d2-≥0
管
理
运
筹
学
14
§3 复杂情况下的目标规划
例7.一工艺品厂商手工生产某两种工艺品A、B,已知生产一件产 品A需要耗费人力2工时,生产一件产品B需要耗费人力3工时。A、
B产品的单位利润分别为250元和125元。为了最大效率地利用人
力资源,确定生产的首要任务是保证人员高负荷生产,要求每周 总耗费人力资源不能低于600工时,但也不能超过680工时的极限; 次要任务是要求每周的利润超过70000元;在前两个任务的前提 下,为了保证库存需要,要求每周产品A和B的产量分别不低于
课号 课名 微积分 线性代数 最优化方法 数据结构 应用统计 计算机模拟 计算机编程 预测理论 数学实验
管
增加约束
9
xi 6,
i 1
以学分最多为目标求解。
最优解: x1 = x2 = x3 = x5 = x7 = x9 =1, 其它为0;总 学分由21增至22。
学分 5 4 4 3 4 3 2 2 3
管 理 运 筹 学
4
显然,此问题属于目标规划问题。它有两个目标变量:一是 限制风险,一是确保收益。在求解之前,应首先考虑两个目标的
优先权。
假设第一个目标(即限制风险)的优先权比第二个目标(确 保收益)大,这意味着求解过程中必须首先满足第一个目标,然
后在此基础上再尽量满足第二个目标。
• 建立模型:
设x1、x2分别表示投资商所购买的A股票和B股票的数量。
管 理 运 筹 学
20
例2 选课策略
课号
1 2 3 4 5 6 7 8 9
课名
微积分 线性代数 最优化方法 数据结构 应用统计 计算机模拟 计算机编程 预测理论 数学实验
学分
5 4 4 3 4 3 2 2 3
所属类别
数学 数学 数学;运筹学 数学;计算机 数学;运筹学 计算机;运筹学 计算机 运筹学 运筹学;计算机
得的目标最优值作为一个新的约束条件加入到当前模型中,并求 解。
管 理 运 筹 学
8
三、图解法 1.针对优先权最高的目标建立线性规划
建立线性规划模型如下:
Min d1+
s.t.
20x1+50x2≤90000 0.5x1 +0.2x2-d1++d1-=700 3x1+4x2-d2++d2-=10000 x1,x2,d1+,d1-≥0
管 理 运 筹 学
9
x2
4000
3000
0.5x1 +0.2x2=700
2000
1000
20x1+50x2≤90000
0
1000
2000
3000
4000
5000
x1
10
2.针对优先权次高的目标建立线性规划 优先权次高(P2)的目标是总收益超过10000。
建立线性规划如下:
管 理 运 筹 学
6
把等式转换,可得到 0.5x1 +0.2x2-d1++d1-=700。
再来考虑年收入:
年收入=3x1+4x2
引入变量d2+和d2-,分别表示年收入超过与低于10000的数量。
于是,第2个目标可以表示为 3x1+4x2-d2++d2-=10000。
管
理
运
筹
学
7
二、有优先权的目标函数 本问题中第一个目标的优先权比第二个目标大。即最重要的
管
理
运
筹
学
19
• 则其目标函数化为: min7d1++7d2-+5d3-+2d4-+4d5这就变成了一个普通的单一目标的线性规划问题 min7d1++7d2-+5d3-+2d4-+4d5-
s.t.
2x1+3x2-d1++d1-=680 2x1+3x2-d2-+d2+=680 250x1+125x2-d3-+d3+=70000 x1-d4++d4-=200 x2-d5++d5-=120 x1,x2,d1+,d1-,d2-,d2+, d3+,d3-,d4+,d4-,d5+,d5-≥0 。
先修课要求
微积分;线性代数 计算机编程 微积分;线性代数 计算机编程
应用统计 微积分;线性代数
要求至少选两门数学课、三门运筹学课和两门计算机课 为了选修课程门数最少,应学习哪些课程 ? 选修课程最少,且学分尽量多,应学习哪些课程 ?
管 理 运 筹 学
21
0-1规划模型
课号 1 2 3 4 5 6 7 8 9 课名 微积分 线性代数 最优化方法 数据结构 应用统计 计算机模拟 计算机编程 预测理论 数学实验 所属类别 数学 数学 数学;运筹学 数学;计算机 数学;运筹学 计算机;运筹学 计算机 运筹学 运筹学;计算机
