中科大近似算法作业
中科大算法导论第一二次和第四次作业答案PPT学习教案

取c 1/ 3,n 2时,有T (n) cn lg n,T (n) (n lg n)
所以T (n) (n lg n). 第5页/共18页
4.1-4证明合并排序算法的“准确”递归式(4.2)的解为
Θ(nlgn)
(1)
如果n 1
T (n) T (n / 2) T (n / 2) (n) 如果n 1
c(n
/
2)
lg(
n
/
2)
c(n/2)Fra biblioteklg(
n
/
2)
(n)
c
n 2
lg(
n 2
)
c
n
1 2
lg(
n
2
1)
(n)
c n lg( n) c n 1lg( n 1) (n) cn lg n 22 2 2
c n lg( n) c n 1lg( n 1) (n) cn lg n 0 22 2 2
14.
i++
15.
else do A[k]=R[j]
16.
j++
17.
k++
18. while(i<=n1) 19. do A[k++]=L[i++]
20. while(j<=n2)
21. do A[k++]=R[j++]
第1页/共18页
第二次作业
3.2-3 证明等式lg(n!)=Θ(nlgn)。并证明等式n!=ω(2n)和
2
2
cn lg n 1 (1 c)n c lg( n 1) c 0 n
lg( n 1) lg(1 1)是递增函数,取n 2,则lg(n 1) 1
26-近似算法(1)
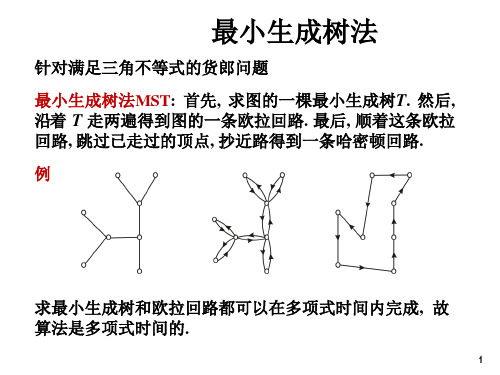
最小生成树法针对满足三角不等式的货郎问题最小生成树法MST: 首先, 求图的一棵最小生成树T. 然后, 沿着T 走两遍得到图的一条欧拉回路. 最后, 顺着这条欧拉回路, 跳过已走过的顶点, 抄近路得到一条哈密顿回路.例求最小生成树和欧拉回路都可以在多项式时间内完成, 故算法是多项式时间的.最小生成树法的性能定理对货郎问题的所有满足三角不等式的实例I,MST(I) < 2OPT(I)证因为从哈密顿回路中删去一条边就得到一棵生成树, 故T 的权小于OPT(I). 沿T 走两遍的长小于2OPT(I). 因为满足三角不等式, 抄近路不会增加长度, 故MST(I) < 2OPT(I).MST是2-近似算法.⎪ 紧实例OPT(I) = 2n MST(I) = 4n-2=⎛2 -⎝1 ⎫OPT( I)n ⎭最小权匹配法最小权匹配法MM:首先求图的一棵最小生成树T.记T 的所有奇度顶点在原图中的导出子图为H, H 有偶数个顶点, 求H 的最小匹配M. 把M 加入T 得到一个欧拉图, 求这个欧拉图的欧拉回路; 最后, 沿着这条欧拉回路, 跳过已走过的顶点, 抄近路得到一条哈密顿回路.求任意图最小权匹配的算法是多项式时间的, 因此MM 是多项式时间的.最小权匹配法的性能定理对货郎问题的所有满足三角不等式的实例I,MM( I) 3OPT( I) 2证由于满足三角不等式, 导出子图H 中的最短哈密顿回路C 的长度不超过原图中最短哈密顿回路的长度OPT(I). 沿着C 隔一条边取一条边, 得到H 的一个匹配. 总可以使这个匹配的权不超过C 长的一半. 因此, H 的最小匹配M 的权不超过OPT(I)/2, 求得的欧拉回路的长小于(3/2)OPT(I). 抄近路不会增加长度, 得证MM(I)< (3/2)OPT(I).MM是3/2 -近似算法货郎问题的难度定理货郎问题(不要求满足三角不等式) 是不可近似的, 除非P = NP.证假设不然, 设A是货郎问题的近似算法, 其近似比r ≤K, K是常数. 任给图G = <V,E>, 如下构造货郎问题的实例I G: 城市集V, ∀u,v∈V,若(u,v)∈E, 则令d(u,v)=1; 否则令d(u,v)=Kn,其中|V| = n. 若G 有哈密顿回路, 则OPT(I G) = n, A(I G) ≤r OPT(I G) ≤Kn否则OPT(I G) > Kn, A(I G) ≥ OPT(I G) > Kn所以, G 有哈密顿回路当且仅当A(I) ≤KnG15K15K15K 1 15K实例1HC货郎问题HC 实例有哈密顿回路,则货郎问题实例有长度不超过 n 的旅行,即近似算法的解不超过 Kn . 若HC 实例没有哈密顿回路,则货郎实例的旅行路线长度大于 Kn .7证明下述算法可以判断图G 是否有哈密顿回路.算法1.由I 构造货郎问题的实例I G2.对I G 运用近似算法A3.若A(I G) Kn, 则输出“Yes”; 否则输出“No”由于K是固定的常数, 构造I可在O(n2) 时间内完成且G| I G| = O(n2). A是多项式时间的, A 对I G 可在n 的多项式时间内完成计算, 所以上述算法是HC 的多项式时间算法. 而HC 是NP 完全的, 推得P=NP.⎨∑ 0-1背包问题0-1背包问题的优化形式: 任给 n 件物品和一个背包, 物品 i 的重量为 w i , 价值为 v i , 1≤ i ≤ n , 背包的重量限制为 B , 其中 w i , v i 以及 B 都是正整数.把哪些物品装入背包才能在不超过重量限制的条件下使得价值最大? 即, 求子集 S *⊆{1,2,⋯,n } 使得∑ v ii ∈S * = max ⎧ v ⎩ i ∈S | ∑ w i i ∈S ≤ B , S ⊆ {1,2. ⎫, n }⎬. ⎭i一个简单的贪心算法贪心算法G-KK1.按单位重量的价值从大到小排列物品. 设v1/w1 ≥v2/w2 ≥⋯≥v n/w n.2.顺序检查每一件物品, 只要能装得下就将它装入背包,设装入背包的总价值为V.3. 求v k = max{ v i | i = 1, 2, ⋯, n }.>V, 则将背包内的物品换成物品k.若vk,v i): (3,7), (4,9), (5,9), (2,2); B=6.实例(wiG-KK给出的解是装入(3,7)和(2,2), 总价值为9.若把第3件物品改为(5,10), 则装入第3件, 总价值为10. 这两个实例的最优解都是装入(4,9)和(2,2), 总价值为11.G-KK的性能定理对0-1背包问题的任何实例I, 有OPT(I) < 2G-KK(I)证设物品l 是第一件未装入背包的物品, 由于物品按单位重量的价值从大到小排列, 故有OPT(I) < G-KK(I) + v l≤ G-KK(I) + v max≤ 2 G-KK(I).G-KK是2-近似算法.多项式时间近似方案算法PTAS 输入ε> 0和实例I.1. 令m = ⎡1/ε⎤.2.按单位重量的价值从大到小排列物品. 设v1/w1 ≥v2/w2 ≥⋯≥v n/w n.3.对每一个t =1,2,⋯, m 和t 件物品, 检查这t 件物品的重量之和. 若它们的重量之和不超过B, 则接着用G-KK把剩余的物品装入背包.4.比较得到的所有装法, 取其中价值最大的作为近似解. PTAS是一簇算法. 对每一个固定的ε> 0, PTAS是一个算法, 记作PTASε.C Cn + + n n n例子取ε =0.1,m =10.t =1: 尝试 n 次, 装入背包物品集分别为{1},{2},…,{n },再使用 G-KK 算法t =2: 尝试 n (n -1)/2次,装入物品集分别是{1, 2},{1, 3}, …, {n -1, n },再使用G-KK 算法.… t =10: 尝试10 次,装入物品集为 {1,…,9,10}, {1,…,9,11},…, {n -9,n -8,…,n -1,n },再用G-KK 算法. 总计运行G-KK 算法次数至多:1 2 ... + 10C C,PTAS的性能定理对每一个ε> 0和0-1 背包问题的实例I,OPT(I) < (1+ε) PTASε(I),且PTASε的时间复杂度为O(n1/ε+2 ) .证设最优解为S*. 若|S*| ≤m, 则算法必得到S*. 设|S*| > m. 考虑计算中以S*中m 件价值最大的物品为基础, 用G-KK 得到的结果S. 设物品l 是S* 中第一件不在S 中的物品, 在此之前G-KK装入不属于S* 的物品(肯定有这样的物品, 否则应该装入物品l ) 单位重量的价值都不小于v/w l , 当然也l不小于S* 中所有没有装入的物品的单位重量的价值, 故有OPT(I) < ∑i∈S v i + v lS 包括S* 中m 件价值最大的物品, 它们的价值都不小于v l ,v≤∑i∈S v/mc + n n≤nm多项式时间近似方案OPT(I) < ∑i∈S v i + v l≤∑i∈S v i + ∑i∈S v i /m≤ (1+1/m) PTASε(I)≤(1+ε) PTASε(I)时间复杂度. 从n 件物品中取t 件( t =1,2,⋯,m), 所有可能取法的个数为1 2 + + m m ⋅nm!≤n m .对每一种取法, G-KK的运行时间为O(n), 故算法的时间复杂度为O(n m+1) = O(n1/ε+2 ).多项式时间近似方案: 以ε>0和问题的实例作为输入I, 对每一个固定的ε> 0, 算法是1+ε- 近似的.c c∑ 伪多项式时间算法与完全多项式时间近似方案完全多项式时间近似方案: 以 ε > 0和问题的实例 I 作为输入, 时间复杂度为二元多项式 p (|I |,1/ε), 且对每一个固定的 ε > 0, 算法的近似比为 1+ε .动态规划算法A 记G k (d ): 当只考虑前 k 件物品时, 为了得到不小于 d 的价值, 至少要装入的物品重量G k (d ) = ⎧ k min ⎨ ⎩ i =1 w i x i| ∑ i =1 v i x i ≥ d , x i = 0或1, 1 ≤ i ⎫ ≤ k ⎬, ⎭ 0 ≤ k ≤ n , 0 ≤ d ≤ D , D = v 1 + v 2 + ⋯ + v n约定: min ∅ = +∞OPT(I ) = max{ d | G n (d ) ≤ B }k⎩ ⎩ k 动态规划算法递推公式G 0 (d ) = ⎧0, ⎨+ ∞, 若d = 0, 若d > 0,G (d ) = ⎧min{G k (d ), w k +1 }, 若d ≤ v k +1 , k +1 ⎨min{G (d ),G (d - v ) + k k +1w k +1 }, 若d > v k +1 ,0 ≤ k ≤ n -1, 0 ≤ d ≤ D . A 的时间复杂度为O (nD )=O (n 2v max ), 是伪多项式时间算法.完全多项式时间近似方案算法FPTAS (Fully Polynomial-Time Approximation Scheme ) 输入 ε > 0和实例 I . 1. 令 ⎧⎢ b = max v max ⎥ ⎫ ⎨⎢(1 + 1 / ε )n ⎥ , 1⎬.⎩⎣⎦ ⎭ 2. 令 v i '=⎡v i /b ⎤, 1≤i ≤n . 把所有 v i 换成 v i ', 记新的实例为I '.3. 对 I ' 应用算法A 得到解 S , 把 S 取作实例 I 的解.定理 对每一个ε > 0和 0-1背包问题的实例 I ,OPT(I ) < (1+ε) FPTAS (I ),并且 FPTAS 的时间复杂度为 O (n 3(1+1/ε)) .证明证 由 于(v i '-1)b < v i ≤ v i 'b(1) 对任意的 T ⊆{1, 2, ⋯ , n }0 ≤ b ∑ i ∈T v i '-∑ i ∈T v i < b |T | ≤ bn (2) 设 I 的最优解为 S *, 注意到 S 是 I ' 的最优解, 故有 OPT(I )-FPTAS(I ) = ∑ i ∈S* v i -∑ i ∈S v i = ( ∑ i ∈S*v i - b ∑i ∈S*v i ' ) (≤0, 由式(1) v i ≤ v i 'b ) + ( b ∑i ∈S*v i '- b ∑i ∈S v i ' ) (≤0, S 是关于输入v i '的最优解) + ( b ∑i ∈S v i '- ∑ i ∈S v i )≤ (b ∑i ∈S v i '-∑i ∈S v i ) < bn (由式(2))ii v '=⎡v /b ⎤ ⎭ ⎦ ⎥ , ⎫. ⎩⎣ v max ⎨⎢(1 + 1 / ε )n ⎥ 1⎬ b = max ⎧⎢证明OPT(I )-FPTAS(I ) < bn 对每一个ε > 0, 若 b =1, 则 I ' 就是 I , S 是 I 的最优解. 设 b >1, 则OPT(I )-FPTAS(I )< v max /(1+1/ε)≤ OPT(I )/(1+1/ε) (因为v max ≤ OPT(I )) 得 OPT(I ) < (1+ε)FPTAS (I ).时间:主要是A 对I ' 的运算,时间复杂度为O (n 2v max /b ) = O (n 3(1+1/ε))20 i i ⎭v '=⎡v /b ⎤ ⎦ ⎥ , ⎫ ⎩⎣ v max ⎨⎢(1 + 1 / ε )n ⎥ 1⎬ b = max ⎧⎢。
近似算法

近似算法12.1 简介到目前为止,我们已经学习了很多可以在多项式时间内高效解决的问题,我们可以很快速的解决这些问题。
然而,在下面几讲,我们将考虑一些不知道如何高效解决的问题。
12.1.1 NP-完全性问题在学习这些问题的时候,我们会遇到这个概念NP-完全性。
NP-完全性问题是由很多组合和最优化问题组成,这些问题都有两个共同点:z没有很高效的算法;然而,我们可以在指数时间内解决这些问题。
z有高效的缩影存在于所有其他的NP-完全性问题中;因此,如果我们有一个黑盒,它能解决其中的一个问题,那么我们就能够高效的解决所有的问题。
下面就列举了一些NP-完全性问题的例子。
除了SAT的每一个问题都可以被阐明为最优化问题,尽管严格来说,它取决于每一个问题的NP-完全性。
另一方面讲,存在一个与SAT相关的最优化问题,称为MAXSAT。
在这个问题中,我们给出一个布尔公式,我们必须找到一些变量的赋值来最大化的满足子句。
可满足性问题(SAT):给定一个布尔公式,是否存在一个变量的赋值使得它满足此公式(即使公式的值为真)?装箱问题:给定一些箱子和物品,这些物品有着特定的大小,这些箱子有着一定的容积,求出能容纳这些物品的所需的最小箱子数。
最大独立子集问题:给定一个图,找出节点的最大子集,使得在这个子集中没有两个节点是相互连接的。
背包问题:给定一个能容纳一定大小的背包和一些物品,这些物品有着特定的大小和价值,求出此背包能容纳的最大价值量。
并行机器调度问题:给定一组相同的机器和一组任务,这些任务都有特定的所需时间,求如何分配任务给这些机器,使得所有的机器完成分配给它们的任务所需的时间最小。
旅行商问题:找出一个最短路径使得旅行商从一个城市出发,最后又回到该城市,并且要求每一个城市只能经过一次。
所有的这些问题不能依赖于这个假定P≠NP高效的解决。
尽管这个推测还没有被证明,但是我们可以相信它是正确的,所以我们可以简单的假定P≠NP。
12.1.2 解决NP-完全性问题如果我们不知道如何高效的解决NP-完全性问题,那我们应该怎么做呢?启发式:一种可能性就是放弃寻求多项式算法,取而代之的是集中开发启发式的算法,它在实践中接近于多项式的时间复杂度。
中科大算法第二章近似算法--黄刘生(调整后适合打印版)

NP-完全性理论
Karp的贡献
理查德·卡普(Richard Karp , 1935- ) 1972 年论文 ”Reducibility among Combinatorial Problems” 发 展和加强了由库克提出的“NP完全性”理论。 尤其是库 克仅证明了命题演算的可满足问题是NP完全的,而卡普则证明了从 组合优化中引出的大多数经典问题(背包问题、覆盖问题、匹配问 题、分区问题、路径问题、调度问题等)都是NP完全问题。只要证 明其中任一个问题是属于P类的,就可解决计算复杂性理论中最大 的一个难题,即P=?NP。
SAT∈P当且仅当P=NP
Cook 于1961 年获 Michigan 大学学士学位, 1962 和 1966年分获哈佛 大学硕士与博士学位。 1966-1970 ,他在 UC Berkeley 担任助教授; 1970年加盟多伦多大学,现为该校CS 和数学系教授,他的论文开启 了NP完备性的研究,令该领域于之后的十年成为计算机科学中最活 跃和重要的研究。因其在计算复杂性理论方面的贡献,尤其是在奠 定NP完全性理论基础上的突出贡献而荣获1982年度的图灵奖。
9
P、NP及NPC类问题
NP=?P
∵确定型图灵机是非确定型图灵机的特例,∴P⊆NP 是否有NP⊆P?即是否NP=P?
美国麻省的Clay数学研究所于2000年5月24日在巴黎法兰西学院宣 布:对七个“千年数学难题”中的每一个均悬赏 100 万美元,而 问题NP=?P位列其首:
1.P问题对NP问题 2.霍奇猜想 3. 庞加莱猜想 (2002.11-2003.7 ,俄罗斯数学家佩雷尔曼在 3 篇 论文预印本中证明了几何化猜想,2006被授予菲尔兹奖) 4.黎曼假设 5.杨-米尔斯存在性和质量缺口 6.纳维叶-斯托克斯方程的存在性与光滑性 7.贝赫和斯维讷通-戴尔猜想
(完整word版)近似算法的特点与计算方法、分类及概率算法的计算过程与应用(DOC)

近似算法和概率算法的特点与计算方法、分类及概率算法的计算过程与应用一.近似算法1近似算法的计算方法设D是一个最优化问题,A是一个算法,若把A用于D的任何一个实例I,都能在|I|的多项式时间内得到I的可行解,则称算法A为问题D的一个近似算法,其中|I|表示实例I的规模或输入长度,进而,设实例I的最优值为OP(I),而算法A所得到实例I 的可行解之值为A(I),则称算法A解实例I的性能比为R A(I)的性能比为R A(D),同时称D有R A—近似解.其中A ( I)OP(I), 若D为最小化问题.R A ( I) =OP(I) ,若D为最大化问题。
A (I)R A(D)=inf{r≥|R A(I)≤r,I∈D}2近似算法的特点(1)解同一个问题的近似算法可能有多个(2)算法的时间复杂性:近似算法的时间复杂性必须是多项式阶的,这是设计近似算法的基本目标。
(3)解的近似程度:近似最优解的近似程度也是设计近似算法的重要目标。
近似程度可能与近似算法本身、问题规模,乃至不同的输入实例都有关。
3近似算法的分类(1)基于线性规划的近似算法(2)基于动态规划的近似算法(3)绝对近似类(4)相对近似类(5)P TAS类和FPTAS类(6)随机近似算法二.概率算法1概率算法的计算方法概率算法允许算法在执行的过程中随机选择下一个计算步骤。
许多情况下,当算法在执行过程中面临一个选择时,随机性选择常比最优选择省时.2概率算法的特点(1)不可再现性。
概率算法的一个特点是对所求解问题的同一实例用同一概率算法求解两次可能得到完全不同的效果。
(2)分析困难。
要求有概率论、统计学和数论的知识。
3概率算法的分类(1)数值概率算法。
数值概率算法常用于数值问题的求解。
这类算法所得到的往往是近似解。
而且近似解的精度随计算时间的增加不断提高.在许多情况下,要计算出问题的精确解是不可能或没有必要的,因此用数值概率算法可得到相当满意的解。
(2)蒙特卡罗(Monte Carlo)算法。
中科大软件学院算法实验报告

算法实验报告快速排序1. 问题描述:实现对数组的普通快速排序与随机快速排序(1)实现上述两个算法(2)统计算法的运行时间(3)分析性能差异,作出总结2. 算法原理:2.1快速排序快速排序是对冒泡排序的一种改进。
它的基本思想是:选取一个基准元素,通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比基准元素小,另外一部分的所有数据都要比基准元素大,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
设要排序的数组是A[0]……A[N-1],首先选取一个数据(普通快速排序选择的是最后一个元素, 随机快速排序是随机选择一个元素)作为关键数据,然后将所有比它小的数都放到它前面,所有比它大的数都放到它后面,这个过程称为一趟快速排序。
一趟快速排序的算法是:1)设置两个变量i、j,排序开始的时候:i=0,j=N-1;2)以第一个数组元素作为关键数据,赋值给key,即key=A[0];3)从j开始向前搜索,即由后开始向前搜索(j--),找到第一个小于key的值A[j],将A[j]赋给A[i];4)从i开始向后搜索,即由前开始向后搜索(i++),找到第一个大于key的A[i],将A[i]赋给A[j];5)重复第3、4步,直到i=j;(3,4步中,没找到符合条件的值,即3中A[j]不小于key,4中A[i]不大于key的时候改变j、i的值,使得j=j-1,i=i+1,直至找到为止。
找到符合条件的值,进行交换的时候i,j指针位置不变。
另外,i==j这一过程一定正好是i+或j-完成的时候,此时令循环结束)。
2.2随机快速排序快速排序的最坏情况基于每次划分对主元的选择。
基本的快速排序选取第一个或者最后一个元素作为主元。
这样在数组已经有序的情况下,每次划分将得到最坏的结果。
一种比较常见的优化方法是随机化算法,即随机选取一个元素作为主元。
这种情况下虽然最坏情况仍然是O(n^2),但最坏情况不再依赖于输入数据,而是由于随机函数取值不佳。
近似算法设计

(*)任务:细节
• 转化后问题的求解
– qj = eps*T + k*eps2*T <= pj k是整数 – 一台机器上的时间,离散后,约Q=1/eps2个 – 一台机器上的任务,至多有P=1/eps个
• 动态规划:任务集合S需要最少机器f(S)
– f(S)=1+min{f(S–R)} R是一台机器的任务集 – 状态数:O(nQ),转移复杂度:O(QP)
– {qj}的工作量,是否可以在T时间内完成 – 证明见下页
(*)任务:细节
• 若转化后的问题有解
– 一台机器上不超过1/eps个任务 – pj – qj < 1/eps2 – 因此一台机器上的延时不超过1/eps – 存在一个最终期限不超过(1+eps)T的解
• 转化后的问题无解
– 由于pj > qj – 显然不存在最终期限不超过T的解
完成的工作
• 确定了二分范围
– [L, 2L]
二分算法
• 设二分上下界为T1, T2 • 二分过程
– 调用判定算法判断中点 (1+eps/2)是否有解
• 停止条件
–
,即
关于 停止
• 二分次数O(log2(1/eps))
(1+eps)-判定算法:细节
• 删去所有的pj <= eps*T • 判断余下的任务是否可以在(1+eps)T时间
• 粒子不同的排列结构,对应着不同的能 量水平。如果退火过程是缓慢进行的, 也就是说,温度的下降如果非常缓慢的 话,使得在每个温度下,粒子的排列都 达到一种平衡态,则当温度趋于0(绝对 温度)时,系统的能量将趋于最小值。
• 如果以粒子的排列或者相应的能量来表 达固体所处的状态,在温度T下,固体所 处的状态具有一定的随机性。一方面, 物理系统倾向于能量较低的状态,另一 方面,热运动又妨碍了系统准确落入低 能状态。
中国科学院大学 2014 秋季学期微积分习题及解答

|f ′(x0) − f ′(ξ)| < ϵ. 这和极限的定义不一致.
解答作业
7.
a)
考察函数
f (x)
=
−
1 αxα
,
我们有
f ′(x) =
. 1
x1+α
根据拉格朗日定理,
我们有
(
)
1 α
1
1
(n − 1)α − nα
=
f (n) − f (n − 1)
=
f ′(ξ)
=
1 ξ1+α
>
1 .
n1+α
中国科学院大学 2014 秋季学期微积分 I-A01 习题 10
课程教师:袁亚湘 助教:刘歆 2014 年 12 月 6 日,8:00-9:40
作业 1. 计算 f ′(x), 如果
{ ()
a) f (x) =
exp
−
1 x2
,
0,
如果x ̸= 0; 如果x = 0,
{
b) f (x) =
x2
sin
1 x
,
如果x ̸= 0;
0, 如果x = 0,
c) 验证问题 a) 中的函数在 R 上任意次可微, 且 f (n)(0) = 0.
d) 验证问题 b) 中的函数的导数在 R 上有定义, 但不是 R 上的连续函数.
e) 证明函数
{(
)
f (x) =
exp
−
1 (1+x)2
−
1 (1−x)2
,
0,
当 − 1 < x < 1, 当|x| ≥ 1,
作业 5. 设函数 y = y(x) 由参数方程 x = a cos3(t); y = a sin3(t) 给出, 求 yx′′x.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
10.证明:G中最大团的size为a当且仅当Gm里最大团的size是ma
解:
(1)必要性
由定义可知,Gm是不同G中任意两顶点连线以及G中原有边形成的图,不妨设G 中的两个图分别标记为p和q,p中的每一个点与q中的一个点都有边相连,所以假如G中的一个最大团的size为a,以此类推,p与q组合形成G2最大团的size为2a,同理,Gm最大团的size为ma
(2)充分性
对于充分性,即对图中的顶点的删除,每删除一个G最大团中的顶点,G最大团的size都减一,以此类推,显然有Gm最大团的size为ma。
11.证明:当最优调度在任何机器上至多包含2个作业时,LPT也是最优的
解:
不妨设n=2m,若n<2m,则令Jn+1,…,J2m的时间均为0,将其加入I,不妨设
P1≥P2≥…≥P2m.
设最优调度使得每台机器恰有2个作业:Ji和Jj,则必有i≤m,j>m。
否则若某最优调度O,有i,j≤m,则定有某台机器上有Js和Jt,使得s,t>m
因为Pi,Pj≥Ps,Pt,交换Pj和Pt,则Pi+Pt≤Pi+Pj,Ps+Pj≤Pi+Pj
交换后的调度O’的最迟完成时间只可能减少,故O’也是最优调度。
对于i,j>m时,因为Pi,Pj≤Ps,Pt,交换Pj和Pt,则Pi+Pt≤Ps+Pt,Ps+Pt≤Ps+Pt,所以必有最优调度使J I,…,Jm分别分配到M1,…,Mm上,当将J m+1,…,J2m分配到M台机器上时,LPT是将长时间的作业分配到轻负载上,必与该最优调度结果相同。
