期权定价模型及其求解
期权定价模型的推导过程

伊藤过程dS=μSdt+σSdz上式是描述股票价格行为的最广泛使用的一种模型形式简单,比较容易处理,对实际情况的合理近似。
σ称为股票价格波动率,μ称为预期收益率伊藤定理:设变量x 遵循ITO 过程dx=a(x,t)dt+b(x,t)dz ,则x 和t 的函数G(x,t)遵循如下过程:bdz xG dt b x G t G a x G dG ∂∂+∂∂+∂∂+∂∂=)21(222其中,dz 是与上述过程中同样的维纳过程。
G 实际上也遵循一个ITO 过程。
的分布这是到期时刻股价对数或因此,相互独立其中,,则时刻的股价为,时刻的股价为设离散时间形式均为常数,因此可写为和其中得定理,由应用令由)](),)(2/([ln ~ln )](),)(2/[(~ln ln ),1,0(~,)(),,0(~,)2(ln ln G S T S )2(1,0,1G IT O ln 22222/12T 2222t T t T r S N S t T t T N S S z N t z t N z t T t zt S S t dzdt dG S S G t G S S S G Sdz Sdt dS T T T ---+----∆∆=∆∆∆-=∆∆+∆-=-=∆+-=-=∂∂=∂∂=∂∂=+=σσσσμεεσσμσμσσμσμ按照风险中性假设,当我们希望以无风险利率r 来贴现期权的价值时,即r 0=r ,股票的期望收益率也应该为无风险利率,即μ=r ,则:)]0,[max(ˆ)(K S E e c T t T r -=--)](),)(2/([ln ~ln 22t T t T r S N S T ---+σσ我们有了lnS T 的概率分布,就可以得到S T 的概率分布,即其密度函数,有了S T 的密度函数,E[max(ST-K,0)]就是一个积分过程,通过积分我们就可以得到结果,即著名的B-S公式。
具体积分过程如下:⎰⎰∞-∞---=====----T x T S S T xT T u d u f S F u d u f x F ex f x S e S f ln 22/1222/12)()()(ln )()()()2()(,ln )2()(ln 22)(2)(ln σσμμσπσπ则:令2)(ln 22)(ln 22/1222/12)2(1)2(1)(ln )()(σσμμσπσπ------=⨯=⨯=⨯=T S T S eS S eS S f S dx dx x dF S f T TTT T T以上是到期股价T S 的密度函数。
期权定价模型

二、期权价值评估的方法(一)期权估价原理1、复制原理基本思想复制原理的基本思想是:构造一个股票和贷款的适当组合,使得无论股价如何变动投资组合的损益都与期权相同,那么创建该投资组合的成本就是期权的价值。
基本公式每份期权价格(买价)=借钱买若干股股票的投资支出=购买股票支出-借款额计算步骤(1)确定可能的到期日股票价格Su和Sd上行股价Su=股票现价S×上行乘数u下行股价Sd=股票现价S×下行乘数d(2)根据执行价格计算确定到期日期权价值Cu和Cd:股价上行时期权到期日价值Cu=上行股价-执行价格股价下行时期权到期日价值Cd=0(3)计算套期保值率:套期保值比率H=期权价值变化/股价变化=(CU-Cd)/(SU-Sd)(4)计算投资组合的成本(期权价值)=购买股票支出-借款数额购买股票支出=套期保值率×股票现价=H×S0借款数额=价格下行时股票收入的现值=(到期日下行股价×套期保值率)/(1+r)= H×Sd/(1+r)2、风险中性原理基本思想假设投资者对待风险的态度是中性的,所有证券的预期收益率都应当是无风险利率;假设股票不派发红利,股票价格的上升百分比就是股票投资的收益率。
因此:期望报酬率(无风险收益率)=(上行概率×股价上升时股价变动百分比)+(下行概率×股价下降时股价变动百分比)=p×股价上升时股价变动百分比+(1-p)×股价下降时股价变动百分比计算步骤(1)确定可能的到期日股票价格Su和Sd(同复制原理)(2)根据执行价格计算确定到期日期权价值Cu和Cd(同复制原理)(3)计算上行概率和下行概率期望报酬率=(上行概率×股价上升百分比)+(下行概率×股价下降百分比)(4)计算期权价值期权价值=(上行概率×Cu+下行概率×Cd)/(1+r)(二)二叉树期权定价模型1、单期二叉树定价模型基本原理风险中性原理的应用计算公式(1)教材公式期权价格=U=股价上行乘数=1+股价上升百分比d=股价下行乘数=1-股价下降百分比(2)理解公式:(与风险中性原理完全一样)2、两期二叉树模型基本原理把到期时间分成两期,由单期模型向两期模型的扩展,实际上就是单期模型的两次应用。
第11章 期权定价模型

第11章 布莱克-舒尔茨-默顿期权定价模型一、基本思路1. 基本思路我们为了给股票期权定价,必须先了解股票本身的走势。
因为股票期权是其标的资产(即股票)的衍生工具,在已知执行价格、期权有效期、无风险利率和标的资产收益的情况下,期权价格变化的唯一来源就是股票价格的变化,股票价格是影响期权价格的最根本因素。
用几何布朗运动表示股票价格的变化过程,具体形式如下:dS dt dz Sμσ=+ 或者表示为dS Sdt Sdz μσ=+伊藤引理表明,当股票价格服从上述随机过程时,作为衍生品的期权价格f 将服从22221()2f f f f df S S dt Sdz S t SS μσσ∂∂∂∂=+++∂∂∂∂ 两式表明:股票价格及其衍生品——期权价格都只受到同一种不确定性的影响,只是两者对随机因素变化的反应程度不同而已。
从数学上看,将两式联立,解方程组可消掉随机项。
其金融含义可看作:买入股票、卖空期权构造一个短期内没有不确定性的投资组合。
在一个无套利市场中,该投资组合必然只能获得无风险利率收益。
由此可得到一个期权价格满足的微分方程,此即为BSM 期权定价模型的微分形式,具体为222212f f f rS S rf t S S σ∂∂∂++=∂∂∂ 由于该公式中不包含反映投资者风险偏好的参数——预期收益,因此可以在风险中性世界里求解该微分方程。
求解该方程可得到期权定价公式。
无股利欧式看涨期权的价格为 ()12()()r T t c SN d Xe N d --=-其中,21221d d d ===- 根据无股利欧式看涨期权和看跌期权平价公式()21()()r T t p Xe N d SN d --=--- 可求出无股利欧式看跌期权定价公式()21()()r T t p Xe N d SN d --=---无收益美式看涨期权是不会提前执行的,因此无收益美式看涨期权定价公式和欧式看涨期权定价公式相同,()12()()r T t C SN d Xe N d --=-对于有收益欧式期权,需要在股票价格中抛去收益的现值,对有收益的美式看涨期权,需要考虑其提前执行的情况,由于不存在美式期权之间的平价公式,因此无法给出美式看跌期权的确切公式。
第二节期权定价模型

C Fe r (T t ) Ke r (T t ) P
(二)平价关系
4、美式期权的平价关系 (1)标的资产无收益的平价关系
S K c p S Ker (T t )
(2)标的资产有收益的平价关系
S D K c p S D Ker (T t )
第二节
金融期权的定价模型
一、金融期权价格构成 (一)金融期权的内在价值 1、含义:期权的内在价值,即履约的价值,指期权合 约本身所具有的价值,也是期权的买方立即执行期权能 获得的收益。 期权的内在价值取决于协定价格与标的物市场价格的 关系。 期权的内在价值不会小于零。 根据内在价值,期权可分为实值、虚值和平值三种。
注意:对看涨期权来说,L 总是负值(总是借入资金)。 问题:导出复制看跌期权组合的计算公式。
• Risk-Neutral Probability
记: q R d
ud
1 q
C=∆S+L C = 1/R × (q × Cu + (1-q) × Cd) 如果q是股票价格上涨的概率,则看涨期权的价格是期权未来 价值的期望值的贴现值。 衍生证券的风险中性定价 如果每个人都是风险中性的,股票的期望收益率将等于无风险 收益率R. 在风险中性的世界中,股票上升的概率为q(注意 在实际中,股票上升的概率为p,投资者是风险厌恶的 ) 看涨期权的价格是期权未来价值的期望值的贴现值: C = 1/R × {q × Cu + (1-q) × Cd} 一般公式为: Derivative Price = EQ[(1/R)(T-t) × Payoff ] 此公式说明衍生证券的价格是其盈亏贴现值的期望值 (风险中 性的世界中)
1、实例
期权定价理论知识

期权定价理论知识期权定价理论是金融市场中重要的工具,它用于确定期权的合理价格。
期权是一种金融衍生品,它赋予持有者在未来某个时间点购买或卖出标的资产的权利,但并不强制执行。
期权的价格由多种因素决定,包括标的资产价格、行权价格、期权到期时间、标的资产的波动性以及无风险利率等。
在期权定价理论中,最著名的模型是布莱克-斯科尔斯期权定价模型(Black-Scholes Option Pricing Model)。
该模型是由费希尔·布莱克和米伦·斯科尔斯于1973年提出的,并且因此获得了诺贝尔经济学奖。
该模型基于一些假设,如市场是完全有效、无风险利率是恒定的等。
根据布莱克-斯科尔斯期权定价模型,期权的价格可以通过以下公式计算:C = S * N(d1) - X * e^(-rt) * N(d2)其中,C表示看涨期权价格,S表示标的资产价格,N(d1)和N(d2)分别是标准正态分布函数,X表示行权价格,r表示无风险利率,t表示期权到期时间。
公式中的d1和d2可以通过以下公式计算:d1 = (ln(S/X) + (r + (σ^2)/2)*t) / (σ * √t)d2 = d1 - σ * √t该模型通过考虑标的资产价格、行权价格、期权到期时间、标的资产的波动性和无风险利率等因素,来确定一个看涨期权的合理价格。
类似地,可以用类似的方法计算看跌期权的价格。
虽然布莱克-斯科尔斯期权定价模型是一个重要的理论框架,但它在实际应用中存在一些限制。
例如,该模型假设市场是完全有效的,但实际市场存在各种交易成本、税收和限制等,这些因素都可能影响期权的价格。
此外,该模型假设无风险利率是恒定的,但实际上利率是变化的。
因此,在实际应用中,需要根据实际情况进行调整和修正。
总之,期权定价理论是金融市场中重要的理论工具,它为期权的定价和交易提供了基础。
布莱克-斯科尔斯期权定价模型是其中最著名的模型之一,它通过考虑标的资产价格、行权价格、期权到期时间、标的资产的波动性和无风险利率等因素来确定期权的合理价格。
第六章布莱克-舒尔斯期权定价模型
第六章 布莱克-舒尔斯期权定价模型一、 影响期权价值的主要因素由前面的分析知道决定期权价值(价格)C V 的因素是到期的股票市场价格m S 和股票的执行价格X 。
但是到期m S 是未知的,它的变化还要受价格趋势和时间价值等因素的影响。
1)标的股票价格与股票执行价格的影响。
标的股票市场价格越高,则买入期权的价值越高,卖出期权的价值越低;期权的执行价越高,则买入的期权价值越低,卖出期权的价值越高。
2)标的股票价格变化范围的影响。
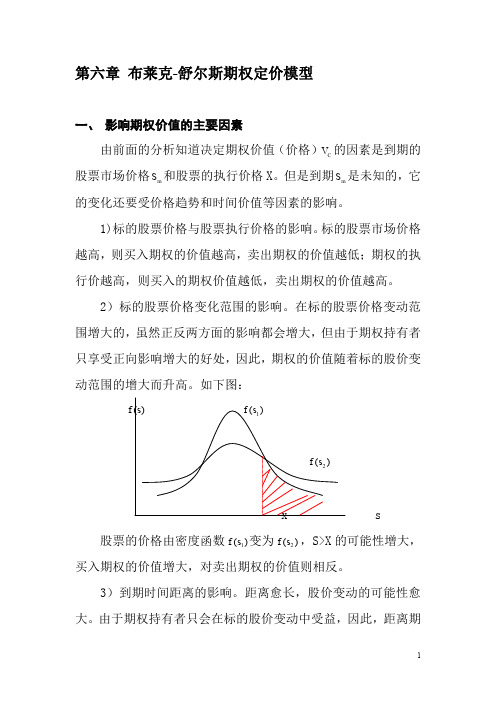
在标的股票价格变动范围增大的,虽然正反两方面的影响都会增大,但由于期权持有者只享受正向影响增大的好处,因此,期权的价值随着标的股价变动范围的增大而升高。
如下图: )(s f )(1s f)(2s fx s股票的价格由密度函数)(1s f 变为)(2s f ,S>X 的可能性增大,买入期权的价值增大,对卖出期权的价值则相反。
3)到期时间距离的影响。
距离愈长,股价变动的可能性愈大。
由于期权持有者只会在标的股价变动中受益,因此,距离期权到期的时间越长,期权的价值就越高。
4)利率的影响。
利率越高,则到期m S 的现值就越低,使得买入期权价值提高,而卖出期权价值降低。
5)现金股利的影响。
股票期权受到股票分割或发放股票股利的保护,期权数量也适应调整,而不受影响,但是期权不受现金股利的保护,因此当股票的价格因公司发放现金股利而下降时,买入期权的价值下降,卖出期权的价值便上升。
二、布莱克-舒尔斯期权定价模型的假设条件B-S 模型是反映欧式不分红的买入期权定价模型,它的假定条件,除了市场无摩擦(例如无税、无交易成本、可以无限制自由借贷等)以外,还有:1. 股票价格是连续的随机变量,所以股票可以无限分割。
2. T 时期内各时段的预期收益率r i 和收益方差σi 保持不变。
3. 在任何时段股票的复利收益率服从对数正态分布,即在t 1-t 2时段内有:()()()2221211()ln ,()S t N t t t t S t μσ⎛⎫-- ⎪⎝⎭因为股票的价格可以用随机过程{},...2,1)(=t t S 表示,其中S (t )表示第t 日股票的价格,它是一个随机变量. 则第t 日股票的收益率(年收益率)为R t :3651)1()(t R t S t S +=-股票的年收益率(单利)R 应该是:)3651()3651)(3651()364()365()1()0()2()1()0()365(136521R R R S S S S S S S S R +++===+为了简化计算两边同时取自然对数可得:∑=+=+3651)3651()1(t tR In R In设r ,r 1,r 2,…,r 365为和R ,R 1,R 2,…,R 365相对应的连续复利。
B-S期权定价模型、公式与数值方法

B-S期权定价公式:假设条件
1.证券价格遵循几何布朗运动,,为常数 2.允许卖空标的证券 3.没有交易费用或税收 4.所有证券都是无限可分的 5.标的证券在有效期内没有红利支付 6.不存在无风险套利机会 7.交易是连续的 8.无风险利率为常数
B-S期权定价公式
经典的B-S期权定价公式是对于欧式股票期权给出的。
期权的价值正是来源于签订合约时,未来标的资产价格与合约执 行价格之间的预期差异变化,在现实中,资产价格总是随机变化 的。需要了解其所遵循的随机过程。
研究变量运动的随机过程,可以帮助我们了解在特定时刻,变量 取值的概率分布情况。在下面几节中我们会用数学的语言来描述 这种定价的思想。
6.1 证券价格的变化过程
**随机微积分与非随机微积分的差别 d ln S dS
S
变量x和t的函数G也遵循Ito 过程:
dG ( G xa G t1 2 2 x G 2b2)d t G xbdz
dSSdtSdz
根据Ito引理,衍生证券的价格G应遵循如下过程:
d G ( G SS G t1 2 S 2 G 22 S2)d t G SSdz
但是当人们开始采用分形理论研究金融市场时,发现它的运行并 不遵循布朗运动,而是服从更为一般的分数布朗运动。
对于标准布朗运动来说:设t 代表一个小的时间
间隔长度,z代表变量z在 t 时间内的变化,遵循标
准布朗运动的 z 具有两种特征:
特征1:z和 t 的关系满足:
z = t
其中, 代表从标准正态分布中取的一个随机值。
的普通布朗运动:
Ito过程
dxadb t dz d xa (x,t)d tb (x,t)dz
or:x( t)x0a t bz(t)x(t)x00 tad s0 tbd
期权定价模型和数值方法

期权及其有关概念
3. 期权旳内在价值 买入期权在执行日旳价值CT为 CT=max(ST -E,0)
式中:E表达行权价;ST表达标旳资产旳市场价。 卖出期权在执行日旳价值PT为 PT=max(E- ST,0) 根据期权旳行权价与标旳资产市场价之间旳关系,期权可分为价内期权(in the
money)(S > E)、平价期权(at the money)(S = E)和价外期权(out of the money)(S < E)。
4. 珞(Rho)ρ ρ为期权旳价值随利率波动旳敏感度,利率增长,使期权价值变大。
5. 伽玛(Gamma)Γ Γ 表达δ与标旳资产价格变动旳关系。
10.3 B-S公式隐含波动率计算
隐含波动率概念
BlackScholes期权定价公式,欧式期权理论价格旳体现式:
式中:
隐含波动率是将市场上旳期权交易价格代入权证理论价格BlackScholes模型反 推出来旳波动率数值。因为期权定价BS模型给出了期权价格与五个基本参数之间旳 定量关系,只要将其中前4个基本参数及期权旳实际市场价格作为已知量代入定价 公式,就能够从中解出惟一旳未知量,其大小就是隐含波动率。
10.3. 3 隐含波动率计算程序
环节3: 函数求解。 M文件TestImpliedVolatility.M代码如下:
%TestImpliedVolatility %市场价格 Price=100; %执行价格 Strike=95; %无风险利率 Rate=0.10; %时间(年) Time=0.25; CallPrice=15.0;%看涨期权交易价格 PutPrice=7.0; %看跌期权交易价格 %调用ImpliedVolatility函数 [Vc,Vp,Cfval,Pfval]=ImpliedVolatility(Price,Strike,Rate,Time,CallPrice,PutPrice)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【实验小结】(收获体会)
通过这次期权定价模型与数值方法综合实验,加深了对Black-Schole期权定价公式的理解,同时培养了运用软件工具解决期权定价问题的应用和动手能力。
三、指导教师评语及成绩:
评语
评语等级
优
良
中
及格
不及格
1.实验报告按时完成,字迹清楚,文字叙述流畅,逻辑性强
(7)可以运用全部的金融资产所得进行卖空操作。
无收益欧式看涨期权的定价公式:
无收益资产欧式看跌期权的定价公式:
其中 ,
算例:股票的价格为100,股票的波动率标准差为0.25,无风险利率为5%,期权的执行价格为100,存续期为0.25年,试计算该股票欧式期权的价格。
【实验环境】
MATLAB2010b
Windows10
2.实验方案设计合理
3.实验过程(实验步骤详细,记录完整,数据合理,分析透彻)
4实验结论正确.
成绩:
指导教师签名:
批阅日期:
附录1:源程序
欧式期权的收益图程序:
subplot(1,2,1)
s=[0:1:99];
E=50;
call=zeros(size(s));
for i=1:100
call(i)=max(s(i)-E,0);
【实验原理】
1.BSM期权价格微分方程
2.看跌期权定价的显性差分法
(1)BSM微分方程中偏导数的差分近似
; ;
(2)差分方程
其中
(3)边界条件
T时刻看跌期权的价值为
下边界 上期权价值为
上边界 上期权价值为
(4)期权的价值
对于差分方程和边界条件
;
解出每个 的期权值,然后再与每个格点的期权内在价值 进行比较,判断是否提前执行,从而得到 时刻每个格点的期权价格。
end
plot(S,put);
ylim([-10 50]);
xlim([0 90]);
xlabel('到期价格S(T)');
ylabel('看跌期权的到期收益');
计算期权定价:
function [Call Put]=bsprice(S0,K,r,T,sigma)
% call:看涨期权
% put:看跌期权
数学与计算科学学院
实验报告
实验项目名称期权定价模型及其求解
所属课程名称微分方程数值解
实验类型验证型
实验日期4月8日
班级
学号
姓名
成绩
一、实验概述:
【实验目的】
(1)通过期权定价模型与数值方法综合实验,使学生加深对期权模型的理解;
(2)熟练掌握运用Matlab软件计算期权价格的有限差分法。
(4)培养学生运用软件工具解决期权定价问题的应用和动手能力。
二、实验内容:
【实验方案】
编写m文件,存储函数和需要求解的方程,在命令窗口输入相关命令调用函数即可得到结果。
【实验过程】(实验步骤、记录、数据、分析)
第一步.利用Matlab绘制欧式期权的收益图
2,计算Black-Scholes期权价格:
(call:看涨期权put:看跌期权
S0:股票的现价K:期权执行价格
(1)在期权有效期内,无风险利率和股票资产期望收益变量和价格波动率是恒定的;
(2)市场无摩擦,即不存在税收和交易成本;
(3)股票资产在期权有效期内不支付红利及其它所得(该假设可以被放弃);(4)该期权是欧式期权,即在期权到期前不可实施;
(5)金融市场不存在无风险套利机会;
(6)金融资产的交易可以是连续进行的;
Put=K*exp(-r*T)*normcdf(-d2)-S0*normcdf(-d1); %利用Black-Schole公式计算看跌期权价格、
依此类推,可以计算出 ,当 等于初始资产价格时,该格点对应的 就是所求的期权价值。
1.参量与符号
(1) :标的资产的价格;(2) :行权价格;(3) :到期期限;
(4) :标的资产价格波动率;(5) :连续复利的无风险利率。
2.Black-Schole期权定价公式
在满足以下条件下,可以有新的计算公式。
% S0:股票的现价
% K:期权执行价格
% r:
d1=(log(S0/K)+(r+0.5*sigma^2)*T)/(sigma*sqrt(T)); % d1的计算
d2=d1-(sigma*sqrt(T)); % d2的计算
Call=S0*normcdf(d1)-K*exp(-r*T)*normcdf(d2); %利用Black-Schole公式计算看涨期权价格
r:无风险利率T:期权存续期
sigma:波动率)
用老师给定的数据s0=100;k=100;r=0.05;sigma=0.5;T=0.25;调用语句[Call,Put]=bsprice(100,100,0.05,0.25,0.5)得到如下结果:
Call =
10.5193
Put =
9.2770
【实验结论】(结果)
end
plot(s,call)
ylim([-10 50]);
xlim([0 90]);
xlabel('到期价格S(T)');
ylabel('看涨期权的到期收益');
subplot(1,2,2)
S=[0:1:99];
put=zeros(size(S));
for i=1:100
put(i)=max(E-S(i),0);
