组合数学 试题及答案09
高中数学选择性必修三 6 2 2 组合及组合数(精练)(含答案)

6.2.2 组合及组合数(精练)【题组一 组合的概念】1.下列问题不是组合问题的是 ( )A .10个朋友聚会,每两人握手一次,一共握手多少次?B .平面上有2015个不同的点,它们中任意三点不共线,连接任意两点可以构成多少条线段?C .集合{a 1,a 2,a 3,…,a n }的含有三个元素的子集有多少个?D .从高三(19)班的54名学生中选出2名学生分别参加校庆晚会的独唱、独舞节目,有多少种选法? 【答案】 D【解析】 组合问题与次序无关,排列问题与次序有关,D 项中,选出的2名学生,如甲、乙,其中“甲参加独唱、乙参加独舞”与“乙参加独唱、甲参加独舞”是两个不同的选法,因此是排列问题,不是组合问题,选D. 2.给出下列问题:(1)从a ,b ,c ,d 四名学生中选2名学生完成一件工作,有多少种不同的选法? (2)从a ,b ,c ,d 四名学生中选2名学生完成两件不同的工作,有多少种不同的选法? (3)a ,b ,c ,d 四支足球队之间进行单循环比赛,共需赛多少场? (4)a ,b ,c ,d 四支足球队争夺冠亚军,有多少种不同的结果?(5)某人射击8枪,命中4枪,且命中的4枪均为2枪连中,不同的结果有多少种? (6)某人射击8枪,命中4枪,且命中的4枪中恰有3枪连中,不同的结果有多少种? 在上述问题中,哪些是组合问题?哪些是排列问题? 【答案】见解析【解析】(1)2名学生完成的是同一件工作,没有顺序,是组合问题. (2)2名学生完成两件不同的工作,有顺序,是排列问题.(3)单循环比赛要求每两支球队之间只打一场比赛,没有顺序,是组合问题. (4)冠亚军是有顺序的,是排列问题.(5)命中的4枪均为2枪连中,为相同的元素,没有顺序,是组合问题. (6)命中的4枪中恰有3枪连中,即连中3枪和单中1枪,有顺序,是排列问题. 【题组二 组合数】1.(2020·山东菏泽·高二期末)已知4m ≥,3441m m m C C C +-+=( )A .1B .mC .1m +D .0【答案】D【解析】3443444411110m m m m m m m m C C C C C C C C ++++=--++-==.故选:D2.(2020·山东莱州一中高二期末)下列等式中,错误的是( )A .11(1)m m n n n A A +++=B .!(2)!(1)n n n n =--C .!m m nnA C n =D .11m mn n A A n m+=- 【答案】C【解析】通过计算得到选项A,B,D 的左右两边都是相等的.对于选项C, !m m nnA C m =,所以选项C 是错误的.故答案为C.3.444444456789C C C C C C +++++=( ).A .410C B .510CC .610CD .410A【答案】B【解析】因为111C C C mm m n nn ++++=, 所以44444454444454444567895567896678C C C C C C C C C C C C C C C C +++++=+++++=+++45444544545977898899910C C C C C C C C C C C +=+++=++=+=.故选:B 4.(2020·广东佛山·高二期末)若3221364n n n A A C +-=,则n =( )A .5B .8C .7D .6【答案】A【解析】∵3221364n n n A A C +-=,∴()()()()13126142n n n n n n n +----=⨯,即()()()3126122n n n n ----=+,求得5n =,或23n =(舍去),故选:A. 5.(多选)(2020·江苏连云港·高二期末)关于排列组合数,下列结论正确的是( ) A .C C mn mn n-=B .11C C C m m m n nn -+=+ C .11A A m m n n m --= D .11A A A mm m n nn m -++=【答案】ABD【解析】根据组合数的性质或组合数的计算公式!()!!m n n C n m m =-,可知A ,B 选项正确;!()!m n n A n m =-,而()111!()!m n m n mA n m ---=-,故C 选项错误;()()111!1!!!!()!(1)!(1)!(1)!(1)!m m mnnn n m n n n m n m n A mAA n m n m n m n m n m -+-+⋅+⋅⋅+=+=+==--+-+-++-, 故D 选项正确;故选:ABD .6.(2020·苏州市第四中学校高二期中)计算()2973100100101CC A +÷的值为__________.(用数字作答) 【答案】16【解析】由组合数的基本性质可得()()297323333100100101100100101101101101!98!13!98!101!6C C A C C A C A +÷=+÷=÷=⨯=⨯.故答案为:16.7.求值:(1)333364530C C C C +++⋅⋅⋅+; (2)12330303030302330C C C C +++⋅⋅⋅+.【答案】(1)31464;(2)29302⋅.【解析】(1)333343333456304456301C C C C C C C C C +++⋅⋅⋅+=++++⋅⋅⋅+-4311C =-31464=(2)()12330012293030303029292929233030C C C C C C C C +++⋅⋅⋅+=+++⋅⋅⋅+29302=⋅【题组三 组合应用 】1.(2020·北京高二期末)若从1,2,3,…,9这9个整数中同时取3个不同的数,其和为奇数,则不同的取法共有( ) A .36种 B .40种 C .44种 D .48种【答案】B【解析】根据题意,将9个数分为2组, 一组为奇数:1、3、5、7、9,一组为偶数:2、4、6、8, 若取出的3个数和为奇数,分2种情况讨论:①取出的3个数全部为奇数,有3510C =种情况, ②取出的3个数有1个奇数,2个偶数,有1254C C 30=种情况,则和为奇数的情况有103040+=种. 故选:B .2.(2020·北京朝阳·高二期末)从3名男生和4名女生中各选2人组成一队参加数学建模比赛,则不同的选法种数是( ) A .12 B .18 C .35 D .36【答案】B【解析】先从3名男生中选出2人有233C =种,再从4名女生中选出2人有246C =种,所以共有1863=⨯种,故选: B3.(2020·新疆乌鲁木齐市第70中高二期中(理))已知集合{1,2,3,4,5}A =,则集合A 各子集中元素之和为( ) A .320 B .240 C .160 D .8【答案】B【解析】当集合A 的子集为空集时,各元素之和为0;当集合A 的子集含有1个元素时,共有155C =个集合,1、2、3、4、5各出现1次; 当集合A 的子集含有2个元素时,共有2510C =个集合,1、2、3、4、5各出现4次;当集合A 的子集含有3个元素时,共有3510C =个集合,1、2、3、4、5各出现6次; 当集合A 的子集含有4个元素时,共有455C =个集合,1、2、3、4、5各出现4次; 当集合A 的子集含有5个元素时,共有551C =个集合,1、2、3、4、5各出现1次;所以集合A 各子集中,1、2、3、4、5各出现了1464116++++=次, 所以集合A 各子集中元素之和为()1234516240++++⨯=. 故选:B.4.(2020·湖北高二月考)2020年春节期间,因新冠肺炎疫情防控工作需要,M 、N 两社区需要招募义务宣传员,现有A 、B 、C 、D 、E 、F 六位大学生和甲、乙、丙三位党员教师志愿参加,现将他们分成两个小组分别派往M 、N 两社区开展疫情防控宣传工作,要求每个社区都至少安排1位党员教师及2位大学生,且B 由于工作原因只能派往M 社区,则不同的选派方案种数为( ) A .120 B .90C .60D .30【答案】C【解析】由于B 只能派往M 社区,所以分组时不用考虑B .按照要求分步将大学生和党员教师分为两组,再分别派往两个社区.第一步:按题意将剩余的5位大学生分成一组2人,一组3人,有2510C=种,第二步:按题意将3位大学生分成一组1人,一组2人,有133C=种,再分别派往两个社区的不同选派种数:103260⨯⨯=种,故选:C。
人教版高中数学选择性必修第三册6.2.2组合及组合数 同步训练(含答案)
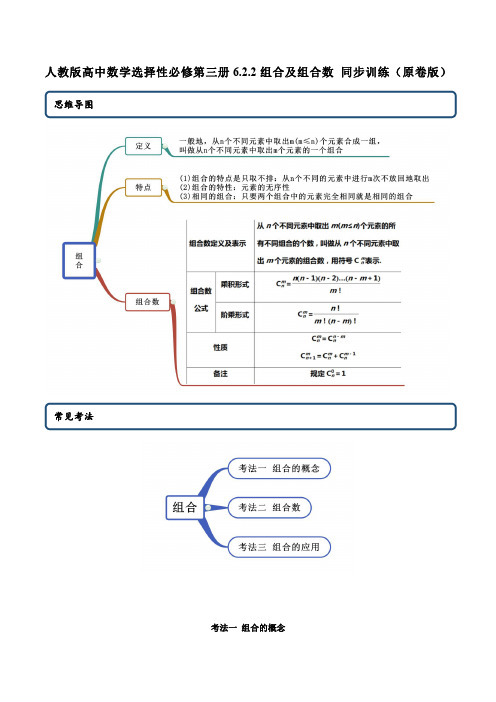
人教版高中数学选择性必修第三册6.2.2组合及组合数同步训练(原卷版)思维导图常见考法考法一组合的概念【例1】(2020·广东湛江高二单元测试)给出下列问题:①有10个车站,共需要准备多少种车票?②有10个车站,共有多少中不同的票价?③平面内有10个点,共可作出多少条不同的有向线段?④有10个同学,假期约定每两人通电话一次,共需通话多少次?⑤从10个同学中选出2名分别参加数学和物理竞赛,有多少中选派方法?以上问题中,属于组合问题的是_________(填写问题序号).【一隅三反】1.(2020·全国高二课时练习)以下四个问题中,属于组合问题的是()A.从3个不同的小球中,取出2个小球排成一列B.老师在排座次时将甲、乙两位同学安排为同桌C.在电视节目中,主持人从100名幸运观众中选出2名幸运之星D.从13位司机中任选出两位分别去往甲、乙两地2.(2020·全国高二课时练习)下列问题属于排列问题的是()①从10个人中选2人分别去种树和扫地;②从10个人中选2人去扫地;③从班上30名男生中选出5人组成一个篮球队;④从数字5,6,7,8中任取两个不同的数作为log a b 中的底数与真数A.①④B.①②C.④D.①③④考法二组合数【例2】(1)(2020·广东云浮·高二期末)333345C C C ++=()A.45C B.56C C.36C D.46C (2)(2020·湖北高二期末)满足条件23n n A C >的自然数n 有()A.7个B.6个C.5个D.4个组合数的两个性质:(1)m n mn n C C -=;(2)11m m mn nn C C C -+=+.【一隅三反】1.(2020·陕西高二期末)若()6671*n n n C C C n +-=∈Ν,则n 等于()A.11B.12C.13D.142.(2020·林芝市第二高级中学高二期中)已知215n C =,那么2n A =()A.20B.30C.42D.723.设n 为满足不等式01222008nn n n n C C C nC ⋅+⋅<⋅+++的最大正整数,则n 的值为().A.11B.10C.9D.84.(多选)下列等式正确的是()A.()111mm nn n A A+++=B.()()!2!1n n n n =--C.!m m nnA C n =D.11m mn nA A n m+=-5.(多选)(2020·江苏省丰县中学高二期末)如下的四个命题中真命题的标号为()A.97100162700C =B.3239910C C C +=C.12345678888888C C C C C C C 254++++++=D.10(12)x +的展开式中二项式系数最大的项是513579(4)5!x ⨯⨯⨯⨯考法三组合应用【例3】男运动员6名,女运动员4名,其中男、女队长各1名.现选派5人外出参加比赛,在下列情形中各有多少种选派方法?(1)男运动员3名,女运动员2名;(2)至少有1名女运动员;(3)队长中至少有1人参加;(4)既要有队长,又要有女运动员.【方法总结】组合问题常有以下两类题型变化:(1)“含有”或“不含有”某些元素的组合题型:“含”,则先将这些元素取出,再由另外元素补足;“不含”,则先将这些元素剔除,再从剩下的元素中去选取.(2)“至少”或“至多”含有几个元素的组合题型:解这类题必须十分重视“至少”与“至多”这两个关键词的含义,谨防重复与漏解.用直接法和间接法都可以求解,通常用直接法分类复杂时,考虑逆向思维,用间接法处理.【一隅三反】1.(2020·江苏金湖中学)一个口袋内有3个不同的红球,4个不同的白球(1)从中任取3个球,红球的个数不比白球少的取法有多少种?(2)若取一个红球记2分,取一个白球记1分,从中任取4个球,使总分不少于6分的取法有多少种?2.(2020·云南省保山第九中学)某车间甲组有10名工人,其中有4名女工人;乙组有5名工人,其中有3名女工人.现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两组中共抽取3名工人进行技术考核.(Ⅰ)求从甲、乙两组各抽取的人数;(Ⅱ)求从甲组抽取的工人中恰好1名女工人的概率;(Ⅲ)求抽取的3名工人中恰有2名男工人的概率.3.(2020·江苏高二)有男运动员6名,女运动员4名,其中男女队长各1名.选派5人外出比赛,在下列情形中各有多少种选派方法?(1)男运动员3名,女运动员2名;(2)至少有1名女运动员;(3)既要有队长,又要有女运动员.人教版高中数学选择性必修第三册6.2.2组合及组合数同步训练(解析版)思维导图常见考法考法一组合的概念【例1】(2020·广东湛江高二单元测试)给出下列问题:①有10个车站,共需要准备多少种车票?②有10个车站,共有多少中不同的票价?③平面内有10个点,共可作出多少条不同的有向线段?④有10个同学,假期约定每两人通电话一次,共需通话多少次?⑤从10个同学中选出2名分别参加数学和物理竞赛,有多少中选派方法?以上问题中,属于组合问题的是_________(填写问题序号).【答案】②④【解析】①有10个车站,共需要准备多少种车票?相当于从10个不同元素任取2个按一定顺序排列起来,属于排列问题;②有10个车站,共有多少中不同的票价?相当于从10个不同元素任取2个并成一组,属于组合问题;③平面内有10个点,共可作出多少条不同的有向线段?相当于从10个不同元素任取2个按一定顺序排列起来,属于排列问题;④有10个同学,假期约定每两人通电话一次,共需通话多少次?相当于从10个不同元素任取2个并成一组,属于组合问题;⑤从10个同学中选出2名分别参加数学和物理竞赛,有多少中选派方法?相当于从10个不同元素任取2个按一定顺序排列起来,属于排列问题;以上问题中,属于排列问题的是②④.【一隅三反】1.(2020·全国高二课时练习)以下四个问题中,属于组合问题的是()A.从3个不同的小球中,取出2个小球排成一列B.老师在排座次时将甲、乙两位同学安排为同桌C.在电视节目中,主持人从100名幸运观众中选出2名幸运之星D.从13位司机中任选出两位分别去往甲、乙两地【答案】C【解析】只有从100名幸运观众中选出2名幸运之星,与顺序无关,是组合问题.故选:C.2.(2020·全国高二课时练习)下列问题属于排列问题的是()①从10个人中选2人分别去种树和扫地;②从10个人中选2人去扫地;③从班上30名男生中选出5人组成一个篮球队;④从数字5,6,7,8中任取两个不同的数作为log a b中的底数与真数A.①④B.①②C.④D.①③④【答案】A【解析】排列的概念:从n 个元素中取()m m n ≤个元素,按照一定顺序排成一列,由题可知:①④中元素的选取有顺序,②③中元素的选取无顺序,由此可判断出:①④是排列问题,故选:A.考法二组合数【例2】(1)(2020·广东云浮·高二期末)333345C C C ++=()A.45C B.56C C.36C D.46C (2)(2020·湖北高二期末)满足条件23n n A C >的自然数n 有()A.7个B.6个C.5个D.4个【答案】(1)D(2)C【解析】(2)333433434345445556C C C C C C C C C ++=++=+=.故选:D.(2)由23n n A C >得(1)(2)(1)321n n n n n --->⨯⨯,即8n <,又3n ≥,且*n N ∈,所以3,4,5,6,7n =.故选:C.组合数的两个性质:(1)mn mn n C C -=;(2)11m m mn nn C C C -+=+.【一隅三反】1.(2020·陕西高二期末)若()6671*n n n C C C n +-=∈Ν,则n 等于()A.11B.12C.13D.14【答案】B【解析】根据题意,6671n n n C C C +-=变形可得,6671n n n C C C +=+;由组合性质可得,6771n n n C C C ++=,即6711n n C C ++=,则可得到16712n n +=+⇒=.故选:B.2.(2020·林芝市第二高级中学高二期中)已知215n C =,那么2n A =()A.20B.30C.42D.72【答案】B【解析】2156n C n =⇒=22630n A A ==答案选B3.设n 为满足不等式01222008nn n n n C C C nC ⋅+⋅<⋅+++的最大正整数,则n 的值为().A.11B.10C.9D.8【答案】D【解析】设0122nn n n n S C C C nC =+++⋅⋅⋅+,则()()12012n n n n nn n S nC n C n C C --=+-+-+⋅⋅⋅+,又r n rn nC C -=,01212222n n n n n n nn n S nC nC nC nC nC C n -∴=++++++=⋅+,121n S n -∴=⋅+,由2008S <得:122007n n -⋅<,72128=,82256=,∴78210242007⨯=<,89223042007⨯=>,n ∴的值为8.故选:D .4.(多选)下列等式正确的是()A.()111mm nn n A A+++=B.()()!2!1n n n n =--C.!m m nnA C n =D.11m mn nA A n m+=-【答案】ABD【解析】A.11!(1)!(1)!(1)(1)()!()![(1)(1)]!mm n n n n n n A n A n m n m n m +++++=+⋅===--+-+,故正确;B.()()!(1)(2)3212!1(1)n n n n n n n n n --⨯⨯⨯⨯==---,故正确;C.!!m m m n nnA A C m n =≠,故错误;D.111!!(1)!()!m mn n n n A A n m n m n m n m +=⋅==-----,故正确.故选:ABD5.(多选)(2020·江苏省丰县中学高二期末)如下的四个命题中真命题的标号为()A.97100162700C =B.3239910C C C +=C.12345678888888C C C C C C C 254++++++=D.10(12)x +的展开式中二项式系数最大的项是513579(4)5!x ⨯⨯⨯⨯【答案】BCD【解析】由于9731001001009998161700321C C ⨯⨯===⨯⨯,故A 错误;由组合数的性质:11mm mn nn C C C -++=,3239910C C C ∴+=,故B 正确;1234567808888888888C C C C C C C 22562254C C ++++++=--=-=,故C 正确;10(12)x +的展开式中二项式系数最大的项是5109876(2)5!x =⨯⨯⨯⨯513579(4)5!x ⨯⨯⨯⨯,故D 正确.故选:BCD考法三组合应用【例3】男运动员6名,女运动员4名,其中男、女队长各1名.现选派5人外出参加比赛,在下列情形中各有多少种选派方法?(1)男运动员3名,女运动员2名;(2)至少有1名女运动员;(3)队长中至少有1人参加;(4)既要有队长,又要有女运动员.【答案】(1)120(2)246(3)196(4)191【解析】(1)分两步完成:第一步,选3名男运动员,有C 36种选法;第二步,选2名女运动员,有C 24种选法.由分步计数原理可得,共有C 36·C 24=120(种)选法.(2)方法一“至少有1名女运动员”包括以下四种情况:1女4男,2女3男,3女2男,4女1男.由分类计数原理可得总选法共有C 14C 46+C 24C 36+C 34C 26+C 44C 16=246(种).方法二“至少有1名女运动员”的反面为“全是男运动员”,可用间接法求解.从10人中任选5人有C 510种选法,其中全是男运动员的选法有C 56种.所以“至少有1名女运动员”的选法有C 510-C 56=246(种).(3)方法一(直接法)可分类求解:“只有男队长”的选法种数为C 48;“只有女队长”的选法种数为C 48;“男、女队长都入选”的选法种数为C 38,所以共有2C 48+C 38=196(种)选法.方法二(间接法)从10人中任选5人有C 510种选法,其中不选队长的方法有C 58种.所以“至少有1名队长”的选法有C 510-C 58=196(种).(4)当有女队长时,其他人任意选,共有C 49种选法;当不选女队长时,必选男队长,共有C 48种选法,其中不含女运动员的选法有C 45种,所以不选女队长时的选法共有(C 48-C 45)种.所以既要有队长又要有女运动员的选法共有C 49+C 48-C 45=191(种).【方法总结】组合问题常有以下两类题型变化:(1)“含有”或“不含有”某些元素的组合题型:“含”,则先将这些元素取出,再由另外元素补足;“不含”,则先将这些元素剔除,再从剩下的元素中去选取.(2)“至少”或“至多”含有几个元素的组合题型:解这类题必须十分重视“至少”与“至多”这两个关键词的含义,谨防重复与漏解.用直接法和间接法都可以求解,通常用直接法分类复杂时,考虑逆向思维,用间接法处理.【一隅三反】1.(2020·江苏金湖中学)一个口袋内有3个不同的红球,4个不同的白球(1)从中任取3个球,红球的个数不比白球少的取法有多少种?(2)若取一个红球记2分,取一个白球记1分,从中任取4个球,使总分不少于6分的取法有多少种?【答案】(1)13;(2)22.【解析】(1)从中任取3个球,红球的个数不比白球少的取法:红球3个,红球2个和白球1个.当取红球3个时,取法有1种;当取红球2个和白球1个时,.取法有213412C C =种.根据分类计数原理,红球的个数不少于白球的个数的取法有11213+=种.(2)使总分不少于6分情况有两种:红球2个和白球2个,红球3个和白球1个.第一种,红球2个和白球2个,取法有223418C C =种;第二种,红球3个和白球1个,取法有31344C C =种,根据分类计数原理,使总分不少于6分的取法有18422+=种.2.(2020·云南省保山第九中学)某车间甲组有10名工人,其中有4名女工人;乙组有5名工人,其中有3名女工人.现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两组中共抽取3名工人进行技术考核.(Ⅰ)求从甲、乙两组各抽取的人数;(Ⅱ)求从甲组抽取的工人中恰好1名女工人的概率;(Ⅲ)求抽取的3名工人中恰有2名男工人的概率.【答案】(Ⅰ)2,1;(Ⅱ)815;(Ⅲ)3175.【解析】(Ⅰ)因为车间甲组有10名工人,乙组有5名工人,所以甲、乙两组的比例是2:1,又因为从甲、乙两组中共抽取3名工人进行技术考核,所以从甲、乙两组各抽取的人数是2,1;(Ⅱ)因为车间甲组有10名工人,其中有4名女工人,所以从甲组抽取的工人中恰好1名女工人的概率1146210815p C CC==;(Ⅲ)因为车间甲组有10名工人,其中有4名女工人;乙组有5名工人,其中有3名女工人,所以求抽取的3名工人中恰有2名男工人的概率112166322121105105131475p C C C C C C C C C=+=.3.(2020·江苏高二)有男运动员6名,女运动员4名,其中男女队长各1名.选派5人外出比赛,在下列情形中各有多少种选派方法?(1)男运动员3名,女运动员2名;(2)至少有1名女运动员;(3)既要有队长,又要有女运动员.【答案】(1)共有3264120C C ∙=(种)选法;(2)246;(3)191.【解析】⑴第一步:选3名男运动员,有36C 种选法.第二步:选2名女运动员,有24C 种选法.共有3264•120C C =(种)选法.⑵“至少1名女运动员”的反面为“全是男运动员”.从10人中任选5人,有510C 种选法,其中全是男运动员的选法有36C 种.所以“至少有1名女运动员”的选法有55106246C C -=(种).(3)当有女队长时,其他人选法任意,共有49C 种选法.不选女队长时,必选男队长,共有48C 种选法.其中不含女运动员的选法有45C 种,所以不选女队长时共有4485C C -种选法.故既要有队长,又要有女运动员的选法有444985191C C C +-=(种).。
组合数学考试题目及答案

组合数学考试题目及答案**组合数学考试题目及答案**一、单项选择题(每题3分,共30分)1. 从10个不同的元素中取出3个元素的组合数为()。
A. 120B. 210C. 100D. 150答案:B2. 以下哪个不是排列数的性质?()。
A. \( P(n, n) = n! \)B. \( P(n, 0) = 1 \)C. \( P(n, k) = \frac{n!}{(n-k)!} \)D. \( P(n, k) = \frac{n!}{k!} \)答案:D3. 从5个不同的元素中取出2个元素的排列数为()。
A. 10B. 20C. 15D. 25答案:B4. 组合数 \( C(n, k) \) 和排列数 \( P(n, k) \) 之间的关系是()。
A. \( C(n, k) = \frac{P(n, k)}{k!} \)B. \( P(n, k) = \frac{C(n, k)}{k!} \)C. \( C(n, k) = k \times P(n, k) \)D. \( P(n, k) = k \times C(n, k) \)答案:A5. 以下哪个是组合数的性质?()。
A. \( C(n, k) = C(n, n-k) \)B. \( C(n, k) = C(n-1, k-1) \)C. \( C(n, k) = C(n, k+1) \)D. \( C(n, k) = C(n+1, k+1) \)答案:A6. 从8个不同的元素中取出3个元素的组合数为()。
A. 56B. 54C. 48D. 35答案:A7. 以下哪个是排列数的递推关系?()。
A. \( P(n, k) = P(n-1, k) + P(n-1, k-1) \)B. \( P(n, k) = P(n-1, k) - P(n-1, k-1) \)C. \( P(n, k) = P(n-1, k) \times P(n, 1) \)D. \( P(n, k) = P(n-1, k-1) \times P(n, 1) \)答案:D8. 从7个不同的元素中取出4个元素的排列数为()。
高中数学精品试题:组合(分类和分步)

组合(分类和分步)
1.将9个1,9个2,9个3, ,9个1000共9000个数填入一个9行、1000列的表格内(每格内填入一个数),使得同一列中任何两数之差的绝对值不超过3.设这个表格中每列中各数之和(共1000个列和)的最小值为M ,试求M 的最大值。
2.空间给定()22≥n n 个点,其中任意4点不共面,它们之间连有12
+n 条线段,求证这些线段至少构成n 个三角形。
3.8个人参加一次聚会。
(1)如果其中任何5个人中都有3个人两两认识,求证:可以从中找出4个人两两认识;
(2)试问,如果其中任何6个人中都有3个人两两认识,那么是否一定可以找出4个人两两认识?
4.已知()6≥n 个人之间互通电话问候,满足:(1)每个人至多与⎥⎦
⎤⎢⎣⎡+-22n n 人互通电话;(2)任何3个人中至少有两人互通了电话。
证明:这n 个人总可以分成不相交的两组,使同组的任何两人之间都互通了电话。
5.求最小整数数n ,使得任何n 个无理数中总有3个数,其中每两个数之后仍为无理数。
6.设有12-n 个不同的数列,每个数列有n 项,每项都等于0或1.已知对于这些数列中任意3个数列,都存在正整数p ,使得这3个数列的第p 项都是1,证明存在唯一的正整数k ,使得所有12-n 个数列的第k 项都等于1.。
组合数学试题及答案

组合数学试题及答案一、选择题(每题3分,共30分)1. 在组合数学中,从n个不同元素中取出m个元素的组合数表示为:A. C(n, m)B. P(n, m)C. A(n, m)D. nCm答案:A2. 如果一个集合有10个元素,从中任取3个元素的组合数为:A. 120B. 210C. 1001D. 1000答案:B3. 组合数学中的排列数与组合数的关系是:A. P(n, m) = C(n, m) * m!B. C(n, m) = P(n, m) / m!C. P(n, m) = C(n, m) + m!D. P(n, m) = C(n, m) * n!答案:B4. 以下哪个公式用于计算组合数?A. C(n, m) = n! / (m! * (n-m)!)B. P(n, m) = n! / (n-m)!C. A(n, m) = n! / (m! * (n-m)!)D. B(n, m) = n! / (m! * (n-m)!)答案:A5. 如果一个集合有8个元素,从中任取2个元素的排列数为:A. 28B. 56C. 8!D. 7!答案:B6. 组合数学中,排列数P(n, m)的定义是:A. 从n个元素中取出m个元素的所有可能的排列方式的数量B. 从n个元素中取出m个元素的所有可能的组合方式的数量C. 从n个元素中取出m个元素的所有可能的排列方式的数量,不考虑顺序D. 从n个元素中取出m个元素的所有可能的组合方式的数量,考虑顺序答案:A7. 以下哪个公式用于计算排列数?A. P(n, m) = n! / (n-m)!B. C(n, m) = n! / (m! * (n-m)!)C. A(n, m) = n! / (m! * (n-m)!)D. B(n, m) = n! / (m! * (n-m)!)答案:A8. 如果一个集合有15个元素,从中任取5个元素的组合数为:A. 3003B. 3000C. 1365D. 15504答案:D9. 组合数学中的二项式系数表示为:A. C(n, m)B. P(n, m)C. A(n, m)D. B(n, m)答案:A10. 以下哪个公式用于计算二项式系数?A. C(n, m) = n! / (m! * (n-m)!)B. P(n, m) = n! / (n-m)!C. A(n, m) = n! / (m! * (n-m)!)D. B(n, m) = n! / (m! * (n-m)!)答案:A二、填空题(每题2分,共20分)1. 从5个不同元素中取出3个元素的组合数为 ________。
猿题库高中组合数练习题及讲解

猿题库高中组合数练习题及讲解# 高中组合数练习题及讲解组合数是高中数学中的一个重要概念,它在概率论、排列组合等领域有着广泛的应用。
本文将提供一些高中组合数的练习题,并给出相应的讲解,帮助学生更好地理解和掌握这一概念。
## 练习题一:基本组合数计算题目:从10个不同的球中任选5个,求不同的选法有多少种?解答:这是一个典型的组合数问题。
组合数的计算公式为 \( C(n, k) = \frac{n!}{k!(n-k)!} \),其中 \( n \) 是总数,\( k \) 是选取的数量。
将题目中的数值代入公式,我们得到 \( C(10, 5) =\frac{10!}{5!(10-5)!} = 252 \)。
所以,不同的选法有252种。
## 练习题二:组合数在实际问题中的应用题目:一个班级有30名学生,需要选出5名学生代表班级参加比赛。
如果不考虑性别,求选出的5名学生的组合数。
解答:这个问题同样可以使用组合数公式来解决。
因为我们不考虑任何额外条件,所以直接使用 \( C(30, 5) \) 来计算。
计算结果为\( C(30, 5) = \frac{30!}{5!(30-5)!} \),计算得出的结果是142506。
因此,有142506种不同的组合方式。
## 练习题三:组合数与排列数的区别题目:从7个不同的数字中选出3个数字,分别放在三个不同的位置上,求不同的排列方式有多少种?解答:这个问题涉及到排列数的计算。
排列数的公式为 \( P(n, k)= \frac{n!}{(n-k)!} \)。
与组合数不同,排列数考虑了元素的顺序。
将题目中的数值代入公式,我们得到 \( P(7, 3) = \frac{7!}{(7-3)!} = 210 \)。
所以,不同的排列方式有210种。
## 练习题四:组合数的边界条件题目:如果从n个不同的元素中选取0个元素,求组合数。
解答:根据组合数的定义,\( C(n, 0) \) 表示从n个元素中不选取任何元素的情况。
高三数学组合与组合的运用试题答案及解析

高三数学组合与组合的运用试题答案及解析1.若从1,2,3,…,9这9个整数中同时取4个不同的数,其和为偶数,则不同的取法共有()A.60种B.63种C.65种D.66种【答案】D【解析】从1,2,3,…,9这9个整数中同时取4个不同的数,其和为偶数的取法分为三类;第一类是取四个偶数,即=5种方法;第二类是取两个奇数,两个偶数,即=60种方法;第三类是取四个奇数,即=1,故有5+60+1=66种方法.故选D.2.高三某班有两个数学课外兴趣小组,第一组有名男生,名女生,第二组有名男生,名女生.现在班主任老师要从第一组选出人,从第二组选出人,请他们在班会上和全班同学分享学习心得.(Ⅰ)求选出的人均是男生的概率;(Ⅱ)求选出的人中有男生也有女生的概率.【答案】(Ⅰ);(Ⅱ).【解析】(Ⅰ)由题意,先将从第一组选出人,从第二组选出人这一基本事件的所有可能情况都列出,可知共有30种情况,其中选出的人均是男生可知共有3种情况,故求得选出的人均是男生的概率为;(Ⅱ)在30种基本事件中找出符合人中有男生也有女生共得到25个基本事件,从而计算得选出的人中有男生也有女生的概率为.试题解析:(Ⅰ)记第一组的4人分别为;第二组的5人分别为 1分设“从第一组选出人,从第二组选出人”组成的基本事件空间为,则共有30种 4分设“选出的人均是男生”为事件,则事件A含有3个基本事件 6分,所以选出的人均是男生的概率为 8分(Ⅱ)设“选出的3个人有男生也有女生”为事件B,则事件B含有25个基本事件, 10分,所以选出的人中有男生也有女生的概率为. 12分【考点】1.随机事件的概率;2.排列组合.3.从8名女生,4名男生中,选出2名女生,1名男生组成课外小组,则不同的选取方案种数为_______________(用数字作答).【答案】【解析】.【考点】组合与组合数公式.4.某动点在平面直角坐标系第一象限的整点上运动(含正半轴上的整点),其运动规律为或。
高二数学组合与组合的运用试题答案及解析

高二数学组合与组合的运用试题答案及解析1.方程-=的解集是________.【答案】【解析】,即,∴x﹣1+2x+2=16,解得x=5.故答案为:{5}.【考点】组合及组合数公式.2.圆上有10个点,过每三个点画一个圆内接三角形,则一共可以画的三角形个数为()A.720B.360C.240D.120【答案】D【解析】圆上有10个点,故无三点共线,因此从中任取三点都能得到一个对应的三角形,因此一共可以画的三角形个数为,注意这里是组合问题,而不是排列问题.【考点】组合应用及转化思想.3.等于()A.B.C.D.【答案】D【解析】直接运用公式计算和,即可选出其答案.【考点】组合数的计算.4.某学校要从5名男生和2名女生中选出2人作为上海世博会志愿者,若用随机变量X表示选出的志愿者中女生的人数,则数学期望E(X)=________(结果用最简分数表示).【答案】【解析】X的可能取值为0,1,2,P(X=0)==,P(X=1)==,P(X=2)==,∴E(X)=×0+×1+×2=.5.设集合A={1,2,3,4},m,n∈A,则关于x,y的方程+=1表示焦点在x轴上的椭圆的个数为________.【答案】6【解析】∵m>n,∴有C42=6(个)焦点在x轴上的不同椭圆.6.从2,3,4,5,6,7,8,9这8个数中任取2个不同的数分别作为一个对数的底数和复数,则可以组成________个不同的对数值.【答案】52【解析】C85=56,又log24=log39,又log39=log24,log23=log49,log49=log23所以可以组成52个对数值.7.已知集合A={1,2,3,4},B={5,6,7},C={8,9}.现在从这三个集合中取出两个集合,再从这两个集合中各取出一个元素,组成一个含有两个元素的集合,则一共可以组成集合的个数为【答案】26【解析】由C41·C31+C31·C21+C41·C21=26.8.要从12人中选出5人参加一项活动,其中A、B、C 3人至多2人入选,有多少种不同选法?【答案】756【解析】解:法一可分三类:①A,B,C三人均不入选,有C95种选法;②A,B,C三人中选一人,有C31·C94种选法;③A,B,C三人中选二人,有C32·C93种选法.由分类计数加法原理,共有选法C95+C31·C94+C32·C93=756(种).法二先从12人中任选5人,再减去A,B,C三人均入选的情况,即共有选法C125-C92=756(种).9.某书店有11种杂志,2元1本的8种,1元1本的3种.小张用10元钱买杂志(每种至多买一本,10元钱刚好用完),则不同买法的种类是________(用数字作答).【答案】266【解析】由题知,按钱数分10元钱,可有两大类,第一类是买2本1元,4本2元的共C32C84种方法;第二类是买5本2元的书,共C85种方法.∴共有C32C84+C85=266(种).10.若C12n=C122n-3,则n=________.【答案】3或5【解析】由C12n=C122n-3,得n=2n-3或n+2n-3=12,解得n=3或n=5.11.有4个不同的球,四个不同的盒子,把球全部放入盒内(结果用数字表示).(1)共有多少种放法?(2)恰有一个盒子不放球,有多少种放法?(3)恰有一个盒内放2个球,有多少种放法?(4)恰有两个盒不放球,有多少种放法?【答案】(1)256(2)144(3)144(4)84【解析】(1)一个球一个球地放到盒子里去,每只球都可有4种独立的放法,由分步乘法计数原理,放法共有:种. 2.5分(2)为保证“恰有一个盒子不放球”,先从四个盒子中任意拿出去1个,即将4个球分成2,1,1的三组,有种分法;然后再从三个盒子中选一个放两个球,其余两个球,两个盒子,全排列即可.由分步乘法计数原理,共有放法:种. 5分(3)“恰有一个盒内放2个球”,即另外三个盒子中恰有一个空盒.因此,“恰有一个盒内放2球”与“恰有一个盒子不放球”是一回事.故也有144种放法. 7.5分(4)先从四个盒子中任意拿走两个有种,问题转化为:“4个球,两个盒子,每盒必放球,有几种放法?”从放球数目看,可分为(3,1),(2,2)两类.第一类:可从4个球中先选3个,然后放入指定的一个盒子中即可,有种放法;第二类:有种放法.因此共有种.由分步乘法计数原理得“恰有两个盒子不放球”的放法有:种. 10分【考点】排列组合点评:本题的求解按照分步计数原理可先将球分组,选择盒子,再将球排列到选定的盒子里,这种先选后排的方法是最常用的思路12.要从10名女生与5名男生中选出6名学生组成课外活动小组,则符合按性别比例分层抽样的概率为()A.B.C.D.【解析】根据题意,要完成要从10名女生与5名男生中选出6名学生组成课外活动小组,那么所有的情况是,那么则符合按性别比例分层抽样的情况积为2:1,说明是4名男生,2名女生,则其概率为,故选C.【考点】组合数的应用点评:主要是考查了组合数公式求解随机事件的概率的应用,属于基础题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
组合数学试题 共 5 页 ,第 1 页电子科技大学研究生试卷 (考试时间: 至 ,共 2 小时)课程名称 组合数学 教师 学时 40 学分 2 教学方式 讲授 考核日期 2009 年 12 月 日 成绩 考核方式: (学生填写)一、(14分) 现安排从星期一至星期五对5个项目A, B, C, D, E 进行评审,每个项目安排一天,每天安排一个项目。
但要求项目A 不安排在星期二评审,项目B 不安排在星期三和星期五评审,项目C 不安排在星期四评审,项目D 不安排在星期一评审,项目E 不安排在星期三和星期四评审。
问有多少种不同的评审安排方案? 解 原问题可模型化为一个5元有禁位的排列. 其禁区棋盘C 如下图的阴影部分。
-----------------4分 由图,可得C 的棋盘多项式为 R(C)= = 1+7x+17x 2+18x 3+8x 4+x 5 -----------------5分 所以安排方案数为 5! - 7·4! + 17·3! - 18·2! + 8-1 -----------------4分 = 25 即共有25种。
-----------------1分 二、(10分)用2种颜色对下图的小圆点着色,证明必存在两列,其着色完全相同。
证明:因每个小圆点有2种颜色可选,故每列恰有8 种着色方案, -------------5分 学号姓名学院……………………密……………封……………线……………以……………内……………答……………题……………无……………效……………………A B C D E 1 2 3 4 5组合数学试题 共 5 页 ,第 2 页现有9列,由鸽笼原理,知必有两列着色相同. -------------5分 三、(16 分)求方程⎩⎨⎧≤≤≤≤≤=+++2,62,63133214321x x x x x x x 的正整数解的个数。
解 等价于求集合S 0={3.A,4.B,1.C,∞.D}的所有6-组合构成的集合。
-----------------4分 令集合S 为{,,,}A B C D ∞⋅∞⋅∞⋅∞⋅的所有6-组合构成的集合。
-----------------2分 则有 |S|=F(4,6) = 84。
令 A 1表示S 中至少含有4个A 的元素构成的集合, A 2表示S 中至少含有5个B 的元素构成的集合, A 3表示S 中至少含有2个C 的元素构成的集合, -----------------4分 于是 10)2,4(||1==F A ,4)1,4(||2==F A ,35)4,4(||3==F A =⋂||31A A 1 0||||||3213221=⋂⋂=⋂=⋂A A A A A A A -----------------2分 由容斥原理,所求的5-组合数为 31231231i i j i i j A A A S A A A A A A =≠=-+-∑∑ -----------------3分 =84– (10+4+35)+1 = 36 -----------------1分 四、(14分)解下列递归关系 ⎩⎨⎧==-=----5,2)2(1451021a a a a a n n n n 解 对应的齐关系的特征方程 x 2-5x -14=0 -----------------3分 有根 x 1 = 7,x 2 = -2。
-----------------1分 故齐关系的通解为*n a =c 17n +c 2(-2)n -----------------1分 设特解 n a = An (-2)n ,代入原关系:An (-2)n -5A (n -1) (-2)n -1-14A (n -2) (-2)n -2 = (-2)n -----------------3分 ⇒ A = 92 ⇒ n a = 922n n )(- -----------------2分 ∴ a n = *n a + n a = c 17n +c 2(-2)n + 922n n )(- -----------------1分……………无……………效……………………学 号姓名学院…………密……………封……………线……………以……………内……………答……………题……………无……………效……………………组合数学试题 共 5 页 ,第 3 页由初值得 ⎪⎩⎪⎨⎧=-=+5942722121-c c c c ⇒ ⎪⎪⎩⎪⎪⎨⎧==8177818521c c -----------------2分 ∴ a n = 81857n +8177 (-2)n + 922n n )(- -----------------1分五、(12分)求1出现奇数次且2出现偶数次的n 位十进制数的个数。
解:设a n 是由0,1,……,9组成的满足“1出现奇数次”且“2出现偶数次”的长为n 的序列的个数, -----------------2分 则a n 的指数母函数为:f e (x ) = 422)!22!11)(!4!21)(!3!1(61088423xx x xx x x e e e e e e e x x x x x x -+-+--=⋅=+++++++ =!)610(410n x n n n n ∑-∞= -----------------4分所以 a n =)n n 610(41- ,n ≥1 -----------------3分 以0为首项的长为n 的序列有a n -1个,在上述序列中去掉以0为首项的长为n 的序列便可得到1出现奇数次且2出现偶数次的n 位十进制数的个数: -----------------2分 a n -a n -1=)--1165109(41n n ⨯-⨯ -----------------1分六、(14分)求由数字0,1,2,3,4,5,6,7组成的r 位数中,1和5都出现偶数次,2和6至少出现一次的r 位数的个数。
解:这是一个排列问题。
设满足条件的r 位数字串的个数为r a ,则序列12(,,,,)r a a a 对应的指数母函数为: -----------------3分f e (x ) = 42242)!22!11()!22!1()!4!21( +++++++x x x x x x + -----------------4分 423432)1()2(2345678422x x x x x x x x x x x e e e e e e e e e e e +-+-+-=-+=- !)232435463728(410n x n r r r r r r n r +⨯-⨯+⨯-⨯+⨯-=∑∞=组合数学试题 共 5 页 ,第 4 页所以r a =)232435463728(41r r r r r r r +⨯-⨯+⨯-⨯+⨯- -----------------3分 首位取0的r 位数字串的个数为1-r a ,故所求的r 位数的个数为r a -1-r a =-----------------2分 ⎪⎩⎪⎨⎧=>+⨯-⨯+⨯-⨯+⨯-⨯-------0r 00r )2344951661571287(411111111r r r r r r r -----------------2分;如果没有针对r=0单独结果的,只得1分七、(6分)设n a 表示一个凸n 边形被它的对角线划分成互不重叠的区域个数(没有三条对角线在该n 边形内交于一点)。
试建立n a 的递规关系(不需要求解)。
解:23 11-+⎪⎪⎭⎫ ⎝⎛-+=-n n a a n n ,n>3. 其中:13=a―――――――――――――――――过程4分,结果2分。
八、(14分)若7个人中有3对夫妇,试问从中取出6个人的夫妇均不相邻的圆排列有多少种?解:分两种情况。
情况1. 取出的6个人中恰含3对夫妇。
-----------------1分 计算如下:取全集S 为6个人的圆排列的集合。
令A i 为S 中第i 对夫妇相邻的圆排列的集合,i = 1,2,3。
有 -----------------1分 | S | = 5!=120, | A i | = 2•4!=48, i = 1,2,3;| A i ∩A j | = 4•3!=24(i j = 1,2,3;i ≠ j );| A 1∩A 2∩A 3 | = 16。
-----------------2分 由容斥原理 -----------------1分 321A A A ⋂⋂ = 120-3•48+3•24-16 =32 -----------------1分情况2. 取出的6个人中恰含2对夫妇。
-----------------1分 此时取6人的方式有6种,对取定的每一种取全集S 为6个人的圆排列的集合。
令组合数学试题 共 5 页 ,第 5 页 A i 为S 中第i 对夫妇相邻的圆排列的集合,i = 1,2。
-----------------2分有| S | = 5!=120, | A i | = 2•4!=48, i = 1,2;| A 1∩A 2 | =4•3!=24。
---------------1分 由容斥原理 -----------------1分 21A A ⋂ = 120-2•48+24 =48 -----------------1分 所以此类总数为 6•48=288 -----------------1分 最终结果为: 32 + 288=320 -----------------1分。
