宁夏银川二中2014届高三下学期第一次模拟考试_数学(文)_Word版含答案 (1)
[VIP专享]】银川一中2014届高三下学期第一次模拟考试_数学(文)_Word版含答案
![[VIP专享]】银川一中2014届高三下学期第一次模拟考试_数学(文)_Word版含答案](https://img.taocdn.com/s3/m/e0eba1fb0b1c59eef9c7b45a.png)
2
3
5
A.f(b)>f(a)>f(c) B. f(b)>f(c)>f(a) C. f(a)>f(b)>f(c) D. f(a)>f(c)>f(b)
1) B2Ak+22+12=+15+c51mc+=5m=2c111++m+12+21+++2=12=2+1+2+1+2+2+22+32k+1+2
88.8918÷.12990.÷1=4214÷3922=.0034=1÷15251371=8.535.78208÷.0232173c0*0÷1=m920.30392.2c=1÷203m=2÷1202.52=3535=42314)c*5232m40341*.31252=3.*1.153.5*03134.2*920522..104455=+21*3*50202.2.0285.4850.13*50+5c8*125*12m0.2+050.+0*014.852*0051000+0+/038.T+0÷+=55*+1011+010+91÷0145405*00010200+5+0+080+40*04+***115.103910*-%*C%6(+÷*M==5M÷5)0*3*0(31÷3110**5*+*÷414.m2371e=%7)8n08%.=s8.5=77.93cc60.mc*m4*m13,101w9.9o.k24mc-.cem5nm2csp2665m*9..03-4.50c60*5.pc3m85,9cm0.5g.i50mr0l-.p.s85p/6c50bc.0om7m.yp.cs6pc5m+;c0m..m7.ckm; 1+1k+12+1+k2234=1c+m1++4+4+2
2010-2023历年宁夏银川二中高三第一次月考文科数学卷

2010-2023历年宁夏银川二中高三第一次月考文科数学卷第1卷一.参考题库(共20题)1.用表示三个数中的最小值.设,则的最大值为 ( )A.4B.5C.6D.72.(本小题满分12分)已知; q:,若是的充分不必要条件,求实数的取值范围。
3.设为正数, 则的最小值为( )A.8B.9C.12D.154.已知,下列命题正确的是()A.B.C.D.5.设f()是R上的奇函数,且当[0,+ )时,f()=(1-),则时f()的表达式是____________;6.(本小题满分12分)设函数,已知是奇函数.(Ⅰ)求、的值;(Ⅱ)求的单调区间与极值.7.若是偶函数,且当的解集是()A.(-1,0)B.(-∞,0)∪(1,2)C.(1,2)D.(0,2)8.(本小题满分12分)建造一个容积为16立方米,深为4米的无盖长方体蓄水池,池壁的造价为每平方米100元,池底的造价为每平方米200元,问怎样设计才能使该蓄水池的总造价最低,最低造价为多少?9.则图中阴影部分表示的集合为()A BC D10.已知实数条件,则2x+y的最大值是_________;11.函数的大致图像是 ( )12.已知函数,则f[f(-1)]的值是( ) A.5B.9C.-5D.-313.函数f(x)=x3-3x+1在区间[0,3]上的最小值是()A.-1B.3C.1D.1914.函数零点的个数为()A.4B.3C.2D.115.(本小题满分10分)若不等式的解集是.(1)解不等式;(2)b为何值时,的解集为R;16.曲线在点A处的切线方程是___________;17.下列函数中在(-,0)上单调递减的是()A.=B.C.D.18.若,,则 ( )A.a>b>cB.b>a>cC.c>a>bD.b>c>a19.(本小题满分12分)设函数若,求关于的方程的解集.20.(本小题满分12分)已知函数R).(Ⅰ)若a=1,函数的图象能否总在直线的下方?说明理由;(Ⅱ)若函数在(0,2)上是增函数,求a的取值范围;(Ⅲ)设为方程的三个根,且,,, 求证:或第1卷参考答案一.参考题库1.参考答案:C2.参考答案:实数的取值范围为。
宁夏银川二中高三数学第一次月考试题 理 新人教A版

银川二中2013届髙三月考试题一理科 数学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,其中第Ⅱ卷第(22)—(24)题为选考题,其它题为必考题。
考生作答时,将答案答在答案题卡上,在本试卷上答题无效。
考试结束后,只收回答题卡和答题纸。
注意事项:1、答题前,考生务必先将自己的姓名、准考证号填写在答题卡上,认真核对条形码上的姓名、准考证号,并将条形码粘贴在答题卡的指定位置上。
2、选择题答案使用2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其它答案的标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚。
3、请按照题号在各题的答题区域(黑色钱框)内作答,超出答题区域书写无效。
4、保持卡面清洁,不折叠,不破损。
5、做选者考题时,考生按照题目要求作答,并用2B 铅笔在答题卡上把所选题目对应的题号涂黑.一、选择题(本大题共12小题,每小题5分,共60分。
在每題给出的四个选中,只有一项是符合题目要求)(1)、设全集{},5,4,3,2,1=⋃=N M U {}4,2)(=⋂N C M U ,则=N A.{}3,2,1 B. {}5,3,1 C. {}5,4,1 D. {}4,3,2 (2)、若)12(log 1)(21+=x x f ,则)(x f 的定义域为A. )0,21(-B. ),21(∝+-C. ),0()0,21(∝+⋃-D. )2,21(- (3) 、设集合{}02|>-∈=x R x A ,{}0|<∈=x R x B ,{}0)2(|>-∈=x x R x C ,则""B A x ⋃∈是""C x ∈的A.充分而不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件(4) 、设ab是向量,命题“若,-==”的逆命题是A.若,-≠≠B.若,-=≠C.≠,则b a -≠D.=,b a -= (5) 、⎰+1)2(dx x e x 等于A.1B.e-1C.eD.e+1 (6) 、已知命题,:R x p ∈∃使;25sin =x 命题R x q ∈∀:,都有012>++x x 。
宁夏银川一中2014届高三4月模拟考试数学(文)试题 扫描版含答案

数学(文科)答案一、选择题:A 卷答案:1-5 CBBAC 6-10 CCBDB 11-12AD B 卷答案:1-5 DBBAD 6-10 DDBCB 11-12AC 二、填空题:13.1(0,)16-14. 015.14π16. 三、解答题:(解答题按步骤给分,本答案只给出一或两种答案,学生除标准答案的其他解法,参照标准酌情设定,且只给整数分)17解:(Ⅰ)设等比数列{}n a 的公比为q ,由已知得21251232a q a q ìï=ïíï=ïî,,……………2分又∵10a >,0q >,解得112a q ì=ïïíï=ïî,,………………3分∴12n n a -=;…………………5分(Ⅱ)由2n S n =得,()211n S n -=-,∴当2n …时,121n n n b S S n -=-=-,………………7分当1n =时,11b =符合上式,∴21n b n =-,(n Î*N )……………8分,∴()1212n n na b n -?- ,()12113252212n n T n -=+??+- L ,()()2312123252232212n nn T n n -=???+-?- L ,………………10分两式相减得 ()()()21122222122323n nnn T n n --=++++--?--?L ,∴()2323n n T n =-+.……………………12分18.证明:(Ⅰ)由题意得:1A B ⊥面ABC ,∴1A B AC ⊥, ------2分又AB AC ⊥,1AB A B B = ∴AC ⊥面1AB B , ------3分∵AC ⊂面1A AC , ∴平面1A AC ⊥平面1AB B ; ------5分(Ⅱ)在三棱锥ABC P -中,因为AB AC ⊥, 所以底面ABC 是等腰直角三角形,又因为点P 到底面的距离B A h 1==2,所以34213131=⋅⋅⋅=⋅=∆-h AB AC h S V ABC ABC P . ------6分由(Ⅰ)可知AC ⊥面1AB B ,因为点P 在11B C 的中点,所以点P 到平面B B AA11距离2h 等于点1C 到平面B B AA 11的距离的一半,即12=h .------8分341223131312121111=⋅⋅⋅=⋅⋅=⋅=-h B A AB h S V B B AA B B AA P 四边形, ------10分所以三棱锥ABC P - 与四棱锥111A B AAP -的体积之比为1:1. ------12分 19. 解:(Ⅰ)东城区的平均分较高. (结论正确即给分)……………………5分 (Ⅱ)从两个区域各选一个优秀厂家,则所有的基本事件共15种,………………7分满足得分差距不超过5的事件(88,85)(88,85)(89,85)(89,94)(89,94)(93,94)(93,94)(94,,94)(94,,94)共9种.……………10分 所以满足条件的概率为35.………………12分 20.解: (Ⅰ)依题意23==a c e , 过焦点F与长轴垂直的直线x=c与椭圆12222=+by a x联立解答弦长为a b 22=1,……………2分所以椭圆的方程1422=+y x .………………4分(Ⅱ)设P(1,t)3210t t k PA =+-=,直线)2(3:+=x t y l PA ,联立得:22(2),3 1.4t y x x y ⎧=+⎪⎪⎨⎪+=⎪⎩即()0361616942222=-+++t x t x t,可知2216362,49M t x t --=+所以2218849M t x t -=+,则222188,4912.49M M t x t t y t ⎧-=⎪⎪+⎨⎪=⎪+⎩……………………6分同理得到22282,414.41N N t x t t y t ⎧-=⎪⎪+⎨⎪=⎪+⎩………………8分由椭圆的对称性可知这样的定点在x 轴, 不妨设这个定点为Q()0,m ,………………10-分又mt t t t k MQ-+-+=948189412222 , m t t t t k NQ-+-+=1428144222, NQMQ k k =,()28326240m t m --+=,4m =.……………12分21.解:(Ⅰ)若0a =,()ln 1f x x x x =-+,'()ln f x x ='(0,1),()0,()x f x f x ∈<为减函数,'(1,),()0,()x f x f x ∈+∞>为增函数 (4)分(Ⅱ)ln (1)(1)0,x x x ax a ---+<在()1,+∞恒成立.01若0a =, ()ln 1f x x x x =-+,'()ln f x x =,'(1,),()0,()x f x f x ∈+∞>∴为增函数.()(1)0f x f ∴>=,即()0f x <不成立;0a ∴=不成立.……………………6分021x > ,(1)(1)ln 0,x ax a x x --+-<在()1,+∞恒成立, 不妨设(1)(1)()ln ,x ax a h x x x --+=-,()1,x ∈+∞()2'221(1)1()x ax a ax x a h x x x -+---+=-=-,()1,x ∈+∞………………8分'121()0,1,ah x x x a -===,若0a <,则211ax a -=<,1x >,'()0h x >,()h x 为增函数,()h x >(1)0h =(不合题意);若102a <<,1(1,)ax a -∈,'()0h x >,()h x 为增函数,()h x >(1)0h =(不合题意);若12a ≥,(1,)x ∈+∞,'()0h x <,()h x 为减函数,()h x <(1)0h =(符合题意).……………11分综上所述若1x >时,()0f x <恒成立,则12a ≥.………………12分22.解:(Ⅰ)连接AB ,在EA 的延长线上取点F ,如图①所示. ∵AE 是⊙O 1的切线,切点为A , ∴∠F AC =∠ABC,.……………1分 ∵∠F AC =∠DAE ,∴∠ABC =∠DAE ,∵∠ABC 是⊙O 2内接四边形ABED 的外角, ∴∠ABC =∠A DE ,……………2分 ∴∠DAE =∠A DE .………………3分 ∴EA =ED ,∵EC EB EA ∙=2, ∴EC EB ED∙=2.………………5分(Ⅱ)当点D 与点A 重合时,直线CA 与⊙O 2只有一个公共点, 所以直线CA 与⊙O 2相切.……………6分 如图②所示,由弦切角定理知:︒⨯=∠=∠∠=∠∠=∠∠=∠18021ABE ABC MAE PAC ABE MAE ABC PAC 因又∴AC 与AE 分别为⊙O 1和⊙O 2的直径.…………8分 ∴由切割线定理知:EA 2=BE ·CE ,而CB =2,BE =6,CE=8 ∴EA 2=6×8=48,AE =34.故⊙O 2的直径为34.………………10分 23.解: (Ⅰ)θρcos = ,…………………2分.…………………4分(Ⅱ)设P (ααsin 2,cos 2),)0,21(2C2PC ===…………………6分1cos ,2α∴=,2min2PC =,…………………8分min PQ =……………………10分 24.解:(Ⅰ)当a=1时,()21f x x x x=-+-≥图(2)Eϑρρcos 2=41212222=+⎪⎭⎫ ⎝⎛-=+y x x y x2x ≥当时,解得3x ≥;当21<<x 时,解得1≤x ,∴无解1x ≤当时,解得1x ≤;……………………………3分综上可得到解集}31{≥≤x x x 或.……………………5分(Ⅱ)依题意, ,()3x f x ∀∈≥R 对都有,则()()3222)(≥-=---≥-+-=a a ax ax a ax ax x f ,……………8分232351(a a a a -≥-≤-∴≥≤-或或舍)5a ∴≥…………………10分。
银川一中2013-2014学年高三第一次月考文科数学试卷(有答案)AKwnAH
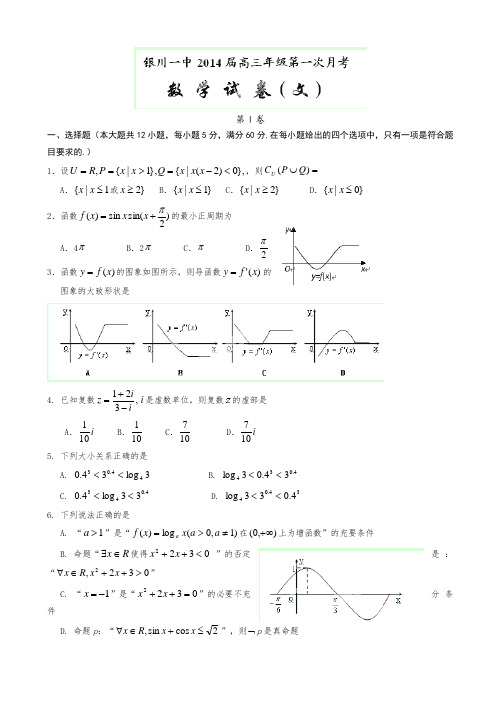
第Ⅰ卷一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.设},0)2(|{},1|{,<-=>==x x x Q x x P R U ,则=⋃)(Q P C UA .1|{≤x x 或}2≥xB .}1|{≤x xC .}2|{≥x xD .}0|{≤x x 2.函数)2sin(sin )(π+=x x x f 的最小正周期为A .4πB .2πC .πD .2π 3.函数)(x f y =的图象如图所示,则导函数)('x f y =的 图象的大致形状是4. 已知复数,321iiz -+=i 是虚数单位,则复数的虚部是 A .i 101 B .101 C .107D .i 1075. 下列大小关系正确的是 A. 3log 34.044.03<< B. 4.03434.03log <<C. 4.04333log 4.0<< D. 34.044.033log <<6. 下列说法正确的是 A. “1>a ”是“)1,0(log )(≠>=a a x x f a 在),0(+∞上为增函数”的充要条件 B. 命题“R x ∈∃使得0322<++x x ”的否定是:“032,2>++∈∀x x R x ”C. “1-=x ”是“0322=++x x ”的必要不充分条件D. 命题p :“2cos sin ,≤+∈∀x x R x ”,则⌝p 是真命题7. 函数)2||,0)(sin()(πϕωϕω<>+=x x f 的部分图像如图所示,如果)3,6(,21ππ-∈x x ,且)()(21x f x f =, 则=+)(21x x f A .21B .22C .23D .18. 已知),0(πα∈,且,21cos sin =+αα则α2cos 的值为A .47±B .47C .47-D .43- 9. 函数ax x x f +=ln )(存在与直线02=-y x 平行的切线,则实数a 的取值范围是A. ]2,(-∞B. )2,(-∞C. ),2(+∞D. ),0(+∞ 10. 已知函数)2cos()(ϕ+=x x f 满足)1()(f x f ≤对R x ∈恒成立,则A. 函数)1(+x f 一定是偶函数B.函数)1(-x f 一定是偶函数C. 函数)1(+x f 一定是奇函数D.函数)1(-x f 一定是奇函数11. 已知函数),1,0(,,ln )(21ex x x x f ∈=且21x x <则下列结论正确的是 A .0)]()()[(2121<--x f x f x x B .2)()()2(2121x f x f x x f +<+C .)()(1221x f x x f x >D .)()(1122x f x x f x >12. 已知函数)(x f 满足)()1(x f x f -=+,且)(x f 是偶函数,当]1,0[∈x 时, 2)(x x f =,若在区间[-1,3]内,函数k kx x f x g --=)()(有4个零点,则实数的取值范围是 A .)31,41[B .)21,0(C .]41,0(D .)21,31(第Ⅱ卷本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须做答.第22题~第24题为选考题,考生根据要求做答. 二、填空题:本大题共4小题,每小题5分.13. 已知函数x a x f 2log )(-=的图象经过点A (1,1),则不等式1)(>x f 的解集为______.14. 已知α为钝角,且53)2cos(-=+απ,则 。
2025届银川第二中学高三第一次模拟考试数学试卷含解析

2025届银川第二中学高三第一次模拟考试数学试卷注意事项:1.答卷前,考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。
用2B 铅笔将试卷类型(B )填涂在答题卡相应位置上。
将条形码粘贴在答题卡右上角"条形码粘贴处"。
2.作答选择题时,选出每小题答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。
答案不能答在试题卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。
不按以上要求作答无效。
4.考生必须保证答题卡的整洁。
考试结束后,请将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.第24届冬奥会将于2022年2月4日至2月20日在北京市和张家口市举行,为了解奥运会会旗中五环所占面积与单独五个环面积之和的比值P ,某学生做如图所示的模拟实验:通过计算机模拟在长为10,宽为6的长方形奥运会旗内随机取N 个点,经统计落入五环内部及其边界上的点数为n 个,已知圆环半径为1,则比值P 的近似值为( )A .8Nnπ B .12nNπ C .8nNπ D .12Nnπ2.已知向量()()1,2,2,2a b λ==-,且a b ⊥,则λ等于( ) A .4B .3C .2D .13.德国数学家莱布尼兹(1646年-1716年)于1674年得到了第一个关于π的级数展开式,该公式于明朝初年传入我国.在我国科技水平业已落后的情况下,我国数学家、天文学家明安图(1692年-1765年)为提高我国的数学研究水平,从乾隆初年(1736年)开始,历时近30年,证明了包括这个公式在内的三个公式,同时求得了展开三角函数和反三角函数的6个新级数公式,著有《割圆密率捷法》一书,为我国用级数计算π开创了先河.如图所示的程序框图可以用莱布尼兹“关于π的级数展开式”计算π的近似值(其中P 表示π的近似值),若输入10n =,则输出的结果是( )A .11114(1)35717P =-+-+⋅⋅⋅+B .11114(1)35719P =-+-+⋅⋅⋅- C .11114(1)35721P =-+-+⋅⋅⋅+D .11114(1)35721P =-+-+⋅⋅⋅-4.某圆柱的高为2,底面周长为16,其三视图如图所示,圆柱表面上的点M 在正视图上的对应点为A ,圆柱表面上的点N 在左视图上的对应点为B ,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为( )A .17B .25C .3D .25.已知函数()1ln 11xf x x x+=++-且()()12f a f a ++>,则实数a 的取值范围是( ) A .11,2⎛⎫--⎪⎝⎭B .1,02⎛⎫-⎪⎝⎭C .10,2⎛⎫ ⎪⎝⎭D .1,12⎛⎫ ⎪⎝⎭6.已知复数z 满足()125z i ⋅+=(i 为虚数单位),则在复平面内复数z 对应的点位于( ) A .第一象限B .第二象限C .第三象限D .第四象限7.已知复数z 满足(1)43z i i +=-,其中i 是虚数单位,则复数z 在复平面中对应的点到原点的距离为( )A 5B .522C .52D .548.将函数()cos f x x =的图象先向右平移56π个单位长度,在把所得函数图象的横坐标变为原来的1ω(0)>ω倍,纵坐标不变,得到函数()g x 的图象,若函数()g x 在3(,)22ππ上没有零点,则ω的取值范围是( )A.228(0,][,]939B.2(0,]9C.28(0,][,1]99D.(0,1]9.函数1()ln1f xx x=--的图象大致是( )A.B.C.D.10.根据党中央关于“精准”脱贫的要求,我市某农业经济部门派四位专家对三个县区进行调研,每个县区至少派一位专家,则甲,乙两位专家派遣至同一县区的概率为()A.16B.14C.13D.1211.洛书,古称龟书,是阴阳五行术数之源,在古代传说中有神龟出于洛水,其甲壳上心有此图象,结构是戴九履一,左三右七,二四为肩,六八为足,以五居中,五方白圈皆阳数,四角黑点为阴数.如图,若从四个阴数和五个阳数中分别随机选取1个数,则其和等于11的概率是().A.15B.25C.310D.1412.圆柱被一平面截去一部分所得几何体的三视图如图所示,则该几何体的体积为()A .12πB .32π C .2π D .3π二、填空题:本题共4小题,每小题5分,共20分。
宁夏银川市第一中学2014高三下第一次模拟考试数学(理)试卷
绝密★启用前2014年普通高等学校招生全国统一考试数学(理)(银川一中第一次模拟考试)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,其中第Ⅱ卷第22~24题为选考题,其它题为必考题。
考生作答时,将答案答在答题卡上,在本试卷上答题无效。
考试结束后,将本试卷和答题卡一并交回。
注意事项:1.答题前,考生务必先将自己的姓名、准考证号填写在答题卡上,认真核对条形码上的姓名、准考证号,并将条形码粘贴在答题卡的指定位置上。
2.选择题答案使用2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案的标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚。
3.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效。
4.保持卡面清洁,不折叠,不破损。
5.做选考题时,考生按照题目要求作答,并用2B 铅笔在答题卡上把所选题目对应的题号涂黑。
第I 卷一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.设集合M={x|1242x ≤≤},N={x|x-k>0},若M∩N=φ,则k 的取值范围为 A. [)2,+∞ B.(2,+∞) C.(-∞,-1) D.(],1-∞- 2.复数()21i 1i+-等于A .-1-iB .1+iC .1-iD .-1+i3.下列说法正确的是A .命题“R x ∈∃使得0322<++x x ”的否定是:“032,2>++∈∀x x R x ” B .a ∈R,“1a<1”是“a>1”的必要不充分条件 C .“p q ∧为真命题”是“q p ∨为真命题”的必要不充分条件理科数学试卷 第1页(共6页)D .命题p :“2cos sin ,≤+∈∀x x R x ”,则⌝p 是真命题4.等差数列{}n a 中,564a a +=,则10122log (222)aaa⋅⋅⋅⋅= A .10B .20C .40D .2+log 255.如图,长方形的四个顶点为)2,0(),2,4(),0,4(),0,0(C B A O ,曲线x y =经过点B .现将一质点随机投入长方形OABC 中,则质点落在图中阴影区域的概率是 A .125 B .21C .32 D .43 6.要从10名女生和5名男生中选出6名学生组成课外兴趣 小组学习,则按分层抽样组成此课外兴趣小组的概率为A .42105615A A C ⋅B .615615C AC .33105615C C C ⋅D .42105615C C C ⋅ 7.执行如图的程序框图,那么输出S 的值是 A .2 B .21C .-1D .18.已知y x z c y x y x x y x +=⎪⎩⎪⎨⎧≥++-≤+≥302,42,且目标函数满足的最小值是5,则z 的最大值是A .10B .12C .14D .159.若c b a ,,均为单位向量,b a ∙21-=,b y a x c +=,),(R y x ∈,则y x +的最大值是 A . 2B. CD. 110.将函数f (x )=3sin (4x +6π)图象上所有点的横坐标伸长到原来的2倍,再向右平移6π个单位长度,得到函数y =g (x )的图象.则y =g (x )图象的一条对称轴是 A .x =12π B .x =6πC .x =3πD .x =23π 11.某四面体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此四面体的外接球的体积为A .34πB .π3C .πD .π23 12.在直线2-=y 上任取一点Q ,过Q 作抛物线y x 42=的切线,切点分别为A 、B ,则直线AB 恒过的点是A .(0,1)B .(0,2)C .(2,0)D .(1,0)第Ⅱ卷本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须做答.第22题~第24题为选考题,考生根据要求做答.二、填空题:本大题共4小题,每小题5分.13.若二项式22nx x ⎛⎫+ ⎪⎝⎭的展开式共7项,则该展开式中的常数项为___________.14.在△ABC 中,AB,AC =1,B =30°,则△ABC 的面积等于 .15.设双曲线22143x y -=的左、右焦点分别为12,F F ,过1F 的直线l 交双曲线左支于,A B 两点,则22BF AF +的最小值为____________.16.已知数列{}n a 的前n 项和为n S ,11a =,12(2)n n a S n -=≥,则n a = .三、解答题:解答应写出文字说明.证明过程或演算步骤17.(本题满分12分)设函数2()sin(π)2cos 1(0).62f x x x ωωω=--+>直线y =()y f x =图象相邻两交点的距离为π.(Ⅰ)求ω的值;(Ⅱ)在△ABC 中,角A 、B 、C 所对的边分别是a 、b 、c ,若点(,02B)是函数()y f x =图象的一个对称中心,且3b =,求△ABC 周长的取值范围.18.(本题满分12分)如图,在梯形ABCD 中,AB ∥CD ,a CB DC AD ===, 60=∠ABC ,平面⊥ACFE 平面ABCD ,四边形ACFE 是矩形,a AE =,点M 在线段EF 上.(1)求证:⊥BC 平面ACFE ;(2)当EM 为何值时,AM ∥平面BDF ?证明你的结论; (3)求二面角D EF B --的平面角的余弦值.MFECD BA理科数学试卷 第3页(共6页)19.(本小题满分12分)为迎接2012年伦敦奥运会,在著名的海滨城市青岛举行了一场奥运选拔赛,其中甲、乙两名运动员为争取最后一个参赛名额进行的7轮比赛的得分如茎叶图所示:(1)若从甲运动员的每轮比赛的得分中任选3个不低于80且不高于90的得分,求甲的三个得分与其每轮比赛的平均得分的差的绝对值都不超过2的概率;(2)若分别从甲、乙两名运动员的每轮比赛不低于80且不高于90的得分中任选1个,求甲、乙两名运动员得分之差的绝对值ξ的分布列与期望.20. (本小题满分12分)已知函数()f x 是奇函数,()f x 的定义域为(,)-∞+∞.当0x <时,()f x ln()ex x-=.(e 为自然对数的底数).(1)若函数()f x 在区间1(,)(0)3a a a +>上存在极值点,求实数a 的取值范围; (2)如果当x ≥1时,不等式()1kf x x ≥+恒成立,求实数k 的取值范围.21.(本小题满分12分)如图,椭圆)0(12222>>=+b a by a x 的一个焦点是F (1,0),O 为坐标原点.(1)已知椭圆短轴的两个三等分点与一个焦点构成 、正三角形,求椭圆的方程;(2)设过点F 的直线l 交椭圆于A 、B 两点.若直线l 绕点F 任意转动,则有|OA |2+|OB |2<|AB |2,求a 的取值范围.8甲乙7 95 4 5 4 18 4 4 6 7 4 191请考生在第22、23、24三题中任选一题做答,如果多做,则按所做的第一题记分.答时用2B 铅笔在答题卡上把所选题目的题号涂黑.22.(本小题满分10分)选修4—1: 几何证明选讲.如图,圆1O 与圆2O 相交于A 、B 两点,AB 是圆2O 的直径,过A 点作圆1O 的切线交圆2O 于点E ,并与BO 1的延长线交于点P ,PB 分别与 圆1O 、圆2O 交于C ,D 两点。
宁夏银川市唐徕回民中学2014届高三数学第一次模拟考试试题 理 新人教A版
高三第一次模拟考试数学〔理〕试题命题人:唐希明、沈学斌 审核人:高三备课组一、选择题〔每一小题5分,共60分〕1.集合A={1,2},B={1,2,3},P={b a x x ⋅=|,∈a A ,∈b B},如此集合P 的元素的个数为 A .3B. 4C. 5D. 62. 假设i 是虚数单位,如此复数i i+-12的实部与虚部之积为 A.43B. 43-C. 43iD. 43-i 3. 假设α,β表示两个不同的平面,b a ,表示两条不同的直线,如此α//a 的一个充分条件是A .βα⊥,β⊥a B. α∩β=b ,b a // C. b a //,α//bD. α//β,β⊂a4. 设双曲线()019222>=-a y ax 的渐近线方程为023=±y x ,如此⎰a dx x 1)1(的值为 A .ln2 B. 0 C. ln3 D. 15. 假设cos231=θ,如此sin 4θ+cos 4θ的值为 A .1813B. 1811C. 95D. 16. 某同学有一样的名信片2张,同样的小饰品3件,从中取出4样送给4位朋友,每位朋友1样,如此不同的赠送方法共有 A .4种B. 10种C. 18种D. 20种7. 执行如下列图的程序框图,假设输入如下四个函数 ①()x x f sin =②()x x f cos = ③()||x e x f =④()|ln |x x f =如此输出的函数的个数为 A . 0个B. 1个C. 2个D. 3个8. 假设0||2||≠=a b ,a c ⊥,b a c +=,如此a 与b 的夹角为 A .300B. 600C. 900D. 1209. 某几何体的正视图与侧视图都是边长为1的正方形,且体积为21, 如此该几何体的俯视图可以是10. 点P 是函数()()0sin 2>+=ωϕωx y 的图像的最高点,M ,N 是与点P 相邻的且该图像与x 轴的两个交点,且N 〔3,0〕,假设0=⋅PN PM ,如此ϕ的值为A .8πB.4π C. 4D. 811. 经过抛物线C 的焦点F 作直线l 与抛物线C 交于A ,B 两点,如果A ,B 在抛物线C 的准线上的射影分别是A 1,B 1,那么∠A 1FB 1为 A .2π B.4π C.6πD. π3212. 函数()()0|11|>-=x xx f ,当b a <<0,假设()()b f a f =时,如此有 A. 1>abB. 1≥abC. 21≥abD. 21>ab 二、填空题〔每一小题5分,共20分〕 13.在△ABC 中,b =1,c =3,∠C=32π,如此①a =________;②∠B=________. 14. 变量y x ,满足条件,假设目标函数y ax z +=〔其中0>a 〕仅在点〔4,2〕处取得最大值,如此a 的取值范围是__________.15. M 〔00,y x 〕是抛物线()022>=p px y 上的一点,过点M 的切线方程的斜率可通过以下方法求解:在px y 22=两边同时对x 求导,得ypy p y y ='⇒='⋅22,如此过M 点的切线的斜率为0y p k =,类比上述方法求出双曲线1222=-y x 在点Q 〔2,2〕处的切线方程为___________________.16. ()()0|cos ≥=x x x f |,)(x g y =是经过原点且与()x f 图像恰有两个交点的直线,这两个交点的横坐标分别为α,β〔0<α<β〕,那么如下结论中正确..的有______. ①()()0≤-x g x f 的解集为[α,)∞+②()()x g x f y -=在〔0,α〕上单调递减 ③0cos cos =+αββα④当π=x 时,()()x g x f y -=取得最小值三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤. 17.〔本大题总分为12分〕等比数列{}n a 中,1a ,2a ,3a 分别是下表一、二、三行中的某一个数,且1a ,2a ,3a 中任何两个数不在下表同一列,且1a <2a <3a ,〔1〕求数列{}n a 的通项公式;〔2〕假设数列{}n b 满足n n n a a b ln +=,求数列{}n b 前n 项和n S .18.〔本大题总分为12分〕唐徕回中随机抽取局部新生调查其上学所需时间〔单位:分钟〕,并将所得数据绘制成频率分布直方图,其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100], 〔1〕求直方图中的x 的值;〔2〕如果上学所需时间不少于1小时的学生可申请住校,请估计学校600名新生中有多少名学生可以申请住校;〔3〕从学校的新生中任选4名学生,这4名学生中上学所需时间少于20分钟的人数记为X ,求X 分布列和数学期望. 〔以直方图中新生上学所需时间少于20分钟的频率作为每名学生上学所需时间少于20分钟的概率.〕19.〔本大题总分为12分〕如图,直三棱柱ABC —A 1B 1C 1中,D ,E 分别是AB ,BB 1的中点,AA 1=AC=CB=AB 22, 〔1〕证明:BC 1//平面A 1CD ; 〔2〕求二面角D —A 1C —E 的正弦值.20.〔本大题总分为12分〕椭圆)0(12222>>=+b a b y a x ,过点A 〔-a ,0〕,B 〔0,b 〕的直线的倾斜角为6π,原点到该直线的距离为22, 〔1〕求椭圆的方程;〔2〕是否存在实数k ,直线2+=kx y 交椭圆于Q ,P 两点,以PQ 为直径的圆过点D 〔-1,0〕,假设存在,求出k 的值;假设不存在,请说明理由.21.〔本大题总分为12分〕设函数()()0≠⋅=k ex x f kx〔1〕求曲线()x f y =在点〔0,()0f 〕处的切线方程; 〔2〕求函数()x f 的单调区间;〔3〕假设函数()x f 在区间〔-1,1〕内单调递增,求k 的取值范围.请考生在22,23,24题中任选一题作答,如果多做,如此按所做的第一题记分。
宁夏银川二中高考数学一模试卷 文(含解析)
2015年宁夏银川二中高考数学一模试卷(文科)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题所给出的四个选项中,只有一项是符合题目要求的)1.设集合M={x|﹣2<x<3},P={x|x≤﹣1},那么“x∈M或x∈P”是“x∈M∩P”的() A.必要不充分条件 B.充分不必要条件C.充要条件 D.既不充分也不必要条件2.设a,b为实数,若复数,则()A. B. a=3,b=1 C. D. a=1,b=33.已知α是第二象限角,P(x,)为其终边上一点,且cosα=x,则x=()A. B.± C.﹣ D.﹣4.如图,若执行该程序,输出结果为48,则输入k值为()A. 4 B. 5 C. 6 D. 75.已知函数和g(x)=alnx,曲线y=f(x)和y=g(x)有交点且在交点处有相同的切线,则a=()A. B. C. D. e6.如图所示,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是等腰梯形,等腰直角三角形和长方形,则该几何体表面积为()A. 14 B. 14+2 C. 8+8 D. 167.设函数f(x)=sin(ωx+φ)+cos(ωx+φ)的最小正周期为π,且f(﹣x)=f(x),则()A. f(x)在单调递减 B. f(x)在(,)单调递减C. f(x)在(0,)单调递增 D. f(x)在(,)单调递增8.已知集合表示的平面区域为Ω,若在区域Ω内任取一点P(x,y),则点P的坐标满足不等式x2+y2≤2的概率为()A. B. C. D.9.已知直线x+y﹣k=0(k>0)与圆x2+y2=4交于不同的两点A、B,O是坐标原点,若,则实数k=()A. 1 B. C. D. 210.在△ABC中,角A、B、C所对的边分别为a,b,c,若,且,则下列关系一定不成立的是()A. a=c B. b=c C. 2a=c D. a2+b2=c211.已知抛物线的方程为y2=4x,过其焦点F的直线l与抛物线交于A,B两点,若S△AOF=3S △BOF(O为坐标原点),则|AB|=()A. B. C. D. 412.已知函数f(x)=x2﹣2x+1+alnx有两个极值点x1,x2,且x1<x2,则()A. f(x2)<﹣ B. f(x2)< C. f(x2)> D. f(x2)>二、填空题:本大题共4小题,每小题5分,共20分,把答案填写在答题卡中横线上.13.某班级有50名学生,现要采取系统抽样的方法在这50名学生中抽出10名学生,将这50名学生随机编号1~50号,并分组,第一组1~5号,第二组6~10号,…,第十组46~50号,若在第三组中抽得号码为12的学生,则在第八组中抽得号码为的学生.14.在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2,AD=1,梯形所在平面内一点P满足,则= .15.设是奇函数,则使f(x)<0的x的取值范围是16.已知四面体P﹣ABC的外接球的球心O在AB上,且PO⊥平面ABC,2AC=AB,若四面体P﹣ABC的体积为,则该球的体积为.三、解答题(本大题共6个小题,共70分.要求解答应写出文字说明,证明过程或演算步骤)17.已知数列{a n}中,a1=1,且点(a n,a n+1)在函数y=x+1的图象上(n∈N*),数列{b n}是各项都为正数的等比数列,且b2=2,b4=8.(Ⅰ)求数列{a n},{b n}的通项公式;(Ⅱ)若数列{c n}满足c n=(﹣1)n a n+b n,记数列{c n}的前n项和为T n,求T100的值.18.从某企业生产的某种产品中抽取20件,测量这些产品的一项质量指标值,由测量得到如图所示的频率分布直方图1,从左到右各组的频数依次记为A1、A2、A3、A4,A5.(1)求图1中a的值;(2)图2是统计图1中各组频数的一个算法流程图,求输出的结果S;(3)从质量指标值分布在[80,90)、[110,120)的产品中随机抽取2件产品,求所抽取两件产品的质量指标之差大于10的概率.19.如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,M是PD的中点,且AB=2,∠BAD=60°.(1)求证:OM∥平面PAB;(2)求证:平面PBD⊥平面PAC;(3)当三棱锥M﹣BCD的体积等于时,求PB的长.20.已知椭圆C:+=1(a>b>0)过点(2,0),且椭圆C的离心率为.(Ⅰ)求椭圆C的方程;(Ⅱ)若动点P在直线x=﹣1上,过P作直线交椭圆C于M,N两点,且P为线段MN中点,再过P:作直线l⊥MN.求直线l是否恒过定点,如果是则求出该定点的坐标,不是请说明理由.21.已知函数f(x)=+lnx(a∈R)(Ⅰ)当a=1时,求f(x)的最小值;(Ⅱ)若f(x)在(0,e]上的最小值为2,求实数a的值;(Ⅲ)当a=﹣1时,试判断函数g(x)=f(x)+在其定义域内的零点的个数.22,23,24题中任选一题作答,如果多做,则按所做的第一题记分.作答时用2B铅笔在答题纸卡上把所选的题目对应的标号涂黑.选修4-1:几何证明选讲22.如图,直线PQ与⊙O相切于点A,AB是⊙O的弦,∠PAB的平分线AC交⊙O于点C,连结CB,并延长与直线PQ相交于点Q,若AQ=6,AC=5.(Ⅰ)求证:QC2﹣QA2=BC•QC;(Ⅱ)求弦AB的长.选修4-4:坐标系与参数方程23.极坐标系与直角坐标系xoy有相同的长度单位,以原点为极点,以x铀正半轴为极轴,已知曲线C1的极坐标方程为ρ=4cosθ,直线l的参数方程为(t为参数),射线与曲线C1交于(不包括极点O)三点A、B、C.(Ⅰ)求曲线C1化成直角坐标方程及直线l的普通方程,并求曲线C1上的点到直线l的最小值.(Ⅱ)求证:.选修4-5:不等式选讲24.(1)设函数f(x)=|x﹣|+|x﹣a|,x∈R,若关于x的不等式f(x)≥a在R上恒成立,求实数a的最大值;(2)已知正数x,y,z满足x+2y+3z=1,求++的最小值.2015年宁夏银川二中高考数学一模试卷(文科)参考答案与试题解析一、选择题(本大题共12个小题,每小题5分,共60分,在每小题所给出的四个选项中,只有一项是符合题目要求的)1.设集合M={x|﹣2<x<3},P={x|x≤﹣1},那么“x∈M或x∈P”是“x∈M∩P”的() A.必要不充分条件 B.充分不必要条件C.充要条件 D.既不充分也不必要条件考点:必要条件、充分条件与充要条件的判断.专题:简易逻辑.分析:根据充分条件和必要条件的定义结合集合的基本运算进行判断即可.解答:解:∵M={x|﹣2<x<3},P={x|x≤﹣1},∴M∪P={x|x<3},M∩P={x|﹣2<x≤﹣1},则M∩P⊊M∪P,即“x∈M或x∈P”是“x∈M∩P”的必要不充分条件,故选:A点评:本题主要考查充分条件和必要条件判断,根据集合的交集和并集进行运算是解决本题的关键.2.设a,b为实数,若复数,则()A. B. a=3,b=1 C. D. a=1,b=3考点:复数相等的充要条件.分析:先化简,然后用复数相等的条件,列方程组求解.解答:解:由可得1+2i=(a﹣b)+(a+b)i,所以,解得,,故选A.点评:本题考查了复数相等的概念及有关运算,考查计算能力.是基础题.3.已知α是第二象限角,P(x,)为其终边上一点,且cosα=x,则x=()A. B.± C.﹣ D.﹣考点:任意角的三角函数的定义.专题:三角函数的求值.分析:根据三角函数的定义有cosα=,条件cosα=x都可以用点P的坐标来表达,借助于角的终边上的点,解关于x的方程,便可求得所求的横坐标.解答:解:∵cosα===x,∴x=0(∵α是第二象限角,舍去)或x=(舍去)或x=﹣.故选:D.点评:本题巧妙运用三角函数的定义,联立方程求出未知量,不失为一种好方法.4.如图,若执行该程序,输出结果为48,则输入k值为()A. 4 B. 5 C. 6 D. 7考点:循环结构.专题:算法和程序框图.分析:根据循环条件进行模拟运行即可.解答:解:输入k,a=2,n=1满足条件1<k,n=2,a=2×2=4,n=2满足条件2<k,n=3,a=3×4=12,n=3满足条件3<k,n=4,a=4×12=48,n=4不满足条件4<k,输出a=12,即k>3成立,而k>4不成立,即输入k的值为4,故选:A点评:本题主要考查程序框图的识别和判断,根据循环结构,进行模拟运算是解决本题的关键.5.已知函数和g(x)=alnx,曲线y=f(x)和y=g(x)有交点且在交点处有相同的切线,则a=()A. B. C. D. e考点:利用导数研究曲线上某点切线方程.专题:计算题;导数的概念及应用.分析:先求出交点,再根据切线相等,建立方程,即可求出a.解答:解:∵函数,g(x)=alnx,a∈R.∴f′(x)=,g′(x)=(x>0),由已知曲线y=f(x)与曲线y=g(x)在交点处有相同的切线,故有=alnx且=,解得a=,故选:B.点评:本题考查利用导数研究曲线上某点切线方程,考查导数的几何意义,正确求导是关键.6.如图所示,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是等腰梯形,等腰直角三角形和长方形,则该几何体表面积为()A. 14 B. 14+2 C. 8+8 D. 16考点:由三视图求面积、体积.专题:空间位置关系与距离.分析:如图所示,底面是矩形ABCD,AB=4,AD=2,EF平行底面,EF=2.DE=AE=.即可得出.解答:解:如图所示,底面是矩形ABCD,AB=4,AD=2,EF平行底面,EF=2.DE=AE=.过点E作EM⊥AB,垂足为M,则AM=1,∴EM==1.∴S梯形ABFE===3=S梯形CDEF,S△ADE=S△BCF==1,S矩形ABCD=2×4=8.∴该几何体表面积=8+2×3+2=16.故选:D.点评:本题考查了五面体的三视图、梯形、等腰直角三角形的面积计算公式,考查了计算能力,属于基础题.7.设函数f(x)=sin(ωx+φ)+cos(ωx+φ)的最小正周期为π,且f(﹣x)=f(x),则()A. f(x)在单调递减 B. f(x)在(,)单调递减C. f(x)在(0,)单调递增 D. f(x)在(,)单调递增考点:由y=Asin(ωx+φ)的部分图象确定其解析式;正弦函数的单调性.专题:三角函数的图像与性质.分析:利用辅助角公式将函数表达式进行化简,根据周期与ω的关系确定出ω的值,根据函数的偶函数性质确定出φ的值,再对各个选项进行考查筛选.解答:解:由于f(x)=sin(ωx+ϕ)+cos(ωx+ϕ)=,由于该函数的最小正周期为T=,得出ω=2,又根据f(﹣x)=f(x),得φ+=+kπ(k∈Z),以及|φ|<,得出φ=.因此,f(x)=cos2x,若x∈,则2x∈(0,π),从而f(x)在单调递减,若x∈(,),则2x∈(,),该区间不为余弦函数的单调区间,故B,C,D都错,A正确.故选A.点评:本题考查三角函数解析式的确定问题,考查辅助角公式的运用,考查三角恒等变换公式的逆用等问题,考查学生分析问题解决问题的能力和意识,考查学生的整体思想和余弦曲线的认识和把握.属于三角中的基本题型.8.已知集合表示的平面区域为Ω,若在区域Ω内任取一点P(x,y),则点P的坐标满足不等式x2+y2≤2的概率为()A. B. C. D.考点:几何概型;简单线性规划.专题:概率与统计.分析:作出不等式组对应的平面区域,求出对应的面积,结合几何概型的概率公式进行求解即可.解答:解:作出不等式组对应的平面区域如图,则对应的区域为△AOB,由,解得,即B(4,﹣4),由,解得,即A(,),直线2x+y﹣4=0与x轴的交点坐标为(2,0),则△OAB的面积S==,点P的坐标满足不等式x2+y2≤2区域面积S=,则由几何概型的概率公式得点P的坐标满足不等式x2+y2≤2的概率为=,故选:D点评:本题考查的知识点是几何概型,二元一次不等式(组)与平面区域,求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据几何概型的概率公式进行求解.9.已知直线x+y﹣k=0(k>0)与圆x2+y2=4交于不同的两点A、B,O是坐标原点,若,则实数k=()A. 1 B. C. D. 2考点:直线与圆的位置关系.专题:计算题;直线与圆.分析:利用向量关系,得出圆心到直线的距离d=||,由勾股定理,建立方程,即可求出k.解答:解:∵,∴圆心到直线的距离d=||,圆心到直线的距离d=,由勾股定理可得()2+(•)2=4,∵k>0,∴k=.故选:B.点评:本题考查直线与圆的位置关系,考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.10.在△ABC中,角A、B、C所对的边分别为a,b,c,若,且,则下列关系一定不成立的是()A. a=c B. b=c C. 2a=c D. a2+b2=c2考点:余弦定理.专题:解三角形.分析:利用余弦定理表示出cosA,将已知第一个等式代入求出cosA的值,确定出A度数,再利用正弦定理化简第二个等式,求出sinB的值,确定出B的度数,进而求出C的度数,确定出三角形ABC形状,即可做出判断.解答:解:∵b2+c2﹣a2=bc,∴cosA==,∴A=30°,由正弦定理化简b=a,得到sinB=sinA=,∴B=60°或120°,当B=60°时,C=90°,此时△ABC为直角三角形,得到a2+b2=c2,2a=c;当B=120°时,C=30°,此时△ABC为等腰三角形,得到a=c,综上,b=c不一定成立,故选:B.点评:此题考查了正弦、余弦定理,以及直角三角形与等腰三角形的性质,熟练掌握定理是解本题的关键.11.已知抛物线的方程为y2=4x,过其焦点F的直线l与抛物线交于A,B两点,若S△AOF=3S △BOF(O为坐标原点),则|AB|=()A. B. C. D. 4考点:直线与圆锥曲线的综合问题;抛物线的简单性质.专题:圆锥曲线的定义、性质与方程.分析:根据对称性可设直线的AB的倾斜角为锐角,利用S△AOF=3S△BOF,求得y A=﹣3y B,设出直线AB的方,与抛物线方程联立消去x,利用韦达定理表示出y A+y B和y A y B,进而求得利用+,求得m,最后利用斜率和A,B的坐标求得|AB|.解答:解:设直线的AB的倾斜角为锐角,∵S△AOF=3S△BOF,∴y A=﹣3y B,∴设AB的方程为x=my+1,与y2=4x联立消去x得,y2﹣4my﹣4=0,∴y A+y B=4m,y A y B=﹣4.∴+==﹣2==﹣3﹣,∴m2=,∴|AB|=•=.故选:A.点评:本题主要考查了抛物线的概念和性质,直线和抛物线的综合问题.要注意解题中出了常规的联立方程,用一元二次方程根与系数的关系表示外,还可考虑运用某些几何性质.12.已知函数f(x)=x2﹣2x+1+alnx有两个极值点x1,x2,且x1<x2,则()A. f(x2)<﹣ B. f(x2)< C. f(x2)> D. f(x2)>考点:利用导数研究函数的极值.专题:计算题;导数的概念及应用.分析:对f(x)求导数,f′(x)=0有两个不同的正实根x1,x2,由x1、x2的关系,用x2把a表示出来,求出f(x2)的表达式最小值即可.解答:解:由题意,f(x)=x2﹣2x+1+alnx的定义域为(0,+∞),∴f′(x)=2x﹣2+=;∵f(x)有两个极值点x1,x2,∴f′(x)=0有两个不同的正实根x1,x2,∵0<x1<x2,且x1+x2=1,∴<x2<1,a=2x2﹣2x22,∴f(x2)=x22﹣2x2+1+(2x2﹣2x22)lnx2.令g(t)=t2﹣2t+1+(2t﹣2t2)lnt,其中<t<1,则g′(t)=2(1﹣2t)lnt.当t∈(,1)时,g′(t)>0,∴g(t)在(,1)上是增函数.∴g(t)>g()=.故f(x2)=g(x2)>.故选:D.点评:本题考查了利用导数研究函数的单调性,研究函数的极值问题,求参数的范围问题,是一道基础题.二、填空题:本大题共4小题,每小题5分,共20分,把答案填写在答题卡中横线上.13.某班级有50名学生,现要采取系统抽样的方法在这50名学生中抽出10名学生,将这50名学生随机编号1~50号,并分组,第一组1~5号,第二组6~10号,…,第十组46~50号,若在第三组中抽得号码为12的学生,则在第八组中抽得号码为37 的学生.考点:系统抽样方法.专题:计算题;概率与统计.分析:由题设知第八组的号码数比第三组的号码数大(8﹣3)×5,由此能求出结果.解答:解:这50名学生随机编号1~50号,并分组,第一组1~5号,第二组6~10号,…,第十组46~50号,在第三组中抽得号码为12的学生,则在第八组中抽得号码为12+(8﹣3)×5=37.故答案为:37.点评:抽样选用哪一种抽样形式,要根据题目所给的总体情况来决定,若总体个数较少,可采用抽签法,若总体个数较多且个体各部分差异不大,可采用系统抽样,若总体的个体差异较大,可采用分层抽样.14.在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2,AD=1,梯形所在平面内一点P满足,则= ﹣1 .考点:平面向量数量积的运算.专题:平面向量及应用.分析:建立坐标系,得到A,B,C,D的坐标,由得到P的坐标,再由向量的数量积运算解答.解答:解:如图在坐标系中,A(0,2),B(0,0),C(2,0),D(1,2),所以=(0,2),=(2,0),由,得到=(1,1),所以=(1,﹣1)(0,1)=﹣1;故答案为:﹣1.点评:本题考查了向量数量积的坐标运算;关键是距离坐标系,利用坐标法解答本题.15.设是奇函数,则使f(x)<0的x的取值范围是(﹣1,0)考点:函数奇偶性的性质;对数的运算性质.分析:根据若f(x)是奇函数且在x=0有定义,则f(0)=0,即可解出a.再根据对数函数的单调性解不等式得到答案.解答:解:依题意,得f(0)=0,即lg(2+a)=0,所以,a=﹣1,,又f(x)<0,所以,,解得:﹣1<x<0.故答案为:(﹣1,0).点评:本题主要考查函数的奇偶性和对数不等式的解法.在解对数不等式时注意对数函数的单调性,即:底数大于1时单调递增,底数大于0小于1时单调递减.16.已知四面体P﹣ABC的外接球的球心O在AB上,且PO⊥平面ABC,2AC=AB,若四面体P﹣ABC的体积为,则该球的体积为4π.考点:球的体积和表面积.专题:空间位置关系与距离.分析:设该球的半径为R,则AB=2R,2AC=AB=×2R,故AC=R,由于AB是球的直径,所以△ABC在大圆所在平面内且有AC⊥BC,由此能求出球的体积.解答:解:设该球的半径为R,则AB=2R,2AC=AB=×2R,∴AC=R,由于AB是球的直径,所以△ABC在大圆所在平面内且有AC⊥BC,在Rt△ABC中,由勾股定理,得:BC2=AB2﹣AC2=R2,所以Rt△ABC面积S=×BC×AC=R2,又PO⊥平面ABC,且PO=R,四面体P﹣ABC的体积为,∴V P﹣ABC=×R××R2=,即R3=9,R3=3,所以:球的体积V球=×πR3=×π×3=4π.故答案为:点评:本题考查四面体的外接球的体积的求法,解题时要认真审题,仔细解答,注意合理地化空间问题为平面问题.三、解答题(本大题共6个小题,共70分.要求解答应写出文字说明,证明过程或演算步骤)17.已知数列{a n}中,a1=1,且点(a n,a n+1)在函数y=x+1的图象上(n∈N*),数列{b n}是各项都为正数的等比数列,且b2=2,b4=8.(Ⅰ)求数列{a n},{b n}的通项公式;(Ⅱ)若数列{c n}满足c n=(﹣1)n a n+b n,记数列{c n}的前n项和为T n,求T100的值.考点:数列的求和;数列递推式.专题:等差数列与等比数列.分析:(I)由于点(a n,a n+1)在函数y=x+1的图象上(n∈N*),可得a n+1=a n+1,利用等差数列的通项公式即可得出.数列{b n}为等比数列,设公比为q,由于b2=2,b4=8,可得b4=b1q3=8,b1q=2.解出即可.(II)数列{c n}满足c n=(﹣1)n a n+b n=(﹣1)n n+2n﹣1,可得T100=(﹣1+2﹣3+4+…+100)+(1+2+22+…+299),利用分组求和与等比数列的前n项和公式即可得出.解答:解:(I)∵点(a n,a n+1)在函数y=x+1的图象上(n∈N*),∴a n+1=a n+1,即a n+1﹣a n=1,∴数列{a n}是以1为首项,1为公差的等差数列.故数列{a n}的通项公式为a n=n.数列{b n}为等比数列,设公比为q,∵b2=2,b4=8,∴b4=b1q3=8,b1q=2.b n>0,∴b1=1,q=2.∴b n=2n﹣1(n∈N*).(Ⅱ)∵数列{c n}满足c n=(﹣1)n a n+b n=(﹣1)n n+2n﹣1,∴T100=(﹣1+2﹣3+4+...+100)+(1+2+22+ (299)=50+=50+2100﹣1=22100+49.点评:本题考查了“分组求和”方法、等差数列与等比数列的通项公式与前n项和公式,考查了推理能力与计算能力,属于中档题.18.从某企业生产的某种产品中抽取20件,测量这些产品的一项质量指标值,由测量得到如图所示的频率分布直方图1,从左到右各组的频数依次记为A1、A2、A3、A4,A5.(1)求图1中a的值;(2)图2是统计图1中各组频数的一个算法流程图,求输出的结果S;(3)从质量指标值分布在[80,90)、[110,120)的产品中随机抽取2件产品,求所抽取两件产品的质量指标之差大于10的概率.考点:列举法计算基本事件数及事件发生的概率;程序框图.专题:图表型;概率与统计;算法和程序框图.分析:解:(1)依题意,利用频率之和为1,直接求解a的值.(2)由频率分布直方图可求A1,A2,A3,A4,A5的值,由程序框图可得S=A2+A3+A4,代入即可求值.(3)记质量指标在[110,120)的4件产品为x1,x2,x3,x4,质量指标在[80,90)的1件产品为y1,可得从5件产品中任取2件产品的结果共10种,记“两件产品的质量指标之差大于10”为事件A,可求事件A中包含的基本事件共4种,从而可求得P(A).解答:解:(1)依题意,(2a+0.02+0.03+0.04)×10=1解得:a=0.005(2)A1=0.005×10×20=1,A2=0.040×10×20=8,A3=0.030×10×20=6,A4=0.020×10×20=4,A5=0.005×10×20=1故输出的S=A2+A3+A4=18(3)记质量指标在[110,120)的4件产品为x1,x2,x3,x4,质量指标在[80,90)的1件产品为y1,则从5件产品中任取2件产品的结果为:(x1,x2),(x1,x3),(x1,x4),(x1,y1),(x2,x3),(x2,x4),(x2,y1),(x3,x4),(x3,y1),(x4,y1)共10种,记“两件产品的质量指标之差大于10”为事件A,则事件A中包含的基本事件为:(x1,y1),(x2,y1),(x3,y1),(x4,y1)共4种所以可得:P(A)==.即从质量指标值分布在[80,90)、[110,120)的产品中随机抽取2件产品,所抽取两件产品的质量指标之差大于10的概率为点评:本题考查读频率分布直方图的能力和利用统计图获取信息的能力,利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题,属于中档题.19.如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,M是PD的中点,且AB=2,∠BAD=60°.(1)求证:OM∥平面PAB;(2)求证:平面PBD⊥平面PAC;(3)当三棱锥M﹣BCD的体积等于时,求PB的长.考点:棱柱、棱锥、棱台的体积;直线与平面平行的判定;平面与平面垂直的判定.专题:空间位置关系与距离.分析:(1)在△PBD中,由O、M分别是BD、PD的中点,利用三角形中位线定理可得:OM ∥PB,再利用线面平行的判定定理可得:OM∥平面PAB;(2)由PA⊥平面ABCD,可得PA⊥BD,由于底面ABCD是菱形,可得AC⊥BD.利用线面面面垂直的判定定理与性质定理即可证明;(3)由底面ABCD是菱形,M是PD的中点,可得V M﹣BCD===,可得V P﹣ABCD=.可得PA=.再利用勾股定理可得PB=,即可得出.解答:(1)证明:在△PBD中,∵O、M分别是BD、PD的中点,∴OM∥PB,又OM⊄平面PAB,PB⊂平面PAB,∴OM∥平面PAB;(2)证明:∵PA⊥平面ABCD,BD⊂平面ABCD,∴PA⊥BD,∵底面ABCD是菱形,∴AC⊥BD.又PA∩AC=A,∴BD⊥平面PAC,∵BD⊂平面PBD,∴平面PBD⊥平面PAC;(3)解:∵底面ABCD是菱形,M是PD的中点,∴V M﹣BCD===,∴V P﹣ABCD=.S ABCD==2.∴=,∴PA=.∵PA⊥平面ABCD,∴PA⊥AB,∴PB===.点评:本题主要考查直线与直线、直线与平面的位置关系、菱形的性质、体积等基础知识,考查空间想象能力、推理论证能力、运算求解能力、化归与转化能力,属于中档题.20.已知椭圆C:+=1(a>b>0)过点(2,0),且椭圆C的离心率为.(Ⅰ)求椭圆C的方程;(Ⅱ)若动点P在直线x=﹣1上,过P作直线交椭圆C于M,N两点,且P为线段MN中点,再过P:作直线l⊥MN.求直线l是否恒过定点,如果是则求出该定点的坐标,不是请说明理由.考点:直线与圆锥曲线的综合问题.专题:圆锥曲线中的最值与范围问题.分析:(Ⅰ)由已知条件推导出a2=4,,由此能求出椭圆C的方程.(Ⅱ)设P(﹣1,y0),,当直线MN的斜率存在时,设直线MN的方程为y﹣y0=k(x+1),由,得,由韦达定理结合已知条件推导出直线l恒过定点;当直线MN的斜率不存在时,直线l也过点.所以直线l恒过定点.解答:解:(Ⅰ)因为点(2,0)在椭圆C上,所以,所以a2=4,(1分)因为椭圆C的离心率为,所以,即,(2分)解得b2=3,所以椭圆C的方程为.(4分)(Ⅱ)设P(﹣1,y0),,①当直线MN的斜率存在时,设直线MN的方程为y﹣y0=k(x+1),M(x1,y1),N(x2,y2),由,得,所以,因为P为MN中点,所以,即.所以,(8分)因为直线l⊥MN,所以,所以直线l的方程为,即,显然直线l恒过定点.(10分)②当直线MN的斜率不存在时,直线MN的方程为x=﹣1,此时直线l为x轴,也过点.综上所述直线l恒过定点.(12分)点评:本题考查椭圆方程的求法,考查直线方程是否恒过定点的判断与求法,解题时要认真审题,注意分类讨论思想的合理运用.21.已知函数f(x)=+lnx(a∈R)(Ⅰ)当a=1时,求f(x)的最小值;(Ⅱ)若f(x)在(0,e]上的最小值为2,求实数a的值;(Ⅲ)当a=﹣1时,试判断函数g(x)=f(x)+在其定义域内的零点的个数.考点:导数在最大值、最小值问题中的应用;函数的最值及其几何意义;根的存在性及根的个数判断.专题:导数的综合应用.分析:(Ⅰ)当a=1时,求出函数的导数,通过函数的单调性求出f(x)的最小值;(Ⅱ)通过①当a≤0时,②当a∈(0,e]时,③当a>e时,通过x∈(0,e利用导函数的符号,判断函数的单调性,通过函数的最值,推出a符合题意的值即可;(Ⅲ)当a=﹣1时,求出函数的定义域,函数的导数求出函数的最值与0比较,判断在其定义域内的零点的个数即可.解答:解:(Ⅰ)当a=1时,,当x∈(0,1)时,f′(x)<0,f(x)单调递减,当x∈(1,+∞)时,f′(x)>0,f(x)单调递增,所以,当x=1时,f(x)有最小值:f(x)min=f(1)=1.(Ⅱ)因为,①当a≤0时,f′(x)>0,f(x)在(0,e]上为增函数,此时f(x)在(0,e]上无最小值.②当a∈(0,e]时,若x∈(0,a),则f′(x)<0,f(x)单调递减,若x∈(a,e],则f′(x)>0,f(x)单调递增,所以f(x)min=f(a)=1+lna=2,∴a=e,符合题意;③当a>e时,x∈(0,e],∴f′(x)<0,f(x)单调递减,所以,∴a=e,不符合题意;综上所述,a=e时符合题意.(Ⅲ)证明当a=﹣1时,函数,,令φ(x)=2+x﹣lnx,(x>0),则,所以x∈(0,1)时,φ′(x)<0,φ(x)单调递减,当x∈(1,+∞)时,φ′(x)>0,φ(x)单调递增,所以,φ(x)min=φ(1)=3>0,在定义域内g′(x)>0,g(x)在(0,+∞)单调递增,又g(1)=﹣1<0,而,因此,函数g(x)在(1,e)上必有零点,又g(x)在(0,+∞)单调递增,所以函数在其定义域内有唯一的零点.点评:本题考查函数的导数的应用,函数的最值的求法,考查分类讨论思想以及转化思想的应用.考查分析问题解决问题的能力.22,23,24题中任选一题作答,如果多做,则按所做的第一题记分.作答时用2B铅笔在答题纸卡上把所选的题目对应的标号涂黑.选修4-1:几何证明选讲22.如图,直线PQ与⊙O相切于点A,AB是⊙O的弦,∠PAB的平分线AC交⊙O于点C,连结CB,并延长与直线PQ相交于点Q,若AQ=6,AC=5.(Ⅰ)求证:QC2﹣QA2=BC•QC;(Ⅱ)求弦AB的长.考点:与圆有关的比例线段.专题:选作题;推理和证明.分析:(Ⅰ)利用切割线定理得:QA2=QB•QC=(QC﹣BC)•QC=QC2﹣BC•QC,即可证明QC2﹣QA2=BC •QC;(Ⅱ)求出AC=BC=5,QC=9,由∠QAB=∠ACQ,知△QAB∽△QCA,即可求弦AB的长.解答:(Ⅰ)证明:∵PQ与⊙O相切于点A,∴由切割线定理得:QA2=QB•QC=(QC﹣BC)•QC=QC2﹣BC•QC.…(4分)∴QC2﹣QA2=BC•QC.…(5分)(Ⅱ)解:∵PQ与⊙O相切于点A,∴∠PAC=∠CBA,∵∠PAC=∠BAC,∴∠BAC=∠CBA,∴AC=BC=5,…(6分)又知AQ=6,由(Ⅰ)可知QA2=QB•QC=(QC﹣BC)•QC,∴QC=9.…(8分)由∠QAB=∠ACQ,知△QAB∽△QCA,∴,…(9分)∴.…(10分)点评:本题考查切割线定理,考查三角形相似的判定与性质,考查学生分析解决问题的能力,属于中档题.选修4-4:坐标系与参数方程23.极坐标系与直角坐标系xoy有相同的长度单位,以原点为极点,以x铀正半轴为极轴,已知曲线C1的极坐标方程为ρ=4cosθ,直线l的参数方程为(t为参数),射线与曲线C1交于(不包括极点O)三点A、B、C.(Ⅰ)求曲线C1化成直角坐标方程及直线l的普通方程,并求曲线C1上的点到直线l的最小值.(Ⅱ)求证:.考点:参数方程化成普通方程.专题:计算题;坐标系和参数方程.分析:(Ⅰ)把曲线C1化成直角坐标方程及直线l的普通方程,求出圆心到直线的距离d,d﹣r即为曲线C1上的点到直线l的最小值;(Ⅱ)设点A,B,C的极坐标分别为(ρ1,φ),(ρ2,φ+),(ρ3,φ﹣),把三点代入曲线C1解析式,表示出ρ1=4cosφ,ρ2=4cos(φ+),ρ3=4cos(φ﹣),代入计算即可得证.解答:(Ⅰ)解:把x=cosθ,y=sinθ,ρ=x2+y2代入得:C1:x2+y2=4x,即(x﹣2)2+y2=4,直线l方程化简得:y=2(x+2),即y=x+2,∵圆心(2,0)到直线l的距离d==2,则曲线C1上的点到直线l的最小值d﹣r=2﹣2;(Ⅱ)证明:设点A,B,C的极坐标分别为(ρ1,φ),(ρ2,φ+),(ρ3,φ﹣),∵点A,B,C在曲线C1上,∴ρ1=4cosφ,ρ2=4cos(φ+),ρ3=4cos(φ﹣),∴|OB|+|OC|=ρ2+ρ3=4cos(φ+)+4cos(φ﹣)=4cosφ=ρ1,则|OB|+|OC|=|OA|.点评:此题考查了参数方程化为普通方程,将参数方程正确的化为普通方程是解本题的关键.选修4-5:不等式选讲24.(1)设函数f(x)=|x﹣|+|x﹣a|,x∈R,若关于x的不等式f(x)≥a在R上恒成立,求实数a的最大值;(2)已知正数x,y,z满足x+2y+3z=1,求++的最小值.考点:二维形式的柯西不等式;绝对值不等式的解法.专题:综合题;不等式的解法及应用.分析:(1)由绝对值三角不等式可得 f(x)≥|a﹣|,可得|a﹣|≥a,由此解得a的范围.(2)运用柯西不等式可得(x+2y+3z)(++)≥(+2+)2=16+8,即可得出结论.解答:解:(1)由绝对值三角不等式可得 f(x)=|x﹣|+|x﹣a|≥|(x﹣)﹣(x﹣a)|=|a﹣|,再由不等式f(x)≥a在R上恒成立,可得|a﹣|≥a,∴a﹣≥a,或a﹣≤﹣a,解得a≤,故a的最大值为.(2)∵正数x,y,z满足x+2y+3z=1,∴由柯西不等式可得(x+2y+3z)(++)≥(+2+)2=16+8,当且仅当x:y:z=3::1时,等号成立,∴++的最小值为16+8.点评:本题主要考查绝对值不等式的解法,函数的恒成立问题,考查三元柯西不等式及应用,考查基本的运算能力,体现了等价转化和分类讨论的数学思想,属于中档题.。
宁夏银川二中、银川九中、唐徕回民中学2014届高三下学期三校联考数学文Word版含答案
绝密★启用前银川市第二中学 2014年高三年级三校联合模拟考试文科数学试卷银川市第九中学 银川唐徕回民中学命题人 银川唐徕回民中学唐希明、沈学斌试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,其中第Ⅱ卷第22~24题为选考题,其它题为必考题。
考生作答时,将答案答在答题卡上,在本试卷上答题无效。
考试结束后,将本试卷和答题卡一并交回。
注意事项:1.答题前,考生务必先将自己的姓名、准考证号填写在答题卡上,认真核对条形码上的姓名、准考证号,并将条形码粘贴在答题卡的指定位置上。
2.选择题答案使用2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案的标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚。
3.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效。
4.保持卡面清洁,不折叠,不破损。
5.做选考题时,考生按照题目要求作答,并用2B 铅笔在答题卡上把所选题目对应的题号涂黑。
第I 卷一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.i 为虚数单位,复数1i i在复平面内对应的点到原点的距离为( ) A .21 B.22 C. 1D. 22. 已知集合A={1,2a},B={a ,b },若A ∩B={21},则A ∪B 为( ) A .{-1,21,1} B. {-1,21}C .{1,21}D. {21,1,b }3. 某单位为了了解用电量y (度)与气温x (℃)之间的关系,随机统计了某4天的用电量(7题图)由表中数据及线性回归方程a bx y+=ˆ,其中b =-2 预测当气温为-4℃时,用电量的度数约为( ) A .65.5 B. 66.5C. 67.5D. 68.54. 已知数列{}n a 是各项均为正数的等比数列, 若2a =2,243a a +=16,则5a =( ) A. 32 B. 16C. 8D. 45. 已知l ,m ,n 为三条不同的直线,α,β为两个不同的平面, 下列命题中正确的是( )A. l ⊥m ,l ⊥n ,且α⊂n m ,,则l ⊥αB .若平面α内有不共线的三点到平面β的距离相等,则βα//C .若α⊥m ,n m ⊥,则α//nD .若n m //,α⊥n ,则α⊥m6. 向量a =(2,0),b =(x ,y ),若b 与b -a 的夹角为6π,则|b |的最大值为( ) A .4B. 32C. 2D.334 7. 如图,在正方体ABCD —A 1B 1C 1D 1中,点P 是上底面A 1B 1C 1D 1内 一动点,则三棱锥P —BCD 的主视图与左视图的面积之比为 ( ) A .1:1 B. 2:1C. 2:3D. 3:28.执行如图所示的程序框图,输出S 的值为( ) A .10B. -6C. 3D. -159. 已知A (A x ,A y )是圆心在坐标原点的单位圆上任意一点,且射线OA 绕原点逆时针旋转300到OB 交单位圆于点B (B x ,B y ),则A x -B y 的最大值为( )A .21B. 1C.23D. 210. 下列说法:(1)命题“R x ∈∃,使得32>x ”的否定是“R x ∈∀,使得32≤x ”(8题图)(2)命题“函数()x f 在0x x =处有极值,则()00='x f ”的否命题是真命题(3)()x f 是(∞-,0)∪(0,∞+)上的奇函数,0>x 时的解析式是()xx f 2=,则0<x的解析式为()x x f --=2其中正确的说法的个数是( )A .0个B. 1个C. 2个D. 3个11. 斜率为2的直线l 过双曲线12222=-by a x ()0,0>>b a 的左焦点,且与双曲线的左、右支分别相交,则双曲线的离心率e 的取值范围是( ) A .(1,2)B.(1,3)C. (1,5)D.(5,∞+)12. 已知()x x f x 2log 3)31(2-⋅=,实数c b a ,,满足()()()()c b a c f b f a f <<<<⋅⋅00,若实数0x 是函数()x f y =的一个零点,那么下列不等式中不可能...成立的是( ) A .0x a <B. 0x b >C. 0x c <D. 0x c >第Ⅱ卷本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须做答.第22题~第24题为选考题,考生根据要求做答.二、填空题:本大题共4小题,每小题5分.13.小明和小华约定第二天早上8:00~9:00在图书馆门口见面,并约定一方先到要等另一方半小时,若等半小时不见另一方可离开,问两人碰面的概率是__________. 14. 设等差数列{}n a 的前n 项和为n S ,若1-m S =-2,m S =0,1+m S =3,则m =___________.15. 已知ω>0,函数())4sin(πω+=x x f 在(2π,π)内单调递减,则ω的取值范围是_______.16. 已知动圆M 过两定点A (1,2),B (-2,-2),则下列说法正确的是__________.(写出所有正确结论的序号) (1)动圆M 与x 轴一定有交点 (2)圆心M 一定在直线21-=x 上 (3)动圆M 的最小面积为π425 (4)直线2+-=x y 与动圆M 一定相交 (5)点(0,32)可能在动圆M 外三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤. 17.(本大题满分12分)在△ABC 中,角A ,B ,C 对边分别为c b a ,,满足:22)(AC AB 2c b a +-=⋅,(Ⅰ)求角A 的大小; (Ⅱ)求)B 34sin(2cos 322--πC 的最大值,并求取得最大值时角B ,C 的大小.18.(本大题满分12分)某校学生会组织部分同学用“10分制”随机调查“阳光”社区人们的幸福度,现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶).(Ⅰ)指出这组数据的众数和中位数;(Ⅱ)若幸福度不低于9.5分,则该人的幸福度为“很幸福”, 按分层抽样的方法从16人中抽取8人,并从8人中随机抽取2人,求2人中至少有1人“很幸福”的概率.19.(本大题满分12分)如图,四边形ABCD 是边长为2的正方形,△ABE 为等腰三角形,AE=BE=2,平面ABCD ⊥平面ABE , (Ⅰ)求证:平面ADE ⊥平面BCE ; (Ⅱ)求三棱锥D —ACE 的体积.20.(本大题满分12分)已知点M (-1,0),N (1,0),动点P (x ,y )满足|PM |+|PN |=32,(Ⅰ)求P 的轨迹C 的方程;(Ⅱ)是否存在过点N (1,0)的直线l 与曲线C 相交于A ,B 两点,并且曲线C 上存在点Q ,使四边形OAQB 为平行四边形?若存在,求出直线l 的方程;若不存在,请说明理由.21.(本大题满分12分)设函数()1-+=ax e x f x(e 为自然对数的底数),(Ⅰ)当a =1时,求过点(1,()1f )处的切线与坐标轴围成的面积; (Ⅱ)若()2x x f ≥在(0,1)恒成立,求实数a 的取值范围.请考生在22,23,24题中任选一题作答,如果多做,则按所做的第一题记分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
绝密★启用前(银川二中第一次模拟考试)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,其中第Ⅱ卷第22~24题为选考题,其它题为必考题。
考生作答时,将答案答在答题卡上,在本试卷上答题无效。
考试结束后,将本试卷和答题卡一并交回。
注意事项:1.答题前,考生务必先将自己的姓名、准考证号填写在答题卡上,认真核对条形码上的姓名、准考证号,并将条形码粘贴在答题卡的指定位置上。
2.选择题答案使用2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案的标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚。
3.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效。
4.保持卡面清洁,不折叠,不破损。
5.做选考题时,考生按照题目要求作答,并用2B 铅笔在答题卡上把所选题目对应的题号涂黑。
参考公式:S 圆台侧面积=L R r )(+π第I 卷一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 设集合M={x|1242x ≤≤},N={x|x-k>0},若M ∩N=φ,则k 的取值范围为 A.[)2,+∞ B.(2,+∞) C.(-∞,-1) D.(],1-∞-2.复数()21i 1i+-等于A .-1+i B. 1+i C.1-i D.-1-i3.设a ∈R,则“1a<1”是“a>1”的 A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件文科数学试卷 第1页(共6页)2014年普通高等学校招生全国统一考试文 科 数 学4.设三角形ABC 的三个内角为A ,B ,C ,向量(3sin ,sin ),(cos ,3cos ),m A B n B A ==1cos(),m n A B ∙=++则C=A.6πB.3πC. 56πD.23π5.在等差数列{a n }中,a 1+a 3+a 5=105, a 2+a 4+a 6=99, 以S n 表示{a n }的前n 项和,则使S n 达到最大值的n 是 A .21B .20C .19D .186.在⊿ABC中,三边a,b,c 所对的角分别为A,B,C,若a 2-b 2则角A=A .300B .450C .1500D .1350 7.运行如下程序框图,如果输入的[1,3]t ∈-,则输出s 属于A .[3,4]-B .[5,2]-C .[4,3]-D .[2,5]-8.已知集合A={(x,y )|-1≤x≤1.0≤y≤y ≤}. 若在区域A 中随机的扔一颗豆子,则该豆子落在区域B 中 的概率为 A .14π- B .4π C .1-8π D .8π 9.A .112π B. 112π+6 C. 11π D.112π10.已知函数f(x)=x 3+ax 2+bx+a 2在x=1处有极值10,则f(2)= A. 11或18, B. 11 C. 17或18D.1811.已知点M 是y=214x 上一点,F 为抛物线的焦点,A 在C :22(x 1)(4)1y -+-= 上,则|MA|+|MF|的最小值为 A .2B. 4C. 8D. 1012.已知定义在R 上的奇函数)(x f 满足)()2(x f e x f -=+(其中e =2.7182…),且在区间[e ,2e ]上是减函数,令55ln ,33ln ,22ln ===c b a ,则f (a ), f (b ), f (c ) 的大小关系(用不等号连接)为 A .f (b )>f (a )>f (c ) B. f (b )>f (c )>f (a ) C. f (a )>f (b )>f (c ) D. f (a )>f (c )>f (b )正视图600 侧视图俯视图PGFE DCBA第Ⅱ卷本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须做答.第22题~第24题为选考题,考生根据要求做答. 二、填空题:本大题共4小题,每小题5分.13.某高中共有900人,其中高一年级300人,高二年级200人,高三年级400人,现采用分层抽样抽取容量为45的样本,那么高一、高二、高三各年级抽取的人数分别为______、_______、________.14.已知关于x,y 的二元一次不等式组24120x y x y x +≤⎧⎪-≤⎨⎪+≥⎩,则x+2y+2的最小值为_________15.设双曲线的一个焦点为F ,虚轴的一个端点为B ,如果直线FB 与该双曲线的一条渐近线垂直,那么此双曲线的离心率为_________.16. 函数f (x )=Asin()x ωφ+(A ,,ωφ为常数,A >0,0ω>,||φ<π)的部分图象如图所示,则f (0)的值是_______.三、解答题:解答应写出文字说明.证明过程或演算步骤17.(本小题满分12分)设{a n }是等差数列,{b n }是各项为正项的等比数列,且a 1=b 1=1, a 3+b 5=21, a 5+b 3=13. (1)求{a n }, {b n }的通项公式; (2)求数列{nnb a }的前n 项和S n ;18.(本题满分12分)如图,在底面是正方形的四棱锥P ABCD -中,PA ⊥面ABCD ,BD 交AC 于点E ,F 是PC 中点,G 为AC 上一动点. (1)求证:BD FG ⊥;(2)确定点G 在线段AC 上的位置,使FG //平面PBD ,并说明理由. (3)如果PA=AB=2,求三棱锥B-CDF 的体积19.(本小题满分12分)从某学校的800名男生中随机抽 取50名测量身高,被测学生身高全部 介于155cm 和195cm 之间,将测量文科数学试卷 第3页(共6页)结果按如下方式分成八组:第一组 [155,160),第二组[160,165),…, 第八组[190,195],右图是按上述分 组方法得到的频率分布直方图的一部 分,已知第一组与第八组人数相同, 第六组的人数为4人.(Ⅰ)求第七组的频率并估计该校800名男生中身高在180cm 以上(含180cm )的人数;(Ⅱ)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为,x y ,事件=E {5x y -≤},事件F ={15->x y },求()P E F .20.(本小题满分12分)已知椭圆C :22221(0)M(2,0),x y a b a b +=>>定点 椭圆短轴的端点是B 1,B 2,且MB 1⊥MB 2。
(1)求椭圆C 的方程(2)设过点M 且斜率不为0的直线交椭圆C 于A 、B 两点,试问X 轴上是否存在定点P ,使PM 平分∠APB ?若存在,求出点P 的坐标;若不存在,说明理由。
21.(本小题满分12分)已知函数f(x)=(2x 2-4ax)lnx+x 2(a>0) (1)求()f x 的单调区间;(2)设[)1,x ∀∈+∞,不等式(2x-4a )lnx>-x 恒成立,求a 的取值范围。
请考生在第22、23、24三题中任选一题做答,如果多做,则按所做的第一题记分.答时用2B 铅笔在答题卡上把所选题目的题号涂黑.22.(本小题满分10分) 选修4—1:几何证明选讲.如图,AB 是⊙O 的直径,弦CA BD ,的延长线 相交于点E ,EF 垂直BA 的延长线于点F . 求证:(1)2CE CE AC DE BE =⋅+⋅;(2)B C F E ,,,四点共圆.23.(本小题满分10分)选修4—4:坐标系与参数方程.极坐标系中,已知圆心C (3,)6π,半径r =1.(1)求圆的直角坐标方程;(2)若直线1(12x t y t ⎧=-+⎪⎪⎨⎪=⎪⎩为参数)与圆交于B A ,两点,求弦AB 的长.24.(本小题满分10分)选修4—5:不等式选讲.已知函数k x x x f +-+-=23)(.(1)若3)(≥x f 恒成立,求k 的取值范围; (2)当1=k 时,解不等式:x x f 3)(<.文科数学试卷 第5页(共6页)PG FE D CB A银川一中2014届高三第一次模拟数学(文科)试卷参考答案1—5.AABDB , 6—10.AACDD 11.B 12.A 13.15,10,20, 14. -6 15.12, 16.217.解:(1)设{a n }的公差为d,{b n }的公比为q,则依题意有q>0,⎪⎩⎪⎨⎧=++=++1341212124q d q d 解得d=2,q=2. 所以a n =2n-1, b n =2n-1((2)1212--=n n n n b a , S n =1+12212122322523---+-+++n n n n2S n =2+3+2523212232---+-++n n n n ,两式相减得:S n =2+2(122212)2121211----++++n n n =2+11123262122112112---+-=----⨯n n n n n 18.解析⑴证空间两直线垂直的常用方法是通过线面垂直来证明,本题中,由于直线FG 在平面PAC 内,所以考虑证明BD ⊥平面APC .⑵注意平面PAC 与平面PBD 相交于PE ,而直线FG 在平面PAC 内,故只需FG PE ∥即可,而这又只需G 为EC 中点即可.(3)求三棱锥B-CDF 的体积中转化为求三棱锥F -BCD 的体积,这样底面面积与高都很易求得.试题解析:⑴∵PA ⊥面ABCD ,四边形ABCD 是正方形,其对角线BD 、AC 交于点E ,∴PA BD ⊥,AC BD ⊥.2分∴BD ⊥平面APC ,∵FG ⊂平面PAC ,∴BD FG ⊥ 4分⑵当G 为EC 中点,即34AG AC =时,FG ∥/平面PBD , 5分理由如下:连结PE ,由F 为PC 中点,G 为EC 中点,知FG PE ∥ 6分 而FG ⊄平面PBD ,PB ⊂平面PBD ,故FG //平面PBD . 8分 (3)三棱锥B-CDF 的体积为112221323B CDF F BCD V V --==⨯⨯⨯⨯=.12分 19. 解:(Ⅰ)第六组的频率为40.0850=,所以第七组的频率为 10.085(0.00820.0160.0420.06)0.06--⨯⨯++⨯+=;由直方图得后三组频率为0.060.080.00850.18++⨯=,所以800名男生中身高在180cm 以上(含180cm )的人数为0.18800144⨯=人(Ⅱ)第六组[180,185)的人数为4人,设为,,,a b c d ,第八组[190,195]的人数为2人, 设为,A B ,则有,,,,,,ab ac ad bc bd cd ,,,,,,,,aA bA cA dA aB bB cB dB AB 共15种情况,因事件=E {5x y -≤}发生当且仅当随机抽取的两名男生在同一组,所以事件E 包含的基本事件为,,,,,,ab ac ad bc bd cd AB 共7种情况,故7()15P E =. 由于max19518015x y -=-=,所以事件F ={15->x y }是不可能事件,()0P F =由于事件E 和事件F 是互斥事件,所以7()()()15P E F P E P F =+=20. 解析:(1)由222222521,93a b b b e a a a -===-=,依题意△MB 1B 2是等腰直角三角形,从而b=2,故a=3,所以椭圆C 的方程是22194x y += (2)设A (x 1,y 1),B(x 2,y 2),直线AB 的方程为x=my+2, 将直线AB 的方程与椭圆C 的方程联立,消去X 得(4m 2+9)y 2+16my-20=0, y 1+y 2=12221620,4949m y y m m --+=++y 1·y 2=94202+-m ,若PM 平分∠APB ,则直线PA ,PB 的倾斜角互补,所以K PA +K PB =0,设P (n,0),则有12120.y yx n x n+=-- 将x 1=my 1+2,x 2=my 2+2,代入得2my 1y 2+(2-n)(y 1+y 2)=0. 整理得(2n-9)m=0.由于上式对任意实数m 都成立,所以n=92,综上,存在定点P(92,0),使PM 平分∠APB 。
