二阶电路冲击响应
合集下载
二阶电路经典篇
1. 二阶电路的零输入响应 + - C i uc
已知： 已知：
R L
uc(0+)=U0
i(0+)=0
列电路方程： 列电路方程：
Ri + uL − uC = 0
di uL = L dt
duC i = −C dt
2
若以电容电压为变量： 若以电容电压为变量： 若以电感电流为变量： 若以电感电流为变量：
d uC duC LC + RC + uC = 0 dt dt 2 di di LC + RC + i = 0 dt dt
求通解的特征方程为； 求通解的特征方程为；
LCP2 + RCP +1 = 0
uc = u + u
' c
" c
特解: 特解 特解
u =E
" c
通解
uc解答形式为： 解答形式为：
uc = E + A e 1
uc = E + A e 1
p1t
−δ t
+ A2e
p2t
−δ t
( p1 ≠ p2 )
( P = P = −δ ) 1 2
2
U0 di = dt t =0+ L
d uC duC 电路方程： 电路方程： LC + RC + uC = 0 dt dt
特征方程： 特征方程：
LCP2 + RCP + 1 = 0
R R 2 1 − R ± R2 − 4L/ C 特征根： 特征根： P = =− ± ( ) − 2L 2L LC 2L
uc
U0
设|P2|>|P1|
已知： 已知：
R L
uc(0+)=U0
i(0+)=0
列电路方程： 列电路方程：
Ri + uL − uC = 0
di uL = L dt
duC i = −C dt
2
若以电容电压为变量： 若以电容电压为变量： 若以电感电流为变量： 若以电感电流为变量：
d uC duC LC + RC + uC = 0 dt dt 2 di di LC + RC + i = 0 dt dt
求通解的特征方程为； 求通解的特征方程为；
LCP2 + RCP +1 = 0
uc = u + u
' c
" c
特解: 特解 特解
u =E
" c
通解
uc解答形式为： 解答形式为：
uc = E + A e 1
uc = E + A e 1
p1t
−δ t
+ A2e
p2t
−δ t
( p1 ≠ p2 )
( P = P = −δ ) 1 2
2
U0 di = dt t =0+ L
d uC duC 电路方程： 电路方程： LC + RC + uC = 0 dt dt
特征方程： 特征方程：
LCP2 + RCP + 1 = 0
R R 2 1 − R ± R2 − 4L/ C 特征根： 特征根： P = =− ± ( ) − 2L 2L LC 2L
uc
U0
设|P2|>|P1|
二阶电路阶跃响应和冲激响应讲解
50 W
50 V
R iR
0.5H L C
100 μF
iL
iC
(5)求iR
iR iL iC
iL
LC
d2iL dt 2
或设解答形式为： iR 1 Ae100t sin(100t )
50W
定常数
R iR
50 V
2A
iC
i
R
(0
)
diR dt
(0
)
1
iC ?
(0
)
1
iR
50 R
uc
5Ω 解 （1） uc(0－)=25V iL(0－)=5A
（2）开关打开为RLC串 联电路，方程为：
LC
d 2uc dt
RC
duc dt
uc
0
特征方程为： 50P2+2500P+106=0
P 25 j139
uc Ae25t sin(139t )
uc Ae25t sin(139t )
0
A U0 ， arctg
sin
ω，ω０，δ间的关系:
ω0
ω
sin
0
A
0
U
0
δ
uc
0
U0e
t
sin(t
)
uc
0
U0e
t
sin(t
)
uc是其振幅以
0
U0为包线依指数衰减的正弦函数。
t=0时 uc=U0
uc U0
0
U0
e
t
uc零点：t = -，2- ... n- uc极值点：t =0， ，2 ... n
L
di dt
二阶电路的冲激响应
0
i(t)
0 Ld
e t cos
cos d t
sin
sindt ε(t)
0 Ld
e
t
cosd t
ε(t)
α称为衰减常数(attenuation constant) ，或阻尼常数
(damping constant)
角频率 d称为阻尼振荡角频率(angular frequency of
the damped oscillation)
阻尼振荡角频率不仅决定于电感L和电容C，也和电
阻R有关。
在R = 0的极限情况下， = 0，d 0
1 LC
θ = 0，在R = 0情况下的响应uC(t)、i (t) 均变为等幅振 荡(unattenuated oscillation)，或称为无阻尼振荡 (undamped oscillation)。其函数表达式为
uC
(
t
)
0
sin
0
t
ε(
t
)
i(t)
1 L
cos
0
t
ε(t)
2. s1和s2为相等的负实根
=0
即
R 2L
1 ，或R 2 LC
L C
电容电压的通解为
uC (t) A1 A2t e t
代入初始条件得
A1 0
A1
A2
1 LC
故
uC (t)
t LC
e tε(t )
i(t) C duc (t) 1 e t 1 t ε(t)
电容上的冲激响应电压为
uC (t)
1 LC(s1
(e s1t s2 )
es2t )ε(t )
冲激响应电流为
i(t)
0 Ld
e t cos
cos d t
sin
sindt ε(t)
0 Ld
e
t
cosd t
ε(t)
α称为衰减常数(attenuation constant) ，或阻尼常数
(damping constant)
角频率 d称为阻尼振荡角频率(angular frequency of
the damped oscillation)
阻尼振荡角频率不仅决定于电感L和电容C，也和电
阻R有关。
在R = 0的极限情况下， = 0，d 0
1 LC
θ = 0，在R = 0情况下的响应uC(t)、i (t) 均变为等幅振 荡(unattenuated oscillation)，或称为无阻尼振荡 (undamped oscillation)。其函数表达式为
uC
(
t
)
0
sin
0
t
ε(
t
)
i(t)
1 L
cos
0
t
ε(t)
2. s1和s2为相等的负实根
=0
即
R 2L
1 ，或R 2 LC
L C
电容电压的通解为
uC (t) A1 A2t e t
代入初始条件得
A1 0
A1
A2
1 LC
故
uC (t)
t LC
e tε(t )
i(t) C duc (t) 1 e t 1 t ε(t)
电容上的冲激响应电压为
uC (t)
1 LC(s1
(e s1t s2 )
es2t )ε(t )
冲激响应电流为
§12-3 二阶电路的阶跃响应和冲激响应
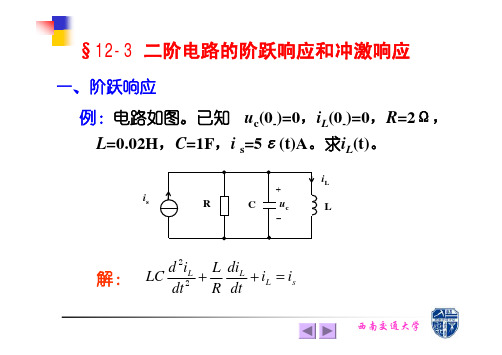
δ (t)V
s(t ) = (1 + K1e p1t + K 2 e p2t ) ε (t )
代入零初始条件：
1 + K 1 + K 2 = 0 K 1 p1 + K 2 p 2 = 0
p2 K1 = p p 2 1 p1 K 2 = p 2 p1
西南交通大学
p2 p1 p1t e p2t )ε (t ) s (t ) = (1 + e + p 2 p1 p 2 p1
ds(t ) p2 p1 p1t uc (t ) = h(t ) = = (e e p2t )ε (t ) dt p2 p1
而
1 p1 p 2 = LC
1 LC (e p1t e p2t )ε (t ) u c (t ) = h(t ) = p 2 p1
∴
西南交通大学
du c LC dt du c t =0+ dt t = 0 + RC [u c ( 0 + ) u c (0 )] +
∫
0+
0
u c dt = 1
∫
0+
0
uc dt :
uc不可能为冲激函数
∴
∫
0+
0
u c dt = 0
u c (0 + ) : uc也不可能在t=0时跳变（阶跃）
du c dt 1 t =0+ = LC
西南交通大学
LCp 2 + RCp + 1 = 0
以特征根为不等实根为例
p1 ≠ p 2
u c = K 1e
p1t
+ K 2e
p2t
du c = K 1 p1e p1t + K 2 p 2 e p2t dt
电路理论第11章二阶电路
R2
响应性质
等幅振荡 (无 阻尼 ) 衰减振荡 (欠阻尼 )
自由分量形式
K sin( 0t )
Ke t sin(t )
L t 相 等 的 实 根 非振荡放电 (临界阻尼 ) e ( A1 A2 t ) C
R2
L 不 等 的 实 根 非振荡放电 ( 过阻尼 ) C
u ,i uC O i
临界状 态
电流
12
电压:
U 0 t te L uL U 0e t (1 t ) i
2019年5月7日
uL
t
小结
第11章 11.1
1. 一阶电路是单调的响应，可用时间常数表示过渡过程。 2. 二阶电路用特征根来表示动态响应。 特征根
R 0 共轭虚根
L R2 共轭复根 C
A1e p1t A2e p2t
13
3. 电路是否振荡取决于特征根，特征根仅仅取决于电路的结 构和参数，而与初始条件和激励的大小没有关系。
2019年5月7日
第11章 11.2
§11-2 二阶电路的零状态响应和阶跃响应
零状态响应: 与一阶电路相同
阶跃响应: 二阶电路在阶跃激励下的零状态响应.
零状态响应 =强制分量+自由分量
duC U 0 t e sin t dt L
uL L
di 0 U 0e t sin( t ) dt
i C
C
+
-
L
t
11
2019年5月7日
第11章 11.1
L 3. R 2 C
临界情况
1 2
U0 ( p2e p t p1e p t ) 此时,p1,p2为两个相等的实根 uC p2 p1
响应性质
等幅振荡 (无 阻尼 ) 衰减振荡 (欠阻尼 )
自由分量形式
K sin( 0t )
Ke t sin(t )
L t 相 等 的 实 根 非振荡放电 (临界阻尼 ) e ( A1 A2 t ) C
R2
L 不 等 的 实 根 非振荡放电 ( 过阻尼 ) C
u ,i uC O i
临界状 态
电流
12
电压:
U 0 t te L uL U 0e t (1 t ) i
2019年5月7日
uL
t
小结
第11章 11.1
1. 一阶电路是单调的响应，可用时间常数表示过渡过程。 2. 二阶电路用特征根来表示动态响应。 特征根
R 0 共轭虚根
L R2 共轭复根 C
A1e p1t A2e p2t
13
3. 电路是否振荡取决于特征根，特征根仅仅取决于电路的结 构和参数，而与初始条件和激励的大小没有关系。
2019年5月7日
第11章 11.2
§11-2 二阶电路的零状态响应和阶跃响应
零状态响应: 与一阶电路相同
阶跃响应: 二阶电路在阶跃激励下的零状态响应.
零状态响应 =强制分量+自由分量
duC U 0 t e sin t dt L
uL L
di 0 U 0e t sin( t ) dt
i C
C
+
-
L
t
11
2019年5月7日
第11章 11.1
L 3. R 2 C
临界情况
1 2
U0 ( p2e p t p1e p t ) 此时,p1,p2为两个相等的实根 uC p2 p1
16第十六讲 二阶电路的零状态响应和全响应阶跃和冲激响应
等幅振荡 π uC = U 0 sin( ω 0 t + ) = uL 无阻尼 2
δ = cos β ω0 ω = sin β ω0 ω β = arctg δ
ω0 uC = U 0 e −δ t sin(ω t + β ) ω
duC U 0 −δ t i = −C = e sin ω t ωL dt di ω0 u L = L = − U 0 e −δ t sin(ω t − β ) ω dt
(2)求通解 自由分量） 求通解(自由分量 求通解 自由分量）
特征方程
特征根
P 2 + 200 P + 20000 = 0
P= -100 ± j100
通解 i L (t ) = Ke−100t sin(100t + β )
(3)求特解（强制分量，稳态解） 求特解（强制分量，稳态解） 求特解
" iL = 1A
U0 uc uC 0
β
π uC = U 0 sin( ω 0 t + ) = uL 2
等幅振荡 无阻尼
ω0 U 0 e − δt ω
t
i
β π π+β 2π-β πβ 2π π
π-β β
t
uL
ω0 − U 0 e −δt ω
L ４ 、R = 2 临 情 界 况 C
R P = P = P2 = − = −δ 1 2L
uC = e −δ t ( A1 + A2 t )
由初始条件 uC (0 + ) = U 0 → A1 = U 0 解出
du C ( 0 + ) = 0 → A1 ( −δ ) + A2 = 0 dt
A1 = U 0 A2 = δU 0
二阶电路的冲激响应
04 二阶电路冲激响应的应用
在控制系统中的应用
控制系统稳定性分
析
通过分析二阶电路的冲激响应， 可以判断控制系统的稳定性，从 而优化系统设计。
控制器设计
利用二阶电路的冲激响应特性， 可以设计出性能更优的控制器， 提高系统的动态性能和稳态性能。
系统故障诊断
通过分析二阶电路的冲激响应， 可以检测出系统中的故障或异常， 及时进行维修和保护。
二阶电路的冲激响应
目录
CONTENTS
• 二阶电路的简介 • 二阶电路的冲激响应 • 二阶电路冲激响应的实例分析 • 二阶电路冲激响应的应用 • 二阶电路冲激响应的展望
01 二阶电路的简介
二阶电路的定义
二阶电路
由两个动态元件（通常是电阻、电容或电感）和 电源组成的电路。
动态元件
具有储能能力的元件，能够存储和释放能量。
在通信系统中的应用
调制解调
在通信系统中，可以利用二阶电路的冲激响应特性进行调制和解 调，实现信号的传输和处理。
信号检测
通过分析二阶电路的冲激响应，可以对通信系统中的信号进行检 测，提取出有用的信息。
信道均衡
在通信系统中，可以利用二阶电路的冲激响应特性进行信道均衡， 消除信号传输过程中的失真和畸变。
输出响应
输出响应是指电路在输入信号的作 用下，产生的输出电压或电流。
冲激响应的求解方法
解析法
通过建立电路的微分方程，并利用初始条件和边界条件求解。
数值法
利用数值计算方法，如欧拉法、龙格-库塔法等，对方程进行离散 化并求解。
符号法
利用符号计算软件，如MATLAB等，对方程进行符号化求解。
冲激响应的特性
发展高精度、高稳定性的测量技 术，以获取更准确的二阶电路冲
电路分析基础第七章__二阶电路
第七章二阶电路重点要求:1. 理解二阶电路零输入响应过渡过程的三种情况;2. 了解二阶电路的阶跃响应和冲击响应。
3.学习数学中的拉普拉斯变换的定义、性质及反变换的方法;4.掌握用拉普拉斯变换求解电路的过渡过程的方法。
1§7-1 二阶电路的零输入响应二阶电路:由二阶微分方程描述的电路。
典型的二阶电路是RLC串联电路。
求全响应方法:1.经典法(时域分析法)全响应= 稳态分量(强制分量) + 暂态分量(自由分量)2.拉普拉斯变换法(频域分析法)2响应曲线:U 0u C , u L , i 0ωtiu Cu L§7-1 二阶电路的零输入响应220p ααω=−±−一. 问题的提出经典法解动态电路过渡过程存在的问题：对较复杂的电路，联立求解微分方程特别是定积分常数比较困难。
若激励不是直流或正弦交流时，特解不容易求得。
二. 拉氏变换法用积分变换的原理简化求解电路过渡过程时域电路解微分方程时域响应f(t)取拉斯变换复频域电路解代数方程复频域响应F(s)取拉斯反变换7.2 动态电路的复频域分析应用拉氏变换法进行电路分析称为电路的一种复频域分析方法，也叫运算法！是数学中的一种积分变换.优点：对复杂电路﹑无稳态情况﹑换路时出现强迫跃变等用拉氏变换法较经典法方便。
三. 拉普拉斯变换的定义设函数f(t)在0≤t ≤∞时有定义，则积分称为原函数f(t)的拉普拉斯变换（象函数）。
()dte tf s F st∫∞−−=0)(式中s=σ+ j ω----复频率。
单位：熟悉的变换:相量法⎩⎨⎧=∫∞+∞−)s (21)(ds e F j t f stj c j c π反变换正变换ZH1.象函数F (s)存在的条件：∞<∫∞−−dt et f st0)(说明：电路分析中的函数都能满足上述条件。
2. 在电路中积分的下限定义为“0-”, 更有实际意义(将奇异函数也包括在内)。
[][]⎩⎨⎧==−)( )()( )( S F t f t f S F 1简写正变换反变换在电路分析中通常直接查表得到。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2LC
2L
R 2 1 2L LC
2 02
def
R
2L
de f
0
1 LC
当s1s2时，微分方程的通解为
uC (t) A1es1t A2es2t
duC dt
S1 A1eS1t
S2 A2eS2t
A1 A2 0
uC (0 ) uC (0 ) 0
duC dt
(0 )
i(0 ) C
§4-5 二阶电路的冲击响应
一、RLC串联电路的h(t) 求 iL(t),uL(t)
解：1. 因为 uC(0-)=0,iL(0-)=0
所以 uL (0) (t)V
iL (0
)
iL (0
)
1 L
0 0
uL
(0)dt
1 L
uC (0 ) 0
iL (0 ) 0
uC (0 ) uC (0 ) 0
S2 )
e S1t
1 LC (S1
S2 )
e S2t ] (t)
正数 慢
负数 快
3．讨论 s1 2 02 s2 2 02
(1)
0
即
R 2L
1 或R 2 LC
L C
过阻尼情形
S1 S2 0 S1 S2
S1-S2>0
当t >0时,uC(t)>0 ,说明电容电压只改变大小,不改变方向 当t = 0+时，uC(0+)=0 当 t 时，uC() = 0
duC dt
A2et ( A1 A2t)et
uC (0 ) 0
duC dt
(0 )
iC (0 ) C
1 LC
A1 0
A2
A1
1 LC
uC (t)
1 tet (t)
LC
i(t) C duc (t) 1 e t 1 t (t) ( 1 et tet ) (t)
dt L
L
L
R2 L C
L(S1 S2 )
负数 正数
负数 慢 正数 快
t=0+时，iL(0+)=1/L 0 t tm时，iL (t) 0
t=tm时，iL(tm)=0
t tm时， 正数 快 负数 慢
iL (t) 0 而iL () 0
因此,在t =tm到t的变化过程
中, iL(t)要出现负的极2值ln。s1
在t =0+到t的变化过程中,uC(t)要出现正的极值。
uC(t)的曲线为
令 duC 0 dt
ln s1
tm
s2
s2 s1
为
R2 L C
S1 S2 0
非 振
荡
为过阻尼情形 为不等的负实根
情
形
iL
(t)
iC
(t)
C
duC dt
[ S1
e S1t
L(S1 S2 )
S2
eS2t ] (t)
阻尼振荡周期(period of the damped oscillation)
< 0的情形称为(阻尼)振荡情形(oscillatory case)，
或欠阻尼情形(underdamped case)。
0
d t
2
2
d t
2
d t
2 dt
R2 L C
欠阻尼情形
S1 S2
d t
3
2
ห้องสมุดไป่ตู้
共轭复根(实部<0)
1 LC (s1
s2 )
(e s1t
es2t ) (t)
02 e e t jdt e te jdt (t) j2d
S1 S2 j2d
02
1 LC
02 d
et
sin dt
(t ) (衰减正弦函数)
uC
(t)
02 d
et
sin
d t
(t)
i(t) C duC (t) C02
dt
1 LC
A1
1 LC(s1
s2 )
s1 A1
s2 A2
1 LC
A2
1 LC(s1
s2 )
uC (t)
1 LC (s1
s2 )
( e s1t
es2t ) (t)
i(t) C duC (t) 1
dt
L(s1 s2 )
s1e s1t s2e s2t
(t)
uC (t)
[
1
LC (S1
d
d dt
e t sin d t (t)
C02 d
e t
sin d t
d
cosd t (t)
d 02 2
arctg d
0 sin d 0 cos
i(t)
0 L0d Ld
e t cos cosd t sin sin d t (t)
e t cosd t (t) (衰减余弦函数)
0 Ld
e t
cosd t
(t)
1 L
c os0 t
(t)
振 荡
无 阻 尼 振
荡
R=0
S1 S2
(unattenuated oscillation)
无阻尼情形 共轭复根(实部=0) (undamped oscillation)
(3) 0
R2 L C
S1 S2
临界阻尼情形
uc (t) A1 A2t e t
2．t>0时电路
RC duC dt
L
d dt
[C
duC dt
]
uC
0
LC d 2uC dt 2
RC
duC dt
uC
0
(t 0)
uC (0 ) 0
iL (0 )
1 L
LC d 2uC dt 2
RC duC dt
uC
0
LCs2 RCs 1 0
(t 0)
RC S1,2
(RC)2 4LC R
令 diL 0 dt
tm
s2
s2 s1
2tm
在 >0的情形下,当t > 0时,电路的能量过程
0 < t < tm
tm < t < tm
t > tm
非振荡
(2)
0
即
R 2L
1 或R 2 LC
L C
欠阻尼情形
S1,2 2 02
令d 02 2
jd
j 1
S1 S2
uC (t)
衰减快慢由 R 决定,叫
2L
衰减系数(attenuation constant) ， 或阻尼系数(damping constant)
振荡角频率 d
2 0
2
1 ( R )2 LC 2L
Td
2 d
叫阻尼振荡角频率(angular frequency of the damped oscillation)
S1 S2 0
为非振荡情形
为临界阻尼情形 为相等的负实根
二、RLC并联电路的h(t) (分析方法同前)
求 uC (t) (t 0)
解：因为 uC (0 ) 0 iL (0 ) 0
所以 uL (0) 10 (t)v
iL
(0
)
iL
(0
)
1 L
u0
0 L
(0)dt
10A
uC (0 ) uC (0 ) 0
阻尼振荡(衰减振荡)
阻尼振荡角频率
d
2 0
2
1 ( R )2 LC 2L
阻尼振荡角频率不仅决定于电感L
和电容C，也和电阻 R有关。
在R = 0时
R 0
2L
arctg 0 d
d 0
1 LC
无阻尼振荡角频率
uC (t)
02 d
e t
sin dt (t)
0
sin 0t
(t)
等 幅
i(t)