实变函数复习题.docx
(完整版)实变函数试题库1及参考答案

实变函数试题库及参考答案(1) 本科一、填空题1.设,A B 为集合,则()\A B B U A B U (用描述集合间关系的符号填写) 2.设A 是B 的子集,则A B (用描述集合间关系的符号填写) 3.如果E 中聚点都属于E ,则称E 是 4.有限个开集的交是5.设1E 、2E 是可测集,则()12m E E U 12mE mE +(用描述集合间关系的符号填写) 6.设nE ⊂¡是可数集,则*m E 07.设()f x 是定义在可测集E 上的实函数,如果1a ∀∈¡,()E x f x a ⎡⎤≥⎣⎦是 ,则称()f x 在E 上可测8.可测函数列的上极限也是 函数9.设()()n f x f x ⇒,()()n g x g x ⇒,则()()n n f x g x +⇒ 10.设()f x 在E 上L 可积,则()f x 在E 上 二、选择题1.下列集合关系成立的是( )A ()\B A A =∅I B ()\A B A =∅IC ()\A B B A =UD ()\B A A B =U2.若nR E ⊂是开集,则( )A E E '⊂B 0E E =C E E =DE E '=3.设(){}n f x 是E 上一列非负可测函数,则( )A ()()lim lim n n E En n f x dx f x dx →∞→∞≤⎰⎰ B ()()lim lim n n E E n n f x dx f x dx →∞→∞≤⎰⎰C ()()lim lim n n E En n f x dx f x dx →∞→∞≤⎰⎰ D ()()lim lim n n EE n n f x dx f x →∞→∞≤⎰⎰三、多项选择题(每题至少有两个以上的正确答案) 1.设[]{}0,1E =中无理数,则( )A E 是不可数集B E 是闭集C E 中没有内点D 1mE =2.设nE ⊂¡是无限集,则( )A E 可以和自身的某个真子集对等B E a ≥(a 为自然数集的基数)C E '≠∅D *0mE >3.设()f x 是E 上的可测函数,则( )A 函数()f x 在E 上可测B ()f x 在E 的可测子集上可测C ()f x 是有界的D ()f x 是简单函数的极限4.设()f x 是[],a b 上的有界函数,且黎曼可积,则( )A ()f x 在[],a b 上可测B ()f x 在[],a b 上L 可积C ()f x 在[],a b 上几乎处处连续D ()f x 在[],a b 上几乎处处等于某个连续函数四、判断题1. 可数个闭集的并是闭集. ( )2. 可数个可测集的并是可测集. ( )3. 相等的集合是对等的. ( )4. 称()(),f x g x 在E 上几乎处处相等是指使()()f x g x ≠的x 全体是可测集. ( ) 五、定义题1. 简述无限集中有基数最小的集合,但没有最大的集合.2. 简述点集的边界点,聚点和内点的关系.3. 简单函数、可测函数与连续函数有什么关系?4. [],a b 上单调函数与有界变差函数有什么关系?六、计算题1. 设()[]230,1\xx E f x xx E⎧∈⎪=⎨∈⎪⎩,其中E 为[]0,1中有理数集,求()[]0,1f x dx ⎰.2. 设{}n r 为[]0,1中全体有理数,(){}[]{}12121,,00,1\,,n n n x r r r f x x r r r ∈⎧⎪=⎨∈⎪⎩L L ,求()[]0,1lim n n f x dx →∞⎰.七、证明题1.证明集合等式:(\)A B B A B =U U2.设E 是[0,1]中的无理数集,则E 是可测集,且1mE =3.设(),()f x g x 是E 上的可测函数,则[|()()]E x f x g x >是可测集4.设()f x 是E 上的可测函数,则对任何常数0a >,有1[|()|]|()|E mE x f x a f x dx a≥≤⎰5.设()f x 是E 上的L -可积函数,{}n E 是E 的一列可测子集,且lim 0n n mE →∞=,则lim ()0nE n f x dx →∞=⎰实变函数试题库及参考答案(1) 本科一、填空题1.=2.≤3.闭集4.开集5.≤6.=7.可测集8.可测9.()()f x g x + 10.可积 二、单选题 ABB三、多选题ACD AB ABD ABC 四、判断题 × √√√ 五、定义题1.答:因为任何无限集均含有可数集,所以可数集是无限集中基数最小的,但无限集没有基数最大的,这是由于任何集合A ,A 的幂集2A 的基数大于A 的基数.2.答: 内点一定是聚点,边界点不一定是聚点,点集的边界点或为孤立点或为聚点.3.答:连续函数一定是可测函数;简单函数一定是可测函数;简单函数可表示成简单函数或连续函数的极限4.答:单调函数是有界变差函数,有界变差函数可表示成两个单调增函数之差.六、解答题1.解:因为0mE =,所以()3,.f x x a e =于[]0,1,于是()[][]30,10,1f x dx x dx =⎰⎰,而3x 在[]0,1上连续,从而黎曼可积,故由黎曼积分与勒贝格积分的关系,[]()41331000,11|44x x dx R x dx ===⎰⎰ 因此()[]0,114f x dx =⎰.2.解:显然()n f x 在[]0,1上可测,另外由()n f x 定义知,()0,.n f x a e =于[]0,1()1n ≥ 所以()[][]0,10,100nf x dx dx ==⎰⎰因此()[]0,1lim0nn f x dx →∞=⎰七、证明题 1.证明(\)()c A B B A B B =U I U ()()()c c A B A B B A B B B A B ===I U I U I U U U2.证明 设F 是[0,1]中的有理数集,则F 是可数集,从而*0m F =,因此F 是可测集,从而c F 可测,又[0,1]\[0,1]cE F F ==I ,故E 是可测集.由于E F =∅I ,所以1[0,1]()0m m E F mE mF mF ===+=+U ,故1mF =3.证明 设{}n r 为全体有理数所成之集,则()11[|()()][|()()][|()][|()]n n n n n E x f x g x E x f x r g x E x f x r E x g x r ∞∞==>=≥>=≥<I U U因为(),()f x g x 是E 上的可测函数,所以[|()]n E x f x r ≥,[|()]n E x g x r <是可测集,1,2,n =L ,于是由可测集性质知[|()()]E x f x g x >是可测集4.证明 因为()f x 在E 上可测,所以|()|f x 在E 上非负可测,由非负可测函数积分性质,[|()|][|()|]|()||()|E x f x a E x f x a Eadx f x dx f x dx ≥≥≤≤⎰⎰⎰而[|()|][|()|]E x f x a adx a mE x f x a ≥=⋅≥⎰,所以1[|()|]|()|E mE x f x a f x dx a≥≤⎰5.证明 因为lim 0n n mE →∞=,所以0,1N δ∀>∃≥,当n N ≥时,n mE δ<,又()f x 在E 上L -可积,所以由积分的绝对连续性,0,0,εδ∀>∃>当,e E me δ⊂<时|()|ef x dx ε<⎰于是当n N ≥时,n mE δ<,因此|()|nE f x dx ε<⎰,即lim ()0nE n f x dx →∞=⎰。
实变函数A卷(解答).docx
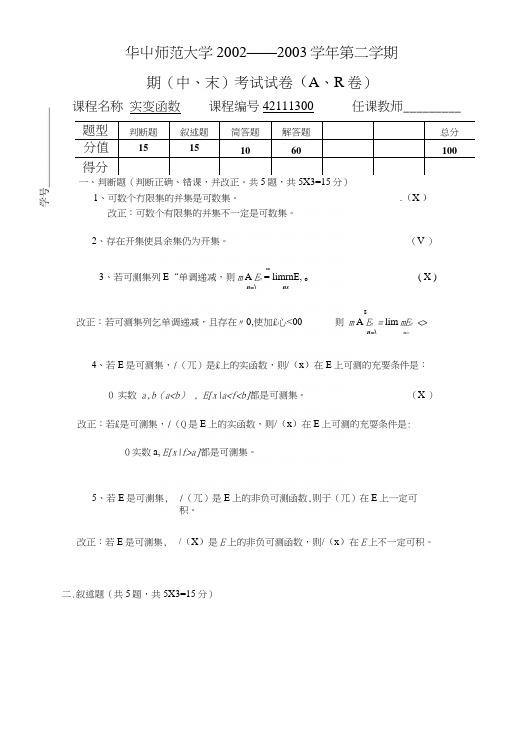
华屮师范大学2002——2003学年第二学期期(中、末)考试试卷(A、R卷)课程名称实变函数课程编号42111300 任课教师_________题型判断题叙述题简答题解答题总分分值151********得分一、判断题(判断正确、错课,并改正。
共5题,共5X3=15分)1、可数个冇限集的并集是可数集。
.(X )改正:可数个有限集的并集不一定是可数集。
2、存在开集使具余集仍为开集。
(V )co3、若可测集列E“单调递减,则m A E n = limrnE, o( X )n=\ ns改正:若可测集列乞单调递减,且存在〃0,使加£心<008则m A E n = lim mE n <>n=\n—4、若E是可测集,/(兀)是£上的实函数,则/(x)在E上可测的充要条件是:0 实数a,b(a<b) , E[x\a<f<b]都是可测集。
(X )改正:若£是可测集,/(Q是E上的实函数,则/(x)在E上可测的充耍条件是: 0实数a, E[x\f>a]都是可测集。
5、若E是可测集, /(兀)是E上的非负可测函数,则于(兀)在E上一定可积。
改正:若E是可测集, /(X)是E上的非负可测函数,则/(x)在E上不一定可积。
二.叙述题(共5题,共5X3=15分)1、集合的对等。
答:设A、B是两个集合,若A、BZ间存在一一对应,则称A与B对等。
2、可测集。
答:设E u R”,如果对任意T uR”,总有mV=/77*(Tn£) + m*(Tn£c),则称E为可测集。
3、可测集与几型集的关系。
答:设E为可测集,则存在人型集F,使F uE且加E二加F、加(E — F) = O。
4、叶果洛夫定理。
答:设mE < +oo , { f n(x))为E上儿乎处处有限的可测函数列,/(兀)也为E上儿乎处处有限的可测函数,如果AU)^/(x) a.e.于E,则对任意£>0,存在可测了集E£^E 使在E&上,f n (兀)一致收敛于/*(兀),而m{E-E G)< 8 o5、九(兀)在可测集E上依测度收敛于/(兀)的定义。
实变函数(复习资料_带答案)资料

集。
0, 开集 G E,使 m* (G E)
,则 E 是可测
(第 7 页,共 19 页)
3. (6 分)在 a, b 上的任一有界变差函数 f ( x) 都可以表示为 两个增函数之差。
5. (8 分)设 f ( x) 在 E a,b 上可积,则对任何 0 ,必存
b
在 E 上的连续函数 ( x) ,使 | f ( x) (x) | dx . a
E
四、解答题 (8 分× 2=16 分) .
1、(8分)设 f (x)
x2, x为无理数 ,则 f ( x) 在 0,1 上是否 R
1, x为有理数
可积,是否 L 可积,若可积,求出积分值。
五、证明题 (6 分× 4+10=34 分) . 1、(6 分)证明 0,1 上的全体无理数作成的集其势为 c
可测集;
二. 填空题 (3 分× 5=15 分)
1、设 An
11 [ , 2 ], n 1,2,
,则 lim An
_________。
nn
n
2、设 P 为 Cantor 集,则 P
o
,mP _____,P =________。
3、设 Si 是一列可测集,则 m i 1 Si ______ mSi i1 4、鲁津定理:
4.(8 分)设函数列 fn (x) ( n 1,2, ) 在有界集 E 上“基本上” 一致收敛于 f ( x) ,证明: fn (x) a.e.收敛于 f ( x) 。
2. x
E , 则存在 E中的互异点列
{
xn },
使 lim n
xn
x ……… .2
分
xn E, f ( xn ) a ………………… .3 分
实变函数(复习资料_带答案)资料

2页,共19页) 3、若|()|fx是可测函数,则()fx必是可测函数 4.设()fx在可测集E上可积分,若,()0xEfx,则()0Efx 四、解答题(8分×2=16分). 1、(8分)设2,()1,xxfxx为无理数为有理数 ,则()fx在0,1上是否R可积,是否L可积,若可积,求出积分值。 2、(8分)求0ln()limcosxnxnexdxn 五、证明题(6分×4+10=34分). 1、(6分)证明0,1上的全体无理数作成的集其势为c
6页,共19页) 又()0,mEF所以()fx是EF上的可测函数,从而是E上的 可测函数……………………..10分 《实变函数》试卷二 一.单项选择题(3分×5=15分) 1.设,MN是两集合,则 ()MMN=( ) (A) M (B) N (C) MN (D) 2. 下列说法不正确的是( ) (A) 0P的任一领域内都有E中无穷多个点,则0P是E的聚点 (B) 0P的任一领域内至少有一个E中异于0P的点,则0P是E的聚点 (C) 存在E中点列nP,使0nPP,则0P是E的聚点 (D) 内点必是聚点 3. 下列断言( )是正确的。 (A)任意个开集的交是开集;(B) 任意个闭集的交是闭集; (C) 任意个闭集的并是闭集;(D) 以上都不对; 4. 下列断言中( )是错误的。 (A)零测集是可测集; (B)可数个零测集的并是零测集; (C)任意个零测集的并是零测集;(D)零测集的任意子集是可测集; 5. 若()fx是可测函数,则下列断言( )是正确的 (A) ()fx在,abL可积|()|fx在,abL可积; (B) (),|()|,fxabRfxabR在可积在可积 (C) (),|()|,fxabLfxabR在可积在可积; (D) (),()fxaRfxL在广义可积在a,+可积 二. 填空题(3分×5=15分) 1、设11[,2],1,2,nAnnn,则nnAlim_________。 2、设P为Cantor集,则 P ,mP_____,oP=________。 3、设iS是一列可测集,则11______iiiimSmS 4、鲁津定理:__________________________________________ 5、设()Fx为,ab上的有限函数,如果_________________则称()Fx为,ab上的绝对连续函数。 三.下列命题是否成立?若成立,则证明之;若不成立,则说明原因或举出反例.(5分×4=20分) 1、由于0,10,10,1,故不存在使0,101和,之间11对应的映射。
实变函数(复习资料,带答案)

《实变函数》试卷一一、单项选择题(3分×5=15分) 1、下列各式正确的是( )(A )1lim n k n n k n A A ∞∞→∞===⋃⋂; (B )1lim n k n k n n A A ∞∞==→∞=⋂⋃;(C )1lim n k n n k nA A ∞∞→∞===⋂⋃; (D )1lim n k n k nn A A ∞∞==→∞=⋂⋂;2、设P 为Cantor 集,则下列各式不成立的是( ) (A )=P c (B) 0mP = (C) P P ='(D) P P =3、下列说法不正确的是( )(A) 凡外侧度为零的集合都可测(B )可测集的任何子集都可测(C) 开集和闭集都是波雷耳集 (D )波雷耳集都可测 4、设{}()n f x 是E 上的..a e 有限的可测函数列,则下面不成立的是( )(A )若()()n f x f x ⇒, 则()()n f x f x → (B){}sup ()n nf x 是可测函数(C ){}inf ()n nf x 是可测函数;(D )若()()n f x f x ⇒,则()f x 可测5、设f(x)是],[b a 上有界变差函数,则下面不成立的是( )(A) )(x f 在],[b a 上有界 (B) )(x f 在],[b a 上几乎处处存在导数(C ))('x f 在],[b a 上L 可积 (D)⎰-=b aa fb f dx x f )()()('二. 填空题(3分×5=15分)1、()(())s s C A C B A A B ⋃⋂--=_________2、设E 是[]0,1上有理点全体,则'E =______,oE =______,E =______.3、设E 是n R 中点集,如果对任一点集T 都_________________________________,则称E 是L 可测的 4、)(x f 可测的________条件是它可以表成一列简单函数的极限函数.(填“充分”,“必要”,“充要”)5、设()f x 为[],a b 上的有限函数,如果对于[],a b 的一切分划,使_____________________________________,则称()f x 为[],a b 上的有界变差函数。
(完整版)实变函数(复习资料_带答案)

《实变函数》试卷一一、单项选择题(3分×5=15分) 1、下列各式正确的是( )(A )1lim n k n n k n A A ∞∞→∞===⋃⋂; (B )1lim n k n k n n A A ∞∞==→∞=⋂⋃;(C )1lim n k n n k nA A ∞∞→∞===⋂⋃; (D )1lim n k n k nn A A ∞∞==→∞=⋂⋂;2、设P 为Cantor 集,则下列各式不成立的是( )(A )=P c (B) 0mP = (C) P P =' (D) P P =ο3、下列说法不正确的是( )(A) 凡外侧度为零的集合都可测(B )可测集的任何子集都可测(C) 开集和闭集都是波雷耳集 (D )波雷耳集都可测 4、设{}()n f x 是E 上的..a e 有限的可测函数列,则下面不成立的是( )(A )若()()n f x f x ⇒, 则()()n f x f x → (B){}sup ()n nf x 是可测函数(C ){}inf ()n nf x 是可测函数;(D )若()()n f x f x ⇒,则()f x 可测5、设f(x)是],[b a 上有界变差函数,则下面不成立的是( )(A) )(x f 在],[b a 上有界 (B) )(x f 在],[b a 上几乎处处存在导数(C ))('x f 在],[b a 上L 可积 (D)⎰-=b aa fb f dx x f )()()('二. 填空题(3分×5=15分)1、()(())s s C A C B A A B ⋃⋂--=_________2、设E 是[]0,1上有理点全体,则'E =______,oE =______,E =______.3、设E 是n R 中点集,如果对任一点集T 都_________________________________,则称E 是L 可测的4、)(x f 可测的________条件是它可以表成一列简单函数的极限函数.(填“充分”,“必要”,“充要”)5、设()f x 为[],a b 上的有限函数,如果对于[],a b 的一切分划,使_____________________________________,则称()f x 为[],a b 上的有界变差函数。
实变函数(复习资料,带答案).doc

《实变函数试卷一一、单项选择题(3分X5=15分)1、下列各式正确的是( )_________ oo oo oo oo(A) limA = u n A ; (B) lim A = n u A ;n—H=1k=n,?一z?=l k=n00 00 00 00(C) limA" = n u ; (D) lim= A k ;打一>oo z:=l k=n z?=l k=n2、设P为Cantor集,则下列各式不成立的是( )(A) ~P= c (B) mP = 0 (C) P = P (D) P=P3、下列说法不正确的是( )(A)凡外侧度为零的集合都可测(B)可测集的任何子集都可测(C)开集和闭集都是波雷耳集(D)波雷耳集都可测4、设以(4是£上的E有限的可测函数列,则下而不成立的是( )(A)若又(x)=>/(x),则又(x) + /(x) (B)sup{/…Cr)}是可测函数(O inf{//%)}是可测函数;(D)若/T H又⑺=>/U),则/(X)可测5、设f(X)是上有界变差函数,则卜*面不成立的是()(A) /(X)在[6Z,/7]上有界(B) /(X)在[6/,刎上儿乎处处存在导数c b(C) / (X)在上L 可积(D) J a f\x)cbc=f(b)-f(a)二.填空题(3分X 5=15分)1、(C s AuC v5)n(A-(A-B))= ________________2、设£是[0,1]上有理点全体,则E - ______ , E- ________ , E- _______ .3、设£是/?。
中点集,如果对任一点集r都,贝1J称£是£可测的4、/⑶可测的________ 条件是它可以表成一列简单函数的极限函数.(填“充分”,“必要”,“充要”)5、设/(x)为上的有限函数,如果对于的一切分划,使_____________________________________ ,则称/(x)为[6Z,/7]上的有界变差函数。
(完整版)实变函数期末复习

实变函数期末复习选择题1.设,...,],)(,[21121=-+=n nA nn 则 ( ) A.],[lim 10=∞→n n A B.],(lim 10=∞→n n A C.],(lim 30=∞→n n A D.),(lim 30=∞→n n A2.设N i i x i x A i ∈+≤≤=},:{23,则=∞=I 1i i A ( ) A.(-1,1) B.[0,1] C.∅ D.{0}3.集合E 的全体聚点所组成的集合称为E 的 ( )A.开集B.边界C.导集D.闭包4.若}{n A 是一闭集列,则Y ∞=1n n A是 ( )A.开集B.闭集C.既非开集又非闭集D.无法判断5若)(x f 可测,则它必是 ( )A.连续函数B.单调函数C.简单函数D.简单函数列的极限 6关于简单函数与可测函数下述结论不正确的是 ( )A.简单函数一定是可测函数B.简单函数列的极限是可测函数C.简单函数与可测函数是同一概念D.简单函数列的极限与可测函数是同一概念7设)(x f 是可测集E 上的非负可测函数,则)(x f ( )A.必可积B.必几乎处处有限C.必积分确定D.不一定积分确定8设E 是可测集,则下列结论中正确的是 ( )A.若)}({x f n 在E 上a.e 收敛于一个a.e 有限的可测函数)(x f ,则)(x f n 一致收敛于)(x fB.若)}({x f n 在E 上基本上一致收敛于)(x f ,则)(x f n a.e 收敛于)(x fC.若)}({x f n 在E 上a.e 收敛于一个a.e 有限的可测函数)(x f ,则)(x f n 基本上一致收敛于)(x fD.若)}({x f n 在E 上a.e 收敛于一个a.e 有限的可测函数)(x f ,则)(x f n ⇒)(x f9设)(x f 是可测集E 上可积,则在E 上 ( )A.)(x f +与)(x f - 只有一个可积B.)(x f +与)(x f - 皆可积C.)(x f +与)(x f - 一定不可积D.)(x f +与)(x f - 至少有一个可积 10.)(x f 在可测集E 上)(L 可积的必要条件是,)(x f 为 ( )A 、连续函数B 、几乎处处连续函数C 、单调函数D 、几乎处处有限的可测函数11设)(x D 为狄立克雷函数,则⎰=10)()(dx x D L ( )A 、 0B 、 1C 、1/2D 、不存在 12设}{nE 是一列可测集,ΛΛ⊃⊃⊃⊃n E E E 21,且+∞<1mE ,则有 ( )(A )n n n n mE E m ∞→∞==⎪⎭⎫ ⎝⎛⋂lim 1 (B) n n n n mE E m ∞→∞=≤⎪⎭⎫ ⎝⎛⋃lim 1 (C )n n n n mE E m ∞→∞=<⎪⎭⎫ ⎝⎛⋂lim 1; (D )以上都不对 13设),0(n A n =, N n ∈, 则=∞→n n A lim( ) A 、Φ B 、[0, n] C 、R D 、(0, ∞)14设)1,0(n A n =, N n ∈, 则=∞→n n A lim ( )A 、(0, 1)B 、(0, n1) C 、{0} D 、Φ、 填空题1、设A 为一集合,B 是A 的所有子集构成的集合;若A =n, 则B =2、设A 为一集合,B 是A 的所有子集构成的集合;若A 是一可数集, 则B =3、若c A =, c B =, 则=⋃B A4、若c A =, B 是一可数集, 则=⋃B A5、若c A =, n B =, 则=⋃B A6、若}{n A 是一集合列, 且c A n =, =⋃∞=n n A 1 7、设}{i S 是一列递增的可测集合,则=∞→)lim (n n S m _______。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《实变函数》 一、单项或多项选择题1、下列正确的是(234(3) (?1UB )\C = ?1U (B C UC )C 2、下列正确的是(24)(1) 无理数集是可数集;(2) 超越数构成的集合是不可数集;(3) 若/?屮两个Lebesgue 可测集A 和B 的基数相等,则它们的测度也相等;(4) 0表示全体有理数集,则Q?。
也是可数集.3、在R 中令A = {1,丄丄…丄,…},则(2 3 n6、设几九 wM(X),则(12 3 4(3) /2 G M(X)7、若/在[0,1]上乙可积,则下列成立的是8、设= 1,2,3,…)是X 上儿乎处处有限的可测函数,则下列结论正确的是(1(1)若人 则£—/,心.;(1) A\(B\C) = (A\B)\C(2) AU(BAC) =(AUB )n (AUC )(4)⑷B)\C = A\(BUC )(1) A 为闭集 (2) A 为开集 (3) 几{0}(4) A 为疏集4、设 AuR 满足 mA = 0 ,贝 ij ( 1 3 (1) A 为Lebesgue 可测集)(2)(3)任意可测函数/在A 上可积(4) 4为疏集5、在/?上定义/(%),当兀为有理数时, f(x) = 1 ,当x 为无理数时,/(x) = 0,贝ij( 3(1) /儿乎处处连续 (2) /不是可测函数(3)/在上处处不连续(4) /在/?上为可测函数⑴\f <+oo 在[0,1 ]上儿乎处处成立 (2) |.f|在[0,1]上厶可积 (3) /在[0,1]±几乎处处连续(4)兀在[of 上非厶可积(2) 若九 T/,d.e.,则九(3) 若 f n —> f ,a.u.,则 f n T f ; (4) 若 f 厶 f,则£->/•,“.・9、若{A“}为降列,且 M = 2,贝(4 )n —>oc、“8 、(1) 0(2) 0(3) “U4(4) “CM1心10、有界实函数/在区间[G , /?]± Riemann 可积的充要条件是/的不连续点集为( 4 )11、设f eBV [a,b ]f 则下列成立的是(1 416、超越数的个数为(3(1) 2 (2) a (3) c (4) 2C(1)空集(2)有限集 (3)可数集 (4)零测度集(1) 于在[a 问上有界; (2) /在[a 问上连续; (3) /在[a 问上可微; (4) /是两个增函数Z 差.12、整数集 的内部和闭包分别为(1)(3) 0,(1) 0, (2) (4)13. 设/(%) =x,xe[0,l]2-x,x w(l ,2]' 令 A = <x\f(x)(1) 0(2) 1(3) 2(4)14、下列哪些集合是测度为零的不可数集(3 )(4)(1) 031O )XEB(2) 1 ,则(1(3) 2 ⑷3100,XG [0,1]\17、f G AC[0,1],/(O) = 2,Kf = 0,a.e , B'J/(x)=_318、 设A ,%是R 的可测集,且A 0A 2,则下列正确的是( 2 4 )(1)< mA.(2) mA l <mA 2(3) mA x -mA 2 =\ A 2)(4) mA x =777(71^X2) + mA 219、 当/在[1,+00)上连续且Lebesgue 可积时,则lim f(x)=1L7X->4<0(1) 0 (2) 1 (3) -1 (4) +0020、 人2”-1=[°」],A” =[°,2],(斤= 1,2,…),则limA “和lim 人分别为" >1(I) [0,1],[0,2] ⑶[0,2],[0,1]21、下列正确的是(1 4 )(1) (4UB )\C =(A\C )U (B\C ) (3) A\(B\C) = (A\B)\C ⑵[0,1],[0,2](4) [0,2],[0,2](2) ACl(BUC) =(4nB )UC (4) (A\B)\C = A\(BUC ))⑵ r 1 2 3(Aus )=r ,(A )ur 1(5) ⑷ /-i (An5)=r i (A )ny 1(B )2 3 )24、 设人是[0,1]上所有有理数构成的集合,则川二(3 )(1) A (2) [0,l]\A (3) El(4)以上都不对25、 下列说法正确的是(12 3)1 A =(3) B = P 7(B )23、下列与 有相同基数的集合是( (1) [0,1] (2)3(4)(1) 0(2) 1 (3) 2 (4) 322、设f:X —X 是一个映射,4,B u X ,下列正确的是(2 4(2)上的开集都可以表示成互不相交的开区间的并(4) 的了集不是开集就是闭集 26、 下列正确的是(1 ) (1) 有理数集是可数集;(2) 代数数构成的集合是不可数集;(3) 若中两个Lebesgue 可测集A 和B 的测度相等,则它们的基数也相等; (4) [0,2]内包含的点比[0,1]内包含的点多。
27、 下列说法不正确的是(24)(1)凡外测度为零的集合都可测 (2)可测集的任何了集都可测 (3)开集和闭集都可测 (4)不存在不可测集28、 设/(x )是X 上的可测函数,则(4)(1) /(兀)是X 上的连续函数 (2) /(X )是X 上的勒贝格可积函数 (3) /(x )是X 上的简单函数(4) /(x ) nJ'表示为一列简单函数的极限 29、设{£}是X 上一列可测函数,贝ijsup f n 是X 上的(3n(1)可导函数 (3)可测函数30、下列说法正确的是(1(1)若/(兀)是X 上的Lebesgue 可积两数,则/(兀)在X d.匕上有界;(2) 若/(兀)是X 上的Lebesgue 可积函数,则/(兀)在X 上有界;(3) 若/(兀)是X 上的Lebesgue 可积函数,则/(兀)在火± Riemann 可积;(4) 以上都不对。
31、设/(兀)是X 上的Lebesgue 可积函数,贝ij ( 1 2 3 4 )(1) |/(x)| Lebesgue ^积; (2) f +Lebesgue 可积;(3) f~ (x) Lebesgue "J 积;(4) .f(x)在X 的任意可测子集上的Lebesgue 可积。
32、下列说法正确的是( 2 3 4)(2)连续函数(4)(1)有界变差函数是单调函数;(2)单调函数是有界变差函数;(3)绝对连续函数是有界变斧函数;(4)Lipschitz函数是绝对连续函数。
00 33、关于A=C\■ (1 一丄,2 +丄、的说法正确的是( 2 4 )H = 11 n n)(1) A是开集(2) A是闭集(3) A = [1,2]⑷ A = (l,2)34、设A =[0,\],则A f,=( 2 )(1) 0⑵(0,1)(3) [0,1]⑷{0,1}35、设/(兀)是上的连续函数,贝IJ对任意实数{x\f(x)>a}是(1)开集(2)闭集(3)可测集(4)零测度集36、设九= 1,2,3,…)是X上几乎处处冇限的可测函数,f n T/,d.e.的(1 )(1)充分条件(2)必要条件(3)充要条件(4)既不充分也不必要条件l,x< 1且兀W37、设/(%) = < 2,X> 1且兀G,则爲心( 4 )2x,x 电£(1) 3(2) 2(3) 1(4) 4则/则(12 4(1 3 ) —> 是38、设/(兀)是X上的可测函数,若{/(x)<^,JX'X(1)/(X)在X上L可积;(2)/(兀)在X上L积分存在;(3)|/(x)| 在X 上/?可积;(4)/(%)在X上ae有限;39、关于零测度集下列说法正确的是(24 )(1)零测度集是可数集;(2)零测度集的任何子集是零测度集;(3)无穷多个冬测度集的并还是冬测度集;(4)可数多个零测度集的并还是零测度机。
40、设//(X1) = /z(X2)<oo,则X]和X?的关系是(4 )(1) X}=X2(2) X]UX2 (3) X, z)X2(4)X], X2至多差一个零测度集41、设f:X^X是一个映射,下列正确的是(124 )⑵ r i(AUB)=r1(^)ur1(^)⑴ /(AUB)= /(A)U/(B)⑷ r,(AnB)=r,(A)nr1(s)7? + 1 —\n = 2,3,…),则(3 4n-1(1) A(zB (2) B^A43、下列基数是c的集合为(2 4 (1) (2) (3)44、下列说法正确的是(12 3(1)开集是可测集;(2)闭集是可测集;(3)可数集是零测度集;(4)零测度集是可数集。
45、设y,g,£wM(X),则(12 3 4 (1) fgeM(X)(3) sup / G M(X)(3) AC\B = 0(4) J(A,B)= 0)(4)所有无理数构成的集合)(2) /xzgwM(X)46、设.九,/(〃 = 1,2,3,…)是X上儿乎处处有限的可测函数,则下列结论正确的是(2 3 )(1)若心仁则£-/>.仏・⑵若心仁则存在{九}为{£}的子列,使得九T/4"(3)若f n—> f ,a.u.9则九 t /;(4)若九T/\a.e.,则九47、设于为[a,b].上增函数,则/为(2 3 450、设九 W AT(X)(M = 1,2,…),则(3 4 )(1)严(九=严/ ⑵ £iim/ = lini£An nn n51、 设M,N 是两集合,则M\(M\N)= ( 3 )(1) M(2) N(3) MflN(4) 052、 设九J© = 1,2,3,…)是X 上几乎处处有限的可测函数,则是九T/的 (1 )(1)充分条件 (2)必要条件(3)充要条件 (4)既不充分也不必要条件53、人0 = 1,2,3,…)是一列集合,则下列正确的是(2 3)8 00liniA,=AUA"T8 ?I =1 m-noo54、设力=U A,基数为C ,则对于4下列说法正确的是(4n=\(2) 4”都是有限集 (4)至少有一个A”是不可数集)(3) T (4) 2C56、关于[0,1] ±的冇限减函数的说法,下列正确的是(13 4(1)绝对连续函数 (3)有界变差函数 (2) nJ'测函数 (4)有界函数0,兀为超越数 1,兀为代数数 (1) 1(2) 0(3) +0049、下列哪些函数是有界变羌函数(13 4(4)以上都不对)(3) Lipschitz 函数(4) 绝对连续函数(1)______ 00 00⑵乔A 严DLKH =1 /n=n<X> 00 ⑶ limA,, =UPl An28W =1 /w =n00 00(4) limA, =UriA刃一>8X 1 1n=l m=n148设 /(%) = - )(1)单调函数 (2)有界函数(1) 是有界变差函数; (2) 是连续函数;(3) 是可测畅数;(4) 是儿乎处处连续的函数。
