《管理运筹学》第12章排序与统筹方法
运筹学答案_第_12_章__排序与统筹方法
习题 1 解：各零件的平均停留时间为： 6p1+5p2 +4p3 +3p4 +2p5 + p1 6 由此公式可知，要让停留的平均时间最短，应该让加工时间越少的零件 排在越前面，加工时间越多的零件排在后面。 所以，此题的加工顺序为：3，7，6，4，1，2，5
习题 2 解：此题为两台机器，n 个零件模型，这种模型加工思路为：钻床上加工时v 1aFra bibliotekv 2
b
v4
c
d
v 3
设第 V 发生的时间为 x ，(V, V)间的工序提前完工的时间为 y
i
ij
目标函数 min f = 4.5(x4 −x1)+ 4y12 + y24 +4y23 + 2y34
s.t. x2 − x1 ≥3− y12 x3 − x2 ≥ 4− y23 x4 − x2 ≥7− y24 x4 − x3 ≥5− y34 x1 = 0 y12 ≤2 y23 ≤2 y24 ≤4 y34 ≤3 xi ≥ 0, yij ≥0
这个正态分布的均值 E(T) =12.08
2
2
2
其方差为：σ ＝σb ＋σd ＋σg ＝０.70 则σ ＝０.84
当以９８％的概率来保证工作如期完成时，即：φ(u) =0.98，所以 u=2.05
此时提前开始工作的时间Ｔ满足： T −12.08 =2.05 0.84
所以Ｔ＝13.8 ≈14
习题 7 解：最短的施工工时仍为４＋５＋６＝１５ 具体的施工措施如下：
以上 i=1，2，3，4； j=1，2，3，4 用管理运筹学软件中的线性规划部分求解，得到如下结果： minf=46.5 x1=0,x2=1, x3=5,x4=7,
管理运筹学—统筹图(免费)
第三节
统筹图的绘制
三、绘制统筹图的步骤
（四）检查调整布局 1、线路有无交叉
2、逻辑关系有无错误 3、是否存在闭合回路 4、作业有无遗漏重复 5、有无多余的结点 （五）进行编号注记 1、给结点编号
2、给作业注记（作业代号、作业时间）
第三节
统筹图的绘制
三、绘制统筹图的步骤
（六）确定关键线路
1、寻找关键线路 统筹图中，时间消耗最长的线路。 2、标注关键线路 关键线路一般用粗箭线、双箭线和彩色箭 线表示。
第二节
三、结点
统筹图的组成
（五）编号： 给结点编号必须遵循每项作业箭头结点的号 码大于箭尾结点的号码的原则。 1、顺序号：从左至右、由小到大给结点编 号。起始结点编号一般为1，最终结点编号最大。
1
2
3
4
2、跳编号：各结点的编号不一定要连续，可 以适当留一些空号，以备修改时用。此种方法一 般用于较为复杂的作业。
B D E
B D
E
第三节
统筹图的绘制
二、常见作业逻辑关系的画法
（六）常见作业逻辑关系画法示例 8、作业A完成后进行D，A、B均完成后进行E，B、 C均完成后进行F A A D D E
F B D F
B
C
E
第三节
统筹图的绘制
二、常见作业逻辑关系的画法
（六）常见作业逻辑关系画法示例
9、作业A、B、C完成 后进行D，B、C完成后E A D 10、作业A、B、C完成 后进行D，C完成后进行E A B D
第四节
统筹图时间参数计算
一、结点时间参数计算
（一）结点最早实现时间 1、概念： 结点最早实现时间是保证其所有紧前作业都 能完成的前提下，该结点最早实现的时限，简称 结早。（指从起始结点到该结点的最长时间和） 2、表示：TE（j） 3、标注：结点上方的方块内。“□”
《管理运筹学》复习提纲
【管理运筹学】复习提纲第一章绪论〔P1-P9)1.决策过程〔解决问题的过程〕〔1〕认清问题。
〔2〕找出一些可供选择的方案。
〔3〕确定目标或评估方案的标准。
〔4〕评估各个方案：解的检验、灵敏性分析等。
〔5〕选出一个最优的方案：决策。
〔6〕执行此方案：回到实践中。
〔7〕进行后评估：考察问题是否得到圆满解决。
其中：〔1〕〔2〕〔3〕形成问题。
〔4〕〔5〕分析问题：定性分析与定量分析，构成决策2.运筹学的分支：线性规划、整数线性规划、动态规划、图与网络模型、存储论、排队论、排序与统筹方法、决策分析、对策论、预测、目标规划，此外，还有多目标规划、随机规划、模糊规划等。
3.运筹学在工商管理中的应用1〕生产方案：生产作业的方案、日程表的编排、合理下料、配料问题、物料管理等，追求利润最大化和本钱最小化。
2〕库存管理：多种物资库存量的管理，某些设备的库存方式、库存量等确实定。
3〕运输问题：确定最小本钱的运输线路、物资的调拨、运输工具的调度以及建厂地址的选择等。
4〕人事管理：对人员的需求和使用的预测，确定人员编制、人员合理分配，建立人才评价体系等。
5〕市场营销：广告预算、媒介选择、定价、产品开发与销售方案制定等。
6〕财务和会计：预测、贷款、本钱分析、定价、证券管理、现金管理等。
此外，还有设备维修、更新，工程选择、评价，工程优化设计与管理等。
3.学习管理运筹学必须使用相应的计算机软件，必须注重学以致用的原那么。
第二章线性规划的图解法(P10-P26)1.一些典型的线性规划在管理上的应用合理利用线材问题：如何在保证生产的条件下，下料最少；配料问题：在原料供给量的限制下如何获取最大利润；投资问题：从投资工程中选取方案，使投资回报最大；产品生产方案：合理利用人力、物力、财力等，使获利最大；劳动力安排：用最少的劳动力来满足工作的需要；运输问题：如何制定调运方案，使总运费最小。
2.线性规划的组成目标函数：max f 或min f ；约束条件：s.t. (subject to)，满足于；决策变量：用符号来表示可控制的因素。
管理运筹学(第3版)章后习题解析(上、下合集)课后习题答案
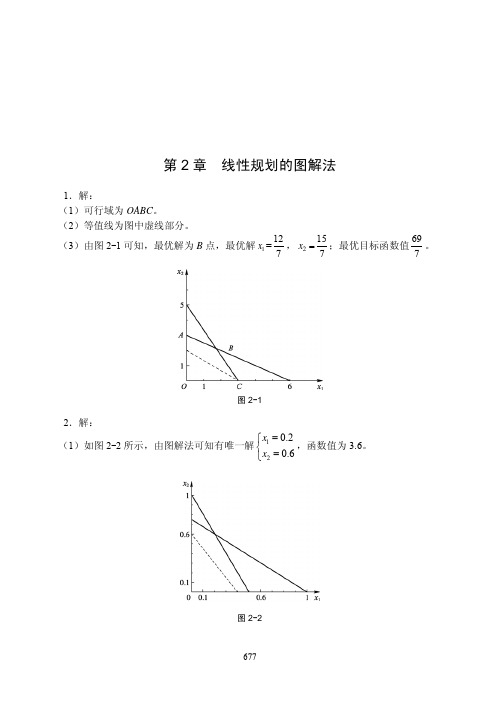
用图解法求解如图 9-2 所示。
717
图 9-2
如图 9-2 所示，解为区域 ABCD，有无穷多解。 （2）由图 9-2 可知，如果不考虑目标 1 和目标 2，仅仅把它们加工时间的最大限度分别为 60 和 180 小时作为约束条件，而以利润最大化为目标，那么最优解为 C 点（360，0） ，即生产 产品 A360 件，最大利润为 1 420 元。结果与（1）是不相同的，原因是追求利润最大化而不仅 仅是要求利润不少于 1 300 元。 （3）如果设目标 3 的优先权为 P1，目标 1 和目标 2 的优先权为 P2，则由图 9-2 可知，满意 解的区域依然是 ABCD，有无穷多解，与（1）的解是相同的，原因是（1）和（3）所设定的目 标只是优先级别不同，但都能够依次达到。 5．解： 设该纸张制造厂需要生产一般类型纸张 x1 吨，生产特种纸张 x2 吨。 （1）目标规划模型如下。 min s.t
716
+ − + − = 0, d 2 = 0,d 3+ = 0, d3− = 4.211, d 4 = 14.316, d 4 = 0。 得 x1 = 9.474, x2 = 20, x3 = 2.105, d1+ = 0, d1− = 0, d 2
所以，食品厂商为了依次达到 4 个活动目标，需在电视上发布广告 9.474 次，报纸上发布 广告 20 次，广播中发布广告 2.105 次。 （使用管理运筹学软件可一次求解上述问题） 3．解： （1） 设该化工厂生产 x1 升粘合剂 A 和 x2 升粘合剂 B。 则根据工厂要求， 建立以下目标规划模型。 min s.t
s.t x1 ≤ 10 x2 ≤ 20 x3 ≤ 15 20 x1 + 10 x2 + 5 x3 − d1+ + d1− = 400
管理运筹学期末复习资料【韩伯棠】
运筹学（Operational Research）复习资料第一章绪论一、名词解释1.运筹学：运筹学是应用分析、试验、量化的方法，对经济管理系统中的人力、物力、财力等资源进行统筹安排，为决策者提供有依据的最优方案，以实现最有效的管理。
二、选择题1.运筹学的主要分支包括（ABDE ）A图论B线性规划C非线性规划D整数规划E目标规划2. 最早运用运筹学理论的是（ A ）A . 二次世界大战期间，英国军事部门将运筹学运用到军事战略部署B . 美国最早将运筹学运用到农业和人口规划问题上C . 二次世界大战期间，英国政府将运筹学运用到政府制定计划D . 50年代，运筹学运用到研究人口，能源，粮食，第三世界经济发展等问题上第二章线性规划的图解法一、选择题/填空题1.线性规划标准式的特点：（1）目标函数最大化（2）约束条件为等式（3 决策变量为非负（4 ) 右端常数项为非负2. 在一定范围内，约束条件右边常数项增加一个单位：（1）如果对偶价格大于0，则其最优目标函数值得到改进，即求最大值时，最优目标函数值变得更大，求最小值时最优目标函数值变得更小。
（2）如果对偶价格小于0，则其最优目标函数值变坏，即求最大值时，最优目标函数值变小了；求最小值时，最优目标函数值变大了。
（3）如果对偶价格等于0，则其最优目标函数值不变。
3.LP模型（线性规划模型）三要素：（1）决策变量（2）约束条件（3）目标函数4. 数学模型中，“s·t”表示约束条件。
5. 将线性规划模型化成标准形式时，“≤”的约束条件要在不等式左端加上松弛变量。
6. 将线性规划模型化成标准形式时，“≥”的约束条件要在不等式左端减去剩余变量。
7．下列图形中阴影部分构成的集合是凸集的是A【解析】：如何判断是凸集？凸集：两点之间连线在图内凹集：两点之间连线在图外8. 线性规划问题有可行解且凸多边形无界，这时CA没有无界解 B 没有可行解 C 有无界解 D 有有限最优解9. 对于线性规划问题，下列说法正确的是（ D ）A. 线性规划问题可能没有可行解B. 在图解法上，线性规划问题的可行解区域都是“凸”区域C. 线性规划问题如有最优解，则最优解可在可行解区域顶点上到达D. 上述说法都正确第三章线性规划问题的计算机求解一、名词解释1.相差值：相应的决策变量的目标系数需要改进的数量，使得决策变量为正值。
管理运筹学讲义 第12 章 排队理论
10
OR:SM
第三节 标准M/M/1模型
一、模型特征
输入过程
顾客源无限； 顾客到达方式是单个到达，且相互独立； 输入过程服从参数为 的泊松分布，到达过程平稳。 队列为单队； 队长无限，即系统容量无限； 系统按先到先服务的等待制规则进行服务 只有一个服务台； 服务方式为单个服务，服务时间相互独立； 服务时间服从相同参数 的负指数分布。
第12 章 排队理论
学习要点 Sub title
正确理解排队系统中排队规则和服务规则 顾客输入过程和服务过程的时间分布函数 排队问题的求解步骤及运行指标间的关系 标准M/M/1模型的状态方程及其运行指标 标准M/M/c模型与c个M/M/1模型的差别 典型排队系统的结构优化和运行优化问题
求运行指标:
• 顾客数 • 排队时间 • 忙期
8 OR:SM
第二节 排队问题求解
二、分布函数
• 泊松分布
条件：
输入流的平稳性 输入流无后效性 输入流的普通性 输入流的有限性
n! 期望E (t ) t 方差 2 t
v0 v0
Pn (t )
性质： ( t ) n
平均等待时间 Wq Ws [服务时间]
忙期概率
P 0 忙 1 P
Ws Wq 1
Ws
1
Ws
Ls Ws
Lq Wq
16
Ls Lq Lq
OR:SM
第三节 标准M/M/1模型
例题
为了评价某单人理发馆随机服务系统，记录了100个工作小时， 每小时来理发的顾客数的统计情况。又记录了100次理发所用的时 间，如表所示。
排序与统筹方法
时间——费用优化
• 正常完成：
– 完成工序j的正常所需时间为Tj – 直接费用为cj
• 最快速度完成：
– 完成工序j的最快速度完成所需时间为Tj’ – 直接费用为cj’
• 直接费用变动率kj：缩短工序j的一天工期所 ' 增加的直接费用 c j cj
kj Tj T
' j
时间——费用优化
• 解：设网络图上第i点发生的时间为xi，工序提前完 工的时间为yij min f=120y27+300y23+400y24+500y25+230y37+350y46+ 400y57+290y67 s.t. x2-x160-y12, x7-x2 45-y27, x3-x210-y23, x4-x220-y24 , x5-x240-y25, x7-x318-y37, x6-x430-y46 , x5-x40 , x7x515-y57, x7-x625-y67, x1 =0, x8 150, y120, y2715, y23 5, y24 10, y25 5, y37 8, y46 10, y575, y780, xi 0，yij 0.（对一切可能的i j)
1. 优先安排关键工序所需的资源。 2. 利用非关键工序的时差，错开各工序的开 始时间。 3. 统筹兼顾工程进度的要求和现有资源的限 制，多次综合平衡。
经过调整，我们让非关 键工序f从第80天开始， 工序h从第110天开始。 找到了时间-资源优化的 方案
58人 64人 42人 26人 65人
60
80
• 若上述工序都按最早开始时间安排，那么从 第60天至第135天的75天里，所需的机械加 工工人人数如下图：
管理运筹学
线性规划标准型
例：将以下线性规划问题转化为标准形式
Min f = 3.6 x1 - 5.2 x2 + 1.8 x3 s. t. 2.3 x1 + 5.2 x2 - 6.1 x3 ≤15.7
4.1 x1 + 3.3 x3 ≥8.9 x1 + x2 + x3 = 38 x1 , x2 , x3 ≥ 0
24
§2 线 性 规 划 的 图 解 法
例1. 目标函数：
Max z = 50 x1 + 100 x2 约束条件：
s.t. x1 + x2 ≤ 300 (A) 2 x1 + x2 ≤ 400 (B)
x2 ≤ 250 (C) x1 ≥ 0 (D) x2 ≥ 0 (E) 得到最优解： x1 = 50， x2 = 250 最优目标值 z = 27500
a21 x1 + a22 x2 + … + a2n xn ≤ （ =, ≥ ）b2 …… …… am1 x1 + am2 x2 + … + amn xn ≤ （ =, ≥ ）bm x1 ，x2 ，… ，xn ≥ 0
• 标准形式 目标函数： 约束条件：
Max z = c1 x1 + c2 x2 + … + cn xn
备台时及A、B两种原材料的消耗以及资源的限制，如下表：
甲
乙
资源限制
设备
1
1
300 台时
原料 A
2
1
400 千克
原料 B
0
1
250 千克
单位产品获利
50 元
100 元
问题：工厂应分别生产多少单位甲、乙产品才能使工厂获利最多？
第十二章排序与统筹
§11.1 车间作业计划模型
如果按照 3、2、4、5、6、1 顺序加工零件， 也可以计算出各零件在车间的停留时间，如表所示
零件 加工时间Pi 停留时间Tj 零件 加工时间Pi 停留时间Tj
3
0.5
0.5
5
1.3
4.7
2
2.0
2.5
6
1.5
6.2
4
0.9
3.4
1
1.8
8
于是各零件平均停留时间为
0.5 2.5 3.4 4.7 6.2 8 4.2（ 2 小时） 6
第一
§11.1 车间作业计划模型
若最小数为 ai，则将零件 i 排在第一位加工； 若最小数为 bj，则将零件 j 排在最后一位加工。
零件 1 2 3 4 5
车床 1.5 2.0 1.0 1.25 0.75
磨床 0.5 0.25 1.75 2.5 1.25
零件加工顺序 第四 第五 第二
第一
§11.1 车间作业计划模型
设 a1， a2，…，an； 和 b1， b2，…，bn 分别是零件 1，2，…，n 在机器 A 和 B 上的加工时间，则使
得全部零件的总加工时间最短的排序算法为：
1). 找出加工时间 a1，a2，…，an，b1，b2，…，bn，中的
最小数。
2). 若最小数为 ai，则将零件 i 排在第一位加工，并从零件集
§11.1 车间作业计划模型
这样可以计算出按照 1、2、3、4、5、6 顺 序加工零件，各零件在车间的停留时间，如表所示
零件 加工时间Pi 停留时间Tj 零件 加工时间Pi 停留时间Tj
1
1.8
1.8
4
0.9
管理运筹学_统筹图
1
A
2
C D
9
K
10
G
统筹方法
练习：根据作业明细表绘制统筹图： I 3、 作业代号 A B C D E F G H 紧前作业 / / / A C B B DF GE
A
2
D F
5
H
1
B
C
3
4
G
7
I
E
6
统筹方法
练习：根据作业明细表绘制统筹图： 4、 作业代号 紧前作业 A
统筹方法
3．工作的表示方法： ⑴实工作： 它是由两个带有编号的圆圈和一个箭杆组成。
i
⑵虚工作：
工作名称 持续时间
j j
i
0
统筹方法
二、节点
1．概念： 指网络图的箭杆进入或引出处带有编号的圆圈。它表示其 前面若干项工作的结束或表示其后面若干项工作的开始。
2．特点：⑴它不消耗时间和资源；
⑵它标志着工作的结束或开始的瞬间； ⑶两个节点编号表示一项工作。 3．节点种类：
作业代号 作业内法 （三）按规则绘制草图 1、统筹图是有向图，箭头一律向右。 2、统筹图中只允许有一个起始结点，一个最终结 点，不允许出现缺口。 3、两个结点之间只能画一个作业相连结。 4、统筹图中不允许出现闭合回路。 （四）检查调整布局 1、线路有无交叉
2、逻辑关系有无错误 3、是否存在闭合回路 4、作业有无遗漏重复 5、有无多余的结点
a
20
d
2 5 4
f
8 8
i
20
h 10 e
10 1 3 7
b
28
6
j
15
9
g 10
c
15 5
l 10
管理运筹学第二版 课后习题答案 (韩伯棠主编) 高教版
第2 章线性规划的图解法1、解：x26A1O01BC36x1a.可行域为 OABC。
b.等值线为图中虚线所示。
c.由图可知，最优解为 B 点，最优解：x1 =1215x2 =，最优目标函数值：7769。
72、解：a x210.60.1O0.10.6x1有唯一解x1 = 0.2x 2 = 0.6函数值为3.6b c d e 无可行解无界解无可行解无穷多解20x1 =923f 有唯一解函数值为83x2 =33、解：a 标准形式：max f = 3x1 + 2 x 2 + 0s1 + 0 s 2 + 0s 39 x1 + 2 x 2 + s1 = 303x1 + 2 x 2 + s 2 = 132 x1 + 2 x 2 + s3 = 9x1 , x 2 , s1 , s 2 , s3 ≥ 0b 标准形式：max f = −4 x1 − 6 x3 − 0s1 − 0s23x1 − x 2 − s1 = 6x1 + 2 x 2 + s 2 = 107 x1 − 6 x 2 = 4x1 , x 2 , s1 , s 2 ≥ 0c 标准形式：max f = − x1' + 2 x2 − 2 x2 − 0s1 − 0s2'''− 3x1 + 5 x 2 − 5 x 2' + s1 = 70''2 x1' − 5 x 2 + 5 x 2' = 50''3x1' + 2 x 2 − 2 x 2' − s 2 = 30''x1' , x 2 , x 2' , s1 , s 2 ≥ 0''4 、解：标准形式：max z = 10 x1 + 5 x 2 + 0 s1 + 0 s 23x1 + 4 x 2 + s1 = 95 x1 + 2 x 2 + s 2 = 8x1 , x 2 , s1 , s 2 ≥ 0s1 = 2, s2 = 0标准形式：min f = 11x1 + 8 x 2 + 0s1 + 0s 2 + 0s310 x1 + 2 x 2 − s1 = 203x1 + 3x 2 − s 2 = 184 x1 + 9 x 2 − s3 = 36x1 , x 2 , s1 , s 2 , s3 ≥ 0 s1 = 0, s2 = 0, s3 = 136 、解：b 1 ≤ c1 ≤ 3c 2 ≤ c2 ≤ 6d x1 = 6x2 = 4x 2 = 16 − 2 x1e x1 ∈[4,8]f 变化。
《管理运筹学统筹》PPT幻灯片
④在网络图中，除了关键线路之外，其余的都是非关键线路； ⑤当管理人员由于工作疏忽，拖长了某些非关键工作的持续
时间，就可能使非关键线路转变为一、 绘制网络图的基本规则
1．必须正确表达已定的逻辑关系；
序号 工作之间的逻辑关系
网络图中的表示方法
说明
1
A、B两项工作依 次施工
A
B
A制约B的开始，
B依赖A的结束
A
2
A、B、C三项工 作同时开始施工
B
C
A、B、C三项 工作为平行施 工方式
第三节 双代号统筹图的绘制
三、线路
1．概念：
指网络图中从起点节点开始，沿箭线方向连续通过一系列箭线 与节点，最后到达终点节点的通路。
2．线路时间： 它是指线路所包含的各项工作持续时间的总和。
A
2
D
4
H
1
9
3
G 6
C 3
1
6
B
3
2
F 1
5
I 7
统筹方法
3．线路种类： ⑴关键线路： 在网络图中线路持续时间最长的线路。 ⑵非关键线路：
i 工作名称 持续时间
j
⑵虚工作：
i0
j
统筹方法
二、节点
1．概念：指网络图的箭杆进入或引出处带有编号的圆圈。它表示其 前面若干项工作的结束或表示其后面若干项工作的开始。
2．特点：⑴它不消耗时间和资源； ⑵它标志着工作的结束或开始的瞬间； ⑶两个节点编号表示一项工作。
运筹学12.2统筹图中有关参数的计算
2019/6/6
8
运 筹 学 Operations Research
3.工序的最早可能开工时间：tES(i, j)
tES (i,j)tES (i)
统筹方法的根本任务就是本着“向关键路线要时间，向非 关键路线要资源”的指导思想，制订出最优的生产计划.
2019/6/6
3
运 筹 学 Operations Research
关键路线的求解：标号法 1.t(1)=0.
2. t( i) m { t( k a ) tx ( k ,i)i} 2 ,3 ,, ,n . k i 将取最大值的弧(k, i)改为粗线.
2019/6/6
6
运 筹 学 Operations Research
有关参数的计算： 1.事项的最早可能开工时间：t ES ( j)
tE(S 1)0; tE(Sj)m ij { atEx (Si)t(i,j)}j ,2, ,n.
2019/6/6
7
运 筹 学 Operations Research
（8）工序的总时差
2019/6/6
20
运 筹 学 Operations Research
（9）工序的单时差
2019/6/6
▍ 21
运 筹 学 Operations Research
Ex. 试为下面的统筹图编号并计算有关参数：
2019/6/6
22
运 筹 学 Operations Research
3.去掉所有细线对应的顶点，即得关键路线，且其长度为 t(n).