初一常用几何证明的定理
(完整版)初中几何几个著名定理及证明

① AC(BP+DP)=AD ・ BC+AB ・ DC ・ 即 AC ・ BD=AB ・ CD+AD ・ BC.2.托勒密定理的逆定理若一个凸四边形两对对边乘积的和等于两条对角线的乘积,则这 个凸四边形內接于一圆。
己知:在凸四边形ABCD 中,AB • CD+AD • BC 二 BD • AC 。
求证:A 、B 、C 、D 四点共圆。
证明:分别以E 、A 为顶点,在 四边形ABCD初屮见何甩个著名炙龌及证明 识玻堵泗阳展療口屮曇蒐疋屮 一.托勒密定理 1.托勒密定理 圆內接四边形中,两条对角线的乘积等于两组对边乘积之和。
己知:圆內接四边形AECD,求证:AC ・BD 二AB • CD+AD ・BC 。
证明:如图所示,过C 作CP 交BD 于P, 使Z1=Z2,又Z3=Z4, AACD^ABCP. 冴 BP BC EP • AC 二 AD • BC 又 ZACB=ZDCP, Z5= Z6,,即 •:A ACB S A DCP . 得需=舘,即DP ・AC =AB ・DC内,作ZABF= ZDBC> ZBAF=ZBDC,—=—=> AB CD^BD-AF则厶ABF^ADBC 〜Ar CDAH _Bn亦—斎又•,• ZABD = Z ABF +ZEBF= ZEBF + ZDBC = ZFBC•'•△ABD S A FB C =x> —=—=>JD-/R-=Hzrc/--HC CF•••AB ・ CD+AD ・ BC=BD* (AF+CF)又VAB・CD+AD ・BC=BD・AC (己知〉,•••AC=AF + CF;「.A、F、C三点共线;ZBAC=ZBAF = ZBDC;:4、B、C、D 四点共圆。
3.托勒密不等式在任意凸四边形中,两组对边乘积的和不小于其两条对角线的乘积。
〈托勒密定理可视作托勒密不等式的特殊情况。
)即在任意凸四边形ABCD中,必有AC ・BDWAB • CD+AD * BC,当且仅当A、B、C、D四点共圆(托勒密定理)或共线(欧扌立几何定理)时取等号。
初中几何证明方法

初中几何证明方法
1. 直角三角形定理证明:利用勾股定理证明直角三角形的特征。
2. 等边三角形定理证明:通过三条边全等证明三角形的三个角都是60度。
3. 同位角证明:沿着一组平行线切割两条平行线,证明同位角相等。
4. 对顶角证明:利用两组平行线切割一条横线,证明对顶角相等。
5. 三角形内角和定理证明:通过将三角形分解成三个直角三角形,证明三角形的内角和为180度。
6. 圆的面积公式证明:通过四个等腰直角三角形的组合和排列得出圆的面积公式。
7. 相似三角形定理证明:通过两个三角形的对应角相等,证明两个三角形相似。
8. 等腰三角形定理证明:通过证明两个底角相等,证明等腰三角形的另外两条边相等。
9. 正方形定理证明:通过证明正方形的四个角都是直角且四条边相等,证明正方形的特征。
10. 角平分线定理证明:利用角平分线将一个角分成两个相等的角,证明相邻的角互补且对顶角相等。
初中几何证明的所有公理和定理

初中几何证明的所有公理和定理几何学是数学的一个分支,研究平面和空间中的图形、形状、大小以及它们之间的关系。
在几何学中,有一些基本的公理和定理被广泛应用于证明其他几何结论。
以下是初中几何中常用的公理和定理。
一、公理1.尺规公理:任意两点可以用直尺连接,任意一点可以用剪刀间距来复原。
2.同位角公理:同位角互等。
3.平行公理:通过点外一条直线的直线,与这条直线平行的直线只有唯一一条。
4.直线偏转公理:过直线和不在直线上的一点,有且只有一条直线与该直线相交。
二、定理1.垂直平分线定理:平分一条线段的直线必垂直于该线段。
2.三角形内角和定理:三角形内角的和为180°。
3.直角三角形定理:在直角三角形中,两个直角三角形的边长和斜边相等。
4.点到直线的距离定理:点到直线的距离等于点到该直线上垂线的距离。
5.等腰三角形定理:等腰三角形的底边中点到顶点的距离等于底边的一半。
6.等边三角形定理:等边三角形的三条边相等。
7.三角形外角定理:三角形外角等于其对应内角的和。
8.直角三角形的勾股定理:在直角三角形中,两直角边的平方和等于斜边的平方。
9.海伦公式:已知三角形的三边长,可以通过海伦公式求解其面积。
10.等周定理:等周的两角相等,反之亦成立。
11.三角形中位线定理:三角形两边中点连线中位线,且平分第三边。
12.周长定理:四边形周长等于各边长的和。
13.三角形周长定理:三角形的周长等于三边长的和。
14.三角形中线定理:三角形中线等分中位线,且平分第三边。
15.三角形终边定理:一个角的终边上的点,到另一个角所在的直线的距离永远相等。
16.五边形内角和定理:五边形的内角和是540°。
17.钝角三角形的边长关系:钝角三角形两边长的平方和小于斜边长的平方。
18.三角形的相似性定理:对应角等价、对应边成比例的两个三角形为相似三角形。
19.平行线的性质定理:平行条边分别过枚角且长度成正比,则连线为平行线。
20.重叠三角形定理:如果两个角和一个边分别相等,则两个三角形相等。
初中几何证明口诀

初中几何证明口诀在初中几何中,证明是学习的重要内容之一、通过证明,可以巩固和提高自己对几何知识的理解和应用能力。
以下是一些常用的初中几何证明口诀:1.三角形的内角和定理:三角形内角和为180度。
可以通过绘制平行线、共线线段等方法证明。
2.外角定理:三角形的外角等于其余两个内角的和。
可以通过绘制平行线等方法证明。
3.垂直角定理:垂直角相等。
可以通过绘制平行线、共线线段等方法证明。
4.同位角定理:同位角相等。
可以通过平行线等方法证明。
5.三角形的相似性定理:相似三角形的对应角相等,对应边成比例。
可以通过AA、SSS、SAS等方法证明。
6.圆周角定理:圆周角是圆心角的两倍。
可以通过绘制弧、使用同位角等方法证明。
7.弦切角定理:弦切角等于其对应的弧的一半。
可以通过绘制切线、弧等方法证明。
8.正方形的特性:正方形的四条边相等,四个角为直角。
可以通过对角线等方法证明。
9.等腰三角形的特性:等腰三角形的两边相等,两个底角相等。
可以通过绘制高线等方法证明。
10.平行四边形的特性:平行四边形的对边相互平行,对角线相互平分。
可以通过角平分线等方法证明。
11.三角形的中线定理:三角形的三个中线交于一点,且这点距离三个顶点的距离是各边长的一半。
可以通过线段等方法证明。
12.直角三角形的勾股定理:直角三角形的两个直角边的平方和等于斜边的平方。
可以通过平行四边形等方法证明。
13.外切圆定理:三角形的外接圆的圆心是三个顶点的垂直平分线的交点。
可以通过角平分线、圆心角等方法证明。
14.圆的切线定理:切线与半径垂直。
可以通过绘制切线、使用垂直角等方法证明。
15.纵横切割定理:两条平行线被一条截线切割,那么两个内角和为180度。
可以通过平行线等方法证明。
这些口诀可以帮助初中生记住一些重要的初中几何证明定理,并引导他们学习如何使用特定的几何性质进行证明。
同时,更重要的是理解定理的证明过程,培养逻辑思维能力和几何推理能力。
初等几何五大ZB定理
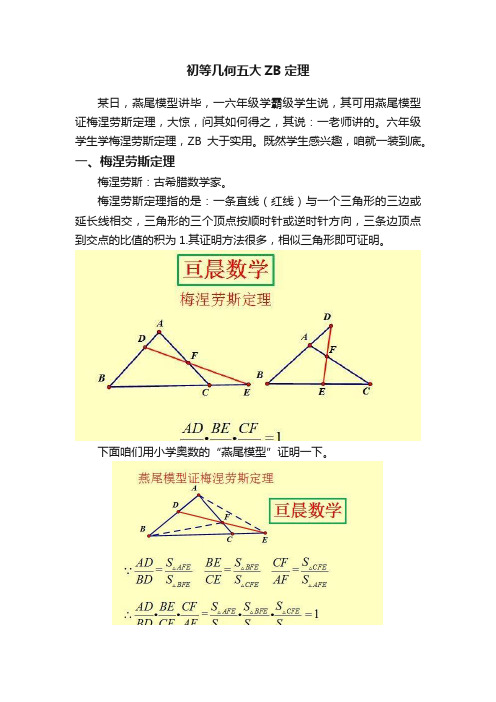
初等几何五大ZB定理某日,燕尾模型讲毕,一六年级学霸级学生说,其可用燕尾模型证梅涅劳斯定理,大惊,问其如何得之,其说:一老师讲的。
六年级学生学梅涅劳斯定理,ZB大于实用。
既然学生感兴趣,咱就一装到底。
一、梅涅劳斯定理梅涅劳斯:古希腊数学家。
梅涅劳斯定理指的是:一条直线(红线)与一个三角形的三边或延长线相交,三角形的三个顶点按顺时针或逆时针方向,三条边顶点到交点的比值的积为1.其证明方法很多,相似三角形即可证明。
下面咱们用小学奥数的“燕尾模型”证明一下。
二、塞瓦定理塞瓦:意大利数学家、水利工程师,该定理于1678年发表于《直线论》一书。
塞瓦定理:可以简单记为三线共点的充要条件是:顺时针或逆时针的分线段的比值积为1.该定理可以用上面的梅涅劳斯定理证明。
三、斯坦纳定理斯坦纳:瑞士几何学家斯坦纳定理:两内角平分线相等的三角形必为等腰三角形。
早在2000多年前,《几何原本》就有定理:等腰三角形的两底角平分线的长相等。
可是它的逆定理书上却只字未提,估计作者也不会,呵呵。
直到1840年,莱默斯请求斯图姆给予纯几何证明,可斯图姆也不会,最后斯坦纳给出了证明,因此该定理也称作:斯坦纳——莱默斯定理。
现在很多高中生也能证明。
大家可以试试有没有难度。
四、托勒密定理托勒密定理:圆内接凸四边形的对边积的和等于对角线的积。
用相似可以证明五、西姆松定理西姆松定理:过三角形外接圆上异于三角形顶点的任意一点作三边所在直线垂线,则三垂足在一点直线上,这条直线我们称作西姆松线。
这些定理一般的中考都不考,一和四和中学的相似联系比较紧密,尽量掌握,培优课上可能会有,感兴趣的同学可以看看。
几何定理证明:几何定理的证明

几何定理证明:几何定理的证明几何定理是数学中非常重要的一部分,它们是建立和推导几何关系的基础。
在几何学中,定理的证明是确保定理的正确性和可靠性的关键步骤。
本文将介绍几何定理的证明过程,并以几个典型的几何定理为例进行详细阐述。
一、直角三角形的勾股定理证明勾股定理是几何中最经典且重要的定理之一,它声称:直角三角形的两条直角边的平方和等于斜边的平方。
该定理的证明可以通过几何方法或代数方法来展开。
几何方法证明:以直角三角形ABC为例,其中∠B为直角。
我们可以通过画图来证明勾股定理。
1. 以BC为边,作一个正方形BCDE。
2. 连接AC和AE。
3. 证明四边形ABED是一个平方。
4. 由于正方形的性质,我们可以得出AE和BD是相等的。
5. 观察三角形ACD和三角形ABC,它们的两个角分别相等,并且一边相等,所以它们是全等三角形。
6. 根据全等三角形的性质,我们可以得出AD和AB相等。
7. AD是直角边的平方,AB是斜边的平方,因此AD的平方加上AB的平方等于斜边AC的平方,从而证明了勾股定理。
代数方法证明:我们可以使用代数方法证明勾股定理。
设直角三角形ABC中,∠B为直角,AB=a,BC=b,AC=c。
根据直角三角形的定义,我们可以得到两个关系式:a² + b² = c²(1)tan(∠B) = a/b (2)将式(2)代入式(1),得到:a² + (a/tan(∠B))² = c²经过变形和化简,我们最终可以得到:(1 + tan²(∠B))a² = c²由于tan²(∠B) + 1 = sec²(∠B)(余切定理),所以我们可以进一步化简为:sec²(∠B) a² = c²最后,我们得到了勾股定理的形式。
二、等腰三角形底角定理证明等腰三角形是指两边相等的三角形。
在等腰三角形中,底角定理成立,即等腰三角形的底角是两个顶角的一半。
初中数学所有几何证明定理

初中数学所有几何证明定理初中数学中的几何证明定理有很多,下面列举一些较为常见和重要的:1.垂线定理:如果两条直线相交,且其中一条直线垂直于另一条直线,那么相交的两条直线分成的两对相邻角互为互补角。
证明:假设直线AB与直线CD相交于点O,且直线AB垂直于直线CD,那么∠AOC和∠BOD构成一对互补角,同时∠AOD和∠BOC构成一对互补角。
2.同位角定理:如果两条平行线被一条横截线相交,那么相交的各对同位角相等。
证明:假设平行线AB与CD被平行于它们的条横截线EF相交于点O,那么∠AEO和∠COF,∠FEO和∠DOF互相等。
3.对顶角定理:如果两条直线AB和CD相交,那么由相交而分成的四个角中的相邻角互为对顶角。
证明:假设直线AB与直线CD相交于点O,那么∠AOB和∠COD、∠BOC和∠AOD互为对顶角。
4.垂直角定理:如果两条直线AB和CD相交,那么由相交而分成的四个角中的互为相对角的两对角中,有一对互为垂直角。
证明:假设直线AB与直线CD相交于点O,那么∠AOC和∠BOC互为相对角,如果直线AB与直线CD垂直,那么∠AOC和∠BOC互为垂直角。
5.三角形的内角和定理:一个三角形的内角的和等于180°。
证明:假设三角形的三个顶点为A、B、C,以AB为边作一个封闭的三角形ABC,再以BC为边作一个封闭的三角形ACB。
根据同位角定理,∠BAC+∠BCE=∠ACB+∠ACD,即∠BAC+∠ACB+∠BCE=∠ACB+∠ACD+∠BCE,因此∠BAC+∠ACB+∠BCE=∠ACB+∠ACB,即∠BAC+∠ACB+∠ACB=180°。
6.线段的三等分定理:对于线段AB上的任意一点C,如果AC与CB 的长度相等,那么AC与CB将线段AB分为三个相等的部分。
证明:利用数学归纳法,首先取一点D在线段AB上,并且AD的长度为BD的两倍,那么根据线段的加法性质,我们有AB=AD+BD=AD+AD=2AD。
空间几何的基本定理和证明

空间几何的基本定理和证明空间几何是研究空间中点、线、面和体之间的位置、形态、大小、相对位置等性质的数学分支。
在空间几何中,有一些基本定理是我们必须要了解和掌握的。
本文将介绍几个常见的空间几何基本定理,并给出相应的证明。
一、平行线定理:平行线是位于同一平面内且不相交的两条直线。
在空间几何中,平行线间的关系有着重要的应用。
平行线定理如下:定理1:如果两条直线与第三条直线相交,且与第三条直线分别平行,则这两条直线互相平行。
证明:设直线l和m与直线n相交,且l与n平行,m与n平行。
我们需证明直线l与m平行。
根据平行线的定义,我们可以得到以下两组对应角相等关系:∠1 = ∠2,∠1 = ∠3;∠4 = ∠5,∠4 = ∠6。
现在我们来证明∠2 = ∠3 = ∠5 = ∠6,这样就证明了直线l与m平行。
根据同位角定理,我们可以得到:∠2 + ∠4 = 180°,∠3 + ∠6 = 180°。
将上述两个等式相加并整理得:∠2 + ∠4 + ∠3 + ∠6 = 360°。
由于∠2 = ∠3,∠4 = ∠5,∠5 = ∠6,代入上式我们可以得到:2∠2 + 2∠5 = 360°。
化简得:∠2 + ∠5 = 180°。
根据同位角的定义,∠2 + ∠5是直线l与m的内错角。
据直线外角定理,直线l与m的内错角相等,即∠2 + ∠5 = 180°。
因此,我们证明了直线l与m平行。
二、垂直定理:在空间几何中,垂直是指两个直线或线段相交时,交点的四个周围角都是直角(90°)。
垂直定理如下:定理2:直线和平面垂直的等价条件是直线上的任意一条直线垂直于平面。
证明:我们设直线l与平面P相交于点A,我们需要证明l上的任意一条直线垂直于平面P。
取直线l上任意一点B,连接OB。
构造平面Q,使得平面Q 过直线l且垂直于平面P。
则由垂直平面的性质得知,直线l就在平面Q内。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初一常用几何证明的定理总结对顶角相等:几何语言:∵∠1、∠2是对顶角∴∠1=∠2(对顶角相等)垂线:几何语言:正用反用:∵∠AOB=90°∵AB⊥CD∴AB⊥CD(垂直的定义)∴∠AOB=90°(垂直的定义)证明线平行的方法:1、平行公理如果两条直线都与第三条直线平行,那么,这两条直线也平行。
简述为:平行于同一直线的两直线平行。
几何语言叙述:如图:∵AB∥EF,CD∥EF∴AB∥CD(平行于同一直线的两直线平行。
)2、同位角相等,两直线平行。
几何语言叙述:如图:∵直线AB、CD被直线EF所截∠1=∠2∴AB∥CD(同位角相等,两直线平行。
)3、内错角相等,两直线平行。
几何语言叙述:如图:∵直线AB、CD被直线EF所截,∠1=∠2 ∴AB∥CD(内错角相等,两直线平行。
)4、同旁内角互补,两直线平行。
几何语言叙述:如图:∵直线AB、CD被直线EF所截,∠1+∠2=180O ∴AB∥CD(同旁内角互补,两直线平行。
)5、垂直于同一直线的两直线平行。
几何语言叙述:如图:∵直线a⊥c,b⊥c∴a∥b(垂直于同一直线的两直线平行。
)平行线的性质:1、两直线平行,同位角相等。
几何语言叙述:∵AB∥CD∴∠1=∠2(两直线平行,同位角相等。
)2、两直线平行,内错角相等。
几何语言叙述:如图:∵AB∥CD∴∠1=∠2(两直线平行,内错角相等。
)3、两直线平行,同旁内角互补。
几何语言叙述:如图:∵AB∥CD∴∠1+∠2=180O(两直线平行,同旁内角互补。
)证明角相等的其余常用方法:1、余角的性质:同角或等角的余角相等。
例:∵如图∠AOB+∠BOC=90°∠BOC+∠COD=90°∴∠AOB=∠COD(同角的余角相等)2、补角的性质:同角或等角的补角相等。
例:∵如图∠AOB+∠BOD=180°,∠AOC+∠COD=180°且∠BOD=∠AOC∴∠AOB=∠COD(同角的补角相等)三角形中三种重要线段:1、三角形的角平分线:几何语言叙述:∵如图BD 是△ABC 的角平分线∴∠ABD =∠CBD=12∠ABC2、三角形的中线:几何语言叙述:∵如图BD 是△ABC 的中线∴AD =BD =12AB3、三角形的高线:几何语言叙述:∵如图AD 是△ABC 的高 ∴∠ADB =∠ADC =90° 三角形的分类:⎧⎪⎧⎨⎨⎪⎩⎩不等边三角形三角形(按边分)底和腰不等的等腰三角形等腰三角形等边三角形⎧⎪⎧⎨⎨⎪⎩⎩直角三角形三角形(按角分)锐角三角形斜三角形钝角三角形三角形三边的关系:三角形两边之和大于第三边,两边之差小于第三边。
如图:|AB -AC|<BC<AB +AC三角形内角和定理及推论三角形内角和定理:三角形三个内角的和等于180°几何语言叙述:如图:∠A+∠B+∠C=108°(三角形三个内角的和等于180°)三角形内角和定理推论1:直角三角形的两锐角互余。
几何语言叙述:如图:∵△ABC中,∠C=90°∴∠A+∠B=90°(直角三角形的两锐角互余)三角形内角和定理推论2:三角形的一个外交等于和它不相邻的两内角之和。
几何语言叙述:如图:∵∠ACD是△ABC的外角∴∠ACD=∠A+∠B(三角形的一个外角等于和它不相邻的两内角之和)三角形内角和定理推论3:三角形的一个外角大于任何一个与它不相邻的内角。
几何语言叙述:如图:∵∠ACD是△ABC的外角∴∠ACD>∠B(三角形的一个外角大于任何一个与它不相邻的内角)平面直角坐标系各个象限内和坐标轴的点的坐标的符号规律:(1)x轴将坐标平面分为两部分,x轴上方的纵坐标为正数;x轴下方的点纵坐标为负数。
即第一、二象限及y轴正方向(也称y轴正半轴)上的点的纵坐标为正数;第三、四象限及y轴负方向(也称y轴负半轴)上的点的纵坐标为负数。
反之,如果点P(a ,b)在x轴上方,则b>0;如果P(a ,b)在x轴下方,则b<0。
(2)y轴将坐标平面分成两部分,y轴左侧的点的横坐标为负数;y轴右侧的点的横坐标为正数。
即第二、三象限和x轴的负半轴上的点的横坐标为负数;第一、四象限和x 轴正半轴上的点的横坐标为正数。
(3)规定坐标原点的坐标为(0 ,0)(4)各个象限内的点的符号规律如下表:上表反推也成立。
如:若点P(a ,b)在第四象限,则a>0,b<0(5)坐标轴上的点的符号规律:定义当两个三角形完全重合时,互相重合的顶点叫做对应顶点,互相重合的边叫做对应边,互相重合的角叫做对应角。
(1)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边。
(2)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角。
(3)有公共边的,公共边一定是对应边。
(4)有公共角的,角一定是对应角。
(5))1、三组对应边分别相等的两个三角形全等(简称“边边边”),这一条也说明了三角形具有稳定性的原因。
2、.有两边及其夹角对应相等的两个三角形全等“边角边”)。
3、.有两角及其夹边对应相等的两个三角形全等“角边角”)。
4、.有两角及其一角的对边对应相等的两个三角形全等“角角边”)5(HL或“斜边,直角边”)。
注意:在全等的判定中,没有AAA(角角角)和SSA(边边角)(特例:直角三角形为HL,属于SSA),这两种情况都不能唯一确定三角形的形状。
性质三角形全等的条件:1.全等三角形的对应角相等。
2.全等三角形的对应边相等3.全等三角形的对应顶点位置相等。
4.全等三角形的对应边上的高对应相等。
5.全等三角形的对应角的角平分线相等。
6.全等三角形的对应中线相等。
78.89.全等三角形可以完全重合要验证全等三角形,不需验证所有边及所有角也对应地相同。
以下判定,是由三个对应的部分组成,即全等三角形可透过以下定义来判定:S.S.S.(Side-Side-Side)(边、边、边):各三角形的三条边的长度都对应地相等的话,该两个三角形就是全等。
S.A.S. (Side-Angle-Side)(边、角、边):各三角形的其中两条边的长度都对应地相等,且两条边夹着的角都对应地相等的话,该两个三角形就是全等。
A.S.A. (Angle-Side-Angle)(角、边、角):各三角形的其中两个角都对应地相等,且两个角夹着的边都对应地相等的话,该两个三角形就是全等。
A.A.S. (Angle-Angle-Side)(角、角、边):各三角形的其中两个角都对应地相等,且没有被两个角夹着的边都对应地相等的话,该两个三角形就是全等。
R.H.S. / H.L.(Right Angle-Hypotenuse-Side):各三角形的直角、斜边及另外一条边都对应地相等的话,该两个三角形就是全等。
但并非运用任何三个相等的部分便能判定三角形是否全等。
以下的判定同样是运用两个三角形的三个相等的部分,但不能判定全等三角形: A.A.A. (Angle-Angle-Angle)(角、角、角):各三角形的任何三个角都对应地相等,但这并不能判定全等三角形,A.S.S. (Angle-Side-Side)(角、边、边):各三角形的其中一个角都相等,且其余的两条边(没有夹着该角),但这并不能判定全等三角形,除非是直角三角形。
但若是直角三角形的话,应以R.H.S.来判定。
1、性质中三角形全等是条件,结论是对应角、对应边相等。
而全等的判定却刚好相反。
2、2.利用性质和判定,学会准确地找出两个全等三角形中的对应边与对应角是关键。
在写两个三角形全等时,一定把对应的顶点,角、边的顺序写一致,为找对应边,角提供方便。
3SAS找全等三角形。
4.用在实际中,一般我们用全等三角形测相等的距离。
以及相等的角,可以用于工业和军事。
5.三角形具有一定的稳定性,所以我们用这个原理来做脚手架及其他支撑物体。
因此我们可以来采取逆思维的方式。
来想要证全等,则需要什么条件要证某某边等于某某边,那么首先要证明含有那两个边的三角形全等。
然后把所得的等式运用(AAS/ASA/SAS/SSS/HL)证明三角形全等。
有时还需要画辅助线帮助解题。
分析完毕以后要注意书写格式,在全等三角形中,如果格式不写好那么就容易出现看漏的现象。
例1、如图,已知CD⊥AB于D,BE⊥AC于E,△ABE≌△ACD,∠C= 20°,AB=10,AD= 4,G为AB延长线上一点.求∠EBG的度数和CE的长.分析:(1)图中可分解出四组基本图形:有公共角的Rt△ACD和Rt△ABE;△ABE≌△ACD,△ABE的外角∠EBG或∠ABE的∠EBG.(2)利用全等三角形的对应角相等性质及外角或邻补角的知识,求得∠EBG等于160°.(3)利用全等三角形对应边相等的性质及等量减等量差相等的关系可得:CE=CA-AE=BA-AD=6.解:∵△ABE≌△ACD ∠C= 20°(已知)∴∠ABE=∠C =20°(全等三角形的对应角相等)∴∠EBG=180°-∠ABE =160°(邻补角的意义)∵△ABE≌△ACD(已知)∴AC=AB(全等三角形对应边相等)AE=AD(全等三角形对应边相等)∴CE=CA-AE =BA-AD =6(等式性质)例1:(2006·浙江金华)如图1,△ABC与△ABD中,AD与BC相交于O 点,∠1=∠2,请你添加一个条件(不再添加其它线段,不再标注或使用其它字母),使AC=BD,并给出证明。
你添加的条件是: . 证明:分析:要说明AC=BD,根据图形想到先说明△ABC≌△BAD,题目中已经知道∠1=∠2,AB=AB,只需一组对边相等或一组对角相等即可。
解:添加的条件是:BC=AD. 证明:在△ABC与△BAD中,∠1=∠2,AB=AB,∠A=∠A' ∴△ABC≌△BAD(SAS)。
∴ AC=BD. 小结:惟一,若按照以下方式之一来添加条件:①BC=AD,②∠C=∠D,③∠CAD=∠DBC,④∠CAB=∠DBA,都可得△CAB≌△DBA,从而有AC=BD. 二、综合开放型例2:(2006·攀枝花)如图2,点E在AB上,AC=AD,请你添加一个条件,使图中存在全等三角形,并给予证明。
所添条件为_______________. 你得到的一对全等三角形是:△≌△ . 证明:分析:在已知条件中已有一组边即可得出全等三角形。
解:所添条件为CE=ED. 得到的一对全等三角形是△CAE≌△DAE. 证明:在△CAE和△DAE中,AC=AD,AE=AE,CE=DE,所以△CAE≌△DAE(SSS)。
小结:本题属于条件和结论同时开放的一道好题目,题目本身并不复杂,但开放程度较高,能激起同学们的发散思维,值得重视.。
