控制工程基础实验指导书[答案解析]
控制工程基础_课后答案
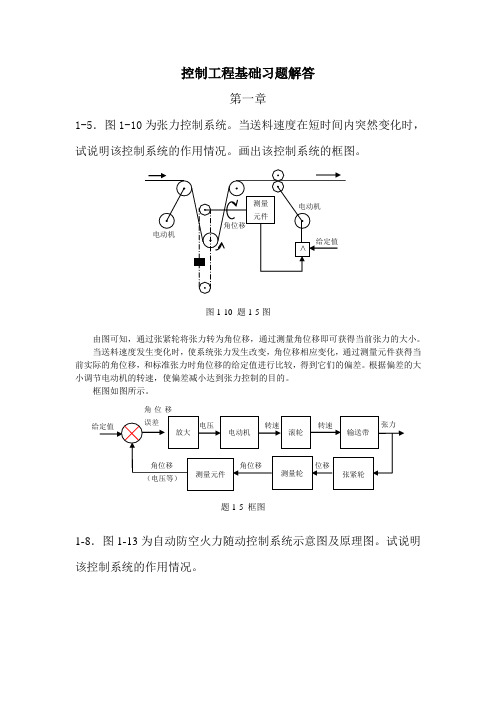
控制工程基础习题解答第一章1-5.图1-10为张力控制系统。
当送料速度在短时间内突然变化时,试说明该控制系统的作用情况。
画出该控制系统的框图。
由图可知,通过张紧轮将张力转为角位移,通过测量角位移即可获得当前张力的大小。
当送料速度发生变化时,使系统张力发生改变,角位移相应变化,通过测量元件获得当前实际的角位移,和标准张力时角位移的给定值进行比较,得到它们的偏差。
根据偏差的大小调节电动机的转速,使偏差减小达到张力控制的目的。
框图如图所示。
1-8.图1-13为自动防空火力随动控制系统示意图及原理图。
试说明该控制系统的作用情况。
题1-5 框图电动机给定值角位移误差张力-转速位移张紧轮滚轮输送带转速测量轮测量元件角位移角位移(电压等)放大电压测量 元件>电动机角位移给定值电动机图1-10 题1-5图该系统由两个自动控制系统串联而成:跟踪控制系统和瞄准控制系统,由跟踪控制系统获得目标的方位角和仰角,经过计算机进行弹道计算后给出火炮瞄准命令作为瞄准系统的给定值,瞄准系统控制火炮的水平旋转和垂直旋转实现瞄准。
跟踪控制系统根据敏感元件的输出获得对目标的跟踪误差,由此调整视线方向,保持敏感元件的最大输出,使视线始终对准目标,实现自动跟踪的功能。
瞄准系统分别由仰角伺服控制系统和方向角伺服控制系统并联组成,根据计算机给出的火炮瞄准命令,和仰角测量装置或水平方向角测量装置获得的火炮实际方位角比较,获得瞄准误差,通过定位伺服机构调整火炮瞄准的角度,实现火炮自动瞄准的功能。
控制工程基础习题解答第二章2-2.试求下列函数的拉氏变换,假定当t<0时,f(t)=0。
(3). ()t et f t10cos 5.0-=解:()[][]()1005.05.010cos 25.0+++==-s s t e L t f L t(5). ()⎪⎭⎫⎝⎛+=35sin πt t f 图1-13 题1-8图敏感 元件定位伺服机构 (方位和仰角)计算机指挥仪目标 方向跟踪环路跟踪 误差瞄准环路火炮方向火炮瞄准命令--视线瞄准 误差伺服机构(控制绕垂直轴转动)伺服机构(控制仰角)视线敏感元件计算机指挥仪解:()[]()252355cos 235sin 2135sin 2++=⎥⎦⎤⎢⎣⎡+=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+=s s t t L t L t f L π2-6.试求下列函数的拉氏反变换。
控制工程基础实验指导书(答案) 2讲解
实验二二阶系统的瞬态响应分析一、实验目的1、熟悉二阶模拟系统的组成。
2、研究二阶系统分别工作在ξ=1,0<ξ<1,和ξ> 1三种状态下的单位阶跃响应。
3、分析增益K对二阶系统单位阶跃响应的超调量σP、峰值时间tp和调整时间ts。
4、研究系统在不同K值时对斜坡输入的稳态跟踪误差。
5、学会使用Matlab软件来仿真二阶系统,并观察结果。
二、实验仪器1、控制理论电子模拟实验箱一台;2、超低频慢扫描数字存储示波器一台;3、数字万用表一只;4、各种长度联接导线。
三、实验原理图2-1为二阶系统的原理方框图,图2-2为其模拟电路图,它是由惯性环节、积分环节和反号器组成,图中K=R2/R1,T1=R2C1,T2=R3C2。
图2-1 二阶系统原理框图图2-1 二阶系统的模拟电路由图2-2求得二阶系统的闭环传递函1222122112/() (1)()/O i K TT U S K U S TT S T S K S T S K TT ==++++ :而二阶系统标准传递函数为(1)(2), 对比式和式得n ωξ==12 T 0.2 , T 0.5 , n S S ωξ====若令则。
调节开环增益K 值,不仅能改变系统无阻尼自然振荡频率ωn 和ξ的值,可以得到过阻尼(ξ>1)、临界阻尼(ξ=1)和欠阻尼(ξ<1)三种情况下的阶跃响应曲线。
(1)当K >0.625, 0 < ξ < 1,系统处在欠阻尼状态,它的单位阶跃响应表达式为:图2-3 0 < ξ < 1时的阶跃响应曲线(2)当K =0.625时,ξ=1,系统处在临界阻尼状态,它的单位阶跃响应表达式为:如图2-4为二阶系统工作临界阻尼时的单位响应曲线。
(2) +2+=222nn nS S )S (G ωξωω1()1sin( 2-3n to d d u t t tgξωωωω--=+=式中图为二阶系统在欠阻尼状态下的单位阶跃响应曲线etn o n t t u ωω-+-=)1(1)(图2-4 ξ=1时的阶跃响应曲线(3)当K < 0.625时,ξ> 1,系统工作在过阻尼状态,它的单位阶跃响应曲线和临界阻尼时的单位阶跃响应一样为单调的指数上升曲线,但后者的上升速度比前者缓慢。
控制工程基础第三版习题答案_清华大学出版社

课 后
答
3-22 解:
案
网
ww w.
kh da
w.
- 31 -
co
m
3-23 解:
3-25 解:
课 后
答
案
网
ww w.
kh da
3-24
w.
- 32 -
co
m
3-26、3-27 缺 3-28 解:
3-29、3-30 缺 3-31 解:
3-32、3-33 缺
课 后
答
案
网
ww w.
kh da
w.
- 33 -
co
m
第四章
4-1 解:
课 后
答
案
网
ww w.
kh da
w.
- 34 -
4-2 解:
co
m
4-3 解:
4-4 解:
课 后 答 案 网 ww w. kh da w. co m
- 35 -
4-5 解:
4-6 解: (a)
课 后
答
案
网
ww w.
kh da
w.
- 36 -
co
m
(b)
(c)
(d)
(e)
目录
第一章…………………………………………………………………………1 第二章…………………………………………………………………………4 第三章…………………………………………………………………………21
第六章…………………………………………………………………………47 第七章…………………………………………………………………………61
S 2 X ( S ) − Sx(0) − x(0) + 6[ SX ( S ) − x(0)] + 8 X ( S ) =
《机械控制工程基础》实验指导书

《机械控制工程基础》实验指导书华东交通大学机电学院实验一 典型环节模拟一、实验目的①了解、掌握计算机模拟典型环节的基本方法。
②熟悉各种典型环节的阶跃响应曲线。
③了解各种参数变化对典型环节动态特性的影响。
④了解计算机辅助分析和设计的特点与优点二、实验要求①通过计算机的仿真图形观测各种典型环节时域响应曲线。
②改变参数,观测参数变化时对典型环节时域响应的影响。
④对实验程序加上注释,写出实验报告。
三、实验内容一般来讲,线性连续控制系统通常都是由一些典型环节构成的,这些典型环节有比例环节、积分环节、一阶微分环节、惯性环节、振荡环节、延迟环节等。
下面分别对其性能进行仿真(建议实验程序在M 文件中用单步执行的方式执行程序,以便于分析):1)比例环节比例环节的传递函数为:k s G =)(编程分析当k=1~10时,比例环节在时域的情况:①当输人信号是单位阶跃信号时,比例环节的输出曲线(单位阶跃响应曲线)是什么形状呢?实验程序如下:for k=1:1:10num=k;den=1;G=tf(num,den);step(G);hold on;end在M 文件的窗口中,输入程序,录入程序完成后,保存该M 文件,在弹出的“保存为”窗工中输人M 文件名bl.m (也可以自己取文件名),选择存放该M 文件的路径,就可以完成保存工作,然后单击“Tools ”菜单中的“Run ”,将在step 图形窗口中显示出响应图形。
试分析系统的输出信号的特点。
2)积分环节积分环节的传递函数为: Ts G 1)(= ① 当输人信号是单位阶跃信号时,积分环节的仿真程序如下:num=1;den=[1,0];G=tf(num,den);step(G)执行程序,试分析系统的输出信号的特点。
若G(s)=k/s ,编程分析当K=1~10时,在单位阶跃信号激励下,积分环节时域响应的情况。
3)一阶微分环节一阶微分环节的传递函数为: 1)(+=Ts s G①当输入信号是单位阶跃信号时,一阶微分环节的输出在MA TLAB 的函数step ()中是无法绘制的。
《控制工程基础》第二版 (董景新 著)课后习题答案 清华出版社

Xi
G1 G2
1+G1 H1+ G2 H2 +G1G2 H3 +G1G2H1H2 )
X0
G (s) =
G 1G 2 1 + G 1 H 1 + G 2 H 2 + G 1G 2 H 3 + G 1G 2 H 1 H 2
第二章习题解
2-7: 求X0(s) 和Xi2(s) (s)之间的闭环传递函数; 求X0(s) 和Xi1(s (s)之间的闭环传递函数;
G (s) =
G1G 2G 3G 4G 5 H 1 1 + G 4 + G1G 2 + G1G 2G 4 − G1G 4G 5 H 1H 2
第二章习题解
4):求出
X 02 ( s ) X i1 ( s )
-
解:第一步,方框图整理
-
G2 G1
Xi1 +
+
+
①
H2 H1
+
② G4 ③
X02 G5 G6
( g )解:设中间变量 : xa (t ) Q k ′ = (Ds + k1 )
x 0(t) k1 k2 m x a(t) (t)
(t) fi(t)
k ′x0 (t ) = k 2 [xa (t ) − x0 (t )] k ′ + k2 D x0 (t ) ∴ xa (t ) = k2 x 又:f i (t ) = m&&a (t ) + k 2 [xa (t ) − x0 (t )] k2 ∴ G (s ) = mDs 3 + m(k1 + k 2 )s 2 + k 2 Ds + k1k 2
控制工程基础课后答案解析

第二章2.1求下列函数的拉氏变换 (1)s s s s F 232)(23++=(2)4310)(2+-=s s s F (3)1)(!)(+-=n a s n s F (4)36)2(6)(2++=s s F(5) 22222)()(a s a s s F +-= (6))14(21)(2s s s s F ++= (7)521)(+-=s s F 2.2 (1)由终值定理:10)(lim )(lim )(0===∞→∞→s t s sF t f f (2)11010)1(10)(+-=+=s s s s s F 由拉斯反变换:t e s F L t f ---==1010)]([)(1 所以10)(lim =∞→t f t2.3(1)0)2()(lim )(lim )0(2=+===∞→→s ss sF t f f s t )0()0()()()](['2''0''f sf s F s dt e t f t f L st --==-+∞⎰)0()0()(lim )(lim'2''0f sf s F s dt e t f s st s --=+∞→-+∞+∞→⎰1)2()(lim )0(222'=+==+∞→s s s F s f s (2)2)2(1)(+=s s F , t te s F L t f 21)]([)(--==∴ ,0)0(2)(22'=-=--f te et f tt又,1)0('=∴f2.4解:dt e t f e t f L s F st s--⎰-==22)(11)]([)(⎰⎰------+-=2121021111dt e e dt e e sts sts)11(11)11(11222s s s s se s e s e e s s e -------+--=22)1(111s s e s e ---∙-=2.5求下列函数的拉氏反变换(1)t t f 2sin 21)(= (2)t e t t f -=361)((3)t t e e t f 32321)(+-=- (4)t t e e t f 235352)(+=-(5)t e t e t f t t 3sin 313cos 2)(22--+= (6)t t t e e te t f 222)(----+-=2.6(1)0)()()(22=--dtt y d m t ky t f(2)0)()()(222121=-+-dt t y d m t y k k k k t f2.7(1)14312)(23++++=s s s s s G(2)210)(22++=-s s e s G s2.8 解 水的流量Q1由调节控制阀的开度控制,流出量Q2则根据需要可通过负载阀来改变,被调量H 反映了。
《控制工程基础》第3版-课后答案解析

lim e(t)
s0
lim
s0
sE(s)
lim s s0 1
G(s)
Xi (s)
所以,输入为 xi2 sin 6t 1(t), ess2 0.8
(对此题来说,还有一种办法:如果记得对于一阶惯性环节, 当输入为阶跃函数,t=4T时输出为输入的98%,则由放入水 中1min时为输入的98%可直接得出: T=1/4=0.25(min)
uo (30) 1 e 4 1V
arctan 1 2 arccos , cos
arctan 1 2 arccos , cos
3—19单位阶跃输人情况下测得某伺服机构的响应为
试求:(1)系统的闭环传递函数; (2)系统的无阻尼自振角频率及阻尼比。
解:ui (t) i(t)R1 uo (t)
uo (t)
1 c
i(t)dt i(t)R2
对方程式进行拉氏变换得:
U
i
(
s)
I (s)R1
UO (s)
UO (s)
1 Cs
I (s)
I (s)R2
Uo (s) R2Cs 1
消去I(s),得:Ui (s) (R1 R2 )Cs 1
Ds( x2 xo ) k2 xo
x2
Ds k2 Ds
xo
k1 x1
k1Ds k1k2 Ds
xo
k2 xo
(k1Ds k2 Ds k1k2 ) xo k1Dsxi
X o (s)
k1Ds
X i (s) (k1 k2 )Ds k1k2
控制工程基础实验指导书

控制工程基础实验指导书目录实验一典型环节的电路模拟┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈3 实验二二阶系统动态性能和稳定性分析┈┈┈┈┈┈┈┈┈┈┈┈┈┈6 实验三控制系统根轨迹分析┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈9 实验四控制系统的频率特性测量┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈10 实验五控制系统串联校正┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈14 附录一 ACCT-III自动控制原理实验箱简介┈┈┈┈┈┈┈┈┈┈┈┈┈18 附录二软件界面及实验参考设置┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈21 附录三 MATLAB语言┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈25实验一 二阶系统动态性能和稳定性分析一、实验目的1.学习和掌握时域性能指标的测试方法。
2.研究二阶系统参数(ξ、ωn )对系统动态性能和稳定性的影响。
二、实验设备1.ACCT-Ⅲ型自动控制理论实验箱 一台 2.方正电脑 一套 3.螺丝刀 一把三、实验原理及线路线性二阶系统的方块结构图如图1所示:其开环传递函数为1()(1)K G S S T S =+,10KK T =其闭环传递函数标准型为222()2n n nW s S S ωξωω=++,取如下二阶系统的模拟电路,图2中参数关系 图1 方块图图2 二阶系统模拟电路102,1R R C R n ==ξω,R0=100K 。
改变图2系统元件参数R1和电容C 大小,即可改变系统的ξ、ωn , 由此来研究不同参数特征下的时域响应。
图3a 、图3b 、图3c 分别对应二阶系统在欠阻尼,临界阻尼,过阻尼三种情况下的阶跃响应曲线:图3a 图3c图3b四、实验内容及步骤1.按图2电路图接线五、预习要求1.求出各种参数下系统的阶跃响应曲线及其动态品质指标。
2.拟定测量系统动态品质指标的方法。
3.如何保证系统为负反馈系统?(注意各运算放大器均使用反相输入端)若将负反馈改为正反馈或开断反馈回路,将是什么结果?4.如果运算放大器饱和,对实验结果会产生什么影响?如何保证和检查各运算放大器均工作在线性范围内?5.深入研究二阶系统有何意义?六、实验报告要求1.测量数据及曲线整理并与理论值比较。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
控制工程基础实验指导书自控原理实验室编印(内部教材)实验项目名称:(所属课程:)院系:专业班级:姓名:学号:实验日期:实验地点:合作者:指导教师:本实验项目成绩:教师签字:日期:(以下为实验报告正文)一、实验目的简述本实验要达到的目的。
目的要明确,要注明属哪一类实验(验证型、设计型、综合型、创新型)。
二、实验仪器设备列出本实验要用到的主要仪器、仪表、实验材料等。
三、实验内容简述要本实验主要内容,包括实验的方案、依据的原理、采用的方法等。
四、实验步骤简述实验操作的步骤以及操作中特别注意事项。
五、实验结果给出实验过程中得到的原始实验数据或结果,并根据需要对原始实验数据或结果进行必要的分析、整理或计算,从而得出本实验最后的结论。
六、讨论分析实验中出现误差、偏差、异常现象甚至实验失败的原因,实验中自己发现了什么问题,产生了哪些疑问或想法,有什么心得或建议等等。
七、参考文献列举自己在本次准备实验、进行实验和撰写实验报告过程中用到的参考文献资料。
格式如下:作者,书名(篇名),出版社(期刊名),出版日期(刊期),页码实验一 控制系统典型环节的模拟一、实验目的1、掌握比例、积分、实际微分及惯性环节的模拟方法;2、通过实验熟悉各种典型环节的传递函数和动态特性;3、了解典型环节中参数的变化对输出动态特性的影响。
二、实验仪器1、控制理论电子模拟实验箱一台;2、超低频慢扫描数字存储示波器一台;3、数字万用表一只;4、各种长度联接导线。
三、实验原理以运算放大器为核心元件,由其不同的R-C 输入网络和反馈网络组成的各种典型环节,如图1-1所示。
图中Z1和Z2为复数阻抗,它们都是R 、C 构成。
图1-1 运放反馈连接基于图中A 点为电位虚地,略去流入运放的电流,则由图1-1得:21()o i u ZG s u Z ==-(1-1) 由上式可以求得下列模拟电路组成的典型环节的传递函数及其单位阶跃响应。
1、比例环节实验模拟电路见图1-2所示图1-2 比例环节传递函数:21()R G s K R =-=- 阶跃输入信号:-2V 实验参数:(1) R 1=100K R 2=100K (2) R 1=100K R 2=200K 2、 惯性环节实验模拟电路见图1-3所示图1-3 惯性环节传递函数:2212211211()11R CS R Z R K CS G s Z R R R CS TS +=-=-=-=-++阶跃输入:-2V 实验参数:(1) R 1=100K R 2=100K C=1µ f23、积分环节实验模拟电路见图1-4所示图1-4 积分环节传递函数:21111()Z CS G s Z R RCS TS=-=-=-= 阶跃输入信号:-2V 实验参数:(1) R=100K C=1µ f (2) R=100K C=2µ f 4、比例微分环节实验模拟电路见图1-5所示图1-5 比例微分环节传递函数:22211111()(1)(1)1D Z R R G S R CS K T S R Z R CS R CS =-=-=-+=-++ 其中 T D =R 1C K=12R R 阶跃输入信号:-2V 实验参数:12(2)R1=100K R2=200K C=1µ f四、实验内容与步骤1、分别画出比例、惯性、积分、比例微分环节的电子电路;2、熟悉实验设备并在实验设备上分别联接各种典型环节;3、按照给定的实验参数,利用实验设备完成各种典型环节的阶跃特性测试,观察并记录其单位阶跃响应波形。
五、实验报告1、画出四种典型环节的实验电路图,并标明相应的参数;2、画出各典型环节的单位阶跃响应波形,并分析参数对响应曲线的影响;3、写出实验心得体会。
六、实验思考题1、用运放模拟典型环节时,其传递函数是在哪两个假设条件下近似导出?(运算放大器开环放大倍数K0很大,运算放大器输入阻抗很高)2、积分环节和惯性环节主要差别是什么?在什么条件下,惯性环节可以近似为积分环节?在什么条件下,又可以视为比例环节?(惯性环节的特点是,当输入x(t)作阶跃变化时,输出y(t)不能立刻达到稳态值,瞬态输出以指数规律变化。
而积分环节,当输入为单位阶跃信号时,输出为输入对时间的积分,输出y(t)随时间呈直线增长。
当t趋于无穷大时,惯性环节可以近似地视为积分环节,当t趋于0时,惯性环节可以近似地视为比例环节。
)3、如何根据阶跃响应的波形,确定积分环节和惯性环节的时间常数?(积分环节的时间常数T由输出曲线斜率的倒数确定,惯性环节的时间常数T等于曲线上升到稳态值的63..2%时的时间t)实验二二阶系统的瞬态响应分析一、实验目的1、熟悉二阶模拟系统的组成。
2、研究二阶系统分别工作在ξ=1, 0<ξ <1,和ξ> 1三种状态下的单位阶跃响应。
3、分析增益K对二阶系统单位阶跃响应的超调量σP、峰值时间tp和调整时间ts。
4、研究系统在不同K值时对斜坡输入的稳态跟踪误差。
5、学会使用Matlab软件来仿真二阶系统,并观察结果。
二、实验仪器1、控制理论电子模拟实验箱一台;2、超低频慢扫描数字存储示波器一台;3、数字万用表一只;4、各种长度联接导线。
三、实验原理图2-1为二阶系统的原理方框图,图2-2为其模拟电路图,它是由惯性环节、积分环节和反号器组成,图中K=R2/R1, T1=R2C1,T2=R3C2。
图2-1 二阶系统原理框图图2-1 二阶系统的模拟电路由图2-2求得二阶系统的闭环传递函1222122112/() (1)()/O i K TT U S K U S TT S T S K S T S K TT ==++++ :而二阶系统标准传递函数为(1)(2), 对比式和式得n ωξ==12 T 0.2 , T 0.5 , n S S ωξ===若令则。
调节开环增益K 值,不仅能改变系统无阻尼自然振荡频率ωn 和ξ的值,可以得到过阻尼(ξ>1)、临界阻尼(ξ=1)和欠阻尼(ξ<1)三种情况下的阶跃响应曲线。
(1)当K>0.625, 0 < ξ < 1,系统处在欠阻尼状态,它的单位阶跃响应表达式为:(2)+2+=222nn nS S )S (G ωξωω1()1sin( 2-3n to d d u t t tgξωωωω--=+=式中图为二阶系统在欠阻尼状态下的单位阶跃响应曲线图2-3 0 < ξ < 1时的阶跃响应曲线(2)当K =0.625时,ξ=1,系统处在临界阻尼状态,它的单位阶跃响应表达式为:如图2-4为二阶系统工作临界阻尼时的单位响应曲线。
图2-4 ξ=1时的阶跃响应曲线(3)当K < 0.625时,ξ> 1,系统工作在过阻尼状态,它的单位阶跃响应曲线和临界阻尼时的单位阶跃响应一样为单调的指数上升曲线,但后者的上升速度比前者缓慢。
四、实验内容与步骤1、根据图1-1,调节相应的参数,使系统的开环传递函数为:2、令ui(t)=1V ,在示波器上观察不同K (K=10,5,2,0.5)时的单位 阶跃响应的波形,并由实验求得相应的σp 、tp 和ts 的值。
3、调节开环增益K ,使二阶系统的阻尼比707.021==ξ ,观察并记录此时的单位阶跃响应波形和σp 、tp 和ts 的值。
4、用三角波或输入为单位正阶跃信号积分器的输出作为二阶系统的斜坡输入信号。
5、观察并记录在不同K 值时,系统跟踪斜坡信号时的稳态误差。
etn o n t t u ωω-+-=)1(1)()1S 2.0(S 5.0K)S (G +=五、实验报告1、画出二阶系统在不同K值(10,5,2,0.5)下的4条瞬态响应曲线,并注明时间坐标轴。
2、按图1-2所示的二阶系统,计算K=0.625,K=1和K=0.312三种情况下 和ωn值。
据此,求得相应的动态性能指标σp、t p和ts,并与实验所得出的结果作一比较。
3、写出本实验的心得与体会。
六、实验思考题1、如果阶跃输入信号的幅值过大,会在实验中产生什么后果?(阶跃信号幅值的大小选择应适当考虑。
过大会使系统动态特性的非线性因素增大,使线性系统变成非线性系统;过小也会使系统信噪比降低并且输出响应曲线不可能清楚显示或记录下来。
)2、在电子模拟系统中,如何实现负反馈和单位负反馈?(以运算放大器为核心,接反馈电路如上图所示,当Z1、Z2不等时,就是负反馈,当Z1、Z2相等时,就是单位负反馈。
)3、为什么本实验的模拟系统中要用三只运算放大器?(由二阶系统的原理方框图可知,它是由惯性环节、积分环节和比例放大环节组成,而每一个典型环节的模拟电路图均只需一个运算放大器)实验三 三阶系统的瞬态响应及稳定性分析一、 实验目的1、掌握三阶系统的模拟电路图;2、由实验证明开环增益K 对三阶系统的动态性能和稳定性能的影响;3、研究时间常数T 对三阶系统稳定性的影响; 二、实验仪器1、控制理论电子模拟实验箱一台;2、超低频慢扫描数字存储示波器一台;3、数字万用表一只;4、各种长度联接导线。
三、实验原理图3-1为三阶系统的方框图,它的模拟电路如图3-2所示,图3-1 三阶系统原理框图图3-2 三阶系统模拟电路闭环传递函数为:该系统的特征方程为T 1T 2T 3S ³+T 3(T 1+T 2)S ²+T 3S+K=0 其中K=R 2/R 1,T 1=R 3C 1,T 2=R 4C 2,T 3=R 5C 3。
K)S T )(S T (S T K)S (U )S (U i o +1+1+=213若令T 1=0.2S ,T 2=0.1S ,T 3=0.5S ,则上式改写为用劳斯稳定判据,求得该系统的临界稳定增益K=7.5。
这表示K>7.5时,系统为不稳定;K<7.5时,系统才能稳定运行;K=7.5时,系统作等幅振荡。
除了开环增益K 对系统的动态性能和稳定性有影响外,系统中任何一个时间常数的变化对系统的稳定性都有影响,对此说明如下:令系统的剪切频率为ωc ,则在该频率时的开环频率特性的相位为: ϕ(ωc )= - 90︒ - t g -1T 1ωc – t g -1T 2ωc 相位裕量γ=180︒+ϕ(ωc )=90︒- t g -1T 1ωc- t g -1T 2ωc 由上式可见,时间常数T 1和T 2的增大都会使γ减小。
四、实验内容与步骤图4-1所示的三阶系统开环传递函数为1、 按K =10,T 1=0.2S , T 2=0.05S , T 3=0.5S 的要求,调整图2-2中的相应参数。
2、 用慢扫描示波器观察并记录三阶系统单位阶跃响应曲线。
3、 令T 1=0.2S ,T 2=0.1S ,T 3=0.5S ,用示波器观察并记录K 分别为5,7.5,和10三种情况下的单位阶跃响应曲线。
