§2-6 LTI系统的零状态响应

合集下载

信号与系统连续时间LTI系统的几种响应求解方法及例题

3
y(t) 5 e2t 11 e4t 1 et , t 0
2
6
3
二、卷积法
系统完全响应 = 零输入响应 + 零状态响应 2.系统的零状态响应
当系统的初始状态为零时，由系统的外部激励f(t) 产生的响应称为系统的零状态响应，用yf (t)表示。
求解系统的零状态响应yf (t)方法：
初始条件y(0)=1, y '(0)=2, 输入信号f (t)=et u(t)，求系统的完全响应y(t)。
解:
(3) 求方程的全解
y(t)

yh (t)
yp (t)
Ae 2t

Be 4t

1 et 3
y(0) A B 1 1
y'
(0)

2 A

3 4B

1

2
解得 A=5/2，B= 11/6
卷积法求解系统零状态响应yft推导tht????????tht????????thftf由时不变特性由均匀特性由积分特性????????????dtftf???????????dthftyfdthtfthftyf?????????????
信号与系统连续时间LTI系统的几种响应求解方法及例题
二、卷积法
[例1] 已知某线性时不变系统的动态方程式为:
y" (t)+5y ' (t) +6y (t) =4f(t), t>0
系统的初始状态为y(0) = 1，y' (0) = 3，求系统的零输入响应yx(t)。
解: 系统的特征方程为 s2 5s 6 0
系统的特征根为 s1 2，s2 3

LTI连续时间系统零状态响应的求解方法

LTI连续时间系统零状态响应的求解方法张楠;李庆华;孙明灿【摘要】目前国内很多“信号与系统”的教材中讨论了LTI连续时间系统零状态响应的一些求解方法，本文根据现有的信号与系统教材中连续时间系统零状态响应的求解方法，分别从利用冲激响应与激励的卷积、微分方程和变换域三方面求解零状态响应，并给出了实例说明了其正确性。

【期刊名称】《齐鲁工业大学学报：自然科学版》【年(卷),期】2014(028)004【总页数】3页(P27-29)【关键词】零状态响应;卷积;连续系统【作者】张楠;李庆华;孙明灿【作者单位】齐鲁工业大学电气工程与自动化学院,山东济南250353;;;【正文语种】中文【中图分类】TP391.9求解线性时不变连续时间系统零状态响应是信号与系统课程中重要的知识点之一。

零状态响应的概念是初始状态为零,完全由激励产生的响应为零状态响应。

目前国内的一些从事信号与系统教学的教育工作者,也总结了一些求解方法[1-5]。

本人根据自己的教学经验,从卷积、微分方程求解和变换域出发，来讨论连续时间系统零状态解的一般方法，并给出实例证明其有效性。

1 求解方法设线性时不变连续时间系统方程如式(1)所示：yn(t)+a1yn-1(t)+…+any(t)=b0fm(t)+b1fm-1(t)+…+bmf(t)(1)式中f(t)是系统的激励信号,响应为y(t),根据零状态响应的定义,可知求零状态响应时,系统初始条件为1.1 利用冲激响应求解的方法通过系统先求出冲激响应,利用冲激响应与激励的卷积得出yzs(t)=h(t)*f(t),该方法重要的是需要先求出系统的冲激响应。

1.2 微分方程求解的方法用微分方程求解零状态响应时需要利用初始条件该方法需要利用函数的匹配,判断初始条件的跳变情况,从而得出据此得出零状态响应的系数。

1.3 变换域方法通过拉普拉斯变换,根据拉普拉斯变换和反变换,求出零状态响应。

该方法要求掌握拉普拉斯反变换的方法。

零输入响应和零状态响应

齐次解
X
第 14
页
两种分解方式的区别：
1、自由响应与零输入响应的系数各不相同
c c 与 i
xi 不相同
c i 由初始状态和激励共同确定
c xi 由初始状态确定
2、自由响应包含了零输入响应和零状态响应中的齐次解
对于系统响应还有一种分解方式，即瞬态响应和稳态响应。所谓瞬态响应指
t 时，响应趋于零的那部分响应分量；而稳态响应指 t
(Cte-t
)
3
d dt
(Cte-t
)
2(Cte-t
)
e-t
特解 yp (t) t et
零状态响应： yzs (t) C1et C2e2t t et
由起始状态导出初始条件
y(0 ) 0 y '(0 ) 0
y(0 ) 0 y '(0 ) 0
y(0 ) C1 y '(0 ) C1
r1(t) rzi (t) rzs (t) 2e3t sin(2t) u(t)
r2 (t) rzi (t) 2rzs (t) [e3t 2sin(2t)]u(t)
X
四.对系统线性的进一步认识
第 17
页
解得 rzi (t) 3e3tu(t) rzs (t) [e3t sin(2t)]u(t)
零输入响应：没有外加激励信号的作用，只由起始状态（起始时刻系统储能）所产生的响应。
零状态响应：不考虑原始时刻系统储能的作用（起始状态等于零），由系统的外加激励信号产生的响应。
X
二．起始状态与激励源的等效转换
第 4
页
在一定条件下，激励源与起始状态之间可以等效转换。即可以将原始储能看作是激励源。

§2-1 LTI系统的零状态响应

1
1 2
x(τ)
1 −1 0 1
τ
τ2 t2 1 当1<t<2 y (t ) = ∫ (t − τ + 1)dτ = (tτ − + τ) t −1 = 2 − 2 2 t −1
∞
h(t − τ)
1
t − 10 t
1
t +1
τ
当t>2
y (t ) =
−∞
∫ x(τ)h(t − τ)dτ = 0
h(t − τ)
−∞
u (t − τ ) d τ
1
0
1
u (−τ)
以上积分式的积分的上下限为(1~t)，积分结果的定义区间为(1~∞)，所以后面要乘分结果的定义区间为(1~ (1~∞ 以u(t-1)。
t t
1
0
t =0
τ
u (t − τ)
1 t <1 0 t
y 2 (t ) = − ∫ e − ( t − τ ) d τ = − e − t ∫ e τ d τ
大连海事大学信息科学技术学院
《信号与系统》信号与系统》
∞ ∞
第二章
LTI系统的时域分析 LTI系统的时域分析
y (t ) =
=
−∞ ∞
∫ x ( τ ) h (t − τ ) d τ =
−(t − τ)
−∞
u ( τ ) e − ( t − τ ) u (t − τ ) d τ ∫
u (τ)
1
0
x (t ) = u (t )
,
h (t ) = e − t u (t )
求系统的零状态响应解：
y (t ) = x (t ) ∗ h (t )

因果周期信号通过LTI系统的零状态响应

ｓｔｙｓｅｍ．
Ｋｅｗｏｄｌｎａｎｉ —ｎｖｒａｔｓｓｅ；ｆｅｕｎｃｏｍａｎａｌｓｓ：ｓｄｍａｎａａｙｉｙｒｓ：ｉｅｒａｄｔｍｅｉａｉｎｙｔｍｒｑｅｙｄｉｎａｙｉ — ｏｉｎｌｓｓ
摘要：文讨论了因果正弦信号或因果周期信号通过线性时不变系统的零状态响应。用频域分析技术分析了单个因果正弦信号通过线性时本
不变系统的零状态响应和因果周期信号通过窄带滤波器的稳态响应；同时用Ｓ分析技术分析了因果周期信号通过宽带滤波器的稳态响应和域暂态响应。给出的计算方法有益于过线性时不变系统时引起的变化。
ＡｂｔａｔＴｈｅｏｓａｅｒｓｏｓｆａｌｅｒｔｍｅｉｖｒａｔ（ｓｒｃ：ｅｚｒ－ｔｔｅｐｎｅｏｉａｉ－ｎａｉｎＬＴＩｙｔｍａｓｄｂａｓｌｓｎｓｉａｉ－ｎ）ｓｓｅｐｓｅｙａｃｕａｉｕｏｄｌｇｓ
经典教材往往未能对因果正弦信号或因果周期
ｓｕｄｎｔｏｕｎｅｓａｈｅｃｎｈｎａｃｕｓｌｓｎｕｓｉａｉｎａｒａｃｕａｅｉｄｉｉａｓｅｎＬＴＩｔｅｓｔｄｒｔｎｄｔｈａｇｅｗｅａａｉｏｄｌｓｇｌｏａｓｌｐｒｏｃｓｇｎｌｐａｓｓａ

离散时间LTI系统零状态响应

x[k]* h[n] ( x[n])* h[k] y[n]
n
n
n
3. 卷积和的性质
[例]
计算
x[k]
{1,
0,
2,
4}与
h[k]
{1,
4,
5,
3}的卷积和。
解: x[k] [k 2] 2[k] 4[k 1]
利用分配律和位移特性
x[k]*h[k] {[k 2] 2[k] 4[k 1]}*h[k]
x[1] h[1]
x[1] h[2]
x[1] h[3]
对角斜线上各数值就是 x[n]h[k－n]的值。
x[ 2 ] x[2] h[0]
x[ 3 ] x[3] h[0]
x[2] h[1] x[3] h[1]
x[2] h[2] x[3] h[2]
x[2] h[3] x[3] h[3]
对角斜线上各数值的和就是y[k]各项的值。
h[k] h [ n ] 1
解：
n
n
0
3
k
02
k
y[k]
综上可知： 3
2 1
k 0 1 2 3 4 56
h[-n] 1
-2 0
n
两个信号的卷积和，卷积和结果仍为一个信号。该信号的起点等于那两个信号起点之和，终点等于那两个信号的终点之和。
2. 卷积和的计算
列表法: 设x[k]和h[k]都是因果序列，则有
2. 卷积和的计算
[例]
计算x [ k ]
{1,
2,
0,
3,
2}
与h [ k ]
{1,
4,
2,
3 } 的卷积和。
解:
h [ -1 ] 1

LTI连续系统产生的零状态响应称为单位阶跃响应

第2章连续系统的时域分析
2.1 LTI连续系统的模型 2.2 LTI连续系统的响应 2.3 冲激响应与阶跃响应 2.4 卷积与零状态响应
2.1 LTI连续系统的模型
2.1.1 LTI连续系统的数学模型 2.1.2 LTI连续系统的框图
返回首页
2.1.1 LTI连续系统的数学模型
对于任意一个线性时不变电路，当电路结构和组成电路的元件参数确定以后，根据元件的伏安关系和基尔霍夫定律，可以建立起与该电路对应的动态方程。
yzi (t) Aie pit
i1
（2）当特征根中含有重根，其他为单根时，零输入响应的一般形式为：
k
N
yzi (t) e p1t Ait (i1)
Aje pjt
i1
jk 1
表2-1 零输入响应形式对照表
2S
1F
1
10 V
8V
1H
i (t)
2
图2-6 例2-14图

y(t)
h2 (t)
图2-18 两个子系统并联
2.4.4 卷积的性质
3．结合律
[ f1 (t) f 2 (t)] f3 (t) f1 (t) [ f 2 (t) f3 (t)]
4．卷积的微分与积分
2.4.4 卷积的性质
5． (t) 与任意信号的卷积
f (t) (t) f (t)
iL (0 )
vC (0 )
iC (0 )
1
1
iL (0 )
y(0 )
图2-4 0-等效电路
图2-5 0+等效电路
返回本节
2.2.2 零输入响应与零状态响应
1．零输入响应 2．零状态响应

§2-6 LTI系统的零状态响应

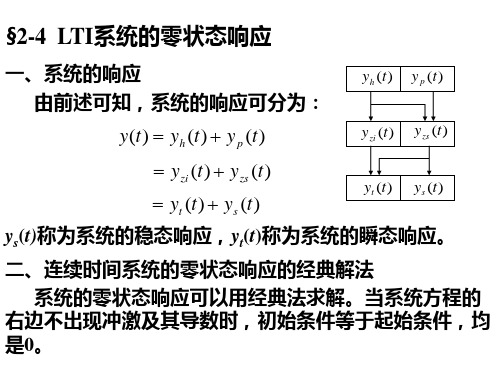
所以求得
1 A1 2
A2 1
于是求得系统的零状态响应
1 t 2 t 1 3t y (t ) e e e 2 2
或表示为
1 t 2 t 1 3t y (t ) ( e e e )u (t ) 2 2
我们下面介绍用卷积积分的方法，求解系统的零状态响应。由信号的冲激分解我们知道，一连续时间信号可表示为： x(t ) x()(t )d
h(n) ,2,3 1
x(n)
3
2 1 2 1 2 1
h(n)
3
0
3
4
n
0
1
2
3
4
n
h(n)
14
结果如上，表示为
y(n) 1, 4, 10, 14, 14, 8, 3
4 1
10 8 3
0 1 2
3 4
5 6 7
n
(9B 9B 2B)e3t e3t
所以
1 1 3t B y p (t ) e 2 2 ⑶ 确定待定系数，求全解。 y (t ) yh (t ) y p (t ) A1e A2 e
t 2t
1 3t e 2
由零状态的条件
1 A1 A2 0 2 3 A1 2 A2 0 2
1 1 a
1
n
例2：设 x(n) {1,2,3,2,1} ,
h(n) ,2,3 1
求卷积和 y(n) x(n) h(n)
解：我们先借助作图的方法，求此卷积和。
两序列的图形为：
x(n)
3
2 1 2 1 2 1
x(m)
h(n)
1

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

x(t )
1 1 1
y1 (t )
1
y(t )
0
t
0
t
y2 (t )
0
1
t
0 1
1
t
四、离散时间系统的零状态响应的求解---卷积和
若以x(n)作用于一零状态的线性时不变系统
(n)
x ( n)
m
x(m)(n m)

LTI系统
h(n)
y ( n)
m
x(m)h(n m)

y(n)就是系统的零状态响应:
y ( n)
m
x(m)h(n m) x(n) h(n)
上式称为序列x(n)与y(n)的卷积和。
卷积和的运算与卷积积分类似，要注意求和限的确定和结果序列的定义区间。 x(n) u(n) , h(n) a nu(n) 例1(复习系统法)：设
求系统的零状态响应 y(n) x(n) h(n) 解：
y(n) x(n) h(n)
m
x(m)h(n m)
u (m)
1

m
u (m)a nmu (n m) a nmu (m)u (n m)

m
u (n m)
1
m
如上例， x(n) {1,2,3,2,1} ,
1，2，3，2，1 × 1，2，3 --------------------------------3，6，9，6，3 2，4，6，4，2 1，2，3，2，1 --------------------------------1，4，10，14，14，8，3
t 1
1
t 2, f1 ( )与f 2 (t )完全分离，f (t ) 0 以上计算结果归纳为
0 .5
f (t )
下页动画演示卷积
0
1
2
t
卷积动画
, x(t ) u (t ) u (t 1) h(t ) et u(t ) 例(复习系统法) ：设
求系统的零状态响应 y (t ) x(t ) h(t )
响应y(t)。
解：⑴ 求方程的齐次通解。知道特征方程与特征根如下：
2 3 2 0 所以，齐次通解设为
1 1, 2 2
yh (t ) A1et A2e2t
y p (t ) Be3t ⑵ 求对应方程自由项的一个特解。设
代入原方程
yp (t ) 3 yp (t ) 2 y p (t ) e3t

若以x(t)作用于一零状态的线性时不变系统
x(t )

LTI系统
y(t )

x()(t )d

x()h(t )d
y(t)就是系统的零状态响应。
根据系统的线性时不变性，当系统的单位冲激响应为 h(t)时，则

x() (t )d

1 1 a
1
n
例2：设 x(n) {1,2,3,2,1} ,
h(n) ,2,3 1
求卷积和 y(n) x(n) h(n)
解：我们先借助作图的方法，求此卷积和。
两序列的图形为：
x(n)
3
2 1 2 1 2 1
x(m)
h(n)
1
3
2
3
0
1
2
3
4
m
0
3
4
n
0
1
2
3
4
n
3
2 1 2 1 0
( t )
u( 1)
y2 (t ) u( 1)e

u(t )d
1
0
以上积分式的积分的上下限为(1~t)，积分结果的定义区间为(1~∞)，所以后面要乘以u(t-1)。
y2 (t ) e
1 t ( t )
u()
1
1

t0
0

t 1
所以求得
1 A1 2
A2 1
于是求得系统的零状态响应
1 t 2 t 1 3t y (t ) e e e 2 2
或表示为
1 t 2 t 1 3t y (t ) ( e e e )u (t ) 2 2
我们下面介绍用卷积积分的方法，求解系统的零状态响应。由信号的冲激分解我们知道，一连续时间信号可表示为： x(t ) x()(t )d
h(m)
当n<0
y ( n) 0
y(0) 11 1
1
2
3
4
m
当n=0
h(1 m)
3
2 1
2 1 0
当n=1 y(1) 1 2 2 1 4
1
2
3
4
m
当n=2
y(2) 1 3 2 2 3 1 10
2 1
x(m)
3
0
1
2
3
4
m
当n=3
y(3) 2 3 3 2 2 1 14

两图形分离，其乘积等于零 0 t 1, f1 ( ) f 2 (t ) 1 0.5, f (t ) 1 0.5d 0.5t
0 t
1 t 2, f1 ( ) f 2 (t ) 1 0.5, f (t ) 1 0.5d 0.5(2 t )
3
2 1 0
h(2 m)
2 1 1 2
3
4
m
当n=4
y(4) 3 3 2 2 11 14
2 1 0
h(3 m)
3
2 1 1 2
3
4
m
h(4 m)
3
2 1
2 1 0
1
2
3
4
m
当n=5
y(5) 2 3 1 2 8
2 1
x(m)
3
01

0 .5
0
1

1
0

第二步：将函数 2 ()沿正轴平移时间，得f 2 (t ) f t
f1 ( )
f1 ( )
1
f 2 (t )
1
0 .5
0.5
f 2 (t )
0.5
0 .5
1
f 2 (t )
t 1
t
0

t 1
0
t

0
t 0(左移)
t 1 1
解： y (t ) x(t ) h(t )

x()h(t )d
x(t )
1
0
1
t
[u() u( 1)]e(t )u(t )d

h(t )
1
y1 (t ) y2 (t )
e t
0
t

y1 (t )

u()e(t )u(t )d (1 e t )u(t )
n
m
y (n) ( a n m )u (n) (a n a m )u (n)
m 0 m 0
n
n
1 a ( n 1) (a n )u (n) 1 1 a
a n a 1 u ( n) 1 1 a
1 a u ( n) 1 a
n 1
y (n)
d e
t
e d
1
t
u(t )
1
t 1
0 t
et (et e1 )u(t 1) [1 e
(t 1)
t

u( 1)u(t )
1
0பைடு நூலகம்
]u(t 1)
t 1
1
t

所以
y(t ) y1 (t ) y2 (t )
(1 et )u(t ) [1 e(t 1) ]u(t 1)
0
1
2
3
4
m
当n=6
y(6) 1 3 3
2 1 0
h(5 m)
3
2 1 1 2
当n≥7
y ( n) 0
h(6 m)
3
2
3
4
5 6
m
1
所以
2 1 0
1
2
3
4
5 6
m
y(n) 1, 4, 10, 14, 14, 8, 3
对于这种两个短序列的卷积和，可以用称为“不进位乘法”的方法求解。
ys(t)称为系统的稳态响应，yt(t)称为系统的瞬态响应。
二、连续时间系统的零状态响应的经典解法系统的零状态响应可以用经典法求解。当系统方程的右边不出现冲激及其导数时，初始条件等于起始条件，均是0。
例如：设系统方程如下，已知激励x(t)=e-3tu(t)，求零状态
y(t ) 3 y(t ) 2 y(t ) x(t )
h(n) ,2,3 1
x(n)
3
2 1 2 1 2 1
h(n)
3
0
3
4
n
0
1
2
3
4
n
h(n)
14
结果如上，表示为
y(n) 1, 4, 10, 14, 14, 8, 3
4 1
10 8 3
0 1 2
3 4
5 6 7
n
(9B 9B 2B)e3t e3t
所以
1 1 3t B y p (t ) e 2 2 ⑶ 确定待定系数，求全解。 y (t ) yh (t ) y p (t ) A1e A2 e