哈工大阵列信号处理第一次作业
哈工大_信号处理技术_习题库(Version201107)

习题库及参考答案(Version2011.7)1. 判断下列信号是否周期函数,是周期函数,确定周期。
(1) )46cos(2.0)2cos()(πππ++=t t t f(2) )814cos(1.0)46cos(2.0)2cos()(πππππ++++=t t t t f(3) )210cos(4)23cos(2)(πππ-++=t t t f(4) )2cos(3][n n f π= 解:(1) 122211===ππωπT , 3162222===ππωπT , 33/1121==T T ,132112===T T T (s)(2) 由上一问可知预求函数的前两项的周期为1s ,第3项周期为:711423==ππT ,77/11312==T T ,17312===T T T 故 该函数为周期信号,周期为1s 。
(3) 3232211===ππωπT , 5102222ππωπ===T , ππ3105/3/221==T T 由于T1/T2不存在正整数比,故 该函数不是周期函数,不存在周期。
(4) )22cos(3))(2cos(3][N n N n n f πππ+=+=122=∴=N N ππ 所以是周期函数,周期为1。
2. 用数学方程描述单位冲激函数的取样特性和移位抽样特性。
解: 取样特性)0()()(f dt t t f =⎰∞∞-δ移位抽样特性 )()()()(000t t t f t t t f -=-δδ3. 试写出信号f(t)与δ(t)的卷积形式,并简要解释其物理含义。
解:信号f(t)与δ(t)的卷积可以写为:ττδτd t f t f )()()(-=⎰∞∞-或)()()(ττδτ∆-∆∆≈∑∞∞-t k f t f其物理含义是:将一个函数(信号)分解为移位、加权和的形式。
也就是将一个信号分解成无数个加权的窄脉冲序列之和。
4. 试分别画出下图信号f(t)的反褶、延迟-1秒、以及反褶+延迟-1秒的波形(共3个波形)。
哈工大信号检测与处理第1章随机过程15-1

1.2 高斯分布与高斯噪声
2 x ( t ) 式中, a 为噪声 的均值; 为噪声 x ( t ) 的方差。称 x ( t ) 是服从均值为 a , 2 2 x ( t ) ~ N ( a , ) 。 为标准差。特别当 方差为 的高斯分布或正态分布,记作 2 a 0 , 1 时, x ( t ) 的分布称为标准正态分布。
1
1.2.3 高斯分布特性的应用
高斯分布最直观的应用是考虑其对数据处理影响程度的分析,如 3 法则。 : 3 法则(标准) 该法则的意义是当噪声服从高斯分布时,噪声的影响主要集中在正负3 倍的标准差之内,即1σ 只考虑了68%的噪声影响,而3σ 几乎考虑了其全部 影响。 大多数噪声(随机过程)瞬时幅度的概率分布是正态的即
F ( x) 1 2
xa xa
用误差函数表示 F(x)的好处是,借助于一般数学手册所提供的误差函数表,可方 便查出不同 x 值时误差函数的近似值,还可以在 Matlab 程序中直接调用 erf(x) 或 erfc(x)计算,避免了复杂积分运算。
误差函数和余补误差函数的主要性质: (1)误差函数是递增函数,它具有如下性质 1) erf ( x) erf ( x) ; 2) erf () 1 。 (2)余补误差函数是递减函数,它具有如下性质 1) erfc() 0 ; 2) erfc( x) 1 exp(x2 ), x x
1 Pn Pn ( )d R(0) 2 2
2)高斯噪声的一维概率密度函数具有如下特性: (1) p( x ) 对称于 x a 直线,即有
p(a x ) p( a x )
(2) p( x ) 在 ( , a ) 内单调上升,在 ( a , ) 内单调下降, 且在点 a 处达到极大值
哈工大数字信号处理实验2011

实验一 离散傅里叶变换的性质一、 实验目的1、 掌握离散傅里叶变换的性质,包括线性特性、时移特性、频移特性、对称性和循环卷积等性质;2、 通过编程验证傅里叶变换的性质,加强对傅里叶变换性质的认识。
二、 实验原理和方法 1. 线性特性1212DFT[()()]()()ax n bx n aX k bX k +=+2. 时移特性DFT[()]()DFT[()]()km kmx n m W X k x n m W X k -+=-=3. 频移特性()()nl N IDFT X k l IDFT X k W +=⎡⎤⎡⎤⎣⎦⎣⎦4. 对称性设由x(n) 延拓成的周期序列为 ()x n 则()()()e o xn x n x n =+ 共轭对称序列()()()*12e xn x n x N n ⎡⎤=+-⎣⎦ 共轭反对称序列()()()*12o x n x n x N n ⎡⎤=--⎣⎦ 将()e xn 和()o x n 截取主周期,分别得 ()()()ep e N x n x n R n = ()()()o p o N x n x n R n= 则()()()()()N ep op x n xn R n x n x n ==+ x(n)序列的实部和虚部的离散立叶变换(){}()Re ep DFT x n X k =⎡⎤⎣⎦ (){}()Im op DFT j x n X k =⎡⎤⎣⎦当x(n)为实数序列[][]()(())()()(())()()()(())()(())()()(())()(())()()()arg ()arg ()N N N N R R N N R N N I I N N I N N X k X k R k X k X N k R k X N k X k X k R k X N k R k X k X k R k X N k R k X k X N k X k X k *=-≅-=-≅-=-=-=--=--=-=--5. 循环卷积()312312()()()()()x n x n x n X k X k X k =⊗⇒=有限长序列线性卷积与循环卷积的关系 x1(n)和x2(n)的线性卷积:111212()()()()()N l m m x n x m x n m x m x n m -∞=-∞==-=-∑∑1120()()N m x m x n m -==-∑将x1(n)和x2(n)延拓成以N 为周期的周期序列11()()r xn x n rN ∞=-∞=+∑ 22()()q xn x n qN ∞=-∞=+∑ 则它们的周期卷积为14120()()()N p m x n xm x n m -==-∑ 1120()()N m x m xn m -==-∑ 1120()()N m q x m x n m qN -∞==-∞=-+∑∑1120()()N q m x m x n qN m ∞-=-∞=⎡⎤=+-⎢⎥⎣⎦∑∑ ()lq x n qN ∞=-∞=+∑x1(n)和x2(n)周期延拓后的周期卷积等于他们的线性卷积的的周期延拓。
哈工大数字信号处理实验一

数字信号处理实验报告实验题目:实验一用FFT做谱分析院系:班级:姓名:学号:哈尔滨工业大学实验一: 用FFT 作谱分析一、实验目的(1) 进一步加深DFT 算法原理和基本性质的理解(因为FFT 只是DFT 的一种快速算法, 所以FFT 的运算结果必然满足DFT 的基本性质)。
(2) 熟悉FFT 算法原理和FFT 子程序的应用。
(3) 学习用FFT 对连续信号和时域离散信号进行谱分析的方法,了解可能出现的分析误差及其原因,以便在实际中正确应用FFT 。
二、实验原理1.DFT 的运算量:一次完整的DFT 运算总共需要2N 次复数乘法和(1)N N -复数加法运算,因而直接计算DFT 时,乘法次数和加法次数都和2N 成正比,当N 很大时,运算量很客观的。
例如,当N=8时,DFT 运算需64位复数乘法,当N=1024时,DFT 运算需1048576次复数乘法。
而N 的取值可能会很大,因而寻找运算量的途径是很必要的。
2.FFT 算法原理:大多数减少离散傅里叶变换运算次数的方法都是基于nkN W 的对称性和周期性。
(1)对称性()*()k N n kn knN N NW W W --== (2)周期性()(mod`)()()kn N kn n N k n k N N N N NW W W W ++===由此可得()()/2(/2)1n N k N n k nk N N N N N k N k N N W W W W W W ---+⎧==⎪=-⎨⎪=-⎩这样:1.利用第三个方程的这些特性,DFT 运算中有些项可以合并;2.利用nkN W 的对称性和周期性,可以将长序列的DFT 分解为短序列的DFT 。
前面已经说过,DFT 的运算量是与2N 成正比的,所以N 越小对计算越有利,因而小点数序列的DFT 比大点数序列的DFT 运算量要小。
快速傅里叶变换算法正是基于这样的基本思路而发展起来的,她的算法基本上可分成两大类,即按时间抽取法和按频率抽取法。
哈尔滨工业大学-试验方法与数字信号处理大作业

Harbin Institute of Technology大作业一课程名称:试验方法与数字信号处理院系:机械电子班级:15S0825学号:姓名:哈尔滨工业大学给出信号x(t)=sin(2π∙10∙t)+sin(2π∙80∙t)+ sin(2π∙200∙t)1.绘出信号波形。
利用matla软件,绘制出的原信号波形如图1所示。
图1 原波形信号2. 低通滤波,分别用FIR,IIR滤波器,保留10Hz,去除80Hz和200Hz,并画出波形,并与10Hz信号对比。
解:原信号的最大F max = 200Hz,取:∆t=10−3<12F max=1400=0.0025此时,满足采样定理。
(1)、用FIR滤波器(附录1)选择低通滤波的截止频率为50Hz,滤波器项数为80,通过FIR滤波器公式,可得到滤波后的信号。
编写matlab程序,对比滤波后信号和10Hz信号,如图2所示。
图2 FIR滤波后信号与10Hz信号对比通过图2可以发现,滤波后的信号大致反应了10Hz信号的变化,相位一致,幅值衰减了一部分,说明滤波后,确实去除了80Hz,200Hz的信号。
为了进一步说明问题,绘制滤波后信号的频谱图,如图3所示。
从图3可以看出,随着N 的增大,10Hz信号幅值衰减的程度变小,会趋于至原幅值的一半,其余信号幅值衰减的程度变大,滤波效果更加明显。
图3 FIR滤波后频谱(N = 8,30,80,800)10Hz尝试用汉宁窗口对泄漏进行修正,修正前后的波形如图4所示。
图4 采用汉宁窗口修正(2)、用IIR滤波器(附录2)选择低通滤波的截止频率为50Hz的二阶IIR滤波器,根据相关公式,可以得到IIR滤波器的滤波因子,进而可得到滤波后的信号。
编写matlab程序,对比滤波后信号和10Hz信号,如图5所示。
图5 IIR滤波后信号与10Hz信号对比通过图5可以发现,滤波后的信号大致反应了10Hz信号的变化,相位一致,幅值衰减了一部分,说明滤波后,确实去除了80Hz,200Hz的信号。
哈工大试验方法和数字信号分析处理作业一

题目:(1)给定数字信号:x(t)=sin(20*pi*t)+sin(100*pi*t)+sin(400*pi*t);即该信号由10HZ,50HZ,200HZ。
三个正弦信号合成。
要求:绘出上述给定数字信号的曲线x(t)。
低通滤波练习:分别用FIR、IIR滤波器滤去50Hz、200Hz信号,保留10Hz信号;绘出滤波前和滤波后的信号曲线,并做对比;滤波过程中的问题讨论。
带通滤波练习:用FIR滤波器滤去10Hz、200Hz信号,保留50Hz信号;绘出滤波前和滤波后的信号曲线,并做对比;滤波过程中的问题讨论。
(2)给定数字信号:X(t)=sin(2*pi*10*t)+sin(2*pi*50*t)+sin(2*pi*200*t)+0.6*randn(1,N)即在原信号上叠加上一个白噪声信号。
要求:绘出上述给定数字信号的曲线x(t)。
分别用低通滤波器和带通滤波器(FIR、IIR任选)滤波、绘曲线对比、讨论。
注:本次作业要求使用我们课上(§3-3、§3-4)所推导的滤波器(公式)滤波;不许使用MATLAB中的滤波函数。
1.数字信号为:x(t)=sin(20*pi*t)+sin(100*pi*t)+sin(400*pi*t);时因为,最大频率为200HZ,故由采样定理dt<=1/2*f max,可得dt<=0.0025s,取dt=0.0003s,满足采样定理。
(1)绘出x(t)图像:Matlab代码:clear allt=0:0.0005:0.6;t1=0.0005;F=15;N=1201;x=sin(2*pi*10*t)+sin(2*pi*50*t)+sin(2*pi*200*t);x1=sin(2*pi*10*t);plot(t,x,'b');图形如下:图1 原始信号图像(2)低通滤波练习:1.FIR滤波器:Matlab代码:clear allt=0:0.0005:0.6;t1=0.0005;F=15;x=sin(2*pi*10*t)+sin(2*pi*50*t)+sin(2*pi*200*t);x1=sin(2*pi*10*t);y(1201)=0;for k=50:1100for i=-20:20if i==0fi=2*F*t1;elsefi=sin(2*pi*F*i*t1)/pi/i;endy(k)=y(k)+fi*x(k-i);endendplot(t,x1,'k',t,x,'b',t,y,'r');图像如下:图2 FIR低通滤波信号图像图3 FIR低通滤波信号图像i=-30:30,k=70:1100时分析讨论:由图可以看出,原始图像有正弦信号叠加后十分混乱,滤波后基本滤出了10HZ的信号,设计滤波器时,通过改变N1和N2以及采样的数量来生成不同的滤波后图像,最终选择了如上代码中的数值。
阵列信号处理仿真作业
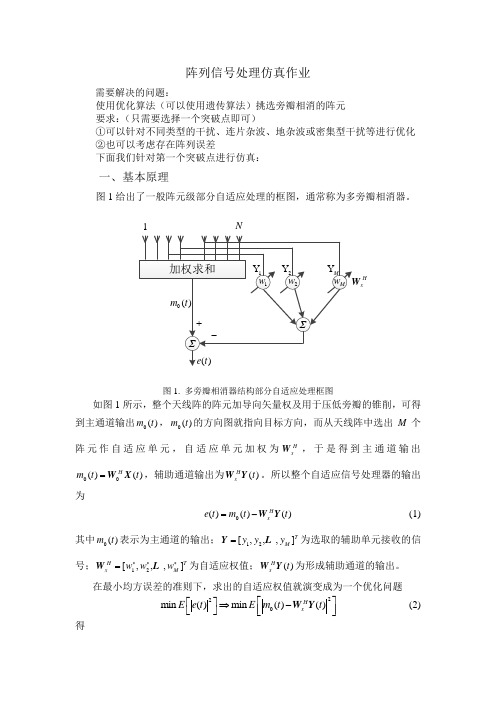
阵列信号处理仿真作业需要解决的问题:使用优化算法(可以使用遗传算法)挑选旁瓣相消的阵元 要求:(只需要选择一个突破点即可)①可以针对不同类型的干扰、连片杂波、地杂波或密集型干扰等进行优化 ②也可以考虑存在阵列误差下面我们针对第一个突破点进行仿真:一、基本原理图1给出了一般阵元级部分自适应处理的框图,通常称为多旁瓣相消器。
1NHx图1. 多旁瓣相消器结构部分自适应处理框图如图1所示,整个天线阵的阵元加导向矢量权及用于压低旁瓣的锥削,可得到主通道输出0()m t ,0()m t 的方向图就指向目标方向,而从天线阵中选出M 个阵元作自适应单元,自适应单元加权为H x W ,于是得到主通道输出00()()H m t t =W X ,辅助通道输出为()H x t W Y 。
所以整个自适应信号处理器的输出为0()()()H x e t m t t =-W Y(1)其中0()m t 表示为主通道的输出;12[,,,]T M y y y =Y L 为选取的辅助单元接收的信号;12[,,,]H Tx M w w w ***=W L 为自适应权值;()H x t W Y 为形成辅助通道的输出。
在最小均方误差的准则下,求出的自适应权值就演变成为一个优化问题220min ()min ()()H x E e t E m t t ⎡⎤⎡⎤⇒-⎢⎥⎣⎦⎣⎦W Y (2)得10()()()()H H xE t t E t m t -*⎡⎤⎡⎤=⎣⎦⎣⎦WY Y Y(3)为了保证目标信号不损失,应对自适应权作约束,约束条件是在目标信号的方向上,阵列自适应处理的增益为一常数。
即在权值调整过程中,无论权x W 怎样变化,对有用信号的增益不变。
这样在使自适应阵输出()e t 的均方值2()E e t ⎡⎤⎣⎦最小时,能最大限度地抑制干扰且不损失有用信号能量。
图1中应用式( 2) 的无约束优化方程显然不合理,它不能保证有用信号增益不变。
哈工大实验方法第一次大作业概要

哈尔滨工业大学试验方法及数字信号处理分析————第一次大作业数字滤波器设计指导老师:包钢学生姓名:陈方鑫学生学号:15S008043第一部分 作业题目一、设计题目1、杂波信号:()sin(210)sin(280)sin(2200)t x t t t πππ=⨯+*+⨯2、要求:(1)绘出杂波信号波形。
(2)分别用FIR IIR 滤波器设计低通和带通滤波器,保留10Hz ,80Hz 频率。
绘出滤波后波形,并与理想波形比较。
(3)在原信号加上白噪声信号,再比较分析。
第二部分 具体设计内容第一节 卷积滤波器的设计一、低通滤波1、低通滤波器参数计算 (1)FIR 滤波频率响应:212()N j fi t i i N H f f e π∆-=-=∑…………①(2)低通期望频率响应:1;0()0;0,f FH f f f F≤≤=≤≥………②(3)通过①、②计算滤波因子 当0i =时,'2f F t ∆= 当0i ≠时,sin(2)'Fi t f iππ=取'f f =可得近似理想低通滤波器:21N k i k ii N y f x -=-=∑(4)由于题目x (t )的最高频率fmax=200。
基于采样定理,f’>2fmax=400。
本例取f’=5fmax=1000。
故 t=0.001s。
2、设计程序程序参数:1t t;F=低通截止频率;t=0:10^-3:0.5;t1=10^-3;F=20;x=sin(2*pi*10*t)+sin(2*pi*80*t)+sin(2*pi*200*t);x1=sin(2*pi*10*t);f(1)=2*F*t1;i=2;while i<60f(i)=sin(2*pi*F*i*t1)/(pi*i);i=i+1;endfor k=61:440y(k)=0;for i=1:60;y(k)=f(i)*(x(k-i)+x(k+i))+y(k);endendy(length(t))=0;plot(t,x,'r',t,x1,'b',t,y,'k');legend('原图','理想图','滤波图');title('F=20');xlabel('x');ylabel('y');3、结果分析F=15放大图放大图放大图分析:上图展示了FIR 低通滤波的总体情况,并分别对F 取15,20,30值时做了对比研究。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Harbin Institute of Technology
阵列信号处理第一次作业课程名称:阵列信号处理
哈尔滨工业大学
1.在球坐标系下,由Maxwell 方程推导自由空间的波动方程
由Maxwell 方程可以推导出电磁波的波动方程为:
22222222()E
E x y z t
εμ∂∂∂∂++=∂∂∂∂ (1) 代入直角坐标与球坐标的关系
sin cos sin sin cos x r y r z r θϕθϕθ=⎧⎪
=⎨⎪=⎩
(2) 可以得到:
22222222
221111()(sin )sin sin s s s
r r r r r r c t
θθθθθϕ∂∂∂∂∂∂++=∂∂∂∂∂∂ (3) 根据球面波方程的球对称性,上式简化为:
222
2211()s s
r r r r c t
∂∂∂=∂∂∂ (4) 即:
222
221rs rs
r c t
∂∂=∂∂ (5) 该方程的一个解为:
exp[()A
s j t kr r
ω=
- (6) 同样有如下关系:
/k c ω=
根据平面波的定义,在球坐标系下,单频平面波的表达式为:
(,)exp[()]A
s r t j t k r r
ω=-⋅ (7)
2.推导空间采样信号的空、时付氏变换的卷积形式
//(,)(,)()2d
d
d
Z k Y l W k l dl
ππ
ωωπ
-=
-⎰
其中()w x 为窗函数。
对于有限孔径的感应器,某一感应器接收的信号可以表示为:
(,)()(,)z x t w x f x t = (1)
其中()w x 为窗函数。
通过空间傅立叶变换可得:
()()exp()W k w x jk x dx ∞
-∞
=⋅⎰ (2)
(,)(,)exp[()F k f x t j t k x dxdt ωω∞
∞
-∞
-∞
=--⋅⎰
⎰
(3)
对接收信号(,)z x t 进行傅立叶变换:
()
()()()[]()()()
(){}
()(),,exp[(),exp exp ,exp ,exp exp ,exp exp o Z k z x t j t k x dxdt
w x f x t j t jk x dxdt
w x F x jk x dx
w x F l jl x dl jk x dx w x F l jl x jk ωωωωωω∞
∞
-∞-∞
∞
∞
-∞-∞∞
-∞∞
∞-∞-∞
∞
∞-∞-∞=--⋅⎡⎤=-⋅⎣⎦⎡⎤=⋅⎣⎦⎡⎤⎡⎤=-⋅⋅⎣⎦⎣⎦⎡⎤=-⋅⋅⎣⎦⎰
⎰⎰
⎰
⎰⎰⎰
⎰⎰()()(){}()(),exp ,x dldx
F l w x j k l x dx dl
W k l F l dl
ωω∞
∞
-∞-∞
∞
-∞
⎡⎤⎣⎦⎡⎤=-⋅⎣⎦
=-⎰⎰⎰
(4)
其中,()()[],,exp o F x f x t j t dt ωω∞
-∞
=-⎰。
综上所述,可得
(,)()(,)Z k W k l F l dl ωω∞
-∞
=-⎰ (5)
3.设在自由空间中有两个平面传播,一接收阵列沿x 方向排列,两平面波传播速度相同为c ,第一个平面波的频率为1w ,与x 轴的夹角为1;,第二个平面波的频率为2w ,与x 轴的夹角为
2
:
A.如果两个信号的空间频率相同,信号频率满足什么关系;
1
1
1
1
11
1
1
12
2
2cos
cos cos cos
2k w c
c
f w
2
2
2
2
22
2
2
22
22cos
cos cos cos
2
k w c
c
f w
若满足:12k k
则有:11
22
cos
cos
w w 信号频率满足:21
2
1
cos cos
w
w
B .如果12w w ,阵列的采样间距应满足什么条件。
为了避免出现模糊,空间采样间隔应该满足:
c d
w
因为12w w ,所以d 应满足两个间距中较小的:
1c d
w
4.两个等间距的线阵,分别由8个阵元构成,间距为d 。
第一个阵列的窗函数为:1,1,1/2,1/2,1/2,1/2,1,1。
第二个阵列的窗函数为:1/2,1/2 ,1,1,1,1,1/2,1/2。
分别计算各阵列的平滑函数(窗函数)。
平滑函数计算公式:
exp W k
w x jk x d x
设8阵元均匀线阵阵元位置如下图所示:
对窗函数计算有限长的傅立叶变换得到:
11(7/2)0
7/25/2
3/2
/2
/23/25/27/2
7/27/25/25/23/23/2exp ()1/2()()()1/2[()(x x x x x x x x x x x x x x x M jk m
d
m jk d jk d jk d jk d jk d jk d jk d jk d jk d jk d jk d jk d jk d jk d jk W k
w x jk x d x w m e e
e
e
e
e e e e e e e e e e e /2
/2)]
2[cos(7/2)cos(5/2)][cos(3/2)cos(/2)]4cos(3)cos(/2)+2cos()cos(/2)2cos(/2)(2cos3cos )
x x d jk d x x x x x x x x x x x e k d k d k d k d k d k d k d k d k d k d k d
21(7/2)0
7/2
5/2
3/2
/2
/23/25/27/27/27/25/25/23/23exp ()1/2()()1/2()
1/2[()()][(x x x x x x x x x x x x x x x M jk m
d
m jk d jk d jk d jk d jk d jk d jk d jk d jk d jk d jk d jk d jk d jk d W k
w x jk x d x w m e e e
e
e
e e e e e e e e e
e /2/2
/2)()]
[cos(7/2)cos(5/2)]2[cos(3/2)cos(/2)]2cos(3)cos(/2)+4cos()cos(/2)2cos(/2)(cos32cos )
x x jk d jk d x x x x x x x x x x x e e k d k d k d k d k d k d k d k d k d k d k d。
