2020-2021初三数学一模试题分类汇编——相似综合
2020-2021初三数学一模试题分类汇编——相似综合及详细答案
2020-2021初三数学一模试题分类汇编——相似综合及详细答案一、相似1．如图，BD是□ABCD的对角线，AB⊥BD，BD=8cm，AD=10cm，动点P从点D出发，以5cm/s的速度沿DA运动到终点A，同时动点Q从点B出发，沿折线BD—DC运动到终点C，在BD、DC上分别以8cm/s、6cm/s的速度运动.过点Q作QM⊥AB，交射线AB于点M，连接PQ，以PQ与QM为边作□PQMN.设点P的运动时间为t(s)（t>0），□PQMN与□ABCD重叠部分图形的面积为S（cm2）.（1）AP=________cm（同含t的代数式表示）.（2）当点N落在边AB上时，求t的值.（3）求S与t之间的函数关系式.（4）连结NQ，当NQ与△ABD的一边平行时，直接写出t的值.【答案】（1）（10-5t）（2）解：如图①，当点N落在边AB上时，四边形PNBQ为矩形．∵PN∥DB，∴△APN∽△ADB，∴AP：AD=PN：DB，∴（10－5t）：10=8t：8，120t=80，∴．（3）解：分三种情况讨论：a)如图②，过点P作PE⊥BD于点E，则PE=3t．当时，．b)如图③，过点P作PE⊥BD于点E，则PE=3t，设PN交AB于点F，则．当时，．c)如图④，当时，PF=8-4t，FB=3t，PN=DB=QM=8，∴FN=4t，DQ=6(t-1)，∴BM=DQ=6(t-1)．∵∠GBM=∠A，∠DBA=∠GMB，∴△BGM∽△ABD，∴GM：BM=DB：AB，解得：GM=8t-8，∴S=S平行四边形PNMQ-S△FMN-S△BMG=8（9t-6）－ ×4t×（9t-6）－ ×（6t-6）（8t-8）= ．综上所述：（4）解：分三种情况讨论．①当NQ∥AB时，如图5，过P作PF⊥BD于F，则PF=3t，DF=4t，PN=FQ=BQ=8t，∴BD=8t+8t+4t=8，解得：．②当AD∥NQ，且Q在BD上时，如图6．∵PNQD和PNBQ都是平行四边形，∴PN=DQ=BQ，∴8t+8t=8，解得：．③当AD∥NQ，且Q在DC上时，如图7，可以证明当Q与C重合，即直线NQ与直线BC重合时，满足条件，如图8，此时DQ=AB= =6，t= =2．综上所述：或或．【解析】【解答】解：（1）（10-5t）；【分析】（1）由题意可得，DP=5t,所以AP=AD-DP=10-5t;（2）由欧勾股定理的逆定理可得∠ABD=，所以根据有一个角是直角的平行四边形是矩形可得，当点N落在边AB上时，四边形PNBQ为矩形；由平行线分线段成比例定理可得比例式：,则可得关于t的方程，解方程即可求解；（3）由（2）知，当□PQMN全部在□ABCD中时，运动时间是秒，由已知条件可知，点Q 在BD边上的运动速度是8cm/s，在DC边上的运动速度是6cm/s，所以当点Q运动到C点时，点P也运动到了点A，所以分3种情况：a)如图②，过点P作PE⊥BD于点E，当0 < t ≤时， S=BQ PE；b)如图③，过点P作PE⊥BD于点E，设PN交AB于点F，当< t ≤ 1 时，S =（PF+BQ）PE；c)如图④，当1 < t ≤ 2 时， S =平行四边形PNMQ的面积-三角形FNM的面积-三角形BMG 的面积；（4）由题意NQ与△ABD的一边平行可知，有3种情况：①当NQ∥AB；②当AD∥NQ，且Q在BD上时；③当AD∥NQ，且Q在DC上时。
2020-2021初三数学一模试题分类汇编——圆的综合综合及答案
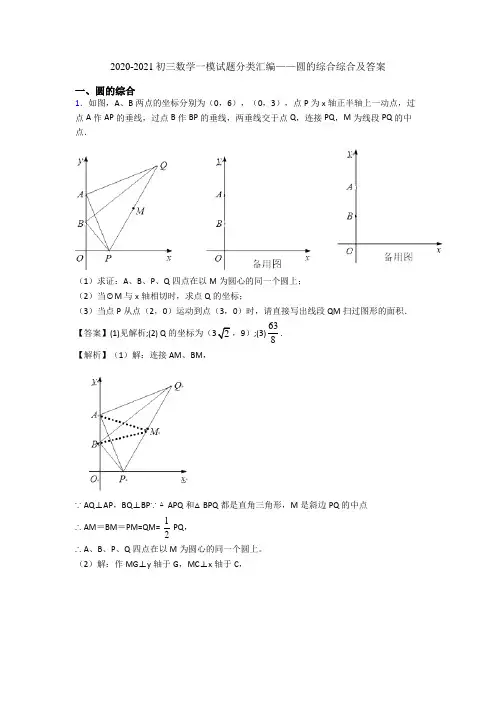
2020-2021初三数学一模试题分类汇编——圆的综合综合及答案一、圆的综合1．如图，A、B两点的坐标分别为（0，6），（0，3），点P为x轴正半轴上一动点，过点A作AP的垂线，过点B作BP的垂线，两垂线交于点Q，连接PQ，M为线段PQ的中点．（1）求证：A、B、P、Q四点在以M为圆心的同一个圆上；（2）当⊙M与x轴相切时，求点Q的坐标；（3）当点P从点（2，0）运动到点（3，0）时，请直接写出线段QM扫过图形的面积．【答案】(1)见解析;(2) Q的坐标为（32，9）;(3)63 8.【解析】（1）解：连接AM、BM，∵AQ⊥AP，BQ⊥BP∵△APQ和△BPQ都是直角三角形，M是斜边PQ的中点∴AM＝BM＝PM=QM= 12 PQ，∴A、B、P、Q四点在以M为圆心的同一个圆上。
（2）解：作MG⊥y轴于G，MC⊥x轴于C，∵AM＝BM∴G是AB的中点，由A（0，6），B（0，3）可得MC＝OG＝4.5∴在点P运动的过程中，点M到x轴的距离始终为4.5则点Q到x轴的距离始终为9，即点Q的纵坐标始终为9，当⊙M与x轴相切时则PQ⊥x轴，作QH⊥y轴于H，HB＝9－3＝6，设OP＝HQ＝x由△BOP∽△QHB，得x2＝3×6＝8，x＝2∴点Q的坐标为（2，9）（3）解：由相似可得：当点P在P1（2，0）时，Q1（4，9）则M1（3，4.5）当点P在P2（3，0）时，Q2（6，9），则M2（4.5，4.5）∴M1M2＝92－3＝32， Q1Q2＝6－4＝2线段QM扫过的图形为梯形M1M2Q2Q1其面积为：12×(32＋2)×4.5＝638.【解析】【分析】根据已知可得出三角形APQ和三角形BPQ都是直角三角形，再根据这个条件结合题意直接解答此题.【详解】（1）解：连接AM、BM，∵AQ⊥AP，BQ⊥BP∵△APQ和△BPQ都是直角三角形，M是斜边PQ的中点∴AM＝BM＝PM=QM= PQ，∴A、B、P、Q四点在以M为圆心的同一个圆上。
2020-2021初三数学一模试题分类汇编——相似综合附答案
2020-2021初三数学一模试题分类汇编——相似综合附答案一、相似1．如图，在□ABCD中，对角线AC、BD相交于点O，点E、F是AD上的点，且AE=EF=FD.连结BE、BF。
使它们分别与AO相交于点G、H（1）求EG ：BG的值（2）求证：AG=OG（3）设AG =a ,GH =b，HO =c，求a : b : c的值【答案】（1）解：∵四边形ABCD是平行四边形，∴AO= AC，AD=BC，AD∥BC，∴△AEG∽△CBG，∴ = = ．∵AE=EF=FD，∴BC=AD=3AE，∴GC=3AG，GB=3EG，∴EG：BG=1：3（2）解：∵GC=3AG（已证），∴AC=4AG，∴AO= AC=2AG，∴GO=AO﹣AG=AG（3）解：∵AE=EF=FD，∴BC=AD=3AE，AF=2AE．∵AD∥BC，∴△AFH∽△CBH，∴ = = = ，∴ = ，即AH= AC．∵AC=4AG，∴a=AG= AC，b=AH﹣AG= AC﹣ AC= AC，c=AO﹣AH= AC﹣ AC= AC，∴a：b：c= ：： =5：3：2【解析】【分析】（1）根据平行四边形的性质可得AO=AC，AD=BC，AD∥BC，从而可证得△AEG∽△CBG，得出对应边成比例，由AE=EF=FD可得BC=3AE，就可证得GB=3EG，即可求出EG：BG的值。
（2）根据相似三角形的性质可得GC=3AG，就可证得AC=4AG，从而可得AO=2AG，即可证得结论。
（3）根据平行可证得三角形相似，再根据相似三角形的性质可得AG=AC，AH=AC，结合AO=AC，即可得到用含AC的代数式分别表示出a、b、c，就可得到a：b：c的值。
2．如图1，在矩形ABCD中，AB=6cm，BC=8cm，E、F分别是AB、BD的中点，连接EF，点P从点E出发，沿EF方向匀速运动，速度为1cm/s，同时，点Q从点D出发，沿DB方向匀速运动，速度为2cm/s，当点P停止运动时，点Q也停止运动．连接PQ，设运动时间为t（0＜t＜4）s，解答下列问题：（1）求证：△BEF∽△DCB；（2）当点Q在线段DF上运动时，若△PQF的面积为0.6cm2，求t的值；（3）当t为何值时，△PQF为等腰三角形？试说明理由．【答案】（1）解：∵四边形ABCD是矩形，∴ AD∥BC，在中，∵别是的中点，∴EF∥AD，∴ EF∥BC，∴∴（2）解：如图1，过点Q作于，∴QM∥BE，∴∴∴（舍）或秒（3）解：当点Q在DF上时，如图2，∴∴ .当点Q在BF上时，，如图3，∴∴时，如图4，∴∴时，如图5，∴∴综上所述，t=1或3或或秒时，△PQF是等腰三角形【解析】【分析】（1）根据题中的已知条件可得△BEF和△DCB中的两角对应相等，从而可证△BEF∽△DCB；（2）过点Q作QM⊥EF 于M ，先根据相似三角形的预备定理可证△QMF ∽△BEF；再由△QM F ∽△BEF可用含t的代数式表示出QM的长；最后代入三角形的面积公式即可求出t的值。
2020-2021中考数学一模试题分类汇编——相似综合含答案
2020-2021中考数学一模试题分类汇编——相似综合含答案一、相似1．如图所示，将二次函数y=x2+2x+1的图象沿x轴翻折，然后向右平移1个单位，再向上平移4个单位，得到二次函数y=ax2+bx+c的图象．函数y=x2+2x+1的图象的顶点为点A．函数y=ax2+bx+c的图象的顶点为点B，和x轴的交点为点C，D（点D位于点C的左侧）．（1）求函数y=ax2+bx+c的解析式；（2）从点A，C，D三个点中任取两个点和点B构造三角形，求构造的三角形是等腰三角形的概率；（3）若点M是线段BC上的动点，点N是△ABC三边上的动点，是否存在以AM为斜边的Rt△AMN，使△AMN的面积为△ABC面积的？若存在，求tan∠MAN的值；若不存在，请说明理由．【答案】（1）解：y=x2+2x+1=（x+1）2的图象沿x轴翻折，得y=﹣（x+1）2，把y=﹣（x+1）2向右平移1个单位，再向上平移4个单位，得y=﹣x2+4，∴所求的函数y=ax2+bx+c的解析式为y=﹣x2+4（2）解：∵y=x2+2x+1=（x+1）2，∴A（﹣1，0），当y=0时，﹣x2+4=0，解得x=±2，则D（﹣2，0），C（2，0）；当x=0时，y=﹣x2+4=4，则B（0，4），从点A，C，D三个点中任取两个点和点B构造三角形的有：△ACB，△ADB，△CDB，∵AC=3，AD=1，CD=4，AB= ，BC=2 ，BD=2 ，∴△BCD为等腰三角形，∴构造的三角形是等腰三角形的概率=（3）解：存在，易得BC的解析是为y=﹣2x+4，S△ABC= AC•OB= ×3×4=6，M点的坐标为（m，﹣2m+4）（0≤m≤2），①当N点在AC上，如图1，∴△AMN的面积为△ABC面积的，∴（m+1）（﹣2m+4）=2，解得m1=0，m2=1，当m=0时，M点的坐标为（0，4），N（0，0），则AN=1，MN=4，∴tan∠MAC= =4；当m=1时，M点的坐标为（1，2），N（1，0），则AN=2，MN=2，∴tan∠MAC= =1；②当N点在BC上，如图2，BC= =2 ，∵BC•AN= AC•BC，解得AN= ，∵S△AMN= AN•MN=2，∴MN= = ，∴∠MAC= ；③当N点在AB上，如图3，作AH⊥BC于H，设AN=t，则BN= ﹣t，由②得AH= ，则BH= ，∵∠NBG=∠HBA，∴△BNM∽△BHA，∴，即，∴MN= ，∵AN•MN=2，即•（﹣t）• =2，整理得3t2﹣3 t+14=0，△=（﹣3 ）2﹣4×3×14=﹣15＜0，方程没有实数解，∴点N在AB上不符合条件，综上所述，tan∠MAN的值为1或4或【解析】【分析】（1）将y=x2+2x+1配方成顶点式，根据轴对称的性质，可得出翻折后的函数解析式，再根据函数图像平移的规律：上加下减，左加右减，可得出答案。
2020-2021九年级数学一模试题分类汇编——相似综合附答案解析
2020-2021九年级数学一模试题分类汇编——相似综合附答案解析一、相似1．如图,在一间黑屋子里用一盏白炽灯照一个球.（1）球在地面上的影子是什么形状?（2）当把白炽灯向上平移时,影子的大小会怎样变化?（3）若白炽灯到球心的距离是1 m,到地面的距离是3 m,球的半径是0.2 m,则球在地面上影子的面积是多少?【答案】（1）解：球在地面上的影子的形状是圆.（2）解：当把白炽灯向上平移时,影子会变小.（3）解：由已知可作轴截面，如图所示：依题可得：OE=1 m，AE=0.2 m，OF=3 m，AB⊥OF于H，在Rt△OAE中，∴OA= = = (m)，∵∠AOH=∠EOA，∠AHO=∠EAO=90°，∴△OAH∽△OEA，∴，∴OH= == (m)，又∵∠OAE=∠AHE=90°，∠AEO=∠HEA，∴△OAE∽△AHE，∴ = ，∴AH= ==2625 (m).依题可得：△AHO∽△CFO，∴ AHCF=OHOF ，∴CF= AH⋅OFOH = 2625×32425=64 (m)，∴S影子=π·CF2=π· (64)2 = 38 π=0.375π(m2).答：球在地面上影子的面积是0.375π m2.【解析】【分析】（1）球在灯光的正下方，根据中心投影的特点可得影子是圆.（2）根据中心投影的特点：在灯光下，离点光源近的物体它的影子短，离点光源远的物体它的影子长；所以白炽灯向上移时，阴影会逐渐变小.（3）作轴截面（如图）由相似三角形的判定得三组三角形相似，再根据相似三角形的性质对应边成比例，可求得阴影的半径，再根据面积公式即可求出面积.2．如图，已知在△ABC中，∠ACB=90°，BC=2，AC=4，点D在射线BC上，以点D为圆心，BD为半径画弧交边AB于点E，过点E作EF⊥AB交边AC于点F，射线ED交射线AC 于点G．（1）求证：△EFG∽△AEG；（2）设FG=x，△EFG的面积为y，求y关于x的函数解析式并写出定义域；（3）联结DF，当△EFD是等腰三角形时，请直接写出FG的长度．【答案】（1）证明：∵ ED=BD，∴∠B=∠BED．∵∠ACB=90°，∴∠B+∠A=90°．∵ EF⊥AB，∴∠BEF=90°．∴∠BED+∠GEF=90°．∴∠A=∠GEF．∵∠G是公共角，∴△EFG∽△AEG（2）解：作EH⊥AF于点H．∵在Rt△ABC中，∠ACB=90°，BC=2，AC=4，∴tanA= = ，∴在Rt△AEF中，∠AEF=90°，tanA= = ,∵△EFG∽△AEG，∴ ,∵ FG=x，∴ EG=2x，AG=4x．∴ AF=3x．∵ EH⊥AF，∴∠AHE=∠EHF=90°．∴∠EFA+∠FEH=90°．∵∠AEF=90°，∴∠A+∠EFA=90°,∴∠A=∠FEH,∴ tanA =tan∠FEH,∴在Rt△EHF中，∠EHF=90°，tan∠FEH= = ,∴ EH=2HF,∵在Rt△AEH中，∠AHE=90°，tanA= = ，∴ AH=2EH，∴ AH=4HF，∴ AF=5HF，∴ HF= ，∴EH= ，∴y= FG·EH= x· = 定义域：（0<x≤ ）（3）解：当△EFD为等腰三角形时，①当ED=EF时，则有∠EDF=∠EFD，∵∠BED=∠EFH，∴∠BEH=∠AHG，∵∠ACB=∠AEH=90°，∴∠CEF=∠HEF，即EF为∠GEH的平分线，则ED=EF=x，DG=8−x，∵anA= ，∴x=3，即BE=3；②若FE=FD, 此时FG的长度是 ;③若DE=DF, 此时FG的长度是 .【解析】【分析】（1）因为ED=BD，所以∠B=∠BED．根据等角的补角相等可得∠A=∠GEF，而∠G是公共角，所以由相似三角形的判定可得△EFG∽△AEG；（2）作EH⊥AF于点H．∠AEF=∠ACB=90°，∠A是公共角，所以可得AEF ACB，所以可得比例式，,由（1）得△EFG∽△AEG，所以可得比例式，,因为FG=x，所以EG=2x，AG=4x．则AF=3x，由同角的余角相等可得∠A=∠FEH,所以tanA =tan∠FEH,在Rt△EHF中，∠EHF=90°，tan∠FEH=,所以EH=2HF,在Rt△AEH中，同理可得AH=2EH，所以AH=4HF，AF=5HF，HF=x ，则EH= x ，△EFG的面积y= FG·EH=x· x=,自变量的取值范围是0<x≤ ；（3）当△EFD为等腰三角形时，分三种情况讨论：①当ED=EF时，则有∠EDF=∠EFD，易得FG=3；②若FE=FD, 易得FG=；③若DE=DF, 易得FG=.3．如图，四边形ABCD内接于⊙O，AB是⊙O的直径，AC和BD相交于点E，且DC2＝CE·CA．（1）求证：BC＝CD；（2）分别延长AB，DC交于点P，若PB＝OB，CD＝，求⊙O的半径．【答案】（1）证明：∵DC2＝CE·CA，∴，∵∠DCE=∠ACD，∴△CDE~△CAD，∴∠CDE=∠CAD，又∵∠CBD=∠CAD，∴∠CDE=∠CBD，∴CD=CB.（2）解：连结OC（如图），设⊙O的半径为r，由（1）知CD=CB，∴弧CD=弧CB，∴∠CDB=∠CBD=∠CAB=∠CAD=∠BAD，∠BOC=2∠CAB，∴∠BOC=∠BAD，∴OC∥AD，∴，∵PB＝OB，∴PB=OB=OA=r，PO=2r，∴=2，∵CD=2，∴PC=4，PD=PC+CD=6，又∵∠PCB=∠CDB+∠CBD，∠PAD=∠PACB+∠CAD，∴∠PCB=∠PAD，∵∠CPB=∠APD，∴△PCB~△PAD，∴，即，解得：r=4.即⊙O的半径为4.【解析】【分析】（1）根据相似三角形的判定：两边对应成比例及夹角相等可得△CDE~△CAD，再由相似三角形的性质：对应角相等，等量代换可得∠CDE=∠CBD，根据等腰三角形的性质即可得证.（2）连结OC，设⊙O的半径为r，根据圆周角定理可得∠BOC=∠BAD，由平行线的判定得OC∥AD，根据平行线所截线段成比例可得=2，从而求得PC、PD长，再根据相似三角形的判定可得△PCB~△PAD，由相似三角形的性质可得，从而求得半径.4．如图，在△ABC中，∠ACB=90°，AC=6cm，BC=8cm，点D从点C出发，以2cm/s 的速度沿折线C→A→B向点B运动，同时点E从点B出发，以1cm/s的速度沿BC边向点C运动，设点E运动的时间为t（单位：s）（0＜t＜8）.（1）当△BDE 是直角三角形时，求t的值；（2）若四边形CDEF是以CD、DE为一组邻边的平行四边形，①设它的面积为S，求S关于t的函数关系式；②是否存在某个时刻t，使平行四边形CDEF为菱形?若存在，求出t 的值；若不存在，请说明理由.【答案】（1）解：如图1，当∠BED=90°时，△BDE是直角三角形，则BE=t，AC+AD=2t，∴BD=6+10-2t=16-2t，∵∠BED=∠C=90°，∴DE∥AC，∴，∴，∴DE= ，∵sinB= ，∴，t= ；如图2，当∠EDB=90°时，△BDE是直角三角形，则BE=t，BD=16-2t，cosB= ，∴，∴t= ；答：当△BDE是直角三角形时，t的值为或（2）解：①如图3，当0＜t≤3时，BE=t，CD=2t，CE=8-t，∴S▱CDEF=2S△CDE=2× ×2t×（8-t）=-2t2+16t，如图4，当3＜t＜8时，BE=t，CE=8-t，过D作DH⊥BC，垂足为H，∴DH∥AC，∴，∴，∴DH= ，∴S▱CDEF=2S△CDE=2× ×CE×DH=CE×DH=（8-t）× = t2− t+ ；∴S于t的函数关系式为：当0＜t≤3时，S=-2t2+16t，当3＜t＜8时，S= t2− t+ ；②存在，如图5，当▱CDEF为菱形时，DH⊥CE，由CD=DE得：CH=HE，BH= ，BE=t，EH= ，∴BH=BE+EH，∴ =t+ ，∴t= ，即当t= 时，▱CDEF为菱形．【解析】【分析】（1）因为△BDE 是直角三角形有两种情况：①当∠BED=90°时，可得DE∥AC，根据平行于三角形一边的直线和其它两边（或其延长线）相交，所构成的三角形与原三角形相似可得,于是可得比例式将DE用含t的代数式表示，再根据sinB=可得关于t的方程，解方程即可求解；② 当∠EDB=90°时，同理可求解；（2）①当0＜t≤3时，S▱CDEF=2S△CDE可得s与t的关系式；当3＜t＜8时，过D作DH⊥BC，垂足为H，根据平行于三角形一边的直线和其它两边（或其延长线）相交，所构成的三角形与原三角形相似可得,于是可得比例式将DH用含t的代数式表示，则S▱CDEF=2S△CDE可得s与t的关系式；当3＜t＜8时，同上；②存在，当▱CDEF为菱形时，DH⊥CE，根据BH=BE+EH可得关于t的方程，解方程即可求解。
2020-2021初三数学一模试题分类汇编——相似综合附答案解析
2020-2021初三数学一模试题分类汇编——相似综合附答案解析一、相似1．如图，已知抛物线经过点A（﹣1，0），B（4，0），C（0，2）三点，点D与点C关于x轴对称，点P是x轴上的一个动点，设点P的坐标为（m，0），过点P做x轴的垂线l交抛物线于点Q，交直线于点M．（1）求该抛物线所表示的二次函数的表达式；（2）已知点F（0，），当点P在x轴上运动时，试求m为何值时，四边形DMQF是平行四边形？（3）点P在线段AB运动过程中，是否存在点Q，使得以点B、Q、M为顶点的三角形与△BOD相似？若存在，求出点Q的坐标；若不存在，请说明理由．【答案】（1）解：由抛物线过点A（-1，0）、B（4，0）可设解析式为y=a（x+1）（x-4），将点C（0，2）代入，得：-4a=2，解得：a=- ，则抛物线解析式为y=- （x+1）（x-4）=- x2+ x+2（2）解：由题意知点D坐标为（0，-2），设直线BD解析式为y=kx+b，将B（4，0）、D（0，-2）代入，得：，解得：，∴直线BD解析式为y= x-2，∵QM⊥x轴，P（m，0），∴Q（m，- m2+ m+2）、M（m， m-2），则QM=- m2+ m+2-（ m-2）=- m2+m+4，∵F（0，）、D（0，-2），∴DF= ，∵QM∥DF，∴当- m2+m+4= 时，四边形DMQF是平行四边形，解得：m=-1或m=3，即m=-1或3时，四边形DMQF是平行四边形。
（3）解：如图所示：∵QM∥DF，∴∠ODB=∠QMB，分以下两种情况：①当∠DOB=∠MBQ=90°时，△DOB∽△MBQ，则，∵∠MBQ=90°，∴∠MBP+∠PBQ=90°，∵∠MPB=∠BPQ=90°，∴∠MBP+∠BMP=90°，∴∠BMP=∠PBQ，∴△MBQ∽△BPQ，∴，即，解得：m1=3、m2=4，当m=4时，点P、Q、M均与点B重合，不能构成三角形，舍去，∴m=3，点Q的坐标为（3，2）；②当∠BQM=90°时，此时点Q与点A重合，△BOD∽△BQM′，此时m=-1，点Q的坐标为（-1，0）；综上，点Q的坐标为（3，2）或（-1，0）时，以点B、Q、M为顶点的三角形与△BOD相似．【解析】【分析】（1）A（-1，0）、B（4，0）是抛物线与x轴的交点，则可由抛物线的两点式，设解析为y=a（x+1）（x-4），代入C（0,2）即可求得a的值；（2）由QM∥DF且四边形DMQF是平行四边形知QM=DF，由D，F的坐标可求得DF的长度；由P（m,0）可得Q（m，-m2+m+2），而M在直线BD上，由B，D的坐标用待定系数法求出直线BD的解析式，并当=m时，表示出点M的坐标，可用m表示出QM的长度。
2020-2021初三数学一模试题分类汇编——圆的综合综合含答案
2020-2021初三数学一模试题分类汇编——圆的综合综合含答案一、圆的综合1．如图，⊙M交x轴于B、C两点，交y轴于A，点M的纵坐标为2．B（﹣33，O），C（3，O）．（1）求⊙M的半径；（2）若CE⊥AB于H，交y轴于F，求证：EH=FH．（3）在（2）的条件下求AF的长．【答案】（1）4；（2）见解析;（3）4．【解析】【分析】（1）过M作MT⊥BC于T连BM，由垂径定理可求出BT的长，再由勾股定理即可求出BM的长；（2）连接AE，由圆周角定理可得出∠AEC=∠ABC，再由AAS定理得出△AEH≌△AFH，进而可得出结论；（3）先由（1）中△BMT的边长确定出∠BMT的度数，再由直角三角形的性质可求出CG 的长，由平行四边形的判定定理判断出四边形AFCG为平行四边形，进而可求出答案．【详解】（1）如图（一），过M作MT⊥BC于T连BM，∵BC是⊙O的一条弦，MT是垂直于BC的直径，∴BT=TC=123∴124；（2）如图（二），连接AE，则∠AEC=∠ABC，∵CE⊥AB，∴∠HBC+∠BCH=90°在△COF中，∵∠OFC+∠OCF=90°，∴∠HBC=∠OFC=∠AFH，在△AEH和△AFH中，∵AFH AEHAHF AHE AH AH∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△AEH≌△AFH（AAS），∴EH=FH；（3）由（1）易知，∠BMT=∠BAC=60°，作直径BG，连CG，则∠BGC=∠BAC=60°，∵⊙O的半径为4，∴CG=4，连AG，∵∠BCG=90°，∴CG⊥x轴，∴CG∥AF，∵∠BAG=90°，∴AG⊥AB，∵CE⊥AB，∴AG∥CE，∴四边形AFCG为平行四边形，∴AF=CG=4．【点睛】本题考查的是垂径定理、圆周角定理、直角三角形的性质及平行四边形的判定与性质，根据题意作出辅助线是解答此题的关键．2．如图，⊙A过▱OBCD的三顶点O、D、C，边OB与⊙A相切于点O，边BC与⊙O相交于点H，射线OA交边CD于点E，交⊙A于点F，点P在射线OA上，且∠PCD=2∠DOF，以O为原点，OP所在的直线为x轴建立平面直角坐标系，点B的坐标为（0，﹣2）．（1）若∠BOH=30°，求点H的坐标；（2）求证：直线PC是⊙A的切线；（3）若10，求⊙A的半径．【答案】（1）（132）详见解析；（3）5 3 .【解析】【分析】（1）先判断出OH=OB=2，利用三角函数求出MH，OM，即可得出结论；（2）先判断出∠PCD=∠DAE，进而判断出∠PCD=∠CAE，即可得出结论；（3）先求出OE═3，进而用勾股定理建立方程，r2-（3-r）2=1，即可得出结论．【详解】（1）解：如图，过点H作HM⊥y轴，垂足为M．∵四边形OBCD是平行四边形，∴∠B=∠ODC∵四边形OHCD是圆内接四边形∴∠OHB=∠ODC∴∠OHB=∠B∴OH=OB=2∴在Rt△OMH中，∵∠BOH=30°，∴MH=12OH=1，33∴点H的坐标为（13（2）连接AC．∵OA=AD，∴∠DOF=∠ADO∴∠DAE=2∠DOF∵∠PCD=2∠DOF，∴∠PCD=∠DAE∵OB与⊙O相切于点A∴OB⊥OF∵OB∥CD∴CD⊥AF∴∠DAE=∠CAE∴∠PCD=∠CAE∴∠PCA=∠PCD+∠ACE=∠CAE+∠ACE=90°∴直线PC是⊙A的切线；（3）解：⊙O的半径为r．在Rt△OED中，DE=12CD=12OB=1，OD=10，∴OE═3∵OA=AD=r，AE=3﹣r．在Rt△DEA中，根据勾股定理得，r2﹣（3﹣r）2=1解得r=53．【点睛】此题是圆的综合题，主要考查了平行四边形的性质，圆内接四边形的性质，勾股定理，切线的性质和判定，构造直角三角形是解本题的关键．3．如图，△ABC的内接三角形，P为BC延长线上一点，∠PAC=∠B，AD为⊙O的直径，过C作CG⊥AD于E，交AB于F，交⊙O于G．（1）判断直线PA与⊙O的位置关系，并说明理由；（2）求证：AG2=AF·AB；（3）若⊙O的直径为10，AC=25，AB=45，求△AFG的面积.【答案】（1）PA与⊙O相切，理由见解析；（2）证明见解析；（3）3.【解析】试题分析：（1）连接CD，由AD为⊙O的直径，可得∠ACD=90°，由圆周角定理，证得∠B=∠D，由已知∠PAC=∠B，可证得DA⊥PA，继而可证得PA与⊙O相切．（2）连接BG，易证得△AFG∽△AGB，由相似三角形的对应边成比例，证得结论.（3）连接BD，由AG2=AF•AB，可求得AF的长，易证得△AEF∽△ABD，即可求得AE的长，继而可求得EF与EG的长，则可求得答案．试题解析：解：（1）PA与⊙O相切．理由如下：如答图1，连接CD，∵AD为⊙O的直径，∴∠ACD=90°.∴∠D+∠CAD=90°.∵∠B=∠D，∠PAC=∠B，∴∠PAC=∠D.∴∠PAC+∠CAD=90°，即DA⊥PA.∵点A在圆上，∴PA与⊙O相切．（2）证明：如答图2，连接BG，∵AD为⊙O的直径，CG⊥AD，∴»».∴∠AGF=∠ABG.AC AD∵∠GAF=∠BAG，∴△AGF∽△ABG.∴AG：AB=AF：AG. ∴AG2=AF•AB.（3）如答图3，连接BD，∵AD是直径，∴∠ABD=90°.∵AG2=AF•AB，55∴5∵CG ⊥AD ，∴∠AEF=∠ABD=90°.∵∠EAF=∠BAD ，∴△AEF ∽△ABD. ∴AE AF AB AD =，即51045=，解得：AE=2. ∴221EF AF AE =-=. ∵224EG AG AE =-=，∴413FG EG EF =-=-=. ∴1132322AFG S FG AE ∆=⋅⋅=⨯⨯=．考点：1. 圆周角定理；2.直角三角形两锐角的关系；3. 相切的判定；4.垂径定理；5.相似三角形的判定和性质；6.勾股定理；7.三角形的面积.4．如图1，在Rt △ABC 中，AC=8cm ，BC=6cm ，D 、E 分别为边AB 、BC 的中点，连结DE ，点P 从点A 出发，沿折线AD ﹣DE 运动，到点E 停止，点P 在AD 上以5cm/s 的速度运动，在DE 上以1cm/s 的速度运动，过点P 作PQ ⊥AC 于点Q ，以PQ 为边作正方形PQMN ．设点P 的运动时间为t （s ）．（1）当点P 在线段DE 上运动时，线段DP 的长为_____cm ．（用含t 的代数式表示） （2）当正方形PQMN 与△ABC 重叠部分图形为五边形时，设五边形的面积为S （cm 2），求S 与t 的函数关系式，并写出t 的取值范围．（3）如图2，若点O 在线段BC 上，且CO=1，以点O 为圆心，1cm 长为半径作圆，当点P 开始运动时，⊙O 的半径以0.2cm/s 的速度开始不断增大，当⊙O 与正方形PQMN 的边所在直线相切时，求此时的t 值．【答案】（1）t ﹣1；（2）S =﹣38t 2+3t +3（1＜t ＜4）；（3）t =103s ． 【解析】 分析：（1）根据勾股定理求出AB ，根据D 为AB 中点，求出AD ，根据点P 在AD 上的速度，即可求出点P 在AD 段的运动时间，再求出点P 在DP 段的运动时间，最后根据DE 段运动速度为1c m/s ，即可求出DP ；（2）由正方形PQMN 与△ABC 重叠部分图形为五边形，可知点P 在DE 上，求出DP =t ﹣1，PQ =3，根据MN ∥BC ，求出FN 的长，从而得到FM 的长，再根据S =S 梯形FMHD +S 矩形DHQP ，列出S 与t 的函数关系式即可；（3）当圆与边PQ 相切时，可求得r =PE =5﹣t ，然后由r 以0.2c m/s 的速度不断增大，r =1+0.2t ，然后列方程求解即可；当圆与MN 相切时，r =CM =8﹣t =1+0.2t ，从而可求得t 的值．详解：（1）由勾股定理可知：AB =22AC BC +=10． ∵D 、E 分别为AB 和BC 的中点，∴DE =12AC =4，AD =12AB =5， ∴点P 在AD 上的运动时间=55=1s ，当点P 在线段DE 上运动时，DP 段的运动时间为（t ﹣1）s ．∵DE 段运动速度为1c m/s ，∴DP =（t ﹣1）cm ．故答案为t ﹣1．（2）当正方形PQMN 与△ABC 重叠部分图形为五边形时，有一种情况，如下图所示．当正方形的边长大于DP 时，重叠部分为五边形，∴3＞t ﹣1，t ＜4，DP ＞0，∴t ﹣1＞0，解得：t ＞1，∴1＜t ＜4．∵△DFN ∽△ABC ，∴DN FN =AC BC =86=43． ∵DN =PN ﹣PD ，∴DN =3﹣（t ﹣1）=4﹣t ， ∴4t FN -=43，∴FN =344t -（）， ∴FM =3﹣344t -（）=34t ，S=S梯形FMHD+S矩形DHQP，∴S=12×（34t+3）×（4﹣t）+3（t﹣1）=﹣38t2+3t+3（1＜t＜4）．（3）①当圆与边PQ相切时，如图：当圆与PQ相切时，r=PE，由（1）可知，PD=（t﹣1）cm，∴PE=DE﹣DP=4﹣（t﹣1）=（5﹣t）cm．∵r以0.2c m/s的速度不断增大，∴r=1+0.2t，∴1+0.2t=5﹣t，解得：t=103s．②当圆与MN相切时，r=CM．由（1）可知，DP=（t﹣1）cm，则PE=CQ=（5﹣t）cm，MQ=3cm，∴MC=MQ+CQ=5﹣t+3=（8﹣t）cm，∴1+0.2t=8﹣t，解得：t=356s．∵P到E点停止，∴t﹣1≤4，即t≤5，∴t=356s（舍）．综上所述：当t=103s时，⊙O与正方形PQMN的边所在直线相切．点睛：本题主要考查的是圆的综合应用，解答本题主要应用了勾股定理、相似三角形的性质和判定、正方形的性质，直线和圆的位置关系，依据题意列出方程是解题的关键．5．如图，已知平行四边形OABC的三个顶点A、B、C在以O为圆心的半圆上，过点C作CD⊥AB，分别交AB、AO的延长线于点D、E，AE交半圆O于点F，连接CF．（1）判断直线DE 与半圆O 的位置关系，并说明理由；（2）若半圆O 的半径为6，求¶AC 的长．【答案】（1）直线CE 与半圆O 相切（2）4π【解析】试题分析：（1）结论：DE 是⊙O 的切线．首先证明△ABO ，△BCO 都是等边三角形，再证明四边形BDCG 是矩形，即可解决问题；（2）只要证明△OCF 是等边三角形即可解决问题，求AC 即可解决问题．试题解析：（1）直线CE 与半圆O 相切，理由如下：∵四边形OABC 是平行四边形，∴AB ∥OC.∵∠D=90°，∴∠OCE=∠D=90°，即OC ⊥DE ，∴直线CE 与半圆O 相切．（2）由（1）可知：∠COF=60°，OC=OF ，∴△OCF 是等边三角形，∴∠AOC=120°∴¶AC 的长为1206180π⨯⨯=4π.6．如图1O e ，的直径12AB P =，是弦BC 上一动点(与点B C ，不重合)30ABC o ，∠=，过点P 作PD OP ⊥交O e 于点D ．()1如图2，当//PD AB 时，求PD 的长；()2如图3，当»»DC AC =时，延长AB 至点E ，使12BE AB =，连接DE ． ①求证：DE 是O e 的切线；②求PC 的长．【答案】（1）262）333①见解析，②．【解析】分析：()1根据题意首先得出半径长，再利用锐角三角函数关系得出OP PD ，的长； ()2①首先得出OBD V 是等边三角形，进而得出ODE OFB 90∠∠==o ，求出答案即可；②首先求出CF 的长，进而利用直角三角形的性质得出PF 的长，进而得出答案． 详解：()1如图2，连接OD ，//OP PD PD AB ⊥Q ，，90POB ∴∠=o ，O Q e 的直径12AB =，6OB OD ∴==，在Rt POB V 中，30ABC o ∠=， 3tan30623OP OB ∴=⋅=⨯=o ， 在Rt POD V 中， 22226(23)26PD OD OP =-=-=；()2①证明：如图3，连接OD ，交CB 于点F ，连接BD ，»»DC AC =Q ，30DBC ABC ∴∠=∠=o ，60ABD o ∴∠=，OB OD =Q ，OBD ∴V 是等边三角形，OD FB ∴⊥，12BE AB =Q ， OB BE ∴=，//BF ED ∴，90ODE OFB o ∴∠=∠=，DE ∴是O e 的切线；②由①知，OD BC ⊥，3cos30633CF FB OB ∴==⋅=⨯=o ， 在Rt POD V 中，OF DF =，13(2PF DO ∴==直角三角形斜边上的中线，等于斜边的一半)， 333CP CF PF ∴=-=-．点睛：此题主要考查了圆的综合以及直角三角形的性质和锐角三角函数关系，正确得出OBD V 是等边三角形是解题关键．7．如图所示，以Rt △ABC 的直角边AB 为直径作圆O ，与斜边交于点D ，E 为BC 边上的中点，连接DE ．（1）求证：DE 是⊙O 的切线；（2）连接OE ，AE ，当∠CAB 为何值时，四边形AOED 是平行四边形？并在此条件下求sin ∠CAE 的值．【答案】(1)见解析;(2)10. 【解析】分析：（1）要证DE 是⊙O 的切线，必须证ED ⊥OD ，即∠EDB+∠ODB=90°（2）要证AOED 是平行四边形，则DE ∥AB ，D 为AC 中点，又BD ⊥AC ，所以△ABC 为等腰直角三角形，所以∠CAB=45°，再由正弦的概念求解即可． 详解：（1）证明：连接O 、D 与B 、D 两点， ∵△BDC 是Rt △，且E 为BC 中点， ∴∠EDB=∠EBD ．（2分） 又∵OD=OB 且∠EBD+∠DBO=90°， ∴∠EDB+∠ODB=90°． ∴DE 是⊙O 的切线． （2）解：∵∠EDO=∠B=90°，若要四边形AOED 是平行四边形，则DE ∥AB ，D 为AC 中点， 又∵BD ⊥AC ，∴△ABC 为等腰直角三角形．∴∠C AB=45°． 过E 作EH ⊥AC 于H ， 设BC=2k ，则EH=22k ，AE=5k ， ∴sin ∠CAE=1010EH AE．点睛：本题考查的是切线的判定，要证某线是圆的切线，已知此线过圆上某点，连接圆心和这点（即为半径），再证垂直即可．8．如图1，延长⊙O 的直径AB 至点C ，使得BC=12AB ，点P 是⊙O 上半部分的一个动点（点P 不与A 、B 重合），连结OP ，CP ． （1）∠C 的最大度数为 ；（2）当⊙O 的半径为3时，△OPC 的面积有没有最大值？若有，说明原因并求出最大值；若没有，请说明理由；（3）如图2，延长PO 交⊙O 于点D ，连结DB ，当CP=DB 时，求证：CP 是⊙O 的切线．【答案】（1）30°；（2）有最大值为9，理由见解析；（3）证明见解析. 【解析】试题分析：（1）当PC 与⊙O 相切时，∠OCP 的度数最大，根据切线的性质即可求得； （2）由△OPC 的边OC 是定值，得到当OC 边上的高为最大值时，△OPC 的面积最大，当PO ⊥OC 时，取得最大值，即此时OC 边上的高最大，于是得到结论；（3）根据全等三角形的性质得到AP=DB ，根据等腰三角形的性质得到∠A=∠C ，得到CO=OB+OB=AB ，推出△APB ≌△CPO ，根据全等三角形的性质得到∠CPO=∠APB ，根据圆周角定理得到∠APB=90°，即可得到结论．试题解析：（1）当PC与⊙O相切时，∠OCP最大．如图1，所示：∵sin∠OCP=OPOC=2 4=12，∴∠OCP=30°∴∠OCP的最大度数为30°，故答案为：30°；（2）有最大值，理由：∵△OPC的边OC是定值，∴当OC边上的高为最大值时，△OPC的面积最大，而点P在⊙O上半圆上运动，当PO⊥OC时，取得最大值，即此时OC边上的高最大，也就是高为半径长，∴最大值S△OPC=12OC•OP=12×6×3=9；（3）连结AP，BP，如图2，在△OAP与△OBD中，OA ODAOP BODOP OB=⎧⎪∠=∠⎨⎪=⎩，∴△OAP≌△OBD，∴AP=DB，∵PC=DB，∴AP=PC，∵PA=PC，∴∠A=∠C，∵BC=12AB=OB，∴CO=OB+OB=AB，在△APB和△CPO中，AP CPA CAB CO=⎧⎪∠=∠⎨⎪=⎩，∴△APB≌△CPO，∴∠CPO=∠APB，∵AB为直径，∴∠APB=90°，∴∠CPO=90°，∴PC切⊙O于点P，即CP是⊙O的切线．9．四边形ABCD内接于⊙O，点E为AD上一点，连接AC，CB，∠B=∠AEC．（1）如图1，求证：CE=CD；（2）如图2，若∠B+∠CAE=120°，∠ACD=2∠BAC，求∠BAD的度数；（3）如图3，在（2）的条件下，延长CE交⊙O于点G，若tan∠BAC= 53，EG=2，求AE的长．【答案】（1）见解析；（2）60°；（3）7.【解析】试题分析：(1)利用圆的内接四边形定理得到∠CED=∠CDE.(2) 作CH⊥DE于H, 设∠ECH=α，由（1）CE=CD，用α表示∠CAE，∠BAC，而∠BAD=∠BAC+∠CAE.（3）连接AG，作GN⊥AC，AM⊥EG，先证明∠CAG=∠BAC，设NG=3m，可得AN=11m，利用直角n AGM,n AEM，勾股定理可以算出m的值并求出AE长.试题解析：（1）解：证明：∵四边形ABCD内接于⊙O.∴∠B+∠D=180°，∵∠B=∠AEC，∴∠AEC+∠D=180°，∵∠AEC+∠CED=180°，∴∠D=∠CED，∴CE=CD．（2）解：作CH⊥DE于H．设∠ECH=α，由（1）CE=CD，∴∠ECD=2α，∵∠B=∠AEC，∠B+∠CAE=120°，∴∠CAE+∠AEC=120°，∴∠ACE=180°﹣∠AEC﹣∠ACE=60°，∴∠CAE=90°﹣∠ACH=90°﹣（60°+α）=30°﹣α，∠ACD=∠ACH+∠HCD=60°+2α，∵∠ACD=2∠BAC，∴∠BAC=30°+α，∴∠BAD=∠BAC+∠CAE=30°+α+30°﹣α=60°．（3）解：连接AG，作GN⊥AC，AM⊥EG，∵∠CED=∠AEG，∠CDE=∠AGE，∠CED=∠CDE，∴∠AEG=∠AGE，∴AE=AG，∴EM=MG=1EG=1，2∴∠EAG=∠ECD=2α，∴∠CAG=∠CAD+∠DAG=30°﹣α+2α=∠BAC，∵tan∠BAC53，∴设NG=3，可得AN=11m，AG22-14m，AG AM∵∠ACG=60°，∴CN=5m，AM3，MG22-m=1，AG AM∴m =12， ∴CE=CD =CG ﹣EG =10m ﹣2=3， ∴AE =22AM EM =221+43（）=7．10．如图，已知在△ABC 中，∠A=90°，（1）请用圆规和直尺作出⊙P ，使圆心P 在AC 边上，且与AB ，BC 两边都相切（保留作图痕迹，不写作法和证明）．（2）若∠B=60°，AB=3，求⊙P 的面积． 【答案】（1）作图见解析；（2）3π 【解析】 【分析】（1）与AB 、BC 两边都相切．根据角平分线的性质可知要作∠ABC 的角平分线，角平分线与AC 的交点就是点P 的位置．（2）根据角平分线的性质和30°角的直角三角形的性质可求半径，然后求圆的面积． 【详解】解：（1）如图所示，则⊙P 为所求作的圆．（2）∵∠ABC=60°，BP 平分∠ABC ， ∴∠ABP=30°， ∵ ∠A=90°， ∴BP=2AP Rt △ABP 中,AB=3，由勾股定理可得：3，∴S ⊙P =3π11．如图，AB 为⊙O 的直径，DA 、DC 分别切⊙O 于点A ，C ，且AB =AD ． （1）求tan ∠AOD 的值． （2）AC ，OD 交于点E ，连结BE ． ①求∠AEB 的度数；②连结BD交⊙O于点H，若BC=1，求CH的长．【答案】（1）2；（2）①∠AEB＝135°；②22 CH=【解析】【分析】（1）根据切线的性质可得∠BAD=90°，由题意可得AD=2AO，即可求tan∠AOD的值；（2）①根据切线长定理可得AD=CD，OD平分∠ADC，根据等腰三角形的性质可得DO⊥AC，AE=CE，根据圆周角定理可求∠ACB=90°，即可证∠ABC=∠CAD，根据“AAS”可证△ABC≌△DAE，可得AE=BC=EC，可求∠BEC=45°，即可求∠AEB的度数；②由BC=1，可求AE=EC=1，BE2=，根据等腰直角三角形的性质可求∠ABE=∠HBC，可证△ABE∽△HBC，可求CH的长．【详解】（1）∵DA是⊙O切线，∴∠BAD=90°．∵AB=AD，AB=2AO，∴AD=2AO，∴tan∠AODADAO==2；（2）①∵DA、DC分别切⊙O于点A，C，∴AD=CD，OD平分∠ADC，∴DO⊥AC，AE=CE．∵AB是直径，∴∠ACB=90°，∴∠BAC+∠ABC=90°，且∠BAC+∠CAD=90°，∴∠ABC=∠CAD，且AB=AD，∠ACB=∠AED=90°，∴△ABC≌△DAE（AAS），∴CB=AE，∴CE=CB，且∠ACB=90°，∴∠BEC=45°=∠EBC，∴∠AEB=135°．②如图，∵BC=1，且BC=AE=CE，∴AE=EC=BC=1，∴BE2=．∵AD=AB，∠BAD=90°，∴∠ABD=45°，且∠EBC=45°，∴∠ABE=∠HBC，且∠BAC=∠CHB，∴△ABE∽△HBC，∴BC CHEB AE=，即12CH=，∴CH22=．【点睛】本题考查了切线的性质，圆周角定理，锐角三角函数，全等三角形的判定和性质，相似三角形的判定和性质，等腰三角形的性质等知识，灵活运用相关的性质定理、综合运用知识是解题的关键．12．（问题情境）如图1，点E 是平行四边形ABCD 的边AD 上一点，连接BE 、CE ．求证：BCE 1S 2=V S 平行四边形ABCD ．（说明：S 表示面积） 请以“问题情境”为基础，继续下面的探究（探究应用1）如图2，以平行四边形ABCD 的边AD 为直径作⊙O ，⊙O 与BC 边相切于点H ，与BD 相交于点M ．若AD ＝6，BD ＝y ，AM ＝x ，试求y 与x 之间的函数关系式． （探究应用2）如图3，在图1的基础上，点F 在CD 上，连接AF 、BF ，AF 与CE 相交于点G ，若AF ＝CE ，求证：BG 平分∠AGC ．（迁移拓展）如图4，平行四边形ABCD 中，AB ：BC ＝4：3，∠ABC ＝120°，E 是AB 的中点，F 在BC 上，且BF ：FC ＝2：1，过D 分别作DG ⊥AF 于G ，DH ⊥CE 于H ，请直接写出DG ：DH 的值．【答案】【问题情境】见解析；【探究应用1】18y x=；【探究应用2】见解析；【迁移1927 【解析】 【分析】（1）作EF ⊥BC 于F ，则S △BCE ＝12BC×EF ，S 平行四边形ABCD ＝BC×EF ，即可得出结论； （2）连接OH ，由切线的性质得出OH ⊥BC ，OH ＝12AD ＝3，求出平行四边形ABCD 的面积＝AD×OH ＝18，由圆周角定理得出AM ⊥BD ，得出△ABD 的面积＝12BD×AM ＝12平行四边形的面积＝9，即可得出结果；（3）作BM ⊥AF 于M ，BN ⊥CE 于N ，同图1得：△ABF 的面积＝△BCE 的面积＝12平行四边形ABCD 的面积，得出12AF×BM ＝12CE×BN ，证出BM ＝BN ，即可得出BG 平分∠AGC ．（4）作AP ⊥BC 于P ，EQ ⊥BC 于Q ，由平行四边形的性质得出∠ABP ＝60°，得出∠BAP ＝30°，设AB ＝4x ，则BC ＝3x ，由直角三角形的性质得出BP ＝12AB ＝2x ，BQ ＝12BE ，AP ＝BP ＝，由已知得出BE ＝2x ，BF ＝2x ，得出BQ ＝x ，EQ x ，PF ＝4x ，QF ＝3x ，QC ＝4x ，由勾股定理求出AF ＝x ，CE，连接DF 、DE ，由三角形的面积关系得出AF×DG ＝CE×DH ，即可得出结果．【详解】（1）证明：作EF ⊥BC 于F ，如图1所示： 则S △BCE ＝12BC×EF ，S 平行四边形ABCD ＝BC×EF ， ∴12BCE ABCD S S =V Y ． （2）解：连接OH ，如图2所示： ∵⊙O 与BC 边相切于点H ， ∴OH ⊥BC ，OH ＝12AD ＝3， ∴平行四边形ABCD 的面积＝AD×OH ＝6×3＝18， ∵AD 是⊙O 的直径， ∴∠AMD ＝90°， ∴AM ⊥BD ， ∴△ABD 的面积＝12BD×AM ＝12平行四边形的面积＝9， 即12xy ＝9， ∴y 与x 之间的函数关系式y ＝18x； （3）证明：作BM ⊥AF 于M ，BN ⊥CE 于N ，如图3所示： 同图1得：△ABF 的面积＝△BCE 的面积＝12平行四边形ABCD 的面积， ∴12AF×BM ＝12CE×BN ， ∵AF ＝CE ， ∴BM ＝BN ，∴BG 平分∠AGC ．（4）解：作AP ⊥BC 于P ，EQ ⊥BC 于Q ，如图4所示： ∵平行四边形ABCD 中，AB ：BC ＝4：3，∠ABC ＝120°， ∴∠ABP ＝60°，∴∠BAP ＝30°，设AB ＝4x ，则BC ＝3x ，∴BP ＝12AB ＝2x ，BQ ＝12BE ，AP ＝3BP ＝23x ， ∵E 是AB 的中点，F 在BC 上，且BF ：FC ＝2：1， ∴BE ＝2x ，BF ＝2x ， ∴BQ ＝x ，∴EQ ＝3x ，PF ＝4x ，QF ＝3x ，QC ＝4x ， 由勾股定理得：AF ＝22AP PF +＝27x ，CE ＝22EQ QC +＝19x ，连接DF 、DE ，则△CDE 的面积＝△ADF 的面积＝12平行四边形ABCD 的面积， ∴AF×DG ＝CE×DH ，∴DG ：DH ＝CE ：AF ＝19x :27x 19:27=．【点睛】本题是圆的综合题目，考查了圆周角定理、平行四边形的性质、三角形面积公式、含30°角的直角三角形的性质、勾股定理、角平分线的判定等知识；本题综合性强，需要添加辅助线，熟练掌握平行四边形的性质和勾股定理是解题的关键．13．如图，四边形ABCD 是⊙O 的内接四边形，AC 为直径，»»BD AD =，DE ⊥BC ，垂足为E ．（1）判断直线ED 与⊙O 的位置关系，并说明理由； （2）若CE =1，AC =4，求阴影部分的面积．【答案】（1）ED 与O e 相切.理由见解析；（2）2=33S π-阴影. 【解析】【分析】 （1）连结OD ，如图，根据圆周角定理，由»»BD AD =得到∠BAD =∠ACD ，再根据圆内接四边形的性质得∠DCE =∠BAD ，所以∠ACD =∠DCE ；利用内错角相等证明OD ∥BC ，而DE ⊥BC ，则OD ⊥DE ，于是根据切线的判定定理可得DE 为⊙O 的切线；（2）作OH ⊥BC 于H ，易得四边形ODEH 为矩形，所以OD =EH =2，则CH =HE ﹣CE =1，于是有∠HOC =30°，得到∠COD =60°，然后根据扇形面积公式、等边三角形的面积公式和阴影部分的面积=S 扇形OCD ﹣S △OCD 进行计算即可．【详解】（1）直线ED 与⊙O 相切．理由如下：连结OD ，如图，∵»»BD AD =，∴∠BAD =∠ACD ．∵∠DCE =∠BAD ，∴∠ACD =∠DCE ．∵OC =OD ，∴∠OCD =∠ODC ，而∠OCD =∠DCE ，∴∠DCE =∠ODC ，∴OD ∥BC ． ∵DE ⊥BC ，∴OD ⊥DE ，∴DE 为⊙O 的切线；（2）作OH ⊥BC 于H ，则四边形ODEH 为矩形，∴OD =EH ．∵CE =1，AC =4，∴OC =OD =2，∴CH =HE ﹣CE =2﹣1=1．在Rt △OHC 中，∵OC =2，CH =1，∠OHC =90°，∠HOC =30°，∴∠COD =60°，∴阴影部分的面积=S 扇形OCD ﹣S △OCD26023360π⋅⋅=-•22 23=π3-．【点睛】本题考查了切线的判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线．要证某线是圆的切线，已知此线过圆上某点，连接圆心与这点（即为半径），再证垂直即可．也考查了扇形面积的计算．14．如图①，已知Rt ABC ∆中，90ACB ∠=o ，8AC =，10AB =，点D 是AC 边上一点（不与C 重合），以AD 为直径作O e ，过C 作CE 切O e 于E ，交AB 于F .（1）若O e 的半径为2，求线段CE 的长；（2）若AF BF =，求O e 的半径；（3）如图②，若CE CB =，点B 关于AC 的对称点为点G ，试求G 、E 两点之间的距离.【答案】(1)42CE =；(2)O e 的半径为3；(3)G 、E 两点之间的距离为9.6.【解析】【分析】（1）根据切线的性质得出∠OEC=90°，然后根据勾股定理即可求得；（2）由勾股定理求得BC ，然后通过证得△OEC ∽△BCA ，得到OE BC =OC BA ，即r 8-r =610，解得即可；（3）证得D 和M 重合，E 和F 重合后，通过证得△GBE ∽△ABC ，GB GE AB AC=，即12108GE =，解得即可． 【详解】(1)如图，连结OE .∵CE 切O e 于E ，∴90OEC ∠=︒.∵8AC =，O e 半径为2，∴6OC =，2OE =. ∴2242CE OC OE =-=；(2)设O e 半径为r .在Rt ABC ∆中，90ACB ∠=︒，10AB =，8AC =，∴226BC AB AC =-=. ∵AF BF =， ∴AF CF BF ==. ∴ACF CAF ∠=∠. ∵CE 切O e 于E ，∴90OEC ∠=︒.∴OEC ACB ∠=∠，∴OEC BCA ∆~∆.∴OE OC BC BA =， ∴8610r r -=， 解得3r =.∴O e 的半径为3；(3)连结EG 、OE ，设EG 交AC 于点M ，由对称性可知，CB CG =.又CE CB =，∴CE CG =.∴EGC GEC ∠=∠.∵CE 切O e 于E ，∴90GEC OEG ∠+∠=︒.又90EGC GMC ∠+∠=︒，∴OEG GMC ∠=∠.又GMC OME ∠=∠，∴OEG OME ∠=∠.∴OE OM =.∴点M 与点D 重合.∴G 、D 、E 三点在同一条直线上.连结AE 、BE ，∵AD 是直径，∴90AED ∠=︒，即90AEG ∠=︒.又CE CB CG ==，∴90BEG ∠=︒.∴180AEB AEG BEG ∠=∠+∠=︒，∴A 、E 、B 三点在同一条直线上.∴E 、F 两点重合.∵90GEB ACB ∠=∠=︒，B B ∠=∠，∴GBE ABC ∆~∆. ∴GB GE AB AC =，即12108GE =. ∴9.6GE =.故G 、E 两点之间的距离为9.6.【点睛】本题考查了切线的判定，轴的性质，勾股定理的应用以及三角形相似的判定和性质，证得G 、D 、E 三点共线以及A 、E 、B 三点在同一条直线上是解题的关键.15．如图，AB 是O e 的直径，DF 切O e 于点D ，BF DF ⊥于F ，过点A 作AC //BF 交BD 的延长线于点C .（1）求证：ABC C ∠∠=；（2）设CA 的延长线交O e 于E BF ，交O e 于G ，若¼DG的度数等于60o ，试简要说明点D 和点E 关于直线AB 对称的理由.【答案】（1）见解析；（2）见解析.【解析】【分析】（1）作辅助线，连接OD ，由DF 为⊙O 的切线，可得OD ⊥DF ，又BF ⊥DF ，AC ∥BF ，所以OD ∥AC ，∠ODB=∠C ，由OB=OD 得∠ABD=∠ODB ，从而可证∠ABC=∠C ；（2）连接OG ，OD ，AD ，由BF ∥OD ，»GD =60°，可求证»BG =»»GD AD ==60°，由平行线的性质及三角形的内角和定理可求出∠OHD=90°，由垂径定理便可得出结论．【详解】（1）连接OD，∵DF为⊙O的切线，∴OD⊥DF．∵BF⊥DF，AC∥BF，∴OD∥AC∥BF．∴∠ODB=∠C．∵OB=OD，∴∠ABD=∠ODB．∴∠ABC=∠C．（2）连接OG，OD，AD，DE，DE交AB于H，∵BF∥OD，∴∠OBG=∠AOD，∠OGB=∠DOG，∴»»==»BG．GD AD∵»GD=60°，∴»BG=»»==60°，GD AD∴∠ABC=∠C=∠E=30°，∵OD//CE∴∠ODE=∠E=30°．在△ODH中，∠ODE=30°，∠AOD=60°，∴∠OHD=90°，∴AB⊥DE．∴点D和点E关于直线AB对称．【点睛】本题考查的是切线的性质、圆周角定理及垂径定理，解答此题的关键是作出辅助线，利用数形结合解答．。
2020-2021全国中考数学相似的综合中考模拟和真题分类汇总含答案解析
2020-2021全国中考数学相似的综合中考模拟和真题分类汇总含答案解析一、相似1．在矩形ABCD中，BC＝6，点E是AD边上一点，∠ABE＝30°，BE＝DE，连接BD.动点M 从点E出发沿射线ED运动，过点M作MN∥BD交直线BE于点N.（1）如图1，当点M在线段ED上时，求证：MN＝ EM；（2）设MN长为x，以M、N、D为顶点的三角形面积为y，求y关于x的函数关系式；（3）当点M运动到线段ED的中点时，连接NC，过点M作MF⊥NC于F，MF交对角线BD于点G（如图2），求线段MG的长.【答案】（1）证明：：∵ °, ° ,∴ °∵ ,∴∵∥ ,∴∴ °,∴过点作于点 ,则 .在中，∴∴（2）解：在中，，∴∵a.当点在线段上时，过点作于点 ,在中，由（1）可知：,∴∴∴b.当点在线段延长线上时，过点作于点在中， ,在中， ,∴ ,∴（3）解：连接 ,交于点 .∵为的中点∴ ,∴ .∵ ,∴ ,∴ ,∴ ,∴ .∵∥∴ ,∴ ,,∵ ,∴ ,又∵ ,∴∽ ,∴，即 ,∴【解析】【分析】（1）过点E作EH⊥MN于点H ,由已知条件易得EN=EM，解直角三角形EMH易得MH和EM的关系，由等腰三角形的三线合一可得MN=2MH即可求解；（2）在Rt△ABE中，由直角三角形的性质易得DE=BE=2AE，由题意动点M从点E出发沿射线ED运动可知点M可在线段ED上，也可在线段ED外，所以可分两种情况求解：①当点M在线段ED上时，过点N作NI⊥AD于点I ,结合（1）中的结论MN=EM即可求解；②当点M在线段ED延长线上时，过点N作NI'⊥AD于点I '，解RtΔNI′M 和可求得NI'和NE，则DM=NE−DE，所以以M、N、D为顶点的三角形面积y=MD.NI可求解；（3）连接CM,交BD于点N'，由（2）中的计算可得MN、CD、MC的长，解直角三角形CDM可得∠DMC的度数，于是由三角形内角和定理可求得∠NMC=，根据平行线的性质可得DMN'是直角三角形，根据直角三角形的性质可得MN′=MD；则NC的长可求，由已知条件易得ΔNMC∽ΔMN′G根据所得的比例式即可求解.,2．如图，抛物线y= x2+bx+c 与x轴交于点A和点B，与y轴交于点C，点B坐标为（6，0），点C坐标为（0，6），点D是抛物线的顶点．（1）求抛物线的解析式及点D的坐标；（2）如图1，抛物线的对称轴与x轴交于点E，连接BD，点F是抛物线上的动点，当∠FBA=∠BDE时，求点F的坐标；（3）如图2，若点M是抛物线上的动点，过点M作MN∥x轴与抛物线交于点N，点P在x轴上，点Q在坐标平面内，以线段MN为对角线作正方形MPNQ，求点Q的坐标．【答案】（1）解：把B（6，0），C（0，6）代入y= x2+bx+c，得解得 ,抛物线的解析式是y= x2+2x+6, 顶点D的坐标是（2，8）（2）解：如图1，过F作FG⊥x轴于点G，设F（x， x2+2x+6），则FG= ，∵∠FBA=∠BDE，∠FGB=∠BED=90°，∴△FBG∽△BDE，∴，∵B（6，0），D（2，8），∴E（2，0），BE=4，DE=8，OB=6，∴BG=6-x，∴当点F在x轴上方时，有，∴x=-1或x=6（舍去），此时F1的坐标为（-1，）,当点F在x轴下方时，有，∴x=-3或x=6（舍去），此时F2的坐标为（-3，）,综上可知F点的坐标为（-1，）或（-3，）（3）解：如图2，不妨M在对称轴的左侧，N在对称轴的左侧，MN和PQ交于点K，由题意得点M，N关于抛物线的对称轴对称，四边形MPNQ为正方形，且点P在x轴上∴点P为抛物线的对称轴与x轴的交点，点Q在抛物线的对称轴上 ,∴KP=KM=k，则Q（2，2k），M坐标为（2-k，k），∵点M在抛物线y= x2+2x+6的图象上，∴k= (2-k)2+2(2-k)+6解得k1= 或k2=∴满足条件的点Q有两个，Q1（2，）或Q2（2，）.【解析】【分析】（1）根据点B、C的坐标，利用待定系数法建立关于b、c的方程组，求解就可得出函数解析式，再求出顶点坐标。
2020-2021初三数学一模试题分类汇编——圆与相似综合及答案
2020-2021初三数学一模试题分类汇编——圆与相似综合及答案一、相似1．如图，在△ABC中，AB=AC，∠BAC=90°，AH⊥BC于点H，过点C作CD⊥AC，连接AD，点M为AC上一点，且AM=CD，连接BM交AH于点N，交AD于点E．（1）若AB=3，AD= ，求△BMC的面积；（2）点E为AD的中点时，求证：AD= BN ．【答案】（1）解：如图1中，在△ABM和△CAD中，∵AB=AC，∠BAM=∠ACD=90°，AM=CD，∴△ABM≌△CAD，∴BM=AD= ，∴AM= =1，∴CM=CA﹣AM=2，∴S△BCM= •CM•BA= ×23=3．（2）解：如图2中，连接EC、CN，作EQ⊥BC于Q，EP⊥BA于P．∵AE=ED，∠ACD=90°，∴AE=CE=ED，∴∠EAC=∠ECA，∵△ABM≌△CAD，∴∠ABM=∠CAD，∴∠ABM=∠MCE，∵∠AMB=∠EMC，∴∠CEM=∠BAM=90°，∴△ABM∽△ECM，∴，∴，∵∠AME=∠BMC，∴△AME∽△BMC，∴∠AEM=∠ACB=45°，∴∠AEC=135°，易知∠PEQ=135°，∴∠PEQ=∠AEC，∴∠AEQ=∠EQC，∵∠P=∠EQC=90°，∴△EPA≌△EQC，∴EP=EQ，∵EP⊥BP，EQ⊥BC∴BE平分∠ABC，∴∠NBC=∠ABN=22.5°，∵AH垂直平分BC，∴NB=NC，∴∠NCB=∠NBC=22.5°，∴∠ENC=∠NBC+∠NCB=45°，∴△ENC的等腰直角三角形，∴NC= EC，∴AD=2EC，∴2NC= AD，∴AD= NC，∵BN=NC，∴AD= BN．【解析】【分析】（1）首先利用SAS判断出△ABM≌△CAD，根据全等三角形对应边相等得出BM=AD= ，根据勾股定理可以算出AM，根据线段的和差得出CM的长，利用S△BCM= •CM•BA即可得出答案；（2）连接EC、CN，作EQ⊥BC于Q，EP⊥BA于P．根据直角三角形斜边上的中线等于斜边的一半得出AE=CE=ED，根据等边对等角得出∠EAC=∠ECA，根据全等三角形对应角相等得出∠ABM=∠CAD，从而得出∠ABM=∠MCE，根据对顶角相等及三角形的内角和得出∠CEM=∠BAM=90°，从而判断出△ABM∽△ECM，由相似三角形对应边成比例得出BM∶CM= AM∶EM,从而得出BM∶AM= CM∶EM，根据两边对应成比例及夹角相等得出△AME∽△BMC，故∠AEM=∠ACB=45°，∠AEC=135°，易知∠PEQ=135°，故∠PEQ=∠AEC，∠AEQ=∠EQC，又∠P=∠EQC=90°，故△EPA≌△EQC，故EP=EQ，根据角平分线的判定得出BE平分∠ABC，故∠NBC=∠ABN=22.5°，根据中垂线定理得出NB=NC，根据等腰三角形的性质得出∠NCB=∠NBC=22.5°，故∠ENC=∠NBC+∠NCB=45°，△ENC的等腰直角三角形，根据等腰直角三角形边之间的关系得出NC= EC，根据AD=2EC，2NC= AD，AD= NC，又BN=NC，故AD= BN．2．如图，AB为的直径，C为上一点，D为BA延长线上一点，．（1）求证：DC为的切线；（2）线段DF分别交AC，BC于点E，F且，的半径为5，，求CF的长．【答案】（1）解：如图，连接OC，为的直径，，，，，，，即，为的切线（2）解：中，，，，，，，∽，，设，，中，，，舍或，，，，设，，，，，∽，，，，【解析】【分析】（1）要证DC为⊙O 的切线，需添加辅助线：连半径OC，证垂直，根据直径所对的圆周角是直角，可得出∠ BCO + ∠ OCA = 90°，再利用等腰三角形的性质，可得出∠ B = ∠BCO ，结合已知，可推出∠OCD=90°，然后利用切线的判定定理，可证得结论。
2020-2021学年上海初三数学一模汇编-专题09 相似三角形(学生版)
2021年上海市16区中考数学一模汇编专题09 相似三角形一、单选题1．（2021·上海长宁区·九年级一模）下列命题中，说法正确的是（ ）A ．四条边对应成比例的两个四边形相似B ．四个内角对应相等的两个四边形相似C ．两边对应成比例且有一个角相等的两个三角形相似D ．斜边与一条直角边对应成比例的两个直角三角形相似2．（2021·上海杨浦区·九年级一模）在梯形ABCD 中，//AD BC ，对角线AC 与BD 相交于点O ，下列说法中，错误的是（ ）A ．AOB DOC S S =△△ B ．AOB BOC S OD S OB =△△ C ．AOD BOC S OA S OC =△△ D ．ABD ABC S AD S BC=△△ 3．（2021·上海黄浦区·九年级一模）已知ABC 与DEF 相似，又40A ∠=︒，60B ∠=︒，那么D ∠不可能是（ ）A ．40°B ．60°C ．80°D ．100°4．（2021·上海宝山区·九年级一模）如图，//AB DE ，//BC DF ，已知::AF FB m n =，BC a =，那么CE 等于（ ）．A ．am nB ．an mC ．am m n +D ．an m n+ 5．（2021·上海金山区·九年级一模）如图，已知点D 、E 分别在ABC ∆的边AB 、AC 上，//DE BC ，2AD =，3BD =，BC a =，那么ED 等于（ ）A ．23aB ．23a -C ．25aD ．25a - 6．（2021·上海徐汇区·九年级一模）下列说法中，正确的是（ ）A ．两个矩形必相似B ．两个含45︒角的等腰三角形必相似C ．两个菱形必相似D ．两个含30角的直角三角形必相似7．（2021·上海长宁区·九年级一模）如图，己知在ABC 中，点D 、点E 是边BC 上的两点，连接AD 、AE ，且AD ＝AE ，如果ABE ∽CBA ，那么下列等式错误的是（ ）A ．AB 2＝BE •BCB ．CD •AB ＝AD •AC C ．AE 2＝CD •BE D ．AB •AC ＝BE •CD8．（2021·上海九年级一模）如图，在ABC 中，点D 在边AB 上，DE BC //，DF AC //，联结BE ，BE 与DF 相交于点G ，则下列结论一定正确的是（ ）A ．AD DE DB BC = B ．AE BF AC BC = C ．BD BF AD DE = D ．DG BF GF FC= 9．（2021·上海黄浦区·九年级一模）如图，在直角梯形ABCD 中，//AB CD ，90BAD ∠=︒，对角线的交点为点O ．如果梯形ABCD 的两底边长不变，而腰长发生变化，那么下列量中不变的是（ ）A ．点O 到边AB 的距离B ．点O 到边BC 的距离 C ．点O 到边CD 的距离D ．点O 到边DA 的距离10．（2021·上海浦东新区·九年级一模）如图，在ABC 中，点D 、F 是边AB 上的点，点E 是边AC 上的点，如果∽ACD=∽B ，DE //BC ，EF //CD ，下列结论不成立的是（ ）A ．2AE AF AD =⋅B ．2AC AD AB =⋅C ．2AF AE AC =⋅D ．2AD AF AB =⋅11．（2021·上海松江区·九年级一模）如图，已知在Rt ABC 中，90C ∠=︒，点G 是ABC 的重心，GE AC ⊥，垂足为E ，如果8CB =，则线段GE 的长为（ ）A ．53B ．73C ．83D ．10312．（2021·上海奉贤区·九年级一模）如图，在梯形ABCD 中，//,3AD BC BC AD =，对角线AC BD 、交于点,O EF 是梯形ABCD 的中位线，EF 与BD AC 、分别交于点G H 、，如果OGH ∆的面积为1，那么梯形ABCD 的面积为（ ）A ．12B ．14C ．16D ．1813．（2021·上海虹口区·九年级一模）如图，在Rt ABC 中，90ACB ∠=︒，D 是边AB 上一点，过D 作DF AB ⊥交边BC 于点E ，交AC 的延长线于点F ，联结AE ，如果1tan 3EAC ∠=，1CEF S =，那么ABC S 的值是（ ）A ．3B ．6C ．9D ．12二、填空题14．（2021·上海崇明区·九年级一模）如果两个相似三角形的一组对应边上的高之比为1:4，那么这两个三角形的面积比为________．15．（2021·上海闵行区·九年级一模）已知两个相似三角形的相似比为4：9，那么这两个三角形的周长之比为__________．16．（2021·上海奉贤区·九年级一模）如果两个相似三角形的周长之比为1:4,那么这两个三角形对应边上的高之比为_______________________．17．（2021·上海徐汇区·九年级一模）如图，在ABC 中，点,D E 分别在边,AB AC 上， //DE BC ，如果AED 和四边形DECB 的面积相等，BC DE 的长是 _____ ．18．（2021·上海长宁区·九年级一模）如果一条对角线把凸四边形分成两个相似的三角形，那么我们把这条对角线叫做这个凸四边形的相似对角线，在凸四边形ABCD 中，AB AC ==32AD CD ==，点E 、点F 分别是边AD ，边BC 上的中点．如果AC 是凸四边形ABCD 的相似对角线，那么EF 的长等于_________． 19．（2021·上海长宁区·九年级一模）如果两个相似三角形对应边上的中线之比为5：4．那么这两个三角形的周长之比为_______________．20．（2021·上海杨浦区·九年级一模）如图，已知在ABC 中，90C ∠=︒，10AB =，1cot 2B =，正方形DEFG 的顶点G 、F 分别在边AC 、BC 上，点D 、E 在斜边AB 上，那么正方形DEFG 的边长为_____．21．（2021·上海浦东新区·九年级一模）如图，矩形DEFG 的边EF 在ABC 的边BC 上，顶点D 、G 分别在边AB 、AC 上，已知ABC 的边BC 长60厘米，高AH 为40厘米，如果DE=2DG ，那么DG=______厘米．22．（2021·上海静安区·九年级一模）如图，在∽ABC 中，点D 、E 分别在边AB 、AC 上，∽AED =∽B ，如果AD =2，AE =3，CE =1，那么BD 长为____．23．（2021·上海宝山区·九年级一模）如图，已知ABC 中，//EF AB ，12AF FC =，如果四边形ABEF 的面积为25，那么ABC 的面积为______．24．（2021·上海闵行区·九年级一模）在ABC 中，点D 、E 分别在边AB 、AC 上，且//DE BC ，如果：25DE BC =，那么AE EC=__________． 25．（2021·上海松江区·九年级一模）如图，正方形DEFG 的边EF 在ABC 的边BC 上，顶点D ，G 分别在AB 、AC 上，已知ABC 的边16BC cm =，高AH 为10cm ，则正方形DEFG 的边长为___．26．（2021·上海虹口区·九年级一模）如图，//AB CD ，AD 、BC 相交于点E ，过E 作//EF CD 交BD 于点F ，如果3AB =，6CD =，那么EF 的长是________．27．（2021·上海虹口区·九年级一模）如图，梯形ABCD 中，//AD BC ，90A ∠=︒，90BDC ∠=︒，4=AD ，9BC =，那么BD =______．28．（2021·上海虹口区·九年级一模）已知△ABC 和△A 'B 'C '，顶点A 、B 、C 分别与顶点A '，B '，C '对应，AD 、A D ''分别是BC 、B C ''边上的中线，如果3BC =， 2.4AD =，2B C ''=，那么A D ''的长是________．29．（2021·上海金山区·九年级一模）已知：如图，ABC ∆的中线AE 与BD 交于点G ，//DF AE 交BC 于F ，那么DF AG=______．30．（2021·上海长宁区·九年级一模）如图，矩形ABCD 沿对角线BD 翻折后，点C 落在点E 处．联结CE 交边AD 于点F ．如果DF ＝1，BC ＝4，那么AE 的长等于_________．31．（2021·上海九年级一模）如果两个相似三角形的周长比为2:3，那么它们的对应角平分线的比为_________________．32．（2021·上海杨浦区·九年级一模）如图，已知在平行四边形ABCD 中，点E 在边AB 上，12AE EB =，联结DE 交对角线AC 于点O ，那么AO OC的值为_____．33．（2021·上海黄浦区·九年级一模）如图，点D 、E 、F 分别位于ABC 的三边上，且//DE BC ，//EF AB ．如果ADE 的面积为2，CEF △的面积为8，那么四边形BFED 的面积是________．34．（2021·上海浦东新区·九年级一模）秦九韶的《数书九章》中有一个“峻积验雪”的例子，其原理为：如图，在Rt ABC 中，∽C=90°，AC=12，BC=5，AD∽AB ，AD=0.4，过点D 作DE //AB 交CB 的延长线于点E ，过点B 作BF∽CE 交DE 于点F ，那么BF=______．35．（2021·上海浦东新区·九年级一模）如图，ABC 中，AB=10，BC=12，AC=8，点D 是边BC 上一点，且BD ：CD=2：1，联结AD ，过AD 中点M 的直线将ABC 分成周长相等的两部分，这条直线分别与边BC 、AC 相交于点E 、F ，那么线段BE 的长为______．36．（2021·上海静安区·九年级一模）如图，在∽ABC 中，点D 、E 分别在边AB 、AC 上，DE ∽BC ，如果AB =12，BC =9，AC =6，四边形BCED 的周长为21，那么DE 的长为____．37．（2021·上海宝山区·九年级一模）在一块直角三角形铁皮上截一块正方形铁皮，如图，已有的铁皮是Rt ABC △，90C ∠=︒，要截得的正方形EFGD 的边FG 在AB 上，顶点E 、D 分别在边CA 、CB 上，如果4AF =，9GB =，那么正方形铁皮的边长为______．38．（2021·上海闵行区·九年级一模）如图，在ABC 中，2AB AC =，点D 在边AB 上，且ACD B ∠=∠，那么ACD ABCS S =△△__________．39．（2021·上海松江区·九年级一模）如图，已知点D ．E 分别在ABC 的边AB 和AC 上，//DE BC ，34DE BC =，四边形DBCE的面积等于7，则ADE的面积为____．40．（2021·上海金山区·九年级一模）如图，在□ABCD中，点E在边BC上，DE交对角线AC于F，若∆的面积等于15，那么FEC∆的面积等于______．CE BE=，ABC2。
2020-2021九年级数学一模试题分类汇编——相似综合附详细答案
2020-2021九年级数学一模试题分类汇编——相似综合附详细答案一、相似1．阅读下列材料，完成任务：自相似图形定义：若某个图形可分割为若干个都与它相似的图形，则称这个图形是自相似图形．例如：正方形ABCD中，点E、F、G、H分别是AB、BC、CD、DA边的中点，连接EG，HF交于点O，易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形，且与原正方形相似，故正方形是自相似图形．任务：（1）图1中正方形ABCD分割成的四个小正方形中，每个正方形与原正方形的相似比为________；（2）如图2，已知△ABC中，∠ACB=90°，AC=4，BC=3，小明发现△ABC也是“自相似图形”，他的思路是：过点C作CD⊥AB于点D，则CD将△ABC分割成2个与它自己相似的小直角三角形．已知△ACD∽△ABC，则△ACD与△ABC的相似比为________；（3）现有一个矩形ABCD是自相似图形，其中长AD=a，宽AB=b（a＞b）．请从下列A、B两题中任选一条作答．A：①如图3﹣1，若将矩形ABCD纵向分割成两个全等矩形，且与原矩形都相似，则a=________（用含b的式子表示）；②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形，且与原矩形都相似，则a=________（用含n，b的式子表示）；B：①如图4﹣1，若将矩形ABCD先纵向分割出2个全等矩形，再将剩余的部分横向分割成3个全等矩形，且分割得到的矩形与原矩形都相似，则a=________（用含b的式子表示）；②如图4﹣2，若将矩形ABCD先纵向分割出m个全等矩形，再将剩余的部分横向分割成n 个全等矩形，且分割得到的矩形与原矩形都相似，则a=________（用含m，n，b的式子表示）．【答案】（1）（2）（3）；；或；或【解析】【解答】（解：（1）∵点H是AD的中点，∴AH= AD，∵正方形AEOH∽正方形ABCD，∴相似比为： == ；故答案为：；（ 2 ）在Rt△ABC中，AC=4，BC=3，根据勾股定理得，AB=5，∴△ACD与△ABC相似的相似比为：，故答案为：；（ 3 ）A、①∵矩形ABEF∽矩形FECD，∴AF：AB=AB：AD，即 a：b=b：a，∴a= b；故答案为：②每个小矩形都是全等的，则其边长为b和 a，则b： a=a：b，∴a= b；故答案为：B、①如图2，由①②可知纵向2块矩形全等，横向3块矩形也全等，∴DN= b，Ⅰ、当FM是矩形DFMN的长时，∵矩形FMND∽矩形ABCD，∴FD：DN=AD：AB，即FD： b=a：b，解得FD= a，∴AF=a﹣ a= a，∴AG= = = a，∵矩形GABH∽矩形ABCD，∴AG：AB=AB：AD即 a：b=b：a得：a= b；Ⅱ、当DF是矩形DFMN的长时，∵矩形DFMN∽矩形ABCD，∴FD：DN=AB：AD即FD： b=b：a解得FD= ，∴AF=a﹣ = ，∴AG= = ，∵矩形GABH∽矩形ABCD，∴AG：AB=AB：AD即：b=b：a，得：a= b；故答案为：或；②如图3，由①②可知纵向m块矩形全等，横向n块矩形也全等，∴DN= b，Ⅰ、当FM是矩形DFMN的长时，∵矩形FMND∽矩形ABCD，∴FD：DN=AD：AB，即FD： b=a：b，解得FD= a，∴AF=a﹣ a，∴AG= = = a，∵矩形GABH∽矩形ABCD，∴AG：AB=AB：AD即 a：b=b：a得：a= b；Ⅱ、当DF是矩形DFMN的长时，∵矩形DFMN∽矩形ABCD，∴FD：DN=AB：AD即FD： b=b：a解得FD= ，∴AF=a﹣，∴AG= = ，∵矩形GABH∽矩形ABCD，∴AG：AB=AB：AD即：b=b：a，得：a= b；故答案为： b或 b．【分析】由题意可知，用相似多边形的性质即可求解。
2020-2021初三数学一模试题分类汇编——圆与相似综合
2020-2021初三数学一模试题分类汇编——圆与相似综合一、相似1．如图，抛物线与x轴交于两点A（﹣4，0）和B（1，0），与y轴交于点C（0，2），动点D沿△ABC的边AB以每秒2个单位长度的速度由起点A向终点B 运动，过点D作x轴的垂线，交△ABC的另一边于点E，将△ADE沿DE折叠，使点A落在点F处，设点D的运动时间为t秒．（1）求抛物线的解析式和对称轴；（2）是否存在某一时刻t，使得△EFC为直角三角形？若存在，求出t的值；若不存在，请说明理由；（3）设四边形DECO的面积为s，求s关于t的函数表达式．【答案】（1）解：把A（﹣4，0），B（1，0），点C（0，2）代入得：，解得：，∴抛物线的解析式为：，对称轴为：直线x=﹣；（2）解：存在，∵AD=2t，∴DF=AD=2t，∴OF=4﹣4t，∴D（2t﹣4，0），∵直线AC的解析式为：，∴E（2t﹣4，t），∵△EFC为直角三角形，分三种情况讨论：①当∠EFC=90°，则△DEF∽△OFC，∴，即，解得：t= ；②当∠FEC=90°，∴∠AEF=90°，∴△AEF是等腰直角三角形，∴DE= AF，即t=2t，∴t=0，（舍去），③当∠ACF=90°，则AC2+CF2=AF2，即（42+22）+[22+（4t﹣4）2]=（4t）2，解得：t= ，∴存在某一时刻t，使得△EFC为直角三角形，此时，t= 或；（3）解：∵B（1，0），C（0，2），∴直线BC的解析式为：y=﹣2x+2，当D在y轴的左侧时，S= （DE+OC）•OD= （t+2）•（4﹣2t）=﹣t2+4 （0＜t＜2）；当D在y轴的右侧时，如图2，∵OD=4t﹣4，DE=﹣8t+10，S= （DE+OC）•OD= （﹣8t+10+2）•（4t﹣4），即（2＜t＜）．综上所述：【解析】【分析】（1）（1）利用待定系数法，将点A、B、C的坐标代入函数解析式，建立方程组求解即可。
2020-2021九年级数学一模试题分类汇编——圆的综合综合附详细答案
2020-2021九年级数学一模试题分类汇编——圆的综合综合附详细答案一、圆的综合1．如图，点A、B、C分别是⊙O上的点， CD是⊙O的直径，P是CD延长线上的一点，AP=AC．（1）若∠B=60°，求证：AP是⊙O的切线；（2）若点B是弧CD的中点，AB交CD于点E，CD=4，求BE·AB的值．【答案】（1）证明见解析；（2）8．【解析】（1）求出∠ADC的度数，求出∠P、∠ACO、∠OAC度数，求出∠OAP=90°，根据切线判定推出即可；（2）求出BD长，求出△DBE和△ABD相似，得出比例式，代入即可求出答案．试题解析：连接AD，OA，∵∠ADC=∠B，∠B=60°，∴∠ADC=60°，∵CD是直径，∴∠DAC=90°，∴∠ACO=180°-90°-60°=30°，∵AP=AC，OA=OC，∴∠OAC=∠ACD=30°，∠P=∠ACD=30°，∴∠OAP=180°-30°-30°-30°=90°，即OA⊥AP，∵OA为半径，∴AP是⊙O切线．（2）连接AD，BD，∵CD是直径，∴∠DBC=90°，∵CD=4，B为弧CD中点，∴BD=BC=，∴∠BDC=∠BCD=45°，∴∠DAB=∠DCB=45°，即∠BDE=∠DAB，∵∠DBE=∠DBA，∴△DBE∽△ABD，∴，∴BE•AB=BD•BD=．考点：1．切线的判定；2．相似三角形的判定与性质．2．如图，在⊙O中，AB为直径，OC⊥AB，弦CD与OB交于点F，在AB的延长线上有点E，且EF=ED．（1）求证：DE是⊙O的切线；（2）若tan A=12，探究线段AB和BE之间的数量关系，并证明；（3）在（2）的条件下，若OF=1，求圆O的半径．【答案】（1）答案见解析；（2）AB=3BE；（3）3．【解析】试题分析：（1）先判断出∠OCF+∠CFO=90°，再判断出∠OCF=∠ODF，即可得出结论；（2）先判断出∠BDE=∠A，进而得出△EBD∽△EDA，得出AE=2DE，DE=2BE，即可得出结论；（3）设BE=x，则DE=EF=2x，AB=3x，半径OD=32x，进而得出OE=1+2x，最后用勾股定理即可得出结论．试题解析：（1）证明：连结OD，如图．∵EF=ED，∴∠EFD=∠EDF．∵∠EFD=∠CFO，∴∠CFO=∠EDF．∵OC⊥OF，∴∠OCF+∠CFO=90°．∵OC=OD，∴∠OCF=∠ODF，∴∠ODC+∠EDF=90°，即∠ODE=90°，∴OD⊥DE．∵点D在⊙O上，∴DE是⊙O的切线；（2）线段AB、BE之间的数量关系为：AB=3BE．证明如下：∵AB为⊙O直径，∴∠ADB=90°，∴∠ADO=∠BDE．∵OA=OD，∴∠ADO=∠A，∴∠BDE=∠A，而∠BED=∠DEA，∴△EBD∽△EDA，∴DE BE BDAE DE AD==．∵Rt△ABD中，tan A=BDAD=12，∴DE BEAE DE==12，∴AE=2DE，DE=2BE，∴AE=4BE，∴AB=3BE；（3）设BE=x，则DE=EF=2x，AB=3x，半径OD=32x．∵OF=1，∴OE=1+2x．在Rt△ODE中，由勾股定理可得：（32x）2+（2x）2=（1+2x）2，∴x=﹣29（舍）或x=2，∴圆O的半径为3．点睛：本题是圆的综合题，主要考查了切线的判定和性质，等腰三角形的性质，锐角三角函数，相似三角形的判定和性质，勾股定理，判断出△EBD∽△EDA是解答本题的关键．3．图 1 和图 2 中，优弧»AB纸片所在⊙O 的半径为 2，AB＝3，点P为优弧»AB上一点（点P 不与A，B 重合），将图形沿BP 折叠，得到点A 的对称点A′．发现：（1）点O 到弦AB 的距离是，当BP 经过点O 时，∠ABA′＝；（2）当BA′与⊙O 相切时，如图 2，求折痕的长．拓展：把上图中的优弧纸片沿直径MN 剪裁，得到半圆形纸片，点P（不与点M， N 重合）为半圆上一点，将圆形沿NP 折叠，分别得到点M，O 的对称点A′， O′，设∠MNP＝α．（1）当α＝15°时，过点A′作A′C∥MN，如图 3，判断A′C 与半圆O 的位置关系，并说明理由；（2）如图 4，当α＝ °时，NA′与半圆O 相切，当α＝ °时，点O′落在»NP上．（3）当线段NO′与半圆O 只有一个公共点N 时，直接写出β的取值范围．【答案】发现：（1）1，60°；（2）3；拓展：（1）相切，理由详见解析；（2）45°；30°；（3）0°＜α＜30°或45°≤α＜90°．【解析】【分析】发现：（1）利用垂径定理和勾股定理即可求出点O到AB的距离；利用锐角三角函数的定义及轴对称性就可求出∠ABA′．（2）根据切线的性质得到∠OBA′=90°，从而得到∠ABA′=120°，就可求出∠ABP，进而求出∠OBP=30°．过点O作OG⊥BP，垂足为G，容易求出OG、BG的长，根据垂径定理就可求出折痕的长．拓展：（1）过A'、O作A'H⊥MN于点H，OD⊥A'C于点D．用含30°角的直角三角形的性质可得OD=A'H=12A'N=12MN=2可判定A′C与半圆相切；（2）当NA′与半圆相切时，可知ON⊥A′N，则可知α=45°，当O′在»PB时，连接MO′，则可知NO′=12MN，可求得∠MNO′=60°，可求得α=30°；（3）根据点A′的位置不同得到线段NO′与半圆O只有一个公共点N时α的取值范围是0°＜α＜30°或45°≤α＜90°．【详解】发现：（1）过点O作OH⊥AB，垂足为H，如图1所示,∵⊙O的半径为2，AB=23，∴OH=22OB HB-=222(3)1-=在△BOH中，OH=1，BO=2∴∠ABO=30°∵图形沿BP折叠，得到点A的对称点A′．∴∠OBA′=∠ABO=30°∴∠ABA′=60°（2）过点O作OG⊥BP，垂足为G，如图2所示．∵BA′与⊙O相切，∴OB⊥A′B．∴∠OBA′=90°．∵∠OBH=30°，∴∠ABA′=120°．∴∠A′BP=∠ABP=60°．∴∠OBP=30°．∴OG=12OB=1．∴3．∵OG⊥BP，∴3．∴3．∴折痕的长为3拓展：（1）相切．分别过A'、O作A'H⊥MN于点H，OD⊥A'C于点D．如图3所示，∵A'C∥MN∴四边形A'HOD是矩形∴A'H=O∵α=15°∴∠A'NH=30∴OD=A'H=12A'N=12MN=2∴A'C与半圆（2）当NA′与半圆O相切时，则ON⊥NA′，∴∠ONA′=2α=90°，∴α=45当O′在»PB上时，连接MO′，则可知NO′=12 MN，∴∠O′MN=0°∴∠MNO′=60°，∴α=30°，故答案为：45°；30°．（3）∵点P，M不重合，∴α＞0，由（2）可知当α增大到30°时，点O′在半圆上，∴当0°＜α＜30°时点O′在半圆内，线段NO′与半圆只有一个公共点B；当α增大到45°时NA′与半圆相切，即线段NO′与半圆只有一个公共点B．当α继续增大时，点P逐渐靠近点N，但是点P，N不重合，∴α＜90°，∴当45°≤α＜90°线段BO′与半圆只有一个公共点B．综上所述0°＜α＜30°或45°≤α＜90°．【点睛】本题考查了切线的性质、垂径定理、勾股定理、三角函数的定义、30°角所对的直角边等于斜边的一半、翻折问题等知识，正确的作出辅助线是解题的关键．4．如图，A、B两点的坐标分别为（0，6），（0，3），点P为x轴正半轴上一动点，过点A作AP的垂线，过点B作BP的垂线，两垂线交于点Q，连接PQ，M为线段PQ的中点．（1）求证：A、B、P、Q四点在以M为圆心的同一个圆上；（2）当⊙M与x轴相切时，求点Q的坐标；（3）当点P从点（2，0）运动到点（3，0）时，请直接写出线段QM扫过图形的面积．【答案】(1)见解析;(2) Q的坐标为（32，9）;(3)63 8.【解析】（1）解：连接AM、BM，∵AQ⊥AP，BQ⊥BP∵△APQ和△BPQ都是直角三角形，M是斜边PQ的中点∴AM＝BM＝PM=QM= 12 PQ，∴A、B、P、Q四点在以M为圆心的同一个圆上。
2020-2021初三数学一模试题分类汇编——相似综合及答案
2020-2021初三数学一模试题分类汇编——相似综合及答案一、相似1．已知线段a，b，c满足，且a＋2b＋c＝26.（1）判断a，2b，c，b2是否成比例；（2）若实数x为a，b的比例中项，求x的值．【答案】（1）解：设，则a=3k，b=2k，c=6k，又∵a+2b+c=26，∴3k+2×2k+6k=26，解得k=2，∴a=6，b=4，c=12；∴2b=8，b2=16∵a=6，2b=8，c=12，b2=16∴2bc=96，ab2=6×16=96∴2bc=ab2a，2b，c，b2是成比例的线段。
（2）解：∵x是a、b的比例中项，∴x2=6ab，∴x2=6×4×6，∴x=12．【解析】【分析】（1）设已知比例式的值为k，可得出a=3k，b=2k，c=6k，再代入a+2b+c=26，建立关于k的方程，求出kl的值，再求出2b、b2,然后利用成比例线段的定义，可判断a，2b，c，b2是否成比例。
（2）根据实数x为a，b的比例中项，可得出x2=ab，建立关于x的方程，求出x的值。
2．已知在△ABC中，∠ABC=90°，AB=3，BC=4.点Q是线段AC上的一个动点，过点Q作AC的垂线交线段AB（如图1）或线段AB的延长线（如图2）于点P.（1）当点P在线段AB上时，求证：△APQ∽△ABC；（2）当△PQB为等腰三角形时，求AP的长.【答案】（1））证明：∵∠A+∠APQ=90°，∠A+∠C=90°，∴∠APQ=∠C.在△APQ与△ABC中，∵∠APQ=∠C，∠A=∠A，∴△APQ∽△ABC.（2）解：在Rt△ABC中，AB=3，BC=4，由勾股定理得：AC=5.∵∠BPQ为钝角，∴当△PQB为等腰三角形时，只可能是PB=PQ.（I）当点P在线段AB上时，如题图1所示，由（1）可知，△APQ∽△ABC，∴，即，解得： .∴ .（II）当点P在线段AB的延长线上时，如题图2所示,∵BP=BQ，∴∠BQP=∠P.∵∠BQP+∠AQB=90°，∠A+∠P=90°，∴∠AQB=∠A。
2020-2021初三数学一模试题分类汇编——相似综合
2020-2021初三数学一模试题分类汇编——相似综合一、相似1．已知：如图，在△ABC中，AB=BC=10，以AB为直径作⊙O分别交AC，BC于点D，E，连接DE和DB，过点E作EF⊥AB，垂足为F，交BD于点P．（1）求证：AD=DE；（2）若CE=2，求线段CD的长；（3）在（2）的条件下，求△DPE的面积．【答案】（1）解：∵AB是⊙O的直径，∴∠ADB=90°，即BD⊥AC∵AB=BC，∴△ABD≌CBD∴∠ABD=∠CBD在⊙O中，AD与DE分别是∠ABD与∠CBD所对的弦∴AD=DE；（2）解：∵四边形ABED内接于⊙O，∴∠CED=∠CAB，∵∠C=∠C，∴△CED∽△CAB，∴，∵AB=BC=10，CE=2，D是AC的中点，∴CD= ；（3）解：延长EF交⊙O于M，在Rt△ABD中，AD= ，AB=10，∴BD=3 ，∵EM⊥AB，AB是⊙O的直径，∴，∴∠BEP=∠EDB，∴△BPE∽△BED，∴，∴BP= ，∴DP=BD-BP= ，∴S△DPE：S△BPE=DP：BP=13：32，∵S△BCD= × ×3 =15，S△BDE：S△BCD=BE：BC=4：5，∴S△BDE=12，∴S△DPE= ．【解析】【分析】（1）根据已知条件AB是⊙O的直径得出∠ADB=90°，再根据等腰三角形的三线合一的性质即可得出结论。
（2）根据圆内接四边形的性质证得∠CED=∠CAB，再根据相似三角形的判定证出△CED∽△CAB，得出对应边成比例，建立关于CD的方程，即可求出CD的长。
（3）延长EF交⊙O于M，在Rt△ABD中，利用勾股定理求出BD的长，再证明△BPE∽△BED，根据相似三角形的性质得对应边成比例求出BP的长，然后根据等高的三角形的面积之比等于对边之比，再由三角形面积公式即可求解。
2．（1）问题发现：如图1，在等边三角形ABC中，点M为BC边上异于B、C的一点，以AM为边作等边三角形AMN，连接CN，NC与AB的位置关系为________；（2）深入探究：如图2，在等腰三角形ABC中，BA=BC，点M为BC边上异于B、C的一点，以AM为边作等腰三角形AMN，使∠ABC=∠AMN，AM=MN，连接CN，试探究∠ABC与∠ACN的数量关系，并说明理由；（3）拓展延伸：如图3，在正方形ADBC中，AD=AC，点M为BC边上异于B、C的一点，以AM为边作正方形AMEF，点N为正方形AMEF的中点，连接CN，若BC=10，CN= ，试求EF的长．【答案】（1）NC∥AB（2）解：∠ABC=∠ACN，理由如下：∵ =1且∠ABC=∠AMN，∴△ABC～△AMN∴，∵AB=BC，∴∠BAC= （180°﹣∠ABC），∵AM=MN∴∠MAN= （180°﹣∠AMN），∵∠ABC=∠AMN，∴∠BAC=∠MAN，∴∠BAM=∠CAN，∴△ABM～△ACN，∴∠ABC=∠ACN（3）解：如图3，连接AB，AN，∵四边形ADBC，AMEF为正方形，∴∠ABC=∠BAC=45°，∠MAN=45°，∴∠BAC﹣∠MAC=∠MAN﹣∠MAC即∠BAM=∠CAN，∵，∴，∴△ABM～△ACN∴，∴ =cos45°= ，∴，∴BM=2，∴CM=BC﹣BM=8，在Rt△AMC，AM= ，∴EF=AM=2 ．【解析】【解答】解：（1）NC∥AB，理由如下：∵△ABC与△MN是等边三角形，∴AB=AC，AM=AN，∠BAC=∠MAN=60°，∴∠BAM=∠CAN，在△ABM与△ACN中，，∴△ABM≌△ACN（SAS），∴∠B=∠ACN=60°，∵∠ANC+∠ACN+∠CAN=∠ANC+60°+∠CAN=180°，∴∠ANC+∠MAN+∠BAM=∠ANC+60°+∠CAN=∠BAN+∠ANC=180°，∴CN∥AB；【分析】（1）由题意用边角边易得△ABM≌△ACN，则可得∠B=∠ACN=60°，所以∠BCN+∠B=∠BCA+∠ACN+∠B=180°，根据平行线的判定即可求解；（2）由题意易得△ABC～△AMN，可得比例式，由三角形内角和定理易得∠BAM=∠CAN，根据相似三角形的判定可得△ABM～△ACN，由相似三角形的性质即可求解；（3）要求EF的值，只须求得CM的值，然后解直角三角形AMC即可求解。
2020-2021初三数学一模试题分类汇编——圆的综合综合及详细答案
2020-2021初三数学一模试题分类汇编——圆的综合综合及详细答案一、圆的综合1．如图，⊙O的半径为6cm，经过⊙O上一点C作⊙O的切线交半径OA的延长于点B，作∠ACO的平分线交⊙O于点D，交OA于点F，延长DA交BC于点E．（1）求证：AC∥OD；（2）如果DE⊥BC，求»AC的长度．【答案】（1）证明见解析；（2）2π．【解析】试题分析：（1）由OC=OD，CD平分∠ACO，易证得∠ACD=∠ODC，即可证得AC∥OD；（2）BC切⊙O于点C，DE⊥BC，易证得平行四边形ADOC是菱形，继而可证得△AOC是等边三角形，则可得：∠AOC=60°，继而求得弧AC的长度．试题解析：（1）证明：∵OC=OD，∴∠OCD=∠ODC．∵CD平分∠ACO，∴∠OCD=∠ACD，∴∠ACD=∠ODC，∴AC∥OD；（2）∵BC切⊙O于点C，∴BC⊥OC．∵DE⊥BC，∴OC∥DE．∵AC∥OD，∴四边形ADOC 是平行四边形．∵OC=OD，∴平行四边形ADOC是菱形，∴OC=AC=OA，∴△AOC是等边三角形，∴∠AOC=60°，∴弧AC的长度=606180π⨯=2π．点睛：本题考查了切线的性质、等腰三角形的判定与性质、菱形的判定与性质以及弧长公式．此题难度适中，注意掌握数形结合思想的应用．2．如图，AB为⊙O的直径，点E在⊙O上，过点E的切线与AB的延长线交于点D，连接BE，过点O作BE的平行线，交⊙O于点F，交切线于点C，连接AC（1）求证：AC是⊙O的切线；（2）连接EF，当∠D=°时，四边形FOBE是菱形．【答案】（1）见解析；（2）30.【解析】【分析】（1）由等角的转换证明出OCA OCE ∆∆≌，根据圆的位置关系证得AC 是⊙O 的切线. （2）根据四边形FOBE 是菱形，得到OF=OB=BF=EF ，得证OBE ∆为等边三角形，而得出60BOE ∠=︒，根据三角形内角和即可求出答案.【详解】（1）证明：∵CD 与⊙O 相切于点E ，∴OE CD ⊥，∴90CEO ∠=︒，又∵OC BE P ，∴COE OEB ∠=∠，∠OBE=∠COA∵OE=OB ，∴OEB OBE ∠=∠，∴COE COA ∠=∠，又∵OC=OC ，OA=OE ，∴OCA OCE SAS ∆∆≌（）， ∴90CAO CEO ∠=∠=︒，又∵AB 为⊙O 的直径，∴AC 为⊙O 的切线；（2）解：∵四边形FOBE 是菱形，∴OF=OB=BF=EF ，∴OE=OB=BE ，∴OBE ∆为等边三角形，∴60BOE ∠=︒，而OE CD ⊥，∴30D ∠=︒．故答案为30．【点睛】本题主要考查与圆有关的位置关系和圆中的计算问题，熟练掌握圆的性质是本题的解题关键.3．如图，在平面直角坐标系xoy 中，E （8,0），F(0 , 6)．（1）当G(4，8)时，则∠FGE= °（2）在图中的网格区域内找一点P ，使∠FPE=90°且四边形OEPF 被过P 点的一条直线分割成两部分后，可以拼成一个正方形．要求：写出点P 点坐标，画出过P 点的分割线并指出分割线（不必说明理由，不写画法）．【答案】（1）90；（2）作图见解析，P（7，7），PH是分割线．【解析】试题分析：（1）根据勾股定理求出△FEG的三边长，根据勾股定理逆定理可判定△FEG是直角三角形，且∠FGE="90" °．（2）一方面，由于∠FPE=90°，从而根据直径所对圆周角直角的性质，点P在以EF为直径的圆上；另一方面，由于四边形OEPF被过P点的一条直线分割成两部分后，可以拼成一个正方形，从而OP是正方形的对角线，即点P在∠FOE的角平分线上，因此可得P（7，7），PH是分割线．试题解析：（1）连接FE，∵E（8,0），F(0 , 6)，G(4，8)，∴根据勾股定理，得FG=，EG=，FE=10．∵，即．∴△FEG是直角三角形，且∠FGE=90 °．（2）作图如下：P（7，7），PH是分割线．考点：1．网格问题；2．勾股定理和逆定理；3．作图（设计）；4．圆周角定理．4．已知▱ABCD的周长为26，∠ABC=120°，BD为一条对角线，⊙O内切于△ABD，E，F，G为切点，已知⊙O的半径为3．求▱ABCD的面积．【答案】203【解析】【分析】首先利用三边及⊙O的半径表示出平行四边形的面积，再根据题意求出AB+AD=13，然后利用切线的性质求出BD的长即可解答.【详解】设⊙O分别切△ABD的边AD、AB、BD于点G、E、F；平行四边形ABCD的面积为S；则S=2S△ABD=2×12(AB·OE+BD·OF+AD·OG)=3（AB+AD+BD）；∵平行四边形ABCD的周长为26，∴AB+AD=13，∴S=3(13+BD)；连接OA；由题意得：∠OAE=30°，∴AG=AE=3；同理可证DF=DG，BF=BE；∴DF+BF=DG+BE=13﹣3﹣3=7，即BD=7，∴S=3（13+7）=203．即平行四边形ABCD的面积为203．5．如图，△ABC的内接三角形，P为BC延长线上一点，∠PAC=∠B，AD为⊙O的直径，过C作CG⊥AD于E，交AB于F，交⊙O于G．（1）判断直线PA与⊙O的位置关系，并说明理由；（2）求证：AG2=AF·AB；（3）若⊙O的直径为10，AC=25，AB=45，求△AFG的面积.【答案】（1）PA与⊙O相切，理由见解析；（2）证明见解析；（3）3.【解析】试题分析：（1）连接CD，由AD为⊙O的直径，可得∠ACD=90°，由圆周角定理，证得∠B=∠D，由已知∠PAC=∠B，可证得DA⊥PA，继而可证得PA与⊙O相切．（2）连接BG，易证得△AFG∽△AGB，由相似三角形的对应边成比例，证得结论.（3）连接BD，由AG2=AF•AB，可求得AF的长，易证得△AEF∽△ABD，即可求得AE的长，继而可求得EF与EG的长，则可求得答案．试题解析：解：（1）PA与⊙O相切．理由如下：如答图1，连接CD，∵AD为⊙O的直径，∴∠ACD=90°.∴∠D+∠CAD=90°.∵∠B=∠D，∠PAC=∠B，∴∠PAC=∠D.∴∠PAC+∠CAD=90°，即DA⊥PA.∵点A在圆上，∴PA与⊙O相切．（2）证明：如答图2，连接BG，∵AD为⊙O的直径，CG⊥AD，∴»».∴∠AGF=∠ABG.AC AD∵∠GAF=∠BAG，∴△AGF∽△ABG.∴AG：AB=AF：AG. ∴AG2=A F•AB.（3）如答图3，连接BD，∵AD 是直径，∴∠ABD=90°.∵AG 2=AF•AB ，AG=AC=25，AB=45，∴AF=5.∵CG ⊥AD ，∴∠AEF=∠ABD=90°.∵∠EAF=∠BAD ，∴△AEF ∽△ABD. ∴AE AF AB AD =，即51045=，解得：AE=2. ∴221EF AF AE =-=. ∵224EG AG AE =-=，∴413FG EG EF =-=-=. ∴1132322AFG S FG AE ∆=⋅⋅=⨯⨯=．考点：1. 圆周角定理；2.直角三角形两锐角的关系；3. 相切的判定；4.垂径定理；5.相似三角形的判定和性质；6.勾股定理；7.三角形的面积.6．四边形 ABCD 的对角线交于点 E ，且 AE ＝EC ，BE ＝ED ，以 AD 为直径的半圆过点 E ，圆心 为 O ．（1）如图①，求证：四边形 ABCD 为菱形；（2）如图②，若 BC 的延长线与半圆相切于点 F ，且直径 AD ＝6，求弧AE 的长．【答案】（1）见解析；（2）π2【解析】 试题分析：（1）先判断出四边形ABCD 是平行四边形，再判断出AC ⊥BD 即可得出结论； （2）先判断出AD =DC 且DE ⊥AC ，∠ADE =∠CDE ，进而得出∠CDA =30°，最后用弧长公式即可得出结论．试题解析：证明：（1）∵四边形ABCD 的对角线交于点E ，且AE =EC ，BE =ED ，∴四边形ABCD 是平行四边形．∵以AD 为直径的半圆过点E ，∴∠AED =90°，即有AC ⊥BD ，∴四边形ABCD 是菱形；（2）由（1）知，四边形ABCD 是菱形，∴△ADC 为等腰三角形，∴AD =DC 且DE ⊥AC ，∠ADE =∠CDE ．如图2，过点C 作CG ⊥AD ，垂足为G ，连接FO ．∵BF 切圆O 于点F ，∴OF ⊥AD ，且132OF AD ==，易知，四边形CGOF 为矩形，∴CG =OF =3． 在Rt △CDG 中，CD =AD =6，sin ∠ADC =CG CD =12，∴∠CDA =30°，∴∠ADE =15°． 连接OE ，则∠AOE =2×∠ADE =30°，∴¶3031802AE ππ⋅⨯==．点睛：本题主要考查菱形的判定即矩形的判定与性质、切线的性质，熟练掌握其判定与性质并结合题意加以灵活运用是解题的关键．7．如图，已知平行四边形OABC 的三个顶点A 、B 、C 在以O 为圆心的半圆上，过点C 作CD ⊥AB ，分别交AB 、AO 的延长线于点D 、E ，AE 交半圆O 于点F ，连接CF ． （1）判断直线DE 与半圆O 的位置关系，并说明理由；（2）若半圆O 的半径为6，求¶AC 的长．【答案】（1）直线CE 与半圆O 相切（2）4π【解析】试题分析：（1）结论：DE 是⊙O 的切线．首先证明△ABO ，△BCO 都是等边三角形，再证明四边形BDCG 是矩形，即可解决问题；（2）只要证明△OCF 是等边三角形即可解决问题，求AC 即可解决问题．试题解析：（1）直线CE 与半圆O 相切，理由如下：∵四边形OABC 是平行四边形，∴AB ∥OC.∵∠D=90°，∴∠OCE=∠D=90°，即OC ⊥DE ，∴直线CE 与半圆O 相切．（2）由（1）可知：∠COF=60°，OC=OF ，∴△OCF 是等边三角形，∴∠AOC=120°∴¶AC 的长为1206180π⨯⨯=4π.8．如图1O e ，的直径12AB P =，是弦BC 上一动点(与点B C ，不重合)30ABC o ，∠=，过点P 作PD OP ⊥交O e 于点D ．()1如图2，当//PD AB 时，求PD 的长；()2如图3，当»»DC AC =时，延长AB 至点E ，使12BE AB =，连接DE ． ①求证：DE 是O e 的切线；②求PC 的长．【答案】（1）26；（2）333-①见解析，②．【解析】分析：()1根据题意首先得出半径长，再利用锐角三角函数关系得出OP PD ，的长； ()2①首先得出OBD V 是等边三角形，进而得出ODE OFB 90∠∠==o ，求出答案即可；②首先求出CF 的长，进而利用直角三角形的性质得出PF 的长，进而得出答案． 详解：()1如图2，连接OD ，//OP PD PD AB ⊥Q ，，90POB ∴∠=o ，O Q e 的直径12AB =，6OB OD ∴==，在Rt POB V 中，30ABC o ∠=，3tan306233OP OB ∴=⋅=⨯=o ， 在Rt POD V 中， 22226(23)26PD OD OP =-=-=；()2①证明：如图3，连接OD ，交CB 于点F ，连接BD ，»»DC AC =Q ，30DBC ABC ∴∠=∠=o ，60ABD o ∴∠=，OB OD =Q ，OBD ∴V 是等边三角形，OD FB ∴⊥，12BE AB =Q ， OB BE ∴=，//BF ED ∴，90ODE OFB o ∴∠=∠=，DE ∴是O e 的切线；②由①知，OD BC ⊥，3cos30633CF FB OB ∴==⋅==o 在Rt POD V 中，OF DF =， 13(2PF DO ∴==直角三角形斜边上的中线，等于斜边的一半)， 333CP CF PF ∴=-=．点睛：此题主要考查了圆的综合以及直角三角形的性质和锐角三角函数关系，正确得出OBD V 是等边三角形是解题关键．9．如图，已知BC 是⊙O 的弦，A 是⊙O 外一点，△ABC 为正三角形，D 为BC 的中点，M 为⊙O 上一点，并且∠BMC=60°．（1）求证：AB是⊙O的切线；（2）若E，F分别是边AB，AC上的两个动点，且∠EDF=120°，⊙O的半径为2，试问BE+CF的值是否为定值？若是，求出这个定值；若不是，请说明理由．【答案】（1）证明见试题解析；（2）BE+CF的值是定值，为等边△ABC边长的一半．【解析】试题分析：（1）连结OB、OD，如图1，由于D为BC的中点，由垂径定理的推理得OD⊥BC，∠BOD=∠COD，即可得到∠BOD=∠M=60°，则∠OBD=30°，所以∠ABO=90°，于是得到AB是⊙O的切线；（2）作DM⊥AB于M，DN⊥AC于N，连结AD，如图2，由△ABC为正三角形，D为BC 的中点，得到AD平分∠BAC，∠BAC=60°，利用角平分线性质得DM=DN，得∠MDN=120°，由∠EDF=120°，得到∠MDE=∠NDF，于是有△DME≌△DNF，得到ME=NF，得到BE+CF=BM+CN，由BM=12BD，CN=12OC，得到BE+CF=12BC，即可判断BE+CF的值是定值，为等边△ABC边长的一半．试题解析：（1）连结OB、OD，如图1，∵D为BC的中点，∴OD⊥BC，∠BOD=∠COD，∴∠ODB=90°，∵∠BMC=12∠BOC，∴∠BOD=∠M=60°，∴∠OBD=30°，∵△ABC为正三角形，∴∠ABC=60°，∴∠ABO=60°+30°=90°，∴AB⊥OB，∴AB是⊙O的切线；（2）BE+CF的值是为定值．作DM⊥AB于M，DN⊥AC于N，连结AD，如图2，∵△ABC为正三角形，D为BC的中点，∴AD平分∠BAC，∠BAC=60°，∴DM=DN，∠MDN=120°，∵∠EDF=120°，∴∠MDE=∠NDF，在△DME和△DNF中，∵∠DME=∠DNF．DM=DN，∠MDE=∠NDF，∴△DME≌△DNF，∴ME=NF，∴BE+CF=BM﹣EM+CN+NF=BM+CN，在Rt△DMB中，∵∠DBM=60°，∴BM=12BD，同理可得CN=12OC，∴BE+CF=12OB+12OC=12BC，∴BE+CF的值是定值，为等边△ABC边长的一半．考点：1．切线的判定；2．等边三角形的性质；3．定值问题；4．探究型；5．综合题；6．压轴题．10．如图1，已知AB是⊙O的直径，AC是⊙O的弦，过O点作OF⊥AB交⊙O于点D，交AC于点E，交BC的延长线于点F，点G是EF的中点，连接CG(1)判断CG与⊙O的位置关系，并说明理由；(2)求证：2OB2＝BC•BF；(3)如图2，当∠DCE＝2∠F，CE＝3，DG＝2.5时，求DE的长．【答案】（1）CG与⊙O相切，理由见解析；（2）见解析；（3）DE＝2【解析】【分析】（1）连接CE，由AB是直径知△ECF是直角三角形，结合G为EF中点知∠AEO＝∠GEC＝∠GCE，再由OA＝OC知∠OCA＝∠OAC，根据OF⊥AB可得∠OCA+∠GCE＝90°，即OC⊥GC，据此即可得证；（2）证△ABC∽△FBO得BC ABBO BF=，结合AB＝2BO即可得；（3）证ECD∽△EGC得EC EDEG EC=，根据CE＝3，DG＝2.5知32.53DEDE=+，解之可得．【详解】解：（1）CG与⊙O相切，理由如下：如图1，连接CE，∵AB 是⊙O 的直径，∴∠ACB ＝∠ACF ＝90°，∵点G 是EF 的中点，∴GF ＝GE ＝GC ，∴∠AEO ＝∠GEC ＝∠GCE ，∵OA ＝OC ，∴∠OCA ＝∠OAC ，∵OF ⊥AB ，∴∠OAC +∠AEO ＝90°，∴∠OCA +∠GCE ＝90°，即OC ⊥GC ，∴CG 与⊙O 相切；（2）∵∠AOE ＝∠FCE ＝90°，∠AEO ＝∠FEC ，∴∠OAE ＝∠F ，又∵∠B ＝∠B ，∴△ABC ∽△FBO ， ∴BC AB BO BF=，即BO •AB ＝BC •BF ， ∵AB ＝2BO ，∴2OB 2＝BC •BF ；（3）由（1）知GC ＝GE ＝GF ，∴∠F ＝∠GCF ，∴∠EGC ＝2∠F ，又∵∠DCE ＝2∠F ，∴∠EGC ＝∠DCE ，∵∠DEC ＝∠CEG ，∴△ECD ∽△EGC ， ∴EC ED EG EC=， ∵CE ＝3，DG ＝2.5， ∴32.53DE DE =+，整理，得：DE 2+2.5DE ﹣9＝0，解得：DE ＝2或DE ＝﹣4.5（舍），故DE ＝2．【点睛】本题是圆的综合问题，解题的关键是掌握圆周角定理、切线的判定、相似三角形的判定与性质及直角三角形的性质等知识点．11．如图，已知在△ABC 中，∠A=90°，（1）请用圆规和直尺作出⊙P ，使圆心P 在AC 边上，且与AB ，BC 两边都相切（保留作图痕迹，不写作法和证明）．（2）若∠B=60°，AB=3，求⊙P 的面积．【答案】（1）作图见解析；（2）3π【解析】【分析】（1）与AB 、BC 两边都相切．根据角平分线的性质可知要作∠ABC 的角平分线，角平分线与AC 的交点就是点P 的位置．（2）根据角平分线的性质和30°角的直角三角形的性质可求半径，然后求圆的面积．【详解】解：（1）如图所示，则⊙P 为所求作的圆．（2）∵∠ABC=60°，BP 平分∠ABC ，∴∠ABP=30°，∵ ∠A=90°，∴BP=2APRt △ABP 中,AB=3，由勾股定理可得：3，∴S ⊙P =3π12．如图所示，AB 是半圆O 的直径，AC 是弦，点P 沿BA 方向，从点B 运动到点A ，速度为1cm/s ，若10AB cm ，点O 到AC 的距离为4cm ．（1）求弦AC的长；（2）问经过多长时间后，△APC是等腰三角形．【答案】（1）AC=6；（2）t=4或5或145s时，△APC是等腰三角形；【解析】【分析】（1）过O作OD⊥AC于D，根据勾股定理求得AD的长，再利用垂径定理即可求得AC的长；（2）分AC=PC、AP=AC、AP=CP三种情况求t值即可.【详解】（1）如图1，过O作OD⊥AC于D，易知AO=5，OD=4，从而AD==3，∴AC=2AD=6；（2）设经过t秒△APC是等腰三角形，则AP=10﹣t①如图2，若AC=PC，过点C作CH⊥AB于H，∵∠A=∠A，∠AHC=∠ODA=90°，∴△AHC∽△ADO，∴AC：AH=OA：AD，即AC： =5：3，解得t=s，∴经过s后△APC是等腰三角形；②如图3，若AP=AC，由PB=x，AB=10，得到AP=10﹣x，又∵AC=6，则10﹣t=6，解得t=4s，∴经过4s后△APC是等腰三角形；③如图4，若AP=CP，P与O重合，则AP=BP=5，∴经过5s后△APC是等腰三角形．综上可知当t=4或5或s时，△APC是等腰三角形．【点睛】本题是圆的综合题，解决问题利用了垂径定理，勾股定理等知识点，解题时要注意当△BPC是等腰三角形时，点P的位置有三种情况．13．如图，已知AB是⊙O的直径，P是BA延长线上一点，PC切⊙O于点C，CD⊥AB，垂足为D．（1）求证：∠PCA＝∠ABC；（2）过点A作AE∥PC交⊙O于点E，交CD于点F，交BC于点M，若∠CAB＝2∠B，CF 3【答案】（1）详见解析；（2633π-.【解析】【分析】（1）如图，连接OC ，利用圆的切线的性质和直径对应的圆周角是直角可得∠PCA=∠OCB ，利用等量代换可得∠PCA=∠ABC.（2）先求出△OCA 是等边三角形，在利用三角形的等边对等角定理求出FA=FC 和CF=FM,然后分别求出AM 、AC 、MO 、CD 的值，分别求出0A E S ∆、BOE S 扇形 、ABM S ∆ 的值，利用0A E ABM BOE S S S S ∆∆=+-阴影部分扇形，然后通过计算即可解答.【详解】解：（1）证明：连接OC ，如图，∵PC 切⊙O 于点C ，∴OC ⊥PC,∴∠PCA+∠ACO=90º,∵AB 是⊙O 的直径，∴∠ACB=∠ACO+OCB=90º∴∠PCA=∠OCB,∵OC=OB,∴∠OBC=∠OCB,∴∠PCA=∠ABC ；（2）连接OE ，如图，∵△ACB 中，∠ACB ＝90º,∠CAB ＝2∠B,∴∠B ＝30º,∠CAB ＝60º,∴△OCA 是等边三角形，∵CD ⊥AB,∴∠ACD+∠CAD ＝∠CAD ＋∠ABC ＝90º,∴∠ACD ＝∠B ＝30º,∵PC ∥AE,∴∠PCA ＝∠CAE ＝30º,∴FC=FA,同理，CF ＝FM,∴AM ＝2CF=3Rt △ACM 中，易得AC=33=3＝OC, ∵∠B ＝∠CAE ＝30º,∴∠AOC=∠COE=60º,∴∠EOB=60º,∴∠EAB=∠ABC=30º,∴MA=MB,连接OM,EG ⊥AB 交AB 于G 点，如图所示，∵OA=OB,∴MO ⊥AB,∴MO ＝OA×tan30º=3 , ∵△CDO ≌△EDO(AAS)， ∴EG=CD=AC×sin60º=332， ∴1332ABM S AB MO ∆=⨯=, 同样，易求93AOE S ∆=， 260333602BOE S ππ⨯==扇形 ∴0A E ABM BOE S S S S ∆∆=+-阴影部分扇形=93363333424ππ-+-=. 【点睛】本题考查了切线的性质、解直角三角形、扇形面积和识图的能力，综合性较强，有一定难度，熟练掌握定理并准确识图是解题的关键.14．如图，AB 为⊙O 的直径，DA 、DC 分别切⊙O 于点A ，C ，且AB =AD ．（1）求tan ∠AOD 的值．（2）AC ，OD 交于点E ，连结BE ．①求∠AEB 的度数；②连结BD 交⊙O 于点H ，若BC =1，求CH 的长．【答案】（1）2；（2）①∠AEB ＝135°；②2CH =【解析】【分析】 （1）根据切线的性质可得∠BAD=90°，由题意可得AD=2AO ，即可求tan ∠AOD 的值； （2）①根据切线长定理可得AD=CD ，OD 平分∠ADC ，根据等腰三角形的性质可得DO ⊥AC ，AE=CE ，根据圆周角定理可求∠ACB=90°，即可证∠ABC=∠CAD ，根据“AAS”可证△ABC≌△DAE，可得AE=BC=EC，可求∠BEC=45°，即可求∠AEB的度数；②由BC=1，可求AE=EC=1，BE2=，根据等腰直角三角形的性质可求∠ABE=∠HBC，可证△ABE∽△HBC，可求CH的长．【详解】（1）∵DA是⊙O切线，∴∠BAD=90°．∵AB=AD，AB=2AO，∴AD=2AO，∴tan∠AODADAO==2；（2）①∵DA、DC分别切⊙O于点A，C，∴AD=CD，OD平分∠ADC，∴DO⊥AC，AE=CE．∵AB是直径，∴∠ACB=90°，∴∠BAC+∠ABC=90°，且∠BAC+∠CAD=90°，∴∠ABC=∠CAD，且AB=AD，∠ACB=∠AED=90°，∴△ABC≌△DAE（AAS），∴CB=AE，∴CE=CB，且∠ACB=90°，∴∠BEC=45°=∠EBC，∴∠AEB=135°．②如图，∵BC=1，且BC=AE=CE，∴AE=EC=BC=1，∴BE2=．∵AD=AB，∠BAD=90°，∴∠ABD=45°，且∠EBC=45°，∴∠ABE=∠HBC，且∠BAC=∠CHB，∴△ABE∽△HBC，∴BC CHEB AE=，即12CH=，∴CH2=．【点睛】本题考查了切线的性质，圆周角定理，锐角三角函数，全等三角形的判定和性质，相似三角形的判定和性质，等腰三角形的性质等知识，灵活运用相关的性质定理、综合运用知识是解题的关键．15．如图，点B在数轴上对应的数是﹣2，以原点O为原心、OB的长为半径作优弧AB，使点A在原点的左上方，且tan∠AOB3C为OB的中点，点D在数轴上对应的数为4．（1）S扇形AOB＝（大于半圆的扇形）；（2）点P是优弧AB上任意一点，则∠PDB的最大值为°（3）在（2）的条件下，当∠PDB最大，且∠AOP＜180°时，固定△OPD的形状和大小，以原点O为旋转中心，将△OPD顺时针旋转α（0°≤α≤360°）①连接CP，AD．在旋转过程中，CP与AD有何数量关系，并说明理由；②当PD∥AO时，求AD2的值；③直接写出在旋转过程中，点C到PD所在直线的距离d的取值范围．【答案】（1）103π（2）30（3）①AD ＝2PC ②20+83或20+83③1≤d ≤3 【解析】【分析】 （1）利用扇形的面积公式计算即可．（2）如图1中，当PD 与⊙O 相切时，∠PDB 的值最大．解直角三角形即可解决问题． （3）①结论：AD ＝2PC ．如图2中，连接AB ，AC ．证明△COP ∽△AOD ，即可解决问题． ②分两种情形：如图3中，当PD ∥OA 时，设OD 交⊙O 于K ，连接PK 交OC 于H ．求出PC 即可．如图④中，当PA ∥OA 时，作PK ⊥OB 于K ，同法可得．③判断出PC 的取值范围即可解决问题．【详解】（1）∵tan ∠AOB ＝3，∴∠AOB ＝60°，∴S 扇形AOB ＝23002103603ππ⋅⋅= （大于半圆的扇形）， （2）如图1中，当PD 与⊙O 相切时，∠PDB 的值最大．∵PD 是⊙O 的切线，∴OP ⊥PD ，∴∠OPD ＝90°，∵21sin 42OP PDO OD ∠=== ∴∠PDB ＝30°， 同法当DP ′与⊙O 相切时，∠BDP ′＝30°，∴∠PDB 的最大值为30°．故答案为30．（3）①结论：AD ＝2PC ．理由：如图2中，连接AB ，AC ．∵OA ＝OB ，∠AOB ＝60°，∴△AOB 是等边三角形，∵BC ＝OC ，∴AC ⊥OB ，∵∠AOC ＝∠DOP ＝60°，∴∠COP ＝∠AOD ， ∵2AO OD OC OP==， ∴△COP ∽△AOD ， ∴2AD AO PC OC==， ∴AD ＝2PC ． ②如图3中，当PD ∥OA 时，设OD 交⊙O 于K ，连接PK 交OC 于H ．∵OP ＝OK ，∠POK ＝60°，∴△OPK 是等边三角形，∵PD ∥OA ，∴∠AOP ＝∠OPD ＝90°， ∴∠POH +∠AOC ＝90°， ∵∠AOC ＝60°，∴∠POH ＝30°，∴PH ＝12OP ＝1，OH 33， ∴PC 2222PH CH 1(13)523+=++=+ ∵AD ＝2PC ，∴AD2＝4（5+23）＝20+83．如图④中，当PA∥OA时，作PK⊥OB于K，同法可得：PC2＝12+（3﹣1）2＝5﹣23，AD2＝4PC2＝20﹣83．③由题意1≤PC≤3，∴在旋转过程中，点C到PD所在直线的距离d的取值范围为1≤d≤3．【点睛】本题属于圆综合题，考查了切线的性质，相似三角形的判定和性质，旋转变换，勾股定理，等边三角形的判定和性质等知识，解题的关键是学会用分类讨论的思想思考问题．。
2020-2021中考数学一模试题分类汇编——圆与相似综合附详细答案
2020-2021中考数学一模试题分类汇编——圆与相似综合附详细答案一、相似1．如图，在四边形ABCD中，AD//BC，，BC=4，DC=3，AD=6.动点P从点D出发，沿射线DA的方向,在射线DA上以每秒2两个单位长的速度运动，动点Q从点C出发，在线段CB上以每秒1个单位长的速度向点B运动，点P、Q分别从点D,C同时出发,当点Q运动到点B时，点P随之停止运动.设运动的时间为t(秒).（1）设的面积为，直接写出与之间的函数关系式是________（不写取值范围）.（2）当B,P,Q三点为顶点的三角形是等腰三角形时，求出此时的值.（3）当线段PQ与线段AB相交于点O，且2OA=OB时，直接写出 =________. （4）是否存在时刻，使得若存在，求出的值；若不存在,请说明理由.【答案】（1）（2）解：如图1，过点P作PH⊥BC于点H，∴∠PHB=∠PHQ=90°，∵∠C=90°，AD∥BC，∴∠CDP=90°，∴四边形PHCD是矩形，∴PH=CD=3，HC=PD=2t，∵CQ=t，BC=4，∴HQ=CH-CQ=t，BH=BC-CH=4-2t，BQ=4-t，∴BQ2= ，BP2= ，PQ2= ，由BQ2=BP2可得：，解得：无解；由BQ2=PQ2可得：，解得：；由BP2= PQ2可得：，解得：或，∵当时，BQ=4-4=0，不符合题意，∴综上所述，或；（3）（4）解：如图3，过点D作DM∥PQ交BC的延长线于点M，则当∠BDM=90°时，PQ⊥BD，即当BM2=DM2+BD2时，PQ⊥BD，∵AD∥BC，DM∥PQ，∴四边形PQMD是平行四边形，∴QM=PD=2t，∵QC=t,∴CM=QM-QC=t，∵∠BCD=∠MCD=90°，∴BD2=BC2+DC2=25，DM2=DC2+CM2=9+t2，∵BM2=(BC+CM)2=(4+t)2，∴由BM2=BD2+DM2可得：，解得：，∴当时，∠BDM=90°，即当时，PQ⊥BD.【解析】【解答】解：（1）由题意可得BQ=BC-CQ=4-t，点P到BC的距离=CD=3，∴S△PBQ= BQ×3= ；（ 3 ）解：如图2，过点P作PM⊥BC交CB的延长线于点M，∴∠PMC=∠C=90°，∵AD∥BC，∴∠D=90°，△OAP∽△OBQ，∴四边形PMCD是矩形，，∴PM=CD=3，CM=PD=2t，∵AD=6，BC=4，CQ=t，∴PA=2t-6，BQ=4-t，MQ=CM-CQ=2t-t=t,∴，解得：，∴MQ= ，又∵PM=3，∠PMQ=90°，∴tan∠BPQ= ；【分析】（1）点P作PM⊥BC，垂足为M，则四边形PDCM为矩形，根据梯形的面积公式就可以利用t表示，就得到s与t之间的函数关系式。
2020-2021初三数学一模试题分类汇编——相似综合附详细答案
2020-2021初三数学一模试题分类汇编——相似综合附详细答案一、相似1．如图，在平面直角坐标系中，直线y=﹣ x+ 与x轴、y轴分别交于点B、A，与直线y= 相交于点C．动点P从O出发在x轴上以每秒5个单位长度的速度向B匀速运动，点Q从C出发在OC上以每秒4个单位长度的速度，向O匀速运动，运动时间为t秒（0＜t＜2）．（1）直接写出点C坐标及OC、BC长；（2）连接PQ，若△OPQ与△OBC相似，求t的值；（3）连接CP、BQ，若CP⊥BQ，直接写出点P坐标．【答案】（1）解：对于直线y=﹣ x+ ，令x=0，得到y= ，∴A（0，），令y=0，则x=10，∴B（10，0），由，解得，∴C（，）．∴OC= =8，BC= =10（2）解：①当时，△OPQ∽△OCB，∴，∴t= ．②当时，△OPQ∽△OBC，∴，∴t=1，综上所述，t的值为或1s时，△OPQ与△OBC相似（3）解：如图作PH⊥OC于H．∵OC=8，BC=6，OB=10，∴OC2+BC2=OB2，∴∠OCB=90°，∴当∠PCH=∠CBQ时，PC⊥BQ．∵∠PHO=∠BCO=90°，∴PH∥BC，∴，∴，∴PH=3t，OH=4t，∴tan∠PCH=tan∠CBQ，∴，∴t= 或0（舍弃），∴t= s时，PC⊥BQ．【解析】【分析】（1）根据直线与坐标轴交点的坐标特点求出A,B点的坐标，解联立直线AB,与直线OC的解析式组成的方程组，求出C点的坐标，根据两点间的距离公式即可直接算出OC,OB的长；（2）根据速度乘以时间表示出OP=5t，CQ=4t，OQ=8-4t，①当OP∶OC=OQ∶OB时，△OPQ∽△OCB，根据比例式列出方程，求解得出t的值；②当OP∶OB=OQ∶OC时，△OPQ∽△OBC，根据比例式列出方程，求解得出t的值，综上所述即可得出t的值；（3）如图作PH⊥OC于H．根据勾股定理的逆定理判断出∠OCB=90°，从而得出当∠PCH=∠CBQ时，PC⊥BQ．根据同位角相等二直线平行得出PH∥BC，根据平行线分线段成比例定理得出OP∶OB=PH∶BC=OH∶OC,根据比例式得出PH=3t，OH=4t，根据等角的同名三角函数值相等及正切函数的定义，由tan∠PCH=tan∠CBQ，列出方程，求解得出t的值，经检验即可得出答案。
2020-2021九年级数学一模试题分类汇编——相似综合附答案
2020-2021九年级数学一模试题分类汇编——相似综合附答案一、相似1．在△ABC中，∠ABC=90°．（1）如图1，分别过A、C两点作经过点B的直线的垂线，垂足分别为M、N，求证：△ABM∽△BCN；（2）如图2，P是边BC上一点，∠BAP=∠C，tan∠PAC= ，求tanC的值；（3）如图3，D是边CA延长线上一点，AE=AB，∠DEB=90°，sin∠BAC= ，，直接写出tan∠CEB的值．【答案】（1）解：∵AM⊥MN，CN⊥MN，∴∠AMB=∠BNC=90°，∴∠BAM+∠ABM=90°，∵∠ABC=90°，∴∠ABM+∠CBN=90°，∴∠BAM=∠CBN，∵∠AMB=∠NBC，∴△ABM∽△BCN（2）解：如图2，过点P作PM⊥AP交AC于M，PN⊥AM于N.∵∠BAP+∠1=∠CPM+∠1=90°，∴∠BAP=∠CPM=∠C，∴MP=MC∵tan∠PAC=，设MN=2m,PN=m,根据勾股定理得，PM=,∴tanC=（3）解：在Rt△ABC中，sin∠BAC= = ，过点A作AG⊥BE于G，过点C作CH⊥BE交EB的延长线于H，∵∠DEB=90°，∴CH∥AG∥DE，∴ =同（1）的方法得，△ABG∽△BCH∴，设BG=4m，CH=3m，AG=4n，BH=3n，∵AB=AE，AG⊥BE，∴EG=BG=4m，∴GH=BG+BH=4m+3n，∴，∴n=2m，∴EH=EG+GH=4m+4m+3n=8m+3n=8m+6m=14m，在Rt△CEH中，tan∠BEC= =【解析】【分析】（1）根据垂直的定义得出∠AMB=∠BNC=90°，根据同角的余角相等得出∠BAM=∠CBN，利用两个角对应相等的两个三角形相似得出：△ABM∽△BCN；（2）过点P作PF⊥AP交AC于F，在Rt△AFP中根据正切函数的定义，由tan∠PAC=,同（1）的方法得，△ABP∽△PQF，故,设AB= a，PQ=2a，BP= b，FQ=2b（a＞0，b＞0），然后判断出△ABP∽△CQF，得从而表示出CQ，进根据线段的和差表示出BC，再判断出△ABP∽△CBA，得出再得出BC，从而列出方程，表示出BC,AB，在Rt△ABC中，根据正切函数的定义得出tanC的值；（3）在Rt△ABC中，利用正弦函数的定义得出：sin∠BAC=,过点A作AG⊥BE于G，过点C作CH⊥BE交EB的延长线于H，根据平行线分线段成比例定理得出，同（1）的方法得，△ABG∽△BCH ，故，设BG=4m，CH=3m，AG=4n，BH=3n，根据等腰三角形的三线合一得出EG=BG=4m，故GH=BG+BH=4m+3n，根据比例式列出方程，求解得出n与m的关系，进而得出EH=EG+GH=4m+4m+3n=8m+3n=8m+6m=14m，在Rt△CEH中根据正切函数的定义得出tan∠BEC的值。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2020-2021初三数学一模试题分类汇编——相似综合一、相似1．已知：如图，在△ABC中，AB=BC=10，以AB为直径作⊙O分别交AC，BC于点D，E，连接DE和DB，过点E作EF⊥AB，垂足为F，交BD于点P．（1）求证：AD=DE；（2）若CE=2，求线段CD的长；（3）在（2）的条件下，求△DPE的面积．【答案】（1）解：∵AB是⊙O的直径，∴∠ADB=90°，即BD⊥AC∵AB=BC，∴△ABD≌CBD∴∠ABD=∠CBD在⊙O中，AD与DE分别是∠ABD与∠CBD所对的弦∴AD=DE；（2）解：∵四边形ABED内接于⊙O，∴∠CED=∠CAB，∵∠C=∠C，∴△CED∽△CAB，∴，∵AB=BC=10，CE=2，D是AC的中点，∴CD= ；（3）解：延长EF交⊙O于M，在Rt△ABD中，AD= ，AB=10，∴BD=3 ，∵EM⊥AB，AB是⊙O的直径，∴，∴∠BEP=∠EDB，∴△BPE∽△BED，∴，∴BP= ，∴DP=BD-BP= ，∴S△DPE：S△BPE=DP：BP=13：32，∵S△BCD= × ×3 =15，S△BDE：S△BCD=BE：BC=4：5，∴S△BDE=12，∴S△DPE= ．【解析】【分析】（1）根据已知条件AB是⊙O的直径得出∠ADB=90°，再根据等腰三角形的三线合一的性质即可得出结论。
（2）根据圆内接四边形的性质证得∠CED=∠CAB，再根据相似三角形的判定证出△CED∽△CAB，得出对应边成比例，建立关于CD的方程，即可求出CD的长。
（3）延长EF交⊙O于M，在Rt△ABD中，利用勾股定理求出BD的长，再证明△BPE∽△BED，根据相似三角形的性质得对应边成比例求出BP的长，然后根据等高的三角形的面积之比等于对边之比，再由三角形面积公式即可求解。
2．（1）问题发现：如图1，在等边三角形ABC中，点M为BC边上异于B、C的一点，以AM为边作等边三角形AMN，连接CN，NC与AB的位置关系为________；（2）深入探究：如图2，在等腰三角形ABC中，BA=BC，点M为BC边上异于B、C的一点，以AM为边作等腰三角形AMN，使∠ABC=∠AMN，AM=MN，连接CN，试探究∠ABC与∠ACN的数量关系，并说明理由；（3）拓展延伸：如图3，在正方形ADBC中，AD=AC，点M为BC边上异于B、C的一点，以AM为边作正方形AMEF，点N为正方形AMEF的中点，连接CN，若BC=10，CN= ，试求EF的长．【答案】（1）NC∥AB（2）解：∠ABC=∠ACN，理由如下：∵ =1且∠ABC=∠AMN，∴△ABC～△AMN∴，∵AB=BC，∴∠BAC= （180°﹣∠ABC），∵AM=MN∴∠MAN= （180°﹣∠AMN），∵∠ABC=∠AMN，∴∠BAC=∠MAN，∴∠BAM=∠CAN，∴△ABM～△ACN，∴∠ABC=∠ACN（3）解：如图3，连接AB，AN，∵四边形ADBC，AMEF为正方形，∴∠ABC=∠BAC=45°，∠MAN=45°，∴∠BAC﹣∠MAC=∠MAN﹣∠MAC即∠BAM=∠CAN，∵，∴，∴△ABM～△ACN∴，∴ =cos45°= ，∴，∴BM=2，∴CM=BC﹣BM=8，在Rt△AMC，AM= ，∴EF=AM=2 ．【解析】【解答】解：（1）NC∥AB，理由如下：∵△ABC与△MN是等边三角形，∴AB=AC，AM=AN，∠BAC=∠MAN=60°，∴∠BAM=∠CAN，在△ABM与△ACN中，，∴△ABM≌△ACN（SAS），∴∠B=∠ACN=60°，∵∠ANC+∠ACN+∠CAN=∠ANC+60°+∠CAN=180°，∴∠ANC+∠MAN+∠BAM=∠ANC+60°+∠CAN=∠BAN+∠ANC=180°，∴CN∥AB；【分析】（1）由题意用边角边易得△ABM≌△ACN，则可得∠B=∠ACN=60°，所以∠BCN+∠B=∠BCA+∠ACN+∠B=180°，根据平行线的判定即可求解；（2）由题意易得△ABC～△AMN，可得比例式，由三角形内角和定理易得∠BAM=∠CAN，根据相似三角形的判定可得△ABM～△ACN，由相似三角形的性质即可求解；（3）要求EF的值，只须求得CM的值，然后解直角三角形AMC即可求解。
连接AB，AN，由正方形的性质和相似三角形的判定易得△ABM～△ACN，可得比例式，可求得BM的值，而CM=BC﹣BM，解直角三角形AMC即可求得AM的值，即为EF的值。
3．如图1，经过原点O的抛物线y=ax2+bx（a≠0）与x轴交于另一点A（，0），在第一象限内与直线y=x交于点B（2，t）．（1）求这条抛物线的表达式；（2）在第四象限内的抛物线上有一点C，满足以B，O，C为顶点的三角形的面积为2，求点C的坐标；（3）如图2，若点M在这条抛物线上，且∠MBO=∠ABO，在（2）的条件下，是否存在点P，使得△POC∽△MOB？若存在，求出点P的坐标；若不存在，请说明理由．【答案】（1）解：∵B（2，t）在直线y=x上，∴t=2，∴B（2，2），把A、B两点坐标代入抛物线解析式可得，解得，∴抛物线解析式为y=2x2﹣3x（2）解：如图1，过C作CD∥y轴，交x轴于点E，交OB于点D，过B作BF⊥CD于点F，∵点C是抛物线上第四象限的点，∴可设C（t，2t2﹣3t），则E（t，0），D（t，t），∴OE=t，BF=2﹣t，CD=t﹣（2t2﹣3t）=﹣2t2+4t，∴S△OBC=S△CDO+S△CDB= CD•OE+ CD•BF= （﹣2t2+4t）（t+2﹣t）=﹣2t2+4t，∵△OBC的面积为2，∴﹣2t2+4t=2，解得t1=t2=1，∴C（1，﹣1）（3）解：存在．设MB交y轴于点N，如图2，∵B（2，2），∴∠AOB=∠NOB=45°，在△AOB和△NOB中∴△AOB≌△NOB（ASA），∴ON=OA= ，∴N（0，），∴可设直线BN解析式为y=kx+ ，把B点坐标代入可得2=2k+ ，解得k= ，∴直线BN的解析式为y= x+ ，联立直线BN和抛物线解析式可得，解得或，∴M（﹣，），∵C（1，﹣1），∴∠COA=∠AOB=45°，且B（2，2），∴OB=2 ，OC= ，∵△POC∽△MOB，∴ = =2，∠POC=∠BOM，当点P在第一象限时，如图3，过M作MG⊥y轴于点G，过P作PH⊥x轴于点H，∵∠COA=∠BOG=45°，∴∠MOG=∠POH，且∠PHO=∠MGO，∴△MOG∽△POH，∴ = = =2，∵M（﹣，），∴MG= ，OG= ，∴PH= MG= ，OH= OG= ，∴P（，）；当点P在第三象限时，如图4，过M作MG⊥y轴于点G，过P作PH⊥y轴于点H，同理可求得PH= MG= ，OH= OG= ，∴P（﹣，）；综上可知存在满足条件的点P，其坐标为（，）或（﹣，）【解析】【分析】（1）根据已知抛物线在第一象限内与直线y=x交于点B（2，t），可求出点B的坐标，再将点A、B的坐标分别代入y=ax2+bx，建立二元一次方程组，求出a、b 的值，即可求得答案。
（2）过C作CD∥y轴，交x轴于点E，交OB于点D，过B作BF⊥CD于点F，可知点C、D、E、F的横坐标相等，因此设设C（t，2t2﹣3t），则E（t，0），D（t，t），F（t，2）,再表示出OE、BF、CD的长，然后根据S△OBC=S△CDO+S△CDB=2，建立关于t的方程，求出t 的值，即可得出点C的坐标。
（3）根据已知条件易证△AOB≌△NOB，就可求出ON的长，得出点N的坐标，再根据点B、N的坐标求出直线BN的函数解析式，再将二次函数和直线BN联立方程组，求出点M的坐标，求出OB、OC的长，再根据△POC∽△MOB，得出，∠POC=∠BOM，然后分情况讨论：当点P在第一象限时，如图3，过M作MG⊥y轴于点G，过P作PH⊥x 轴于点H，证△MOG∽△POH，得出对应边成比例，即可求出点P的坐标；当点P在第三象限时，如图4，过M作MG⊥y轴于点G，过P作PH⊥y轴于点H，同理可得出点P的坐标，即可得出答案。
4．如图（1），在矩形DEFG中，DE=3，EG=6，在Rt△ABC中，∠ABC=90°，BC=3，AC=6，△ABC的一边BC和矩形的一边DG在同一直线上，点C和点D重合，Rt△ABC将从D以每秒1个单位的速度向DG方向匀速平移，当点C与点G重合时停止运动，设运动时间为t秒，解答下列问题：（1）如图（2），当AC过点E时，求t的值；（2）如图（3），当AB与DE重合时，AC与EF、EG分别交于点M、N，求CN的长；（3）在整个运动过程中，设Rt△ABC与△EFG重叠部分面积为y，请求出y与t的函数关系式，并写出相应t的取值范围．【答案】（1）解：如图（2），当AC过点E时，在Rt△ABC中，BC=3，AC=6，∴BC所对锐角∠A=30°，∴∠ACB=60°，依题意可知∠ABC=∠EDC=90°，∵∠ACB=∠ECD，∴△ABC∽△EDC，∴，即，∴CD= ，∴t=CD= ；（2）解：如图（3），∵∠EDG=90°，DE=3，EG=6，∴DG= =3 ，在Rt△EDG中，sin∠EGD= ，∴∠EGD=30°，∵∠NCB=∠CNG+∠EGD，∴∠CNG=∠NCB﹣∠EGD=60°﹣30°=30°，∴∠CNG=∠EGD，∴NC=CG=DG﹣BC=3 ﹣3；（3）解：由（1）可知，当x＞时，△ABC与△EFG有重叠部分．分两种情况：①当＜t≤3时，如图（4），△ABC与△EFG有重叠部分为△EMN，设AC与EF、EG分别交于点M、N，过点N作直线NP⊥EF于P，交DG于Q，则∠EPN=∠CQN=90°，∵NC=CG，∴NC=DG﹣DC=3 ﹣t，在Rt△NQC中，NQ=sin∠NCQ×NC=sin60°×（3 ﹣t）= ，∴PN=PQ﹣NQ=3﹣ = ，∵∠PMN=∠NCQ=60°，∴sin∠PMN= ，MN= =t﹣，在矩形DEFG中，EF∥DG，∴∠MEN=∠CGN，∵∠MNE=∠CNG，∠CNG=∠CGN，∴∠EMN=∠MNE，∴EM=MN，∴EM=MN=t﹣，∴y=S△EMN= EM•PN= × ；②当3＜t≤3 时，如图（5），△ABC与△EFG重叠部分为四边形PQNM，设AB与EF、EG分别交于点P、Q，AC与EF、EG分别交于点M、N，则∠EPQ=90°，∵CG=3 ﹣t，∴S△EMN= ，∵EP=DB=t﹣3，∠PEQ=30°，∴在Rt△EPQ中，PQ=tan∠PEQ×EP=tan30°×（t﹣3）= ，∴S△EPQ= EP•PQ= （t﹣3）× = ，∴y=S△EMN﹣S△EPQ=（）﹣（）= +（﹣，综上所述，y与t的函数关系式：y= ．【解析】【分析】（1）证△ABC∽△EDC，由相似三角形的性质可求出CD的值，即可求t；（2）利用勾股定理求出DG的值，则由三角函数可∠EGD=30°，进而可证得∠CNG=∠EGD，则NC=CG=DG﹣BC，可求出答案；（3）根据重叠部分可确定x的取值范围，再由三角形的面积公式可求出函数解析式.5．定义：如图，若点D在的边AB上，且满足，则称满足这样条件的点为的“理想点”（1）如图，若点D是的边AB的中点，，，试判断点D是不是的“理想点”，并说明理由；（2）如图，在中，，，，若点D是的“理想点”，求CD的长；（3）如图，已知平面直角坐标系中，点，，C为x轴正半轴上一点，且满足，在y轴上是否存在一点D，使点A，B，C，D中的某一点是其余三点围成的三角形的“理想点” 若存在，请求出点D的坐标；若不存在，请说明理由.【答案】（1）解：结论：点D是的“理想点”.理由：如图中，是AB中点，，，，，，，，∽，，点D是的“理想点”，（2）解：如图中，点D是的“理想点”，或，当时，，，，当时，同法证明：，在中，，，，，，.（3）解：如图中，存在有三种情形：过点A作交CB的延长线于M，作轴于H.，，，，，，，≌，，，设，，，，，，，，，，解得或舍弃，经检验是分式方程的解，，，①当时，点A是的“理想点” 设，，，∽，，，解得，.②当时，点A是的“理想点”.易知：，，.③当时，点B是的“理想点”.易知：，，.综上所述，满足条件的点D坐标为或或 .【解析】【分析】（1）结论：点D是的“理想点” 只要证明∽即可解决问题；（2）只要证明即可解决问题；（3）如图中，存在有三种情形：过点A作交CB的延长线于M，作轴于构造全等三角形，利用平行线分线段成比例定理构建方程求出点C坐标，分三种情形求解即可解决问题；6．如图，在△ABC中，∠ACB=90°，AC=6cm，BC=8cm，点D从点C出发，以2cm/s 的速度沿折线C→A→B向点B运动，同时点E从点B出发，以1cm/s的速度沿BC边向点C运动，设点E运动的时间为t（单位：s）（0＜t＜8）.（1）当△BDE 是直角三角形时，求t的值；（2）若四边形CDEF是以CD、DE为一组邻边的平行四边形，①设它的面积为S，求S关于t的函数关系式；②是否存在某个时刻t，使平行四边形CDEF为菱形?若存在，求出t 的值；若不存在，请说明理由.【答案】（1）解：如图1，当∠BED=90°时，△BDE是直角三角形，则BE=t，AC+AD=2t，∴BD=6+10-2t=16-2t，∵∠BED=∠C=90°，∴DE∥AC，∴，∴，∴DE= ，∵sinB= ，∴，t= ；如图2，当∠EDB=90°时，△BDE是直角三角形，则BE=t，BD=16-2t，cosB= ，∴，∴t= ；答：当△BDE是直角三角形时，t的值为或（2）解：①如图3，当0＜t≤3时，BE=t，CD=2t，CE=8-t，∴S▱CDEF=2S△CDE=2× ×2t×（8-t）=-2t2+16t，如图4，当3＜t＜8时，BE=t，CE=8-t，过D作DH⊥BC，垂足为H，∴DH∥AC，∴，∴，∴DH= ，∴S▱CDEF=2S△CDE=2× ×CE×DH=CE×DH=（8-t）× = t2− t+ ；∴S于t的函数关系式为：当0＜t≤3时，S=-2t2+16t，当3＜t＜8时，S= t2− t+ ；②存在，如图5，当▱CDEF为菱形时，DH⊥CE，由CD=DE得：CH=HE，BH= ，BE=t，EH= ，∴BH=BE+EH，∴ =t+ ，∴t= ，即当t= 时，▱CDEF为菱形．【解析】【分析】（1）因为△BDE 是直角三角形有两种情况：①当∠BED=90°时，可得DE∥AC，根据平行于三角形一边的直线和其它两边（或其延长线）相交，所构成的三角形与原三角形相似可得,于是可得比例式将DE用含t的代数式表示，再根据sinB=可得关于t的方程，解方程即可求解；② 当∠EDB=90°时，同理可求解；（2）①当0＜t≤3时，S▱CDEF=2S△CDE可得s与t的关系式；当3＜t＜8时，过D作DH⊥BC，垂足为H，根据平行于三角形一边的直线和其它两边（或其延长线）相交，所构成的三角形与原三角形相似可得,于是可得比例式将DH用含t的代数式表示，则S▱CDEF=2S△CDE可得s与t的关系式；当3＜t＜8时，同上；②存在，当▱CDEF为菱形时，DH⊥CE，根据BH=BE+EH可得关于t的方程，解方程即可求解。