信号与系统matlab实验傅里叶分析及应用报告答案
信号与系统的傅立叶分析实验报告(共10篇)

信号与系统的傅立叶分析实验报告(共10篇)信号与系统实验报告周期信号的傅立叶级数分析信号与系统实验报告实验名称:姓学班时一、实验目的周期信号的傅立叶级数分析名:号:级:间:2013.4.191、掌握周期信号的频谱分析;2、学会对一般周期信号在时域上进行合成;二、实验基本原理在“信号与系统”中,任何周期信号只要满足狄利赫利条件就可以用傅立叶级数表示,即可分解成直流分量及一系列谐波分量之和。
以周期矩形脉冲信号为例,设周期矩形脉冲信号f~(t)的脉冲宽带为?,脉冲幅度为E,周期为T1,如图1.1所示。
图1.1 周期矩形脉冲信号的波形它可以展开成如下三角形式的傅立叶级数:E?2E?f(t)??T1T1~n?1?Sa()cosn?1t ?2n?1从上式可得出直流分量、基波及各次谐波分量的幅度:E?T12E?n??c?Sa()T2c0?1n1根据式(1-2)、(1-3)可以分别画出周期矩形脉冲信号三角形式表示的幅度谱和相位谱,如图1.2所示。
(a)(b)图1.2 周期矩形脉冲信号的频谱从上图中可以看出,周期矩形脉冲信号可以分解成无穷多个频率分量,也就是说,周期信号是由多个单一频率的正弦信号合成的,各正弦信号的频率n?1是周期信号频率?1的整数倍。
同样,任一周期信号也可以由一系列单一的频率分量按式(1-1)式所定的频率、幅度和相位进行合成。
理论上需要谐波个数为无限,但由于谐波幅度随着谐波次数的增加信号幅度减少,因而只需取一定数目的谐波数即可。
三、实验内容及结果1、周期方波信号的傅里叶级数分析(1)五路谐波分量的幅值1)一次谐波的波形(2)2)一、二次谐波合成的波形3)一、二、三次谐波合成的波形4)一、二、三、四次谐波合成的波形5)一、二、三、四、五次谐(3)画出周期方波信号的幅度谱波合成的波形篇二:实验一信号与系统的傅立叶分析实验一信号与系统的傅立叶分析一. 实验目的用傅立叶变换对信号和系统进行频域分析。
二.实验仪器装有matlab软件的计算机三.实验内容及步骤(1)已知系统用下面差分方程描述:y(n)?x(n)?ay(n?1)试在a?0.95和a?0.5两种情况下用傅立叶变换分析系统的频率特性。
信号与系统实验报告-傅立叶变换
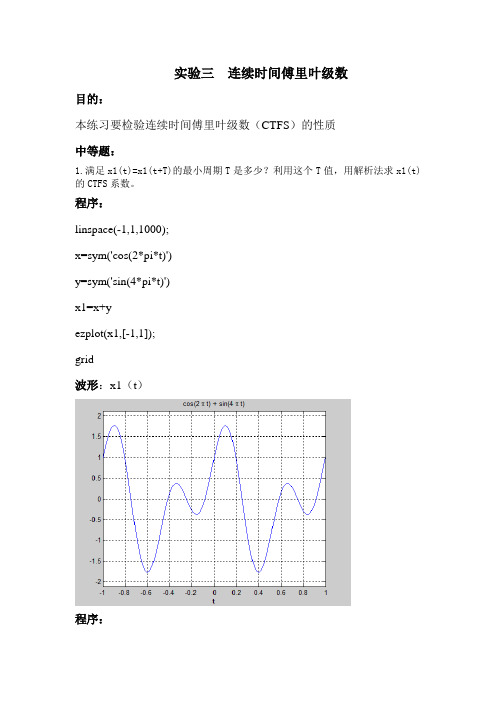
实验三连续时间傅里叶级数目的:本练习要检验连续时间傅里叶级数(CTFS)的性质中等题:1.满足x1(t)=x1(t+T)的最小周期T是多少?利用这个T值,用解析法求x1(t)的CTFS系数。
程序:linspace(-1,1,1000);x=sym('cos(2*pi*t)')y=sym('sin(4*pi*t)')x1=x+yezplot(x1,[-1,1]);grid波形:x1(t)程序:t=linspace(-1,1,1000);x=sym('cos(2*pi*t)')y=sym('sin(4*pi*t)')x1=x+yezplot(x1,[-1,1]);grid %可以从图形求出T=1 k=[-5:5]syms te=exp(-i*2*pi*t*k)f=x1*eFn=int(f,t,0,1);F=abs(Fn) %求Fn系数的绝对值subplot(1,2,1);Fn=double(Fn)subplot(1,2,1)stem(k,Fn)set(gca,'YLim',[-1 1.2])set(gca,'ytick',[0.1 0.2 0.3 0.4 0.5 0.6 1])set(gca,'xtick',[-5 -4 -3 -2 -1 0 1 2 3 4 5])gridF=double(F)subplot(1,2,2)stem(k,F)set(gca,'YLim',[-1 1.2])set(gca,'ytick',[0.1 0.2 0.3 0.4 0.5 0.6 1])set(gca,'xtick',[-5 -4 -3 -2 -1 0 1 2 3 4 5])grid波形:x1(t)的CTFS系数为Fn(左)以及其绝对值,比较可以得出虚部的系数。
信号与系统实验报告

信号与系统实验报告一、实验目的(1) 理解周期信号的傅里叶分解,掌握傅里叶系数的计算方法;(2)深刻理解和掌握非周期信号的傅里叶变换及其计算方法;(3) 熟悉傅里叶变换的性质,并能应用其性质实现信号的幅度调制;(4) 理解连续时间系统的频域分析原理和方法,掌握连续系统的频率响应求解方法,并画出相应的幅频、相频响应曲线。
二、实验原理、原理图及电路图(1) 周期信号的傅里叶分解设有连续时间周期信号()f t ,它的周期为T ,角频率22fT,且满足狄里赫利条件,则该周期信号可以展开成傅里叶级数,即可表示为一系列不同频率的正弦或复指数信号之和。
傅里叶级数有三角形式和指数形式两种。
1)三角形式的傅里叶级数:01212011()cos()cos(2)sin()sin(2)2cos()sin()2n n n n a f t a t a t b t b t a a n t b n t 式中系数n a ,n b 称为傅里叶系数,可由下式求得:222222()cos(),()sin()T T T T nna f t n t dtb f t n t dtTT2)指数形式的傅里叶级数:()jn tn nf t F e式中系数n F 称为傅里叶复系数,可由下式求得:221()T jn tT nF f t edtT周期信号的傅里叶分解用Matlab进行计算时,本质上是对信号进行数值积分运算。
Matlab中进行数值积分运算的函数有quad函数和int函数。
其中int函数主要用于符号运算,而quad函数(包括quad8,quadl)可以直接对信号进行积分运算。
因此利用Matlab进行周期信号的傅里叶分解可以直接对信号进行运算,也可以采用符号运算方法。
quadl函数(quad系)的调用形式为:y=quadl(‘func’,a,b)或y=quadl(@myfun,a,b)。
其中func是一个字符串,表示被积函数的.m文件名(函数名);a、b分别表示定积分的下限和上限。
快速傅里叶变换fft的Matlab实现 实验报告

一、实验目的1在理论学习的基础上,通过本实验加深对快速傅立叶变换的理解;2熟悉并掌握按时间抽取FFT算法的程序;3了解应用FFT进行信号频谱分析过程中可能出现的问题,例如混淆、泄漏、栅栏效应等,以便在实际中正确应用FFT。
二、实验内容1仔细分析教材第六章‘时间抽取法FFT’的算法结构,编制出相应的用FFT 进行信号分析的C语言(或MATLAB语言)程序;用MATLAB语言编写的FFT源程序如下:%%输入数据f、N、T及是否补零clc;clear;f=input('输入信号频率f:');N=input('输入采样点数N:');T=input('输入采样间隔T:');C=input('信号是否补零(补零输入1,不补零输入0):');%补零则输入1,不补则输入0if(C==0)t=0:T:(N-1)*T;x=sin(2*pi*f*t);b=0;e lseb=input('输入补零的个数:');while(log2(N+b)~=fix(log2(N+b)))b=input('输入错误,请重新输入补零的个数:');endt=0:T:(N+b-1)*T;x=sin(2*pi*f*t).*(t<=(N-1)*T);end%%fft算法的实现A=bitrevorder(x);%将序列按二进制倒序N=N+b;M=log2(N);%M为蝶形算法的层数W=exp(-j*2*pi/N);for L=1:1:M%第L层蝶形算法B=2^L/2;%B为每层蝶形算法进行加减运算的两个数的间隔K=N/(2^L);%K为每层蝶形算法中独立模块的个数for k=0:1:K-1for J=0:1:B-1p=J*2^(M-L);%p是W的指数q=A(k*2^L+J+1);%用q来代替运算前面那个数A(k*2^L+J+1)=q+W^p*A(k*2^L+J+B+1);A(k*2^L+J+B+1)=q-W^p*A(k*2^L+J+B+1);endendend%%画模特性的频谱图z=abs(A);%取模z=z./max(z);%归一化hold onsubplot(2,1,1);stem(0:1:N-1,x,'DisplayName','z');title('时域信号');subplot(2,1,2);stem(0:1:N-1,z,'DisplayName','z');title('频谱图');figure(gcf)%画图2用FFT 程序计算有限长度正弦信号()sin(2),0*y t f t t N Tπ=≤<分别在以下情况下所得的DFT 结果并进行分析和讨论:a )信号频率f =50Hz ,采样点数N=32,采样间隔T=0.000625sb )信号频率f =50Hz ,采样点数N=32,采样间隔T=0.005sT=0.0046875sc)信号频率f=50Hz,采样点数N=32,采样间隔051015202530350510152025303505101520253035 e)信号频率f=50Hz,采样点数N=64,采样间隔T=0.000625sg)将c)信号后补32个0,做64点FFT三、实验分析DFT是对有限序列做傅里叶变换后在频域上进行采样,而相对应的时域以频谱上的采样频率的倒数进行周期拓展。
MATLAB实验二 傅里叶分析及应用复习课程

M A T L A B实验二傅里叶分析及应用实验二傅里叶分析及应用一、实验目的(一)掌握使用Matlab进行周期信号傅里叶级数展开和频谱分析1、学会使用Matlab分析傅里叶级数展开,深入理解傅里叶级数的物理含义2、学会使用Matlab分析周期信号的频谱特性(二)掌握使用Matlab求解信号的傅里叶变换并分析傅里叶变换的性质1、学会运用Matlab求连续时间信号的傅里叶变换2、学会运用Matlab求连续时间信号的频谱图3、学会运用Matlab分析连续时间信号的傅里叶变换的性质(三)掌握使用Matlab完成信号抽样并验证抽样定理1、学会运用MATLAB完成信号抽样以及对抽样信号的频谱进行分析2、学会运用MATLAB改变抽样时间间隔,观察抽样后信号的频谱变化3、学会运用MATLAB对抽样后的信号进行重建二、实验条件Win7系统,MATLAB R2015a三、实验内容1、分别利用Matlab符号运算求解法和数值计算法求下图所示信号的FT,并画出其频谱图(包括幅度谱和相位谱)[注:图中时间单位为:毫秒(ms)]。
Code:ft = sym('(t+2)*(heaviside(t+2)-heaviside(t+1))+(heaviside(t+1)-heaviside(t-1))+(2-t)*(heaviside(t-1)-heaviside(t-2))');fw = simplify(fourier(ft));subplot(2, 1, 1);ezplot(abs(fw)); grid on;title('amp spectrum');phi = atan(imag(fw) /real(fw));subplot(2, 1, 2);ezplot(phi); grid on;符号运算法Code:dt = 0.01;t = -2: dt: 2;ft = (t+2).*(uCT(t+2)-uCT(t+1))+(uCT(t+1)-uCT(t-1))+(2-t).*(uCT(t-1)-uCT(t-2));N = 2000;k = -N: N;w = pi * k / (N*dt);fw = dt*ft*exp(-i*t'*w);fw = abs(fw);plot(w, fw), grid on;axis([-2*pi 2*pi -1 3.5]);t(20 π ex p(-3 t) heaviside(t) - 8 π ex p(-5 t) heaviside(t))/(2 π)数值运算法2、试用Matlab 命令求ωωωj 54-j 310)F(j ++=的傅里叶反变换,并绘出其时域信号图。
信号与系统matlab实验四

实验四 连续时间信号的傅立叶变换一、实验目的(1)掌握连续信号傅立叶变换与逆变换的计算方法(2)掌握利用MATLAB 实现连续时间信号傅立叶变换的方法二、实验内容1利用fourier()命令求解如下信号的傅立叶变换,给出)(t f 的波形图以及)(ωj F 的表达式和幅度频谱图:(1) 钟形脉冲:∞<<∞-=-t e t f t ,)(2)2(;(2)符号函数:⎩⎨⎧<->=0101)(t t t f)(ωF 的表达式:(1)22)(ωπω-=e F(2)ωωi F 2)(-=函数一程序如下:syms t v w x;x=exp(-(t/2)*(t/2));F=fourier(x);subplot(211);ezplot(x);subplot(212);ezplot(F);函数二:syms t v w x;x=Heaviside(t)-Heaviside(-t);F=fourier(x);subplot(211);ezplot(x,[-1,1]);subplot(212);ezplot(abs(F));运行结果如图:(1)(2)2求解如下信号的傅立叶变换,绘出信号的时域波形及幅度频谱图:(1) 升余弦脉冲:10)],cos(1[21)(≤≤+=t t t f π;(2)⎪⎩⎪⎨⎧><-=20221)(t t t t f)(ωF 的表达式:(1)()()[]πωπωωω++-+=Sa Sa Sa F 21)()( (2)()()222sin 22)(ωωωω==Sa F函数一:R=0.02;t=-1:R:1;f=1/2*(1+cos(pi*t));N=200;k=0:N;W=2*pi*k/(10*N*R);F=R*f*exp(-j*t'*W);F=real(F);W=[-fliplr(W),W(2:N+1)];F=[fliplr(F),F(2:N+1)];subplot(2,1,1);plot(t,f);xlabel('t');ylabel('f(t)');title('f(t)=u(t+1)-u(t-1)');axis([-1,1,-0.1,1.1]);subplot(2,1,2);plot(W,F);xlabel('w');ylabel('F(w)');title(' f(t)的傅氏变换F(w)');axis([-30,30,-0.1,1.1]);函数二:R=0.01;t=-2:R:2;f=(1-abs(t)/2);N=400;k=0:N;W=2*pi*k/(10*N*R);F=R*f*exp(-j*t'*W);F=real(F);W=[-fliplr(W),W(2:N+1)];F=[fliplr(F),F(2:N+1)];subplot(2,1,1);plot(t,f);xlabel('t');ylabel('f(t)');title('f(t)=(1-abs(t)/2)*[u(t+2)-u(t-2)]');axis([-2,2,-0.1,1.1]);subplot(2,1,2);plot(W,F);xlabel('w');ylabel('F(w)'); title('f(t)的傅氏变换F(w)'); axis([-25,25,-0.1,2.1]);运行结果如图:(1)(2)3已知)(1t f 的波形如下图所示且)()(11ωj F t f ↔;设)()(*)()(11ωj F t f t f t f ↔=,试用MATLAB 给出)(1t f 、)(t f 、)(1ωj F 及)(ωj F ,并验证时域卷积定理。
(完整版)信号与系统Matlab实验作业

(完整版)信号与系统Matlab实验作业实验一典型连续时间信号和离散时间信号一、实验目的掌握利用Matlab 画图函数和符号函数显示典型连续时间信号波形、典型时间离散信号、连续时间信号在时域中的自变量变换。
二、实验内容1、典型连续信号的波形表示(单边指数信号、复指数信号、抽样信号、单位阶跃信号、单位冲击信号)1)画出教材P28习题1-1(3) ()[(63)(63)]t f t e u t u t =----的波形图。
function y=u(t) y=t>=0; t=-3:0.01:3;f='exp(t)*(u(6-3*t)-u(-6-3*t))'; ezplot(f,t); grid on;2)画出复指数信号()()j t f t e σω+=当0.4, 8σω==(0<t<10)时的实部和虚部的< p="">波形图。
t=0:0.01:10;f1='exp(0.4*t)*cos(8*t)'; f2='exp(0.4*t)*sin(8*t)'; figure(1) ezplot(f1,t); grid on; figure(2) ezplot(f2,t); grid on;t=-10:0.01:10; f='sin(t)/t'; ezplot(f,t); grid on;t=0:0.01:10;f='(sign(t-3)+1)/2'; ezplot(f,t);grid on;5)单位冲击信号可看作是宽度为?,幅度为1/?的矩形脉冲,即t=t 1处的冲击信号为11111()()0 t t t x t t t otherδ??<<+?=-=画出0.2?=, t 1=1的单位冲击信号。
t=0:0.01:2;f='5*(u(t-1)-u(t-1.2))'; ezplot(f,t); grid on;axis([0 2 -1 6]);2、典型离散信号的表示(单位样值序列、单位阶跃序列、实指数序列、正弦序列、复指数序列)编写函数产生下列序列:1)单位脉冲序列,起点n0,终点n f,在n s处有一单位脉冲。
信号与系统MATLAB实验报告

一、实验名称MATLAB对连续信号与系统的时域分析、频域分析和s域分析;MATLAB对离散信号与系统的时域分析。
二、实验目的1.学习用MATLAB描述常用信号的方法。
2.掌握连续时间信号和离散时间信号的描述。
3.利用MATLAB计算信号卷积。
4.掌握信号频谱的定义,理解非周期信号频谱密度的概念。
5.掌握用MATLAB分析并绘制连续系统零极点图以判断因果系统稳定的方法。
三、实验原理1.连续系统的冲击响应和阶跃响应(1)连续系统的冲击响应在MATLAB中,利用函数impulse可求解系统冲击响应,其调y=impulse(sys,t)式中:sys表示LTI系统模型,用来表示微分方程、差分方程、状态方程。
利用函数tf获得微分方程的LTI系统模型,其调用形式为:sys=tf(b,a)式中:b和a分别为微分方程右端和左端的各项系数向量。
2.常用连续信号的傅里叶变换在MTLAB中,利用函数fourier实现信号f(t)的傅里叶变换,其调用形式是:F=fourier(f)(1)矩形脉冲矩形脉冲函数可以表示为:f(t)=AGr(t)=A, |t||<τ/2;f(t)=0, |t|>τ/2其傅里叶变换为F(jw)=Aτsa(wτ/2)式中:sa(·)表示采样函数。
3.连续系统函数H(s)的零极点分布和稳定性MATLAB信号处理工具箱提供的zplane函数可以直接求解H(s)的零极点分布,其调用形式为:zplane(b,a)式中:b和a分别为系统函数H(s)的分子多项式和分母多项式的系数向量,该函数的作用是在平面上画出单位圆及系统的零点和极点。
MATLAB信号处理工具箱提供的roots函数可求解多项式的根,其调用形式为:poles=roots(a)4.常用离散信号的MATLAB表示(1)正弦序列离散正弦信号与连续正弦信号类似,就是连续信号的离散型式。
正弦序列的一般序列为:f(k)=Acos(Ωk+φ)式中:A、Ω、φ分别为正弦序列的振幅、数字角频率和初相位。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验二傅里叶分析及应用姓名学号班级一、实验目的(一)掌握使用Matlab进行周期信号傅里叶级数展开和频谱分析1、学会使用Matlab分析傅里叶级数展开,深入理解傅里叶级数的物理含义2、学会使用Matlab分析周期信号的频谱特性(二)掌握使用Matlab求解信号的傅里叶变换并分析傅里叶变换的性质1、学会运用Matlab求连续时间信号的傅里叶变换2、学会运用Matlab求连续时间信号的频谱图3、学会运用Matlab分析连续时间信号的傅里叶变换的性质(三)掌握使用Matlab完成信号抽样并验证抽样定理1、学会运用MATLAB完成信号抽样以及对抽样信号的频谱进行分析2、学会运用MATLAB改变抽样时间间隔,观察抽样后信号的频谱变化3、学会运用MATLAB对抽样后的信号进行重建二、实验条件需要一台PC机和一定的matlab编程能力三、实验内容2、分别利用Matlab符号运算求解法和数值计算法求下图所示信号的FT,并画出其频谱图(包括幅度谱和相位谱)[注:图中时间单位为:毫秒(ms)]。
符号运算法:Ft= sym('t*(Heaviside(t+2)-Heaviside(t+1))+Heaviside(t+1)-Heaviside(t-1)+(-t)*(Heavi side(t-1)-Heaviside(t-2))');Fw = fourier(Ft);ezplot(abs(Fw)),grid on;phase = atan(imag(Fw)/real(Fw));ezplot(phase);grid on;title('|F|');title('phase');w+4 sin(w) w sin(lZ2 conj(f2 sin(1/2 cos(w)-nsin(1Z2 v^2-sin(w) w+4 sin(w) w sin(lZ2 w)2)/w*))/(2 (2 sin(1/2 w)2cos(w)+sin(l^0---------------------------------------------------------------4-6 ・2 0 2 4 6w3、试用Matlab命令求Fj ■)二103 j ■的傅里叶反变换,并绘出其时域信号图4 abs((2 sm(1/2 w)2c o s(w)+s i n(1 fi. w)2-sin(w) w+4 w sm(W 戒时3210[注意:⑴写代码时j i]abs((2 hBavisidB(l)-1) (5 exp(-3 i exp[-5 i t]))syms tFw = sym('10/(3+iw)-/(5+iw)'); ft = ifourier(Fw,t);F = abs(ft);ezplot(F,[-3,3]),grid on;4、已知门函数自身卷积为三角波信号,试用Matlab命令验证FT的时域卷积定理。
[注:即验证门函数FT的平方与相应三角波信号的FT后结果是否一致,可结合频谱图观察分析]Fw*Fw4 3 2 1 0wf = sym('Heaviside(t+1)-Heaviside(t-1)');Fw = simplify(fourier(f));F = Fw.*Fw;ezplot(abs(F)),grid ontitle('Fw*Fw');triangle = sym('(t+2)*Heaviside(t+2)-2*t*Heaviside(t)+(t-2)*Heaviside(t-2)'); Fttriangle = fourier (triangle);F = simplify (Fttriangle);ezplot(abs(F),[-6,6]),grid on;title('triangle FT');5、设有两个不同频率的余弦信号,频率分别为仏=100Hz , f^ 3800Hz ;现在使用抽样频率f s = 4000Hz对这三个信号进行抽样,使用MATLAB命令画出各抽样信号的波形和频谱,并分析其频率混叠现象[建议:抽样信号的频谱图横坐标范围不小于-10000Hz~10000Hz或-20000*pi~20000*pi rad/s]。
F1=100Hz M,实验代码如下:Ts=14000;dt=0.0001;t1=-0.006:dt:0.006; ft=cos(2*pi*100*t1);subplot(221);plot(t1,ft),grid on; axis([-0.006 0.006 -1.6 1.6]); xlabel('Time(sec)'),ylabel('f(t)') title('余弦信号波形');N=5000; k=-N:N;W=2*pi*k/((2*N+1)*dt);Fw=dt*ft*exp(-j*t1'*W); subplot(222);plot(W,abs(Fw));grid on;axis([-20000 20000 0 0.006]); xlabel('\omega'),ylabel('F(w)'); title(' 余弦信号的频谱'); t2=-0.006:Ts:0.006; fst=cos(2.*pi.*100*t2);subplot(223)plot(t1,ft,':'),hold on stem(t2,fst),grid on axis([-0.006 0.006 -1.5 1.5]) xlabel('Time (sec)'),ylabel('fs(t)') title(' 抽样后的信号'),hold off Fsw=Ts*fst*exp(-j*t2'*W);subplot(224) plot(W,abs(Fsw)),grid on axis([-20000 20000 0 0.006])xlabel('\omega'),ylabel('Fsw') title(' 抽样信号的频谱')F2=3800Hz 时,实验代码如下:Ts=14000; dt=0.0001;t 仁-0.006:dt:0.006; ft=cos(2*pi*3800*t1); subplot(221);plot(t1,ft),grid on; axis([-0.006 0.006 -1.6 1.6]); xlabel('Time(sec)'),ylabel('f(t)') title('余弦信号波形');N=5000; k=-N:N; W=2*pi*k/((2*N+1)*dt);Fw=dt*ft*exp(-j*t1'*W); subplot(222); plot(W,abs(Fw)); grid on;axis([-20000 20000 0 0.006]); xlabel('\omega'),ylabel('F(w)'); title('余弦信号的频谱'); t2=-0.006:Ts:0.006; fst=cos(2.*pi.*100*t2);64Ll_21A ___________ ■ ___ __i ■ i i i ■ i4r I i ■ 1~ —八 丁 八-=—1> 1 1 A |■丄I L Bu-6 0 5 Time(sec) x 让 抽样后的信号余弦信号液形買1屮余弦信号的频谱-2-10120 5 Time (sec)x 10'3北1代抽样信号的频谱subplot(223)plot(t1,ft,':'),hold on stem(t2,fst),grid onaxis([-0.006 0.006 -1.5 1.5]) xlabel('Time (sec)'),ylabel('fs (t )') title('抽样后的信号'),hold off Fsw=Ts*fst*exp(-j*t2'*W);subplot(224) plot(W,abs(Fsw)),grid on axis([-20000 20000 0 0.006]) xlabel('\omega'),ylabel('Fsw') title('抽样信号的频谱')(六)结合抽样定理,利用MATLAB 编程实现Sa(t)信号经过冲激脉冲抽样后得到的抽样信 号f s t 及其频谱[建议:冲激脉冲的周期分别取 4*pi/3 s 、pi s 、2*pi/3 s 三种情况对比],并 利用f s t 构建Sa(t)信号。
周期取4*pi/ 3 s:\ I \II||余弦信号液形Time(sec)抽样启的信号61屮抽样信号的频谱L JL2-10 12①x 104出(t)抽样信的信号0.5 -0 —_i --------- ----- iL.*I1I* 九心5——-;——;——[——||■ I I 4 I I1I■1 ---------- ' ---------- ----------- ■ --------- -4-2024Time (sec)由代订司信号重建得到 现)信号Saffltt 样信号的频谱105CA ■L周期取pi s :wm=2; wc=1.2*wm; Ts=4*pi/3; dt=0.1; t 仁-4:dt:4;ft=sinc(ti/pi).*( heaviside (ti+io )- heaviside (ti-10)); N=500; k=-N:N;W=2*pi*k/((2*N+1)*dt); n=-100:100; nTs=n *Ts;fst=s inc(n Ts/pi).*( heaviside ( nTs+10)- heaviside ( nTs-10)); subplot(221); plot(t1,ft,':'),hold on stem (n Ts,fst),grid on axis([-4 4 -1 1]);xlabel('Time (sec)'),ylabel('fs (t )')-10-5 0 5 10*10 -5 051100?title('Sa(t)抽样后的信号'),hold off; Fsw=Ts*fst*exp(-j* nTs'*W); subplot(222)11plot(W,abs(Fsw),'c'),grid onaxis([-10 10 -3 10])xlabel('\omega'),ylabel('Fsw')title('Sa(t)抽样信号的频谱')t=-1O:dt:1O;f=fst*Ts*wc/pi*si nc((wc/pi)*(o nes(le ngth( nTs),1)*t-nTs'*o nes(1,le ngth(t)))); subplot(223);plot(t,f,'m:'),grid on;axis([-10 10 -2 9]);xlabel('t'),ylabel('f(t)');title('由f(nTs)信号重建得到Sa(t)信号');周期取2*pi/3 s :实验代码如下:wm=2;wc=1.2*wm;Ts=2*pi/3;dt=0.1;t1=-4:dt:4;ft=si nc(t1/pi).*( heaviside (t1+10)- heaviside (t1-10));N=500;k=-N:N;W=2*pi*k/((2*N+1)*dt);n=-100:100;丸⑴抽样启的信号 ---------------------------- ' --------------------- 7^ i * ii ■ d * i *%*■ ■■■■■■ ■■严■ "i z 1 * i* Nili|■1= - J _____ ______ J ______ --亠 M iil 4 q <i ii10*10 10 1 1 ■1 ri i■1>1il■■■■■■J ■■■■■■■■1 ilil■1 dil ■i E ■-厂一 ■■•苗 d Iil J小 八 ・―■ — N L W 手■=■ h 齐'b — !l ' • i *■||1I-■=「F " X.d",二書■齐皤■亠■ •0.5 C 0-0 5 5-5 0 56 8 2 0 ■4-2024 Time (sec) 由f(nT£)信号重建得到酮①信号12 nTs=n *Ts;fst=sinc(nTs/pi).*( heaviside (nTs+10)- heaviside (nTs-10)); subplot(221);plot(t1,ft,':'),hold onstem(nTs,fst),grid onaxis([-4 4 -1 1]);xlabel('Time (sec)'),ylabel('fs (t )')title('Sa(t)抽样后的信号'),hold off;Fsw=Ts*fst*exp(-j* nTs'*W);subplot(222) plot(W,abs(Fsw),'c'),grid on axis([-10 10 -3 10])xlabel('\omega'),ylabel('Fsw') title('Sa(t)抽样信号的频谱') t=-10:dt:10;f=fst*Ts*wc/pi*si nc((wc/pi)*(o nes(le ngth( nTs),1)*t- nTs'*o nes(1,length(t)))); subplot(223);plot(t,f,'m:'),grid on;axis([-10 10 -2 9]);xlabel('t'),ylabel('f(t)');title(' 由 f(nTs 信号重建得到Sa(t)信号');出(t)抽样信的信号射①抽样信号的频谱 5 0 -5 0 5 110 o Time (sec)由信号重建得到SaffliS 号86e 42四、实验结论和讨论信号的时域与频域呈离散与周期的对应关系。
