勾股定理的方程思想
勾股定理的公式,勾股定理的公式是什么 怎么计算

勾股定理的公式,勾股定理的公式是什么怎么计算勾股定理的公式,勾股定理的公式是什么怎么计算?-华宇考试网在平面上的一个直角三角形中,两个直角边边长的平方加起来等于斜边长的平方。
假设设直角三角形的两条直角边长度分别是和,斜边长度是,既然如此那,可以用数学语言表达:勾股定理是余弦定理中的一个特例。
勾股定理的证明请看下方具体内容答:勾股定理公式:a的平方+b的平方=c的平方。
勾股定理:在任何一个平面直角三角形中的两直角边的平方之和一定等于斜边的平方。
在△abc中,∠c=90°,则a²+b²=c²。
勾股定理是几何学中一颗光彩夺目标明珠,被称为“几何学的基石”,而且,在高等数学和其他学科中也有着非常广泛的应用。
1发展历程中国是发现和研究勾股定理古老的国家之一。
中国古代数学家称直角三角形为勾股形,较短的直角边称为勾,另一直角边称为股,斜边称为弦,故此,勾股定理也称为勾股弦定理。
在公元前1000多年,据记载,商高(约公元前1120年)答周公曰“故折矩,以为勾广三,股修四,径隅五。
既方之,外半其一矩,环而共盘,得成三四五。
两矩共长二十有五是谓积矩。
”因为这个原因,勾股定理在中国又称“商高定理”。
在公元前7至6世纪一中国学者陈子,曾经给出过任意直角三角形的三边关系:以日下为勾,日高为股,勾、股各乘并开方除之得斜至日。
2主要意义1、勾股定理是联系数学中基本也是原始的两个对象-数与形的第一定理。
2、勾股定理致使不可通约量的发现,以此深入透彻揭示了数与量的区别,即这里说的“无理数与有理数的差别,那就是这里说的首次数学危机。
3、勾股定理启动把数学由计算与测量的技术转变为证明与推理的科学。
4、勾股定理中的公式是第一个不定方程,也是早得出完整解答的不定方程,它一个方面引导到各式各样的不定方程,另外一个方面也为不定方程的解题程序培养了一个范式。
两条直角边的平方和等于斜边的平方勾股定理计算:直角三角形的两条直角边的平方和等于斜边的平方。
勾股定理

第1讲勾股定理第一部分知识梳理1.勾股定理:直角三角形的两直角边的平方和等于斜边的平方。
若直角三角形的两条直角边为a、b,斜边为c,则a²+b²=c²。
2.勾股定理的逆定理:如果三角形的三边长a,b,c有下面关系:a²+b²=c²,那么这个三角形是直角三角形。
3.满足a²+b²=c²的三个正整数,称为勾股数。
若a,b,c是一组勾股数,则ak,bk,ck(k为正整数)也必然是一组勾股数。
常用的几组勾股数有3,4,5;5,12,13;6,8,10;7,24,25;8,15,17;9,40,41等。
4.勾股定理的应用:①圆柱形物体表面上的两点间的最短距离;②长方体或正方体表面上两点间的最短距离问题。
5.直角三角形的判别:①定义,判断一个三角形中有一个角是直角;②根据勾股定理的逆定理,三角形一边的平方等于另外两边的平方和,则该三角形是直角三角形。
6.勾股定理中的方程思想:勾股定理三角形有一个直角的“形”的特征,转化为三边“数”的关系,因此它是数形结合的一个典范.对于一些几何问题,往往借助于勾股定理,利用代数方法来解决.把一条边的长设为未知数,根据勾股定理列出方程,解方程求出未知数的值,即使有时出现了二次方程,大多可通过抵消而去掉二次项。
7.勾股定理中的转化思想:在利用勾股定理计算时,常先利用转化的数学思想构造出直角三角形,比如立体图形上两点之间的最短距离的求解,解答时先把立体图形转化为平面图形,在平面图形中构造直角三角形求解。
8.拓展:特殊角的直角三角形相关性质定理。
第二部分精讲点拨考点1. 勾股定理【例1】在Rt△ABC中,已知两边长为3、4,则第三边的长为变式1 等腰三角形的两边长为10和12,则周长为______,底边上的高是________,面积是_________。
变式2 等边三角形的边长为6,则它的高是________变式3 在Rt△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C所对的边,(1)已知c=4,b=3,求a;(2)若a:b=3:4,c=10cm,求a、b。
公开课-勾股定理中的方程思想

《勾股定理中的方程思想》教学设计
(七)作业布置.(多媒体课件11和12)1、、有一根高为16米的电线杆在点A 处断裂,电线杆顶部C落到离电线杆底部B点8米远的地方,求电线杆的断裂处A离地面的距离。
2、在一棵树BD的5m高A处有两只小猴子,其中一只猴子爬到树顶D后跳到离树10m的地面C处,另外一只猴子爬下树后恰好也走到地面C处,如果两个猴子经过的距离相等,
问这棵树有多高?
小溪边长着两棵树,恰好隔岸相望,一棵树高30尺,另外一棵树高20尺;
两棵树干间的距离是50尺,每棵树
上都停着一只鸟,忽然两只鸟同时
看到两树间水面上游出一条鱼,它
们立刻以同样的速度飞去抓鱼,结
果同时到达目标。
问这条鱼出现在
两树之间的何处?学案上完成
加强知识的应用。
巩固知
识。
数学勾股定理论文

数学勾股定理论文勾股定理是数学史上一个伟大的定理,同时也是一个历史悠久的定理.下面店铺给你分享数学勾股定理论文,欢迎阅读。
数学勾股定理论文篇一数学思想是数学知识的精髓,又是把知识转化为能力的桥梁.灵活运用数学思想,能够有效地提高分析问题和解决问题的能力,增强应用数学知识的意识.在《勾股定理》这一章中,蕴含着许多重要的数学思想,现举例介绍如下.一、方程思想在含有直角三角形的图形中,求线段的长往往要使用勾股定理,如果无法直接用勾股定理来计算,则需要列方程解决.二、化归思想化归思想就是通过一定的方法或途径,把需要解决的问题变换形式,变化成另一类已经解决或易于解决的问题,从而使原来的问题得到解决.例3如图3,长方体的长为15cm,宽为10cm,高为20cm.点B 与点C的距离为5cm,一只蜗牛如果要沿着长方体的表面从点A爬到点B,需爬行的最短路程是多少?分析:由于蜗牛是沿着长方体的表面爬行的,故需把长方体展开成平面图形.根据两点之间线段最短,蜗牛爬行的较短路程有两种可能,如图4、图5所示.利用勾股定理容易求出两种图中AB的长度,比较后即可求得蜗牛爬行的最短路程是25cm.说明:这里通过长方体的展开图,把立体图形转化为平面图形,把求蜗牛爬行的最短路程问题化归成利用勾股定理求两点间的距离问题.例4如图6,是一块四边形的草地ABCD,其中∠A = 60O,∠B =∠D = 90O,AB = 20m,CD = 10m,求AD、BC的长(精确到0.1m,≈1.732).(2004年天津市中考题)分析:图中无直角三角形,怎么办?联想到含30O角的直角三角形,因而延长AD、BC交于点E,则∠E = 30O,AE = 2AB = 40m,CE = 2CD = 20m. 由勾股定理得DE == m,BE == m,所以AD = 40≈22.7m,BC = 20≈14.6m.说明:本题充分利用已知图形的特点,通过构造新图形,将四边形问题巧妙地转化成了直角三角形问题.三、数形结合思想数形结合,就是抓住数与形之间本质上的联系,将抽象的数学语言与直观的图形结合起来,通过“以形助数”或“以数解形”,使复杂问题简单化、抽象问题具体化,从而达到迅速解题的目的.例5在一棵树的10m高处有两只猴子,其中一只爬下树直奔离树20m的池塘,而另一只爬到树顶后直扑池塘,如果两只猴子经过的距离相等,问这棵树有多高?(2005年福建省龙岩市中考题)分析:依题意画出示意图7,D为树顶,AB = 10m,C为池塘,AC = 20m. 设BD = (m),则树高AD = ( +10)m.因为AC + AB = BD + DC,所以DC = (30)m. 在Rt△ACD中,由勾股定理可得方程202 + ( + 10)2 = (30)2,解得 = 5,所以 +10 = 15,即树高15m.说明:勾股定理本身就是数形结合的一个典范,它把直角三角形有一个直角的“形”的特点,转化为三边“数”的关系.利用勾股定理解决实际问题,关键是利用数形结合思想将实际问题转换成直角三角形模型,再利用方程来解决.四、分类讨论思想在解题过程中,当条件或结论不确定或不惟一时,往往会产生几种可能的情况,这就需要依据一定的标准对问题进行分类,再针对各种不同的情况分别予以解决.最后综合各类结果得到整个问题的结论.分类讨论实质上是一种“化整为零,各个击破,再积零为整”的数学方法.例6 一直角三角形的两边长分别为3cm、4cm,则第三边的长为______.分析:此题中已知一个直角三角形的两边长,并没有指明是直角边还是斜边,因此要分类讨论,答案是5cm或cm.例7“曙光中学”有一块三角形形状的花圃ABC,现可直接测量到∠A = 30O,AC = 40米,BC = 25米,请你求出这块花圃的面积. (2003年黑龙江省中考题)分析:由于题目中没有明确告诉我们△ABC的形状,故需分两种情况讨论.在图8中,S△ABC=10 (20 + 15)米2;在图9中,S△ABC= 10(2015)米2.说明:此类问题由于题目中没有图形,常需分类讨论,解答时极易因考虑不周而导致漏解,希望同学们用心体会.五、整体思想对于某些数学问题,如果拘泥常规,从局部着手,则难以求解;如果把问题的某个部分或几个部分看成一个整体进行思考,就能开阔思路,较快解答题目.例8已知一个直角三角形的周长为30cm,斜边长为13cm,那么这个三角形的面积为______.分析:设这个直角三角形的两条直角边长为,斜边为,则= 3013 = 17,于是( + )2 = 2 + 2 + 2 = 172 = 289,由勾股定理知2 + 2 = 289,即132+ 2 = 289,所以 = 60,故所求三角形面积S == 30cm2.说明:我们要求的是面积,即,不一定要分别求出和的值,只要从整体上求出即可.例9 如图10所示,在直线上依次摆放着七个正方形.已知斜放置的三个正方形的面积分别是1,2,3,正放置的四个正方形的面积依次是S1,S2,S3,S4,则S1 + S2 + S3 + S4 = ______.(2005年浙江省温州市中考题)分析:根据已知条件可知AC = EC,∠ABC = ∠CDE = 90O,由角的互余关系易证∠ACB =∠CED,这样可得△ABC ≌ △CDE,所以BC = ED,在Rt△ABC中,由勾股定理,得AC2 = AB2 + BC2 = AB2 + DE2.由S1 = AB2,S2 = DE2,AC2 = 1,有S1 + S2 = 1,同理可得S3 + S4 = 3,所以S1+ S2 + S3 + S4 = 1+3 = 4.说明:本题不是直接求出S1,S2,S3,S4,而是借助勾股定理求得S1 + S2,S3 +S4,体现了整体思想在解决问题中的灵活应用.数学勾股定理论文篇二数学思想方法是以具体数学内容为载体,又高于具体数学内容的一种指导思想和普遍适用的方法.它能使人领悟到数学的真谛,并对人们学习和应用数学知识解决问题的思维活动起着指导和调控的作用.日本数学教育家米山国藏认为,学生在进入社会以后,如果没有什么机会应用数学,那么作为知识的数学,通常在出校门后不到一两年就会忘掉,然而不管他们从事什么业务工作,那种铭刻在人脑中的数学精神和数学思想方法,会长期地在他们的生活和工作中发挥重要作用.灵活运用数学思想方法解决问题,往往可以化难为易、化腐朽为神奇,事半功倍.下面以勾股定理中渗透的数学思想为例说明.一、分类思想例1.(2013年贵州黔西南州)一直角三角形的两边长分别为3和4,则第三边的长为( )点评:本题的易错点是受“勾三股四弦五”的影响,直接把边长为4的边当作直角边,从而误选A,犯了考虑问题不全面的错误.二、方程思想例2.(2013年山东济南)如图1,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端距离地面2m,则旗杆的高度(滑轮上方的部分忽略不计)为()A.12mB.13mC.16mD.17m分析:观察图形,当绳子末端拉到距离旗杆8m处,可过绳子末端向旗杆作垂线,这样可以得到一个直角三角形,然后设旗杆的高度为未知数,进而运用勾股定理列方程求解.解:如图2,设旗杆的高度为x,则AC=AD=x,AB=x-2,BC=8.在Rt△ABC中,由勾股定理,得(x-2)2+82=x2.解得x=17m,即旗杆的高度为17m,答案选D.三、整体思想例3.(2013年江苏扬州)矩形的两邻边长的差为2,对角线长为4,则矩形的面积为____________.分析:设矩形的两邻边长分别为a、b(a>b),则依据题意有a-b=2,a2+b2=16.而矩形的面积等于ab,关键要设法将两个等式转化为含有ab的式子.解:设矩形的两邻边长分别为a、b (a>b),则a-b=2.五、数形结合思想例5.(2013年湖南张家界)如图4,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(10,0)、(0,4),点D是OA的中点,点P在BC上运动.当△ODP是腰长为5的等腰三角形时,点P的坐标为________.分析:易知OD=5,要使△ODP为腰长为5的等腰三角形,可以点O为圆心,OD为半径作圆;也可以点D为圆心,OD为半径作圆.解:由C(10,0)可知OD=5.(1)以点O为圆心,OD为半径作圆交边六、构造思想例6.同例3分析:根据已知条件,联想到证明勾股定理的弦图,本例便有如下巧妙解法.数学勾股定理论文篇三正确的数学思想是成功解题的关键所在.在运用勾股定理解题时,若能正确把握数学思想,则可使思路开阔,方法简便快捷.下面列举在应用勾股定理时经常用到的数学思想,供同学们参考.一、方程思想◆例1如图1,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上且点C落到E点,则CD等于( ).A.2cmB.3cmC.4cmD.5cm分析:由题意可知,ΔACD 和ΔAED关于直线AD对称,因而有ΔACD ≌ΔAED .进一步则有AE=AC=6cm,CD=ED,DE⊥AB.设CD=ED=xcm,则在ΔDEB中,由勾股定理可得DE2+BE2=BD2.又因在ΔABC中,AB2=AC2+BC2=62+82=100,得AB=10.所以有x2+(10- 6) 2=(8- x)2,解得x=3.故选B.二、转化思想◆例2如图2,长方体的高为3cm,底面是正方形,边长为2cm.现有一小虫从A出发,沿长方体表面爬行,到达C处,问小虫走的路程最短为多少厘米?分析:求几何体表面最短距离问题,通常可将几何体表面展开,把立体图形转化为平面图形.对于此题,可将该长方体的右表面翻折至前表面,使A、C两点共面,连结AC,线段AC的长度即为最短路程(如图3).由勾股定理可知AC2=32+42=52,即小虫所走的最短路程为5cm.三、分类讨论思想◆例3在ΔABC中,AB=15,AC=20,BC边上的高AD=12,试求BC的长.分析:三角形中某边上的高既可在三角形内部,也可在三角形的外部,故此题应分两种情况来考虑.当BC边上的高AD在ΔABC的内部时,如图4,由勾股定理得BD2=AB2-AD2,得BD=9;CD2=AC2-AD2,得CD=16,则BC=BD+CD=9+16=25;当BC上的高AD在ΔABC的外部时,如图5,同样由勾股定理可求得CD=16,BD=9,这时,BC=CD-BD=16- 9=7,故BC的长为25或7.四、数形结合思想勾股定理本身就是数形结合的定理,它的验证和应用,都体现了数形结合的思想.这里不再举例,请同学们在平时的练习中仔细体会.。
勾股定理解方程

勾股定理解方程
勾股定理解方程是数学中的一个经典问题,其主要思想是利用勾股定理来解决方程的求解问题。
勾股定理指出,在一个直角三角形中,直角边的平方和等于斜边的平方。
换句话说,如果三角形的直角边长度分别为 a 和 b,斜边长度为 c,那么有:
a2 + b2 = c2
这是一个关于 c 的二次方程,可以使用勾股定理解方程方法来解决。
具体来说,可以将方程变形为:
c2 = a2 + b2 - 2ab cosC
其中 C 是直角三角形的斜边与一条直角边之间的角度差,即 C =
arctan(b/a)。
然后将方程两边同时除以 a2 + b2,得到:
c = sqrt(a2 + b2) / (a2 + b2)
这意味着,如果我们有一个二次方程,其根为 c,那么我们可以使用勾股定理解方程方法来求解 c 的值。
例如,考虑以下方程:
x2 + 2x + 1 = 0
这个方程有一个解为 x = 1,我们可以使用勾股定理解方程方法来解决: c2 = x2 + 2x + 1
c2 = 1 + 2 + 1
c2 = 5
因此,c 的值为 sqrt(5)。
勾股定理解方程方法的主要思想是利用勾股定理将方程转化为一个关于 c
的二次方程,然后求解 c 的值。
这种方法可以用于解决许多不同类型的方程,特别是在解决线性方程组时非常有用。
勾股定理(毕达哥拉斯定理)及各种证明方法
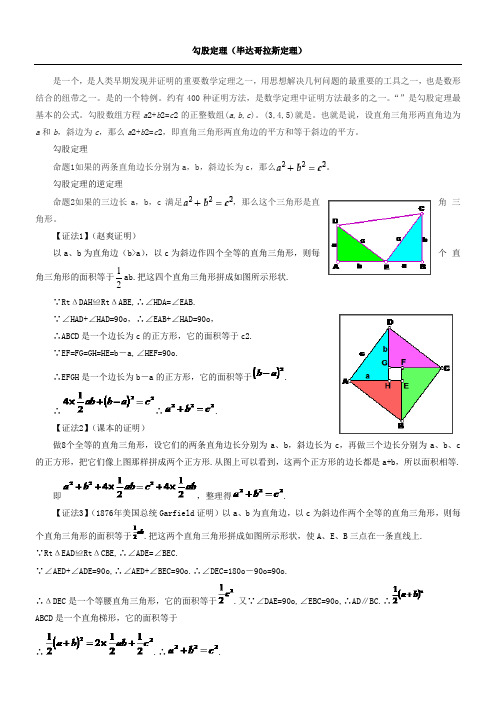
勾股定理(毕达哥拉斯定理) 是一个,是人类早期发现并证明的重要数学定理之一,用思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一。
是的一个特例。
约有400种证明方法,是数学定理中证明方法最多的之一。
“”是勾股定理最基本的公式。
勾股数组方程a 2+b 2=c 2的正整数组(a ,b ,c )。
(3,4,5)就是。
也就是说,设直角三角形两直角边为a 和b ,斜边为c ,那么a 2+b 2=c 2,即直角三角形两直角边的平方和等于斜边的平方。
勾股定理命题1如果的两条直角边长分别为a ,b ,斜边长为c ,那么。
勾股定理的逆定理命题2如果的三边长a ,b ,c 满足,那么这个三角形是直角三角形。
【证法1】(赵爽证明)以a 、b 为直角边(b>a ),以c 为斜边作四个全等的直角三角形,则每个直角三角形的面积等于21ab.把这四个直角三角形拼成如图所示形状. ∵RtΔDAH≌RtΔABE,∴∠HDA=∠EAB.∵∠HAD+∠HAD=90o,∴∠EAB+∠HAD=90o,∴ABCD 是一个边长为c 的正方形,它的面积等于c2.∵EF=FG=GH=HE=b―a,∠HEF=90o.∴EFGH 是一个边长为b―a 的正方形,它的面积等于.∴∴.【证法2】(课本的证明) 做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形.从图上可以看到,这两个正方形的边长都是a+b ,所以面积相等.即,整理得.【证法3】(1876年美国总统Garfield 证明)以a 、b 为直角边,以c 为斜边作两个全等的直角三角形,则每个直角三角形的面积等于.把这两个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上. ∵RtΔEAD≌RtΔCBE,∴∠ADE=∠BEC.∵∠AED+∠ADE=90o,∴∠AED+∠BEC=90o.∴∠DEC=180o―90o=90o.∴ΔDEC 是一个等腰直角三角形,它的面积等于.又∵∠DAE=90o,∠EBC=90o,∴AD∥BC.∴ABCD 是一个直角梯形,它的面积等于 ∴.∴.【趣闻】:在1876年一个周末的傍晚,在美国华盛顿的郊外,有一位中年人正在散步,欣赏黄昏的美景,他就是当时美国俄亥俄州共和党议员伽菲尔德。
勾股定理中的方程思想和参数方法复制

在一棵树的10米高的D处有两只猴子,其中一只 猴子爬下树走到离树20米的池塘A处,另一只爬到 树顶后直接跃向池塘A处,如果两只猴子所经过的 距离相等,试问这棵树有多高?
C
15米
D
10米
┏
20米
B
A
方程思想:
•方程的思想是分析问题中的变量间的等量关系,构建 方程或方程组,或利用方程的性质去分析、转换、解 决问题。
Δ ABC中,周长是24,∠C=90°,且AB=9,则三角 形的面积是多少? 解:设BC=a,AC=b,依题意得:
B
c
A b a C
如图,小颖同学折叠一个直角三角形的纸片,使A与 B重合,折痕为DE,若已知AC=10cm,BC=6cm, 你能求出CE的长吗?
B D
A E
C
如图,铁路上A,B两点相距25km,C,D为两村庄, DA⊥AB于A,CB⊥AB于B,已知:DA=15km, CB=10km,现在要在铁路AB上 建一个土特产品收购 站E,使得C,D两村到E站的距离相等,则E站应建在 离A站多少km 处?
B
x
8
D
C
如图,在正方形ABDC中,E是CD的中点,F为BD上一 点,且BF=3FD,试猜想线段AE,EF的位置关系并证明.
A C
解: ∠AEF=900,证明如下: 设FD=a,则BF=3a,BD=AB= AC=CD=4a, DE=CE=2a, 在RtΔ ABF中,AF2=AB2+BF2=25a2
E
B
F
D
在RtΔ DEF中,EF2=DF2+DE2=5a2
在RtΔ AEC,AE2=AC2+EC2=20 a2 ∴EF2+AE2=AF2 ∴∠AEF=900
勾股定理的方程思想总结

勾股定理的方程思想总结勾股定理是数学中的一条重要定理,由中国古代数学家所发现和证明。
它为解决直角三角形中的问题提供了重要的数学工具,也是数学推理中的一种经典的思想方法。
在这1000字的总结中,我将详细介绍勾股定理的方程思想,包括其背景、推导过程和应用领域。
首先,我们来介绍一下勾股定理的背景。
在古代,古希腊的毕达哥拉斯学派和古中国的《周髀算经》中都有类似的关于直角三角形的边长的关系。
然而,勾股定理最早的证明是由中国古代的《周髀算经》所给出的,可以追溯到约公元前500年左右。
根据《周髀算经》中的记载,古代算术家商高在解题时发现了直角三角形中三边的关系,并用文字形式进行了描述。
这一发现被后来的数学家所发扬光大,成为了后来的勾股定理。
接下来,我们探讨一下勾股定理的推导过程。
勾股定理的推导思想可以用几何和代数方法进行证明。
首先,我们以直角三角形的三个边为对象进行分析。
假设直角三角形的两个直角边分别为a和b,斜边为c。
根据勾股定理,我们有a² + b² = c²。
为了证明这个定理,我们可以使用几何方法进行推导。
具体步骤如下:1. 通过画图,我们可以得到一个直角三角形,其中直角边a和b构成直角,斜边c位于直角边的对面。
2. 将直角边a和b延长,分别延长到直角边b的竖直延长线和直角边a的水平延长线上。
3. 直角边a和b所延长后的部分构成一个正方形和一个长方形。
4. 根据几何性质,我们可以得到正方形的边长为a+b,长方形的边长为a和b。
5. 正方形的面积可以表示为边长的平方,即(a+b)²。
长方形的面积可以表示为a*b。
6. 根据几何性质,正方形的面积可以等于两个长方形面积之和。
7. 将上述两个公式相等,我们可以得到(a+b)² = a² + b²。
8. 展开上述式子后,我们可以得到一个等式 a² + 2ab + b² = a² + b²。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学生读题解题
出示练习
出示解答过程
小结
今天我们学习了已知直角三角形一边及另两边的数量关系求各边长的这类问题,解决这类问题的关键是先从数量关系入手设未知数,再根好的,同学们理清思路了吗我们一起来完成解答过程。
解:设水深有x尺,则芦苇长(x+1) 尺。由题意,得
x2+52=(x+1)2
解得: x=12
答:水深12尺,芦苇长13尺。
读题思考
幻灯片:出示例3题目
出示示意图
出示解答过程
随堂解题
师:刚才老师举了几个例子,同学们是否都掌握了呢下面请大家做一个随堂练习。
幻灯片:出示例1题目
出示解答过程
出示解答过程
出示流程图
讲解例2
师:我们再来看一个例子。请同学们先读一下题目。
例2如图,在Rt△ABC中,∠C=900, AC=1,BC=3. AB的中垂线DE交BC于点D,连结AD,求AD的长.
师:首先我们来分析一下条件.已知AB的中垂线DE交BC于点D,即D在线段AB的中垂线上,则有AD=BD.根据BC=3可得到BD+CD=AD+CD=3.这个时候我们来看Rt△ACD,AC的长已知,AD、CD满足和等于3,那么我们不妨设AD=x,则CD=3- x,根据勾股定理列方程就可以求出AD的长.
师:首先我们根据题意画出示意图。芦苇可以用线段AD来表示,其中BD表示露出水面的部分,拉动芦苇后的位置用线段AC来表示。根据拉动后芦苇的顶端恰好到达水面可以知道,若连结BC,则有BC⊥AD. 根据题意,BD=1尺,BC=丈=5尺,特别地,在芦苇拉动过程中长度不改变,即AC=AD. 这个时候我们来看Rt△ABC,BC的长已知,AC比AB长1尺,那么我们不妨设AB=x尺,则AC=(x+1) 尺,根据勾股定理列方程就可以求出x的值.
【授课内容】勾股定理的方程思想
【适用年级】八年级上
【执教教师】宁波镇海蛟川书院 滕丽
【教学目标】能根据勾股定理列方程,体会方程的思想方法。
【教学过程】
教学板块
教师教学
学生活动
媒体插入
揭示课题,
明确任务
师:同学们,我们已经学习了勾股定理。我们知道任意的一个直角三角形,它的两条直角边的平方和等于斜边的平方,这个结论就称为勾股定理,即如果 为直角三角形的两条直角边长, 为斜边长,则 。在直角三角中,如果已知两边的长,利用勾股定理就可以求第三边的长;那么如果已知一条边长及另两边的数量关系,能否求各边长呢这就是今天我们所要学习内容。
幻灯片:勾股定理
讲解例1
师:我们先来看一个简单的问题。
例1在△ABC中,∠C=Rt∠,
(1)如果BC=16,AB:AC=5:3,求AB、AC的长.
(2)如果AC=5,AB=BC+1,求AB、BC的长.
师:在第(1)小题中,已知了直角三角形ABC的一条边BC的长及另两边的数量关系: AB:AC=5:3,根据这个数量关系,可以把AB设成5x, AC为3x,根据勾股定理得 就能列出含x的方程,从而求出x的值。下面我们一起来解答这个小题。
练习如图,有一张直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边沿直线AD折叠,使点C落在斜边AB上的点E,求CD的长.
师:请同学们先独立思考完成。(停顿)
师:好,我们简单理一下思路:由折叠可知,AE=AC=6cm,CD=DE,∠C= ∠AED=90°。在Rt△BDE中,BE=ABAE 106=4cm,而BD+DE=BD+CD=BC=8cm,这样我们可以从这个数量关系入手设未知数列方程。下面我们一起来看解答。
解:(1)设AB=5x,则AC=3x(x>0)
由勾股定理得162+(3x)2=(5x)2
解得: x2=16
∵x>0∴x=4
∴AB=20,AC=12.
师:下面我们来看第(2)小题,同学们你们会求吗(停顿)
师:是的。我们可以从AB=BC+1这个数量关系入手,设BC= x, 则AB=x+1,根据勾股定理列方程。下面我们一起来解答这个小题。
读题思考
幻灯片:出示例2题目
依次出现两个结论
出示解答过程
讲解例3
师:我们最后来看一个课本中的练习题,请同学们先读题目。
例3在《九章算术》中记载了一道有趣的数学题:“今有池方一丈,葭生其中央,出水一尺。引葭赴岸,始与岸齐,问水深、葭长各几何”这道题的意思是说:有一个边长为1丈的正方形水池,在池的正中央长着一根芦苇,芦苇露出水面1尺。若将芦苇拉到池边中点处,芦苇的顶端恰好到达水面。问水有多深芦苇多长请解这道题。
解:在Rt△ABC中, AC=6cm,BC=8cm
∴ AB=10cm
由折叠可知AE=AC=6cm,CD=DE,
∠C= ∠AED=90°
∴BE=10-6=4cm, ∠BED=90°
设CD=DE=xcm,则BD=(8-x)cm
在Rt△BDE中,由勾股定理可得(8-x)2=x2+42
解得x=3
∴ CD=DE=3cm
师:好的,同学们理清思路了吗我们一起来完成解答过程。
解:∵D在线段AB的中垂线上
∴AD=BD
∵BC=3
∴BD+CD=AD+CD=3
设AD=x,则CD=3- x,
由勾股定理得:x2=(3-x)2+12
解得: x=
∴AD=
师:从这个例题我们可以看到在许多问题中,直角三角形某两边的数量关系并不是条件直接给出的,而是通过条件推理得到,在这种情况下,同学们要仔细分析条件,把数量关系都集中到一个直角三角形中,就可以转化成例1中的类型了。
(2)设BC= x, 则AB=x+1(x>0)
由勾股定理得x2+52=( x+1)2
解得: x=12
∴BC=12,AB=13.
师:我们总结一下步骤:
在直角三角形中(已知两边的数量关系)
设其中一边为x利用勾股定理列方程
解方程求各边长
这就是我们今天所学习的《勾股定理的方程思想求边长》,你掌握了吗
读题思考
