5.2 简谐振动的旋转矢量表示法
合集下载
大学物理简谐振动

tan A1 sin 1 A2 sin 2 A1 cos1 A2 cos2
A2
A
A2 sin 2
2 -1
2
O
1 A1 x2
A1 sin 1
x2 x
x1x1
x2
x
A1 cos1 A2 cos2
合振动振幅:A A12 A22 2A1A2 cos(2 1)
1. 两个分振动的相位相同(同相)
5 (或 3 )
4
4
第六章
机械波
mechanical wave
6.1 机械波的产生、传播和描述 波动: 振动在空间中的传播过程.
机械波: 机械振动在弹性介质中的传播过程. 波动
电磁波: 交变电磁场在空间中的传播过程. 6.1.1 机械波的产生
当弹性介质中的一部分发生振动时,由于介质各个 部分之间的弹性力作用,振动就由近及远地传播出去. (1) 机械波实质上是介质中大量质点参与的集体振动;
20 0.47
(2) 30为何值时, x1+x3 的振幅为最大; 30为何值时, x2+x3的振幅为最小.
x1 0.05cos10t 3 4
x2 0.06cos10t 4
x3 0.07 cos10t 30
30
10
0 时,x1+x3 振幅最大:30
10
3
4
30 20 时,x2+x3 振幅最小:30 20
t 时刻点 P 的振动状态
P点在
t
时刻的位移
y P ,t
yO ,t x
u
A c os [ (t
x) u
0 ]
波函数 (波方程)
y( x, t )
A cos[ (t
A2
A
A2 sin 2
2 -1
2
O
1 A1 x2
A1 sin 1
x2 x
x1x1
x2
x
A1 cos1 A2 cos2
合振动振幅:A A12 A22 2A1A2 cos(2 1)
1. 两个分振动的相位相同(同相)
5 (或 3 )
4
4
第六章
机械波
mechanical wave
6.1 机械波的产生、传播和描述 波动: 振动在空间中的传播过程.
机械波: 机械振动在弹性介质中的传播过程. 波动
电磁波: 交变电磁场在空间中的传播过程. 6.1.1 机械波的产生
当弹性介质中的一部分发生振动时,由于介质各个 部分之间的弹性力作用,振动就由近及远地传播出去. (1) 机械波实质上是介质中大量质点参与的集体振动;
20 0.47
(2) 30为何值时, x1+x3 的振幅为最大; 30为何值时, x2+x3的振幅为最小.
x1 0.05cos10t 3 4
x2 0.06cos10t 4
x3 0.07 cos10t 30
30
10
0 时,x1+x3 振幅最大:30
10
3
4
30 20 时,x2+x3 振幅最小:30 20
t 时刻点 P 的振动状态
P点在
t
时刻的位移
y P ,t
yO ,t x
u
A c os [ (t
x) u
0 ]
波函数 (波方程)
y( x, t )
A cos[ (t
大学物理B(Ⅱ)旋转矢量

2
t 0.667s
x
A
00 7.5 A 2
A v
t0
例 一简谐运动的运动
曲线如图所示,求振动周
期.
t(s) t 0
A A2 0 A x
t 7.5
2π T T
t 7.5s
T 18s
例 已知谐振动的 A 、T ,求 1)如图简谐运动方
A'
44
因为 v0 0 ,由旋转矢量图可知 ' π 4
x Acos(t ) 0.0707cos(6.0t π)
4
例2 一质量为 0.01kg 的物体作简谐运动,其振
幅为 0.08m,周期为 4s ,起始时刻物体在 x 0.04m
处,向 Ox轴负方向运动(如图).试求
(1)t 1.0s 时,物体所处的位置和所受的力;
A/2 t ta
A 0 A x
t0
π ( π) 2π
3 33
tb
T
2π
T 3
的最短时间.
v
x/m
0.08 0.04 o 0.04 0.08
法一 设由起始位置运动到 x 0.04m 处所
需要的最短时间为 t
0.04 0.08cos(π t π) 23
t 0.667s
解法二
t 时刻
t
π3 π3
0.08 0.04 o 0.04
起始时刻
x/m
0.08
t π
3
π s1
x 0.08cos(π t π ) 23
m 0.01kg
v
x/m
0.08 0.04 o 0.04 0.08
x 0.08cos(π t π ) 23
t 1.0s 代入上式得 x 0.069m
t 0.667s
x
A
00 7.5 A 2
A v
t0
例 一简谐运动的运动
曲线如图所示,求振动周
期.
t(s) t 0
A A2 0 A x
t 7.5
2π T T
t 7.5s
T 18s
例 已知谐振动的 A 、T ,求 1)如图简谐运动方
A'
44
因为 v0 0 ,由旋转矢量图可知 ' π 4
x Acos(t ) 0.0707cos(6.0t π)
4
例2 一质量为 0.01kg 的物体作简谐运动,其振
幅为 0.08m,周期为 4s ,起始时刻物体在 x 0.04m
处,向 Ox轴负方向运动(如图).试求
(1)t 1.0s 时,物体所处的位置和所受的力;
A/2 t ta
A 0 A x
t0
π ( π) 2π
3 33
tb
T
2π
T 3
的最短时间.
v
x/m
0.08 0.04 o 0.04 0.08
法一 设由起始位置运动到 x 0.04m 处所
需要的最短时间为 t
0.04 0.08cos(π t π) 23
t 0.667s
解法二
t 时刻
t
π3 π3
0.08 0.04 o 0.04
起始时刻
x/m
0.08
t π
3
π s1
x 0.08cos(π t π ) 23
m 0.01kg
v
x/m
0.08 0.04 o 0.04 0.08
x 0.08cos(π t π ) 23
t 1.0s 代入上式得 x 0.069m
简谐运动的旋转矢量描述法

π
4
A g a'*
h' * g'* *
t f O b*' T T f'* 3T T 5T
e
c' 4* 2*e' 4
4
-A
d*'
T 2 (旋转矢量旋转一周所需的时间)
用旋转矢量图画简谐运动的 x t 图
T 2π (旋转矢量旋转一周所需的时间)
二、旋转矢量法对相位的表示
若某时刻t,测得质点的位移为x =A/2,向OX轴负方
简谐运动的旋转 矢量表示法
一、简谐运动的旋转矢量表示法
P
t=t
t+
o
A t=0
A
x·
x
x Aco(s t )
x Aco(s t )
旋 转 矢量 A的
x 端点在
轴上的投
影点的运
动为简谐
运动.
x Acos(t )
用旋转矢量图画简谐运动的 x t 图
x
Ah
a
bO
c -Ad
x
x Acos(t )
向运动
M
A
O 3P
X
M
三、旋转矢量法对相位差的表示
A2
A1
O
相位差 2 1 2kπ
x
(k 0,1, 2,)
两个振动同相,步调相同
A1
O
A2
相位差 2 1 (2k 1)π
x
(k 0,1,)
两个振动反相,步调相反
例题 两个同方向、同频率的谐振动,频率为2s-1,
当第一个振子从平衡位置向正向运振动的相位差。
解:
2 1
A 2
t
o
简谐振动-旋转矢量法
sin2 (2 1)
y
2) 2 1 π
y A2 x A1
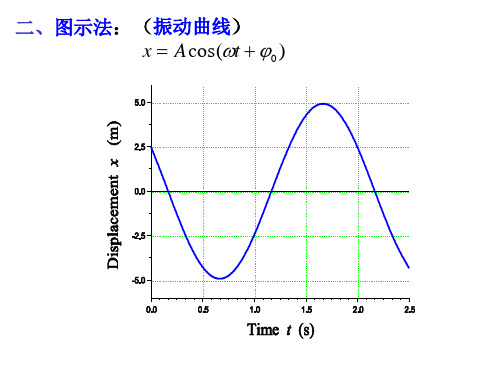
3)2 1 π 2
x A2
o A1
x2 A12
பைடு நூலகம்
y2 A22
1
x A1 cost
y
A2
cos(t
π) 2
A2 y
o A1 x
用 旋 转 矢 量 描 绘 振 动 合 成 图
两
相
互 垂 直 同 频 率 不 同 相
简 谐 运 动 的 合 成 图
x
x
A1 o
o
A
A2
A A1 A2
Tt
结论
A A12 A22 2A1 A2 cos(2 1 )
若两分振动同相位:
2 1 2k k 0,1, 2,
A A1 A2
若两分振动反相位:
两分振动相互加强
2 1 (2k 1) k 0,1, 2,
A A1 A2
两分振动相互减弱
再若 A1= A2 , 则 A= 0
M
A
P
x
注意:旋转矢量在第 2 象限
速度v <0
M
PA
x
注意:旋转矢量在第 2 象限
速度v <0
M
PA
x
<
注意:旋转矢量在第 3 象限
速度v 0
P x
MA
<
注意:旋转矢量在第 3 象限
速度v 0
P x
A
M
<
注意:旋转矢量在第 3 象限
速度v 0
P x
A
M
<
注意:旋转矢量在第 3 象限
速度v 0
找到谐振动的特征量,问题就解决了。
简谐运动及其旋转矢量表示法简谐运动的能量讲课文档

简谐运动及其旋转矢量表示法简谐运动的能量
现在一页,总共十五页。
9.1 简谐振动
一、弹簧振子 1. 受力特点
线性恢复力 F kx
2. 运动方程
据牛顿第二定律得:
若令 ω k m
kx
m
d2 dt
x
2
上式改写为
d2 dt
x
2
2
x
0
解得 x(t) Acos(ω t )
现在二页,总共十五页。
二、简谐振动
x
现在十三页,总共十五页。
2. 同相和反相
x
A1
x1
A2
x2
T
o
- A2
t
-A1
= 2n
两运动步调相同, 称同相
A2
A1
x
A1
x1
A2
T
o
- A2
x2
t
-A1
= (2n+1)
两运动步调相反 ,称反相
A2
O
x
O
x
A1
现在十四页,总共十五页。
例 如图所示,一质点作简谐振动,在一个周期内先后通过距
相位反映了物 体某一时刻的
运动状态
现在三页,总共十五页。
3. 由初始条件求振幅和初相位
熟练掌握
x0 v0
x Acos(ω t ) v ω Asin(ω t )
初位移 x0 Acos 初速度 v0 ω Asin
A
x02
v
2 0
2
tan1( v0 ) x0
注意: 确定 的象限
现在四页,总共十五页。
逆时针旋转 。其端点在
x 轴上的投影
点的运动为 简谐运动, 有:
现在一页,总共十五页。
9.1 简谐振动
一、弹簧振子 1. 受力特点
线性恢复力 F kx
2. 运动方程
据牛顿第二定律得:
若令 ω k m
kx
m
d2 dt
x
2
上式改写为
d2 dt
x
2
2
x
0
解得 x(t) Acos(ω t )
现在二页,总共十五页。
二、简谐振动
x
现在十三页,总共十五页。
2. 同相和反相
x
A1
x1
A2
x2
T
o
- A2
t
-A1
= 2n
两运动步调相同, 称同相
A2
A1
x
A1
x1
A2
T
o
- A2
x2
t
-A1
= (2n+1)
两运动步调相反 ,称反相
A2
O
x
O
x
A1
现在十四页,总共十五页。
例 如图所示,一质点作简谐振动,在一个周期内先后通过距
相位反映了物 体某一时刻的
运动状态
现在三页,总共十五页。
3. 由初始条件求振幅和初相位
熟练掌握
x0 v0
x Acos(ω t ) v ω Asin(ω t )
初位移 x0 Acos 初速度 v0 ω Asin
A
x02
v
2 0
2
tan1( v0 ) x0
注意: 确定 的象限
现在四页,总共十五页。
逆时针旋转 。其端点在
x 轴上的投影
点的运动为 简谐运动, 有:
简谐振动旋转矢量图

2
T
t
)
8
例1:一个沿 x 轴作谐振动的弹簧振子,振幅为
A,周期为T,其振动方程用余弦函数表示。若 t
= 0 时,质点的状态分别为:(1)x0=-A;试 求相应的初相,并写出振动方程。
解: x
A cos( t
)
Acos( 2
T
t
)
(1)解析法(x0=-A)
由x0 Acos A, cos 1, =
7
例1:一个沿 x 轴作谐振动的弹簧振子,振 幅为 A,周期为T,若 t = 0 时,质点的状 态分别为:(1)x0=-A;(2)过平衡位 置向x正向运动;(3)过 x = A/2 处向x负 方向运动;试求相应的初相,并写出用余 弦函数表示的振动方程。
解:所求振动方程为
x
A cos( t
)
A
cos(
下落: v 2gh
碰撞:mv (m M )v0 t 0, y0 (2 1 )
A
y02
v02
2
arctan(
,
v0
y0
),
(2)
1
y
2
O
h
A
cos(
2
T
t
y
)
16
本节课小结: (1)A,ω, 的确定。 (2)掌握旋转矢量法。 作业:7-5
17
T
t
3
)
11
例2:画出质点处于①平衡位置且速度小于 零,②正最大位移,③(1/2)位移处且速度 为正值的旋转矢量,说明初相的大小并画出 振动曲线。
解:①
xx
A
0o
2
Tt
12
②正最大位移 x
A
第四章振动下
结论: 结论:
振子在振动过程中, (1) 振子在振动过程中,动能和势能分别随时间 变化,但任一时刻总机械能保持不变。 变化,但任一时刻总机械能保持不变。 (2) 动能和势能的变化频率是弹簧振子振动频 率的两倍。 频率一定时, (3)频率一定时,谐振动的总能量与振幅的平方 成正比。(适合于任何谐振系统) 。(适合于任何谐振系统 成正比。(适合于任何谐振系统) 弹性势能
小结:
描述简谐振动的三种方法: 描述简谐振动的三种方法: 运动方程,振动曲线,旋转矢量。 运动方程,振动曲线,旋转矢量。
的简谐振动, 例1:一物体沿 轴作振 幅为 A 的简谐振动,若初始时该球的 :一物体沿x轴作振 状态为( ) ;(2)在平衡位置且向X轴正方向运动 轴正方向运动; 状态为(1)X0= -A;( )在平衡位置且向 轴正方向运动; ;( 处向X轴负方向运动;(4) 轴负方向运动;( (3)在 X0=1/2 A 处向 轴负方向运动;( )在 ) / 方向运动。试用旋转矢量法确定相应的初相位。 处向正 方向运动。试用旋转矢量法确定相应的初相位。 3π r ϕ = ϕ =π
k = m
得
X
g b
mg
b, v 0 = 0
g t+π) b
A =b, φ = π
[ 例2] 一谐振动的振动曲线如图所示。 一谐振动的振动曲线如图所示。
ω 以及振动方程。 求: ϕ 0 以及振动方程。
−
π
x
x
A 2
3r
A
1.0
0
解:
t
r A
A
π
2
x
π
3
t=
A x0 = = A cos ϕ 0 2 0时 v 0 = − ω A sin ϕ 0 > 0
简谐振动的旋转矢量图示.ppt
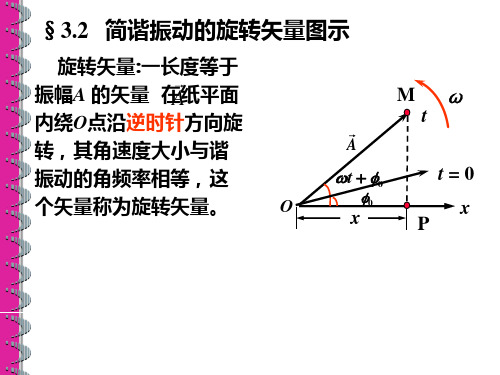
角频率ω
A 与参考方向x 的夹角
振动相位ωt+φ0
3、两个谐振动的相位差
x1 A1 cos(t 1 ) x2 A2 cos(t 2 )
相位差为 (t 2 ) (t 1) 2 1
采用旋转矢量表示为:
A2
2
A1
1
O
x
例1、两个同频率的谐振动,它们都沿x轴振动,且振
幅相等,当t =0时质点1在x=A/2处向左运动,另一质点
F kx m 2x
(0.01kg)(π s1)2 (0.069m) 1.70103 N
2
(2)由起始位置运动到 x 0.04m 处所需要
的最短时间.
v
x/m
0.08 0.04 o 0.04 0.08
解法一 设由起始位置运动到 x 0.04m 处所
需要的最短时间为 t
0.04m (0.08m) cos[(π s1)t π ]
x 0.12cos( 0.5 ) 0.104 m
3
v 0.12 sin( 0.5 ) 0.18 m/s
3 a 0.12 2 cos( 0.5 ) 1.03 m/s2
3
在t =T/4=0.5s时,可得
可得x 0.12cos( 0.5 ) 0.104 m
3
v 0.12 sin( 0.5 ) 0.18 m/s
sin0 0
0
3
简谐振动表达式 x 0.12cos( t ) m
3
因为
(2)由简谐振动的运动方程 x 0.12cos( t ) m
3
可得
v dx 0.12 sin( t ) m/s
dt
3
a dv 0.12 2 cos( t ) m/s2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
π v A cos( t ) 2
a A cos(t )
2
第5章 机械振动
5.2 简谐振动的旋转矢量表示法
用旋转矢量图画简谐振动的
x
A
x
A
*
x A cos(t )
*
T * 3T 2 4
x t
*
* T
图
π 4
O -A
O * T
4
*
-A
*
x1 A1 cos(t 1 )
x2 A2 cos(t 2 )
2 1
为其它
(t 2 ) (t 1 )
0 同步
π 反相
超前 落后
x
x
x
o
t
o
t
o
t
第5章 机械振动
5.2 简谐振动的旋转矢量表示法
例 一放置在水平桌面上的弹簧振子,振幅 , 2 A 1.0 10 m ,周期 T 1 s。当 t 0 时,试分别 振幅 写出以下两种初始条件下简谐振动的运动学方程。( 1) 3 x0 5.0 10 m x轴负方向运动;(2) 质点位于 处,向 3 x0 5.0 10 m x轴正方向运动。 质点位于 处,向 ,且v0 <0,可得旋转矢量的初始位置如 图(a)所示。由图(a)可得简 谐振动的初相位 。由此 3 及 2 / T 2 rad / s,A 1.0 102 m, 可得简谐振动运动学方程为
A
o
v A sin t
A 2
x
0.26m s
1
(负号表示速度沿 Ox 轴负方向)
第5章 机械振动
5.2 简谐振动的旋转矢量表示法
(3)如果物体在 x 0.05 m 处时速度不等于零, 1 而是具有向右的初速度 v0 0.30m s ,求其运动方程 . 解 A'
x0 解 (1)t 0 时, A 2
A O v0 x0 a)
3
x0v0
4 3
x
A
O
x
b)
x 1.0 102 cos(2 t ) m 3
第5章 机械振动
5.2 简谐振动的旋转矢量表示法
量的初始位置如图(b)所示。由图(b)可得振动 4 2 初相位 或 。因此,简谐振动运动学方程 3 3 为 2 2 x 1.0 10 cos(2 t )m 3
量 A的端点
在
o
x0 A cos
x0
x
x 轴上的
投影点的运 动为简谐运 动.
第5章 机械振动
5.2 简谐振动的旋转矢量表示法
2π T
A M
t t
时
M0
以 o为 原点旋转矢
t
量 A的端点
在
o
x
x0
x
x 轴上的
投影点的运 动为简谐运 动.
第5章 机械振动
x A cos(t )
A O v0 x0 a)
3
4 x0v0 3
A (2)根据题意,x0 2 ,且 v0 >0,可得旋转矢
x
A
O
x
b)
第5章 机械振动
5.2 简谐振动的旋转矢量表示法
例 如图所示,一轻弹簧的右端连着一物体,弹簧 1 的劲度系数 k 0.72N m ,物体的质量 m 20g .
*
5T 4
t
T 2π (旋转矢量旋转一周所需的时间)
第5章 机械振动
5.2 简谐振动的旋转矢量表示法
用旋转矢量图画简谐振动的
x t
图
T 2π (旋转矢量旋转一周所需的时间)
第5章 机械振动
5.2 简谐振动的旋转矢量表示法 讨论
相位差:表示两个相位之差 . 1)对同一简谐振动,相位差可以给出两运动状 态间变化所需的时间. (t 2 ) (t1 )
5.2 简谐振动的旋转矢量表示法
简谐振动的规律除了用简谐振动的运动学 方程和振动曲线表示外,还可以采用旋转矢量 表示法。 旋转矢量表示法可以更直观地说明简谐振动 运动学方程中各个特征物理量的意义。
第5章 机械振动
5.2 简谐振动的旋转矢量表示法
2π T
当
t 0时
A M
0
以 o为 原点旋转矢
解
A 0.08 m
2π π 1 s T 2
第5章 机械振动
t 0, x 0.04m
π v0 0 3
5.2 简谐振动的旋转矢量表示法 2π π 1 A 0.08 m s T 2
代入 x
0.04 0.08cos
A cos(t ) π 3
由旋转矢量图可知
第5章 机械振动
5.2 简谐振动的旋转矢量表示法 A (2)求物体从初位置运动到第一次经过 处时的 2 速度;
解
x A cos(t ) A cos(t )
A
x 1 cos( t ) A 2 π 5π t 或 3 3 π 由旋转矢量图可知 t 3
x
A
A2
x A cos(t1 ) x A cos(t2 )
t t 2 t1
a
b
π 3
Ab
o
A
v
t
A
0 A
x
π 3 1 t T T 2π 6
2
Aa A
第5章 机械振动
5.2 简谐振动的旋转矢量表示法
2)对于两个同频率的简谐振动,相位差表示它 们间步调上的差异.(解决振动合成问题)
(1)把物体从平衡位置向右拉到 x 0.05 m 处停 下后再释放,求简谐振动方程; A (2)求物体从初位置运动到第一次经过 处时的 2 速度; (3)如果物体在 x 0.05 m 处时速度不等于零, 1 而是具有向右的初速度 v0 0.30m s ,求其运动方程 .
x/m
o
0.05
A
π 3
0.08 0.04
0.04 π x 0.08 cos( t 2
o
x/m
0.08 π ) 3
第5章 机械振动
5.2 简谐振动的旋转矢量表示法
m 0.01kg
0.08 0.04
v
o
0.04 0.08
x/m
π π x 0.08 cos( t ) 2 3
t 1.0s 代入上式得
5.2 简谐振动的旋转矢量表示法
例 一质量为 0.01kg的物体作简谐振动,其振 幅为 0.08 m ,周期为 4s ,起始时刻物体在 x 0.04 m 处,向 Ox 轴负方向运动(如图).试求 (1 ) t
1.0s
时,物体所处的位置和所受的力;
v
0.08 0.04
o
x/m
0.04 0.08
5.2 简谐振动的旋转矢量表示法
x A cos(t )
矢量 A的
端点在 轴上的投 影点的运
旋转
x
动为简谐
运动.
第5章 机械振动
5.2 简谐振动的旋转矢量表示法
y vm
t
0
an
π t 2
A
vm A
v a
x
an A
2
x A cos(t )
2
x 0.069 m
F kx m x 1.70 103 N
第5章 机械振动
5.2 简谐振动的旋转矢量表示法 (2)由起始位置运动到 x 0.04 m 处所需要
的最短时间.
v
0.08 0.04
o
x/m
0.04 0.08
解法一 设由起始位置运动到 x 0.04 m 处 所需要的最短时间为 t
π π 0.04 0.08 cos( t ) 2 3
t 0.667 s
第5章 机械振动
5.2 简谐振动的旋转矢量表示法
解法二
Hale Waihona Puke t时刻π 3
t
o
起始时刻
π 3
0.04 0.08
x/m
0.08 0.04
π t 3
π 1 s 2
t 0.667 s
第5章 机械振动
第5章 机械振动
5.2 简谐振动的旋转矢量表示法
k 0.72N m 解 ( 1) m 0.02kg
1
6.0s 1
v A x x0 0.05m v0 tan 0 x0 0 或 π
2 0
2 0 2
o
A
x
0 x A cos(t ) 0.05 cos 6.0t m
0 ,由旋转矢量图可知 ' π 4 π x A cos(t ) 0.0707 cos( 6.0t )
因为 v 0
v0 tan' 1 x0 π 3π ' 或 4 4
x
2 0
v
2 0 2
0.0707m
o
π 4
x
A'
4
第5章 机械振动
