大学物理学教学中初相位的求解_旋转矢量法
大学物理-旋转矢量
x oA
y
x
A
A 0
o
x
o
l
t
2.初始条件
x
t 0
o
l
x0 0
v0 0
y
x
0 A cos
cos 0
A
o
A
2
x
o
t
/ 2 , 3 / 2
v0 A sin 0, sin 0 取 / 2
3.初始条件
t 0
x
l
x0 A v0 0
o A
y
x
A A cos
A 处时的
速度；
2
（3）如果物体在 x 0.05m 处时速度不等于零，
而是具有向右的初速度 v0 0.30m s，1 求其运动方程.
x/m
o 0.05
解 （1） x Acos(t )
k 0.72N m1 6.0s1
m
0.02kg
A 0.05m
由旋转矢量图可知 0
x Acos(t )
（3）如果物体在 x 0.05m 处时速度不等于零，
而是具有向右的初速度 v0 0.30m s，1 求其运动方程.
解 x Acos(t )
6.0s1
A
x02
v02
2
0.0707m
o π 4 x A＇
由旋转矢量图可知 π 4
x Acos(t ) 0.0707cos(6.0t π)
轴上的投
影点的运
动为简谐
运动.
x Acos(t )
y vm t π
2
t
0
an A
a v x
vm A an A 2
x Acos(t )
大学物理学教学中初相位的求解_旋转矢量法
图3
图4
3
简谐振动运动中初相位的应用
有关简谐振动的问题也可利用旋转矢量法来求解质点从一位置运动到另一位置的时间 。 例 1 一质量为 0 ． 1 kg 的物体做简谐振动， 振幅为 24 cm， 周期为 4． 0 s。 当 t = 0 时， 位移为 24 cm。
［2 ］ 求由起始位置运动到 x = 12 cm 处所需最短时间？ 根据题意可知振幅 A = 24 cm， 初始位置为 x0 = 24 cm， 终点位置 x1 = 12 cm。 利用旋转矢量法可作
Feb． 2012 Vol． 18 No． 1
— — 旋转矢量法 大学物理学教学中初相位的求解 —
马业万， 刘全金， 章礼华， 张 杰
（ 安庆师范学院 物理与电气工程学院，安徽 安庆 246133 ）
摘
要： 在大学物理中有关振动方程和波动方程的教学中发现， 很多学生不知怎么求解振动方程和波动方程， 其主
x x π π ） + ］ = 0 ． 04cos［ 0 ． 8 π（ tห้องสมุดไป่ตู้－ ） + ］ u 2 0 ． 08 2
大学物理B(Ⅱ)旋转矢量
t 0.667s
x
A
00 7.5 A 2
A v
t0
例 一简谐运动的运动
曲线如图所示，求振动周
期.
t(s) t 0
A A2 0 A x
t 7.5
2π T T
t 7.5s
T 18s
例 已知谐振动的 A 、T ，求 1）如图简谐运动方
A＇
44
因为 v0 0 ，由旋转矢量图可知 ＇ π 4
x Acos(t ) 0.0707cos(6.0t π)
4
例2 一质量为 0.01kg 的物体作简谐运动，其振
幅为 0.08m，周期为 4s ，起始时刻物体在 x 0.04m
处，向 Ox轴负方向运动（如图）.试求
（1）t 1.0s 时，物体所处的位置和所受的力；
A/2 t ta
A 0 A x
t0
π ( π) 2π
3 33
tb
T
2π
T 3
的最短时间.
v
x/m
0.08 0.04 o 0.04 0.08
法一 设由起始位置运动到 x 0.04m 处所
需要的最短时间为 t
0.04 0.08cos(π t π) 23
t 0.667s
解法二
t 时刻
t
π3 π3
0.08 0.04 o 0.04
起始时刻
x/m
0.08
t π
3
π s1
x 0.08cos(π t π ) 23
m 0.01kg
v
x/m
0.08 0.04 o 0.04 0.08
x 0.08cos(π t π ) 23
t 1.0s 代入上式得 x 0.069m
旋转矢量法(干货分享)
2A x
a
o
2
A
v
3
4 t
例：一质点沿 x 轴作简谐振动，振幅 A = 0.12m，周期 T = 2s，当 t = 0 时， x0 = 0.06m，此时质点向 x 轴正向运动。求： （1）此简谐振动的表达式； （2）从初始时刻开始第一次通过平衡位置所需时间。 （3）ｔ=T/4时质点的 位置、速度和加速度； （4）从 x = - 0.06m 向 x 轴负向运动，第一次回到平衡位置所需的时间（思 考？）。
解：
2
1
23 6
质点 ２ 的振动超前质点 １的振动613xO
A
2
2
比较一下简谐运动的位移、速度、加速度的相位关系。
xA cots()
A si n t ()Acost(π)
aA 2cost()A 2cots( 2π)
速度的相位比位移的相位超前π/2 ，加速度的相位比位
x,v,a 移的相位超前π/2 。
5t
32 6
t
0.83(s)
y
x
o A3
求：（3）ｔ= T/4 时刻质点的位置、速度和加速度；
解： 由 振 动x表 0.1达 c2o式 st()： m ()
可 得 A ： si n t ( )
3
0.12sin(t-)(m/s)
3
aA 2cost()
0.062cots()(m /s2)
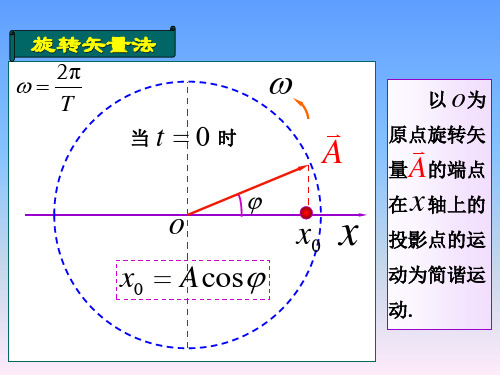
x0Acos
A 在 轴上的
x x 投影点的运 动为简谐运
动。
t t 时
A
t
o 以 为
原点旋转矢
量 的端点 A 在 轴上的
o
x x 投影点的运 动为简谐运
动。
xAcots()
旋转矢量求波动方程初相位
旋转矢量求波动方程初相位波动方程是描述波动传播的数学模型，在物理学中有着广泛的应用。
而确定波动方程的初相位，也就是波动的起始状态，对于理解波动的性质和特点起着重要的作用。
在研究波动方程的初相位之前，我们先了解一下什么是旋转矢量。
旋转矢量是指在空间中旋转方向和角度都确定的向量，它可以用来表示物体在空间中的旋转状态。
在电磁波的研究中，旋转矢量常常用来描述电磁波的偏振状态。
当电磁波传播时，光束中的光子会随着波动的传播而发生旋转。
这种旋转可以用旋转矢量来描述，它的大小和方向表示了波动的相位和偏振方向。
因此，确定波动方程的初相位就是确定旋转矢量的大小和方向。
在确定波动方程的初相位时，我们可以通过将电磁波的传播方向与垂直方向的夹角来确定旋转矢量的方向。
而旋转矢量的大小可以根据波动的振幅来确定。
波动的振幅表示了波动的强度，它越大，表示波动的能量越强。
除了振幅和传播方向外，确定波动方程的初相位还与波动的频率有关。
频率表示了波动的周期性，它与波长之间有一个固定的关系。
我们可以通过波动的频率来确定旋转矢量的速度，从而确定初相位。
总结起来，确定波动方程的初相位需要考虑波动的振幅、传播方向和频率。
通过将电磁波的传播方向与垂直方向的夹角确定旋转矢量的方向，再根据波动的振幅和频率确定旋转矢量的大小和速度，就可以确定波动方程的初相位。
确定波动方程的初相位对于研究波动的行为和性质具有重要的意义。
它可以帮助我们理解波动的传播机制以及与其相关的物理现象。
在实际应用中，通过确定波动方程的初相位，我们可以更好地控制和调整波动的特性，为光通信、雷达、医学成像等领域的技术发展提供有力支持。
通过对旋转矢量和波动方程初相位的探讨，我们可以更深入地理解波动现象的本质和特点。
这不仅是对物理学的研究有着重要的指导意义，也是为我们更好地理解和应用波动方程提供了有力的支撑。
我们期待在未来的研究中，能够进一步深化对波动方程初相位的认识，以推动科学技术的进步和发展。
16.3旋转矢量法
x x1 x2 xn
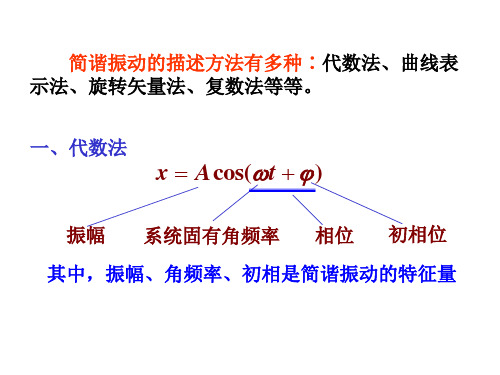
x A cos(t )
o
1 A1
2
A2
3
x
多个同方向同频率简谐运动合成仍为简谐运动 多个分振动的合成在说明光的干涉和衍射规 律时有重要的应用。
二
两个相互垂直的同频率简谐运动的合成
x A1 cos(t 1 ) y A2 cos(t 2 )
三个同方向、同频率的谐振动为
x 1 = 0.1cos(10t+π/6)m x 2 = 0.1cos(10t+π/2)m x 3 = 0.1cos(10t+5π/6)m
试利用旋转矢量法求出合振动的表达式。
解： A 1 = A 2 = A 3 = 0.1 φ1 = π φ2 = π 6 2 A´ = A 1 + A 3 A = A1 + A2 + A3 = A 2 + A´ A = 2 A 1 = 0.2 φ =π 2 A3
李 萨 如 图
1 0
π π 3π π 2 0, , , , 8 4 8 2
x ny x达到最大的次数 y nx y达到最大的次数
测量振动频率 和相位的方法
利用李萨如图形在无线电技术中可以测量频
率：在示波器上，垂直方向与水平方向同时输入
两个振动，已知其中一个频率，则可根据所成图 形与已知标准的李萨如图形去比较，就可得知另 一个未知的频率。
A
P x
注意：旋转矢量在第 2 象限 M 速度v < 0
A
P x
注意：旋转矢量在第 2 象限 速度 v 0 < M
A
P x
注意：旋转矢量在第 2 象限 速度v < 0
用旋转矢量法求受迫振动的振幅和初相
P H ASE OF FO R CED VIBRATI O N BY R OTATING VECTO RXu You w en Xu D i yu( D epa r t ment of Physics , S ichua n Vocatio n al and Technical College , S ui n i n g , S ichuan 629000)Abstract A cco r d i n g to t h e dyna m ic a n d ki n e matic equatio n s of fo r ced vi b ratio n , t h e a mp li2 t u de a n d i n itial p h a s e of fo rce d vi b ratio n a r e o b t a i n ed .K ey Words fo rced vi b ratio n ; ro t a ti n g vecto r ; a m p lit u de ; i n itial p ha s e系统在周期性外力作用下被强迫进行的振动,称为受迫振动. 受迫振动是工程技术中常见的振动. 研究受迫振动具有很大的意义. 求解受迫振动达到稳定状态时的振幅和初相, 一般书籍[ 1～6 ] 都是通过求解受迫振动的动力学方程而得出的,本文用旋转矢量法求受迫振动的振幅和初相.图 1受迫振动的动力学方程旋转矢量受迫振动所受的作用力有:准弹性力- k x 、如图1 所示,从O x坐标轴的原点O , 作一矢量 A ,其长度A 等于谐振动的振幅; t = 0 时 A 与O x 轴夹角等于初相φ; 并使 A 以大小等于谐振动角频率ω的角速度, 沿逆时针方向匀速转动, 这个矢量A 就称为旋转矢量.旋转矢量法是直观地研究谐振动的几何方法. 它不仅可以帮助人们形象地了解谐振动各物理量的含义及其相互关系, 而且便于对谐振动进谐激励力F0 co sωt 、与速度成反比的阻尼力- cv 因此,作受迫振动物体所受的合力为+ F0 co sωt -F = - k x由牛顿第二定律,得cv2md x= - k x + F0 co sωt - cv2d t2d x= - k x +F0sωt - c v∴d t2m m m取ω2 = k/ m ,2β= c/ m , f 0 = F0 / m ,并注意v =d x,0 d t代入上式得受迫振动的动力学方程为d2 x d x2+ 2βd t+ ω0 x = f 0 co sωt(1)d t2这是一个非齐次的常系数二阶微分方程.它的通解为A 0e -βt co s( 0 - β2 t + φ0 )ω2+ A c o s(ωt - δ)x =经过足够长的时间后, 其中第一项解减弱到可以忽略不计,只有第二项是振幅不变的振动.因此,受迫振动达到稳定状态时的运动学方程为[ 7]图 2作H G ⊥O G,在Rt △O G H 中,x = A c o s(ωt - δ)(2)F2 = ( B - D) 2 + C2式中A 是受迫振动稳态时的振幅;角频率等于简谐激励的角频率ω;δ是稳态响应与简谐激励的相差, 即受迫振动的初相. 式(2) 表示稳定状态的受迫振动是一个与简谐激励力同频率的简谐振动.f 2(ω2ω2 ) 2( βω) 2即=0 A - A + 2 A= A2 [ (ω2ω2 ) 2β2ω20 - + 4 ]βωA2βωC 2t a nδ===ω2 2 2 20 A -ω Aω0- ωB - D于是得受迫振动的振幅A 和初相δ分别为f 0用旋转矢量法求受迫振动的振幅和初相 A =(ω20- ω2 ) 2 + 4β2ω22βω由式( 2) 得δ= a r ct a nω2 2- ωd2 x= - ω A c o s(ωt - δ)2由此可知, 用旋转矢量法求受迫振动的振幅和初相,比用解微分方程的方法求解直观简单得多, 充分显示了用旋转矢量描述谐振动的优越性其实,任何谐振量都可以用旋转矢量来描述. 因此, 只要用得上旋转矢量法, 就要尽量应用它.d t2= ω2 A c o s[π+ (ωt - δ) ]2βd x = - 2βωA si n(ωt - δ)( 3)d tπ+ (ωt - δ)= 2βωA co s( 4)2参考文献ω20 x =ω0 A c o s(ωt - δ)2 (5)令B =ω2 A 、C = 2βωA 、D = ω2 A 、F = f 0 , 则式(3) 、0 [ 1 ] 赵景员, 王淑贤. 力学[ M ] . 北京: 人民教育出版社, 1979 .470～473赵凯华, 罗蔚茵. 力学[ M ] . 北京: 高等教育出版社, 1995 .273～275张三慧. 波动与光学[ M ]第2 版. 北京: 清华大学出版社,2000 . 24～25马文蔚,解希顺等. 物理学( 下册)[ M ] 第4 版. 北京:高等教育出版社,1999 . 30～31卢德馨. 大学物理学[ M ] . 北京: 高等教育出版社, 1998 .142～143刘克哲. 物理学(上卷) [ M ] 第2 版. 北京: 高等教育出版社,1999 . 155～156周圣源,黄伟民. 高工专物理学[ M ] . 北京: 高等教育出版社,1996 . 61 ,75( 4) 、( 5) 与式( 1) 的右边变为d2 x[ 2 ]= D co s[π+ (ωt - δ) ](6)d t2[ 3 ]π+ (ωt - δ)2βd x = C co s(7)2d t[ 4 ]ω20 x = B c o s(ωt - δ)( 8)(9)f 0 co sωt = F co sωt[ 5 ]将式(6) 、(7) 、(8) 、(9) 代入式(1) ,并用旋转矢量B 、C、D 、F 表示各谐振量, 则有F = B + C + D并且C ⊥B , D ⊥C.旋转矢量图如图2 所示.[ 6 ][ 7 ]。
大学物理12机械振动2
A
x x−t 图
T
ω v = − A ω sin( ω t + ϕ )
π = Aω cos(ωt +ϕ + ) 2 2 a = − A ω cos( ω t + ϕ )
= Aω cos(ωt +ϕ + π)
2
T=
2π
取ϕ = 0
− Aω
v v −t图 Aω o T
l = l0 1− (v / c)2
在飞船B上测得飞船 相对于飞船 的速度： 在飞船 上测得飞船A相对于飞船 的速度： 上测得飞船 相对于飞船B的速度
v = l / ∆t = (l0 / ∆t) 1−(v / c)
解得：v = l0 / ∆t 1 + (l0 / c∆t )
2
2
= 2.68 ×10
8
∆φ > π 3π 称振动（ ）落后于振动（ ） φ2 −φ1 > 0 例：φ2 −φ1= 2 称振动（2）落后于振动（1） 2π − ∆φ
分别作出四种情况的矢量图! 分别作出四种情况的矢量图!
2 4
∆ϕ21 = (ω t + ϕ2 ) - (ω t + ϕ1) = ϕ2 - ϕ1
φ2 −φ1 < 0 例：φ2 −φ1= − 3π称振动（2）超前振动（1） 2π + ∆φ 称振动（ ）超前振动（ ）
90
v am
ω
0
ω t+ϕ
·
x
1、用旋转矢量方法确定初相位ϕ： 、 要求条件： 的关系， 要求条件：已知 x0 与A的关系，初速度的方向。 的关系 初速度的方向。 例1： 已知一物体做简谐振动。1）x0=(1/2)A且向位移的 ： 已知一物体做简谐振动。 ） 且向位移的 且向位移的正方向运动。 负方向运动； ） 且向位移的正方向运动 负方向运动； 2）x 0= 0且向位移的正方向运动。试求 两种情况下的初相。 两种情况下的初相。 ϕ = π/3
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
x x π π ） + ］ = 0 ． 04cos［ 0 ． 8 π（ t － ） + ］ u 2 0 ． 08 2
若初始时刻质点不在原点， 可用类似的方法处理。 5 结 论 综上所述， 利用旋转矢量法可很方便地求解初相位问题 。实际教学表明， 利用这种方法讲解、 教学， 学生易懂且能很好的掌握。随着高校教学课时的不断压缩， 若老师直接讲解课本内容或不进行思考 ， 学 《大学物理》 《大学物理》 生在学习 时枯燥无味， 长期将厌恶 的学习。作为老师， 要想上好课， 则要求教师 利用课余时间多思考、 多总结、 多探究新的教学方法、 思路， 而不拘于课本。通过这样的教学方法可有效 提高教学效果。 参考文献：
第1 期
— —旋转矢量法 马业万， 刘全金， 等： 大学物理学教学中初相位的求解 —
· 99·
N 两点。 图 4， 初始位置为 M1 ， 末位置 M2 在 x 轴上的位置为 x1 = 12 cm， 过 x1 点作 x 轴的垂线可得 M2 ， 根据题意最先到达， 因旋转矢量是逆时针旋转， 所以 M1 最先旋转到的位置应为 M2 点， 这样即可确定旋 转矢量在 Δ t 时间所转过的角度为 ωΔ t = T T 4 π π π ， = × = = = 0 ． 667 s。 得 Δt = 3 3ω 3 2π 6 6 若初始时刻质点在其他位置， 可用类似的方法处理。 波动方程中求初相位的应用 波动方程的物理意义为： 空间所有质点位移随时间变化的整体情况 ， 且空间每个质点都在各自的位
· 98·
安庆师范学院学报（ 自然科学版）
2012 年
再看看旋转矢量图 1 中含有的隐含信息： ① 矢 量在轴上的投影即为简谐振动的质点在振动过程中 离开平衡位置的位移或质点的位置； ② 旋转矢量沿 逆时针旋转， 此即相当于说明矢量 A 在各位置的运 动方向。 在 y 轴正方向的所有点都沿 x 轴的负向运 动， 而在 y 轴负方向的所有点都沿 x 轴的正向运动。 因而当给出质点的初始位置及运动方向 ， 利用上述 性质可以很方便地找出与此相对应旋转矢量的位 置。
图2
以（ 1 ） 为例， 此类问题的求解， 可以按照以下五个步骤来求解： y 方向及原点 O， ① 首先做一个圆代表旋转矢量的旋转路径 ， 并分别标出 x， 图 2 中的（ a） ； 1 ② 其次确定质点的初始位置 x0 （ 质点在 x 轴上的位置， 本题即 x0 = A） ， 图 2 中的（ b） ； 2 M2 ， ③ 过 x0 作 x 轴的垂线， 垂线与圆的交点即为旋转矢量的初始位置 ， 此垂线与圆有两个交点 M1 ， 对应图 2 中的（ c） ； y 轴下方沿 x 轴的正向运动） 。 ④ 根据运动方向确定到底是 M1 还是 M2 （ y 轴上方沿 x 轴的负向运动， 本题物体沿 x 轴负向运动， 故选取 M1 ， 对应图 2 中的（ d） ； ⑤ 连接 OM1 ， 则 OM1 与 x 轴的夹角即为初相位。 利用直角三 角 形 关 系 可 很 方 便 地 求 解 其 初 相 位 为 φ = Acos（ π ， 因此相应的简谐振动方程为 x = 3
4
置作简谐振动。 在波动方程的推导过程中， 也是先求解坐标原点的振动方程 ， 再根据波传播的特点， 空间 其他点滞后或超前原点振动进而求得波动方程 。 因而波动方程的求解归根到底仍然要求解原点的振动 方程， 而坐标原点做简谐振动， 故同样涉及求解初相位问题。 在有关波的问题中通常给出波传播的波形 图， 首先必须根据波形图来确定坐标原点的振动方程 。 这一点可根据“左上左传， 右上右传 ”方法来判 断。 其含义为： 以波形图中的波峰为分界线， 波峰至最临近的波谷分别称为左侧与右侧 ， 见图 6 （ a） 。 如 果波峰左侧点向上振动（ 或波峰右侧点向下振动） ， 则波向左传播； 若波峰右侧点向上振动 （ 或波峰左侧 点向下振动） ， 则波向右传播。 同理， 如果波向左传播， 则波峰左侧点向上振动 （ 或波峰右侧点向下振 反之波向右传播， 则波峰右侧点向上振动（ 或波峰左侧点向下振动） 。 动） ， 一平面余弦波沿 x 轴正向传播， 其波速为 u = 0 ． 08 m / s， 波长为 λ = 0 ． 2 m。 当 t = 0 时其波 ［2 ］ 求波动方程 。 形曲线如图 5 所示， 例2
图3
图4
3
简谐振动运动中初相位的应用
有关简谐振动的问题也可利用旋转矢量法来求解质点从一位置运动到另一位置的时间 。 例 1 一质量为 0 ． 1 kg 的物体做简谐振动， 振幅为 24 cm， 周期为 4． 0 s。 当 t = 0 时， 位移为 24 cm。
［2 ］ 求由起始位置运动到 x = 12 cm 处所需最短时间？ 根据题意可知振幅 A = 24 cm， 初始位置为 x0 = 24 cm， 终点位置 x1 = 12 cm。 利用旋转矢量法可作
引 言 《大学物理》 教材中， 初相位的确定方法有两种： ① 根据简谐振动的初始条件求解。 教材中对这种 方法做了四种约定， 此方法比较繁琐， 学生在学习过程中不易掌握、 应用时易出错。②旋转矢量法求解。 0 实际教学中发现很多的学生不知如何运用旋转矢量法 。文章以此为出发点， 主要介绍用旋转矢量法求 解初相位的几点应用。 1 旋转矢量法的基本原理
2π 3π π π π t + ） ； 同理可求得 ⑵ 的初相位（ 图 3 ） 为 φ = － － =－ （ 注： 这里初相位的范围取 T 3 2 4 4 3π 7π 2π 3π + 2π = ）， t － ）。 相应的简谐振动表达式 x = Acos（ 4 4 T 4
（ － π， ， π］ 也有教材取 φ = －
图1
时针方向转过的角度为 ωt， 此时矢量 A（ 矢端位置 M2 ） 与 x 轴的夹角为 ωt + φ， 见图 1 。 由图 1 可知， 矢量 A 在 x 轴上的投影点 p 的位置为 x = Acos（ ωt + φ） ， 此表达式正是简谐振动的表达式 。 因此， 旋转矢量 A 的矢端 M2 在 x 轴上的投影点 p 的运动， 可表示为物体在 x 轴上的简谐振动。 矢量 A 旋转一周， 相当于物 体在 x 轴上作一次完整的全振动。 由图 1 不难看出， 当 t = 0 时即初始时刻， 矢量 A 与 x 轴的夹角 φ 即为初相位， 因而在旋转矢量图示 。 中， 简谐振动的初相位即为初始时刻矢量 A 与 x 轴的夹角。 初相位的取值范围通常为（ － π， π］ 因此， 利 用旋转矢量法的图示可很方便地求解初相位 。 2 旋转矢量法求解初相位 在利用旋转矢量法求解初相位时 ， 前提必须要找到 t = 0 时刻矢量 A 的位置， 只有这样才可以判断 其与 ox 轴的夹角。 那么如何判断其初始位置？ 一般来讲， 题目通常都会给出初始时刻简谐振动质点的初 始位置及运动方向（ 即速度沿 x 轴正或负向运动） ， 那么这些信息是如何体现在旋转矢量法的图示中呢 ？
《操作系统》 、 《计算机组装原理 》 的其它一些计算机专业课程教学中去 ， 如 等。 这就要求教师多用类比 教学法， 将抽象的理论知识结合日常生活中的实例 ， 进行形象类比。 对抽象知识点概念讲解的基础上， 类比生活中的一些熟悉实例， 这样才能降低学生对抽象专业知识理解的难度 ， 从而激发学生学习兴趣， 这也正是形象类比法在教学中的优势所在 。 参考文献：
* 收稿日期： 2011 － 11 － 14
基金项目： 安庆师范学院青年基金项目（ KJ201008 ） 资助。 作者简介： 马业万， 男， 安徽六安人， 安庆师范学院物理与电气工程学院讲师， 研究方向： 近场光学数值计算、 金属纳米光学性质； 刘全金， 男， 安徽六安人， 安庆师范学院物理与电气工程学院副教授； 章礼华， 男， 安徽太湖人， 安庆师范学院物理与电气工程学院副教授； 张 杰， 男， 安徽桐城人， 安庆师范学院物理与电气工程学院教授。
［2 ］ 《大学物理学 》 教材课后习题中有这样一道 习题， 一个沿 x 轴作简谐振动的弹簧振子， 振幅为 A，
周期为 T， 求其振动方程并用余弦函数表示。 如果 t 1 = 0 时质点的状态方程分别为： （ 1 ） 过 x0 = A 处向 2 2 x 轴负方向； （ 2 ） 过 x0 = － 槡 A 处向 x 轴正方向； 2
— — 旋转矢量法 大学物理学教学中初相位的求解 —
马业万， 刘全金， 章礼华， 张 杰
（ 安庆师范学院 物理与电气工程学院，安徽 安庆 246133 ）
摘
要： 在大学物理中有关振动方程和波动方程的教学中发现， 很多学生不知怎么求解振动方程和波动方程， 其主
论述如何用旋转矢量法来求解初相位 。 通过旋转 要原因是大多学生不知如何求解初相位 。文章从实际教学过程出发， 矢量法来求解初相位， 方法简捷， 学生学习起来方便、 易懂。 关键词： 旋转矢量法； 初相位； 振动方程； 波动方程 中图分类号： O4 － 42 文献标识码： A 文章编号： 1007 － 4260 （ 2012 ） 01 － 0097 － 03
图5
图6
根据此性质可很方便地求得波形图中各点的振动特点 。 本题中给出波向右传播而波源点 O 在波峰 6 （ a ） ， O 。 的左侧见图 故 点向下振动 因坐标原点的初始位置在原点或平衡位置 ， 这表明坐标原点初始位 置在平衡位置且沿负向运动。 因而利用旋转矢量法（ 图 6 （ b） ） 可很方便地确定 O 点的初相位为 φ = 所以 O 点的简谐振动方程为 y = Acos（ ωt + φ） = 0 ． 04cos（ 0 ． 8 πt + y（ x， t） = 0 ． 04cos［ 0 ． 8 π（ t － π ）， 相应的波动方程为 2 π ， 2