旋转矢量法
旋转矢量法在简谐振动中的应用探讨
旋转矢量法在简谐振动中的应用探讨摘要：结合旋转矢量法的理论依据探究旋转矢量法在简谐振动中的应用，探究结果发现：旋转矢量法的理论依据是两个振幅相等，频率相同的简谐振动，相位差等于π/2，沿垂直方向的合成就是圆周运动；而旋转矢量法可计算简谐振动的矢端速度与加速度、相位与初相位、运动时间间隔及合振动。
关键词：旋转矢量法；简谐振动；应用0.旋转矢量法旋转矢量法[1]，也叫匀速圆周运动法，参考圆法，用其方法来解决简谐振动中的问题，相对来说比较简单。
如图1，做一个圆周，以O为原点，向右为正方向建立坐标轴，根据题目条件确定半径位置，要观察的是半径的端点在x轴上的投影的位置，如果速度为正，半径端点一定处于x轴下方，反之在x轴上方，比如，t＝0时，质点正经过平衡位置向正方向运动，那么这个半径端点就是在原点正下方，即端点的投影刚好在原点[2]。
而以O为原点的旋转向量A的端点与在x 轴上的投影点的运动为简谐振动。
图1 旋转矢量图2 相位差为π/2互相垂直简谐振动的合成1.简谐振动矢量法的理论依据互相垂直相同频率简谐振动的合成[3]，现将分振动的运动学方程表示为，，质点既沿Ox轴又沿Oy轴运动，实际上是在Oxy平面上运动。
从上面方程消去t，得合振动的轨迹方程：=。
当相位差为时，，表明合振动的轨迹为以x和y为轴的椭圆，如图2所示这里又可分为两种情况，时，x方向的振动比y方向的振动超前，即，当某一瞬时，则x=0，y=A2，即质点在图2(a)中的P点，经过很短时间后略大于零，y将略小于A2，为正，而略大于，x将为负，故质点运动到第二象限，即质点沿椭圆逆时针运动。
反之，时，y方向的振动比x方向的振动超前，质点沿椭圆顺时针方向运动，如图2（b）。
以上两分运动中，若=且相位差为，则其合运动轨迹方程褪化为圆。
两个振幅相等，频率相同的简谐振动，相位差等于沿互相垂直方向合成的为圆周运动；反推理可得，圆周运动亦能分解为两互相垂直的同振幅同频率的简谐振动。
简谐振动的旋转矢量图示法
解：
点 2 在 x = - A / 2 处 向 右 运 动 ， 试 用 旋
转 矢 量 法 求 两 质 点 的 相 位 差 。 1
3
x
2
4
3
2
A
2A
O
1
A 2
2143 3
例2、一物体沿x轴作简谐振动，振幅A=0.12m,周期 T=2s。当t=0时,物体的位移x=0.06m,且向x轴正向运
动。求: (1)简谐振动表达式;
向正方向运动,求运动方程。
解：(1) k 0.726.0s-1
m 0.02
由旋转矢量可知初相位 谐振动方程为
0 0
0.05
O
x
x0.05cos(6.0t) m
第一次经过A/2时，相位
(2) v dx 0.056.0sin(6.0t) dt
=0.3sin(6.0t) m/s
6.0t 3
OA
0, x=0.06m可
得0 3
或
3
简谐振动表达式
01
02
03
04
v0Asin00
由于t=0时质点 向x轴正向运动
0 3
因而
可知
x0.12cos(t) m
3
(2)由简谐振动的运动方程可得:
vdx0.12sin(t) m /s
dt
3
adv 0.12 2cos(t)m /s2
dt
3
在t =T/4=0.5s时，可得
A 的长度
振幅A
A 旋转的角速度
角频率ω
A 与参考方向x 的夹角
振动相位ωt+φ0
相位之差为
x1A1cos(t1)
x2A2cos(t2)
旋转矢量表示法B版
1 2
⎞ ⎟ ⎠
−
π⎤
3
⎥ ⎦
=
2 π
⎡ 2π ⎢⎣ 3
−
π⎤ 3 ⎥⎦
=
2 3
=
0.667(s)
四、相图（phase diagram）
利用相图描述非线性动力学的方 法是19世纪末法国数学家亨利·庞加 莱（H.Poincare）发明的.
现以坐标和速度为坐标轴定义一 个平面, 称为相平面. 系统的一个运 动状态对应于相平面上的一个点, 称 为相点. 当系统的运动状态发生变化 时, 相点在相平面内运动, 相点的轨 迹则称为相图.
A 端投影:
x = A cos(ωt + ϕ )
与简谐运动方程完全相同, 所以投影点的运动为简谐运动.
二、初相位
ϕ = π平衡位置 2
旋转矢量表示法
π <ϕ <π 2
ϕ
ϕ=π
负向最大
π 0<ϕ<
2
x ϕ=0
正向最大
π < ϕ < 3π 2
3π < ϕ < 2π 2
ϕ = 3π 平衡位置 2
初相位讨论
大学物理
振动学基础
第3讲 旋转矢量表示法
旋转矢量表示法
旋转矢量表示法
一、旋转矢量表示法(参考圆法)
是研究简谐运动规律时所采用的直观的几何描述方法.
自 Ox 轴原点作矢量 A , 其模等 于振幅. A 绕 O点逆时针旋转, 角 速度为ω (其数值即为简谐运动的 角频率) , 则 A 称为旋转振幅矢量. 设初始时刻 t = 0 时 A 与 x 轴夹角 等于初相位 ϕ , 经过时间 t , A 与 x 轴夹角等于相位ω t +ϕ .
旋转矢量法简谐运动的动力学能量实例
旋转矢量与简谐运动的关联
旋转矢量与简谐运动的振动方向和速度相关联，通过旋转矢量的几何特性可以推 导出简谐运动的振动方程和能量表达式。
旋转矢量法可以直观地表示简谐运动的振动形式，帮助理解振动的合成与分解， 以及振动在不同方向上的表现。
对未来研究的展望
随着科学技术的不断发展，旋转矢量法在简谐运动研究中 的应用将更加广泛和深入。未来可以进Байду номын сангаас步探索旋转矢量 法在其他领域的应用，如量子力学、光学等。
未来研究可以进一步优化旋转矢量法的计算方法和可视化 效果，提高其精度和直观性，以更好地服务于科学研究和 技术创新。
THANKS
感谢观看
旋转矢量法简介
01
旋转矢量法是一种描述简谐运动 的直观方法，通过引入一个旋转 矢量来表示振动的状态。
02
旋转矢量具有长度和方向，分别 对应振动的振幅和相位，矢量的 旋转速度则与角频率有关。
02
旋转矢量法在简谐运动中的应用
旋转矢量表示
旋转矢量表示是一种用于描述简谐运 动的几何方法，通过引入一个旋转矢 量来表示简谐运动的相位和振幅。
简谐运动的定义
简谐运动
物体在一定力的作用下，以一定的初速度做周期 性往复运动。
描述参数
振幅、角频率、初相角、周期等。
实例
单摆、弹簧振子等。
简谐运动的数学模型
微分方程
$mfrac{d^2x}{dt^2}
+
cfrac{dx}{dt} + kx = F$
旋转矢量法
通过旋转矢量表示简谐运动的相 位和振幅，简化分析过程。
简谐振动-旋转矢量法
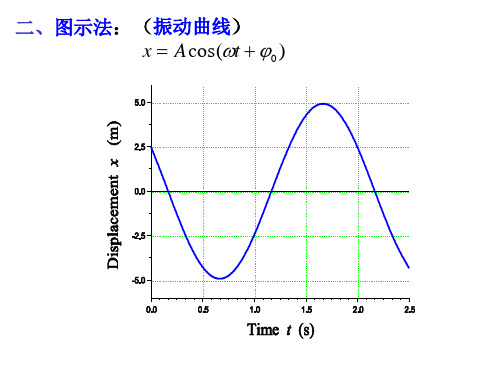
sin2 (2 1)
y
2） 2 1 π
y A2 x A1
3）2 1 π 2
x A2
o A1
x2 A12
பைடு நூலகம்
y2 A22
1
x A1 cost
y
A2
cos(t
π) 2
A2 y
o A1 x
用 旋 转 矢 量 描 绘 振 动 合 成 图
两
相
互 垂 直 同 频 率 不 同 相
简 谐 运 动 的 合 成 图
x
x
A1 o
o
A
A2
A A1 A2
Tt
结论
A A12 A22 2A1 A2 cos(2 1 )
若两分振动同相位：
2 1 2k k 0,1, 2,
A A1 A2
若两分振动反相位:
两分振动相互加强
2 1 (2k 1) k 0,1, 2,
A A1 A2
两分振动相互减弱
再若 A1= A2 , 则 A= 0
M
A
P
x
注意：旋转矢量在第 2 象限
速度v <0
M
PA
x
注意：旋转矢量在第 2 象限
速度v <0
M
PA
x
<
注意：旋转矢量在第 3 象限
速度v 0
P x
MA
<
注意：旋转矢量在第 3 象限
速度v 0
P x
A
M
<
注意：旋转矢量在第 3 象限
速度v 0
P x
A
M
<
注意：旋转矢量在第 3 象限
速度v 0
找到谐振动的特征量，问题就解决了。
4-1-2简谐运动旋转矢量法简谐运动的动力学讲解
-A1
的相位角来判断。
1
2
, 2
0
1
3
2
,
2
0
2-1>0 ，x2比x1超前 π/2 1-2>0 ，x1比x2超前 3π/2
位 移 ：x(t) Acos(t )
速 度 ：(t) Asin(t )
加 速 度 ：a(t) 2 x(t)
x、 、a
2A
A
A
x
o
-A
- A
dt
2
a(t)
d 2 x(t) dt 2
2 Acos(t
)
2 x(t)
m
加速度与位移成正比而反向
x、 、a
2A
A
A
x
o
-A
- A
- 2A
a < 0 a<0 加速
<0 >0 减速
o
x
x
>0 >0 加速
T t
>0 <0 减速
三. 描述简谐运动的特征量 x(t)=Acos( t+)
1.振幅A(amplitude) 偏离平衡位置的最大距离 其值与运动如何开始有关
波动与光学
第1章 振 动 (Vibration)
生活中观察的：摇曳的树枝、飘荡的小船， 人类发明中的：颤动的琴弦或鼓膜， 人类自身中的：声带、耳膜、心脏， 不易感觉的：传递声音的空气分子的振动、
传递温度的固体内原子的振动、 传递信息的天线中电子的振动…… 周期性过程：指不断有规律重复的过程或状态。
2.周期T (period) 振动往复一次所需时间 频率v (frequency) 单位时间内的振动次数
旋转矢量
v
x/m
0.08 0.04 o 0.04 0.08
第九章 振 动
11
物理学
第五版
9-2 旋转矢量
已知 m 0.01kg, A 0.08 m,T 4 s
t 0, x 0.04 m, v0 0 求（1）t 1.0 s, x, F
解 A 0.08 m 2 π π s1
第九章 振 动
4
物理学
第五版
9-2 旋转矢量
用旋转矢量图画简谐运动的x t图
第九章 振 动
5
物理学
第五版
9-2 旋转矢量
讨论 相位差：表示两个相位之差
（1）对同一简谐运动，相位差可以给出 两运动状态间变化所需的时间．
x1 Acos(t1 )
x Acos(t )
2
2
(t ) (t )
(A) 0～π/2之间． (B) π/2～π之间． (C) π～3π/2之间． (D) 3π/2～2π之间。
解：位移向下为正。当小盘处在最低位置时刻有一个小
物体落到盘上，则振子系统向下还是向上运动？
考虑到新的平衡位置相对原平衡位置向下移动的距离小于 原振幅，位移接近正的最大值，速度向下。采用旋转矢量 法可知初相位在第四象限。
物理学
第五版
选择进入下一节：
本章目录
9-1 简谐运动 振幅 周期和频率 相位
9-2 旋转矢量
9-3 单摆和复摆
9-4 简谐运动的能量
9-5 简谐运动的合成
* 9-6 阻尼振动 受迫振动 共振
第九章 振 动
19
法一 设由起始位置运动到x= -0.04 m处所 需要的最短时间为t
v x/m
9-2旋转矢量
理学院 物理系
大学物理
§9-2 旋转矢量
一质量为0.01 kg的物体作简谐运动, 的物体作简谐运动, 例 一质量为 的物体作简谐运动 其振幅为0.08 m,周期为 s,起始时刻物体在 其振幅为 ,周期为4 , x=0.04 m处,向ox轴负方向运动(如图).试求 轴负方向运动( 轴负方向运动 如图) (1)t=1.0 s时,物体所处的位置和所受的力; ) 时 物体所处的位置和所受的力; 2)由起始位置运动到x m处所需要 (2)由起始位置运动到x = -0.04 m处所需要 的最短时间. 的最短时间
t = 0, x = 0 . 04 m 代入 x = A cos( ω t + )
π ∵ v 0 < 0 ∴ = 3
0.08 0.04
ωቤተ መጻሕፍቲ ባይዱ
π =± 3
A
o
π 3
x/m
0.08
0.04
理学院 物理系
大学物理
§9-2 旋转矢量
π ∵ = 3 π π ∴ x = 0.08cos( t + ) 2 3 t 可求( ) 可求(1) = 1.0 s, x, F t = 1 .0 s 代入上式得 x = 0.069 m
大学物理
§9-2 旋转矢量
速度也是简谐振动
dx v= = ωAsin(ωt + 0 ) dt
v(t ) = ωAcos(ω t +0 +
x=Acos(ω t+0 )
π
2
)
v 比 x 超前 π/2
加速度也是简谐振动, 加速度也是简谐振动,a 比 x 超前 π
8.2 简谐振动的旋转矢量表示法
简谐振动的矢量图 这与简谐振动定义式完全相同。由此可知，旋转矢量的端点在x轴上的投影的运动就是简谐振动。显然，一个旋转矢量与一个简谐振动相对应，其对应关系是：旋转矢量的长度就是振动的振幅，因而旋转矢量又称为振幅矢量；矢量的角位置就是振动的相位，矢量的初角位置就是振动的初相，矢量的角位移就是振动相位的变化；矢量的角速度就是振动的角频率，即相位变化的速率；矢量旋转的周期和频率就是振动的周期和频率。我们在讨论一个简谐振动时，用上述方法作一个旋转矢量来帮助分析，可以使运动的各个物理量表现得直观，运动过程显示得清晰，有利于问题的解决。
ω=ΔΦ/Δt=2π/3
故质点的振动方程为
(cm)
【例3】一质点沿x轴作简谐振动，振幅A=0.12m，周期T=2s，当t=0时，质点对平衡位置的位移x0=0.06m，此时刻质点向x正向运动。求：
(1)简谐振动的运动方程；
(2)t=T/4时，质点的位移、速度、加速度。
8.2 简谐振动的旋转矢量表示法
简谐振动除了用谐振方程和谐振曲线来描述以外，还有一种很直观，很方便的描述方法，称为旋转矢量表示法。在一个平面上作一个Ox坐标轴，以原点O为起点作一个长度为A的矢量A，A绕原点O以匀角速度ω沿逆时针方向旋转，称为旋转矢量，矢量端点在平面上将画出一个圆，称为参考圆。设t=0时矢量A与x轴的夹角即初角位置为φ，则任意t时A与x轴的夹角即角位置为，矢量的端点M在x轴上投影点P的坐标为
【解】
(1) 取平衡位置为坐标原点。设位移表达式为
其中 A=0.12m，，下面我们用矢量图来求初相φ。由初始条件，t=0时x0=0.06m=A/2，质点向x正向运动，可画出如图(a)所示的旋转矢量的初始位置（图中略去了参考圆），从而得出。于是此简谐振动的运动方程为
简谐振动的旋转矢量图示法
6.0t 6.0t =
π
π
3
A 2
x
3 v = −0.3sin( ) = −0.3 × = −0.26 m/s 3 2
(3) 由初始条件，t=0,v0=0.30m/s, x0=0.05m,可得 由初始条件， 可得
A′ = x0 2 +
ω
v0 2
2
= 0.0707 m
v0 ϕ0 = arctan − （ ）= arctan − 1 （ ） x0ω
k = m
0.72 = 6.0 s -1 0.02
由旋转矢量可知初相位 谐振动方程为
ϕ0 = 0
O
0.05
x
x = 0.05cos(6.0t ) m
dx = −0.05 × 6.0sin(6.0t ) (2) v = dt = − 0.3sin(6.0t ) m/s
第一次经过A/2时 第一次经过 时，相位
3π 设物体在t 时刻第一次回到平衡位置， 设物体在 2时刻第一次回到平衡位置，相位是 2
1 π 2π 4π π t1 − = 或 cos(π t1 − ) = − 3 3 3 3 2 π π 2π ∴π t1 − = Qv0 = −ω Asin(π t1 − ) < 0 3 3 3 t1 = 1s
3π ϕ0 = − 或 4 4
π
O
4
x
x = 0.0707 cos(6.0 t −
π
4
)m
v0 = −ω Asinφ0 > 0
因而 简谐振动表达式
φ0 = −
π
3
x = 0.12 cos(π t − ) m 3
π
(2)由简谐振动的运动方程可得 由简谐振动的运动方程可得: 由简谐振动的运动方程可得
旋转矢量法的原理和应用
旋转矢量法的原理和应用1. 原理介绍旋转矢量法是一种用于描述物体在三维空间中进行旋转的数学方法。
它通过使用矢量的旋转运算来表示物体的旋转姿态。
旋转矢量法基于欧拉角的表达方式，但它使用四元数来进行计算，避免了欧拉角的一些问题，例如万向锁问题。
2. 旋转矢量的表示旋转矢量通常由一个单位四元数表示，该四元数可以表示物体绕任意轴的旋转。
一个旋转矢量可以通过一个轴向量和一个旋转角度来确定。
轴向量定义了旋转轴的方向，旋转角度表示物体绕轴旋转的量。
3. 旋转矢量的计算为了应用旋转矢量进行对象的旋转，需要进行一些数学计算。
首先，需要将旋转矢量转换为一个旋转矩阵。
然后，可以使用该旋转矩阵将对象的顶点或其他坐标进行变换，以实现旋转效果。
4. 旋转矢量的应用旋转矢量法在计算机图形学和游戏开发中得到了广泛应用。
它可以用于实现物体的旋转、旋转动画和摄像机的旋转等效果。
此外，旋转矢量法还可以用于物体的插值和平滑过渡，例如在两个姿态之间进行插值，以实现流畅的动画效果。
5. 旋转矢量法的优势相比于传统的欧拉角表示，旋转矢量法具有以下几个优势： - 万向锁问题：使用旋转矢量法可以避免欧拉角的万向锁问题，使得旋转计算更加稳定和可靠。
- 插值效果：旋转矢量法可以实现更顺滑的插值效果，使得物体在动画中的过渡更加自然。
- 计算效率：由于使用四元数进行计算，旋转矢量法通常比欧拉角计算更快，尤其是在需要进行大量的旋转计算时。
6. 示例应用场景下面是一些示例应用场景，展示了旋转矢量法的一些实际应用： - 3D建模软件：在3D建模软件中，旋转矢量法被用于实现物体的旋转和变换操作，帮助用户进行建模和设计。
- 游戏开发：旋转矢量法在游戏开发中被广泛使用，用于实现游戏角色的旋转、摄像机的控制以及动画的实现。
- 航空航天领域：旋转矢量法可以应用于飞行器的姿态控制，帮助飞行器保持平稳的飞行姿态和准确的导航。
7. 总结旋转矢量法是一种用于描述物体旋转的数学方法，通过使用旋转矢量来表示物体的旋转姿态。
旋转矢量法详细讲解
旋转矢量法详细讲解
旋转矢量法是一种常用的三维刚体运动描述方法，它可以描述刚体在空间中的旋转状态。
本文将详细介绍旋转矢量法的原理、应用以及计算方法。
一、原理
旋转矢量法的基本原理是将刚体的旋转运动分解为绕三个互相垂直的轴的旋转运动的组合。
这三个轴分别称为x轴、y轴和z轴，它们的方向与刚体的坐标系有关。
在旋转矢量法中，用一个三维向量来表示刚体的旋转状态，这个向量被称为旋转矢量。
二、应用
旋转矢量法广泛应用于机械工程、航空航天、地球物理学等领域。
在机械工程中，旋转矢量法可以用于描述机械零件的旋转状态，从而进行运动学和动力学分析。
在航空航天领域，旋转矢量法可以用于描述飞行器的姿态和轨迹，从而进行导航和控制。
在地球物理学中，旋转矢量法可以用于描述地球的自转和地震波的传播，从而进行地震学研究。
三、计算方法
旋转矢量的计算方法有多种，其中最常用的是欧拉角法和四元数法。
欧拉角法是将旋转运动分解为三个绕不同轴的旋转运动的组合，然后通过三个角度来描述这三个旋转运动的大小和方向。
四元数法是将旋转运动表示为一个四元数，通过四元数的乘法和加法来描述旋转运动的组合。
四、总结
旋转矢量法是一种常用的三维刚体运动描述方法，它可以描述刚体在空间中的旋转状态。
旋转矢量法广泛应用于机械工程、航空航天、地球物理学等领域。
旋转矢量的计算方法有多种，其中最常用的是欧拉角法和四元数法。
掌握旋转矢量法的原理和计算方法，对于进行三维刚体运动分析和控制具有重要的意义。
旋转矢量法
2.旋转矢量图法及其应用同学们好！旋转矢量法可以形象地表示简谐振动位移和时间关系，便于确定初相位，研究振动的合成。
下面我们一起学习旋转矢量法。
简谐振动的平衡位置为坐标原点O 点，水平向右为轴正方向，自原点O 点做一个矢量，矢量长度等于振幅A ，叫振幅矢量。
初始时刻，矢量A 与x 轴夹角等于振动的初相位ψ。
矢量A 从这位置以ω的角速度沿逆时针方向匀速转动，在任一时刻t ， 矢量A 与轴所成角度为ωt+ψ。
矢量A 在轴上的投影点与简谐振子的小球同步运动，位移相等，它在x 轴上的投影与时间用关系可用简谐振动方程表示。
矢量A 旋转一周，同时矢量的矢端在轴上的投影点完成一次简谐振动，投影点的运动可以形象地表示简谐振动，这种方法叫做旋转矢量法。
使用旋转矢量法还可以形象地了解简谐振动的振幅、角频率、初相位的物理意义。
显然，矢量A 做圆周运动的周期对应简谐振动的周期T ；矢量A 的圆周运动角速度对应简谐振动的角频率ω；初始时刻，旋转矢量的角度对应简谐振动的初相位ψ。
另外，使用旋转矢量法可以方便的确定物体的振动状态或初相位。
1. 由相位确定振动状态(1)简谐振动的相位是π/3，求振动状态I .旋转矢量图中，矢量A 的相位等于π/3，矢量A 的投影是物体的位移，等于A /2, 下一时刻矢量A 逆时针转动，所以简谐振动的小球向x 轴负方向运动。
(2)如果简谐振动的相位等于3π/2，求振动状态。
在旋转矢量图中，矢量A 的相位等于3π/2，矢量的投影点在x 轴的投影恰好在原点O , 所以物体的位移等于0， 矢量A 做逆时针转动，所以简谐振动的小球向x 轴正方向运动。
x x x2.由振动状态求初相位初始时刻，简谐振动的物体位移是A/2, 物体向x轴正方向运动，也就是速度大于0，初相位是多少？图中，矢量A在x轴的投影是A/2，表明矢量在第一或第四象限，且投影点向x轴正方向运动，从图示来看矢量A只能在第四象限。
因此初相位等于5π/3或-π/3。
9-2旋转矢量法求相位
9-2
旋转矢量
旋转矢量
自Ox轴的原点 O作一矢量 A，使 它的模等于振动的 振幅A ，并使矢量A 在 Oxy平面内绕点 O作逆时针方向的 匀角速转动，其角 速度 与振动频率 相等，这个矢量就 叫做旋转矢量.
第九章 振 动
1
物理学
9-2
旋转矢量
x A cos(t )
以 o 为原 点旋转矢量 A 的端点在 x 轴 上的投影点的 运动为简谐运 动.
第九章 振 动
2
物理学
9-2
旋转矢量
t 0
A
o
x0
x
x0 A cos
以 o 为原 点旋转矢量 A 的端点在 x 轴 上的投影点的 运动为简谐运 动.
第九章 振 动
3
物理学
9-2
旋转矢量
t t
t
A
x
o
x A cos(t )
以 o 为原 点旋转矢量 A 的端点在 x 轴 上的投影点的 运动为简谐运 动.
0.08 0.04
o
0.04
0.08
12
第九章 振 动
物理学
9-2
旋转矢量
π 3 π π x 0.08 cos( t ) 2 3 t 1.0 s, x, F 可求（1） t 1.0 s 代入上式得 x 0.069 m
F kx m 2 x 1.70 10 3 N
x2 Acos( t2 )
第九章 振 动
7
物理学
9-2
旋转矢量
x
A A2
a
b
t
o
A
旋转矢量法求初相位_概述及解释说明
旋转矢量法求初相位概述及解释说明1. 引言1.1 概述旋转矢量法是一种用于求解信号初始相位的数学方法，广泛应用于信号处理领域。
在许多实际问题中，准确确定信号的初相位对于数据分析和系统性能评估至关重要。
通过应用旋转矢量法，我们可以有效地估计信号的初相位，并将其应用于各种领域，如通信、雷达、图像处理等。
1.2 文章结构本文将按照以下结构进行介绍和解释：- 引言部分将对旋转矢量法求初相位的背景和意义进行概述。
- 旋转矢量法求初相位的理论基础将在第2节中详细阐述。
- 第3节将解释和说明旋转矢量的定义、性质以及该方法在信号处理中的作用。
- 第4节将介绍相关实验验证和结果分析。
- 最后一节为总结与展望，对本文内容进行概括，并探讨旋转矢量法求初相位在未来的应用前景。
1.3 目的本文的目的是全面介绍旋转矢量法求初相位这一方法，并从理论到实践层面进行详细阐述。
通过对方法的解释和说明，我们将揭示旋转矢量法在信号处理中的作用以及确定初相位的优势和局限性。
此外，通过实验验证和结果分析，我们将进一步验证该方法的有效性并提供相关数据支持。
最终，本文旨在为读者提供一个清晰全面的概述，并展望旋转矢量法求初相位在未来应用中可能发挥的重要作用。
2. 旋转矢量法求初相位2.1 理论基础旋转矢量法是一种用于求解信号的初相位的方法，基于信号在复平面上的表示和分析。
该方法利用了旋转矢量在复平面上的特性，通过对信号进行复数域运算和变换，得到信号的频率和初相位信息。
在时域中表示的信号可以看作是复平面上绕原点进行旋转的矢量。
根据欧拉公式，可以将一个复数表示为振幅与相位之间关系的指数形式：A*e^(jφ)，其中A为振幅，φ为相位角。
2.2 方法步骤旋转矢量法求解信号的初相位主要包括以下几个步骤：步骤1：获取待处理的信号数据，并进行预处理。
这一步通常包括去除噪声、滤波和采样等操作，以确保信号质量。
步骤2：对信号进行傅里叶变换或小波变换等频域变换，得到信号在频域上的表示。
大学物理第三讲：8.1.3旋转矢量法
瞬时对应
1、旋转矢量A的长度为简谐振动的振幅 2、φ为t=0时的相位（初相位） 3、（ωt+φ)为t时刻的相位 4、旋转矢量A作逆时针匀速运动（ω角速度）
5、旋转矢量A的末端在参考坐标轴上的投影点的运动即代表质 点做简谐振动。
二、旋转矢量的长处
1、用旋转矢量A来表示简谐振动的位移
x Acost 当 0时 x t曲线
x/cm
t/s
o
9
三、应用举例
已知两个同方向，同频率的简谐振动如下：
x1 5cos10t / 2 x2 5cos10t
A 50cm
5 / 4或 3 / 4
用计算法求它们合振动的振幅和初相位。
已知：A1 A2 5cm；
x/cm
1 / 2;2
t/s
o 求：1合振动的振幅：A A12 A22 ;
16
谢谢大家！ 欢迎大家多提宝贵意见！
2015.10.10
17
18
合振动的初相位：2 ?
8-18 已知两个同方向、同频率的简谐振动如下： x1 5102 cos(10t 3 / 5) SI x2 6102 cos(10t / 5) SI
（1）求它们合振动的振幅与初相位；
（2）另有一个同方向简谐振动 x3 7 102 cos(10t )SI
问值为何值时， x1 x2的振幅最大？ 问值为何值时， x2 x3的振幅最小？
0.05sin 3 0.06sin
5
0.05cos 3
5
0.06 c os
arctan2.5 1.19rad 6813
5
5
12
（2）已知：
x1 5102 cos(10t 3 / 5) SI x2 6102 cos(10t / 5) SI
旋转矢量法
同学们好！
弹簧的伸长 势能
总能
F kx
离系统平衡位置的位移
kx2 2 准弹性势能，
kx2 2
弹性势能
重力势能和弹性势能的总和
1 1 1 mv 2 kx2 kA2 2 2 2
统一描述：只要以平衡位置为坐标原点和零势点
1 2 准弹性势能: 1 Ep kx E kA2 2 （包括重力势能、弹性势能） 2
运动 cos( t ) m 方程：
由初始条件决定
l T 2 g
2
二、复摆：绕不通过质心的光滑水平轴摆动的刚体 由刚体定轴转动定律
M J
d 2 m ghsin J 2 dt d 2 m gh sin 0 2
dt J
o
C
h
J
令
mgh J
{ v A sin( t )
0
x A cos( t 0 )
1 E Ep Ek kA 2 恒量 2
孤立谐振动系统机械能守恒
x, v
E-t 曲线
o
能量
x t
T
0 t x Acost v t v A sin t
1 2 E kA 2 1 2 Ep kA cos 2 t 2
简谐运动的描述和特征 1）物体受线性回复力作用
F kx 平衡位置 x 0
旋转矢量法详细讲解
旋转矢量法详细讲解
旋转矢量法是一种常用的三维空间中的旋转变换方法，它可以将一个三维向量绕着某个轴旋转一定的角度，从而得到一个新的向量。
这种方法在计算机图形学、机器人学、航空航天等领域都有广泛的应用。
旋转矢量法的基本思想是，将旋转变换分解为两个步骤：先将原向量绕着一个固定的轴旋转到一个特定的位置，再将其绕着另一个轴旋转到最终的位置。
这两个步骤可以用两个旋转矩阵来表示，它们的乘积就是最终的旋转矩阵。
具体来说，假设我们要将一个向量v绕着轴n旋转θ角度，那么首先需要将v投影到n所在的平面上，得到一个新的向量v'。
然后，将v'绕着n旋转θ/2角度，得到一个新的向量v''。
最后，将v''再绕着n的负方向旋转θ/2角度，就得到了最终的旋转向量。
旋转矢量法的优点在于，它可以避免旋转矩阵中的奇异性问题，从而提高计算的稳定性和精度。
此外，它还可以方便地进行复合旋转，即将多个旋转变换组合起来进行计算。
需要注意的是，旋转矢量法只适用于绕着固定轴进行旋转的情况，如果需要进行任意方向的旋转，就需要使用四元数或欧拉角等其他方法。
旋转矢量法是一种简单而有效的三维旋转变换方法，它在计算机图
形学、机器人学、航空航天等领域都有广泛的应用。
掌握旋转矢量法的原理和应用，对于进行三维空间中的旋转变换具有重要的意义。
旋转矢量法
旋转矢量法
矢量分析是研究数量物理学中最重要的方法之一，也是数学上最重要的分析工具之一。
矢量是两个平行线段（或者轴），用两个点表示，一个点是矢量的“起点”，另一个点是“终点”。
矢量的长度是从矢量的起点到终点的距离。
此外，矢量具有向量的属性，如方向和向量的场性质。
矢量的分析应用于几何、力学和电磁学等领域。
旋转矢量法（RVM）
旋转矢量法是一种应用于矢量分析的经典方法，它可以用于计算矢量的图形表示，也可以用于计算基本的向量图形。
一般来说，旋转矢量法是一种可以将一个向量从一个坐标系统转换到另一个坐标系统的方法。
原理介绍
旋转矢量法的基本原理是使用两个向量的叉积来旋转一个向量到另一个坐标系统，这两个向量分别称为被旋转矢量和旋转矢量。
如果从一个坐标系(A)旋转到另一个坐标系(B)，则使用被旋转矢量与旋转矢量的叉积，即可计算出旋转矢量在坐标系B中的表达式。
旋转矢量法还可以用来求解向量平面间的夹角和两个向量分量的夹角。
应用
旋转矢量法可用于计算图形学中的位置和方向，也可以应用于机器人、空间分析和三维图形模拟等技术。
此外，旋转矢量法还可以用于解决由向量和仿射变换组成的更复杂的数学问题。
总结
本文简要介绍了旋转矢量法，这是一种矢量分析的经典方法，可以用于计算矢量的图形表示和基本的向量图形，也可以用于解决由向量和仿射变换组成的更复杂的数学问题。
矢量分析方面的必要知识是可以理解旋转矢量法的基础，它需要计算坐标系之间的变换，以及向量的方向和向量的场性质。
在机器人，空间分析和三维图形模拟等技术中，旋转矢量法可以用于计算位置和方向。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
• 能量法求谐振动的振幅
机械能守恒：
1 1 2 1 2 mv kx kA2 2 2 2
• 能量法求谐振动的周期 两边对时间求导：
d2 x a 2 2 x T 2 dt
自学 教材
P381 [例6]、[例7]
/ P.12 [例5]
例：能量法求谐振动的周期
T=2/ t+ 0
位移
速度
x =Acos(t+ 0)
v =- Asin(t+ 0) a =- 2Acos(t+ 0)
加速度
直观地表达谐振动的各特征量 旋转矢量法优点： 由 x、v 的符号确定 便于解题, 特别是确定初相位 便于振动合成 r A 所在的象限：
已知： A = 24cm, T = 3s, t = 0时 x0 12cm, v0 0,
2
mg
d 2 sin 0 2 dt
2
—— 复摆运动的微分方程也是非线性微分方程
当 很小时 sin
d 2 2 0 2 dt
角谐振动
运动 cos( t ) m 方程：
J 周期：T 2 mgh
2
由初始条件决定
由小角度摆动都是谐振动，可推广到 一切微振动均可用谐振动模型处理。 例如晶体中原子或离子在晶格点平衡位置附近的振动。
练 习
教材P.410 13-6 / P.40 12-6
r 解：作t = 0时刻的旋转矢量 A0
求：质点运动到 x = -12 cm处所需最短时间。
r 作x = -12cm处的旋转矢量 A r A
-12
r A0
o 12 24 x(cm)
t min
1 T 0.5 s 6
练 习
两个小球a和b分别沿o-x轴作简谐振动，在
1 1 2 2 k ( x x0 ) kx 0 x kx 0 2 2
m
mg=kx0
x
1 2 kx 2
1 1 2 1 2 2 E Ek Ep mv kx kA 2 2 2
比较
水平放置的弹簧振子
竖直悬挂的弹簧振子
回复力 弹簧的弹力
准弹性力：弹力与重力的合力
F kx
2
x
振动系统机械能守恒：
E Ek Ep 1 1 v 1 mv 2 J kx2 c 恒量 2 2 R 2
2
两边对时间求导：
Jva mva kxv 0 2 R
d2 x kx 2 a 2 x 2 dt mJ R
得：
k ; 2 mJ R 2 m J R2 T 2 k
弹簧的伸长 势能
总能
F kx
离系统平衡位置的位移
kx2 2 准弹性势能，
kx2 2
弹性势能
重力势能和弹性势能的总和
1 1 1 mv 2 kx2 kA2 2 2 2
统一描述：只要以平衡位置为坐标原点和零势点
1 2 准弹性势能: 1 Ep kx E kA2 2 （包括重力势能、弹性势能） 2
三.旋转矢量法
四.能量（以平衡位置为坐标原点和势能零点）
1 1 1 2 2 E Ek Ep mv kx kA2 2 2 2
用旋转矢量图画简谐运动的
x t
图
T 2π （旋转矢量旋转一周所需的时间）
简谐运动的描述和特征 1）物体受线性回复力作用
F kx 平衡位置 x 0
2
d x 2 2）简谐运动的动力学描述 x 2 dt
3）简谐运动的运动学描述
x A cos(t )
v A sin(t )
4）加速度与位移成正比而方向相反
弹簧振子
km 复摆
t=0时，两球均在平衡位置，且球a向x轴的正方向
运动，球b向x轴的负方向运动，比较t=4/3s时两球
的振动相位差。（Ta=2Tb=2s）
四. 孤立谐振动系统的能量 不计振动传播带来的能量损失 —— 辐射阻尼 不计摩擦产生的热损耗 —— 摩擦阻尼 水平放置的弹簧振子 以平衡位置为坐标原点
1 2 1 2 Εp kx kA cos 2 ( t 0 ) 2 2 1 2 1 1 2 2 2 2 2 Ek mv mA sin ( t 0 ) kA sin ( t 0 ) 2 2 2
d 2 g sin 0 2 dt l
d 2 2 sin 0 2 dt
令 2
g
l
得：
单摆运动的微分方程
sin
3
3!
5
5!
非线性微分方程 无解析解
当 很小时 sin
d 2 2 0 2 dt
角谐振动 周期：
同学们好！
k
上 讲 内 容
一. 简谐振动的运动方程(平衡位置为坐标原点）
F kx
d2 x 2 x0 2 dt
x Acos(t 0 )
角频率 k m 二. 特征量
振幅
初相
v02 A x 2
2 0
v0 0 arctg ( ) x0
三. 旋转矢量法
思考：
写出质点 m 以角速率 沿 半径 A 的圆周匀速运动的 参数方程
y A 0
m
o
x
x A cos(t 0 )
y A sin(t 0 )
x、y 方向分运动均为简谐振动
x A cos(t )
量 A的
旋转矢
端点在 x 轴上的投 影点的运 动为简谐 运动.
已知： k , R , J , m
求： T 解：以平衡位置为坐标原点
和零势点，向下为正，任意
m
时刻 t 系统的机械能为：
1 1 1 1 v 2 2 2 Ek mv J mv J 2 2 2 2 R
1 1 2 Ep kx Ep滑 轮 kx2 c 2 2
a x 单摆 g l
2
mgl
J
小
F kx
结：
x A cos( t 0 )
一.简谐振动的运动方程(平衡位置为坐标原点）
d2 x 2 x0 2 dt
角频率
k m
2 v 2 A x0 02
二.
特征量
振幅
初相
v0 0 arct g ( ) x0
1 2 1 1 2 1 2 1 2 2 E EP EK ( kx m v ) kx0 kA kx0 恒量 2 2 2 2 2
恰当选择零势点，可去掉第二项。
如何选？以平衡位置为坐标原点和势能零点
k
x0 EP=0
k
O
k x
1 1 2 2 Ep k ( x x0 ) mgx kx 0 2 2
质量为 0.10kg的物体，以振幅 1.0 102 m 作简谐振动，其最大加速度为 4.0m s 2,求： （1）振动的周期； （2）通过平衡位置的动能； （3）总能量； （4）物体在何处其动能和势能相等？
练 习
解 （ 1）
amax A
T
2
amax 1 20s A
0.314 s
运动 cos( t ) m 方程：
由初始条件决定
l T 2 g
2
二、复摆：绕不通过质心的光滑水平轴摆动的刚体 由刚体定轴转动定律
M J
d 2 m ghsin J 2 dt d 2 m gh sin 0 2
dt J
o
C
h
J
令
mgh J
o
T 4
T 2
3T 4
T
t
1 Ek m 2 A2 sin 2 t 2
E - x 曲线
Ek , Ep变化频率为 x 的2倍 Ek , Ep彼此变化步调相反
竖直悬挂的弹簧振子 以弹簧原长处为重力势能、弹性势能零点 以平衡位置为坐标原点 k
EP=0 x 0
mg-kx0=0 x
k m
O
k x
1 2 Ep k ( x x0 ) mg ( x x0) ) 2 1 k ( x x0 ) 2 kx0 ( x x0 ) 2 1 2 1 2 kx kx0 2 2
2π
（2） Ek ,max （ 3）
1 1 2 mvmax m 2 A2 2.0 103 J 2 2
3
E Ek ,max 2.0 10 J
Ep 时， Ep 1.0 10 J
3
（4） Ek
1 2 1 由 Ep kx m 2 x 2 2 2 2 Ep 4 2 2 0.5 10 m x 2 m
x 0.707 cm
摆动（单摆、复摆介绍）
研究摆动的理想模型 —— 单摆和复摆 一、单摆：无伸长的轻线下悬挂质点作无阻尼摆动 建立如图自然坐标 受力分析如图 切向运动方程 n N
l
m
mg
F ma ml d2 mgsin ml 2 dt
d 2 g sin 0 2 dt l
{ v A sin( t )
0
x A cos( t 0 )
1 E Ep Ek kA 2 恒量 2
孤立谐振动系统机械能守恒
x, v
E-t 曲线
o
能量
x t
T
0 t x Acost v t v A sin t
1 2 E kA 2 1 2 Ep kA cos 2 t 2