工程力学第9章

合集下载

工程力学C-第9章扭转

T 1000 0.04 3 Wp (1 0.54 )
max
84.88MPa
16
min max
10 42.44MPa 20
§9-6 圆轴扭转破坏与强度条件
一、圆轴扭转时的破坏现象
脆性材料扭转破坏
沿450螺旋曲面被拉断
塑性材料扭转破坏
沿横截面被剪断
二、圆轴扭转的强度条件
D 1.192 得： d1
2
D2
A空 A实 4
(1 0.8 )
d1
4
2
0.512
例6 传动轴AB传递的功率为 P =7.5kW，转速n=360r/min。轴的 AC 段为实心圆轴， CB 段为空心圆轴。已知：D =30mm，d =20mm。试计算AC段的最大剪应力，CB 段横截面上内、外缘处的剪应力。解：（1）计算外力偶矩和扭矩 P AC段最大剪应力： m 9549 198.9N m n Tmax D 1max 37.5 10 6 Pa 37.5MPa T m 198.9N m I P1 2 （2）计算极惯性矩 CB段上内外缘的剪应力： D 4 T d 8 4 AC段：I P1 7.95 10 m 2内 I P2 2 32 D 4 4 31.2 10 6 Pa 31.2MPa (1 ) CB段：I P 2 T D 32 2外 8 4 6.38 10 m I P2 2 46.8 10 6 Pa 46.8MPa （3）计算应力
A
ρτ
ρ
dA T
d 2 G ρ dA T dx A
令：
ρ dA I P
2 A
极惯性矩
d G IP T dx

工程力学第九章杆件变形及结构的位移计算

应的（直线图形）的竖标，再除以杆的弯曲刚度。应用图乘法计算时，应注意以下几点：
（1）竖标要在直线段弯矩图上取得；（2）每一个面积只对应一条直线段的弯矩图。
当与在杆的同一侧时，两者乘积取正号，反之取负号。
§9–4 图乘法
二、几种常见图形的面积和形心位置的确定方法
二次抛物线
§9–4 图乘法
例1:求图示梁(EI=常数,跨长为l)B截面转角 B
(
1 2
l 2
1 2
2 3
Pl 4
B l l 1 Pl 1 l 1 1 Pl) 2 22 4 2223 4
l/2
l/2
Pl2 ( ) 16EI
1
Mi
1/ 2
取 yc的图形必
须是直线,不能是曲
B
1 EI
(1 2
l
Pl 4
1) 2
Pl 2 16 EI
(
)
线或折线.
§9–4 图乘法
q
A
B
1
2
1
MP 图
解:
1 ql2
M图
8
B
1 EI
[(2 3
l
1 8
ql2 )
1] 2
1 ql3 （）
24 EI
§9–4图乘法
例2. 试求图示结构B点竖向位移.
P
1
Pl
l
EI
B
l EI MP
Mi
l
解:
By
MM P EI
ds
yc
EI
§9–4 图乘法
解:
yc
EI
1 ( 1 Pl l 2 l Pl l l)
ql3 ( 24 EI
)

工程力学高斌第九章答案

2 2
15kN . m
5kN . m
15kN . m
-
Q qa/2 +
-
qa/2 + x
qa/2
M q a 2/8 +
-
x
q a 2/8
5. 设梁的剪力图如图所示，试作弯矩图及载荷图。已知梁上设有作用集中力偶。 (a)
4kN q=1kN/m
3kN
Q
3kN
2kN
3kN
1kN
A
B
1kN
C
D
x
5
3kN 2m 2m 4m
3
2
⎡ 50 × 2003 ⎤ 150 × 503 Iz = ⎢ + 50 × 200 × 53.62 + + 50 × 150 × 71.4 2 ⎥ mm 4 12 ⎣ 12 ⎦ = 10180 cm 4
根据弯曲正应力强度条件
M
0.8p
σ max
M = ymax ≤ [σ ] , M≤[σ].Iz/ymax Iz
解：梁的弯矩图如图，弯矩的两个极值分别为
µ1 = 0.8P , MA =2P×1.4 - P×2= 0.8P µ2 = 0.6 P , MC = -0.6 P
截面对形心轴的惯性矩为
8
(Iz =bh /12 + Ah1 , h1 腹 = 153.6–100=53.6mm ,h1 翼 =200-153.6+25 =71.4mm )
实心圆截面梁的最大应力
σ max =
空心圆截面最大应力
′ = σ max
空心圆截面梁比实心圆截面梁的最大正应力减少了
′ σ max − σ max 159 − 93.6 = = 41.1% σ max 159

工程力学第九章

下一页返回
9.4

梁的弯曲变形与刚度
2.
挠度和转角
(1) 挠度是指梁轴线上的一点在垂直于轴线方向上的位移，通常用y表示。

一般规定向上的挠度为正，向上的挠度为负。它的单位是mm。 (2) 转角是指梁的各截面相对原来位置转过的角度，用θ 表
示。

一般规定，逆时针方向的转角为正，顺时针的转角为负。它的单位是弧度(rad)或度(º)。
远的边缘处。其计算公式为
max

(2) 梁的正应力强度条件为
M max y max M max Iz Wz
M max ≤[σ ] Wz
下一页返回
max
小

结

max
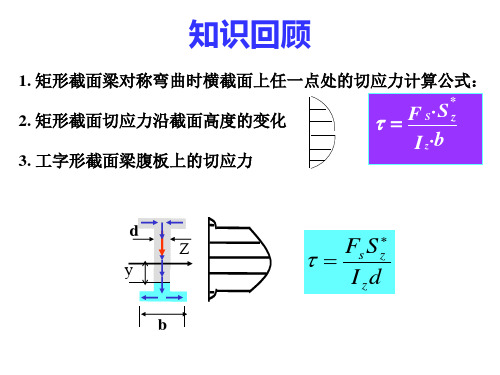
* FQ S z
(3) 梁横截面上的切应力与切应力强度条件对矩形截面梁，横截面上的切应力计算公式为其最大切应力在截面的中性轴上，计算公式为梁的切应力强度条件为τ max≤[τ ]
上一页返回
9.2

梁弯曲时正应力强度计算
梁弯曲时正应力强度计算
9.2
为了保证梁在载荷作用下能够正常工作，必须使梁具备足够的强度。也就是说，梁的最大正应力值不得超过梁材料在单向受力状态(轴向拉、压情况)下的许用应力值[σ ]，即 M max max ≤[σ ] （9.10） Wz 式(9.10)就是梁弯曲时的正应力强度条件。需要指出的是，式(9.10)只适用于许用拉应力[σ l]和许用压应力[σ y]相等的材料。如果两者不相等(例如铸铁等脆性材料)，为保证梁的受拉部分和受压部分都能正常工作，应该按拉伸式
上一页下一页返回
My Iz
(9.4)

工程力学第9章梁弯曲时的刚度计算

挠曲线

w

x
qx
F
x
9.1 挠曲线近似微分方程
9.1.2 挠度和转角的关系
◆挠曲线方程： w f x
w
挠曲线

w

x
qx
F
x
tan dw
dx
dw
dx
9.1.3 挠曲线近似微分方程
一、挠曲线的曲率公式
1M EI

1
x

M x
EI
d2w

1
x

6EI 2l
l 2
2l 2

l 2
2

11Fl3 96EI
未知约束力单独作用引起的B处挠度
wB FB

FB 2l 3
48EI

FBl 3 6EI
将上述结果代入式（b），得到补充方程
11Fl3 FBl3 0 96EI 6EI
w Mex x2 l2 6EIl
（c）
Me 3x2 l2 6EIl
（d）
（4）计算最大挠度与截面的转角
作出梁的弯矩图如下图所示，全梁弯矩为正。其最大挠度处的转角为零。故由式（c）有
dw Me 3x2 l2 0 dx 6EIl
从而得最大挠度所在截面的坐标为
2
在集中力 F 单独作用下，大梁跨度中点C的挠度由教材表
7–1第5栏中查出为
wC
F

Fl 3 48EI
将以上结果叠加，即得在均布载荷和q 集中力的F 共同作用
下，大梁跨度中点C的挠度

工程力学(基础力学、材料力学)14(30)第九章6节

158.4 106 170
158.4kNm
930 103 ( m m3 )
查表选36c型号 I z 17310 cm 4 ; d 14 mm ; I z
3、切应力校核 max
4、结论：选36c型号
F
s max z
S Fs max 112.5 10 27( MPa) I z d 29.9 1014 Izd S z
q B l/2 17 KN 12 KN 12KN.m
F C l/2 D
检查此梁是否安全。
解：（1）作内力图
Fs图
13KN
max
M max Wz
M图
max
Fs max S zmax I zb
39KN.m
（2）计算几何性质
查表得
W z 309cm 3 0.309 103 m 3 Iz S z , max 18.9cm 0.189m
max [ ]
对于等直梁
F
S ,max
S
b
* z max
I
[ ]
z
b 为中性轴处的宽度。
对于横力弯曲下的等直梁，其横截面上一般既有弯矩
又有剪力。梁上最大正应力发生在弯矩最大的横截面上距中性轴最远的各点处。而梁上最大的切应力发生在剪力最大的横截面上中性轴上的各点处。
梁除满足正应力强度条件外，还需满足切应力强度条件。
z
b 120(m m) F max 1.5 h 180(m m) bh b=140mm；h=210mm
lx Fs ( x) F x 0; Fs max F l x Fs1 ( x) F x l ; Fs1max F l

工程力学(第七版)(作者：蒙晓影)习题参考答案 (9)[4页]

第9章压杆稳定9-1解：求柔度值查表得Q235钢：a=304MPa, b=1.12MPa 3.99==p p Eσπλ 57=-=b a s s σλ （2）求各杆的临界压力P cr1杆：p l d l i l λμλ>=⨯==12541111 644d I π= KN l EI P cr 2540)(221==∴μπ 2杆： 5.6222==i l l μλ p l s λλλ<<2 MPa b a cr 2342=-=∴λσKN A P cr cr 470522==σ3杆：s l i l λμλ<==25.3133 KN A P s cr 47253==∴σ9-2解：查表得I=158cm 4,A=35.578cm 2μ=1 KN l EI P cr 5.19741015810200)(28922=⨯⨯⨯⨯==-πμπMPa A P cr cr5.5510578.35105.19743=⨯⨯==-σ9-3 解：473108200120121mm I y ⨯=⨯⨯=，463108.28120200121mm I z ⨯=⨯⨯=112115120200108.284000146=>=⨯⨯⨯==p mmi lλμλa cr MP E 4.7115101023222=⨯⨯==πλπσ9-4解：i=d/4=13mm查表得μ=2，则 λ=μl/i=76.9查表得45号钢 λp=100, λs=60 所以为中长杆查表11-2得，a=578Mpa, b=3.744 Mpaσcr = a-b λ=290.08MPa Pcr=σcr A=639.41KNn w = Pcr/P=4.19-5解：（1）受力分析以梁AC 为研究对象，由静力平衡方程可求得 N BD =106.7KN（2）BD 压杆的柔度查型钢表，20号槽钢： A=32.837cm 2 i y =2.09cm I y =14.1cm 4μ=1，l=1.5/cos30=1.732m 87.82==y i lμλ ∴ p s λλλ<<BD 杆为中长杆（3）计算临界压力KNA b a A P cr cr 5.693)(=-==λσ（4）稳定性校核0.5][5.6=>==w BDcr n N P n 满足稳定要求。

工程力学第九章刚度设计新

的影响。
刚度设计在实际工程中的应用前景
航空航天领域
刚度设计在航空航天领域具有广泛应用，如飞机机身、机翼等结构的刚度设计，以确保飞行安全。
汽车工业
汽车工业中，刚度设计对于提高车辆性能、降低噪音和振动等方面具有重要作用。
建筑行业
在建筑行业中，刚度设计有助于提高结构的稳定性和安全性，保障人民生命财产安全。
机械零件的刚度设计
总结词
确保机械零件的稳定性和精度
详细描述
机械零件的刚度设计对于确保机械系统的稳定性和精度至关重要。在设计中，应考虑零件的形状、尺寸、材料等因素，以及其在机械系统中的作用和所受载荷的类型和大小，以确保零件具有足够的刚度，防止在使用过程中发生变形或振动，从而影响机械系统的性能和精度。
可持续性原则
刚度设计应考虑材料的可再生性和环保性，尽量减少对环境的负面影响。
03
新型刚度设计方法
基于有限元的刚度设计方法
优点
可以处理复杂的几何形状和边界条件，精度高，可以模拟各种复杂的应力分布和变形情况。
缺点
计算量大，需要较高的计算机技术和较长的计算时间。
基于仿生的刚度设计方法
优点
可以借鉴生物经过亿万年进化的优秀结构和功能，具有很高的鲁棒性和适应性。
总结词
考虑多种因素
详细描述
桥梁结构的刚度设计需要综合考虑多种因素，包括桥梁跨度、载荷类型和大小、材料特性、环境条件等。在设计中，应确保桥梁结构在承受载荷时具有足够的刚度，以避免过度的变形和振动，同时还要考虑施工的可行性和经济性。
建筑结构的刚度设计
总结词
满足建筑功能和安全性要求
详细描述
建筑结构的刚度设计必须满足建筑功能和安全性要求。在设计中，应考虑建筑物的使用功能、结构形式、材料选择等因素，以确保结构在承受载荷时具有足够的刚度和稳定性，同时还要考虑建筑物的抗震、抗风等性能要求。

名师讲义【赵堔】工程力学第9章扭转强度与刚度

d MTn x dx
GI p
AB 截面相对扭转角为：
l
d
l
MTn x dx
GI p
# 图示为变截面圆杆，A、B 两端直径分别为 d1、d2 。
从中取 dx 段，该段相邻两截面的扭转角为：
d T dx
GI P (x)
AB 截面相对扭转角为：
d
T dx
L
L GI P ( x)
三、扭转杆的刚度计算
圆管强度。
解：1. 计算扭矩作扭矩图
2. 强度校核
危险截面：截面 A 与 B
A
TA
2πR02d1
ml
2πR02d1
44.6
MPa [
]
ml
B
TB
2π 2
27.9
MPa [
]
圆管强度足够
例图示阶梯状圆轴，AB段直径 d1=120mm，BC段直径
d2=100mm 。扭转力偶矩 MA=22 kN•m， MB=36 kN•m，
d
5、切应力的计算公式：
dA 对圆心的矩 → dAr0
T
AdA.r0
2 0
r0
2td
r02t2
T
2r0 2t
薄壁圆筒扭转时横截面上的切应力计算式
二、关于切应力的若干重要性质
1、剪切虎克定律
为扭转角 r0 l
l
r0 即
l
做薄壁圆筒的扭转试验可得 T
纵轴 T——
T
2r02t
核轴的刚度解：1. 内力、变形分析
T1 MA 180 N m
AB
T1l GIp
1.5010-2
rad
T2 MC 140 N m

工程力学课后习题答案第9章题解g

−
a)
对应的最大正应力
σ2
=
M2 Wz
=
F(l − a) / 4 Wz
据题意有σ 2 = [σ ]，及
σ 1 − σ 2 ×100% = 30% σ2
将σ 1 ,σ 2 的值代入，得
Fl / 4 − F (l − a) / 4
Wz
Wz
F(l − a) / 4
= 0.3
Wz
整理得
70
a = 0.3 l = 0.231l = 0.231× 6 = 1.39 m 1.3
1 qa 2 2
=
0，F
=
P 3
，q
=
P l
即
Pa − 1 ⋅ P a 2 = 0 ， a = 2 l
3 2l
3
（2） M (x) = Fx − 1 qx2 = P x − P x2
2
3 2l
M ′(x) = 0 ， P − P x = 0 ， x = 2
3l
3
M ⎜⎛ l ⎟⎞ = P ⋅ l − 1 ⋅ P ⋅ ⎜⎛ l ⎟⎞2 = Pl ⎝ 3 ⎠ 3 3 2 l ⎝ 3 ⎠ 18
因此，辅助梁应有的最小跨长为：1.39 m 。 9-8 一桥式起重机梁跨 l = 10.5 m ，横截面为 36a 工字钢。已知梁的许用应力
[σ ] = 140 MPa ，电葫芦自重 12 kN，当起吊重量为 50 kN 时，梁的强度不够。为满足正应力强度要求，在梁中段的上、下各焊一快钢板，如图。求加固钢板的最小长度 l0 。
(a）
(b)
( ) 解 ∑ M A = 0 ， FB = 7.64 kN ↑ ( ) ∑ Fy = 0 ， FA = 3.36 kN ↑

工程力学第9章杆件横截面上的切应力分析

第 9 章弹性杆件横截面上的切应力分析
对于实心截面杆件以及某些薄壁截面杆件，当其横截面上仅有扭矩（Mx）或剪力（FQy 或 FQz）时，与这些内力分量相对应的分布内力，其作用面与横截面重合。这时分布内力在一点处的集度，即为切应力。分析与扭矩和剪力对应的切应力方法不完全相同。对于扭矩存在的情形，依然借助于平衡、变形协调与物性关系，其过程与正应力分析相似。对于剪力存在的情形，在一定的前提下，则仅借助于平衡方程。本章重点介绍圆截面杆在扭矩作用下其横截面切应力以及薄壁杆件的弯曲切应力分析。
§ 9-1 圆轴扭转时横截面上的切应力
９－１－１圆轴扭转变形特征－反对称性论证圆轴扭转时横截面保持平面９－１－２变形协调方程９－１－３物性关系－剪切胡克定律９－１－４静力学方程９－１－５圆轴扭转时横截面上的切应力表达式
§ 9-2 非圆截面杆扭转时的切应力
图 9－8 例 9－2 图
解： 1．各轴所承受的扭矩各轴所传递的功率分别为 P1 ＝14 kw ， P 2 ＝ P3 ＝P 1 ／2＝7 kw 转速分别为 n1 ＝ 120 r／min
n 3＝n1 ×
据此，算得各轴承受的扭矩：
z1 36 ＝120 × r/min ＝360r/min z3 12
14 M x1 = M e1 = 9549 × N ⋅ m = 1114 N ⋅ m 120 7 M x2 = M e2 = 9549 × N ⋅ m = 557 N ⋅ m 120 7 M x2 = M e2 = 9549 × N ⋅ m = 185 .7 N ⋅ m 360
2．计算最大切应力 E 、H、C 轴横截面上的最大切应力分别为

工程力学第9章圆轴的扭转

τ ′d x d z
d
τ
c
τ d yd z
x
∑F = 0 ∑F = 0 ∑M = 0
y x z
自动满足存在τ'
(τ d y d z ) d x = (τ ′ d x d z ) d y
得
τ′ =τ
y
τ'
a dy b z
切应力互等定理 d
在相互垂直的两个面上，在相互垂直的两个面上，切应力总是成对出现，并且大小相应力总是成对出现，并且大小相等，方向同时指向或同时背离两个面的交线。个面的交线。
一、圆轴扭转时横截面上的应力 1、几何关系：由实验找出变形规律应变的变化规律几何关系由实验找出变形规律→应变的变化规律 1）实验：实验：
2）观察变形规律：观察变形规律：
圆周线——形状、大小、间距不变，各圆周线只是绕轴线转动形状、大小、间距不变，圆周线形状了一个不同的角度。了一个不同的角度。纵向线——倾斜了同一个角度，小方格变成了平行四边形。倾斜了同一个角度，小方格变成了平行四边形。纵向线倾斜了同一个角度扭转平面假设：变形前的横截面，变形后仍为平面，扭转平面假设变形前的横截面，变形后仍为平面，且形状、大小以及间距不变，半径仍为直线。以及间距不变，半径仍为直线。
3
) 16T 3 16(1.5×103N⋅m = = 0.0535 m d ≥ 6 π(50×10 Pa) π[τ ]
m 取： d = 54 m
2. 确定空心圆轴内、外径确定空心圆轴内、
Wp =
3
πD3 16
(1−α )
4
16T π 3 D (1−α 4) 16
结论：结论：
横截面上

工程力学课后答案第9章

第9章平面体系的几何组成分析习题.【解】若上部结构与地基之间的连接比较多（N4）,能够考虑先将上部结构中的某•刚片与地基连成一个大刚片。

然后，在考虑这个大刚片与上部其它杆件的连接。

本例中，上部结构与地基之间用4个约束连接。

杆件ABE与地基之间用钗A和一根不同过该絞的链杆B相连，组成几何不变体系，且没有多余约束。

所以，能够将杆件ABE与地基看成一个没有多余约束的大刚片。

杆件FCD用三根既不相互平行又不相交于一点的链杆（链杆EF、链杆C、链杆D）与这个大刚片相连，组成一个更大的几何不变体系，且没有多余约束。

杆件ABE与地基之间用平行链杆A和一根不同过该絞的链杆B相连，组成几何不变体系，且没有多余约束。

将杆件ABE与地基看成一个没有多余约束的大刚片。

杆件FCD用三根既不相互平行又不相交于一点的链杆（链杆EF、链杆C、链杆D）与这个大刚片相连，组成一个更大的几何不变体系，且没有多余约束。

-I*羡诊为习题（C）图若上部结构中有皎接三角形，能够考虑将这些三角形看成刚片，然后在进行分析。

刚片I与地基组成•个没有多余约束的大刚片。

这个大刚片与刚片II用三根既不相互平行又不相交于一点的链杆相连，组成一个更大的几何不变体系，且没有多余约束。

习题（d）图将扩大的三角形看成刚片。

先分析一部分：左边的刚片与地基组成一个大刚片ABCD。

增加二元体：在大刚片ABCD上增加二元体DE杆和链杆E,组成一个更大的刚片。

此刚片与刚片GH1F由三根延长线交于H点的链杆（杆件CG、杆件FE、链杆1）相连。

故，体系为瞬变体系。

若上部结构与地基之间用三个约束连接，且符合几何不变体系的组成规律，能够只分析上部结构。

上部结构的分析结论就是整个体系的分析结论。

若折杆只用两个较与其它物体相连，能够将折杆看成是连接两个钗的直杆。

去掉二元体。

剩下部分为两个刚片用两个钗连接，为几何不变体系,且有一个多余约束。

故，整体体系也为几何不变体系，且有一个多余约束。

工程力学第九章梁的应力及强度计算

平面弯曲时，如果某段梁的横截面上只有弯矩M，而无剪力Q = 0，这种弯曲称为纯弯曲。
1、矩形截面梁纯弯曲时的变形观察
现象：
（1）变形后各横向线仍为直线，只是相对旋转了一个角度，且与变形后的梁轴曲线保持垂直，即小矩形格仍为直角；
（2）梁表面的纵向直线均弯曲成弧线，而且，靠顶面的纵线缩短，靠底面的纵线拉长，而位于中间位置的纵线长度不变。
对剪应力的分布作如下假设：
(1)横截面上各点处剪应力均与剪力Q同向且平行；
(2)横截面上距中性轴等距离各点处剪应力大小相。
根据以上假设，可推导出剪应力计算公式：
式中:τ—横截面上距中性轴z距离为y处各点的剪应力；
Q—该截面上的剪力；
b—需求剪应力作用点处的截面宽度；
Iz—横截面对其中性轴的惯性矩；
Sz*—所求剪应力作用点处的横线以下(或以上）的截面积A*对中性轴的面积矩。
应力σ的正负号直接由弯矩M的正负来判断。M为正时，中性轴上部截面为压应力，下部为拉应力；M为负时，中性轴上部截面为拉应力，下部为压应力。
第二节梁的正应力强度条件
一、弯曲正应力的强度条件
等直梁的最大弯曲正应力，发生在最大弯矩所在横截面上距中性轴最远的各点处，即
对于工程上的细长梁，强度的主要控制因素是弯曲正应力。为了保证梁能安全、正常地工作，必须使梁内最大正应力σmax不超过材料的许用应力[σ]，故梁的正应力强度条件为：
圆形截面横梁截面上的最大竖向剪应力也都发生在中性轴上，沿中性轴均匀分布。
其它形状的截面上，一般地说，最大剪应力也出现在中性轴上各点。
结合书P161-162 例8-3进行详细讲解。
五、梁的剪应力强度校核
梁的剪应力强度条件为：
在梁的强度计算时，必须同时满足弯曲正应力强度条件和剪应力强度条件。但在一般情况下，满足了正应力强度条件后，剪应力强度都能满足，故通常只需按正应力条件进行计算。

工程力学第九章梁的强度刚度计算

由结果知，梁的强度不满足要求。
返回下一张上一张
y2
z
例9-6 试为图示钢轨枕木选择矩形截面。已知矩形截面尺寸的比例为b:h=3:4,枕木的弯曲许用正应力[]=15.6MPa,许用剪应力 P P 0 0 .2 m 1 .6 m []=1.7MPa,钢轨传给枕木的压力P=49KN。 .2 m
a
M D ya Iz
返回下一张上一张
10.7
第二节梁横截面上的剪应力
一、矩形截面梁：
矩形截面剪应力计算公式： τ沿截面高度按抛物线规律变化：
2Iz 4
3
QS
* z
I zb
bh
4
τ m ax
2 3
y
h 2
, 0 ; y 0 , max
6 Qh 4 bh
校核梁的正应力强度。
解：(1) 内力及抗弯截面模量计算: MC=3.0KN.m; MD=-4.8KN.m
W1 W2
P1
A
a C a
P2
D
a B
y1

z

763 5 .2
146 . 7 cm
3
y1

z

763 8 .8
86 . 7 cm
3
4 .8 k N m
y2
(2)C截面的正应力强度校核:
4 Q 3 A1
max 2
Q A2
返回下一张上一张
例9-3 矩形截面简支梁如图,已知：l=2m，h=15cm，b=10cm， h1=3cm，q=3kN/m。试求A支座截面上K点的剪应力及该截面的最 b q 大剪应力。解：1.求剪力：QA=3kN

工程力学第9章应力状态分析习题及解析

习题9-1图 x15-'x x'σy'x'τ 1.25MPa15 (b-1)15a 4MP15-y'x'τx'x'σa1.6MP x (a-1) 习题9-2图302MPa 0.5MPa-60x'σ'x ''y x τ 工程力学（工程静力学与材料力学）习题与解答第9章应力状态分析9－1 木制构件中的微元受力如图所示，其中所示的角度为木纹方向与铅垂方向的夹角。

试求： 1．面内平行于木纹方向的切应力；2．垂直于木纹方向的正应力。

知识点：平面应力状态、任意方向面上的应力分析难度：易解答：（a ）平行于木纹方向切应力6.0))15(2cos(0))15(2sin(2)6.1(4=︒-⨯⋅+︒-⨯---=''y x τMPa 垂直于木纹方向正应力84.30))15(2cos(2)6.1(42)6.1(4-=+︒-⨯---+-+-='x σMPa （b ）切应力08.1))15(2cos(25.1-=︒-⨯-=''y x τMPa正应力625.0))15(2sin()25.1(-=︒-⨯--='x σMPa9－2 层合板构件中微元受力如图所示，各层板之间用胶粘接，接缝方向如图中所示。

若已知胶层切应力不得超过1MPa 。

试分析是否满足这一要求。

知识点：平面应力状态、任意方向面上的应力分析难度：易解答：55.1))60(2cos(5.0))60(2sin(2)1(2-=︒-⨯⋅+︒-⨯---=''y x τMPa 1MPa 55.1||>=''y x τMPa ，不满足。

9－3 结构中某点处的应力状态为两种应力状态的叠加结果。

试求叠加后所得应力状态的主应力、面内最大切应力和该点处的最大切应力。

知识点：平面应力状态分析难度：难解答：习题9-2图yσxσxyτ=yσxσxyτx=yσxσxyτ=左微元⎪⎪⎪⎩⎪⎪⎪⎨⎧-='-='-=-='+=--+='000000022cos 122sin )2sin(222cos 10)2cos(22σθσσσσθθστσθθσσσx y xy x 叠加 ⎪⎪⎪⎩⎪⎪⎪⎨⎧-=+'=-=+=+=+'=''000022cos 1022sin 022cos 3σθσσσθττσθσσσy y y x xy x x0)cos 1()cos 1( )22sin (4)22cos 122cos 3(21222cos 122cos 330020202021=⎩⎨⎧-+=-+--+±-++=⎭⎬⎫σσθσθσθσθθσθθσσ 面内最大切应力：θσσστcos 2021max=-='该点最大切应力：031max2cos 12σθσστ+=-=左微元0023))30(2sin()(ττσ=︒-⨯-='x ，0230τσσ-='-='x y ，2))30(2cos(00τττ=︒-⨯='xy 右微元0023)302sin()(ττσ=︒⨯-=''x，0230τσσ-=''-=''x y ，2))30(2cos()(00τττ-=︒⨯-=''xy 叠加 03τσσσ='+'=y x x ，03τσσσ-=''+'=y y y ，0=''+'=xyxy xy τττ 013τσ=，02=σ，033τσ-= 面内031max32||τσστ=-='xABOσOσαα(a)习题9-4图A60CB60100-x σxσyxτxyτ92MPa(a)习题9-5图该点031max 32||τσστ=-=叠加[]⎪⎪⎪⎩⎪⎪⎪⎨⎧=⎥⎦⎤⎢⎣⎡︒-⨯--+==--+==⎥⎦⎤⎢⎣⎡︒-⨯--+-++=MPa 30))45(2sin(2)30(5070MPa 1010)3050(0MPa 90))45(2cos(2)30(502)30(5080xy y x σσσ主应力0MPa 0MPa100304)]100(90[212109022231=⎩⎨⎧=⨯+-±+=⎭⎬⎫σσσ面内及该点：5021002||||31max max=-=-=='σσττMPa9－4 已知平面应力状态的最大正应力发生在与外力作用的自由表面AB 相垂直的面上，其值为0σ。

工程力学--材料力学(北京科大、东北大学版)第4版第九章习题答案

第九章习题9-1 图示的细长压杆均为圆杆，其直径d均相同．材料是Q 235钢．E＝。

其中：图a为两端铰支；图b为—端固定，一端210 GPa铰支；图c为两端固定，试判别哪一种情形的t临界力最大，哪种其次，。

哪种最小?若四杆直径d＝16cm，试求最大的临界力Pcr9-2 图示压杆的材料为Q 235钢，E＝210GPa在正视图a的平面内，两端为铰支，在俯视图b的平面内，两端认为固定。

试求此杆的临界力。

SHAPE \* MERGEFORMAT9-3 图示立柱由两根10号槽钢组成，立柱上端为球铰，下端固定，柱长L＝6m，试求两槽钢距离a值取多少立柱的临界力最大?其佰是多少?已知材料的弹性模量E＝200 GPa．比例极限σp＝200MPa。

9-4 图示结构AB为圆截面直杆，直径d＝80mm，A端固定，B端与BC 直秆球铰连接。

BC杆为正方形截面，边长a＝70 mm，C端也是球铰。

两杆材料相同，弹性模量E＝200GPa，比例极限σp＝200 MPa，长度l＝3m，求该结构的临界力。

9-5 图示托架中杆AB的直径d＝4 cm，长度l＝80 cm．两端可视为铰支，材料是Q235钢。

(1)试按杆AB的稳定条件求托架的临界力Qcr;(2)若巳知实际载荷Q=70 kN，稳定安全]＝2，问此托架是否安全?系数[nst9-6 悬臀回转吊车如图所示，斜杆AB由钢管制成，在B点铰支；铜管的外径D＝100mm，内径d＝86mm，杆长l＝3m,材料为Q235钢,E＝200 GPa、起重量Q＝20 kN，稳定安全系数[n]＝2．5。

试校核斜杆的稳定性。

st9—7 矿井采空区在充填前为防止顶板陷落，常用木柱支撑，若木柱为]＝4,求木红松，弹性模量E＝10GPa．直径d＝l 4cm规定稳定安全系数[nst柱所允许承受的顶板最大压力。

9—8 螺旋千斤顶（图9-16）的最大起重量P＝150 kN，丝杠长l＝0.5m,]材料为45号钢，E＝210 GPa．规定稳定安全系数[nst＝4.2，求丝杠所允许的最小内直径d。

工程力学(高教版)教案：第九章压杆稳定

第九章压杆稳定第一节压杆稳定的概念对于一般的构件，其满足强度及刚度条件时，就能确保其安全工作。

但对于细长压杆，不仅要满足强度及刚度条件，而且还必须满足稳定条件，才能安全工作。

例如，取两根截面（宽300mm ，厚5mm ）相同；其抗压强度极限40=c σMpa 的松木杆；长度分别为30mm 和1000mm ，进行轴向压缩试验。

试验结果，长为30mm 的短杆，承受的轴向压力可高达6kN （A c σ），属于强度问题；长为1000mm 的细长杆，在承受不足30N 的轴向压力时起就突然发生弯曲，如继续加大压力就会发生折断，而丧失承载能力，属于压杆稳定性问题。

如图9-1(a)所示，下端固定，上端自由的理想细长直杆，在上端施加一轴向压力P 。

试验发现当压力P 小于某一数值cr P 时，若在横向作用一个不大的干扰力，如图9-1b 所示，杆将产生横向弯曲变形。

但是，若横向干扰力消失，其横向弯曲变形也随之消失，如图9-1c 所示，杆仍然保持原直线平衡状态，这种平衡形式称为稳定平衡。

当压力cr P P =时，杆仍然保持直线平衡，但此时再在横向作用一个不大的干扰力，其立刻转为微弯平衡，但此时在，如图9-1d 所示，并且当干扰力消失后，其不能再回到原来的直线平衡状态，这种平衡形式称为不稳定平衡。

压杆由原直线平衡状态转为曲线平衡状态，称为丧失稳定性，简称失稳。

使压杆原直线的平衡由稳定转变为不稳定的轴向压力值cr P ，称为压杆的临界载荷。

在临界载荷作用下，压杆既能在直线状态下保持平衡，也能在微弯状态保持平衡。

所以，当轴向压力达到或超过压杆的临界载荷时，压杆将产生失稳现象。

图9-1在工程实际中，考虑细长压杆的稳定性问题非常重要。

因为这类构件的失稳常发生在其强度破坏之前，而且是瞬间发生的，以至于人们猝不及防，所以更具危险性。

例如：1907年，加拿大魁北克的圣劳伦斯河上一座跨度为548m 的钢桥，在施工过程中，由于两根受压杆件失稳，而导致全桥突然坍塌的严重事故；1912年，德国汉堡一座煤气库由于其一根受压槽钢压杆失稳，而致致使其破坏。

《工程力学(工程静力学与材料力学)(第3版)》习题解答：第9章应力状态分析

1． MPa
MPa
MPa
2．
MPa
MPa
9－13图示外径为300mm的钢管由厚度为8mm的钢带沿20°角的螺旋线卷曲焊接而成。试求下列情形下，焊缝上沿焊缝方向的切应力和垂直于焊缝方向的正应力。
1．只承受轴向载荷FP = 250kN；
2．只承受内压p=5.0MPa（两端封闭）
3．同时承受轴向载荷FP = 250kN和内压p=5.0MPa（两端封闭）
难度：一般
解答：
（1）当 = 40℃
mm＜
mm＜
所以铝板内无温度应力，
（2）当 = 80℃
mm＞
mm＞
∴ （1）
（2）
所以解得qx = qy=70MPa（压）
， MPa
MPa
9－18对于一般平面应力状态，已知材料的弹性常数E、，且由实验测得和。试证明：
知识点：广义胡克定律、三者之间的关系
难度：一般
难度：一般
解答：
正确答案是C。
（A）不满足切应力互等定律；
（B）不满足平衡；
（C）既可满足切应力互等，又能达到双向的平衡；
（D）不满足两个方向的平衡。
9－27微元受力如图所示，图中应力单位为MPa。试根据不为零主应力的数目，它是：
（A）二向应力状态；
（B）单向应力状态；
（C）三向应力状态；
（D）纯切应力状态。
MPa
9－7受力物体中某一点处的应力状态如图所示（图中p为单位面积上的力）。试求该点处的主应力。
知识点：应力圆的应用
难度：难
解答：
应力圆半径
9－8从构件中取出的微元，受力如图所示。试：
1．求主应力和最大切应力；
2．确定主平面和最大切应力作用面位置。