两异面直线所成的角.ppt
合集下载
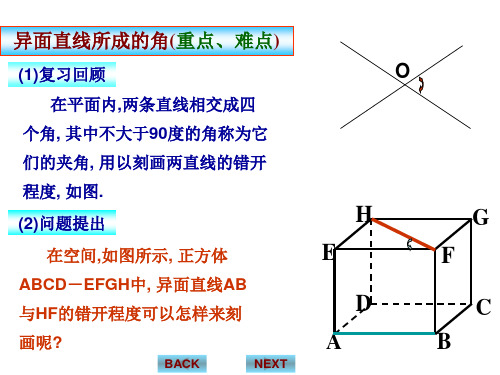
高中数学精品课件:空间角

图7-46-8
与平面ABCD所成的角,由已知得∠MBA=45°,则MA=MB,此时O为AB的中点.
连接OC,由∠BAD=∠ADC=90°,AB=AD=2DC,得四边形AOCD为矩形,所以
OC⊥AB,所以CO⊥平面MAB,又MA⊂平面MAB,所以OC⊥MA.
图7-46-8
[总结反思] (1)求解二面角的大小问题,关键是要合理作出它的平面角,当找到 二面角棱的一个垂面时,即可确定平面角,作二面角的平面角最常用的方法是 利用三垂线定理(或三垂线定理的逆定理). (2)对于建立空间直角坐标系比较简便的几何体,我们可以直接利用向量求出 两个平面的法向量,并转化为求两个法向量的夹角来完成.
.
题组二 常错题 ◆索引:二面角取值范围出错;线面角范围出错;不能正确构建线面垂直及斜线 段在底面上的射影.
6.在一个二面角的两个半平面内都和二面角的棱垂直的两个向量分别为
(0,-1,3),(2,2,4),则这个二面角的余弦值为
.
7.正四棱锥的侧棱长与底面边长都是1,则侧棱与底面所成的角为 45° .
图7-46-8
图7-46-8
方法二:二面角D-MA-C的大小即为二面角B-MA-D的大小与二面角B-MA-C大
小的差,由(1)可知二面角B-MA-D的大小为90°,
所以二面角D-MA-C的正弦值即为二面角B-MA-C的余弦值.
过M作MO⊥AB于O(图略),因为平面MAB⊥平面ABCD,平面 MAB∩平面ABCD=AB,所以MO⊥平面ABCD,∠MBO即为MB
A
证明:连接AC(图略),由题知△ACD为等边三角形,因为M为AD的中点,所以 CM⊥AD,又AD∥BC,所以CM⊥BC,因为平面ABCD⊥平面PBC,且平面 ABCD∩平面PBC=BC,CM⊂平面ABCD,所以CM⊥平面PBC,故CM⊥PB.
异面直线所成的角求法课件

答案解析
答案一解析
首先,由于AB和CD为异面直线,且AB ⟂ CD,我们可以知道异面直线AB与CD所成的 角为∠BAC。因为∠BAC = 60°,所以异面直线AB与CD所成的角也为60°。
答案二解析
首先,找到与AB和AD₁都平行的平面或线段。在长方体中,这样的平面或线段是A₁D和 A₁B₁。然后,利用平移将异面直线AB和AD₁平移到同一个起点,例如点A。最后,利用 余弦公式计算异面直线AB与AD₁所成角的余弦值。具体计算过程涉及长方体的边长和
常见误区
列举了在求解过程中可能出现 的常见错误和误区,并给出了
正确的解释和纠正方法。
展望
01
02
03
04
进一步研究
鼓励学习者在掌握基本方法的 基础上,深入研究异面直线所 成的角的更多性质和应用。
与其他知识的结合
提倡将异面直线所成的角与其 他几何知识进行结合,形成更
完整的知识体系。
实际应用拓展
强调将所学知识应用于实际问 题解决中,培养解决实际问题
在空间向量中的应用
异面直线所成的角在空间向量中也有着重要的应用。向量 的数量积、向量的模长以及向量的夹角都可以通过异面直 线所成的角来表示。
在解决空间向量的加法、数乘以及向量的模长和夹角等问 题时,常常需要利用异面直线所成的角来建立向量关系, 从而得到向量的具体表示和运算结果。
在物理问题中的应用
成的角的余弦值等于 $frac{overset{longrightarrow}{a} cdot overset{longrightarrow}{b}}{|overset{lon
grightarrow}{a}| cdot
利用向量的夹角公式求异面直线所成的角
要点一
异面直线所成的角求法课件

解:首先计算$\vec{a}$和$\vec{b}$的点积,$\vec{a} \cdot \vec{b} = 1 \times 2 + 2 \times 1 + 3 \times 0 = 4$;
然后求出$\vec{a}$和$\vec{b}$的模, $|\vec{a}|=\sqrt{1^2+2^2+3^2}=\sqrt{14}$, $|\vec{b}|=\sqrt{2^2+1^2+0^2}=\sqrt{5}$;
异面直线所成的角求法 课件
目录
• 引入 • 向量法求解异面直线所成角 • 几何法求解异面直线所成角 • 坐标法求解异面直线所成角 • 实际应用与拓展 • 总结与回顾
01
引入
异面直线的定义
定义 判定定理
异面直线所成角的概念
定义
范围
两条异面直线所成角的范围是(0°,90°], 若两条异面直线互相垂直,则说它们 所成的角是90°;若两条异面直线所成 的角是锐角或直角,则就按照锐角或 直角来度量。
求解异面直线所成角的意义
实际应用
拓展思维
02
向量法求解异面直线所成角
向量点积与夹角关系
点积定义
夹角与点积关系
利用向量点积求解异面直线所成角步骤
01
02
03
04
典型例题解析
例1:已知两异面直线上的向量分别为$\vec{a}=(1,2,3)$和 $\vec{b}=(2,1,0)$,求异面直线所成的角。
05
实际应用与拓展
异面直线所成角在实际问题中的应用
建筑设计 机器人路径规划 航空航天
拓展:其他空间几何角的求解方法
向量法
三角函数法
06
然后求出$\vec{a}$和$\vec{b}$的模, $|\vec{a}|=\sqrt{1^2+2^2+3^2}=\sqrt{14}$, $|\vec{b}|=\sqrt{2^2+1^2+0^2}=\sqrt{5}$;
异面直线所成的角求法 课件
目录
• 引入 • 向量法求解异面直线所成角 • 几何法求解异面直线所成角 • 坐标法求解异面直线所成角 • 实际应用与拓展 • 总结与回顾
01
引入
异面直线的定义
定义 判定定理
异面直线所成角的概念
定义
范围
两条异面直线所成角的范围是(0°,90°], 若两条异面直线互相垂直,则说它们 所成的角是90°;若两条异面直线所成 的角是锐角或直角,则就按照锐角或 直角来度量。
求解异面直线所成角的意义
实际应用
拓展思维
02
向量法求解异面直线所成角
向量点积与夹角关系
点积定义
夹角与点积关系
利用向量点积求解异面直线所成角步骤
01
02
03
04
典型例题解析
例1:已知两异面直线上的向量分别为$\vec{a}=(1,2,3)$和 $\vec{b}=(2,1,0)$,求异面直线所成的角。
05
实际应用与拓展
异面直线所成角在实际问题中的应用
建筑设计 机器人路径规划 航空航天
拓展:其他空间几何角的求解方法
向量法
三角函数法
06
2024-2025学年高二数学选择性必修第一册(配北师大版)课件4.3第1课时空间中的角

如图:
名师点睛
不要将两直线所成的角与其方向向量的夹角等同起来,因为两直线所成角
π
的范围是 0, ,而两个向量夹角的范围是[0,π],事实上,两直线所成的角与
2
其方向向量的夹角是相等或互补的关系.
思考辨析
怎样用向量法求两条异面直线所成的角的余弦值?
提示 设两条异面直线a与b的夹角为θ,直线a,b的方向向量分别为a,b,且其
知识点2 直线与平面所成的角 指直线和它在平面内的投影所成角
设向量l为直线l的一个方向向量,n是平面α的一个法向量,则直线l与平面α
所成的角θ∈
π
0, 2
,且
π
θ= -<l,n>(如图
2
π
θ=<l,n>- (如图
2
2),
sin θ=sin < , >
π
-2
1)或
故sin θ=|cos<l,n>|.
π
π
3.若<l,n>是一个锐角,则θ= -<l,n>;若<l,n>是一个钝角,则θ=<l,n>- .
2
2
自主诊断
1.判断正误.(正确的画√,错误的画×)
(1)直线与平面所成的角等于直线的方向向量与该平面法向量夹角的余
角.( × )
(2)直线与平面所成的角可以是钝角.( × )
2.已知向量m,n分别是直线l的方向向量和平面α的法向量,若cos<m,n>=则l与α所成的角为( A )
目录索引
基础落实·必备知识一遍过
重难探究·能力素养速提升
学以致用·随堂检测促达标
1.理解两异面直线所成的角与它们的方向向量之间的关系,会用
异面直线所成的角课件-2023学年高二上学期高教版(2021)中职数学拓展模块一(上册)

A.45° B.60° C.90° D.120°
解:连接A1B,BC1,A1C1
∵A1B // EF,BC1 // GH
A1
∴∠A1B C1为EF1与GH所成的角 在三角形A1BC1中,A1B= BC1= A1C1
E
∴∠A1B C1=60°
A
∴异面直线EF与GH所成的角等于60°
D1
D1
C1 (1)AB1与CD
A1
B1
(2)AB1与CC1
D
C解(1) ∵DC∥AB, 2.说明
A
B
∴∠BAB1为异面直线
1.平移
AB1与CD所成的角, 3.解答
即所求角为30°。
例: 如图:正方体ABCD A1B1C1D1
求异面直线BA1和CC1所成的角。
D1 A1
D A
第四章 立体几何
4.2.3 异面直线所成的角
空间两条直线的位置关系:
位置关系
图形
所成的角
平行
00
相交
00 900
异面
?
2、异面直线的画法:平面衬托法
一、定义
经过空间任意一点分别作与两条异面直线 平行的直线,这两条相交直线的夹角叫做两条 异面直线所成的角。
n n′
m m′
O
n
o
m m′
m与两异n所条面成直直角线线的垂所大直成小,角与它的点们范O一围的定是位相什置交么有吗?关?吗?
G
C B
变式2:(05福建卷)如图,长方体ABCD-A1B1C1D1中, AA1 = AB = 2,AD = 1,E、F、G分别是DD1、AB、 CC1的中点,则异面直线A1E与GF所成的角是__________。
解:连接A1B,BC1,A1C1
∵A1B // EF,BC1 // GH
A1
∴∠A1B C1为EF1与GH所成的角 在三角形A1BC1中,A1B= BC1= A1C1
E
∴∠A1B C1=60°
A
∴异面直线EF与GH所成的角等于60°
D1
D1
C1 (1)AB1与CD
A1
B1
(2)AB1与CC1
D
C解(1) ∵DC∥AB, 2.说明
A
B
∴∠BAB1为异面直线
1.平移
AB1与CD所成的角, 3.解答
即所求角为30°。
例: 如图:正方体ABCD A1B1C1D1
求异面直线BA1和CC1所成的角。
D1 A1
D A
第四章 立体几何
4.2.3 异面直线所成的角
空间两条直线的位置关系:
位置关系
图形
所成的角
平行
00
相交
00 900
异面
?
2、异面直线的画法:平面衬托法
一、定义
经过空间任意一点分别作与两条异面直线 平行的直线,这两条相交直线的夹角叫做两条 异面直线所成的角。
n n′
m m′
O
n
o
m m′
m与两异n所条面成直直角线线的垂所大直成小,角与它的点们范O一围的定是位相什置交么有吗?关?吗?
G
C B
变式2:(05福建卷)如图,长方体ABCD-A1B1C1D1中, AA1 = AB = 2,AD = 1,E、F、G分别是DD1、AB、 CC1的中点,则异面直线A1E与GF所成的角是__________。
必修2课件:异面直线所成的角
BACK NEXT
O
H E D A B F
G
C
(3)解决问题 解决问题
平移转化成相交直线所成的角,即化空间图形问题为平面图形问题 思想方法 : 平移转化成相交直线所成的角 即化空间图形问题为平面图形问题 异面直线所成角的定义: 如图,已知两条异面直线 经过空间任一点O作 异面直线所成角的定义 如图 已知两条异面直线 a , b , 经过空间任一点 作 所成的锐角(或直角 直线 a′∥a , b ′∥b 则把 a ′与 b ′所成的锐角 或直角 叫做异面直线所成的角 ∥ ∥ 与 所成的锐角 或直角)叫做异面直线所成的角 (或夹角 或夹角). 或夹角 异面直线所成的角的范围( 0 , 90 ]
b
b′
a″ a
∠2
α
a′
O
∠1
BACK
NEXT
在求作异面直线所成的角时,O点 在求作异面直线所成的角时 点 常选在其中的一条直线上 (如线段的端点,线段的中点等) 如线段的端点 线段的中点等 如线段的端点 线段的中点
例2
如图,正方体 为侧面ADHE的中心,求 的中心, 如图,正方体ABCD-EFGH中,O为侧面 中 为侧面 的中心 (1)BE与CG所成的角? 与 所成的角? 所成的角 (2)FO与BD所成的角? 与 所成的角 所成的角?
这个角的大小与O点的位置有关吗 点位置不同时, 思考 : 这个角的大小与 点的位置有关吗 ? 即O点位置不同时 这一角的大小 点位置不同时 是否改变? 是否改变
解答: 解答: 如图
答: 这个角的大小与O点的位置无关. 点的位置无关 这个角的大小与 点的位置无关
相交所成的角为∠ 设a ′与 b ′相交所成的角为∠1, a ″与 b 所成的角为∠2 , 与 相交所成的角为 与 所成的角为∠ 公理4), ∵ a′∥a , a″ ∥a∴ a′∥ a″ (公理 ∥ ∴ ∥ 公理 同理 b′∥b″, ∴ ∠1 = ∠2 (等角定理 等角定理) ∥ 等角定理
O
H E D A B F
G
C
(3)解决问题 解决问题
平移转化成相交直线所成的角,即化空间图形问题为平面图形问题 思想方法 : 平移转化成相交直线所成的角 即化空间图形问题为平面图形问题 异面直线所成角的定义: 如图,已知两条异面直线 经过空间任一点O作 异面直线所成角的定义 如图 已知两条异面直线 a , b , 经过空间任一点 作 所成的锐角(或直角 直线 a′∥a , b ′∥b 则把 a ′与 b ′所成的锐角 或直角 叫做异面直线所成的角 ∥ ∥ 与 所成的锐角 或直角)叫做异面直线所成的角 (或夹角 或夹角). 或夹角 异面直线所成的角的范围( 0 , 90 ]
b
b′
a″ a
∠2
α
a′
O
∠1
BACK
NEXT
在求作异面直线所成的角时,O点 在求作异面直线所成的角时 点 常选在其中的一条直线上 (如线段的端点,线段的中点等) 如线段的端点 线段的中点等 如线段的端点 线段的中点
例2
如图,正方体 为侧面ADHE的中心,求 的中心, 如图,正方体ABCD-EFGH中,O为侧面 中 为侧面 的中心 (1)BE与CG所成的角? 与 所成的角? 所成的角 (2)FO与BD所成的角? 与 所成的角 所成的角?
这个角的大小与O点的位置有关吗 点位置不同时, 思考 : 这个角的大小与 点的位置有关吗 ? 即O点位置不同时 这一角的大小 点位置不同时 是否改变? 是否改变
解答: 解答: 如图
答: 这个角的大小与O点的位置无关. 点的位置无关 这个角的大小与 点的位置无关
相交所成的角为∠ 设a ′与 b ′相交所成的角为∠1, a ″与 b 所成的角为∠2 , 与 相交所成的角为 与 所成的角为∠ 公理4), ∵ a′∥a , a″ ∥a∴ a′∥ a″ (公理 ∥ ∴ ∥ 公理 同理 b′∥b″, ∴ ∠1 = ∠2 (等角定理 等角定理) ∥ 等角定理
第二课时 异面直线所成的角PPT全文课件

D′ A′
D
C′ B′
C
第二课时 异面直线所成的角PPT名师课件
A
B
*
第二课时 异面直线所成的角PPT名师课件
例2 如图,在四面体ABCD中,E,F分 别是棱AD,BC上的点,且 AE BF 1
ED FC 2
已知AB=CD=3,EF 3 ,求异面直线AB和
CD所成的角.
A
E
M
第二课时 异面直线所成的角PPT名师课件
b bˊ
a
o
*
b a α
b'
a' o
对于两条异面直线a,b,经过空间 任一点O作直线a′∥a, b′∥b,则 a′与b′所成的锐角(或直角)叫做异 面直线a与b所成的角(或夹角)
*
思考5:若点O的位置不同,则直线a′与
b′的夹角大小发生变化吗?为什么?为
了作图方便,点O宜选在何处?
b
b'
O
a
a' o
•
6.抓住课文中的主要内容和重点句子 ,引导 学生从 “摇花 乐”中 体会到 作者对 童年生 活的和 对家乡 的怀念 之情。
•
7.桂花是没有区别的,问题是母亲不 是在用 嗅觉区 分桂花 ,而是 用情感 在体味 它们。 一亲一 疏,感 觉自然 就泾渭 分明了 。从中 ,我们 不难看 出,家 乡在母 亲心中 的分量 。
•
2.许地山这样说,也是这样做的,他 长大后 埋头苦 干,默 默奉献 ,成为 著名的 教授和 作家, 他也因 此取了 个笔名 叫落花 生,这 就是他 笔名的 由来。
•
3.在伟大庄严的教堂里,从彩色玻璃 窗透进 一股不 很明亮 的光线 ,沉重 的琴声 好像是 把人的 心都洗 淘了一 番似的 ,我感 到了我 自己的 渺小。
异面直线所成角(公开课)ppt课件
异面直线平移成相交直线(在平面上适当的平移) 由两相交直线构造一个平面图形(三角形)
求出平面图形上对应的角θ
注意θ若为钝角,则异面直线所成角为π- θ
可编辑课件
18
b
O
a’
a
α
借助于平面α,使两条异面直线移动到相交,
是研究异面直线所成的角时必备法宝.
可编辑课件
19
思路整理:
异面直线所成角的求法
例1.已知ABCD-A1B1C1D1是棱长为1的正方
B
o
D
M 可编辑课件
14
C
新课讲解:
异面直线所成角的求法
例3.已知空间四边形ABCD中,AB=AC=AD=BC=BD
=CD=a, M 、 N分别是BC、AD的中点
(1)求异面直线AB、MN所成的角。
(2)求异面直线AB、CD所成的角。
A
N
B
o
D
M 可编辑课件
15
C
新课讲解:
异面直线所成角的求法
例3.已知空间四边形ABCD中,AB=AC=AD=BC=BD
=CD=a, M 、 N分别是BC、AD的中点
(1)求异面直线AB、MN所成的角。
(2)求异面直线AB、CD所成的角。
A
(3)求异面直线AM、CN所成的角。
N
B
D
E
M 可编辑课件
16
C
新课讲解:
异面直线所成角的求法
练习1.已知空间四边形ABCD中,AD=BC, M 、 N分别是
AB、CD的中点
(1) M N=
C1 N
A1
M
D
B1
C
B
N
C
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2. 两条异面直线所成的角指的是( )
①两别平行的两条相交直线
所成的锐角或直角;③过其中一条上的一点
作与另一条平行的直线,这两条相交直线所
成的锐角或直角;④两条直线既不相交也不
平行,无法成角
A.①②
B.②③
C.③④
D.①④
3. 若直线a//b,c与a所成的角为θ,则c与b所 成2. 的两角条异为面(直线所成)的角指的是( ) A点.与①θ 两两条 条相 异交 面直 直线线所分B成别.π的平-角行θ;的②两过条空相间 交任 直一 线 C所.成不的是锐θ角或直角;D③.不过其是中π一-条θ上的一点
c
b
a
直线a与b, 直线a与c, 直线a与d 都是异面直线,它们有什么区别?
N
c
d
b
a M
四. 异面直线所成的角的定义
直线a,b是异面直线,经过空间任意 一点O,分别引直线a1∥a, b1∥b, 我们把 直线a1和b1所成的锐角(或直角)叫做异面 直线a和b所成的角。
. bbbb11b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1ba1b1b1a1b1b1a1b1b1a1baa1b11b1a1ba1b11b1a1ba1b1aa1b11b11a1b1b1a111a1ao1a1a1 a1aa1a11
4. 通常采用平移的方法化异面直线为相交
直线所成的角
5. 异面直线垂直的概念。
教材:P298 2、3、4、5
M
O是空间中的任意一点
所成的锐角是否相等?
点O常 取在两条 异面直线 中的一条 上
b2
a2
.
b1
o1
a1
b
.
o
a M
相交直线所成角的大 小,就是异面直线所成 角的大小
b
o
α
0°﹤0 90° 相成交的异的异所直角面角面成线?直的直的≤a线范,b线角所围?成?
a
点O常取在两条异面直线中的一条上
例
正方体ABCD-A1B1C1D1,求:
两异面直线所成的角
一、复习
1. 填空: ⑴平行于同一条直线的两条直线_, 此结论又叫做空间平行直线的_; ⑵如果一个角的两边和另一个角的两 边__并且___,那么这两个 角相等;
二、异面直线
1. 定义:不同在任何一个平面内的两条直线 叫做异面直线。
注意:①“不同在任何一个平面内”,指 这 两条直线永不具备确定平面的条件,因此, 异面直线既不相交也不平行;②不能把异面 直线误解为:分别在不同平面内的两条直线 为异面直线。
D1
①A1B与CC1所成的角是多少度? A1
②④与棱A在1正BB11方B与垂体C直CA1的B所C棱成D有的-A几角1B条是1C?多1D少1棱度中?,
D
③ A1C1与BC所成的角是多少度?
A
C1 B1
C B
= + “垂直”
“相交垂直”
“异面垂直”
五. 课堂练习:
1. 异面直线是指( ) A.空间中两条不相交的直线 B.分别位于两个不同平面内的直线 C.平面内的一条直线与平面外的一条直线 D.不同在任何一个平面内的两条直线
三、异面直线的判定
1. 思考:如图所示,已知直线AB与平面α 相交于点B,点A在α外,直线L在α内但不 过点B,试判断直线AB与直线L的位置关系?
A
l
B
2.异面直线判定定理
• 过平面外一点与平面内一点的直线,和平 面内不经过该点的直线是异面直线。
A'
C
A
B
A'' B'
C' B'
a与b是相交直线,a与c也是相交直线, 它们之间又有什么区别?
作与另一条平行的直线,这两条相交直线所
4. 若则A成平a.的行相a、AC、锐 ,..交① ③b角 无c是② ④的、或 法异直 成位平角 角面置行;直关或④线系异两,条是面BD..直②b①(、线③④既cB也不).相相是交交异也或面不平直行线,
C.异面
D.平行或异面
5. 如图,在长方体ABCD-A’B‘C’D‘中:
⑴哪些棱所在直线与直线AA’成异面直线
且互相垂直?
⑵已知AB= 3,AA’=1,求异面直线
BA‘与CC’所成角的度数。
D’
C‘
A‘ D
B’ C
A
B
六. 课堂小结: 1. 异面直线的概念。 2. 异面直线的判定定理:连结平面内一点
与平面外一点的直线,和这个平面内不 经过此点的直线是异面直线。 3. 异面直线夹角的概念。
