§2.4 粘弹性流体
粘弹性流体的特性及其在药物输送和生物流体力学中的应用

粘弹性流体的特性及其在药物输送和生物流体力学中的应用粘弹性流体是一种特殊的流体,具有粘性和弹性的双重特性。
在物理学、化学和工程学等领域中,粘弹性流体的研究与应用日益受到关注。
本文将介绍粘弹性流体的特性,并探讨其在药物输送和生物流体力学中的应用。
一、粘弹性流体的特性粘弹性流体的特性可以归结为两个方面:粘性和弹性。
1. 粘性:粘弹性流体表现出与黏度相关的特性。
黏度是流体内部分子间相互作用引起的阻力大小。
粘性使得粘弹性流体具有黏滞的特性,即流动缓慢且阻力较大。
2. 弹性:粘弹性流体在受力后能够产生应力,当施加的力消失后,流体能够恢复原貌。
这种特性使得粘弹性流体具有一定的形变能力。
二、粘弹性流体在药物输送中的应用1. 控释药物输送系统:粘弹性流体可用于制备控释药物输送系统。
通过调节粘弹性流体的黏度和弹性,可以使药物以缓慢且持续的方式释放,从而提高药物治疗效果并减少药物的频繁使用。
2. 口腔和皮肤黏附剂:粘弹性流体作为黏附剂可以在口腔和皮肤表面保持一定时间。
在药物输送中,它可以增加药物在局部的停留时间,从而提高药效。
三、粘弹性流体在生物流体力学中的应用1. 血液模拟体:粘弹性流体可以用于生物流体力学的研究中,模拟血液的流动行为。
通过调节粘弹性流体的黏度和弹性,可以模拟不同状态下的血流情况,研究血流动力学特性,从而为心血管疾病的诊断和治疗提供依据。
2. 细胞培养基:粘弹性流体还可以作为细胞培养基的替代品,提供更接近细胞体内环境的生物力学条件。
这可以帮助研究者更好地理解细胞生长、分化和迁移等过程,为组织工程和再生医学提供指导。
四、结语粘弹性流体作为一种特殊的流体,具有粘性和弹性的特性,广泛应用于药物输送和生物流体力学领域。
在药物输送中,粘弹性流体可以用于制备控释药物输送系统,以及口腔和皮肤黏附剂的制备。
在生物流体力学中,粘弹性流体可以模拟血液流动行为,用作血液模拟体,同时也可以作为细胞培养基,提供更接近细胞体内环境的生物力学条件。
黏弹性流体力学研究中的弹性效应分析

黏弹性流体力学研究中的弹性效应分析引言黏弹性流体是一种特殊的流体,其流动特性既受到黏性的影响,也受到弹性的影响。
在研究黏弹性流体力学时,必须考虑到弹性效应对流体流动行为的影响。
本文将详细分析黏弹性流体力学研究中的弹性效应,以期深入理解这一领域。
黏弹性流体的特性黏弹性流体具有独特的流动特性,其特点如下: 1. 延展性: 黏弹性流体能够以较小的应力下发生很大的变形。
2. 回弹性: 黏弹性流体在停止外力作用后能够恢复原状或接近原状。
3. 补偿时间: 黏弹性流体具有补偿能力,可以在流动中适应外界环境变化。
4. 结构耗散: 黏弹性流体的流动过程中存在结构的重组和破坏。
弹性效应对黏弹性流体力学研究的影响黏弹性流体力学研究在很大程度上依赖于弹性效应的考虑,弹性效应对流体流动的影响主要体现在以下几个方面:弹性模量的测定弹性模量是衡量黏弹性流体中弹性效应的重要参数,它可以通过实验方法测定得到。
常用的测定方法包括剪切杆测试、剪切振动测试和动态拉伸测试等。
这些方法通过施加外力并测量流体的应变来计算弹性模量,从而揭示流体中弹性效应的特征。
力学行为的描述黏弹性流体力学中,弹性效应对力学行为的描述起着重要的作用。
流体的粘滞效应和弹性效应共同决定了流体的力学行为。
根据流变学理论,可以通过引入弹性效应的流体模型来描述流体的力学行为,例如,Maxwell模型、Kelvin模型和Oldroyd模型等。
这些模型可用于模拟黏弹性流体的应力-应变关系。
流动行为的预测弹性效应在预测黏弹性流体流动行为中发挥着重要作用。
在模拟黏弹性流体的流动过程时,必须考虑到弹性效应对流体动力学行为的影响。
通过引入弹性效应的流体模型,可以预测黏弹性流体在不同流动条件下的行为,如层流和湍流过渡、流动的稳定性和剪切层的形成等。
弹性效应的尺度依赖性弹性效应在黏弹性流体力学中的研究中还表现出尺度依赖性。
尺度效应是指由于尺度效应引起的材料力学性质随尺度的改变而发生变化,在弹性效应的研究中,尺度效应尤为重要。
粘弹性流体力学的理论与实验研究

粘弹性流体力学的理论与实验研究引言粘弹性流体力学是研究流体在同时具有粘性和弹性特性时的行为的学科。
这一领域的研究在多个领域具有重要的应用,包括材料科学、生物医学以及地球科学等领域。
本文将深入探讨粘弹性流体力学的理论基础,并介绍一些经典的实验研究。
理论基础粘弹性流体的概念粘弹性流体是指既具有粘性又具有弹性的液体或软固体。
粘性是指流体内部分子之间相互摩擦的现象,而弹性是指流体内部分子在外力作用下出现回弹的现象。
粘弹性流体的宏观性质在很大程度上取决于物质的微观结构与分子间力的相互作用。
粘弹性流体的模型粘弹性流体的模型通常基于两种基本模型:弹性体模型和粘性流体模型。
弹性体模型可以用弹簧和阻尼器串联的方式来描述,而粘性流体模型则可以用牛顿黏滞定律来表示。
实际的粘弹性流体通常需要综合考虑这两种模型。
粘弹性流体的本构方程粘弹性流体的本构方程用于描述物质的应力-应变关系。
最常用的本构方程是Maxwell模型和Kelvin模型。
Maxwell模型将弹性元素和粘性元素串联起来,可以较好地描述物质的粘弹性行为。
而Kelvin模型通过并联弹性元素和粘性元素来描述物质的行为。
粘弹性流体的流变特性粘弹性流体的流变特性包括黏度、屈服应力、流变曲线等。
黏度是指流体流动时所表现出的阻力大小,是刻画流体流动难易程度的物理量。
屈服应力是指流体在外力作用下开始产生可观测的流动行为所需要的最小应力。
流变曲线则是描述流体在剪切应力施加下产生的剪切应变与时间的关系。
实验研究粘弹性流体的流变性能测试粘弹性流体的流变性能可以通过实验测试来获得。
常见的实验方法有旋转粘度计法、振荡剪切法、迎风试验法等。
旋转粘度计法是通过测量粘弹性流体在旋转圆盘上产生的剪切应力与剪切速率的关系来确定其黏度。
振荡剪切法则是通过频率和振幅的变化来研究粘弹性流体的流变特性。
迎风试验法则是在流体流动中施加外界气流压力来研究粘弹性流体的变形和流动行为。
粘弹性流体的微观结构表征粘弹性流体的微观结构对其宏观行为具有重要影响。
§2.4 粘弹性流体
τ13= τ31 , τ23= τ32 。对简单的剪切流动, τ13= τ31=0, τ23= τ32 =0, 故只有剪切应力τ12起作用。
τ 11-τ 22=N1 为 第 一 法 向 应 力 差 , 产 生 轴 向 压 力 , 引 起
Weissenberg效应和挤出物胀大现象。
τ 22-τ 33=N 2为第二法向应力差,产生径向压力,通常很小,
3.同心套管轴向流动现象
4.回弹现象
5.无管虹吸现象
6.次级流现象
7.紊流减阻现象
二、粘弹性流体的流变特征 1.法向应力与法向应力差 当力F作用于物体时,物体内部体积元所受的总应力(或物体内
τ 部某一点所受到的总应力) 可用九个应力分量τ
τ
可分解为九个应力分量 τ
ij
ij
表示,或者说
,其中i代表应力分量作用的平面
法向方向,j代表应力分量的方向,如下图所示,可用张量表示如 下。
τ 11 τ 12 τ 13 τ τ ij = 21 τ 22 τ 23 τ 31 τ 32 τ 33
其中,应力分量的下标1、2、3分别对应于x、y、z方向。τ11 、 τ
22、
τ33为法向应力,其它6个为剪切应力,并且, τ12= τ21 ,
并为负值。 为描述剪切流场中流体流变性随剪切速率的变化性质,需要 下面3个物料函数: (1)剪切粘度
µ (γɺ )=τ 12 γɺ
ψ 1 (γɺ )= N 1 2 (2)第一法向应力系数 γɺ
(3)第二法向应力系数
ψ 2 (γɺ )= N 2
γɺ 2
ψ µ对于牛顿流体, 1 (γɺ )和 ψ 2 (γɺ ) 均为0, (γɺ ) 为常数。
应力松弛曲线示意图
粘弹性流体物理特性的研究及其在工业化加工中的应用研究

粘弹性流体物理特性的研究及其在工业化加工中的应用研究第一章粘弹性流体的概念与分类粘弹性流体是指在应力下表现出固体特性和流体特性的一类复杂非牛顿流体,广泛应用于化工、生物医学、食品加工等领域。
粘弹性流体常见的物质有聚合物、胶体、水泥、淀粉等。
根据流变学的分类,粘弹性流体可以分为黏弹性体、黏塑性体、粘弹性液体三类。
第二章粘弹性流体的物理特性2.1 流动行为粘弹性流体与牛顿流体不同,其流动规律不同,随着剪切速率的增加,黏度呈现不同程度的变化,即存在剪切率的效应。
为了描述流体的这种特性,研究者提出了流变学的概念,即研究流体随剪切力的变化而产生的结构演变和性质变化。
2.2 破坏形变当粘弹性流体在剪切场中进行变形时,其分子链会因为外力而断裂,形成流化结构,导致物理性质的改变。
这种流化结构可以随着外力的停止而缓慢恢复,称为“记忆效应”。
2.3 外场响应在外力场的作用下,粘弹性流体内部会产生很大的内应变和相应的能量损失,具有优异的阻尼特性。
因此,在工程实践中可以利用这种特性来制作减震、隔音等工业产品。
第三章粘弹性流体在工业化加工中的应用研究3.1 液压系统液压系统在航空、机械、汽车等领域非常常见,而粘弹性流体的阻尼特性很适合用来制作减震器,提升车辆乘坐的舒适度和行驶的平稳性。
3.2 食品加工粘弹性流体在食品加工中的应用非常广泛,如在果酱、果泥等加工过程中,加入一定量的黏性增稠剂使其提高流动性。
3.3 生物医学在生物医学领域中,粘弹性流体的应用也得到了广泛的关注。
例如,利用粘弹性流体可以制作出仿生材料,来模拟肌肉组织及生物材料的特性。
第四章粘弹性流体应用的优点与不足4.1 优点①显著的阻尼特性:液压减震器、阻尼材料等领域中广泛使用这种特性。
②柔顺的流动性:在食品、化妆品、纺织品等领域中广泛应用于改善质地和流动性。
③增强的粘附性:在油墨、染料等工业中广泛应用,可以有效地提高粘附性。
4.2 不足由于粘弹性流体本身结构复杂,且理论研究尚未完备,因此在实际应用中容易出现应变失稳、流动不稳定等问题。
流体动力学中的黏弹性流体研究

流体动力学中的黏弹性流体研究引言流体动力学是研究流体运动规律的物理学科,黏弹性流体是其中的一个重要分支。
黏弹性流体具有介于液体和固体之间的特性,既具有流体的流动性,又具有固体的弹性。
在工程领域中,黏弹性流体的研究在物料加工、油田开发、生物医学等多个方面具有重要应用价值。
本文将探讨黏弹性流体的定义、性质、流动行为以及相关研究方法与应用领域。
一、黏弹性流体的定义与分类1.1 定义黏弹性流体是指在外力作用下具有应力和应变关系不仅取决于变形速度和应变量,而且还取决于变形历史的流体。
与牛顿流体和非牛顿流体相比,黏弹性流体展现出了更为复杂的性质。
1.2 分类黏弹性流体按照性质可分为两类:线性黏弹性流体和非线性黏弹性流体。
线性黏弹性流体的应力与应变呈线性关系,而非线性黏弹性流体的应力与应变则不是线性关系。
二、黏弹性流体的性质与特点黏弹性流体具有以下几个基本性质与特点:2.1 弹性本质黏弹性流体具有固体的形变回复能力,即具有弹性本质。
当外力停止作用时,黏弹性流体会恢复到初始状态,这与牛顿流体和非牛顿流体在停止外力作用后无法恢复的特性有所区别。
2.2 流变性黏弹性流体的应力-应变关系与变形速率密切相关,即流体的黏度会随着变形速度的变化而发生变化。
这种特性使得黏弹性流体具有复杂的流变性质。
2.3 液体性质与固体相比,黏弹性流体更接近液体,具有流动性。
黏弹性流体的流动性使得其在流体力学中具有重要地位,并广泛应用于工程领域。
黏弹性流体的流动行为比较复杂,受多个因素的影响。
主要包括应变速率、外力作用、温度等因素。
3.1 应变速率的影响黏弹性流体的黏度随应变速率的变化而变化。
当应变速率较低时,黏弹性流体呈现出较低的黏度值;当应变速率增加时,黏度也会随之增加。
这种应变速率对黏度的敏感性使得黏弹性流体在实际应用中需要进行合适的设定与控制,以满足不同流动条件的要求。
3.2 外力作用的影响外力的作用对黏弹性流体的流动行为具有重要影响。
流体动力学中的粘弹性流体研究

流体动力学中的粘弹性流体研究引言流体力学是研究流体运动规律的科学领域,其中粘弹性流体是一种特殊的流体,具有既有液体的流动性,又具有可变形的固体的特性。
粘弹性流体在工程和科学研究中具有重要应用价值,对其进行深入研究有助于我们更好地理解和掌握流体动力学的基本原理。
本文将介绍粘弹性流体的基本概念和特性,并介绍流体动力学中的粘弹性流体研究的主要内容和方法。
粘弹性流体的定义和特性粘弹性流体是介于固体和液体之间的一类流体。
与牛顿流体(如水和空气)不同,粘弹性流体在外力作用下不仅会流动,还会发生变形。
粘弹性流体的主要特性包括粘度、弹性、流变性和记忆效应。
粘度粘度是粘弹性流体的一种基本特性,它描述了流体内部的黏性阻力。
粘度可以分为静态粘度和动态粘度两种。
静态粘度指的是流体在不应变条件下的黏性阻力,动态粘度则指的是流体在受到应变时的黏性阻力。
粘度可用来描述流体的流动阻力大小,常用单位是帕斯卡·秒(Pa·s)。
弹性粘弹性流体的弹性是指其在受力作用下会发生恢复变形的特性。
与刚体不同,粘弹性流体在受到外力后会发生弹性变形,当外力去除时会恢复到原始状态。
粘弹性流体的弹性可用弹性模量来描述,常用单位是帕斯卡(Pa)。
流变性粘弹性流体的流变性是指其在外力作用下会发生非线性变形的特性。
由于流体具有粘度和弹性,其应力-应变关系不遵循线性规律,而呈现出非线性的行为。
流变性可用流变学来研究和描述。
记忆效应粘弹性流体的记忆效应是指其在经历过一定变形后,会在一定的时间范围内保持相同的应力-应变关系。
这使得粘弹性流体具有一定的时间依赖性。
记忆效应是粘弹性流体独特的特性之一。
粘弹性流体的研究内容和方法在流体动力学中,粘弹性流体的研究主要集中在以下几个方面:流变学、模型和仿真、实验测量和应用。
流变学研究流变学是研究粘弹性流体变形和流动规律的学科。
通过建立流变学模型来描述粘弹性流体的应力-应变关系,从而深入了解粘弹性流体的流变性质。
粘弹性流体的本构模型及其应用

粘弹性流体的本构模型及其应用随着人们对物质性质的深入研究,越来越多的特殊性质的物质被人们所发现,粘弹性流体就是其中之一。
粘弹性流体既具有粘性又具有弹性,被广泛运用于化学、医学、生物学和工程等领域中。
而对于粘弹性流体的本构模型的研究,则是这些应用的基础。
本篇文章将对粘弹性流体的本构模型及其应用进行详细的论述。
一、粘弹性流体的性质粘弹性流体是介于粘性流体和弹性体之间的物质,它既具有流变性质,也具有力学弹性。
它的流变特性表现为,当它受到作用力时会出现变形,而当这种作用力减小或消失时,它的变形又会逐渐恢复。
这种特殊的性质使得它在许多领域具有广泛的应用。
二、粘弹性流体的本构模型粘弹性流体的本构模型是用数学方式来描述流体变形特性的模型。
它是通过实验数据和理论推导确定的粘弹性流体性质的一种数学表示,用于预测和计算其在不同外力下的流变特性。
在粘弹性流体的本构模型中,最常见的是Maxwell模型、Kelvin模型以及Jeffreys模型。
1、Maxwell模型Maxwell模型是由Maxwell在1867年提出的一种模型,是最早被使用的粘弹性流体本构模型之一。
它被广泛应用于石油工程、高分子材料工程、生物领域等领域中。
Maxwell模型的基本原理是将粘性流体和弹性体的模型结合而成。
在Maxwell模型中,流体被视为一个简单的线性弹性体,它由一个弹簧和一个阻尼器组成。
当给该模型施加一个外力时,其中的弹簧会产生弹性变形,而其中的阻尼器会产生粘性变形,使模型发生流变。
而在外力消失后,这两种变形也会随之减小或消失。
2、Kelvin模型Kelvin模型是由Lord Kelvin在1855年提出的一种模型,它将Maxwell模型中的一个弹簧换成为一个螺旋状的弹性体。
和Maxwell模型一样,Kelvin模型也是一种线性的本构模型,它可以更好地描述时间依赖性粘弹性流体的行为。
3、Jeffreys模型Jeffreys模型是由Jeffreys在1927年提出的一种模型,它是Maxwell模型的一种变体。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
并为负值。 为描述剪切流场中流体流变性随剪切速率的变化性质,需要 下面3个物料函数: (1)剪切粘度
µ (γɺ )=τ 12 γɺ
ψ 1 (γɺ )= N 1 2 (2)第一法向应力系数 γɺ
(3)第二法向应力系数
ψ 2 (γɺ )= N 2
γɺ 2
ψ µ 对于牛顿流体, 1 (γɺ )和 ψ 2 (γɺ ) 均为0, (γɺ ) 为常数。
蠕变与回复曲线
5.线性粘弹性与非线性粘弹性 流体的粘弹性可分为线性粘弹性和非线性粘弹性。线性粘弹 性即应力、应变和应变速率之间成线性关系。粘弹性流体往往 只能在较小的形变或形变速率下才出现线性特性。在较大的应 变或剪切速率下,应力、应变和应变速率之间一般不成线性关 系,即流体呈现非线性粘弹性。对非线性粘弹性状态下的流体, 所测的流变性数据受实验参数和测量系统几何尺寸的影响非常 大,不是绝对值,只能用作比较。目前人们对粘弹性流体流变 性的认识、描述在很大程度上仍停留在线性粘弹性范围。
2.应力松弛 对粘弹性流体施加一恒定的应变,即保持应变随时间不变 见 图中的曲线a,那么流体内所受到的应力随时间而逐渐减小,这 种特性称应力松弛。
τ → ∞ 时, > 0 当 t → ∞ 时, = 0 τ
当t
,称部分应力松弛,如图中的曲线b所示; ,称完全应力松弛,如图中的曲线c所示。
τ ϒ
a
b
c t
τ
a
b
ϒ
弹性滞后曲线示意图
4.蠕变与回复 对理想固体施加一恒定的应力时,固体中瞬间产生对应的 应变;当应力消除时,产生的应变也瞬间完全回复。对理想流 体施加恒定的应力时,流体内产生的应变会随应力作用时间的 增加而逐渐增大;当应力消除后,流体内产生的应变不会回复。 对粘弹性流体,对于应力的突然施加与突然消除,得到的应变 -时间曲线是介于理想固体与理想流体之间的独特的特性曲线。 在应力施加阶段的应变-时间曲线为蠕变曲线,在应力消除后 对应的应变-时间曲线为回复曲线变曲线为通过原点的直线,而且应力上 升与下降对应的应力-应变曲线完全重合,如图中的曲线a。 而粘弹性流体的应力-应变曲线不是直线,而且其应力上升与 下降对应的应力-应变曲线不重合,如图中的曲线b,这种特 性称弹性滞后。滞后环的面积与应变随时间的变化速率有关, 即应力是应变与时间的函数。
法向方向,j代表应力分量的方向,如下图所示,可用张量表示如 下。
τ 11 τ 12 τ 13 τ τ ij = 21 τ 22 τ 23 τ 31 τ 32 τ 33
其中,应力分量的下标1、2、3分别对应于x、y、z方向。τ11 、 τ
22、
τ33为法向应力,其它6个为剪切应力,并且, τ12= τ21 ,
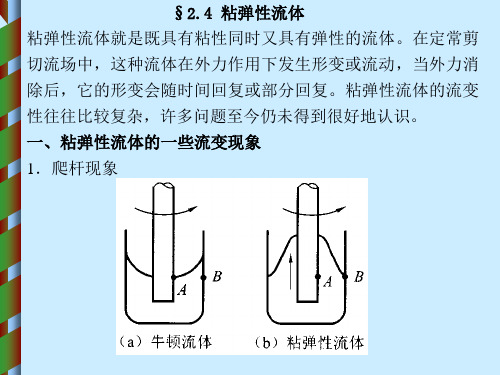
§2.4 粘弹性流体 粘弹性流体就是既具有粘性同时又具有弹性的流体。在定常剪 切流场中,这种流体在外力作用下发生形变或流动,当外力消 除后,它的形变会随时间回复或部分回复。粘弹性流体的流变 性往往比较复杂,许多问题至今仍未得到很好地认识。 一、粘弹性流体的一些流变现象 1.爬杆现象
2.挤出胀大现象
3.同心套管轴向流动现象
4.回弹现象
5.无管虹吸现象
6.次级流现象
7.紊流减阻现象
二、粘弹性流体的流变特征 1.法向应力与法向应力差 当力F作用于物体时,物体内部体积元所受的总应力(或物体内
τ 部某一点所受到的总应力) 可用九个应力分量τ
τ
可分解为九个应力分量 τ
ij
ij
表示,或者说
,其中i代表应力分量作用的平面
τ13= τ31 , τ23= τ32 。对简单的剪切流动, τ13= τ31=0, τ23= τ32 =0, 故只有剪切应力τ12起作用。
τ 11-τ 22=N1 为 第 一 法 向 应 力 差 , 产 生 轴 向 压 力 , 引 起
Weissenberg效应和挤出物胀大现象。
τ 22-τ 33=N 2为第二法向应力差,产生径向压力,通常很小,
