线性回归问题与非线性回归分析
《非线性回归分析》课件
封装式
• 基于模型的错误率和复 杂性进行特征选择。
• 常用的封装方法包括递 归特征消除法和遗传算 法等。
嵌入式
• 特征选择和模型训练同 时进行。
• 与算法结合在一起的特 征选择方法,例如正则 化(Lasso、Ridge)。
数据处理方法:缺失值填充、异常值 处理等
1
网格搜索
通过预定义的参数空间中的方格进行搜
随机搜索
2
索。
在预定义的参数空间中进行随机搜索。
3
贝叶斯调参
使用贝叶斯优化方法对超参数进行优化。
集成学习在非线性回归中的应用
集成学习是一种将若干个基学习器集成在一起以获得更好分类效果的方法,也可以用于非线性回归建模中。
1 堆叠
使用多层模型来组成一个 超级学习器,每个模型继 承前一模型的输出做为自 己的输入。
不可避免地存在数据缺失、异常值等问题,需要使用相应的方法对其进行处理。这是非线性回归 分析中至关重要的一环。
1 缺失值填充
常见的方法包括插值法、代入法和主成分分析等。
2 异常值处理
常见的方法包括删除、截尾、平滑等。
3 特征缩放和标准化
为了提高模型的计算速度和准确性,需要对特征进行缩放和标准化。
偏差-方差平衡与模型复杂度
一种广泛用于图像识别和计算机 视觉领域的神经网络。
循环神经网络
一种用于处理序列数据的神经网 络,如自然语言处理。
sklearn库在非线性回归中的应用
scikit-learn是Python中最受欢迎的机器学习库之一,可以用于非线性回归的建模、评估和调参。
1 模型建立
scikit-learn提供各种非线 性回归算法的实现,如 KNN回归、决策树回归和 支持向量机回归等。
非线性回归分析的入门知识

非线性回归分析的入门知识在统计学和机器学习领域,回归分析是一种重要的数据分析方法,用于研究自变量和因变量之间的关系。
在实际问题中,很多情况下自变量和因变量之间的关系并不是简单的线性关系,而是呈现出一种复杂的非线性关系。
因此,非线性回归分析就应运而生,用于描述和预测这种非线性关系。
本文将介绍非线性回归分析的入门知识,包括非线性回归模型的基本概念、常见的非线性回归模型以及参数估计方法等内容。
一、非线性回归模型的基本概念在回归分析中,线性回归模型是最简单和最常用的模型之一,其数学表达式为:$$Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + ... + \beta_pX_p +\varepsilon$$其中,$Y$表示因变量,$X_1, X_2, ..., X_p$表示自变量,$\beta_0, \beta_1, \beta_2, ..., \beta_p$表示模型的参数,$\varepsilon$表示误差项。
线性回归模型的关键特点是因变量$Y$与自变量$X$之间呈线性关系。
而非线性回归模型则允许因变量$Y$与自变量$X$之间呈现非线性关系,其数学表达式可以是各种形式的非线性函数,例如指数函数、对数函数、多项式函数等。
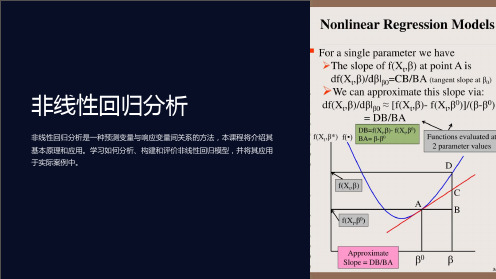
一般来说,非线性回归模型可以表示为:$$Y = f(X, \beta) + \varepsilon$$其中,$f(X, \beta)$表示非线性函数,$\beta$表示模型的参数。
非线性回归模型的关键在于确定合适的非线性函数形式$f(X,\beta)$以及估计参数$\beta$。
二、常见的非线性回归模型1. 多项式回归模型多项式回归模型是一种简单且常见的非线性回归模型,其形式为: $$Y = \beta_0 + \beta_1X + \beta_2X^2 + ... + \beta_nX^n +\varepsilon$$其中,$X^2, X^3, ..., X^n$表示自变量$X$的高次项,$\beta_0, \beta_1, \beta_2, ..., \beta_n$表示模型的参数。
回归分析非线性回归

回归分析非线性回归回归分析是一种用于研究自变量与因变量之间关系的统计分析方法。
在回归分析中,我们使用自变量来解释因变量的变化,并建立一个数学模型来描述这种关系。
通常情况下,我们假设自变量与因变量之间是线性关系。
因此,在大多数回归分析应用中,我们使用线性回归模型。
然而,有时候我们可能会发现实际数据不符合线性关系的假设。
这时,我们就需要使用非线性回归模型来更好地解释数据。
非线性回归分析是一种通过建立非线性模型来描述自变量和因变量之间关系的方法。
在这种情况下,模型可以是各种形式的非线性函数,如指数函数、对数函数、多项式函数等。
非线性回归模型的形式取决于实际数据。
非线性回归模型的建立通常包括以下几个步骤:1.数据收集:首先需要收集与自变量和因变量相关的数据。
这些数据应该能够反映出二者之间的关系。
2.模型选择:根据实际情况选择合适的非线性模型。
常见的非线性模型有指数模型、对数模型、幂函数等。
3.参数估计:使用最小二乘法或其他拟合方法来估计模型中的参数。
这些参数描述了自变量和因变量之间的关系。
4.模型检验:对估计得到的模型进行检验,评估模型的拟合程度。
常见的检验方法有残差分析、F检验、t检验等。
5.模型解释与预测:解释模型的参数和拟合程度,根据模型进行预测和分析。
非线性回归分析的主要优点是可以更准确地描述自变量和因变量之间的关系。
与线性回归不同,非线性回归可以拟合一些复杂的实际情况,并提供更准确的预测。
此外,非线性回归还可以帮助发现自变量和因变量之间的非线性效应。
然而,非线性回归模型的建立和分析相对复杂。
首先,选择适当的非线性模型需要一定的经验和专业知识。
其次,参数估计和模型检验也可能更加困难。
因此,在进行非线性回归分析时,需要谨慎选择合适的模型和方法。
最后,非线性回归分析还需要考虑共线性、异方差性、多重共线性等统计问题。
这些问题可能影响到模型的稳定性和可靠性,需要在分析过程中加以注意。
总之,非线性回归分析是一种用于解释自变量和因变量之间非线性关系的方法。
第3章 线性回归与非线性回归

Yt B1 B2 X t ut
假设 u t u t -1 v t -1 1 其中,v满足OLS假定,并且 是已知的。
Yt 1 B1 B2 X t 1 ut 1
方程(9 - 2)的两边同时乘以 , 得到 :
Yt -1 B1 B2 X t -1 u t -1
View/Residual Tests/Heteroskedasticity Tests 或者 eq01.hettest(type=Glejser) c car pmg pop rgnp
斯皮尔曼(Spearman)秩相关检验。 戈德费尔德-匡特(Goldfeld-Quandt)检验 巴特莱特(Bartlett)检验 匹克(Peak)检验 布鲁尔什-培甘(Breusch-Pagan)检验 CUSUMSQ检验
在方程定义窗口的定义栏中输入: 线性化方法:ls log(Y) c log(K) log(L) 非线性方法:ls Y=c(1)*K^c(2)*L^c(3)
有时遇到估计结果不符合常规或显示出无法收敛 的错误信息时,需要设定选项重新估计。 (1)初始值(Start Value) 初始值是EViews进行第一次迭代计算时参数所取 的数值。这个值保存在与回归函数有关的系数向 量中。回归函数必须定义初始值。例如如果回归 函数包含表达式1/C (1),就不能把C (1)的初始值 设定为0,同样如果包含表达式LOG (C (2)),那C (2)必须大于零。
建模过程仍是先打开方程定义窗口,在定义栏中输 入模型的非线性表达式即可。不同的是有时候可能 迭代无法收敛,则需要通过修改选项设置来重新估 计。 与例3.6比较,可以看出,线性化与NLS法的参数估 计值完全一样,统计量输出相同,这是由于线性化 仅改变了变量的形式,而NLS法也没有改变y和1/x 的线性关系,在这两种情况下进行最小二乘估计对 于待估参数来说是等价的。
多元线性回归和非线性回归

2
SSR R SST
2 ˆ ( y y ) i 2 ( y y ) i i 1 i 1 n
n
,x ,x 称 y 关于 x 1 2, p 的样本复相关系数,R 的大小可以
反映作为一个整体的 x ,x ,x 1 2, p与 y 的线性相关的密切 程度.
修正多重决定系数(adjusted multiple coefficient of determination)
回归参数的估计
估计的多元线性回归的方程
(estimated multiple linear regression equation)
1.
2. 3.
ˆ ,b ˆ ,b ˆ, ˆ 估计回归方程 ,b 用样本统计量 b 0 1 2 p 中的 参数 b 时得到的方程 , b , b , , b 0 1 2 p 由最小二乘法求得 一般形式为
ˆ ˆ ˆ ˆ ˆ y b b x b x b x 0 1 1 2 2 p p
ˆ, ˆ, ˆ, ˆ是 b , b , b , , b b , b 0 1 2 p 0 b 1 b 2 p
估计值 ˆ 是 y 的估计值 y
参数的最小二乘法
1. 使因变量的观察值与估计值之间的离差平方和 ˆ, ˆ, ˆ, ˆ 。即 b b , b 达到最小来求得 b 0 1 2 p
i 1
3. 确定显著性水平和分子自由度p、分母自由度np-1找出临界值F 4. 作出决策:若F>F ,拒绝H0
方差分析表
前面的这些计算结果可以列成表格的形式,称为方差分析表. 方差分析表
方差来源 平方和 回归 残差 总和 SSR SSE SST 自由度 p 方差 SSR / p F 值
第 2 讲(1) 一元线性、非线性回归分析

2
14
• 因此,点估计:
ˆ y ( x0 ) = a + bx0
• 区间估计:
ˆ y1 ( x0 ) = a + bx0 − δ ( x0 )
ˆ y 2 ( x0 ) = a + bx0 + δ ( x0 )
15
进似地, 很大( 进似地,当n很大(即 n → ∞ )时,t α 很大
α = 0.05
② 单侧控制
y < y,或 y < y 2
' 1 '
19
• 回归分析注意事项
(1)自变量、因变量的选择 )自变量、 (2)样本回归方程 ) (3)必须进行显著性检验 ) (4)任何回归方程都具有使用范围 )
20
二、一元非线性回归分析
1. 可化为线性回归的非线性回归
某石灰土强度与龄期关系 强度(Mpa Mpa) 2.5 2 1.5 1 0.5 0 0 50 100 150 200 龄期(d)
y1 < y < y2
' '
为此我们要合理控制x的取值,参照式(1)有下式:
P{
y1 < y < y2
' '
}≥ 1 − α
17
• 一般情况下可参照图求解:
′ y1 = a + bx −
t α ( n − 2 ) σˆ
2
1 (x − x )2 1 + + n L xx
′ y 2 = a + bx + t α
ˆ δ ( x0 ) ≈ 1.96σ
x0 又在 x 的平均值附近,取
= 1.96
2
ˆ ˆ y1 ( x0 ) ≈ a + bx0 − 1.96σ
如何使用Matlab进行线性回归与非线性回归

如何使用Matlab进行线性回归与非线性回归使用Matlab进行线性回归与非线性回归简介:线性回归和非线性回归是统计分析中常用的两种回归模型。
线性回归假设自变量与因变量之间存在线性关系,而非线性回归则假设二者之间存在非线性关系。
本文将介绍如何使用Matlab进行线性回归和非线性回归分析,并分析其应用领域和优缺点。
一、线性回归分析线性回归是一种最基本的回归分析方法,广泛应用于统计学、经济学、金融学等领域。
在Matlab中,可以使用fitlm函数进行线性回归分析。
回归模型的基本形式如下所示:Y = β0 + β1X1 + β2X2 + ... + ε其中Y是因变量,X1,X2等是自变量,β0,β1,β2等是回归系数,ε是误差项。
线性回归模型的参数估计可以采用最小二乘法。
在Matlab中,可以使用fitlm 函数进行参数估计和显著性检验。
显著性检验可以帮助我们确定回归系数的是否显著不等于零,从而判断自变量对因变量的影响是否显著。
二、非线性回归分析在某些情况下,变量之间的关系不是线性的,而是呈现出曲线的形式。
这时,我们需要使用非线性回归模型进行分析。
在Matlab中,可以使用cftool函数进行非线性回归分析。
cftool是一个交互式的拟合工具箱,通过界面操作可以方便地进行曲线拟合。
用户可以选择不同的拟合模型,并根据数据点进行拟合。
cftool提供了各种常见的非线性回归模型,如指数模型、幂函数模型、对数模型等。
用户可以根据实际需求选择合适的模型进行分析。
非线性回归模型的参数估计可以使用最小二乘法、最大似然估计等方法。
在Matlab的cftool中,可以直接进行参数估计,并生成相应的拟合曲线。
三、线性回归与非线性回归的应用领域线性回归和非线性回归分析在各个领域都有广泛的应用。
线性回归常用于预测、趋势分析、经济建模等方面。
非线性回归则更适用于描述非线性关系的数据,常用于生物医学、环境科学、物理学等领域。
以医学领域为例,线性回归可以用于预测患者的生存时间、评估药物的剂量-效应关系等。
生物统计学:第10章 多元线性回归分析及一元非线性回归分析

H0 : 1 2 k 0 H A : 至少有一个i 0
拒绝H0意味着至少有一个自变量对因变量是有影 响的。
检验的程序与一元的情况基本相同,即用方差
胸围X2 186.0 186.0 193.0 193.0 172.0 188.0 187.0 175.0 175.0 185.0
体重Y 462.0 496.0 458.0 463.0 388.0 485.0 455.0 392.0 398.0 437.0
序号 体长X1 胸围X2 体重Y 11 138.0 172.0 378.0 12 142.5 192.0 446.0 13 141.5 180.0 396.0 14 149.0 183.0 426.0 15 154.2 193.0 506.0 16 152.0 187.0 457.0 17 158.0 190.0 506.0 18 146.8 189.0 455.0 19 147.3 183.0 478.0 20 151.3 191.0 454.0
R r Y•1,2,,k
yp yˆ p
,
p 1,2,, n
对复相关系数的显著性检验,相当于对整个回 归的方差分析。在做过方差分析之后,就不必再检 验复相关系数的显著性,也可以不做方差分析。
例10.1的RY·1,2为:
RY •1,2
24327 .8 0.9088 29457 .2
从附表(相关系数检验表)中查出,当独立
表示。同样在多元回归问题中,可以用复相关系数表 示。对于一个多元回归问题,Y与X1,X2,… ,Xk 的线性关系密切程度,可以用多元回归平方和与总平 方和的比来表示。因此复相关系数由下式给出,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例3.1 根据例2.1计算特征值及条件指数 多重共线性检验SPSS
• 打开[Linear Regression: Statistics]子对话框,选择 [Collinearity diagnostics(共线性诊断)],单击[Continue]返 回主对话框并单击[OK]按钮。这样SPSS 便可输出所有检 查多重共线性的指标。
注意: 剩余解释变量参数的经济含义和数值都发生了变化。
例2.1 删去POP,再进行回归
2.增大样本容量
由于多重共线性是一样本特征,故有可能 在关于同样变量的另一样本中共线性没有第一个 样本那么严重。一般认为:解释变量之间的相关 程度与样本容量成反比,即样本容量越小,相关 程度越高;样本容量越大,相关程度越小。因此, 收集更多观测值,增加样本容量,就可以避免或 减轻多重共线性的危害。 在实践中,当我们所选的变量个数接近样 本容量时,自变量间就容易产生共线性。所以, 我们在运用回归分析研究经济问题时,要尽可能 使样本容量远大于自变量个数。
3.方差扩大因子法
与特征根法比较,方差扩大因子法可以较准确地说明哪些变量 与其他变量有严重的共线性,严重程度如何
例3.2 承接例3.1,用方差扩大因子法检验 多重共线性检验SPSS 除PMG外,其他变量都与别的变量存在程度不同的 共线性问题,其中MOB的共线性最严重。
Coefficientsa Unstandardized Coefficients B Std. Error 2E+007 3E+007 1.419 .267 -3E+007 5027085 -59.875 198.552 -30540.9 9557.981 Standardized Coefficients Beta 2.484 -.415 -.071 -1.099 Collinearity Statistics Tolerance VIF .005 .180 .018 .008 218.079 5.548 55.074 118.205
Model 1
t .979 5.315 -ຫໍສະໝຸດ .569 -.302 -3.195
(Constant) MOB PMG POP GNP
Sig . .335 .000 .000 .765 .003
a. Dependent Variable: QMG
克服多重共线性的方法
1.排除引起共线性的变量
找出引起多重共线性的解释变量,将它排除出去, 是最为有效的克服多重共线性问题的方法。
a Collinearity Diagnostics
Model 1
Dimension 1 2 3 4 5
Eig envalue 4.797 .175 .027 .001 .000
Condition Index 1.000 5.240 13.250 88.903 162.804
(Constant) .00 .00 .01 .08 .92
2.条件指数
m ki , i 0,1, 2, p i
条件指数(condition index)可以用来判断多重共线性是否存在 以及多重共线性的严重程度,通常认为:
0 k 10, 没有多重共线性 10 k 100, 存在较强的多重共线性 k 100,存在严重的多重共线性
如果某两个或多个解释变量之间出现了相关性, 则称为多重共线性(Multicollinearity)。
如果存在 c1X1i+c2X2i+…+ckXki=0
i =1,2,…,n
其中: ci 不全为0,则称为解释变量间存在完全共线性。
多重共线性在实际的多元线性回归分析尤其是涉及经济变里
的模型中很常见。即在决定一个因变量的多个自变量中,有
(2)滞后变量的引入
在经济计量模型中,往往需要引入滞后经济变量来反 映真实的经济关系。 例如,消费=f(当期收入, 前期收入)
显然,两期收入间有较强的线性相关性。
(3)样本资料的限制
由于完全符合理论模型所要求的样本数据较难收集,特 定样本可能存在某种程度的多重共线性 一般经验:
诊断方法
1.一些经验方法
部分自变量呈高度相关,也就是说,这些变量被用来解释因 变量时导致所提供的信息出现“重叠”。例如、模型中如果
有多个自变量有共同的上升趋势,它们之间很可能有高度的
相关关系导致共线性。
实际经济问题中的多重共线性
(1)经济变量相关的共同趋势 时间序列样本:经济繁荣时期,各基本经济 变量(收入、消费、投资、价格)都趋于增长; 衰退时期,又同时趋于下降。 横截面数据:生产函数中,资本投入与劳动 力投入往往出现高度相关情况,大企业二者都大, 小企业都小。
3.差分法
时间序列数据、线性模型:将原模型 变换为差分模型: Yi =1X1i+2 X2i ++k Xki+ i 可以相对有效地消除原模型中的多 重共线性。
一般讲,增量之间的线性关系远比总量 之间的线性关系弱得多。
例如:
Year 1980 GDP NA CONS 2976
中国GDP与居民消费C的总量与增量数据 CONS/GDP NA ΔGDP NA ΔCONS NA ΔCONS / ΔGDP NA
Variance Proportions MOB PMG POP .00 .00 .00 .00 .13 .00 .00 .61 .00 .26 .01 .08 .74 .25 .92
GNP .00 .00 .01 .81 .18
a. Dependent Variable: QMG
从条件指数可以看到,最大的条件数为162.804,说明自变 量间存在严重的共线性。 如果有某几个自变量的方差比例值在某一行同时较大(接 近1),则这几个自变量间就存在共线性。
第3章 线性回归问题与非线性回 归分析
3.1 线性回归的常见问题
3.1.1 多重共线性 3.1.2 异方差性 3.1.3 自相关性
3.1.1 多重共线性 1.概念
对于模型 Yi 0 1 X 1i 2 X 2i k X ki i
i=1,2,…,n 其基本假设之一是解释变量之间不存在完 全共线性。
