09华南农业大学珠江学院期末考试试卷A及答案
华南农业大学珠江学院概率论与数理统计考试试卷A答案
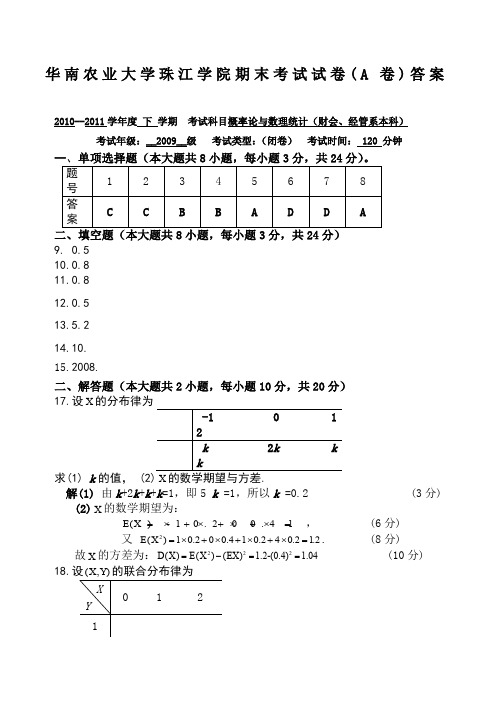
华南农业大学珠江学院期末考试试卷(A卷)答案2010--2011学年度下学期考试科目概率论与数理统计(财会、经管系本科)考试年级:__2009__级考试类型:(闭卷)考试时间: 120 分钟一、单项选择题(本大题共8小题,每小题3分,共24分)。
9.0.510.0.811.0.812.0.513.5.214.10.15.2008.二、解答题(本大题共2小题,每小题10分,共20分)17.设X的分布律为求(1)k的值,X解(1)由k+2k+k+k=1,即5 k =1,所以k =0.2 (3分)(2)X的数学期望为:()-10.200.410E X=⨯+⨯+⨯+⨯=,(6分)又2E X=⨯+⨯+⨯+⨯=. (8分)()10.200.410.240.21.2故X的方差为:222=-==(10分)D XE X EX()()() 1.2-(0.4) 1.0418.设(,)X Y的联合分布律为求 ,αβ,αβ取什么值时,X 与Y 相互独立?解 (1)由联合分布律的基本性质可以知道:1121161893αβαβ≥≥+++++=0,0,,故得 2+=9αβαβ≥≥0,0且(3分)(2) (,)X Y 的联合分布律表:X 与Y 相互独立⇔,i j i jp p p =知1121=()6299αα+⇒= , (7分) 2199βα=-=(10分)三、综合题(共12分)19.设二维随机变量(,)X Y 的联合概率分布如下:Z XY =cov(,)X Y 和XY ρ; (3)证明:X 与Y 不相关,但X 与Y 不相互独立. 解 (1) 由已知),(Y X 的联合分布律可得下表(4分)(2) 111()-1010424E XY =⨯+⨯+⨯=,1()0,(),2E X E Y ==cov(,)()()()0X Y E XY E X E Y =-=,0XY ρ= (8分)(3)因0XY ρ=,故X 与Y 不相关 (10分) 故X 与Y 不相互独立 (12分)四、 应用题(本大题共3小题,19题必做,20与21题任选1题,每小题10分,共20分)20.某批钢材的强度()2200,16X N ~.现从中任取一件,问:(1) 求取出的钢材强度不低于1802/N mm 的概率; (2) 如果要以99%的概率保证强度不低于1602/N mm ,问这批钢材是否合格?(参考数据:(1.11)0.8665,(1.25)0.8944,(2.3)0.9893,(2.5)0.9938Φ=Φ=Φ=Φ=) 解 (1){}{}1802001801180116P X P X -⎛⎫≥=-<=-Φ ⎪⎝⎭(3分) ()1 1.25=-Φ-()1.250.8944=Φ=(5分)(2){}{}1602001601160116P X P X -⎛⎫≥=-<=-Φ⎪⎝⎭(7分)故这批钢材合格 (10分)21.某车站的5路车到站时间X (分钟)服从均匀分布:[]~0,X U θ,X 1,X 2,…,X n 为X 的一个样本.(1) 求未知参数θ的矩估计量;(2) 若有样本观察值为:5,8,10,12,6.求θ的矩估计值; (3) 判断θ的矩估计量是否为θ的无偏估计量?并说明理由. 解 (1)总体的一阶矩1=()=2E X θμ,1=2θμ,用1=A X 代替1μ得θ的矩估计量为=2X θ (3分)(2)θ的矩估计值为5810126=2216.45x θ++++=⨯=(6分)(3) ()(2)2()22E E X E X θθθ===⨯=, (8分)故θ的矩估计量=2X θ是θ的无偏估计量 (10分) 22.从一批钉子中随机抽取16枚,测得其平均长度为 2.125x =,样本标准差为0.017s =,若钉子的长度2~(,)X N μσ,在下列两种情况下分别求总体均值的置信度为190%α-=的置信区间(取小数点后3位).(1)已知0.01σ=; (2)σ未知.(参考数据:0.050.05(1.285)0.90,(1.645)0.95,(15)=1.753,(16)=1.746t t Φ=Φ=)解 (1) 0.01σ=,190%,0.05,162n αα-===,构造样本函数~(0,1)X U N =.μ的置信度为1α-置信区间为22X X αα⎛⎫⎪⎝⎭, (3分) 20.05=1.645u u α=, 2.125x =, (4分)代入得所求的置信区间为:()2.1212.129, (5分) (2) 在2σ未知的情形下,μ的置信度为1α-的置信区间为22(1)(1)X t n X t n αα⎛⎫-- ⎪⎝⎭, (8分) 对于置信度为1α-=0.90(α=0.10),有20.05(1)=(15)=1.753t n t α-, (9分)将已知的数据代入,得所求的置信区间为:()2.1172.133,. (10分)。
11级年《电子测量与仪表》期末试卷A及答案

华南农业大学珠江学院期末考试试卷2011学年度下学期考试科目:电子测量与仪表考试年级:09_级考试类型:(开卷)A卷考试时间:120 分钟学号姓名年级专业一、简答题(本大题共5小题,每小题5分,共25分)1. 将下列数据进行舍入处理,要求保留四位有效数字。
3.14159; 3.21650;3.6235;6.378501;7.691499。
2.电子测量对电压测量的几个基本要求是什么?3.测频误差主要由哪两部分组成?什么叫量化误差?使用电子计数器时,怎样减小量化误差?4.扫频测量与点频测量相比有什么优点?5.自动测试系统的结构特点是什么?它对计算机的要求如何?二、分析计算题(要求列出所求未知量的算式或关系式,最后计算结果一般保留三位有效数字,误差保留两位,中间单纯数学运算过程可以省略。
本大题共6题,每小题7分,共42分)1. 附图2-1为RC衰减电路,调节C2可以补偿引线对地寄生电容:若C1调节范围为3~30pF,C2调节范围为3—15pF,则寄生电容在什么范围内,可以通过C2调节获得正确补偿。
附图2-12. 设有两只电阻,R1=200±0.8Ω,R2=51Ω±1%,试求这两只电阻并联时的总阻值及误差。
3. 测量电阻R消耗的功率时,可间接测量电阻值R、电阻上的电压V、流过电阻的电流I,然后采用三种方案来计算功率:(1)请给出三种方案;(2)设电阻、电压、电流测量的相对误差分别为νR=±1%,νv=±2%,νI±2.5%,问采用哪种测量方案较好?4. .欲用电子计数器测量一个f X=200Hz的信号频率,采用测频(选闸门时间为1s)和测周(选时标为0.1μs)两种方法,试比较这两种方法由±1误差所引起的测量误差,并讨论所得结果。
5.利用正弦有效值刻度的均值表测量正弦波、方波和三角波,读数均为1V,试求三种波形信号的有效值分别为多少?6.已知示波器偏转灵敏度Dy=0.2V/cm,荧光屏有效宽度10cm(1)若扫描速度为0.05ms/cm(放“校正”位置),所观察的波形如下图所示,求被测信号的峰—峰值及频率;(2)若想在屏上显示10个周期该信号的波形,扫描速度应取多大?三、测量方法简述题(本大题共2题,每小题10分,本大题共20分)1. 如何对低频放大器的电压放大倍数、功率放大倍数进行测量?要求画出放大器放大倍数测量连线图,说明测量方法。
《华南农业大学期末考试试卷》模板(4)(1)

华南农业大学期末考试试卷(A 卷)学年第 学期 考试科目: 微观经济学 考试类型:(闭卷)考试 考试时间: 120 分钟学号 姓名 年级专业一、选择题(本大题共 40小题,每小题 1分,共 40 分,写在答题纸上) 1。
经济学中的“稀缺性”是指( )A 世界上大多数人生活在贫困中B 、相对于资源的需求而言,资源总是不足的C 用资源必须考虑下一代D 、世界上的资源终将被人类消耗光 2。
下列项目中可称为固定成本的是( )A.管理人员的工资 B 。
生产工人的工资 C.原料及燃料D 。
以上三者中无固定成本 3.假定某商品的需求价格为P =100-4Q,供给价格为P =40+2Q ,均衡价格和均衡产量应为( )A .P =60,Q =10B .P =10,Q =6C .P =40,Q =6D .P =20,Q =20 4.冰棒的需求价格弹性( )药品的需求价格弹性 A 、大于 B 、小于 C 、等于 D 、大于或等于5。
下列命题中哪个是规范经济学的命题?( )A.征税对中等收入家庭是不公平的B. 1982年8月政府把贴现率降到10% C 。
1981年失业率超过9% D 。
社会保险税的课税依据现已超过30000美元6。
如果消费者的预算收入为50美元,商品X和Y的价格均为5美元,消费者打算购买6单位X和4单位Y,商品X、Y的边际效用分别为25和20,那么,要达到效用最大化,他应该( )A、按原计划购买B、减少X和Y的购买量C、增加X、Y的购买量D、增加X的同时减少Y的量7.如果价格下降10%能使需求量增加5%,则该商品价格上升会使销售收益( )A.增加 B.不变 C.下降 D.可能增加也可能下降8.建筑工人工资提高将使()A.新房子供给曲线左移并使房子价格上升B.新房子供给曲线右移并使房子价格下降C.新房子需求曲线左移并使房子价格下降D.新房子需求曲线右移并使房子价格上升9。
蛛网模型是以下列哪个假定为前提的( )A.需求量对价格缺乏弹性 B.供给量对价格缺乏弹性 C.生产者按本期价格决定下期的供给量 D.消费者改变对价格的预期10. 某工人在工资率为每小时2美元的时候每周挣80美元,每小时3美元的时候每周挣105美元,由此可以断定()A.收入效应起着主要作用 B.替代效应起着主要作用C.收入效应没有发生作用 D.替代效应没有发生作用11。
华南农业大学期末考试试卷(A卷)(标准答案)
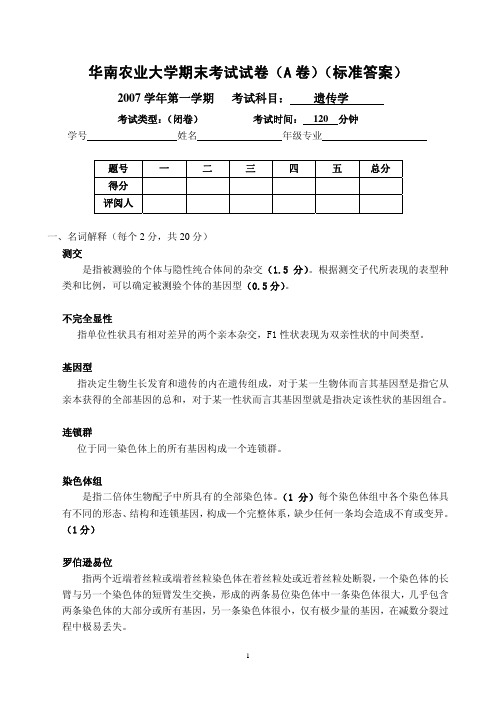
规律:控制不同性状的非等位基因分布在非同源染色体上,在减数分裂形成配子时非同源染 色体之间发生随机组合,因而这些非等位基因可以自由组合。(2.5 分)
3. 测量矮脚鸡和芦花鸡以及它们杂种的体重,得到下列的平均体重和表型方差(见下表), 请计算体重的广义和狭义遗传率。
矮脚鸡 芦花鸡 F1 F2 B1B B2B
华南农业大学期末考试试卷(A 卷)(标准答案)
2007 学年第一学期 考试科目: 遗传学
学号
考试类型:(闭卷) 姓名
考试时间: 120 分钟 年级专业
题号
一
二
三
四
五
总分
得分
评阅人
一、名词解释(每个 2 分,共 20 分) 测交 是指被测验的个体与隐性纯合体间的杂交(1.5 分)。根据测交子代所表现的表型种 类和比例,可以确定被测验个体的基因型(0.5 分)。
度,可确定物种分歧的大致时间。(√)
四、简答题(每题 5 分,共 30 分)
1. 写出下列专业术语的英文名称
(1)等位基因; (2)染色体组; (3)连锁;
allele;
genome;
linkage;
(4)遗传; heredity;
(5)表型 phenotype
2. 分离规律及自由组合规律的遗传实质是什么? 答:分离规律:控制相对性状的一对等位基因位于同源染色体上,在减数分裂形成配子时两 条同源染色体被分配到不同的细胞中,其上的等位基因也随之发生分离。(2.5 分)自由组合
平均(斤) 方差
1.4
0.1
6.6
0.5
3.4
0.3
3.6
1.2
2.5
0.8
4.8
1.0
华南农业大学期末考试试卷(A经济学专用)(DOC)

华南农业大学期末考试试卷(A 卷)答题纸2012-2013学年第 1学期 考试科目: 经济计量学 考试类型:(闭卷)考试 考试时间: 120 分钟学号 姓名 年级专业一、单选题(本大题共20小题,每小题1分,共20分)【答题要求:请将该大题的答案依次抄写在下列指定空格处】1.变量显著性检验t 统计量的表达式是( )。
2.在双对数线性模型lnY i =ln β0+β1lnX i +u i 中,β1的含义是( ) A .Y 关于X 的增长量 B .Y 关于X 的发展速度 C .Y 关于X 的边际倾向 D .Y 关于X 的弹性3.在二元线性回归模型:i i 22i 110i u XX Y +β+β+β=中,1β表示( ) A .当X 2不变、X 1变动一个单位时,Y 的平均变动 B .当X 1不变、X 2变动一个单位时,Y 的平均变动 C .当X 1和X 2都保持不变时, Y 的平均变动 D .当X 1和X 2都变动一个单位时, Y 的平均变动4.关于多元线性回归模型的F 检验与t 检验的关系,描述正确的是( )。
A.关于变量的显著性t 检验全部通过时,模型总体显著的F 检验一定通过。
B.关于模型总体显著的F 检验通过时,变量的显著性t 检验一定全部通过。
)var(.11..ˆ.ˆˆˆˆ2222b b b ye e y s b b jj jii i ijjt D k n n t C t B b t A j-=---•==-=∑∑∑∑C. F检验与t检验是等价的。
D.F检验与t检验没有任何关系。
5.DW检验法适用于检验()A.异方差B.序列相关C.多重共线性D.设定误差6.如果X为随机解释变量,Xi 与随机误差项ui相关,即有Cov(Xi,ui)≠0,则普通最小二乘估计 ˆ是()A.有偏的、一致的B.有偏的、非一致的C.无偏的、一致的D.无偏的、非一致的7.设某商品需求模型为Yt =β+β1Xt+ ut,其中Y是商品的需求量,X是商品价格,为了考虑全年4个季节变动的影响,假设模型中引入了4个虚拟变量,则会产生的问题为()A.异方差性B.序列相关C.不完全的多重共线性D.完全的多重共线性8.当截距和斜率同时变动模型Yi =α+α1D+β1Xi+β2(DXi)+ui退化为截距变动模型时,能通过统计检验的是()A.α1≠0,β2≠0 B.α1=0,β2=0C.α1≠0,β2=0 D.α1=0,β2≠09.若随着解释变量的变动,被解释变量的变动存在两个转折点,即有三种变动模式,则在分段线性回归模型中应引入虚拟变量的个数为()A.1个B.2个C.3个D.4个10.对于无限分布滞后模型Yt =α+βXt+β1Xt-1+β2Xt-2+…+ut,无法用最小二乘法估计其参数是因为()A.参数有无限多个B.没有足够的自由度C.存在严重的多重共线性D.存在序列相关11.对自回归模型进行自相关检验时,若直接使用DW检验,则DW值趋于()A .0B .1C .2D .412.当某商品的价格下降时,如果其需求量的增加幅度稍大于价格的下降幅度,则该商品的需求( ) A .缺乏弹性 B .富有弹性 C .完全无弹性 D .完全有弹性13.根据实际样本资料建立的回归模型是( ) A .理论模型 B .回归模型 C .样本回归模型 D .实际模型14.双对数模型Y=A e rt K a L ß u 中,Y 、K 和L 分别表示产出、资本和劳动投入,则参数a 的经济含义是( )A .Y 关于K 的增长率 B. Y 关于K 的发展速度 C. 资本产出弹性 D. 资本产出乘数15回归分析中使用的距离是点到直线的垂直坐标距离。
级珠江学院期末考试复变函数试卷

华南农业大学珠江学院期末考试试卷2009--2010学年 上 学期 考试科目: 复变函数考试年级:__2008__级 考试类型:(闭卷)A 卷 考试时间: 120 分钟 学号 姓名 年级专业一、填空题(本大题共8小题,每小题3分,共24分) 1.ie。
2.设11iz i-=+,则zz = 。
3.设21()(1)f z z z=++,则()f z '= 。
4.0z =为函数31()z e f z z -=的 级极点。
5.1z dzz ==⎰ 。
(1z =为正向圆周) 6.幂级数nn nz∞=∑的收敛半径为 。
7.Ln(1)。
8.当||1z 时,21nzz z 。
9小题6分,其余每小题10分,共76分) 9.判断函数2()||f z z 在何处可导,在何处解析。
10.计算积分(1)Cz dz ,其中积分路径C 为从点0到点2i 的直线段。
11.计算积分221zz e dz z。
(2z =为正向圆周)12.计算积分511z ze dz z 。
(1z =为正向圆周)13.将12()zf z z e 在0z内展开成罗朗级数。
14.计算()cot f z z 在每个有限奇点处的留数。
15.求函数 1 , ||1()0 , ||1t F t t 的傅里叶变换及其积分表达式。
16.求阶跃函数 1 , 0()0 , 0t u t t的拉普拉斯变换。
参考答案一.填空题1.1 2.1 3.212(1)z z+- 4.二 5.2i 6.1 7.(21) (0,1,2,)ki k8.11z二.计算题 9.解:因为222()||f z z x y ,所以22(,)u x y x y ,(,)0v x y .则....1分 2 ,2 ,0 ,0 .uu v v x y xyxy............3分上述四个偏导数处处连续,但仅当0x y 时C-R 方程成立。
因此函数仅在0z 可导,从而在复平面内处处不解析。
...........6分10.解:曲线C 的方程为(2) , (01)z i t t ...........2分 10(1)[(2)1][(2)]Cz dz i t d i t ............6分 120[(2)2]i t i dt ...........7分 123[(2)(2)]2i ti t ...........9分 732i ...........10分11.解:被积函数2()1z e f z z 在||2z 的内部有两个奇点1z,在2z =的内部作两个互不包含互不相交的正向圆周1C 和2C ,其中1C 的内部只包含奇点1z ,2C 的内部只包含奇点1z,则由复合闭路定理有 ...........2分 122222111zzzz C C e e e dzdz dz z z z ............5分 12111111zzC C e e dzdz z z z z ............7分112211z z zze e iiz z ............9分11()eie i e e i ............10分12.解:令()1zf z e,则55111()zz z e f z dzdz zz 。
09珠江学院期末考试PLC试卷及答案
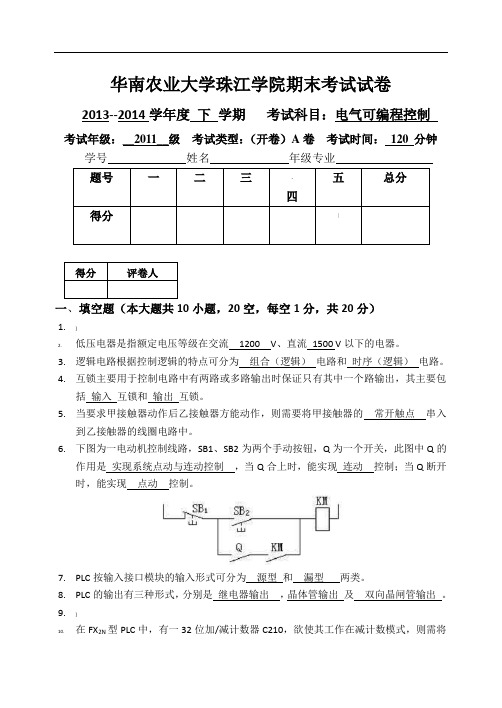
华南农业大学珠江学院期末考试试卷2013--2014学年度下学期考试科目:电气可编程控制考试年级:__2011__级考试类型:(开卷)A卷考试时间:120 分钟学号姓名年级专业题号一二三.四五总分得分|得分评卷人一、填空题(本大题共10小题,20空,每空1分,共20分)1.]2.低压电器是指额定电压等级在交流1200 V、直流1500 V以下的电器。
3.逻辑电路根据控制逻辑的特点可分为组合(逻辑)电路和时序(逻辑)电路。
4.互锁主要用于控制电路中有两路或多路输出时保证只有其中一个路输出,其主要包括输入互锁和输出互锁。
5.当要求甲接触器动作后乙接触器方能动作,则需要将甲接触器的常开触点串入到乙接触器的线圈电路中。
6.下图为一电动机控制线路,SB1、SB2为两个手动按钮,Q为一个开关,此图中Q的作用是实现系统点动与连动控制,当Q合上时,能实现连动控制;当Q断开时,能实现点动控制。
7.PLC按输入接口模块的输入形式可分为源型和漏型两类。
8.PLC的输出有三种形式,分别是继电器输出,晶体管输出及双向晶闸管输出。
9.]10.在FX2N型PLC中,有一32位加/减计数器C210,欲使其工作在减计数模式,则需将对应的特殊辅助继电器M8210 置1即可。
11.已知一定时器T234,欲使其在10S后动作,则该定时器的设定值应为K1000 。
12.对于一个状态转移图而言,其通常由三部分组成,分别是:状态步,转移条件和驱动负载。
(二、选择题(本大题共10小题,每小题1分,共10分)在每小题列出的四个备选项中只有一个是最符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.时间继电器的作用是【D 】。
A. 短路保护B. 过电流保护C. 延时通断主回路D. 延时通断控制回路2.由于电弧的存在,将导致【B 】。
A.电路的分断时间缩短B. 电路的分断时间延长C. 电路的分断时间不变D. 分断能力不变3.|4.三相笼型异步电动能耗制动是将正在运转的电动机从交流电源上切除后,【B 】。
华南农业大学珠江学院期末高数考试A卷和答案

华南农业大学珠江学院期末考试试卷2020学年度下学期 考试科目:高等数学考试年级:信工系08本科_ 考试类型:(闭卷)A 卷 考试时刻:120 分钟 学号 姓名 年级专业一、填空题(本大题共8小题,每题2分,共16分)1.微分方程2323230d y d y dx x dx ⎛⎫+= ⎪⎝⎭的阶数为 .2.已知{}1,2,2a =,{}b ,,=λ-21,且b a ⊥,那么=λ .3.已知函数2x yz e=, 那么 1 2x y dz=== _ .4.已知ln 1(,)exdx f x y dy ⎰⎰, 那么改变积分顺序后,二次积分变成 _ .5.已知三重积分(,,),I f x y z dv Ω=Ω⎰⎰⎰: 由旋转抛物面22z xy =+ 与平面1z =围成,将其化成三次积分为 _ _ .6.曲面222236x y z ++=在点(1,1,1)处的法线方程为 ________________________7.若是级数1nn u∞=∑收敛,那么必然知足的条件是lim n n u →∞= _ .8.已知 L 为连接(1, 0)及( 0 ,1 )两点的直线段,那么积分 ()Lx y ds +⎰= _ .二、单项选择题(本大题共6小题,每题3分,共18分)在每题列出的四个备选项中只有一个是最符合题目要求的,请将其代码填写在题后的括号内。
错选、多项选择或未选均无分。
9.二元函数(,)z f x y =在00,)x y 点(处可微是偏导数 00 00,),,)x y f x y f x y ((存在的( ). A. 必要条件 ; B. 充要条件 ; C. 充分条件 ; D. 既非充分又非必要条件.10.方程22212y x z -+=所表示的曲面是( ). A. 双曲抛物面 ; B.椭圆锥面 ; C. 双叶旋转双曲面 ; D. 单叶旋转双曲面 . 11.点(0,0)是函数z xy =的( ).A. 极值点;B. 驻点 ;C. 最大值点 ;D. 不持续点 . 12.设D 由圆22(1)1x y -+= 所围成,那么(,)Df x y dxdy ⎰⎰=( )A. 2cos 0(cos ,sin )d f d πθθρθρθρρ⎰⎰; B.2cos 2 02(cos ,sin )d f d πθθρθρθρρ⎰⎰;C.2cos 22(cos ,sin )d f d πθπθρθρθρρ-⎰⎰; D.22 0(cos ,sin )d f d πθρθρθρρ⎰⎰ .13.已知L 为从点(1,1)到点(4,2)的直线段,那么()()Lx y dx y x dy ++-⎰值为( ).A. 10 ;B. 11 ;C. 8 ;D. 9 . 14.以下级数中绝对收敛的是( ).A. 1(1)nn n ∞=-∑ ; B.1!3n n n ∞=∑ ; C. 121(1)n n n -∞=-∑ ;D. 1(1)nn ∞=-∑ . 三、计算题(本大题共7小题,每题7分,共49分)15.求微分方程440y y y '''-+=知足初始条件01,4x x y y =='==的特解.16.过点(2,0,-3)且与直线 247035210x y z x y z -+-=⎧⎨+-+=⎩垂直的平面方程.17.设22(,)y z f x y x =-,f 具有一阶持续编导数,求z z x y∂∂∂∂及.18.函数(,)z z x y = 由方程zx y z e +-=所确信,求2z zx x y∂∂∂∂∂及.19.求22Dx d yσ⎰⎰,其中D 是由直线2,x y x ==与双曲线1xy =所围成的闭区域.20.计算222(2sin )cos L y xy x dx x dy -+⎰ ,其中L 为椭圆22221x y a b+=的右半部份,取逆时针方向.21.求1(1)321n n nn x n ∞=--∑ 的收敛半径及收敛域.四、应用题(本大题共1题,共12分)22.在曲面22()1x y z --=上求出点的坐标,使其到原点的距离最短,并求出此最短距离.五、证明题(本大题共1题,共5分)23.设(()),u x y ϕψ=+其中,ϕψ具有二阶导数,证明:222u u u u x x y y x ∂∂∂∂⋅=⋅∂∂∂∂∂ .A 卷答案及评分标准一、填空题(本大题共8小题,每题2分,共16分) 1. 3; 2. 0; 3. 2(4)e dx dy +; 4.1ee (,)ydy f x y dx ⎰⎰;5.2211-1(,,)x y dx f x y z dz +⎰⎰⎰; 6.111123x y z ---==; 7. 0; 8..二、单项选择题(本大题共6小题,每题3分,共18分)9. C; ; 11. B; 12. C; 13. B; 14. C.三、计算题(本大题共7小题,每题7分,共49分) 15.解:所给微分方程的特点方程为 2440r r -+=解得两相等实根122r r == …………2分故所给微分方程的通解为:212()xy C C x e =+将初始条件01,x y==代入通解,得11C =,将11C =再代回通解,得22(1)xy C x e =+ …………5分 对上式求导,得2222(1)2x x y C e C x e '=++再将初始条件04x y ='=代入上式,得22C =,将其代回通解中,得特解:2(12)xy x e =+ …………7分 16. 解:依照题意,所求平面的法向量n 可取直线的方向向量s ,即 n = s =124352i j k-- …………3分{}16,14,11=- …………5分由已知点(2,0,-3)(平面点法式方程),所求平面方程为:16(2)14(0)11(3)0x y z --+-++=即161411650x y z ---= …………7分17.解:令22,yu x y v x=-=…………1分2z z z z z 2z z z 1z 2u v x u x v xy x u x vz u v y u y v yy u x v∂∂∂∂∂=+∂∂∂∂∂∂∂=-∂∂∂∂∂∂∂=+∂∂∂∂∂∂∂=-+∂∂ …………4分…………7分 18.解:(可用公式法, 也能够直接方程两边同时对自变量求偏导方式) 方程两边同时对x 求偏导,z z 1z 11z ze x xx e ∂∂-=∂∂∂=∂+ …………2分…………3分方程两边同时对y 求偏导,z z 1z 11z ze y yy e ∂∂-=∂∂∂=∂+因此 …………5分23z z 1()()1(1)zzz z x y y x y eee ∂∂∂∂==∂∂∂∂∂+=-+…………7分19. 解:由题意可知: D=1(,)12,x y x y x x ⎧⎫≤≤≤≤⎨⎬⎩⎭…………2分因此:222 x 122 1 221 1 23 122411()()19()244x Dx xx x d dx dyy y x dxyx x dxx x σ==-=-+=-+=⎰⎰⎰⎰⎰⎰ …………5分…………7分20. 解:设1L 是从点(0,)b -到点(0,b)的有向直线段,由1L 与L 所围成的闭区域为D , 那么由L 与1L -组成的有向闭曲线是D 的正向边界曲线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
华南农业大学珠江学院期末考试试卷
学年度 下 学期 考试科目:高等数学(信工本科)
考试年级:级 考试类型:(闭卷)卷 考试时间: 分钟 学号 姓名 年级专业
. 直线
1
1
121-+=
=-z y x 与平面1=+-z y x 的位置关系是 ( ) 例五
() 垂直; () 平行; () 夹角为π4; () 夹角为π
4
-. . 设D :1≤2
2
y x +≤4;则
=+⎰⎰
y x y x D
d d 22 ( )
()2π4
2
01
d d r r θ⎰⎰; ()2π4
01
d d r r θ⎰
⎰;
()
2π2
20
1
d d r r θ⎰
⎰; ()2π2
1
d d r r θ⎰
⎰.
. 若(,)z f x y =的偏导数
z x ∂∂及z
y
∂∂在点)(00,y x 都存在,则 ( )
() (,)z f x y =在点)(00,y x 可微; () (,)z f x y =在点)(00,y x 连续; () (,)z f x y =在点)(00,y x 不一定可微; () 以上结论都不对.
. 正项级数
∑∞
=1
n n
a
若满足下面哪个条件必收敛, ( )
()0lim =∞
→n n a ; ()1lim
1<+∞→n n n a a ; ()1lim 1n n n
a
a +→∞≤; ()1lim 1>=+∞→λn n n a a .
试卷第页(共 页)
.关于幂函数∑∞
=1
n n
n x ,下列结论正确的是 ( )
()当且仅当1<x 时收敛; ()当1≤x 时收敛; ()当11<≤-x 时收敛; ()当11≤<-x 时收敛.
.微分方程 22x
y y xe '''-=的特解*
y 的形式为(其中,a b 为待定系数) ( ) ()2x axe () 2()x ax b e + () 22x ax e () 2()x
x ax b e + .已知Ω由12,0,0,0=++===z y x z y x 所围成,则⎰⎰⎰Ω
=xdxdydz ( )
() 1
1 1 0 0 0x y
dx dy xdz --⎰⎰⎰
; ()12
1
12 0 0 0
x x y
dx dy xdz ---⎰⎰
⎰
;
()
1
2 1
1
dx dy xdz ⎰
⎰⎰; ()12
1 1
2 0
x y
dx dy xdz --⎰⎰⎰
.
2
1
0(1)1!2!!
n x x x dx n +++++⎰ ( )
(); ()e ; ()2
e ; ()1-e .
.设2||=→
a ,1||=→
b ,且3
),(π
=
∠→
→b a ,则=-⋅+→
→→→)()(b a b a 332 .
.曲线22
21
z x y z ⎧=+⎨=⎩在xOy 平面上的投影曲线方程为 .
.若(
)xy
e
y x f z ,22-=,其中f 具有一阶连续偏导,则x
z ∂∂ ;
y
z
∂∂ . .积分区域D 由曲线x y =及抛物线x y 42
=所围成,化二重积分⎰⎰=
D
y x f I σd ),(为
试卷第页(共 页)。
