最新嵊州市初三数学竞赛试题
2020年浙江省中考数学竞赛试题附解析

2020年浙江省中考数学竞赛试题学校:__________ 姓名:__________ 班级:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上一、选择题1.右图是方格纸上画出的小旗图案,如果用(0,0)表示A点,(0,4)表示B点,那么C 点的位置可表示为()A.(0,3)B.(2,3)C.(3,2)D.(3,0)2.把12与 6作和、差、积、商、幂的运算,结果中为正数的有()A. 4个B.3个C.2个D.1个3.以x=-3为解的方程是()A.3x-7=2 B.5x-2=-x C.6x+8=-26 D.x+7=4x+164.已知∠AOB=150°,0C平分∠AOB,OD在∠AOB的内部,且∠AOD=13∠AOB,则∠COD= ()A.15°B.25°C.35°D.45°5.如图,下午2点30分时,时钟的分针与时针所成角的度数为()A.90°B.105°C.120°D.135°6.计算x10÷x4×x6的结果是()A.1 B.0 C.x12D.x367.在下列的计算中,正确的是()A.2x+3y=5xy B.(a+2)(a-2)=a2+4C.a2•ab=a3b D.(x-3)2=x2+6x+98.在运用分配律计算 3. 96×(-99)时,下列变形较合理的是()A.(3+0.96)×(-99)B.(4-0.O4)×(-99)C.3.96×(-100+1)D.3.96×(-90-9)9.数据0,-1,6,1,x的众数为-l,则这组数据的方差是()A.2 B .345 C .2 D .26510.有一个质地均匀且六个面上分别刻有1到6的点数的正方体骰子,掷一次骰子,向上的一面的点数为2的概率是( )A .0B .12C .16D .1 11.直角梯形的一腰长为l0 cm ,这条腰与底所成的角为30°,则它的另一腰长为 ( ) A .2.5 cmB .5 cmC .10 cmD .15 cm 12.抛物线212y x =的函数值是( ) A . 大于零B .小于零C . 不大于零D . 不小于零 13. 如图,以圆柱的下底面为底面,上底面圆心为顶点的圆锥的母线长为4,高线长为 3,则圆柱的侧面积为( )A . 30πB .67πC .20πD .47π14.有一拦水坝的截面是等腰梯形,它的上底为6m ,下底为 lOm ,高为23,则此拦水坝斜坡的坡度和坡角分别是( )A 3°B 3°C 3°D .3,60°15.已知⊙O 的半径为r ,圆心O 到直线l 的距离为d .若直线l 与⊙O 有交点,则下列结论正确的是( )A .d =rB .d ≤rC .d ≥rD .d <r16.设⊙O 的半径为 r ,直线 1l 、2l 、3l 分别与⊙O 相切、相交、相离,它们到圆心 0的距离分别为l d 、2,l d 、3,d ,则有( )A .123d r d d >=>B .123d r d d =<<C .213d d r d <=<D .123d r d d =>>17.在一副完整的扑克牌中摸牌,第一张是红桃3,第二张黑桃7,第三张方片4,第四张是小王,那么第五张出现可能性最大的是( )A .红桃B .黑桃C .方片D .梅花二、填空题如图,地面A 处有一支燃烧的蜡烛(长度不计),一个人在A 与墙BC 之间运动,则他在墙上投影长度随着他离墙的距离变小而 (填“变大”、“变小”或“不变”).19.两个相似三角形对应边的比为6,则它们周长的比为_____________.20.如图,∠1 =40°,∠2=40°,那么直线a 与b 的位置关系是 ,理由是 .21.如果关于x 的方程2324+=-x m x 和m x x 32-=的解相同,则m = .22.写出下列各式分解因式时应提取的公因式: (1)ax ay -应提取的公因式是 ;(2)236x mx n -应提取的公因式是 ;(3)2x xy xz -+-应提取的公因式是 ;(4)322225520x y x y x y --应提取的公因式是 ;(5)()()a x y b x y +-+应提取的公因式是 .23.将3,5x-2,13x -两两用等号连结,可组成 个一元一次方程,它们分别是 .24.-5的相反数是 ,122-的绝对值是 . 三、解答题25.已知:如图,在△ABC 中,AB =AC ,AD ⊥BC ,垂足为点D ,AN 是△ABC 外角∠CAM 的平分线,CE ⊥AN ,垂足为点E .(1)求证:四边形ADCE 为矩形;(2)当△ABC 满足什么条件时,四边形ADCE 是一个正方形?并给出证明.26.图中标明了李明同学家附近的一些地方.(1)根据图中所建立的平面直角坐标系,写出学校,邮局的坐标;(2)某个星期日早晨,李明同学从家里出发,沿着(-2,-l)→(-1,-2) →(1,-2) →(2,-l) →(1,-l) →(1,3) →(-1,O) →(0,-l)的路线转了一下,写出他路上经过的地方;(3)连结他在(2)中经过的地点,你能得到什么图形?27. (1)计算:22(105)5x y xy xy -÷; (2)因式分解:3228m mn -28.如图所示,在△ABC 中,∠ABC=∠ACB ,且∠ACB=2∠A ,BD ⊥AC 于D ,求∠DBC 的度数.29.观察“工”“田”“土”等汉字,我们能找到直线与直线的哪几种位置关系?请你再举几个这样的汉字?30.比较a 与a -的大小.【参考答案】学校:__________ 姓名:__________ 班级:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上一、选择题1.C2.C3.D4.B5.B6.C7.C8.C9.B10.C11.B12.D13.B14.D15.B16.C17.D二、填空题18.变小19.620.a ∥b ;同位角相等,两直线平行21.222.(1) a ;(2)3x ;(3)x -;(4)25x y ;(5)x y +23.3;523x -=,133x -=,5213x x -=- 24.5,122三、解答题25.(1)证明:在△A BC 中, AB =AC ,AD ⊥BC .∴ ∠BAD =∠DAC .∵ AN 是△ABC 外角∠CAM 的平分线,∴ MAE CAE ∠=∠. ∴ ∠DAE =∠DAC +∠CAE =⨯21180°=90°. 又 ∵ AD ⊥BC ,CE ⊥AN ,∴ ADC CEA ∠=∠=90°,∴ 四边形ADCE 为矩形.(2)例如,当AD =12BC 时,四边形ADCE 是正方形. 证明:∵ AB =AC ,AD ⊥BC 于D .∴ DC =12BC .又 AD =12BC ,∴ DC =AD . 由(1)四边形ADCE 为矩形,∴ 矩形ADCE 是正方形.26.(1)学校(1,3),邮局(0,-1) (2)商店、公园、汽车站、水果店、学校、游乐场、邮局 (3)一只小船27.(1)2x y - (2)2(2)(2)m mn n m n +-28.18°29.垂直、平行、中、丰、王、圭等30.分情况:a>0 ,a=0,a<0 进行讨。
2023年浙江省绍兴市中考数学竞赛试卷附解析

2023年浙江省绍兴市中考数学竞赛试卷学校:__________ 姓名:__________ 班级:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上一、选择题1.若三角形三边的比是3:4:5,周长为60 cm,则此三角形中最长的中位线是()A.15 cm B.l2.5 cm C.10cm D.8 cm2.点M在y轴的左侧,到x轴、y轴的距离分别是3和5,则点M的坐标是()A.(一5,3)B.(-5,-3)C.(5,3)或(-5,3)D.(-5,3)或(-5,-3)3.如图,AD是△ABC的角平分线,DE是△ABD的高,DF是△ACD的高,则()A.∠B=∠C B.∠EDB=∠FDC C.∠ADE=∠ADF D.∠ADB=∠ADC4.如图,△ABC的两个外角平分线交于点O, 若∠BOC=76°,则∠A的值为()A.76°B.52°C.28°D.38°5.在△ABC中,∠A是锐角,那么△ABC是()A.锐角三角形B.直角三角形C.钝角三角形D.不能确定6.两个5次多项式的和的次数一定()A.是5次B.是10次C.不大于5次D.大于5次二、填空题7.如图,两个同心圆的半径分别为2和1,∠AOB= 120°,则阴影部分的面积是.8.已知AD∥BC,要使四边形ABCD为平行四边形,需要增加的条件是__________(•填一个你认为正确的条件).9.天河宾馆在重新装修后,准备在大厅的主楼梯上铺设某种红色地毯,已知这种地毯每平方米售价30元,主楼梯宽2 m,其侧面图如图所示,则购买地毯至少需要元.10.下表是食品营养成分表的一部分.(每100g 食品中部分营养成分的含量) 蔬菜种类 绿豆芽 白菜 油菜 卷心菜 菠菜 韭菜 胡萝卜(红) 碳水化合物(g)4344247在表中提供的碳水化合物的克数所组成的数据中,中位数是 ,平均数是 .11.地面气温是20℃,若每升高100 m ,气温下降6℃,则气温t(℃)与高度h(m)的函数解析式是 .12.如果一个立体图形的主视图为长方形,则这个立体图形可能是 (只需填上一个立图形) 13.如图是在平面镜里看到背向墙壁的电子钟示数,这时的实际时间应该是 .14.足球比赛前,裁判用抛一枚硬币猜正反面的方式让甲、乙两个队长选进攻方向,猜对正面的队长先选,则队长甲先选的概率是 .15.A 表示一个多项式,若()23A a b a b ÷-=+,则A= . 16.当1a =-,2b =-,2c =时,分式244ac b a-的值为 .17.填空:(1)6()mn ÷ =22m n ; (2)32(1)(1)a a +÷--= ; (3)54n n a a ++÷= . 18.若12x y =⎧⎨=⎩是关于 x ,y 方程312mx y -=的一个解,则m= . 19.下列叙述中,哪些数是准确数?哪些数是近似数? (1)我们班里有18位女同学,“l8”是 数; (2)小红体重约38千克,“38”是 数;(3)1999年7月1日香港回归祖国,“1999”、“7”、“1”都是 数; (4)我国科盲达5亿之多,5是 数;(5)1998年首都机场起降各类飞机159307架次,“l59307”是 数.三、解答题20.在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:摸球的次数n 100 200 300 500 800 1000 3000 摸到白球的次数m 65 124 178 302 481 599 1803 摸到白球的频率mn0.650.620.5930.6040.6010.5990.601ABPQMN(1)请估计:当n 很大时,摸到白球的频率将会接近 .(精确到0.1) (2)假如你摸一次,你摸到白球的概率()P 白球 . (3)试估算盒子里黑、白两种颜色的球各有多少只?21.已知梯形 ABCD ,AD ∥BC ,若 EF ∥BC ,且所分成的梯形 AEFD ∽梯形 EBCF ,AD=12,BC = 18,求 EF 的长.22.已如图,在△ABC 中,AB=AC, ∠ABC=2∠A, BM 平分∠ABC 交外接圆于点M,ME ∥BC 交AB 于点 E. 试判断四边形EBCM 的形状,并加以证明.23.已知,如图,⊙O 中 弦AB 、CD 相交于 P ,且.求证:AP=DP .24.如图,已知PQ ∥MN ,夹在两条平行线间的线段AB 长为 3 cm ,∠ABM =60°.求PQ 与MN 之间的距离.25.如图所示,△ACB,△ECD都是等腰直角三角形,且点 C在AD上,AE的延长线与BD 交于点F. 请你在图中找出一对全等三角形,并写出证明它们全等的过程.26.某学校要印刷一批资料,甲印刷公司提出收制版费900元,另外每份材料收印刷费0.5元;乙印刷公司提出不收制版费,每从头材料收印刷费0.8元.(1)分别写出两家印刷公司的收费y(元)与印刷材料x(份)之间的函数解析式;(2)若学校预计要印刷2500份宣传材料,请问学校应选择哪一家印刷公司更合算?27.如图,将△ABC先向上平移5格得到△A′B′C′,再以直线MN为对称轴,将△A′B′C′作轴对称变换,得到△A″B″C″,作出△A′B′C′和△A″B″C″.28.先化简,再求值.(1)222963()3x x x x +--,其中2x =-;(2)222222(53)()(53)a b a b a b -++-+,其中1a =-,1b =.29.如果 5 个人7 天可以做 10 个工艺品,那么7 个人用相同的速度做8个相同的工艺品需要多少天?30.一个多边形的内角和与其中一个外角之和为2007°,求这个多边形的内角和.【参考答案】学校:__________ 姓名:__________ 班级:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上一、选择题1.B2.D3.C4.C5.D6.C二、填空题7.8.AD=BC(答案不惟一)9.480°10.4g,4g11.200.06t h=-12.答案不唯一,如长方体13.20:5114.2115.2223a ab b+-16.317.(1)4()mn;(2)1a+;(3)a18.5319.(1)准确 (2)近似(3)准确 (4)近似 (5)准确三、解答题20.(1)0.6,(2)0.6,(3)白球24个,黑球16个.21.梯形 AEFD∽梯形 EBCF梯形,∴AD EFEF BC=,1218EFEF=,21218EF=⨯,∴EEF= 22.四边形 EBCM是菱形.∵∠ABM=∠MBC=12∠ABC,∠ABC= 2∠A , ∴∠A=∠ABM,∵∠A=∠BMC,∴∠ABM=∠BMC,∴BE∥CM,∵ME∥BC,∴四边形 EBCM 是平行四边形.∵∠A= ∠MBC, ∴⌒BC =⌒MC , ∴BC=MC,∴□EBCM 是菱形. 23.作 OE⊥AB于E,OF⊥CD于F,连结OP.∴AE=12AB ,DF=12CD.∵⌒AC =⌒BD,∴⌒AB =⌒CD,∴AB=CD,OE=OF,∴AE=DF.在Rt△OPE 和 Rt△OPF 中,∵OE= OF,OP= OP,∴Rt△OPE≌Rt△OPF,∴PE=PF,∴AE+PE=DF+PF,即AP=DP.24.32 cm.25.△ACE≌△BCD,证明略26.(1)0.5900y x=+甲,0.8y x=乙;(2)选择乙印刷公司27.略28.(1) 268x x+,20 (2) 225a b-,-4 29.4 天30.1980°。
九年级数学竞赛题

九年级数学竞赛题(全卷满分120分 考试时间100分钟) 一选择题(共10小题,每小题3分,计30分。
每小题只有一个选项是符合题意) 1.三角形的下列线段中能将三角形的面积分成相等两部分的是( )2.三角形的两边长分别为2和6,第三是方程x 2-2x-3=0的解,则第三边的长为( ) A. 7 B.3 C.7或3 D.无法确定 3下列旋转体中三视图相同的是( )4若顺次连接四边形ABCD 各边的中点所得四边形是矩形,则四边形ABCD 一定是( ) A.矩形 B.菱形 C.对角线互相垂直的四边形 D.对角线相等的四边形5在Rt △ABC 中,若∠C=90O,BC=6,AC=8,sinA 的值为( ) A. 45 B. 35 C.43 D. 346若二次函数y=ax 2+bx+c 的x 与y 的部分对应值如下表则当x=1时,y 的值为A. 5B.-3 C-13 D.-277若二次函数y=ax 2+c,当x 取x 1,x 2(x 1≠x 2)时,函数值相等,则当x 取x 1+x 2时,函数值为( )A.a+c B.a-c C.-c D.c8.已知抛物线y=x 2+2x+m 的顶点在直线y=-2x+1上,则m 的值为( ) A.2 B.3 C.4 D.59.在平面直角坐标系中,A(-3,4),B(3,2)在x 轴上找一点p,使PA+PB 最小,则点P 的坐标是( )A.(-1,0) B.(0,0) C.(1,0) D.(3,0)10.一个暗箱里装有10个黑球,8个白球,12个红球,每个球出颜色外都相同,从中任意摸出一个球,摸到白球的概率是( ) (A )31 (B)81 (C)154 (D)114 二填空题(本题共6小题,每小题4分共计24分)11、方程(m 2-1)x 2+(m -1)x+1=0,当m 时,是一元二次方程;当m 时,是一元一次方程. 12.、已知函数xy 41-=,当x <0时,y _______0,此时,其图象的相应部分在第_______象限; 13王老师假期中去参加高中同学聚会,聚会时,所有到会的同学都互相握了一次手,王老师发现共握手435次,则参加聚会的同学共有多少人?设参加聚会的同学共有x 人,则根据题意,可列方程: .14.如图,已知AB 是线段CD 的垂直平分线,E 是AB 上的一点,如果EC=7cm ,那么ED= cm ;如果∠ECD=60°,那么∠EDC=CA DBE15、一元二次方程(m-1)x 2+3mx+(m+4)(m-1)=0有一个根为0,则m 的值是 . 16.若等腰梯形ABCD 的上、下底之和为2,并且两条对角线所成的锐角为600,则等腰梯形ABCD 的面积为 . 三解答题 17解方程和计算(1)(x+1)2+5(x+1)+4=0 (2) 22sin45°+sin60°-2cos45°18.、一艘轮船以20海里/时的速度由西向东航行,途中接到台风警报,台风中心正以40海里/时的速度由南向北移动,距台风中心2010海里的圆形区域(包括边界)都属台风区.当轮船到A 处时,测得台风中心移到位于点A 正南方向B 处,且AB=100海里.若这艘轮船自A 处按原速度继续航行,在途中会不会遇到台风?若会,试求轮船最初遇到 台风的时间;若不会,请说明理由.19如图,已知:△ABC ,CF ⊥AB ,BE ⊥AC ,M 、N 分别为BC 、EF 中点,求证:MN ⊥EF 。
初三数学竞赛试卷及答案

初三数学竞赛试卷学校___________________年级___________班 姓名_________________ 一、选择题(共5小题,每小题6分,满分30分)1、已知非零实数a ,b 满足 2242(3)42a b a b a -+++-+=,则a b +等于( ) A .-1 B.0 C.1 D.22、如图1,已知AB 是⊙O 的弦,P 是AB 上一点,若AB=10,PB=4,OP=5,则⊙O 的半径等于( )A 、5B 、6C 、7D 、8 3、方程|2x -x 2|=x2的正根个数是 ( )A. 0B. 1C. 2D. 34、抛物线2221y ax ax b =+++的一部分如图所示,设该抛 物线与x 轴的交点为()3,0A -和B ,与y 轴的交点为C ,若△ACO ∽△CBO ,则21b +的值为 ( )A 、1B 、2C 、3D 、35、如图,菱形ABCD 的边长为a ,点O 是对角线AC 上的一点, 且OA =a ,OB =OC =OD =1,则a 等于( )A.512+ B.512- C.1 D.2 二、填空题(共5小题,每小题6分,满分30分)6、若直线b y =(b 为实数)与函数342+-=x x y 的图象至少有三个公共点,则实数b 的取值范围是_________.7、母亲节到了,小红,小莉,小莹到花店买花送给自己的母亲.小红买了3枝玫瑰,7枝康乃馨,1枝百合花,付了14元;小莉买了4枝玫瑰,10枝康乃馨,1枝百合花,付了16元;小莹买上面三种花各2枝,则她应付 元.(第5题)8、把一枚六个面编号分别为1,2,3,4,5,6的质地均匀的正方体骰子先后投掷2次,若两个正面朝上的编号分别为m ,n ,则二次函数2y x mx n =++的图象与x 轴有两个不同交点的概率是 .9、若关于x 的函数()()22212y a x a x a =+--+-的图象与坐标轴有两个交点,则a 的值为 。
初三数学竞赛试题(含答案)

初三数学竞赛试题(含答案) 初三数学竞赛试题一、选择题(共8小题,每小题5分,共40分)1.要使方程组 $3x+2y=a$,$2x+3y=2$ 的解是一对异号的数,则 $a$ 的取值范围是()。
A) $4\sqrt{3}<a<3$B) $a<4\sqrt{3}$C) $a>3$D) $a>3$ 或 $a<4\sqrt{3}$2.一块含有 $30^\circ$ 角的直角三角形(如图),它的斜边 $AB=8$ cm,里面空心 $\triangle DEF$ 的各边与 $\triangle ABC$ 的对应边平行,且各对应边的距离都是 $1$ cm,那么$\triangle DEF$ 的周长是()。
A) $5$ cmB) $6$ cmC) $(6-3)$ cmD) $(3+3)$ cm3.将长为 $15$ cm 的木棒截成长度为整数的三段,使它们构成一个三角形的三边,则不同的截法有()。
A) $5$ 种B) $6$ 种C) $7$ 种D) $8$ 种4.作抛物线 $A$ 关于 $x$ 轴对称的抛物线 $B$,再将抛物线 $B$ 向左平移 $2$ 个单位,向上平移 $1$ 个单位,得到的抛物线 $C$ 的函数解析式是 $y=2(x+1)^2-1$,则抛物线$A$ 所对应的函数表达式是()。
A) $y=-2(x+3)^2-2$B) $y=-2(x+3)^2+2$C) $y=-2(x-1)^2-2$D) $y=-2(x+3)^2+2$5.书架上有两套同样的教材,每套分上、下两册,在这四册教材中随机抽取两册,恰好组成一套教材的概率是()。
A) $\frac{2}{11}$B) $\frac{3}{32}$C) $\frac{3}{26}$D) $\frac{3}{26}$6.如图,一枚棋子放在七边形 $ABCDEFG$ 的顶点处,现顺时针方向移动这枚棋子 $10$ 次,移动规则是:第 $k$ 次依次移动 $k$ 个顶点。
2019年浙江省嵊州市“天乐杯”九年级数学竞赛试题
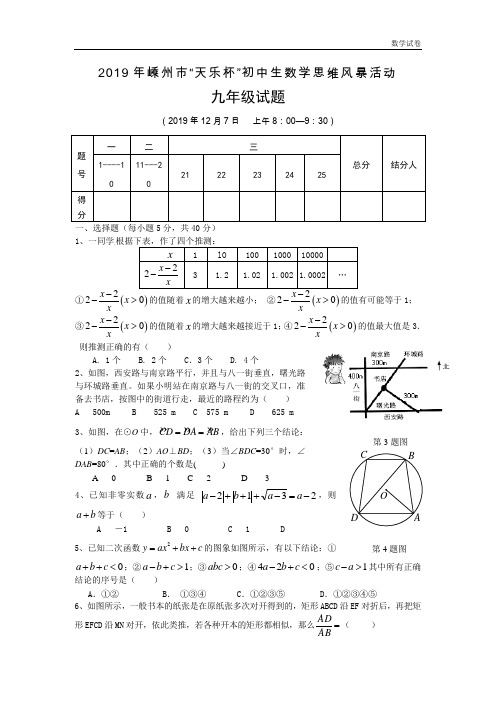
2019年嵊州市“天乐杯”初中生数学思维风暴活动九年级试题(2019年12月7日 上午8:00—9:30)一、选择题(每小题5分,共40分) 1、一同学 1.02①()220x x x -->的值随着x 的增大越来越小; ②()20x x ->的值有可能等于1;③()220x x x -->的值随着x 的增大越来越接近于1;④()220x x x-->的值最大值是3.则推测正确的有( )A. 1个B. 2个 C .3个 D. 4个2、如图,西安路与南京路平行,并且与八一街垂直,曙光路与环城路垂直。
如果小明站在南京路与八一街的交叉口,准备去书店,按图中的街道行走,最近的路程约为( ) A 500m B 525 m C 575 m D 625 m3、如图,在⊙O 中,CD DA AB ==,给出下列三个结论:(1)DC =AB ;(2)AO ⊥BD ;(3)当∠BDC =30°时,∠DAB =80°.其中正确的个数是( )A 0B 1C 2D 34、已知非零实数a ,b 满足2312-=-+++-a a b a ,则a b +等于( )A -1B 0C 1 D5、已知二次函数2y ax bx c =++的图象如图所示,有以下结论:①0a b c ++<;②1a b c -+>;③0abc >;④420a b c -+<;⑤1c a ->其中所有正确结论的序号是( )A .①②B . ①③④C .①②③⑤D .①②③④⑤6、如图所示,一般书本的纸张是在原纸张多次对开得到的,矩形ABCD 沿EF 对折后,再把矩形EFCD 沿MN 对开,依此类推,若各种开本的矩形都相似,那么=ABAD( ) 第4题图第3题图A 22B 2C 3D 27、已知函数()()()()22113513x x y x x ⎧--⎪=⎨--⎪⎩≤>,则使y =k 成立的x 值恰好有三个,则k 的值为( )A .0B .1C .2D .38、如图,设正方体ABCD -A 1B 1C 1D 1的棱长为1,黑、白两个甲壳虫同时从A 点出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA 1→A 1D 1→……,白甲壳虫爬行的路线是AB →BB 1→……,并且都遵循如下规则:所爬行的第n n 与第2+条棱所在的直线必须是既不平行也不相交(其中n 是正整数).那么当黑、白两个甲壳虫各爬行完第2019条棱分别停止在所到的正方体顶点处时,它们之间的距离是( )A 0B 1 C2 D 3二、填空题(每小题5分,共40分) 9、若关于x ,y 的二元一次方程组3133x y ax y +=+⎧⎨+=⎩的解满足2x y +<,则a 的取值范围为______. 10、设15-=a ,则代数式142323+-+a a a 的值为11、读一读:式子“1+2+3+4+……+100”表示从1开始的100个连续自然数的和,由于式子比较长,书写不方便,为了简便起见,我们将其表示为∑=1001n n ,这里“∑”是求和符号,通过以上材料的阅读,计算∑=+20121n 1)(n 1n = .12、在直角坐标系中,点A 是抛物线y=x 2在第二象限上的点,连接OA ,过点O 作OB ⊥OA ,交抛物线于点B ,以OA 、OB 为边构造矩形AOBC 。
2020版初三数学竞赛试卷含答案
2020版初三数学竞赛试卷含答案2020版初三数学竞赛试卷一、选择题(共5小题,每小题6分,共30分)1.已知a≠0,14(a2b2c2)=(a2b3c)2,那么a:b:c=()A、2:3:6B、1:2:3C、1:3:4D、1:2:42.抛物线y=kx2-7x-7的图象和x轴有交点,则k的取值范围是()A、B、且k≠0;C、D、且k≠03.如图,已知P是正方形ABCD内一点,△PBC是等边三角形,若△PAD的外接圆半径为a,则正方形ABCD边长为()A、B、C、D、4.一个等腰三角形被过一个顶点的一条直线分割成两个较小的等腰三角形,那么这个等腰三角形的顶的角度数的值可能有()A、2种B、3种C、4种D、5种5.如图所示,二次函数y=ax 2+bx+c 的图象经过点(-1,2),且与x 轴交点的横坐标分别为x 1,x 2,其中-2<x 1<-1,0<x 2<1,下列结论:①4a-2bc<0;②2a-b<0;③a<-1;④b 28a>4ac。
其中正确的有()(A)1个(B)2个(C)3个(D)4个二、填空题(共5小题,每小题6分,共30分)6.已知x 2xy y=14①,y 2xy x=28②,则x y 的值为.7.已知a,b 均为质数,且满足a 2b a =13,则a b b 2=.8.设整数a 使得关于x 的一元二次方程的两个根都是整数,则整数a的值=.9.如图是一个数的转换器,每次输入3个不为零的数,经转换器转换后输出3个新数,规律如下:当输入数分别为x,y,z时,对应输出的新数依次为,,.例如,输入1,2,3,则输出,,.那么当输出的新数为,,时,输入的3个数依次为.10.若实数a、b满足a2ab b2=1,且t=ab-a2-b2,则t的取值范围是。
三、解答题(共4题,满分60分)11、规定符号[x]表示不超过x的最大整数,例[3.1]=3,[-73]=-3,[6]=6。
求:满足方程2-x2=[x]且大于-3的x的解。
2020年浙江省绍兴市中考数学竞赛试卷附解析
2020年浙江省绍兴市中考数学竞赛试卷 学校:__________ 姓名:__________ 班级:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上一、选择题1.已知抛物线y =x 2-x -1与x 轴的一个交点为(m ,0),则代数式m 2-m +2008的值为( )A .2006B .2007C .2008D .2009 2.抛物线2255y x x =++与坐标轴的交点个数是( )A .O 个B .1个C . 2个D .3 个 3.正方形具有而菱形不一定具有的特征有( ) A .对角线互相垂直平分 B .内角和为360°C .对角线相等D .对角线平分内角4.下列图形中,是中心对称图形而不是轴对称图形的是( ) A .平行四边形 B .正三角形 C .正方形D .线段AB 5.如图,已知在△ABC 中,AB=AC ,∠C=30°,AB ⊥AD ,AD=2cm ,则BC 的长为( )A .8 cmB .6cmC .4cmD .2cm6.如图,AB ∥CD ,则∠α,∠β,∠γ之间的关系为( )A .∠α+∠β+∠γ=360°B .∠α-∠β+∠γ=180°C .∠α+∠β-∠γ=180°D .∠α+∠β+∠γ=180°7.不等式组⎩⎨⎧>->-03042x x 的解集为( )A .x >2B .x <3C .x >2或 x <-3D .2<x <38.关于x 、y 的方程组244x y a x y a +=⎧⎨-=⎩解是方程3210x y +=的解,那么a 的值为( ) A . -2 B . 2 C .-1 D . 19.小王只带2元和 5元两种面值的人民币,他买一件学习用品要支付27元,则付款的方式有( )A . 1种B . 2种C .3种D .4种10.如图,将四边形AEFG 变换到四边形ABCD ,其中E ,G 分别是AB 、AD 的中点,下列叙述不正确...的是( ) A .这种变换是相似变换B .对应边扩大到原来到2倍C .各对应角度数不变D .面积是原来2倍11.已知一叠2元和5元两种面值的人民币,其价值是24元,则面值为2元的人民币的张数是 ( )A .2张B .7张C 12张D .2张或7张 二、填空题12.如图,已知AB 是⊙O 的直径,弦CD AB ⊥,22AC =,1BC =,那么sin ABD ∠的值是 .13.如图,口袋中有5张完全相同的卡片,分别写有1cm ,2cm ,3cm ,4cm 和5cm ,口袋外有2张卡片,分别写有4cm 和5cm .现随机从袋内取出一张卡片,与口袋外两张卡片放在一起,以卡片上的数量分别作为三条线段的长度,回答下列问题:(1)求这三条线段能构成三角形的概率;(2)求这三条线段能构成直角三角形的概率;(3)求这三条线段能构成等腰三角形的概率.解答题14.如果一扇形的半径为15,弧长为4π,则此扇形的面积是 。
浙江初三初中数学竞赛测试带答案解析
浙江初三初中数学竞赛测试班级:___________ 姓名:___________ 分数:___________一、选择题1.下列等式一定成立的是()A.B.C.D.2.下列式子成立的是()A.a a=a B.(a b)= a bC.0.0081=8.1×10D.3.以下列各组数为边长,能构成直角三角形的是 ( )A.,,B.,,C.32,42,52D.1,2,34.使式子有意义的x的取值范围是()A.x≤1B.x≤1且x≠-2C.x≠-2D.x<1且x≠-25.解关于x的方程时产生增根,则m的值等于()A.-2B.-1C.1D.26.二次函数的图象可能是()7.如图几何体的俯视图是()8.已知:如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上一动点,则DN+MN的最小值为()A.8B.10C.11D.129.如图,已知矩形ABCD,R、P分别是DC、BC上的点,E、F分别是AP,RP的中点,当P在BC上从B向C 移动而R不动时,那么下列结论成立的是()A.线段EF的长逐渐增大 B.线段EF的长逐渐减小C.线段EF的长不改变 D.线段EF的长不能确定二、填空题1.⊙O的半径是13,弦AB∥CD,AB=24,CD=10,则AB与CD的距离是 .2.规定"*"为一种运算,它满足a*b=,那么1992*(1992*1992)=____。
3.已知直角三角形的两条边x、y的长满足,则第三边长为4.有五根木条,分别为12cm,10cm,8cm,6cm,4cm,则从中任取三根能组成三角形的概率为5.如图所示,二次函数的图象经过点,且与x轴交点的横坐标为、,其中、下列结论:①;②;③;④;正确的结论是 .三、解答题1.解方程:2.某商场将进价40元一个的某种商品按50元一个售出时,能卖出500个,已知这种商品每个涨价一元,销量减少10个,为赚得最大利润,售价定为多少?最大利润是多少?3.如图,在△ABC中,点O是AC边上的一动点,过点O作直线MN//BC,MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F。
嵊州市初三数学竞赛试卷
嵊州市初三数学竞赛试卷一、选择题(每题有且只有一个正确答案,每小题5分,共30分)1.民航规定:乘坐飞机普通舱旅客一人最多可免费携带行李,超过部分每千克按飞机票价的1.5 % 购买很行李票。
一名旅客带了35千克行李乘机,机票连同行李费共付1323元,则该旅客的机票票价为( )A.1000元B.1080元C.1100元D.12.已知x 1、x 2 是方程20x p x q ++=的两个根,且1(5)x -,2(5)x -是方程20x qx p ++=的两个根,则p q +的值为( )A.-3B.-4C.3D.4 3.=,满足上式的自然数对(x ,y ,z )的个数是( )A.1B.2C.3D.44.如图,在平行四边形ABCD 中,EF 、GH 把它分成四个小的平行四边形,其中12S =,23S =,36S =,则4S = ( )A.8B.9C.12D.155.某中学科技窗户设计如图(1)所示,如果每个符号(窗户形状)代表一个阿拉伯数码,每横行三个符号自左至右成一个三位数,这四层组成四个三位数,它们是450,172,396,857,则按图(1)所示规律写出应是图(2)中的( )+图(1) 图(2)6.抛物线2y ax bx c =++与x 轴交于A 、B 两点,Q (2,k )是该抛物线上一点,且AQ ⊥BQ ,则ak 的值等于( )A.-1B.-2C.2D.3 二、填空题(每小题5分,共30分)7.定义一种新运算“▲”为x ▲y =ax+by (a 、b 为常数),若1▲2=5,2▲3=8,那么4▲1000=______________.8.方程组22513x y x y +=⎧⎨+=⎩的两组解为1111x a y b =⎧⎨=⎩,2222x a y b =⎧⎨=⎩,则1221a b a b +的 S 4S 3S 2S 1H P GFEDC BA 3 913值为__________.9.如图,正方体的每个面上都有一个正整数,已知相对的两个面上两数之和都相等,如果13、9、3的对面分别是a 、b 、c ,试求222a b c bc ca ab ++---的值为_____________. 10.如图,△ABC 中,BC =a ,若D 1、E 1分别是AB 、AC 的中点,则D 1E 1=21a ;若D 2 、E 2分别是D 1 B 、E 1 C 的中点,则D 2E 2=137248a a a ⎛⎫+= ⎪⎝⎭;…若n n D E 分别是1n D B -、1n E C -的中点,则n n D E =___________(n ≥1,且n 为整数)11.如图,在△ABC 中,D 、E 是BC 边上的两个点,且CD ∶DE ∶BE =1∶2∶1,F 是AC 的中点,AD 与EF 交于O ,若OF OE =1n,则n =____________. 12.如图,已知边长为4的正方形截去一角成五边形ABCDE ,其中AF =2,BF =1.在AB 上的一点P ,使得矩形PNDM 有最大面积,则矩形PNDM 面积的最大值是________________.三、解答题(60分) 13.(15分)已知关于x 的方程211111x mx x x --=+--,求m 为何值时,方程有两个不相等的实数根?14.(15分)将自然数1、2、3 …按下图排列,从1开始,右边写2,然后向下转弯写3,再向左转弯写4、5,再向上转弯写6、7…,这样,第一次转弯是2,第二次转弯是3,E 1E 2E 3E 4D 4D 3D 2D 1CBAOFE DCB AMPF ED CBA第三次转弯是5,第四次转弯是7,…….请同学们先阅读下面的解答过程,然后再解答第(1)、(2)两题解:第一次转弯是2第二次转弯是2321=+个第三次转弯是35=212++个第四次转弯是47=2122+++个……请解答(1)第弯是几?(2)第n 次转弯是几?15.(15分)如图所示,ABCD 为☉O 的内接四边形,E 是BD 上的一点,且有∠BAE=∠DAC. (1)求证:△ABC ∽△AED ; (2)求证:AB •DC + AD •BC = AC •BD.16.(15分)某商场为提高彩电销售人员的积极性,制定了新的工资分配方案.方案规定:每位销售人员的工资总额=基本工资+奖励工资,每位销售人员的月销售定额为10000元,在销售定额内,得基本工资;超过销售定额,超过部分的销售额按相应比例作为奖励工资.奖励工资发放比例如表1所示.(1)已知销售员甲本月领到的工资总额为800元,请问销售员甲本月的销售额为多少元?(2)依法纳税是每个公民应尽的义务.根据我国税法规定,每月工资总额不超过800元不要缴纳个人所得税;超过800元的部分为“全月应税所得额”,表2是缴纳个人所得税税率表.若销售员乙本月共销售A、B两种型号的彩电27台,缴纳个人所得税后实际得到的工资为1860元,又知A型彩电的销售价为每台1000元,B型彩电表1 表2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
嵊州市2004年初三数学竞赛试题题号一二三总分1-67-12 13 14 15 16 得分一、选择题:(每小题5分,共30分) 1.小明同学买了一包弹球,其中14是绿色的,18是黄色的,余下的15是蓝色的。
如果有12个蓝色的弹球,那么,他总共买了弹球 ( )A.48个B.60个C.96个D.720个 2.一种儿童游戏,以确定这个人是“谁”。
孩子们站成一个圆圈,并唱一首有九个单词的诗歌。
按这个圆圈的顺时针方向连续计数,将第九个孩子淘汰出圈。
开始时,一圈有六个孩子。
按顺时针方向分别记为a ,b ,…,f 。
最后剩下的这个孩子是c 。
开始记数的位置是 ( ) A.b B.d C.c D.f 3.若123456789123456786x =⨯,123456788123456787y =⨯,则x ,y 的大小关系是 ( ) A.x y = B.x y <C.x y >D.不确定的4.已知动点P 在边长为2的正方形ABCD 的边上沿着A -B -C -D 运动,x 表示点P 由A 点出发所经过的路程,y 表示△APD 的面积,则y 和x 函数关系的图像大致为 ( )A.B.C.D.5.如图,平行四边形ABCD 中,E 是AD 上的一点,且AE =13AD ,对角线AC ,BD 交于点O ,EC 交BD 于F ,BE 交AC 于G ,如果Y ABCD的面积为S ,那么,△GEF 的面积为( ) A.110S B.115S C.120S D.130S6.二次函数2y ax bx c =++的图象如图所示,Q (n ,2)是图象上的一点,且AQ ⊥BQ ,则a 的值为( ) A.13-B.12-C.-1D.-2二、填空题(每小题5分,共30分) 7.若关于x 的方程212x ax +=-+的解为正数,则实数a 的取值范围是 。
8.已知四边形ABCD 内接于⊙O ,分别延长AB 和DC 相交于点P ,»»CBCD =,AB =12,CD =6,PB =8,则⊙O 的面积为 。
9.观察图形,用i S 表示第i个三角形的面积,有12S =;22S =;32S =,…,若12310n S S S S ++++>L ,则n 的最小值为 。
10.观察下面各组数:(3,4,5)、(5,12,13)、(7,24,25)、(9,40,41)、(11,60,61)……,发现:()24312=-÷,()212512=-÷,()224712=-÷……,若设某组数的第一个数为k ,则这组数为(k , , )。
11.如图已知二次函数2y ax bx c =++的图象过(-1,0)和(0,-1)两点,则化简代数式= 。
12.某水池有编号为1,2,……,9的9个水管,有的是进水管,有的是出水管。
已知所开的水管号与水池灌满的时间如下表,则9个水管一起开,灌满水池的时间为 。
第6题第 8 题P 11111111S 7S 1S 2S 3S 4S 5S 6A 8A 7A 6A 5A 4A 3A2第 9 题A 1第11题三、解答题(每小题15分,共60分) 13.某市自来水公司,为鼓励居民节约用水,采用分段计费的方法计算水费,(2)小王家第二季度交纳水费情况如下:问小王家第二季度共用水多少度?14.已知:关于x 的方程①()2220x m x m -++-=有两个符号不同的实数根1x ,2x ,且1x >2x >0;关于x 的方程②()22230mx n x m +-+-=有两个有理数根且两根之积等于2。
求整数n 的值。
15.如图,在半径为6,圆心角为90°的扇形OAB 的»AB 上,有一个动点P ,PH ⊥OA ,垂足为H ,△OPH 的重心为G 。
(1)当点P 在»AB 上运动时,线段GO 、GP 、GH 中,有无长度保持不变的线段?如果有,请指出这样的线段,并求出相应的长度;(2)如果△PGH 是直角三角形,试求OG ∶PG ∶HG 的值; (3)如果△PGH 是等腰三角形,试求出线段PH 的长。
16.在密码学中,称直接可以看懂的内容为明码,对明码进行某种处理后得到的内容为密码,对于英文,人们将26个字母按顺序分别对应整数0到25,如12,4表示“me ”,即“我”。
现在4个字母构成的密码单词,记4个字母对应的数字分别为1x ,2x ,3x ,4x 。
已知整数122x x +,23x ,342x x +,43x 除以26的余数分别为9,16,23,12,问这个密码单词是什么意思?G B PA H O命题:嵊州市教研室 蔡建锋参考答案及评分标准:一、选择题(30分)1.C2.C3.B4.A5.C6.B 二、填空题(30分)7.a <-2 8.45π 9.n =10 10.212k -,212k + 11.2a12.2小时三、解答题(60分)13.(1)解:12 2.006 2.502 3.0045⨯+⨯+⨯=(元) ············· (6分) (2)∵22<12×2.00 ∴22÷2.00=11(度) ····················· (3分) ∵34>12×2.00 ∴12×2.00+(x -12)×2.50=34 ∴x =16(度)························································ (3分) ∵54>12×2.00+6×2.50 ∴12×2.00+6×2.50+(x -18)×3.00=54∴ x =23(度)∴11+16+23=50(度) ············································· (3分)14.由方程①知:∵120x x ⋅<,1x >2x >0 ∴1x >0,20x < ·················· (3分) ∵△=()2280m -+> ∴1220x x m +=+> 1220x x m ⋅=-<∴-2<m <2 ······························································ (3分)由方程②知:232m m-= ∴2230m m --= ∴3m =(舍去),1m =-(3分) 代入②得:2(2)20x n x --+= ∵方程的两根为有理数∴△=()2228n k --= ∴△=()2228n k --= ()()228n k n k -+--=∴2422n k n k -+=⎧⎨--=⎩或2224n k n k -+=-⎧⎨--=-⎩∴5n =或1n =- ······ (6分)15.(1)延长HG 交OP 于点F ∵G 是重心 ∴F 为OP 边中点 · (2分) ∵PH ⊥OA ∴∠PHO =90° ∴FH =12OP =3 ∴GH =23HF =23×3=2 ··········································· (3分) (2)延长OG 交PH 于点K∵△PGH 为Rt △ FG =1,PF =3 ∴PG =∴PH =∴KG ∴OG =∴OG ∶PG ∶HG =∶2∶1 ········· (5分) (3)△PGH 是等腰三角形有3种可能性①当GH =PH 时,PH ②当GP =GH 时,PH =0(不存在)③当PH =GH 时,PH =2∴PH 或PH =2 ················································· (5分) 16.显然1x ,2x ,3x ,4x 都在0~25间 ∵23x 除以26余16,∴23x =16或42或68又∵23x 是3的倍数 ∴23x =42 即2x =14 ···················· (2分) ∵122x x +=1x +28除以26余数为9 ∴1x +28=26+9∴1x =7 ····································································· (2分) ∵43x 除以26余数为12 ∴43x =12或38或64∴4x =4 ···································································· (2分) 又∵342x x =3x +8除以26余23 ∴3x +8=23或49∴3x =15 ··································································· (2分) 所以1x =7,2x =14,3x =15,4x =4 ····························· (2分) 它们分别对应的英语字母是7-h ,14-o ,15-p ,4-e ∴这个密码单词为hope ,意思是“希望”. ························ (5分) 评分要求:(1) 推理过于简单,得到的数正确,结论正确,得10~12分。
