结构力学 结构的位移计算作业答案
结构力学位移法题及答案
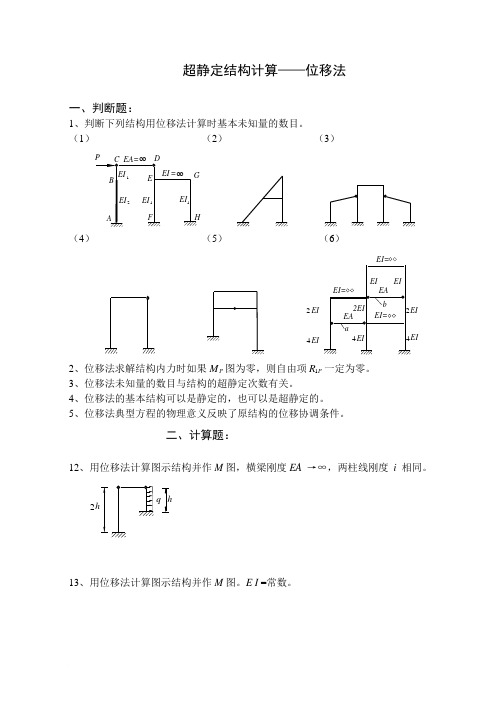
超静定结构计算——位移法一、判断题:1、判断下列结构用位移法计算时基本未知量的数目。
(1) (2) (3)(4) (5) (6)EIEIEIEI 2EI EI EIEIEAEA ab EI=EI=EI=244422、位移法求解结构内力时如果P M 图为零,则自由项1P R 一定为零。
3、位移法未知量的数目与结构的超静定次数有关。
4、位移法的基本结构可以是静定的,也可以是超静定的。
5、位移法典型方程的物理意义反映了原结构的位移协调条件。
二、计算题:12、用位移法计算图示结构并作M 图,横梁刚度EA →∞,两柱线刚度 i 相同。
213、用位移法计算图示结构并作M 图。
E I =常数。
—— 41 ——ll /2l /214、求对应的荷载集度q 。
图示结构横梁刚度无限大。
已知柱顶的水平位移为 ()5123/()EI →。
12m12m8mq15、用位移法计算图示结构并作M 图。
EI =常数。
ll ll16、用位移法计算图示结构,求出未知量,各杆EI 相同。
4m19、用位移法计算图示结构并作M 图。
qll20、用位移法计算图示结构并作M 图。
各杆EI =常数,q = 20kN/m 。
6m6m23、用位移法计算图示结构并作M 图。
EI =常数。
ll 224、用位移法计算图示结构并作M 图。
EI =常数。
q29、用位移法计算图示结构并作M 图。
设各杆的EI 相同。
qql l /2/232、用位移法作图示结构M 图。
E I =常数。
—— 43 ——qql l/2l /2l36、用位移法计算图示对称刚架并作M 图。
各杆EI =常数。
l l38、用位移法计算图示结构并作M 图。
EI =常数。
ql l l l42、用位移法计算图示结构并作M 图。
2m 2m43、用位移法计算图示结构并作M 图。
EI =常数。
lllql48、已知B 点的位移∆,求P 。
ll/2/2A∆51、用位移法计算图示结构并作M 图。
超静定结构计算——位移法(参考答案)1、(1)、4; (2)、4; (3)、9; (4)、5; (5)、7;(6)、7。
结构力学 第八章 作业参考答案
D
Z2
B
2I 2FL/9 I
M图
D
L
B
A
L
B
2FL/9
A
L
FL/9
B
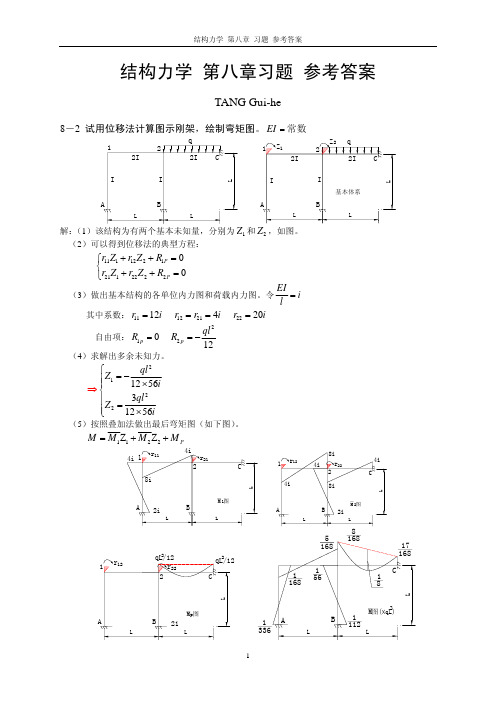
解: (1)该结构为有两个基本未知量,分别为 Z1 和 Z 2 ,如图。 (2)可以得到位移法的典型方程:
⎧r11Z1 + r12 Z 2 + R1P = 0 ⎨ ⎩r21Z1 + r22 Z 2 + R2 P = 0
(3)做出基本结构的各单位内力图和荷载内力图。令 其中系数: r11 = 14i 自由项: R1 p = 0 (4)求解出多余未知力。
4
1m
E
E
E r12 2I
4m
I
I
4m
I
I
1m
0.75 E
1m
结构力学 第八章 习题 参考答案
(2)可以得到位移法的典型方程:
⎧r11Z1 + r12 Z 2 + R1P = 0 ⎨ ⎩r21Z1 + r22 Z 2 + R2 P = 0
(3)做出基本结构的各单位内力图和荷载内力图。 其中系数: r11 = r22 =
8-7 试用位移法计算连续梁,绘制弯矩图。 EI = 常数
A Z1 B 6m 6m
基本体系
Z1 C 6m
A B 6m 6m C 6m
D
D
解: (1)该结构为有两个基本未知量,分别为 Z1 和 Z 2 ,如图。 (2)可以得到位移法的典型方程:
⎧r11Z1 + r12 Z 2 + R1P = 0 ⎨ ⎩r21Z1 + r22 Z 2 + R2 P = 0
结构力学4静定结构的位移计算习题解答

第4章 静定结构的位移计算习题解答习题 是非判定题(1) 变形体虚功原理仅适用于弹性体系,不适用于非弹性体系。
( ) (2) 虚功原理中的力状态和位移状态都是虚设的。
( )(3) 功的互等定理仅适用于线弹性体系,不适用于非线弹性体系。
( ) (4) 反力互等定理仅适用于超静定结构,不适用于静定结构。
( ) (5) 关于静定结构,有变形就必然有内力。
( ) (6) 关于静定结构,有位移就必然有变形。
( )(7) 习题(7)图所示体系中各杆EA 相同,那么两图中C 点的水平位移相等。
( ) (8) M P 图,M 图如习题(8)图所示,EI =常数。
以下图乘结果是正确的:4)832(12ll ql EI ⨯⨯⨯ ( )(9) M P 图、M 图如习题(9)图所示,以下图乘结果是正确的:033202201111)(1y A EI y A y A EI ++ ( )(10) 习题(10)图所示结构的两个平稳状态中,有一个为温度转变,现在功的互等定理不成立。
( )(a)(b)习题 (7)图图(b)M图(a)M P 81qM 图(b)P M 图(a)习题 (8)图 习题 (9)图(a)P习题 (10)图【解】(1)错误。
变形体虚功原理适用于弹性和非弹性的所有体系。
(2)错误。
只有一个状态是虚设的。
(3)正确。
(4)错误。
反力互等定理适用于线弹性的静定和超静定结构。
(5)错误。
譬如静定结构在温度转变作用下,有变形但没有内力。
(6)错误。
譬如静定结构在支座移动作用下,有位移但没有变形。
(7)正确。
由桁架的位移计算公式可知。
(8)错误。
由于取0y 的M 图为折线图,应分段图乘。
(9)正确。
(10)正确。
习题 填空题(1) 习题(1)图所示刚架,由于支座B 下沉∆所引发D 点的水平位移∆D H =______。
(2) 虚功原理有两种不同的应用形式,即_______原理和_______原理。
其中,用于求位移的是_______原理。
结构力学(5.1.2)--位移法习题及参考答案
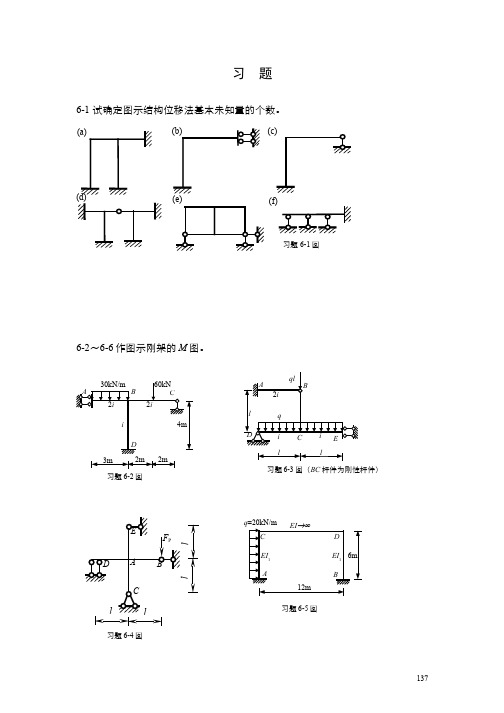
习 题6-1 试确定图示结构位移法基本未知量的个数。
6-2~6-6作图示刚架的M 图。
(a)(f)习题6-1图(d)习题6-2图习题6-5图习题6-3图(BC 杆件为刚性杆件)习题6-4图6-6 试用位移法计算图示结构,并作内力图。
6-7 试用位移法计算图示结构,并作内力图。
6-8 试用位移法计算图示结构,并作内力图。
EI 为常数。
6-9试用位移法计算图示结构,并作弯矩图。
EI 为常数。
6-10 试用位移法计算图示结构,并作弯矩图(提示:结构对称)。
习题6-9图习题6-7图6-11作图示刚架的体系内力图。
6-12 设支座 B 下沉0.5cm B D =,试作图示刚架的M 图。
6-13如图所示连续梁,设支座C 下沉淀1cm ,试作M 图。
6-14图示等截面正方形刚架,内部温度升高+t°C ,杆截面厚度h ,温度膨胀系数为 ,试作M 图。
10 kN/m( a )( b)40 kN习题6-10图BGH习题6-11图(a )(b )q6-15试作图示有弹性支座的梁的弯矩图,332EIk l=,EI =常数。
6-16 试用弯矩分配法计算图示连续梁,并作M 图。
6-176-18 用力矩分配法计算图示结构,并作M 图。
6-19 已知图示结构的力矩分配系数1238/13,2/13,3/13,A A A m m m ===作M 图。
6-20 求图示结构的力矩分配系数和固端弯矩。
已知q=20kN/m,各杆EI 相同。
习题6-17图习题6-13图习题6-14图6-21~6-22 用力矩分配法计算图示连续梁,作M 图,并计算支座反力。
EI=常数。
6-23~6-25用力矩分配法计算图示刚架,作M 图。
EI=常数。
参考答案6.1 (a) 2 (b) 1 (c) 2 (d) 3 (e) 6 (f) 26.2 15BD M =kN·m (右侧受拉)20kN/m 40kN习题6-22图习题6-21图15kN/m习题6-23图F P =10kN 习题6-24图习题6-25图6.321112AB M ql =(上侧受拉)6.4P 0.4AD M F l =(上侧受拉)6.5150AC M =kN·m (左侧受拉)6.651.3AB M =kN·m (左侧受拉)6.780AB M =kN·m (上侧受拉)6.816.9AB M =kN·m (左侧受拉)6.9 (a) 10.43CA M =kN·m (左侧受拉) (b) 56.84CE M =kN·m (下侧受拉)6.10 (a) 8.5AB M =kN·m (上侧受拉) (b) 34.3AC M =kN·m (左侧受拉)6.11 (a) 20.794DC M ql =(右侧受拉) (b) 6.14GD M q =(右侧受拉)6.1223.68AC M =kN·m (右侧受拉)6.1359.3310BA M =ᅲkN·m (上侧受拉)6.142/M EIt h a =(外侧受拉)6.152/32BA M ql =(下侧受拉)6.1617.5CB M =kN·m (下侧受拉)6.1778.75CD M =kN·m (上侧受拉)6.1827/12AB M ql =(上侧受拉)6.191117.95A M =kN·m (上侧受拉)6.200.34AD m =,13.33AD M =kN·m 6.2142.3BA M =kN·m (上侧受拉)6.2217.35BA M =kN·m (上侧受拉)6.2357.4BA M =kN·m (上侧受拉)6.2428.5BA M =kN·m (上侧受拉)6.2573.8BD M =kN·m (左侧受拉)。
结构力学习题集及答案

第三章 静定结构的位移计算一、判断题:1、虚位移原理等价于变形谐调条件,可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下,静定结构不产生内力,但会有位移且位移只与杆件相对刚度有关。
4、求图示梁铰C 左侧截面的转角时,其虚拟状态应取:A.;;B.D.C.M =1=15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知M p 、M k 图,用图乘法求位移的结果为:()/()ωω1122y y EI +。
M kM p21y 1y 2**ωω( a )M 17、图a 、b 两种状态中,粱的转角ϕ与竖向位移δ间的关系为:δ=ϕ 。
8、图示桁架各杆E A 相同,结点A 和结点B 的竖向位移均为零。
9、图示桁架各杆EA =常数,由于荷载P 是反对称性质的,故结点B 的竖向位移等于零。
二、计算题:10、求图示结构铰A 两侧截面的相对转角ϕA ,EI = 常数。
q11、求图示静定梁D 端的竖向位移 ∆DV 。
EI = 常数 ,a = 2m 。
10kN/m12、求图示结构E 点的竖向位移。
EI = 常数 。
ll l /32 /3/3q13、图示结构,EI=常数 ,M =⋅90kN m , P = 30kN 。
求D 点的竖向位移。
P14、求图示刚架B 端的竖向位移。
q15、求图示刚架结点C 的转角和水平位移,EI = 常数 。
q16、求图示刚架中D点的竖向位移。
EI =常数。
l/217、求图示刚架横梁中D点的竖向位移。
EI=常数。
18、求图示刚架中D点的竖向位移。
E I = 常数。
qll l/l/2219、求图示结构A、B两截面的相对转角,EI=常数。
l/23l/320、求图示结构A、B两点的相对水平位移,E I = 常数。
ll21、求图示结构B点的竖向位移,EI = 常数。
ll22、图示结构充满水后,求A 、B 两点的相对水平位移。
结构力学作业及答案土木工程管理本科课程

(C)第j个结点位移等于单位位移时,产生的第i个附加约束中的反力(矩)
(D)第j个结点位移产生的第j个附加约束中的反力(矩)
正确答案:C
解答参考:
7.
考虑各杆件轴向变形,图示结构若用边界条件先处理法,结构刚度矩阵的容量为:
(A)15×15
(C)可求得支座结点位移
(D)无法求得结点位移
正确答案:D
解答参考:
14.单元刚度矩阵中元素 的物理意义是:( )
(A)当且仅当 时引起的与 相应的杆端力
(B)当且仅当 时引起的与 相应的杆端力
(C)当 时引起的与 相应的杆端力
(D)当 时引起的与 相应的杆端力
正确答案:C
解答参考:
15.
图示桁架的动力自由度数为( )
正确答案:说法错误
解答参考:
46.频率、主振型是体系本身的固有特性,与外荷载无关。( )
正确答案:说法正确
解答参考:
47.在动力荷载作用下,结构的内力和变形不仅与动力荷载的幅值有关,而且与动力荷载的变化规律以及结构本身的动力特性(自振频率、振型和阻尼等因素)有关。( )
正确答案:说法正确
解答参考:
48.结构的自振频率与质量、刚度及荷载有关。 ( )
正确答案:说法正确
解答参考:
33.一般情况下,矩阵位移法的基本未知量的数目比传统位移法的基本未知量的数目要多。( )
正确答案:说法正确
解答参考:
34.单元刚度矩阵均具有对称性和奇异性。( )
正确答案:说法错误
解答参考:
35.
图示四单元的l、EA、EI相同,所以它们整体坐标系下的单元刚度矩阵也相同。( )
长沙理工大学结构力学期末考试题库及详细答案-第五章 结构位移
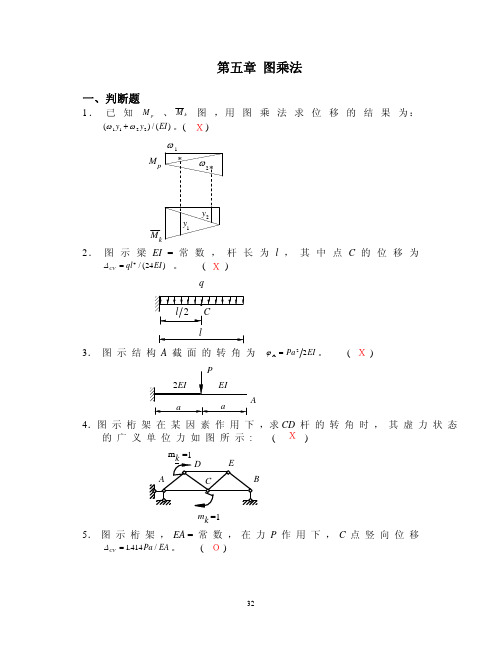
第五章 图乘法一、判断题1. 已 知 、M p M k 图 ,用 图 乘 法 求 位 移 的 结 果 为:()/()ωω1122y y E +I 。
( ) M kM p21y 1y 2**ωω2. 图 示 梁 EI = 常 数 , 杆 长 为 l , 其 中 点 C 的 位 移 为。
( )ΔCV ql EI =424/() q3. 图 示 结 构A 截 面 的 转 角 为 A ϕ=Pa EI 22。
( )A4.图 示 桁 架 在 某 因 素 作 用 下 ,求CD 杆 的 转 角 时 , 其 虚 力 状 态的 广 义 单 位 力 如 图 所 示 : ()m k=1m =1 5. 图 示 桁 架 , EA = 常 数 , 在 力 P 作 用 下 , C 点 竖 向 位 移ΔCV Pa EA =1414./。
( )XXXXO二、选择题6.图 示 结 构 , 求 A 、B 两 点 相 对 线 位 移 时 , 虚 力 状 态 应 在 两 点 分 别 施 加 的 单 位 力 为 : ( ) A 。
竖 向 反 向 力 ; B 。
水 平 反 向 力 ; C 。
连 线 方 向 反 向 力 ; D 。
反 向 力 偶 。
AB7. 四 个 互 等 定 理 适 用 于 :( )A .刚 体 ;B .变 形 体;C .线 性 弹 性 体 系 ;D .非 线 性 体 系 。
8. 图 示 结 构 A 截 面 转 角(设 顺 时 针 为 正)为 :( )A .22Pa EI / ; B .−Pa EI 2/ ; C .5 ;42Pa EI /() D .-5 。
42Pa EI /()PA9.图 示 梁 A 点 的 竖 向 位 移 为 ( 向 下 为 正 ):() A . ; Pl EI 324/()B .;Pl EI 316/()CCCCC .5 ; 963Pl EI /()D .。
5483Pl EI /()P10. 图 示 结 构 (E I = 常 数), D 点 水 平 位 移 ( 向 右 为 正 ) 为 :( )A. ; (qa EI 43/)B. qa ; EI 46/()C. - qa ;EI 43/()D. - 。
结构力学_第六章_作业参考答案(整理_BY_TANG_Gui-he)

结构力学 第六章习题 参考答案TANG Gui-he6-1 试用积分法求图示刚架B 点的水平位移。
q解:(1) 实际状态下的内力AC 杆:22P qx M qlx =−+BC 杆:2P qlxM =(2) 虚拟状态下的内力AC 杆:M x = BC 杆:M x = (3)求Bx Δ200411()223 ()8l lp Bx M M ds qlx qx xdx qlx xdx EIEI EI qlΔ==+−+=∑∫∫∫i i→6-2 图示曲梁为圆弧形,EI =常数。
试求B 的水平位移。
1解:(1) 实际状态下的内力(sin 2p FM R R )θ=− (2) 虚拟状态下的内力1sin M R θ=i (3)求 Bx Δ/2312(sin )sin 22p Bx M M ds F F R R R Rd EIEIEIπθθθΔ==→−=∑∫∫ii i ()R6-3B AAB解:(1) 实际状态下的内力20sin()(1cos )p M qRd R qR θϕθϕθ=−=−∫i(2) 虚拟状态下的内力1sin M R θ=i(3)求 Bx Δ/2421(1cos )sin ()2p Bx M M ds FR qR R Rd EIEIEIπθθθΔ==←−=∑∫∫i i6-4 图示桁架各杆截面均为,32210m A −=×210 GPa E =,40 kN F =,。
试求:(a) C 点的竖向位移;(b) 角ADC 的改变量。
2 m d =F (kN)NP解: 实际状态下的桁架内力如上图。
(a )在C 点加上一个单位荷载,得到虚拟状态下的内力如上图。
11[2()(222322]22210)()N Np Cy F F l F d F d EAEA FdEAΔ==−−+↓++=+∑i i i i i i iNPNP(b)虚拟状态下的内力如上图。
11(22()(]4) ()N NpADCF F lF dEA EA dFEAϕ∠Δ==++−=∑ii i i增大6-6 试用图乘法求指定位移。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B
0.5
0.5
17/72
-0.8
4m
0 C
1
1.5
1.5
2.5
A
M1(m)
0.5
t1 t2
t1=25℃
C
t1=15℃
A
3m
2m 2m
-0.8
B 0.5
t1 t2
B
3m
受弯构件
t0
t1 t2 2
20
Δt 25 15 5 2
DCV
a t0Ni
a
Dt h
Mi
DCV a 20 (0.8) 5 2
第五章 结构的位移计算 作业详解
Last Edit: 2009.8.12
本章课后作业
2/72
【作业1】
等截面伸臂梁,在图示荷载作用下,求截面C的角位移jC
(郑版5-2)
10kN/m
40kN
EI
EI C
A
6m
B 2m
3/72
10kN/m
EI
A
6m
EI
A
6m
MP图(kN·m)
40
5
M1图(kN·m)
180
20
MP
(kN·m)
MDA 60 4 10 4 2 0 MDA 160
A
B
-70kN
11/72
1
C
2
4
D
E
6
-1
1
A
1
180 5C
M1(m) 6m
20
D
160
B
0
1 2m
60 E
-70kN
180
20
MP
(kN·m)
A
B
4m
2m
3)确定虚拟状态,并画出M1图 4)图乘
ΔCH
1 EI
[(4 160
1 2
4
2 3
2 3
4 20 2)
(20 2 1 2 2 2 2 51) 23 3
(1 180 6 2 6 1 6 60 1 6)]
2
32
3
1 (4 701) EA
1 (960 20 1800) 4 280
EI
EI
3900 EI
方向向右
12/72
【作业4】等截面刚架各杆截面均为矩形,截面高度 h = 0.25m, 材
60kN C
3m
3m
40kN B
A
3m
3m
5/72
60kN C
1)静定结构计算反力,并画出MP图
60kN
C
FCx FCx
3m
40kN
A 3m
B 3m
3m
FCy 40kN
FAx
A
FCy
FBx
B
FBy
FCx FBx FCy FBy
FAy 代入前面结果
CB部分 MC 0 FBx FBy AC部分 M A 0
Δj 1 [ 1 3100 2 2 1 3100 (1 1 2 2)
EI 2
33 2
3 33
1 380 (1 1 2 4) 1 680 2 4 1 680 1 4)
2
3 33 2
33 2
23
1 EI
( 1270) 3
1270 2.1104 3
0.02rad
Hale Waihona Puke 9/72【作业3】组合结构如图示荷载作用下,已知链杆BE的轴向刚度 EA=EI/4 (1/m2) 其余为受弯杆件,EI = 常数 求C点的水平位移
100
40kN
80 40 3 3 20
2
6
20/3kN
20
B
MP (kN·m)
100/3kN
100/3kN A
80/3kN
7/72
2)确定虚拟状态,并画出M1图
1
C
FCx
FCy
1
B
A
FAx FAy
FCx 3 FCy 3 1 0
FBx
FBy 1
FCx
FBx
2 9
FCy
FBy
1 9
1 FCx FCy
t1=25℃
C
t1=15℃ t1
t2
t2 t1
4m
A
3m
2m 2m
B
3m
14/72
DBH
t1 t2
A
3m
t1=25℃
C
t1=15℃
2m 2m
1
A
t2 t1
B
3m
1
4m
0.6
1)确定虚拟状态。
2)画出虚拟状态下的弯矩图,轴 力图(受弯构件在温度变化影响下, 必须考虑轴力。)
1
0.6
4
4
(m)
A
B
1
B
2
t1
520a ()
t2
B
3m
16/72
DCV
t1 t2
A
3m
t1=25℃
C
t1=15℃
2m 2m
C 1
A 0.5
t2 t1
B
3m
B 0.5
4m
-0.8
1)确定虚拟状态。
2)画出虚拟状态下的弯矩图,轴 力图(受弯构件在温度变化影响下, 必须考虑轴力。)
0 C
-0.8
1
1.5
1.5
2.5
A
M1(m)
DCH (郑版5-17)
C
30kN
2m
D
E
10kN/m
4m
A
B
6m
2m
10/72
C
30kN
D
E
10kN/m
A 60kN
40kN
B 0kN
6m
2m
70kN
4m
2m
1)求反力 EB 二力构件
2)画出MP图 计算MDC MDE MDA
180
5C 60
20
D
160
E
M DC 10 21 0 M DC 20 MDE 308 706 0 MDE 180
40kN
EI C B 2m
1 EI C B 2m
80
1) 确定虚拟状态
2)画出实际状态和虚拟状态的弯矩图
3)图乘
1 y1
1 2
6 80
2 3
2 3
6
45
1 2
70
2
y2
1 2
2801
80
y 1y1 2 y2 70 80 150
jC
150 EI
1
1
方向:顺时针。
4/72
【作业2】图乘法 已知各杆的EI = 2.1×104kN·m2,求图示刚架 铰C 左右截面的相对角位移。
FCx 6 FCy 3 1 0
FAx
2 9
FAy
1 9
8/72
2)确定虚拟状态,并画出M1图
C
4/3
2/3
2/3
4/3
1
100 80
60kN
C 80
D
100 E
2/9
B
M1
1/9
40kN
20
B
MP (kN·m)
100/3kN
A 2/9
1/9 3)图乘求解
20/3kN
A 80/3kN
100/3kN
1
15/72
DBH
1
A
t1 t2
A
3m
0.6
4m
1
4
4
(m)
t1=25℃
C
t1=15℃
2m 2m
0.6
受弯构件
t0
t1 t2 2
20
Δt 25 15 5 2
B
DB1H
a t0Ni
a
Dt h
Mi
DBH a 20[5 0.6 2 1 4]
a 5 (4 5 1 2 4 4)
0.25
a 5 (2 51.5 1
0.25
2
1.5 4 41 1) 2
300 100
300 9FBx 0 FBy FBx
考虑整体平衡
9
3
kN
40 3 60 3 FCx 6 FCy 3 0
FAx
20 3
kN
FAy
80 3
kN
6/72
1)静定结构计算反力,并画出MP图
MD
20 3
6
40 3
80
80
80
D
100 60kN C
E
ME
100 3
3
100
料线膨胀系数为a , 试求B的水平位移DBH,和横梁中点C的竖向位 移DCV。(郑版习题5-21)
t1=25℃
C
t1=15℃ t1
t2
t2 t1
4m
A
3m
2m 2m
B
3m
13/72
【作业4】等截面刚架各杆截面均为矩形,截面高度 h = 0.25m, 材
料线膨胀系数为a , 试求B的水平位移DBH,和横梁中点C的竖向位 移DCV。(郑版习题5-21)
