1.4.2正弦函数余弦函数的性质2(教学设计)
正弦函数余弦函数的性质教学设计

正弦函数余弦函数的性质教学设计教学设计题目:正弦函数和余弦函数的性质一、教学目标:1.理解正弦函数和余弦函数的定义和图像特点;2.掌握正弦函数和余弦函数的周期、振幅、相位等性质;3.能够利用正弦函数和余弦函数的性质解决实际问题。
二、教学内容:1.正弦函数和余弦函数的定义和图像特点;2.正弦函数和余弦函数的周期、振幅、相位等性质;3.正弦函数和余弦函数在实际问题中的应用。
三、教学流程:【导入】(5分钟)1.利用实物或幻灯片展示一个周期性的物体(如钟摆、运动员腕表);2.引导学生思考:你能观察出这个物体有哪些规律性的变化吗?3.引导学生回忆中学过的函数,提到是否有一些函数能够描述这种规律性的变化?【探究】(20分钟)1.引导学生尝试利用直尺、铅笔在纸上标出正弦函数和余弦函数的图像;2.让学生观察图像,找出正弦曲线和余弦曲线的相似之处和不同之处;3.分组讨论并总结正弦函数和余弦函数的定义和图像特点。
【归纳】(15分钟)1.教师引导学生对上述内容进行归纳总结,将正弦函数和余弦函数的定义和图像特点整理成导学笔记;2.教师对学生的总结进行点评,给予肯定和指导。
【深化】(15分钟)1.教师拿出钟表,让学生观察时针的运动;2.引导学生思考:时针的运动是否具有周期性?有什么规律性的变化?是否可以用函数来描述?3.通过时针的运动,引入正弦函数和余弦函数的周期概念。
【拓展】(20分钟)1.教师引导学生观察不同振幅、不同相位的正弦函数和余弦函数的图像;2.教师解释振幅和相位的概念,并给出具体的定义;3.引导学生思考振幅和相位对函数图像的影响。
【展示】(15分钟)1.教师运用课件或黑板展示正弦函数和余弦函数的定义和图像特点,以及周期、振幅、相位等性质;2.教师通过示例演示如何求解正弦函数和余弦函数的周期、振幅、相位等具体数值。
【练习】(30分钟)1.学生进行练习题的训练,巩固对于正弦函数和余弦函数性质的掌握;2.教师巡视指导,及时给予反馈和纠正。
1.4.2 正弦函数、余弦函数的性质(第1课时) 优秀教学设计

余弦函数也具有同样的性质,这种性质我们就称之为周期性。
二、 新课 讲解
1.周期函数定义:对于函数 f (x),如果存在一个非零常数 T,使得当 x 取 对于上述周
1.4.2 正弦、余弦函数的性质
【课题】:正弦、余弦函数的性质(1)
【三维目标】:
一、知识与技能
1.正弦函数的图象
2.余弦函数的图象
二、过程与方法
1.会用单位圆中的线段画出正弦函数的图象
2.用诱导公式画出余弦函数的图象
3.会用“五点法”画出正、余弦函数的图象
三、情感态度与价值观
1.培养学生的数形结合思想
(3)∵
2
sin(
1 2
x
6
2 )
2
sin
1 2
(x
4 )
6
2
sin(
1 2
x
6
)
∴自变量
x
只要并且至少要增加到
x
4
,函数
y
2
sin(
1 的值才能重复出现,
所以,函数
y
2
sin(
1 2
x
6
)
,
x
R
的周期是
4
.
例 3 : 下 列 三 角 函 数 的 周 期 : ① y 3cos x ② y sin 2x ( 3 )
y
2
sin(
人教版高中数学必修四《正弦函数余弦函数的性质》教学设计

1.4.2 正弦函数、余弦函数的性质2 教学设计一、教学目标知识目标:观察正弦、余弦函数图像得到正弦函数、余弦函数的性质,并灵活应用性质解题。
能力目标:培养分析、探索、类比和数形结合等数学思想方法在解决问题中的应用能力;增强自主探究的能力。
情感目标:学生亲身经历数学的研究过程,感受数学的魅力,享受成功的喜悦。
二、教材分析本节课是《数学必修4》的第一章三角函数的内容,是学习了正弦函数、余弦函数的图像和周期性之后,进一步学习正弦函数、余弦函数的性质。
该内容共两课时,这里讲的是第二课时。
正弦、余弦函数的图像和性质是三角函数里的重点内容,也是高考热点考察的内容之一。
通过本节课的学习,不仅可以培养学生的观察能力,分析问题、解决问题的能力,而且渗透了数形结合、类比、分类讨论等重要的数学思想方法,为以后、为高考的学习打下基础。
三、教学重难点教学重点: 正弦函数、余弦函数的单调性、最值。
教学难点: 确定函数的单调区间,应该对单调性的应用进行多层次练习,在练习中掌握正弦、余弦函数的性质及应用。
四、教学过程 复习引入: (1)单调性:正弦曲线下面是正弦函数sin ()y x x R =∈图像的一部分:-11y x-6π-5π6π5π-4π-3π-2π-π4π3π2ππf x () = sin x ()sin ()y x x R =∈在)](22,22[Z k k k ∈++-ππππ上单调增,函数值从-1增加到1,在)](223,22[Z k k k ∈++ππππ上单调减,函数值从1减小到-1. 余弦曲线 cos ()y x x R =∈cos ()y x x R =∈在)](2,2[Z k k k ∈+-πππ上单调增,函数值从-1增加到1,在)](2,2[Z k k k ∈+πππ上单调减,函数值从1减小到-1.(2)最值:正弦函数R x x y ∈=,sin ①当且仅当Z k k x ∈+=,22ππ时,取得最大值1②当且仅当Z k k x ∈+-=,22ππ时,取得最小值1-余弦函数R x x y ∈=,cos①当且仅当Z k k x ∈=,2π时,取得最大值1 ②当且仅当Z k k x ∈+=,2ππ时,取得最小值1- 应用一: 正、余弦函数的最值问题例1.以下函数有最大、最小值吗?如果有,求出最大值、最小值,并写出取最大、最小值时的自变量 x 的集合.练习1.求函数y=-3sin2x 的最大最小值,并写出取最大最小值时自变量x 的集合 解:令2t x =,函数sin y t =max 3(1)3y =-⨯-=.4x k ππ=-+Rx x y ∈-=,sin 3)2(Rx x y ∈+=,1cos )1(此时 得:因此 此时x 的取值集合是同理此时x 的取值集合是 方法总结:对形如类型的函数求最值时,主要是利用三角函数的图象求解,在解题时注意函数的定义域。
正弦函数余弦函数的性质教学设计
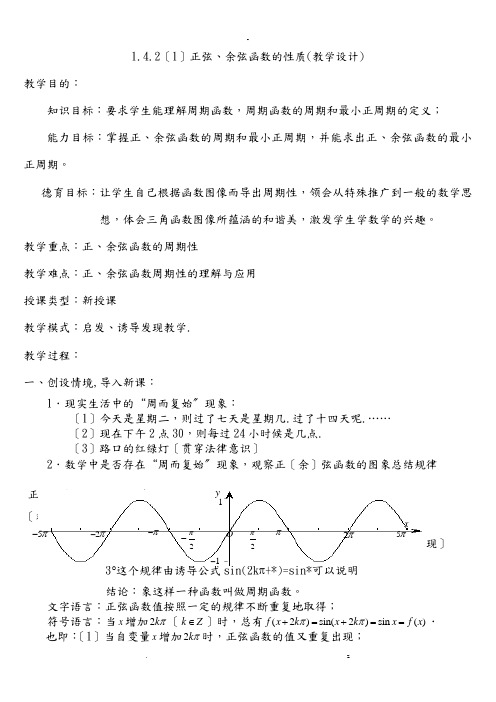
1.4.2〔1〕正弦、余弦函数的性质(教学设计)教学目的:知识目标:要求学生能理解周期函数,周期函数的周期和最小正周期的定义; 能力目标:掌握正、余弦函数的周期和最小正周期,并能求出正、余弦函数的最小正周期。
德育目标:让学生自己根据函数图像而导出周期性,领会从特殊推广到一般的数学思想,体会三角函数图像所蕴涵的和谐美,激发学生学数学的兴趣。
教学重点:正、余弦函数的周期性教学难点:正、余弦函数周期性的理解与应用 授课类型:新授课教学模式:启发、诱导发现教学. 教学过程:一、创设情境,导入新课:1.现实生活中的“周而复始〞现象:〔1〕今天是星期二,则过了七天是星期几.过了十四天呢.……〔2〕现在下午2点30,则每过24小时候是几点. 〔3〕路口的红绿灯〔贯穿法律意识〕2.数学中是否存在“周而复始〞现象,观察正〔余〕弦函数的图象总结规律正弦函数()sin f x x =性质如下: 〔观察图象〕 1︒正弦函数的图象是有规律不断重复出现的;2︒规律是:每隔2π重复出现一次〔或者说每隔2k π,k ∈Z 重复出现〕 3︒这个规律由诱导公式sin(2k π+*)=sin*可以说明结论:象这样一种函数叫做周期函数。
文字语言:正弦函数值按照一定的规律不断重复地取得;符号语言:当x 增加2k π〔k Z ∈〕时,总有(2)sin(2)sin ()f x k x k x f x ππ+=+==. 也即:〔1〕当自变量x 增加2k π时,正弦函数的值又重复出现;––π2π2π-2π5ππ-2π-5π-Oxy 11-〔2〕对于定义域的任意x ,sin(2)sin x k x π+=恒成立。
余弦函数也具有同样的性质,这种性质我们就称之为周期性。
二、师生互动,新课讲解:1.周期函数定义:对于函数f (*),如果存在一个非零常数T ,使得当*取定义域的每一个值时,都有:f (*+T)=f (*)则函数f (*)就叫做周期函数,非零常数T 叫做这个函数的周期。
1.4.2正弦函数、余弦函数的性质课件-高一上学期数学人教A版必修4

此时x=2kπ-
,k∈Z.
[0,2]
4.若cos x=m-1有意义,则m的取值范围是________.
因为-1≤cos x≤1
要使cos x=m-1有意义,须有-1≤m-1≤1,
所以0≤m≤2.
新知探究
[-1,1]
[-1,1]
思考:y=sin x和y=cos x在区间(m,
n)(其中0<m<n<2π)上都是减函数,
你能确定m的最小值、n的最大值吗?
提示:由正弦函数和余弦函数的单调
性可知m= ,n=π.
题型突破
典例深度剖析
重点多维探究
题型一
[例1]
正弦函数、余弦函数的单调性
(1)函数y=cos x在区间[-π,a]上为增函数,则
a的取值范围是________.
思路点拨
确定a的范围 → y=cos x在区间[-π,a]上为增函数 → y=
5
4
23
−
5
<cos
=cos
π
.
4
x在[0,π]上是减函数,
,
17
−
4
π
)
4
.
三角函数值大小比较的策略
解
题
策
略
1利用诱导公式,对于正弦函数来说,一般将两个角转
化到
− ,
2 2
或
3
,
2 2
内;对于余弦函数来说,一般将两个
角转化到[-π,0]或[0,π]内.
2不同名的函数化为同名的函数.
所以函数y=cos2x+2sin x-2,x∈R的值域为[-4,0].
[例3]
(2)已知函数f(x)=asin
1.4.2(2)正弦_余弦函数的性质(奇偶性、单调性)上课用(全)

关键:借助y sin z的单调性。
1 思考:函数y sin( x ), x [2 ,2 ]的 2 3 单调递减区间。
小
结:
奇偶性 [ 单调性(单调区间)
+2k, +2k],kZ 单调递增 2 2 3 [ +2k, +2k],kZ 单调递减 2 2
例3 下列函数有最大值、最小值吗?如果有,请 写出取最大值、最小值时的自变量x的集合, 并说出最大值、最小值分别是什么?
(1)y= cosx +1, x∈R
(2)y= –3sin2x, x∈R
例4 利用三角函数的单调性,比较下列各组数的大小: (1) sin( ) 与 sin( ) 18 10 解: 2 10 18 2 又 y=sinx 在[ , ] 上是增函数
正弦、余弦函数的奇偶性:
y
1 -4 -3 -2 -
o
-1
2
3
4
5
6
x
sin(-x)= - sinx (xR)
y=sinx (xR) 是奇函数 定义域关于原点对称
cos(-x)= cosx (xR)
y
1 -4 -3 -2 -
y=cosx (xR) 是偶函数
o
-1
5 2
-2
3 2
-
2
o
-1
2
3 2
2
5 2
x
3
7 2
4
x
cosx
- -1
…
2
…
0
1
…
2
…
正弦函数余弦函数的性质2(教学设计)

1.4.2(2)正弦、余弦函数的性质(教学设计)教学目的:知识目标:要求学生能理解三角函数的奇、偶性和单调性,最值,值域的求法;能力目标:掌握正、余弦函数的奇、偶性的判断,并能求出正、余弦函数的单调区间。
德育目标:激发学生学习数学的兴趣和积极性,陶冶学生的情操,培养学生坚忍不拔的意志,实事求是的科学学习态度和勇于创新的精神。
教学重点:正、余弦函数单调性和最值;教学难点:正、余弦函数单调性的理解与应用授课类型:新授课教学模式:启发、诱导发现教学.教学过程:一、复习回顾,导入新课:1、一般结论:函数sin()y A x b ωϕ=++及函数cos()y A x b ωϕ=++,x R ∈的周期2||T πω=2、y=sinx 为奇函数,图象关于原点对称;y=cosx 是偶函数,图象关于y 轴对称。
3、正弦函数y=sinx 每一个闭区间[-2π+2k π,2π+2k π](k ∈Z )上都是增函数,其值从-1增大到1;在每一个闭区间[2π+2k π,23π+2k π](k ∈Z )上都是减函数,其值从1减小到-1. 余弦函数y=cosx 在每一个闭区间[(2k -1)π,2k π](k ∈Z )上都是增函数,其值从-1增加到1;在每一个闭区间[2k π,(2k +1)π](k ∈Z )上都是减函数,其值从1减小到-1.4、正弦函数y=sinx 当x=22k ππ+时取最大值1,当x=322k ππ+时取最小值-1。
余弦函数y=cosx 当x=2k π时取最大值1,当x=2k ππ+最取最小值-1。
(以上k Z ∈) 二、师生互动,新课讲解:1、对称轴观察正、余弦函数的图形,可知(1)y=sinx 的对称轴为x=2ππ+k k ∈Z(2)y=cosx 的对称轴为x=πk k ∈Z特别提示:当x 为对称轴时,三角函数达到最大(小)值。
2、对称中心观察正、余弦函数的图形,可知(1)y=sinx 的对称中心(,0)k π k ∈Z(2)y=cosx 的对称中心(,0)2k ππ+k ∈Z例1:写出函数x y 2sin 3=的对称轴;变式训练1:)4sin(π+=x y 的一条对称轴是( C )(A) x 轴, (B) y 轴, (C) 直线4π=x , (D) 直线4π-=x例2:(课本P39例5)求函数y=sin()32π+x ,x ]2,2[ππ-∈的单调区间?变式训练2:求函数y= -sinx 的单调递增区间。
正弦函数余弦函数性质2教案

正弦函数余弦函数性质2教案教案:正弦函数余弦函数性质一、教学内容:正弦函数与余弦函数性质2二、教学目标:1.理解正弦函数与余弦函数的周期性;2.掌握正弦函数与余弦函数的奇偶性;3.运用正弦函数与余弦函数的性质解决具体问题。
三、教学重难点:1.正弦函数与余弦函数的周期性;2.正弦函数与余弦函数的奇偶性。
四、教学方法:1.讲解法;2.举例法;3.练习与讨论相结合。
五、教学准备:课本、教学课件、黑板、白板笔、多媒体设备。
六、教学过程:Step 1 理解正弦函数与余弦函数的周期性(15分钟)1.引导学生回顾正弦函数与余弦函数的图像,并解释周期的概念。
2.将周期性进行形象化的说明,告诉学生周期是指在一定的区间内,函数的图像会重复出现。
3.让学生观察正弦函数与余弦函数的图像,指出周期是2π,即在区间[0,2π)内,正弦函数和余弦函数的图像会重复出现。
Step 2 掌握正弦函数与余弦函数的奇偶性(20分钟)1.针对正弦函数与余弦函数的性质,引导学生回忆奇函数与偶函数的性质。
2.提出正弦函数的奇函数性质和余弦函数的偶函数性质,并用图像进行说明。
3.引导学生通过改变x的正负值来验证正弦函数和余弦函数的奇偶性。
Step 3 运用正弦函数与余弦函数的性质解决具体问题(25分钟)1.指导学生通过观察正弦函数与余弦函数的图像,得出一些结论。
例:sin(x + π/2) = cosx,sin(x - π/2) = - cosx2.引导学生应用这些结论解决具体问题。
例:已知正弦函数的一个周期为2π,求cos(x-π/2)的一个周期。
Step 4 练习与讨论(25分钟)1.分发练习题给学生进行独立解答。
2.教师巡视指导学生解题过程,并提供必要的帮助。
3.讨论答案,解析题目的解题方法和思路。
Step 5 总结与拓展(15分钟)1.总结正弦函数与余弦函数的性质,并强调正弦函数的奇函数性质、余弦函数的偶函数性质以及周期为2π。
2.提醒学生要注意在应用正弦函数与余弦函数的性质时,要根据题目考察的具体内容进行灵活运用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.4.2(2)正弦、余弦函数的性质(教学设计)
教学目的:
知识目标:要求学生能理解三角函数的奇、偶性和单调性,最值,值域的求法;
能力目标:掌握正、余弦函数的奇、偶性的判断,并能求出正、余弦函数的单调区间。
德育目标:激发学生学习数学的兴趣和积极性,陶冶学生的情操,培养学生坚忍不拔的意志,实事求是的科学学
习态度和勇于创新的精神。
教学重点:正、余弦函数单调性和最值;
教学难点:正、余弦函数单调性的理解与应用
授课类型:新授课
教学模式:启发、诱导发现教学.
教学过程:
一、复习回顾,导入新课:
1、一般结论:函数sin()y A x b ωϕ=++及函数cos()y A x b ωϕ=++,x R ∈的周期2||T πω=
2、y=sinx 为奇函数,图象关于原点对称;y=cosx 是偶函数,图象关于y 轴对称。
3、正弦函数y=sinx 每一个闭区间[-
2π+2k π,2π+2k π](k ∈Z )上都是增函数,其值从-1增大到1;在每一个闭区间[2
π+2k π,23π+2k π](k ∈Z )上都是减函数,其值从1减小到-1. 余弦函数y=cosx 在每一个闭区间[(2k -1)π,2k π](k ∈Z )上都是增函数,其值从-1增加到1;在每一个闭区间[2k π,(2k +1)π](k ∈Z )上都是减函数,其值从1减小到-1.
4、正弦函数y=sinx 当x=22k ππ+时取最大值1,当x=
322
k ππ+时取最小值-1。
余弦函数y=cosx 当x=2k π时取最大值1,当x=2k ππ+最取最小值-1。
(以上k Z ∈) 二、师生互动,新课讲解:
1、对称轴
观察正、余弦函数的图形,可知
(1)y=sinx 的对称轴为x=2π
π+k k ∈Z
(2)y=cosx 的对称轴为x=πk k ∈Z
特别提示:当x 为对称轴时,三角函数达到最大(小)值。
2、对称中心
观察正、余弦函数的图形,可知
(1)y=sinx 的对称中心(,0)k π k ∈Z
(2)y=cosx 的对称中心(,0)2k π
π+
k ∈Z
例1:写出函数x y 2sin 3=的对称轴;
变式训练1:)4sin(π
+=x y 的一条对称轴是( C )
(A) x 轴, (B) y 轴, (C) 直线4π=
x , (D) 直线4π-=x
例2:(课本P39例5)求函数y=sin()32π
+x
,x ]2,2[ππ-∈的单调区间?
变式训练2:求函数y= -sinx 的单调递增区间。
例3:求函数y=1-cos 3x
的单调递减区间。
变式训练3:求函数y= 2-sin2x 的单调递增区间。
例4:(tb0135503)求下列函数的单调区间,并求出它们的最值:
(1) y=sin(3x-3π
);(2) y= -2cos(2x+3π
)
变式训练4:求函数y=sin (-2x )的单调递增区间。
例5:作出下列函数的图象,若是周期函数,请写出它的周期
(1)y=|sinx| (2)y=|cosx|
变式训练5:作出下列函数的图象,若是周期函数,请写出它的周期
(1)y=sin|x| (2)y=cos|x|
例6:已知函数)42sin(3π
-=x y ,用“五点法”画出函数在长度为一个周期的闭区间上的图象;
课堂巩固练习(课本P40练习NO :4;5;6)
三、课堂小结,巩固反思:
1、会求三角函数的最小正周期、会判断函数的奇偶性,会求单调区间,会求最值,以及会判断对称轴与对称中心。
四、课时必记:
1、对称轴
观察正、余弦函数的图形,可知
(1)y=sinx 的对称轴为x=2π
π+k k ∈Z
(2)y=cosx 的对称轴为x=πk k ∈Z
特别提示:当x 为对称轴时,三角函数达到最大(小)值。
2、对称中心
观察正、余弦函数的图形,可知
(1)y=sinx 的对称中心(,0)k π k ∈Z
(2)y=cosx 的对称中心(,0)2k π
π+
k ∈Z
五、[分层作业]
A 组:
1.观察函数sin y x =的图象,它的一条对称轴为 ( B )
A . 0x =
B . 2x π
= C . x π= D . 2x π=
2.函数sin(2)4y x π
=+的最小值为 ,相应的x 的值是 .
3、已知函数3sin )(+⋅=x m x f 的最大值是7,则常数=m ____________。
4、求下列函数的最值,并求使函数取得最值时的自变量x 的集合。
(1)x y cos 21
1-= (2))322sin(3π
-=x y
5、求下列函数的单调区间:
(1)sin(2)4y x π
=+ (2)3cos 21y x =+ (3)y=cos(-2x) (4)y= -cosx
B 组:
1、(tb3806301)下列四个函数中,在),2(ππ
上为增函数的是( )
(A )y=sinx (B) y=sin2x (C)y=cosx (D)y=cos2x
2、函数y ( )
A . 5[,]66π
π
B . 5[2,2]()66k k k Z ππ
ππ++∈
C . 57[2,2]()66k k k Z π
π
ππ++∈ D . 513[2,2]()66k k k Z π
π
ππ++∈
3、已知函数2sin(2)3y x π
=-,用“五点法”画出函数在长度为一个周期的闭区间上的图象;
C 组:
1、(课本P46习题1.4B 组 NO :3)
2、在(0,2)π内使sin cos x x >成立的x 的取值范围是 ( ) A 5(,)(,)424π
π
ππ⋃ B (,)4π
π C 5(,)44π
π D 53(,)(,)442πππ
π⋃
【分析】(解法一)在单位圆中用正弦线、余弦线比较即等C (解法二)在同一坐标系内作出sin ,cos y x y x ==的图象,观察它们的位置关系,选C (解法三)取x π=,要满足sin cos x x >,对照选项,排除后选C。
