数学高考(理)二轮专题复习检测:第一部分专题五 立体几何与空间向量13Word版含答案
数学高三立体几何与空间向量专题复习检测(含答案)

数学高三立体几何与空间向量专题复习检测(含答案)平面几何是3维欧氏空间的几何的传统称号,下面是平面几何与空间向量专题温习检测,请考生练习。
一、选择题1.(2021武汉调研)一个几何体的三视图如下图,那么该几何体的直观图可以是()解析 A、B、C与仰望图不符.答案 D2.将长方体截去一个四棱锥,失掉的几何体如下图,那么该几何体的侧(左)视图为()解析抓住其一条对角线被遮住应为虚线,可知正确答案在C,D中,又结合直观图知,D正确.答案 D3.(2021安徽卷)一个多面体的三视图如下图,那么该多面体的外表积为()A.21+3B.18+3C.21D.18解析由三视图知,该多面体是由正方体割去两个角所成的图形,如下图,那么S=S正方体-2S三棱锥侧+2S三棱锥底=24-231211+234(2)2=21+3.答案 A4.S,A,B,C是球O外表上的点,SA平面ABCD,ABBC,SA=AB=1,BC=2,那么球O的外表积等于()A.4B.3C.2解析如下图,由ABBC知,AC为过A,B,C,D四点小圆直径,所以ADDC.又SA平面ABCD,设SB1C1D1-ABCD为SA,AB,BC为棱长结构的长方体,得体对角线长为12+12+22=2R,所以R=1,球O的外表积S=4.故选A.答案 A5.(2021湖南卷)一块石材表示的几何体的三视图如下图.将该石材切削、打磨,加工成球,那么能失掉的最大球的半径等于()A.1B.2C.3D.4解析由三视图可得原石材为如下图的直三棱柱A1B1C1-ABC,且AB=8,BC=6,BB1=12.假定要失掉半径最大的球,那么此球与平面A1B1BA,BCC1B1,ACC1A1相切,故此时球的半径与△ABC内切圆的半径相等,故半径r=6+8-102=2.应选B.答案 B6.点A,B,C,D均在同一球面上,其中△ABC是正三角形,AD平面ABC,AD=2AB=6,那么该球的体积为()A.323B.48C.643D.163解析如下图,O1为三角形ABC的外心,过O做OEAD,OO1面ABC,AO1=33AB=3.∵OD=O A,E为DA的中点.∵AD面ABC,AD∥OO1,EO=AO1=3.DO=DE2+OE2=23.R=DO= 23.V=43(23)3=323.答案 A二、填空题7.某四棱锥的三视图如下图,该四棱锥的体积是________. 解析由三视图可知,四棱锥的高为2,底面为直角梯形ABCD.其中DC=2,AB=3,BC=3,所以四棱锥的体积为132+3322=533. 答案 5338.如图,在三棱柱A1B1C1-ABC中,D,E,F区分是AB,AC,AA1的中点,设三棱锥F-ADE的体积为V1,三棱柱A1B1C1-ABC 的体积为V2,那么V1V2=________.解析设三棱柱A1B1C1-ABC的高为h,底面三角形ABC的面积为S,那么V1=1314S12h=124Sh=124V2,即V1V2=124. 答案 1249.在四面体ABCD中,AB=CD=6,AC=BD=4,AD=BC=5,那么四面体ABCD的外接球的外表积为________.解析结构一个长方体,使得它的三条面对角线区分为4、5、6,设长方体的三条边区分为x,y,z,那么x2+y2+z2=772,而长方体的外接球就是四面体的外接球,所以S=4R2=772. 答案 772三、解答题10.以下三个图中,左边是一个正方体截去一个角后所得多面体的直观图.左边两个是其正(主)视图和侧(左)视图. (1)请在正(主)视图的下方,依照画三视图的要求画出该多面体的仰望图(不要求表达作图进程).(2)求该多面体的体积(尺寸如图).解 (1)作出仰望图如下图.(2)依题意,该多面体是由一个正方体(ABCD-A1B1C1D1)截去一个三棱锥(E-A1B1D1)失掉的,所以截去的三棱锥体积VE-A1B1D1=13S△A1B1D1A1E=1312221=23,正方体体积V正方体AC1=23=8,所以所求多面体的体积V=8-23=223.11.(2021安徽卷)如图,四棱柱ABCD-A1B1C1D1中,A1A底面ABCD.四边形ABCD为梯形,AD∥BC,且AD=2BC.过 A1,C,D三点的平面记为,BB1与的交点为Q.(1)证明:Q为BB1的中点;(2)求此四棱柱被平面所分红上下两局部的体积之比.解 (1)证明:由于BQ∥AA1,BC∥AD,BCBQ=B,ADAA1=A,所以平面QBC∥平面A1AD.从而平面A1CD与这两个平面的交线相互平行,即QC∥A1D.故△QBC与△A1AD的对应边相互平行,于是△QBC∽△A1AD.所以BQBB1=BQAA1=BCAD=12,即Q为BB1的中点.(2)如图,衔接QA,QD.设AA1=h,梯形ABCD的高为d,四棱柱被平面所分红上下两局部的体积区分为V上和V下,BC=a,那么AD=2a.VQ-A1AD=13122ahd=13ahd,VQ-ABCD=13a+2a2d12h=14ahd,所以V下=VQ-A1AD+VQ-ABCD=712ahd,又V四棱柱A1B1C1D1-ABCD=32ahd,所以V上=V四棱柱A1B1C1D1-ABCD-V下=32ahd-712ahd=1112ahd.故V上V下=117.B级才干提高组1.(2021北京卷)在空间直角坐标系Oxyz中,A(2,0,0),B(2,2,0),C(0,2,0),D(1,1,2).假定S1,S2,S3区分是三棱锥D-ABC在xOy,yOz,zOx坐标平面上的正投影图形的面积,那么()A.S1=S2=S3B.S2=S1且S2S3C.S3=S1且S3 S2D.S3=S2且S3S1解析作出三棱锥在三个坐标平面上的正投影,计算三角形的面积.如下图,△ABC为三棱锥在坐标平面xOy上的正投影,所以S1=1222=2.三棱锥在坐标平面yOz上的正投影与△DE F(E,F 区分为OA,BC的中点)全等,所以S2=1222=2.三棱锥在坐标平面xOz上的正投影与△DGH(G,H区分为AB,OC 的中点)全等,所以S3=1222=2.所以S2=S3且S1S3.应选D. 答案 D2.(2021山东卷)三棱锥P-ABC中,D,E区分为PB,PC的中点,记三棱锥D-ABE的体积为V1,P-ABC的体积为V2,那么V1V2=________.解析由于VP-ABE=VC-ABE,所以VP-ABE=12VP-ABC,又因VD-ABE=12VP-ABE,所以VD-ABE=14VP-ABC,V1V2=14.答案 143.(理)(2021课标全国卷Ⅱ)如图,四棱锥P-ABCD中,底面ABCD为矩形,PA平面ABCD,E为PD的中点.(1)证明:PB∥平面AEC;(2)设二面角D-AE-C为60,AP=1,AD=3,求三棱锥E-ACD的体积.解 (1)衔接BD交AC于点O,衔接EO.由于ABCD为矩形,所以O为BD的中点.又E为PD的中点,所以EO∥PB.EO平面AEC,PB平面AEC,所以PB∥平面AEC.(2)由于PA平面ABCD,ABCD为矩形,所以AB,AD,AP两两垂直.如图,以A为坐标原点,AB的方向为x轴的正方向,|PA|为单位长,树立空间直角坐标系A-xyz.那么D(0,3,0),E0,32,12, AE=0,32,12.设B(m,0,0)(m0),那么C(m,3,0),AC=(m,3,0),设n1=(x,y,z)为平面ACE的法向量,那么n1AC=0,n1AE=0,即mx+3y=0,32y+12z=0,可取n1=3m,-1,3.又n2=(1,0,0)为平面DAE的法向量,由题设|cos〈n1,n2〉|=12,即 33+4m2=12,解得m=32.由于E为PD的中点,所以三棱锥E-ACD的高为12.三棱锥E-ACD的体积V=131233212=38.3.(文)如图,在Rt△ABC中,AB=BC=4,点E在线段AB上.过点E作EF∥BC交AC于点F,将△AEF沿EF折起到△PEF 的位置(点A与P重合),使得PEB=30.(1)求证:EF(2)试问:当点E在何处时,四棱锥P-EFCB的正面PEB的面积最大?并求此时四棱锥P-EFCB的体积.解 (1)证明:∵AB=BC,BCAB,又∵EF∥BC,EFAB,即EFBE,EFPE.又BEPE=E,EF平面PBE,EFPB.(2)设BE=x,PE=y,那么x+y=4.S△PEB=12BEPEsinPEB=14xy14x+y22=1.当且仅当x=y=2时,S△PEB的面积最大.此时,BE=PE=2.由(1)知EF平面PBE,平面PBE平面EFCB,在平面PBE中,作POBE于O,那么PO平面EFCB.即PO为四棱锥P-EFCB的高.又PO=PEsin30=212=1.S梯形EFCB =12(2+4)2=6.VP-BCFE=1361=2.平面几何与空间向量专题温习检测及答案的全部内容就是这些,查字典数学网预祝考生可以取得更好的效果。
2022届高考数学(理)二轮专题复习课时作业:专题五 立体几何 (十三) Word版含答案

课时作业(十三) 空间向量与立体几何1.如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2a,F为CD的中点.(1)求证:AF∥平面BCE;(2)推断平面BCE与平面CDE的位置关系,并证明你的结论.解析:建立如图所示的空间直角坐标系A-xyz,则A(0,0,0),C(2a,0,0),B(0,0,a),D(a,3a,0),E(a,3a,2a).由于F为CD的中点,所以F⎝⎛⎭⎪⎫32a,32a,0.(1)证明:AF→=⎝⎛⎭⎪⎫32a,32a,0,BE→=(a,3a,a),BC→=(2a,0,-a).由于AF→=12(BE→+BC→),AF⊄平面BCE,所以AF∥平面BCE.(2)平面BCE⊥平面CDE.证明如下:由于AF→=⎝⎛⎭⎪⎫32a,32a,0,CD→=(-a,3a,0),ED→=(0,0,-2a),所以AF→·CD→=0,A F→·ED→=0,所以AF→⊥CD→,AF→⊥ED→.所以AF⊥平面CDE,又AF∥平面BCE,所以平面BCE⊥平面CDE.2.(2021·广西南宁、梧州摸底联考)如图,已知四棱锥P-ABCD,底面ABCD为菱形,且∠DAB=60°,△PAB是边长为a的正三角形,且平面PAB⊥平面ABCD,已知点M是PD的中点.(1)证明:PB∥平面AMC;(2)求直线BD与平面AMC所成角的正弦值.解析:(1)证明:连接BD交AC于点O,连接OM,由于四边形ABCD为菱形,OB=OD,又M为PD的中点,所以OM∥PB.由PB⊄平面AMC,OM⊂平面AMC,所以PB∥平面ACM.(2)取AB的中点N,连接PN,ND,则∠AND=90°,分别以NB,ND,NP为x轴、y轴、z轴建立空间直角坐标系N-xyz,则B⎝⎛⎭⎪⎫a2,0,0,C⎝⎛⎭⎪⎫a,32a,0,A⎝⎛⎭⎪⎫-a2,0,0,D⎝⎛⎭⎪⎫0,32a,0,P⎝⎛⎭⎪⎫0,0,32a,M⎝⎛⎭⎪⎫0,34a,34a,则AC→=⎝⎛⎭⎪⎫32a,32a,0,AM→=⎝⎛⎭⎪⎫a2,34a,34a.设平面AMC的法向量为n=(x,y,z),则⎩⎪⎨⎪⎧32ax+32ay=0,a2x+34ay+34az=0,令y=3,则x=-1,z=-33,即n=⎝⎛⎭⎪⎫-1,3,-33.又BD→=⎝⎛⎭⎪⎫-a2,32a,0,设直线BD与n所成的角为θ,则cosθ=n·BD→|n||BD→|=23913,故直线BD与平面AMC所成角的正弦值为23913.3.(2021·河北石家庄模拟)如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AD∥BC,CD ⊥BC ,AD =2,AB =BC =3,PA =4,M 为AD 的中点,N 为PC 上一点,且PC =3PN .(1)求证:MN ∥平面PAB ; (2)求二面角P AN M 的余弦值. 解析:(1)证明:在平面PBC 内作NH ∥BC 交PB 于点H ,连接AH , 在△PBC 中,NH ∥BC ,且NH =13BC =1,AM =12AD =1.∵AD ∥BC ,∴NH ∥AM ,且NH =AM ,∴四边形AMNH 为平行四边形,∴MN ∥AH . ∵AH ⊂平面PAB ,MN ⊄平面PAB ,∴MN ∥平面PAB . (2)解:在平面ABCD 内作AE ∥CD 交BC 于E ,则AE ⊥AD .分别以AE ,AD ,AP 所在直线为x 轴、y 轴、z 轴建立空间直角坐标系A -xyz ,则P (0,0,4),M (0,1,0),C (22,2,0),N ⎝⎛⎭⎪⎫223,23,83. 设平面AMN 的法向量m =(x ,y ,z ),AM →=(0,1,0),AN →=⎝ ⎛⎭⎪⎫223,23,83,则⎩⎪⎨⎪⎧y =0,223x +23y +83z =0,取m =⎝⎛⎭⎪⎫2,0,-12.设平面PAN 的法向量n =(x ,y ,z ),AP →=(0,0,4),AN →=⎝ ⎛⎭⎪⎫223,23,83,则⎩⎪⎨⎪⎧4z =0,223x +23y +83z =0,取n =(1,-2,0),则cos 〈m ,n 〉=m·n |m ||n |=269.故二面角P AN M 的余弦值为269.4.(2021·山东卷)如图,几何体是圆柱的一部分,它是由矩形ABCD (及其内部)以AB 边所在直线为旋转轴旋转120°得到的,G 是DF 的中点.(1)设P 是CE 上的一点,且AP ⊥BE ,求∠CBP 的大小; (2)当AB =3,AD =2时,求二面角E AG C 的大小.解析:(1)由于AP ⊥BE ,AB ⊥BE ,AB ,AP ⊂平面ABP ,AB ∩AP =A ,所以BE ⊥平面ABP . 又BP ⊂平面ABP ,所以BE ⊥BP . 又∠EBC =120°,所以∠CBP =30°.(2)方法一:如图,取EC 的中点H ,连接EH ,GH ,CH .由于∠EBC =120°, 所以四边形BEHC 为菱形,所以AE =GE =AC =GC =32+22=13. 取AG 的中点M ,连接EM ,CM ,EC , 则EM ⊥AG ,CM ⊥AG ,所以∠EMC 为所求二面角的平面角.又AM =1,所以EM =CM =13-1=2 3. 在△BEC 中,由于∠EBC =120°,所以二面角CEMN的正弦值为10521.(3)依题意,设AH=h(0≤h≤4),则H(0,0,h),进而可得NH→=(-1,-2,h),BE→=(-2,2,2).由已知,得|cos〈NH→,BE→〉|=|NH→·BE→||NH→||BE→|=|2h-2|h2+5×23=721,整理得10h2-21h+8=0,解得h=85,或h=12.所以,线段AH的长为85或12.6.(2021·湖北孝感联考)如图,四棱锥P-ABCD的底面为直角梯形,AD∥BC,AD=2BC=2,BC⊥DC,∠BAD=60°,平面PAD⊥底面ABCD,E为AD的中点,△PAD为正三角形,M是棱PC上的一点(异于端点).(1)若M为PC的中点,求证:PA∥平面BME;(2)是否存在点M,使二面角MBED的大小为30°.若存在,求出点M的位置;若不存在,说明理由.解析:(1)证明:如图,连接AC交BE于点F,连接CE.由题意知BC∥AE,且BC=AE,故四边形ABCE为平行四边形,∴F为AC的中点,在△PAC中,又由M为PC的中点,得MF∥PA.又MF⊂平面BME,PA⊄平面BME,∴PA∥平面BME.(2)连接PE,则由题意知PE⊥平面ABCD.故以E为坐标原点建立如图所示空间直角坐标系E-xyz,则E(0,0,0),P(0,0,3),B(3,0,0),C(3,-1,0).设PM→=λPC→=(0<λ<1),则M(3λ,-λ,3(1-λ)).∴EM→=(3λ,-λ,3(1-λ)),EB→=(3,0,0).取平面DBE的法向量n1=(0,0,1),设平面BME的法向量n2=(x,y,z),则由⎩⎨⎧n2·EM→=0,n2·EB→=0得⎩⎨⎧3λx-λy+31-λz=0,3x=0.令y=3,得n2=⎝⎛⎭⎪⎫0,3,λ1-λ.又由⎪⎪⎪⎪⎪⎪n1·n2|n1||n2|=cos30°,得λ=34,即M⎝⎛⎭⎪⎫334,-34,34.故存在点M满足要求,且M为棱PC上靠近端点C的四等分点.。
立体几何与空间向量综合测试卷(新高考专用)(解析版)-高中数学

立体几何与空间向量综合测试卷(考试时间:120分钟;满分:150分)注意事项:1.本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第I卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。
写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
第I卷(选择题)一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合要求的。
1.(5分)(2024·湖南·三模)已知m,n是两条不重合的直线,α,β是两个不重合的平面,下列命题正确的是()A.若m//α,n//β,α//β,则m//nB.若m⊂α,n⊂α,m//β,n//β,则α//βC.若m⊥α,m//n,α⊥β,则n⊥βD.若m⊥α,n⊥β,m⊥n,则α⊥β【解题思路】利用空间线线的关系、面面平行、面面垂直的判定定理和性质逐一判定各选项,即可得出结论.【解答过程】对于A,若n//β,α//β,则n//α或n⊂α,则m,n相交、平行、异面都有可能,A错误;对于B,若m⊂α,n⊂α,m//β,n//β,则α与β相交或平行,B错误;对于C,若m⊥α,m//n,则n⊥α,又α⊥β,则n//β或n⊂β,C错误;对于D,由m⊥α,m⊥n,得n//α或n⊂a,若n//α,则存在过n的平面与α相交,令交线为l,则n//l,而n⊥β,于是l⊥β,α⊥β;若n⊂a,而n⊥β,则α⊥β,因此α⊥β,D正确.故选:D.2.(5分)(2024·浙江嘉兴·模拟预测)设x,y∈R,a=(1,1,1),b=(1,y,z),c=(x,―4,2),且a⊥c,b∥c,则|2a+b|=()A.B.0C.3D.【解题思路】根据向量的垂直和平行,先求出x,y,z的值,再求所给向量的模.【解答过程】由a⊥c⇒a⋅c=0⇒x―4+2=0⇒x=2,由b∥c⇒12=y―4=z2⇒y=―2,z=1.所以|2a+b|=|2(1,1,1)+(1,―2,1)|=|(3,0,3)|=故选:D.3.(5分)(2024·新疆乌鲁木齐·三模)三棱锥A―BCD中,AD⊥平面ABC,∠BAC=60°,AB=1,AC=2,AD=4,则三棱锥A―BCD外接球的表面积为()A.10πB.20πC.25πD.30π【解题思路】利用余弦定理先求出底面三角形ABC的外接圆半径r,再利用R2=r2+(ℎ2)2(ℎ为三棱锥的高,R为外接球半径),即可求解.【解答过程】在△ABC中,∠BAC=60°,AB=1,AC=2,由余弦定理可得BC2=AB2+AC2―2AB⋅AC⋅cos∠BAC,即BC2=1+4―2×1×2×cos60°=3,所以BC=设△ABC的外接圆半径为r,则2r=BCsin∠BAC==2,所以r=1,AD⊥平面ABC,且AD=4,设三棱锥A―BCD外接球半径为R,则R2=r2+(12AD)2,即R2=1+4=5,所以三棱锥A―BCD外接球的表面积为4πR2=20π.故选:B.4.(5分)(2024·辽宁沈阳·模拟预测)已知直三棱柱ABC ―A 1B 1C 1中,∠ABC =120°,AB =CC 1=2,BC =1,则异面直线AB 1与BC 1所成角的余弦值为( )A B C D 【解题思路】根据空间向量法求线线角即可.【解答过程】以B 为原点,在平面ABC 内过B 作BC 的垂线交AC 于D ,以BD 为x 轴,以BC 为y 轴,以BB 1为z 轴,建立空间直角坐标系,因为直三棱柱ABC ―A 1B 1C 1中,∠ABC =120°,AB =CC 1=2,BC =1,所以―1,0),B 1(0,0,2),B(0,0,0),C 1(0,1,2),所以AB 1=(―BC 1=(0,1,2),设异面直线AB 1与BC 1所成角为θ,所以cos θ=|AB 1⋅BC ||AB 1|⋅|BC 1|==故选:C.5.(5分)(2024·贵州·模拟预测)为了美化广场环境,县政府计划定购一批石墩.已知这批石墩可以看作是一个圆台和一个圆柱拼接而成,其轴截面如下图所示,其中AB =2CE =2EF =40cm ,AC =,则该石墩的体积为( )A .10000π3cm 3B .11000π3cm 3C .4000πcm 3D .13000π3cm 3【解题思路】过点C 作CM ⊥AB 于M ,根据条件,求出圆台的高,再利用圆台与圆柱的体积公式,即可求出结果.【解答过程】如图,过点C 作CM ⊥AB 于M ,因为|AB |=2|CE |=2|EF |=40cm ,|AC |=,所以|AM |=10,|CM |===10,所以圆台的体积为V =13(S 上+S 下+=13(π×102+π×202+×10=7000π3(cm 3),又圆柱的体积为V 1=Sℎ=π×102×20=2000π(cm 3),所以该石墩的体积为7000π3+2000π=13000π3(cm 3),故选:D.6.(5分)(2024·江西赣州·二模)已知球O 内切于正四棱锥P ―ABCD ,PA =AB =2,EF 是球O 的一条直径,点Q 为正四棱锥表面上的点,则QE ⋅QF 的取值范围为( )A .[0,2]B .[4―C .[0,4D .[0,4―【解题思路】根据给定条件,利用体积法求出球O 半径,再利用向量数量积的运算律计算即得.【解答过程】令H 是正四棱锥P ―ABCD 底面正方形中心,则PH ⊥平面ABCD ,而AH =则PH ==P ―ABCD 的体积V =13×22×=正四棱锥P ―ABCD 的表面积S =422+22=,显然球O 的球心O 在线段PH 上,设球半径为r ,则V =13Sr ,即r =3VS=在△POA 中,∠PAO <45∘=∠APO ,于是OA >OP ,又EF 是球O 的一条直径,因此QE ⋅QF =(QO +OE )⋅(QO ―OE )=QO 2―OE 2=QO 2―OH 2,显然OH ≤QO ≤AO ,则(QE ⋅QF )min =0,(QE ⋅QF )max =AO 2―OH 2=AH 2=2,所以QE ⋅QF 的取值范围为[0,2].故选:A.7.(5分)(2024·陕西榆林·模拟预测)在正方体ABCD―A1B1C1D1中,E,F分别是DD1,BC1的中点,则()A.EF//BD B.FD1//平面BCEC.EF⊥BC1D.AF⊥平面BCC1B1【解题思路】对于A,说明EF,BD异面即可判断;对于B,说明平面BCE//平面GHD1即可判断;对于C,可以用反证法导出矛盾,进而判断;对于D,显然不垂直.【解答过程】对于A,设G为BB1中点,则EG//BD,但EG,EF相交,所以EF,BD异面,故A错误;对于B,设CC1的中点为H,则BC//GH,BE//GD1,因为GH⊄平面BEC,BC⊂平面BEC,GD1⊄平面BEC,BE⊂平面BEC,所以GH//平面BEC,GD1//平面BEC,又因为GH∩GD1=G,GH,GD1⊂平面GHD1,故平面BCE//平面GHD1,又FD1⊂平面GHD1,故FD1//平面BCE,选项B正确.对于C,在△EBC1中,BE≠EC1,BF=FC1,故EF与BC1不可能垂直(否则EF垂直平分BC1,会得到EB=EC1,这与BE≠EC1矛盾),C选项错误.对于D ,易知AB ⊥平面BCC 1B 1,又AB ∩AF =A ,故D 选项错误.故选:B.8.(5分)(2024·山东临沂·二模)已知正方体ABCD ―A 1B 1C 1D 1中,M ,N 分别为CC 1,C 1D 的中点,则( )A .直线MN 与A 1CB .平面BMN 与平面BC 1D 1C .在BC 1上存在点Q ,使得B 1Q ⊥BD 1D .在B 1D 上存在点P ,使得PA //平面BMN【解题思路】以D 为坐标原点,建立如图所示的空间直角坐标系,设正方体的边长为1,由空间向量计算异面直线所成角,二面角和线线垂直可判断ABC ;由N,M,B,A 四点共面,而A ∈平面BMN 可判断D.【解答过程】以D 为坐标原点,建立如图所示的空间直角坐标系,设正方体的边长为1,所以A (1,0,0),D (0,0,0),B (1,1,0),C (0,1,0),A 1(1,0,1),D 1(0,0,1),B 1(1,1,1),C 1(0,1,1),M0,1,0,12对于A ,MN =0,―12,0,A 1C =(―1,1,―1),直线MN 与A 1C 所成角的余弦值为|cos ⟨MN ,A 1C ⟩|=|MN⋅A C ||MN ||A 1C |=1=A 错误;对于B ,MN =0,―12,0,BM =―设平面BMN 的法向量为n =(x,y,z ),则n ⋅MN =―12y =0n ⋅BM =―x +12z =0,取x =1,可得y =0,z =2,所以n =(1,0,2),C 1D 1=(0,―1,0),BC 1=(―1,0,1),设平面BC 1D 1的法向量为m =(x 1,y 1,z 1),则n ⋅C 1D 1=―y 1=0n ⋅BC 1=―x 1+z 1=0,取x 1=1,可得y 1=0,z 1=1,所以m =(1,0,1),平面BMN 与平面BC 1D 1夹角的余弦值为:cos⟨m,n⟩=m⋅n==B错误;对于C,因为Q在BC1上,设Q(x0,1,z0),所以C1Q=λC1B,0≤λ≤1,则C1Q=(x0,0,z0―1),C1B=(1,0,―1),所以x0=λ,z0=―λ+1,所以Q(λ,1,―λ+1),B1Q=(λ―1,0,―λ),BD1=(―1,―1,1),.所以B1Q⋅BD1=1―λ―λ=0,解得:λ=12故BC1上存在点B1Q⊥BD1,故C正确;对于D,因为MN//DC//AB,所以N,M,B,A四点共面,而A∈平面BMN,所以B1D上不存在点P,使得PA//平面BMN,故D错误.故选:C.二、多项选择题:本题共3小题,每小题6分,共18分,在每小题给出的四个选项中,有多项符合题目的要求,全部选对的得6分,部分选对的得部分分,有选错的得0分。
高考数学二轮复习空间向量与立体几何专题训练(含解析)
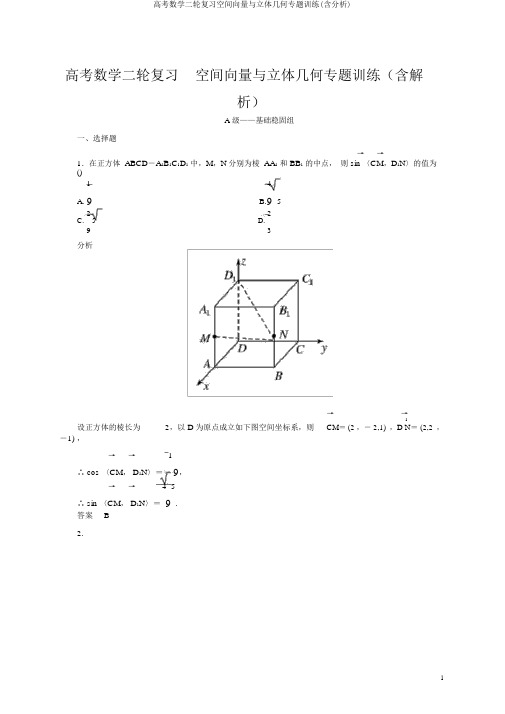
高考数学二轮复习空间向量与立体几何专题训练(含解析)A 级——基础稳固组一、选择题→ →1.在正方体ABCD-A1B1C1D1中,M,N分别为棱AA1和BB1的中点,则 sin 〈CM,D1N〉的值为()14A. 9B.9 522C. 5D.93分析→→设正方体的棱长为2,以D为原点成立如下图空间坐标系,则CM=(2,-2,1)1,,D N=(2,2-1) ,→ →1∴ cos 〈CM,D1N〉=-9,→ → 4 5∴ sin 〈CM,D1N〉=9 .答案B2.如图, 三棱锥 A - BCD 的棱长全相等, E 为 AD 的中点, 则直线 CE 与 BD 所成角的余弦值为 ()33A.B.62331C.D.62→→→→→→ 1→ 2 1→→→→→→1 1 分析设 AB = 1,则 CE · BD = ( AE - A C ) ·(AD - AB ) = 2AD - 2AD · AB -AC · AD + AC · AB = 2-21cos60°- cos60°+ cos60°= 4.→ →1→ → 4 3CE · BD∴ cos 〈CE , BD 〉= → → =3 = 6.应选 A.||| |CE BD2答案A3.如图,点 P 是单位正方体 ABCD - A B CD→ →中异于 A 的一个极点,则 AP · AB 的值为 ()1 1 1 1A . 0B . 1C .0或 1D .随意实数分析 →7 个向量: →→→→→→→ → → →AP 可为以下 AB , AC , AD ,AA 1, AB 1,AC 1, AD 1,此中一个与 AB 重合, AP · AB =| → | 2= 1;→,→1,→ 1与→垂直,这时 → · → = 0; → ,→1与→的夹角为45°,这时→·→= 2AB AD AD AA AB AP ABAC AB ABAP AB×1×cos π = 1,最后 →1· →= 3×1×cos ∠1= 3× 1 = 1,应选 C.4 ACABBAC3答案 C4.(201 3·山东卷 ) 已知三棱柱- 1 11的侧棱与底面垂直,体积为 9,底面是边长为3的正ABC ABC4三角形.若 P 为底面 A 1B 1C 1 的中心,则 PA 与平面 ABC 所成角的大小为 ()5ππ A. 12B. 3πD.πC.64分析如下图,设△ABC1 3 3ABC 的中心为 O , S= 2× 3× 3×sin60 °= 4 .3 39∴ VABC - A 1B 1C 1 =S ABC ×OP =4 × OP = 4,∴ OP = 3.32又 OA = 2 × 3× 3=1,OP ∴ tan ∠ OAP == 3,OAπ又 0<∠ OAP < 2 ,π∴∠ OAP = 3 .5.在正方体 ABCD - A 1B 1C 1D 1 中,点 E 为 BB 1 的中点,则平面 A 1ED 与平面 ABCD 所成的锐二面角的余弦值为 ()1 2 A. 2B. 332C. 3D. 2分析以 A 为坐标原点成立空间直角坐标系,如图.设棱长为 1,则 1(0,0,1) ,E 1, 0, 1, (0,1,0) ,A2 D→→1, 0,-1,112所以 AD =(0,1 ,- 1),AE =设平面 1 的一个法向量为 1=(1 , y , ) ,A EDn zy - z =0,y =2,则1所以 n = (1,2,2) .所以1- 2z = 0, z =2,1由于平面 ABCD 的一个法向量为 n = (0,0,1) ,2所以 |cos 〈n 1, n 2〉 | =223×1 = .3即平面 A ED 与平面 ABCD 所成的锐二面角的余弦值为23. 应选 B.1答案 B6. P 是二面角 α-AB - β 棱上的一点,分别在 α, β 平面上引射线PM ,PN ,假如∠ BPM =∠=45°,∠=60°,那么二面角 - -的大小为 ()A.60° B .70°C.80° D .90°分析不如设 PM= a, PN= b,作 ME⊥ AB于点 E, NF⊥AB于点 F,如图.由于∠ EPM=∠ FPN=45°,所以 PE=22a, PF=22b,→ →→ →→→所以 EM· FN=( PM-PE)·(PN- PF)→ → →→ →→→ →= PM· PN-PM· PF- PE· PN+ PE·PF2222=ab cos60°- a×2 b cos45°-2 ab cos45°+2 a×2 b abab ab ab=2-2-2+2=0.→→所以 EM⊥ FN,所以二面角α-AB-β 的大小为90°.答案D二、填空题7.已知a= (2 ,-1,1),b=(-1,4,-2),c=(11,5,λ).若向量 a,b,c 共面,则λ=________.分析由向量,,c 共面可得c=xa+(x,∈R) ,a b yb y11= 2x-y,x=7,故有 5=-x+ 4y,解得 y=3,λ =x-2y,λ=1.答案18.已知空间不共面四点,,,,→·→=→·→=→·→=0,且 |→| =|→|=|→|,→O A B COAOBOAOCOBOC OA OB OC AM →= MB,则 OM与平面 ABC所成角的正切值是________.分析由题意可知, OA , OB , OC 两两垂直,如图,成立空间直角坐标系O - xyz ,设 OA = OB = OC = 1,1 1则 A (1,0,0) , B (0,1,0) , C (0,0,1) , M 2 ,2, 0 ,→→ → 1 1故 AB = ( - 1,1,0) ,AC = ( - 1,0,1) , OM = 2,2,0 .设平面 ABC 的法向量为 n = ( x ,y , z ) ,→- x +y = 0,n ⊥AB ,则由得→ - x +z = 0,n ⊥AC ,令 x = 1,得平面 ABC 的一个法向量为 n = (1,1,1) .→1= 6故 cos 〈n , OM 〉=,2 33× 2→6 2 3sin 〈 n ,OM 〉=1-3 = 3 ,→→2sin 〈n , OM 〉tan 〈 n ,OM 〉= cos 〈 , →〉=2.nOM答案229.已知点 E , F 分别在正方体 ABCD - A 1B 1C 1D 1 的棱 BB 1, CC 1 上,且 B 1E = 2EB , CF = 2FC 1,则平面与平面所成的二面角的正切值为________.AEFABC分析如图,成立空间直角坐标系.设= 1,由已知条件得(1,0,0),E1, 1,1,F0, 1,2,DA A33→1AE=0, 1,3,→2AF=-1,1,3,设平面 AEF的法向量为n=( x,y, z),平面 AEF与平面→n· AE=0,由→n· AF=0,ABC所成的二面角为θ,1y+3z=0,得2-x+ y+3z=0.令 y=1,得 z=-3, x=-1,则 n=(-1,1,-3),平面 ABC的法向量为 m=(0,0,-1),cos θ= cos〈n,m〉=3,tanθ=2. 113答案2 3三、解答题10.如下图,四棱锥S- ABCD的底面是正方形,SD⊥平面 ABCD, SD= AD= a,点 E 是 SD上的点,且 DE=λa(0<λ≤1).(1)求证:对随意的λ∈(0,1],都有AC⊥BE;(2)若二面角 C- AE- D的大小为60°,求λ的值.解(1) 证明:如下图,成立空间直角坐标系D -xyz ,则 A ( a, 0,0) ,B ( a ,a, 0) ,C (0 ,a, 0) ,D (0,0,0) ,E (0,0 , λa ) ,∴→=(- ,0) ,→=( - ,- ,) ,ACaa, BEaa λa→ →对随意 λ∈ (0,1]都成立,∴ AC · BE =0即对随意的 λ∈ (0,1] ,都有 AC ⊥ BE .(2) 明显n = (0,1,0) 是平面的一个法向量,ADE设平面 ACE 的法向量为 m = ( x ,y , z ) ,→→- a, 0, λa ), ∵ AC = ( - a , a, 0) , AE =(→- ax + ay =0, x - y = 0, m · AC = 0, ∴ →即+= 0,∴-= 0.· = 0, -ax λazxλzm AE令 z = 1,则 x = y =λ,∴ m =( λ, λ, 1) .∵二面角 C - AE - D 的大小为 60°,∴ cos 〈n ,m 〉=n ·mλ1== ,| n || m |1+ 2λ222 ∵ λ∈ (0,1] ,∴ λ=.211.(2014 ·北京卷 ) 如图,正方形AMDE的边长为 2,B,C分别为AM,MD的中点.在五棱锥P-ABCDE中, F为棱 PE的中点,平面 ABF与棱 PD,PC分别交于点 G, H.(1)求证: AB∥ FG;(2) 若PA⊥底面ABCDE,且PA=AE,求直线BC与平面ABF所成角的大小,并求线段PH的长.解 (1) 证明:在正方形AMDE中,由于B是AM的中点,所以 AB∥ DE.又由于 AB?平面 PDE,所以 AB∥平面 PDE.由于 AB?平面 ABF,且平面 ABF∩平面 PDE= FG,所以 AB∥ FG.(2)由于 PA⊥底面 ABCDE,所以 PA⊥AB,PA⊥ AE.如图成立空间直角坐标系A- xyz,则 A(0,0,0),B(1,0,0), C(2,1,0), P(0,0,2), F(0,1,1)→., BC=(1,1,0)设平面 ABF的法向量为 n=( x,y, z),→x=0,n· AB=0,则即n ·→=0,y+ z=0. AF令 z=1,则 y=-1.所以 n=(0,-1,1).设直线 BC 与平面 ABF 所成角为 α,→1则 sin=|cos 〈,→〉 | = n ·BCα= .n BC→2| n || BC |π所以直线 BC 与平面 ABF 所成角的大小为 6 .设点 H 的坐标为 ( u ,v , w ) .→→由于点 H 在棱 PC 上,所以可设 PH = λPC (0< λ<1) ,即 ( u , v , w - 2) = λ(2,1 ,- 2) ,所以 u = 2λ , v = λ, w = 2- 2λ.由于 n 是平面 ABF 的法向量,→所以 n ·AH = 0,即 (0 ,- 1,1) ·(2 λ,λ, 2- 2λ) = 0,2解得 λ=3.所以点 H 的坐标为4 2 2, ,3 3 3 .所以 = 4 2 2 2 42+ + - =2.PH 3 3 3B 级——能力提升组1.(2014 ·江西卷 ) 如图,四棱锥 P - ABCD 中, ABCD 为矩形,平面 PAD ⊥平面 ABCD .(1) 求证: AB ⊥ PD ;(2) 若∠ BPC =90°, PB = 2,PC = 2,问 AB 为什么值时,四棱锥 P - ABCD 的体积最大?并求此时平面 PBC 与平面 DPC 夹角的余弦值.解 (1) 证明: ABCD 为矩形,故 AB ⊥ AD .又平面 PAD ⊥平面 ABCD ,平面 PAD ∩平面 ABCD = AD ,所以 AB ⊥平面 PAD ,故 AB ⊥ PD .故 PO⊥平面 ABCD, BC⊥平面 POG, BC⊥ PG,23266在 Rt △BPC中,PG=3,GC=3,BG=3,2242设 AB= m,则 OP=PG- OG=3- m,故四棱锥 P- ABCD的体积为142m2V=3·6· m·3- m=38-6m.由于-2=24-2228m-=6m-+,86m8m 6m3366P-ABCD的体积最大.此时,成立如下图的坐标系,各故当 m=,即 AB=时,四棱锥3366626266点的坐标为 O(0,0,0), B3,-3, 0, C3,3, 0,D 0,3, 0,P 0,0,3.→6266→故 PC=3,3,-3, BC=(0,6,0),→6.CD=-3,0,0设平面 BPC的法向量 n =( x, y, 1),16266→→3 x+3 y-3=0,则由 n ⊥ PC, n ⊥ BC,得116y=0,解得 x=1, y=0,n1=(1,0,1).21同理可求出平面=0,,1,DPC的法向量n2进而平面与平面夹角的余弦值为11| n·n |110cos θ12=5 .=| n1|| n2|=12·4+ 12.如图,在长方体ABCD- A1B1C1D1中, AA1= AD=1,E 为 CD的中点.(1)求证: B1E⊥ AD1;(2)在棱 AA1上能否存在一点 P,使得 DP∥平面 B1AE?若存在,求 AP的长;若不存在,说明原因;(3)若二面角 A- B1E-A1的大小为30°,求 AB的长.解 (1) 证明:以A 为原点,→,→,→x轴、y轴、z轴的正方向成立空间直角1的方向分别为AB AD AA1a1,1,0坐标系 ( 如图 ) ,设AB=a,则A(0,0,0), D(0,1,0), D(0,1,1), E2, B ( a, 0,1),→→a→→a,1,011-,1,- 11, AE=2.故 AD=(0,1,1),BE=2,AB=( a, 0,1)→→a∵ AD1· B1E=-2×0+1×1+(-1)×1=0,∴B1E⊥ AD1.(2)假定在棱 AA1上存在一点 P(0,0, z0)(0≤ z0≤1),使得 DP∥平面 B1AE.高考数学二轮复习空间向量与立体几何专题训练(含分析)→此时 DP = (0 ,- 1, z 0) .又设平面 B 1AE 的法向量 n = ( x , y , z ) .→→ax + z =0, ax由 n ⊥ AB ,n ⊥ AE ,得12+ y = 0. 取 x = 1,得平面 B 1AE 的一个法向量an = 1,- 2,- a .→a要使 DP ∥平面 B 1AE ,只需 n ⊥DP ,有 2- az 0= 0,1解得 z 0= 2. 又 DP ?平面 B 1AE ,1∴存在点P ,知足 DP ∥平面 B 1AE ,此时 AP = 2.(3) 连结 A 1D , B 1C ,由长方体 ABCD - A 1B 1C 1D 1 及 AA 1= AD = 1,得 AD 1⊥ A 1D .∵ B 1C ∥ A 1D ,∴ AD 1⊥ B 1C .又由 (1) 知 B 1E ⊥ AD 1,且 B 1C ∩ B 1E = B 1,∴ AD 1⊥平面 DCB 1A 1.→→.∴ AD 1是平面 A 1B 1E 的一个法向量,此时 AD 1= (0,1,1) → 设 AD 1与 n 所成的角为 θ ,a· →1- 2-aAD.则 cos θ= → =2| n || AD 1|21+ a+ a 24∵二面角- 1- 1 的大小为 30°,A B E A3a∴ |cos θ| =cos30°,即235a 2=2 ,21+ 4解得 a = 2,即 AB 的长为 2.。
2025届高考数学二轮专题复习与测试第一部分专题三立体几何02命题分析03知识方法

专题三 立体几何1.高考立体几何试题具有较强的综合性,重视基础学问、基本技能和创新意识的考查,突出直观想象、逻辑推理、数学运算等学科核心素养的考查.内容包括“空间几何体”“点、直线、平面之间的位置关系”和“空间向量与立体几何”.2. 从近几年高考数学试题考查的状况来看,题目难度和题量相对稳定,一般是一个大题,两个小题,占22分,难度基本是中等.3.立体几何高考选择题或填空题有两个常考的热点:一是空间几何体的表面积、体积的计算,有时和数学文化、科技情境交汇命题,特殊要留意的是球与球的组合体问题,常作为小题的压轴题出现,难度较大,对空间想象实力和推理实力都有较高的要求.二是空间中点、直线、平面之间的位置关系的判定,或空间角的计算,若出现在压轴小题的位置,则类型一般为立体几何动态问题或翻折问题.4.立体几何高考解答题常以棱柱或棱锥为载体,一般设置两问,“一证一算”,一问是定性分析,一问是定量分析.其中定性分析以线、面平行、垂直的证明为主,考查逻辑推理实力及学科素养;而定量分析主要是应用空间向量求线面角、二面角,考查数学运算实力与学科素养.1.几何体的表面积与体积公式(1)柱体的体积和表面积:V =S 底h ;S 圆柱侧=2πrl ;S 表面积=S 侧+2S 底.(2)台体的体积和表面积:V =13(S 上+S 下+S 上S 下)h ;S 圆台侧=π(r 1+r 2)l ;S 表面积=S 侧+S 上+S 下.(3)锥体的体积和表面积:V =13S 底h ;S 圆锥侧=πrl ;S 表面积=S 侧+S 底. (4)球的体积和表面积:V =43πR 3;S =4πR 2. 2.三个基本领实(1)基本领实1:过不在同一条直线上的三点,有且只有一个平面.(2)基本领实2:假如一条直线上的两点在一个平面内,那么这条直线在此平面内.(3)基本领实3:假如两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.3.线面平行、垂直的定理(1)线面平行的判定定理:a ⊄α,b ⊂α,a ∥b ⇒a ∥α.(2)线面平行的性质定理:a ∥α,a ⊂β,α∩β=b ⇒a ∥b .(3)面面平行的判定定理:a ⊂α,b ⊂α,a ∩b =P ,a ∥β,b ∥β⇒α∥β.(4)面面平行的性质定理:α∥β,α∩γ=a ,β∩γ=b ⇒a ∥b .(5)线面垂直的判定定理:⎭⎪⎬⎪⎫l ⊥a l ⊥b a ∩b =O a ⊂αb ⊂α⇒l ⊥α. (6)线面垂直的性质定理:⎭⎪⎬⎪⎫a ⊥αb ⊥α⇒a ∥b . (7)面面垂直的判定定理: ⎭⎪⎬⎪⎫l ⊥αl ⊂β⇒α⊥β.(8)面面垂直的性质定理: ⎭⎪⎬⎪⎫α⊥βα∩β=al ⊥al ⊂β⇒l ⊥α. 4.三种空间角的求法设直线l ,m 的方向向量分别为a =(a 1,b 1,c 1),b =(a 2,b 2,c 2),平面α,β的法向量分别为μ=(a 3,b 3,c 3),v =(a 4,b 4,c 4)(以下相同).(1)线线夹角:设l ,m 的夹角为θ⎝ ⎛⎭⎪⎫0≤θ≤π2,则cos θ=|a ·b ||a ||b |=|a 1a 2+b 1b 2+c 1c 2|a 21+b 21+c 21·a 22+b 22+c 22 .(2)线面夹角:设直线l 与平面α的夹角为θ⎝⎛⎭⎪⎫0≤θ≤π2,则sin θ=|a ·μ||a ||μ|=|cos 〈a ,μ〉|.(3)面面夹角:设平面α,β的夹角为θ(0≤θ<π),则|cos θ|=|μ·v ||μ||v |=|cos 〈μ,v 〉|.5.空间距离(1)点到直线的距离直线l 的单位方向向量为u ,A 是直线l 上的任一点,P 为直线l 外一点,设AP →=a ,则点P到直线l 的距离d =a 2-(a ·u )2.(2)点到平面的距离平面α的法向量为n ,A 是平面α内任一点,P 为平面α外一点,则点P 到平面α的距离为d =|AP →·n ||n |.。
2022届高考数学二轮专题:空间向量与立体几何

空间向量与立体几何1.如图,在四棱锥P ABCD 中,底面ABCD 是平行四边形,已知PA u u r a ,PB u u r b ,PC u u u rc ,12PE PD u u r u u u r,则BE u u r ()A.131222a b c B.111222a b c C.131222a b c D.113222a b c 【答案】A【解析】连接BD ,如图,则1111122222BE BP BD PB BA BC PB PA PB PC PBu u r u u r u u u r u u r u u r u u u r u u r u ur u u r u u u r u u r11131131222222222PB PA PB PC PA PB PC u u r u u r u u r u u u r u u r u u r u u u r a b c ,故选A.2.已知长方体1111ABCD A B C D 中1AB BC ,12AA ,E 是棱1BB 的中点,P 是平面11D C CD 内一点,且AP ⊥平面1A DE ,则EP 长度为()B.2C.2D.32【答案】B【解析】如图,以点D 为原点,分别以直线DA ,DC ,1DD 为x 轴,y 轴,z 轴,建立空间直角坐标系,则 1,0,0A , 11,0,2A , 0,0,0D , 1,1,1E ,设 0,,P y z ,所以 11,0,2DA u u u r , 1,1,1DE u u u r , 1,,AP y z u u u r,设平面1A DE 的法向量为 ,,x y z n ,由100DA DE n n ,得200x z x y z,取 2,1,1 n ,因为AP 平面1A DE ,所以AP ∥u u u r n ,则1211y z ,解得12y z ,所以110,,22P,则111,,22PEu u r,所以2EP u u r ,故选B.3.如图,已知圆锥的底面半径为1,,AB 为圆锥底面圆的直径,C 是圆弧AB 的中点,D 是母线SA 的中点,则异面直线SC 与BD所成角的余弦值为()A.23B.105C.510D.1010【答案】C【解析】连接OC 、OS ,因为AB 为圆锥底面圆的直径,C 是圆弧AB 的中点,则AC BC ,O Q 为AB 的中点,则OC AB ,以点O 为坐标原点,OC 、OB 、OS 所在直线分别为x 、y 、z轴建立空间直角坐标系,因为SA1AO ,易知SO AB,则1SO ,所以, 0,1,0B 、 1,0,0C 、110,,22D、 0,0,1S , 1,0,1SC u u r ,310,,22BDu u u r ,则12cos ,10SC BDSC BD SC BDu u r u u u ru u r u u u r u u r u u u r ,因此,异面直线SC 与BD所成角的余弦值为10,故选C.4.(多选)如图,在长方体1111ABCD A B C D中,1AD AA 2AB ,点P ,E 分别为AB ,1AA 的中点,点M 为直线1CD 上的动点,点N 为直线11C D上的动点,则()A.对任意的点N ,一定存在点M ,使得PM DNB.向量PM u u u r ,1A B u u u r ,1D E u u u r共面C.异面直线PM 和1AA 所成角的最小值为4D.存在点M ,使得直线PM 与平面11DCC D 所成角为3【答案】BCD【解析】建立如图所示的空间直角坐标系,则,2,0,0,2,0,0,0,0ABC D,1111,2,,0,2,,0,0,A B C D ,故 P,设 0,N t ,11D M D C u u u u r u u u r,02,01t ,而 10,2,D C u u u r,故 10,2,D M u u u u r,即 0,2M ,故 0,DN t u u u r, 2PM u u u r,若PM DN ,则0DN PM u u u r u u u r,即 21330t ,当1t 时, 不存在,故当N 为11D C 中点,不存在M ,使得PM DN ,故A 错误;连接EP ,则1//EP A B ,由长方体可得11//D C A B ,故1//EP CD ,故PM u u u r ,EP u u r ,1D E u u u r ,即PM u u u r ,1A B u u u r ,1D E u u u r共面,故B正确;1AA u u u r,故1cos ,AA PMu u u r uu u r当1 时,1cos ,0AA PM ,此时1AA PM ;当01时,1cos ,AA PMu u u r u u u r,令2211t ,设 10,1u ,则21133244t u ,故1cos ,2AA PMu u u r u u u r,所以异面直线PM 和1AA 所成角的范围为,42 ,故直线PM 和1AA 所成角的最小值为4,故C 正确;平面11DCC D 的法向量为 1,0,0 n ,故cos ,PMu u u rn ,若直线PM 与平面11DCCD 所成角为3,则32,故271030 ,所以37或1 ,故D 正确,故选BCD.5.(多选)已知正方体1111ABCD A B C D 的棱长为2,点P 满足1AP xAB y AD z AA u u u r u u u r u u u r u u u r,则下列选项正确的为()A.若01x ,1y ,12z,则二面角P AB D 为30 B.若1z ,则三棱锥P ABD 的体积为定值C.若0x ,01y ,01z ,且直线AP 与平面ABCD 所成的角为45 ,则点P 的轨迹长度为D.若AP uu u r P 的轨迹与正方体表面交线的总长度为3【答案】BCD【解析】建立如图所示空间直角坐标系,则 2,2,2P x y z , 2,0,0B ,平面ABD ,也即平面ABCD 的法向量为 10,0,1 n ,对于A 选项, 2,2,1,01P x x ,设平面PAB 的法向量为 2111,,x y z n ,则12112120220AB x AP x x y z u u u r u u u r n n ,故可设 20,1,2 n ,设二面角P AB D 为,则1212cos 52n n n n ,所以A 选项错误;对于B 选项,1z ,则 2,2,2P x y ,即P 到平面ABD 也即平面ABCD 的距离为定值2,而三角形ABD 的面积是定值,所以三棱锥P ABD 的体积为定值,所以B 选项正确;对于C 选项,当0x 时, 0,2,2P y z ,且022,022y z ,依题意直线AP 与平面ABCD 所成角为45 ,所以11sin 452AP APu u u ru u u rn n ,两边平方并化简得22,y z y z .所以P 点的轨迹是线段1AD,1AD,C 选项正确;对于D选项,AP u u u r P 到A所以P 的轨迹是以A为球心,半径r 的球,注意到4323 2222343233,所以球与正方形ABCD ,正方形11ABB A ,正方形11ADD A 相交形成的轨迹是如下图中的弧形,三段弧长和为π3633.球与正方形11BCC B ,正方形11CDD C ,正方形1111A B C D 相交形成的轨迹是如下图中的弧形,三段弧长和为π2333π23,所以点P 的轨迹与正方体表面交线的总长度为23π33ππ33,D 选项正确,故选BCD.6.(多选)如图,四棱锥P ABCD 的底面是正方形,平面PAB 平面ABCD ,1PB AB ,E 为BC 中点,F 为线段PD 上一点()A.若60PBA ,则AE PD B.若F 为PD 中点,则EF PDC.若90PBA ,则四棱锥P ABCD 外接球表面积为6πD.直线AE 与平面PAD 所成的角的余弦值的取值范围是5,1)5【答案】ABD【解析】B选项,2DE ,由于平面PAB 平面ABCD 且交线为AB ,BC AB ,所以BC 平面PAB ,所以BC PB,所以52PE DE ,当F 是PD 中点时,EF PD ,B选项正确;C 选项,90PBA ,即PB AB ,由于平面PAB 平面ABCD 且交线为AB ,所以PB 平面ABCD ,所以PB BC ,而AB BC ,即,,AB BC PB 两两相互垂直,所以四棱锥P ABCD外接球的直径2R,所以外接球的表面积为24π3πR ,C 选项错误;以B 为空间坐标原点建立如图所示空间直角坐标系,则 11,0,0,1,1,0,0,,02A D E, 10,1,0,1,,02AD AEu u u r u u u r ,A 选项,当60PBA 时,三角形PAB 是等边三角形,所以11,0,,,1,2222P PDu u u r,111,,0,1,0222AE PDu u u r u u u r ,所以AE PD ,所以A 选项正确;D 选项,设 ,0,P x z ,其中220,1z x z ,则11x ,1,0,AP x z u u u r , 0,1,0AD u u u r,设平面PAD 的法向量为 111,,x y z n ,则11110AP x x z zAD yu u u ru u u rnn,故可设,0,11zxn,设直线AE与平面PAD所成的角为 ,则sinAEAEu u u ru u u rnn,由于线面角的范围是π0,2,所以cos ,将221z x代入上式并化简得cos ,由于11x,222123,1555555x x,所以cos,15,所以D选项正确,故选ABD.7.长方体1111ABCD A B C D中,2AB AD,11AA ,已知点H,A,1C三点共线,且110AC B Hu u u r u u u r,则点H到平面ABCD的距离为________.【答案】59【解析】在长方体1111ABCD A B C D中,以点A为原点建立如图所示的空间直角坐标系,则11(0,0,0),(2,0,1),(2,2,1)A B C ,1(2,2,1)AC u u u r,因点H ,A ,1C 三点共线,令1(2,2,)AH t AC t t t u u u r u u u r,点(2,2,)H t t t ,则1(22,2,1)B H t t t u u u r,又110AC B H u u u r u u u r ,则2(22)410t t t ,解得59t ,所以点10105(,,)999H 到平面ABCD 的距离为59,故答案为59.8.如图,已知菱形ABCD ,2,3AB ADC,沿直线AC 将ACD △翻折成ACS V ,,E F 分别为SA SB ,的中点,SA 与平面ABC 所成角的正弦值为63,M 为线段AC 上一点(含端点),则AE 与平面EFM 所成角的正弦值的最大值为___________.【答案】22211【解析】设顶点S 在平面ABC 内的射影为点O ,因为SA 与平面ABC 所成角的正弦值为63,2SA ,所以263SO ,因为2SA SC ,所以233OA OC,又因为AB AC ,所以,如图1,在平面ABC 中,ABC V 为等边三角形,C AOB OB △V,所以OB 平分ABC ,即6ABO,所以在AOB V中,2222443cos 242OB OB AB OAABO OB ABOB,解得3OB,3OB,所以点O 为ABC V 的中心,故三棱锥S ABC 是棱长为2的正四面体,故如图2,以AB 中点H 为坐标原点,,HC HB 分别为,x y轴建立空间直角坐标系,则 326316316(0,0,0),(0,1,0),0,1,0,,0,,,,,,,33623623H A B S E F,设,1,0,03M x x x1,,6323EM x xu u u r , 0,1,0EF u uu r ,设平面EFM 的一个法向量为 000,,x y z n ,则00EF EM u u u r u u u r n n,即000063y x x z,令0z,得6n ,因为1,,623AE u u u r ,设AE 与平面EFM 所成角为 ,所以sin cos ,AE AE AEu u u ru u u ru u u rn n n令1t x ,则33t,因为函数2962y t 在3,3上单调递增,所以s in在,3上单调递减,所以当33t时,AE 与平面EFM 所成角的正弦值最大,最大值为22211,故答案为11.9.如图,在四棱锥P ABCD 中,底面ABCD 为矩形,PA 平面ABCD ,//AP CQ ,22AB BC ,332CQ AP.(1)求直线PD 与平面BPQ 所成角的正弦值;(2)求平面APQ 与平面BPQ 所成角的余弦值.【答案】(1)11;(2)55.【解析】(1)解:因为PA 平面ABCD ,四边形ABCD 为矩形,以点A 为坐标原点,AB 、AD 、AP 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系,则 0,0,0A 、 2,0,0B 、 2,1,0C 、 0,1,0D 、 0,0,2P 、 2,1,3Q ,设平面BPQ 的法向量为 111,,x y z m ,2,0,2BP u u r , 0,1,3BQ u u u r,由111122030BP x z BQ y z u u r u u u r m m ,取11z ,可的 1,3,1 m , 0,1,2PD u u u r,则cos ,11PD PD PD u u u ru u u r u u u rm m m,因此,直线PD 与平面BPQ所成角的正弦值为11.(2)解:设平面APQ 的法向量为 222,,x y z n ,0,0,2AP u u u r , 2,1,3AQ u u u r,由222220230AP z AQ x y z u u u r u u u r n n ,取21x ,可得 1,2,0 n,cos ,55m n m n m n .由图可知,平面APQ 与平面BPQ 所成角为锐角,因此,平面APQ 与平面BPQ所成角的余弦值为55.10.如图,已知圆柱的上,下底面圆心分别为11,,P Q AA C C 是圆柱的轴截面,正方形ABCD 内接于下底面圆Q ,2AB ,1AA k .(1)当k 为何值时,点Q 在平面PBC 内的射影恰好是△PBC 的重心;(2)若 2,4k ,当平面PAD 与平面PBC 所成的锐二面角最大时,求该锐二面角的余弦值.【答案】(1)2k(2)35.【解析】(1)取BC 中点E ,连接QE ,PE ,PQ ,则QE BC ,PE BC ,又QE PE E I ,所以BC 平面PQE ,过Q 作QF PE ,交PE 于F ,因为QF 平面PQE ,所以BC QF ,又BC PE E I ,所以QF 平面PBC ,即F 是Q 点在平面PBC 内的射影.因为F 恰好是PBC V 的重心,所以3PE EF ,在PQE Rt △中,112QE AB ,223QE EF PE EF ,所以33EF ,3PE ,所以2(3)12PQ 12AA .所以当2kQ 点在平面PBC 内的射影恰好是PBC V 的重心.(2)以D 为原点,DA 为x 轴,DC 为y 轴,作1DM AA ∥,以DM 为z 轴,建立如图所示的空间直角坐标系,则 0,0,0D , 1,1,P k , 2,0,0A , 2,2,0B , 0,2,0C ,2,0,0DA u u u r , 1,1,DP k u u u r , 1,1,PB k u u r , 1,1,PC k u u u r.设平面PAD 的法向量 111,,x y z m ,则0DA DP u u u r u u u rm m ,即1111200x x y kz ,取11z ,得 0,,1k m ,设平面PBC 的法向量 222,,x y z n ,则0PB PC u u r u u u rn n ,即2222220x y kz x y kz,取21z ,得 0,,1k n ,222220112cos ,1111k k k k k m n .因为24k ,所以当2k 时,上式取得最小值35,此时二面角最大,所以平面PAD 与平面PBC 所成锐二面角最大时,其余弦值为35.11.如图,在直三棱柱111ABC A B C 中,90BAC ,12AB AC AA ,E 是BC中点.(1)求点1A 到平面1AEC 的距离;(2)求平面1AEC 与平面11ABB A 夹角的余弦值.【答案】(1)233;(2)33.【解析】(1)解:(1)以A 为原点,AB 为x 轴,AC 为y 轴,1AA 为z 轴建立空间直角坐标系,所以111(0,0,0),(0,0,2),(2,0,0),(2,0,2),(0,2,0),(0,2,2),(1,1,0)A A B B C C E ,因为1(1,1,0),(0,2,2)AE AC u u u r u u u r ,1(0,0,2)AA u u u r,设平面1AEC 的法向量为(,,)x y z n ,则有10AE AC u u u r u u u rn n ,得00x y y z ,令1y ,则1,1x z ,所以可以取(1,1,1) n ,设点1A 到平面1AEC 的距离为d,则1||||3AA du u u rn n ,所以点1A 到平面1AEC的距离为3.(2)因为AC 平面11ABB A ,取平面11ABB A 的法向量为(0,2,0)AC u u u r,设平面1AEC 与平面11ABB A 的夹角为 ,所以cos |cos ,|3||||AC AC AC u u u r u u u r u u u r n n n ,平面1AEC 与平面11ABB A夹角的余弦值3.12.如图,在四棱锥P ABCD 中,PA 面ABCD ,//AB CD ,且2CD ,1AB,BC 1PA ,AB BC ,N 为PD 的中点.(1)求证:AN ∥平面PBC ;(2)在线段PD 上是否存在一点M ,使得直线CM 与平面PBC 所成角的正弦值是13.若存在,求出DMDP的值;若不存在,说明理由.【答案】(1)证明见解析;(2)存在,且12DM DP .【解析】(1)设E 是CD 的中点,连接AE ,由于//,,AB CE AB CE AB BC ,所以四边形ABCE 是矩形,所以AE AB ,由于PA 平面ABCD ,所以,PA AB PA AE ,以A 为空间坐标原点建立如图所示空间直角坐标系,0,0,1,0,1,0,2,1,0,2,1,0P B C D ,112,,22N ,0,1,1,2,1,1PB PC u u r u u u r,设平面PBC 的法向量为 ,,x y z n ,则0220PB y z PC y z u u r u u u r n n ,故可设 0,1,1 n ,0AN u u u rn ,且A 平面PBC ,所以//AN 平面PBC .(2)2,1,1DP u u u r ,设 01DM t t DP,则 2,,DM tDP t t t u u u u r u u u r ,222,1,AM AD DM t t t u u u r u u u r u u u u r,2,2,CM AM AC t t t u u u r u u u r u u u r,设直线CM 与平面PBC 所成角为 ,则1sin 3CM CMu u u r u u u r n n22222132222t t t t,两边平方并化简得241670t t ,解得12t或72t (舍去),所以存在M ,使直线CM 与平面PBC 所成角的正弦值是13,且12DM DP .13.如图在直三棱柱111ABC A B C 中,90BAC o ,12AB AC AA ,M 为AB 的中点,N 为11B C 的中点,H 是11A B 中点,P 是1BC 与1B C 的交点,Q 是1A N 与1C H 的交点.(1)求证:11A C BC ;(2)求证:PQ ∥平面1A CM ;(3)求直线PQ 与平面1A CM 的距离.【答案】(1)证明见解析;(2)证明见解析;(3)63.【解析】(1)证明:法一:在直三棱柱111ABC A B C 中,因为90BAC ,以点A 为坐标原点,1AB CA AA u u u r u u r u u u r 、、方向分别为x y z 、、轴正方向建立如图所示空间直角坐标系.因为12AB AC AA ,所以 10,0,2,0,2,0A C , 12,0,0,0,2,2B C ,所以 12,2,2BC u u u r , 10,2,2A C u u u r,所以 110,2,22,2,20A C BC u u u r u u u r,所以11A C BC .法二:连接1AC ,在直三棱柱111ABC A B C 中,有1AA 面ABC ,AB 面ABC ,所以1AA AB ,又90BAC ,则AB AC ,因为1AA AC A I ,所以AB 面11ACC A ,因为1A C 面11ACC A ,所以1AB A C ,因为11,2AA AC AC AA ,所以四边形11AA C C 为正方形,所以11A C AC ,因为1AB AC A I ,所以1A C 面1ABC ,因为1BC 面1ABC ,所以11A C BC .法三:用三垂线定理证明:连接1AC ,在直三棱柱111ABC A B C 中,有1AA 面ABC ,因为AB 面ABC ,所以1AA AB ,又90BAC o ,则AB AC ,因为1AA AC A I ,所以AB 面11ACC A ,所以1BC 在平面11ACC A 内的射影为1AC ,因为四边形11AA C C 为正方形,所以11A C AC ,因此根据三垂线定理可知11A C BC .(2)证明:法一:因为12,AB AC AA M 为AB 的中点,N 为11B C 的中点,H 为11A B 中点,P 是1BC 与1B C 的交点,所以 10,0,20,2,01,1,1A C P 、、、 1,0,01,1,21,0,2M N H 、、,依题意可知Q 为111A B C △重心,则1123A Q A N u u u r u u u r ,可得22,,233Q,所以11,,133PQ u u u r ,10,2,2A C u u u r , 11,0,2A M u u u u r,设 ,,x y z n 为平面1A CM 的法向量,则1100AC A M u u u r u u u u r n n ,即22020y z x z,取1z ,得2,1x y ,则平面1A CM 的一个法向量为 2,1,1 n .所以 11,,12,1,1033PQu u u r n ,则PQ u u u r n ,因为PQ 平面1A CM ,所以//PQ 平面1A CM .法二:连接BH MH 、.在正方形11AA B B 中,M 为AB 的中点,所以1//BM A H 且1BM A H ,所以四边形1BMA H 是平行四边形,所以1//BH A M,又H 为11A B 中点,所以四边形1AA HM 是矩形,所以1//MH AA 且1MH AA ,因为11//AA C C 且11AA C C ,所以1//MH CC ,1MH C C ,21所以四边形1MHC C 为平行四边形,所以1//C H CM .因为1C H BH H I ,1C H 平面1BHC ,BH 平面1BHC ,CM 平面1A MC ,1A M 平面1A MC ,所以平面1//BHC 平面1A MC ,PQ 平面1BHC ,所以//PQ 平面1A CM .(3)法一:由(2)知平面1A CM 的一个法向量 2,1,1 n ,且//PQ 平面1A CM ,所以PQ 到平面1A CM 的距离与P 到平面1A CM 的距离相等, 10,0,2A , 1,1,1P ,所以 11,1,1PA u u u r,所以点P 到平面1A CM的距离13PA d u u u rn n ,所以PQ 到平面1A CM的距离为3.法二:因为N H 、分别为11B C 和11A B 中点,所以Q 为111A B C △的重心,所以1123A Q A N ,所以Q 到平面1A CM 的距离是N 到平面1A CM 距离的23,取1B H 中点E ,则1//NE C H ,又1//,//C H CM NE CM ,NE 平面1A CM ,CM 平面1A CM ,所以//NE 平面1A CM ,所以N 到平面1A CM 的距离与E 到平面1A CM 的距离相等.设点E 到平面1A CM 的距离为h ,由11E A CM C A ME V V ,得11ΔΔ1133A CM A ME S h S AC ,又1A CM S V 132A ME S V ,所以62h ,所以Q 到平面1A CM的距离是3,所以PQ 到平面1A CM的距离为3.。
2023高考数学二轮专题复习与测试第一部分专题三微专题2立体几何与空间向量课件
专题三 立体几何
所以 AF2=AP2-PF2=14,即 AF=12, 过 F 做 FH⊥BC 交 BC 于 H,分别以 FH、FE、FP 所在的直线为 x,y、z 轴的正方向建立空间直角坐标系,如下图所示:
专题三 立体几何
B(1,-12,0),A(0,-12,0)P(0,0, 23),D(-1,32,0)A→P=(0,12, 23), A→D=(-1,2,0),P→B=(1,-12,- 23), 设平面 PAD 的一个法向量为 n=(x,y,z), 所以AA→→DP··nn==00,,即12-y+x+223yz==00,, 令 x=2,则 y=1,z=- 33, 所以 n=(2,1,- 33),
→ DB·n →
=-
|DB|·|n|
3, 5
所以平面 A1AC1 与平面 AC1D 所成角的正弦值为
1-(-
3)2= 5
10 5.
专题三 立体几何
大题考法 3 平行与垂直关系的证明及空间距离的求解 (2022·广州三模)如图,在四棱锥中 P-ABCD 中,PA⊥AB,PC⊥CD,
BC∥AD,∠BAD=23π,PA=AB=BC=2,AD=4.
专题三 立体几何
设 AB=2,则 A(1,0,0),B(1,2,0),C(-1,2,0), P(0,0, 3),D(-1,0,0),M(-12,0, 23), 所以A→M=(-32,0, 23),P→B=(1,2,- 3), P→C=(-1,2,- 3), 设平面 PBC 的一个法向量为 n=(x,y,z), 则PP→→BC··nn==x-+x2+y-2y-3z=3z0=,0, 令 z= 3,则 y=32,x=0,则 n=(0,32, 3),
专题三 立体几何
设平面 ACF 的一个法向量为 n=(x,y,z),
高考数学第二轮复习专题测试(立体几何与空间向量)
立体几何与空间向量一、选择题:本大题共12小题,每小题5分,共60分.1.(理)空间四边形OABC . 其对角线为OB 、AC 、M 、N 分别为对边OA 、BC 的中点,点G 在线段MN 上,且2||||=GN MG ,现用基向量OC ••OB ••OA ,,表示向量=OC z OB y OA x ++,则x ,y ,z 的值分别为( ) A .••z ••y •x 31,31,31=== B .••z ••y •x 31,31,61=== C .••z ••y •x 31,61,31===D .••z ••y •x 61,31,31=== (文)已知△ABC 所在平面内的一点P ,满足:AP 的中点为Q ,BQ 的中点为R ,GR 的中点P . 设b •a •==,,用a ,b 表示向量AP =( )A .b a 7274+B .b a 7472-C .b a 7274- D .b a 7472+ 2.有以下命题:①如果向量a ,b 与任何向量不能构成空间向量的一组基底,那么a ,b 关系是不共线;②O ,A ,B ,C 为空间四点,且向量••••,,不构成空间的一个基底,那么点O ,A ,B ,C 一定共面;③已知向量a ,b ,c 是空间的一个基底,则向量a +b ,a -b ,c 也是空间的一个基底,其中正确的命题是( )A .①②B .①③C .②③D .①②③3.在棱长为1的正方体ABCD —A 1B 1C 1D 1中,若点P 为△BCD 的重心,则D 1P 与平面ADD 1A 1所成的角的大小为( )A .510arctanB .13132arctanC .1010arctan D .32arctan4.(理)已知正四面体O —ABC ,E 、F 分别为AB 、OC 的中点,则OE 与BF 所成角的余弦值为( )A .32B .31C .61D .53 (文)若O 为原点,对一切θ∈R ,向量cos 1(+=θ,sin 2-θ)的长度的最大值为( )A .15-B .1C .51+D .55.P 为四面体S —ABC 的侧面SBC 内一点,若动点P 到底面ABC 的距离与P 到S 的距离相等,则动点P 的轨迹是侧面SBC 内的( )A .椭圆的一部分B .椭圆或双曲线的一部分C .双曲线或抛物线的一部分D .抛物线或椭圆的一部分6.如图,设P 、Q 为△ABC 内的两点,且AC AB AQ ••AC AB AP 4132,5152+=+=, 则△ABP 的面积与△ABQ 的面积之比为( )A .51B .54 C .41 D .31 7.已知ABCD —A 1B 1C 1D 1为长方体,对角线AC 1与平面A 1BD 相交于点G ,则G 是△A 1BD 的( )A .重心B .垂心C .内心D .外心8.ABCD —A 1B 1C 1D 1是正方体,点P 在线段A 1C 1上运动,异面直线BP 与AD 1所成的角为θ,则θ的取值范围是( )A .)4,0(π••B .)6,0(π••C .⎥⎦⎤ ⎝⎛π3,0•• D .)3,0(π•• 9.已知三棱锥P —ABC 的四个顶点均在半径为1的球面上,且满足••,0=∙ 0=∙PC PB •,0=∙PA PC •,则三棱锥P —ABC 的侧面积的最大值为( )A .2B .1C .21D .41 10.直三棱柱ABC ——A 1B 1C 1中,AC 1与B 1C 在侧面ABB 1A 1上的射影长相等,则△ABC 一定是( )A .直角三角形B .等腰三角形C .等边三角形D .等腰直角三角形11.如果一条直线与一个平面垂直,那么,称此直线与平面构成一个“正交线面对”. 在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是A .48B .18C .24D .3612.对于已知直线a ,如果直线b 同时满足下列三个条件:①与直线a 异面;②与直线a 所成的角为定值θ;③与直线a 的距离为定值d .那么这样的直线b 有( )A .1条B .2条C .3条D .无数条二、填空题:本大题共4小题,每小题5分,共20分,把答案填在题中的横线上.13.已知空间三点A (1,1,1)、B (-1,0,4)、C (2,-2,3),则与的夹角θ的大小是 .14.三棱锥中,已知两相对棱长分别为16和18,其余四条棱长都是17,则此三棱锥的体积是 .15.在平行四边形ABCD 中,AB=AC =1,∠ACD =90°,将它沿对角线AC 折起,使AB 与CD 成60°角,则B 、D 间的距离为 .16.(理)设有四个条件:①平面γ与平面α、β所成的锐二面角相等;②直线a ∥b ,a ⊥平面α、b ⊥平面β;③a ,b 是异面直线,β⊂α⊂•b •a ,,且a ∥β,b ∥α;④平面α内距离为d 的两条平行直线在平面β内的射影仍为两条距离为d 的平行直线;其中能推出α∥β的条件有 .(文)有如下四个命题:①平面α和平面β垂直的充要条件是平面α内至少有一条直线与平面β垂直;②平面α和平面β平行的一个必要不充分条件是α内有无数条直线与平面β平行;③直线a 与平面α平行的一个充分不必要条件是平面α内有一条直线与直线a 平行;④两条直线平行是这两条直线在一个平面内的射影互相平行的既不充分也不必要条件.其中正确的序号是 .三、解答题:本大题共6小题,共70分. 解答应写出文字说明、证明过程或演算步骤.17.(本小题满分10分)如图,已知四棱锥P —ABCD 的底面是直角梯形. ︒=∠=∠90BCD ABC ,AB=BC=PB=PC =2CD ,侧面PBC ⊥底面ABCD .(1)P A 与BD 是否相互垂直,请证明你的结论.(2)求二面角P —BD —C 的大小.(3)求证:平面P AD ⊥平面P AB .18.(本小题满分12分)已知直四棱柱ABCD —A ′B ′C ′D ′的底面是菱形,︒=∠60ABC ,E 、F分别是棱CC ′与BB ′上的点,且EC=BC =2FB =2.(1)求证:平面AEF ⊥平面AA ′C ′C ;(2)求截面AEF 与底面ABCD 所成二面角的大小.19.(本小题满分12分)如图,在四棱锥P —ABCD 中,PD ⊥底面ABCD ,底面ABCD 为正方形,PD=DC ,E 、F 分别是AB ,PB 的中点.(1)求证:EF ⊥CD ;(2)在平面P AD 内求一点G ,使GF ⊥平面PCB ,并证明你的结论.(3)(只理科做)求DB 与平面DEF 所成角的大小.20.(本小题满分12分)如图,已知直三棱柱ABC —A 1B 1C 1的侧棱长为2,底面△ABC 是等腰直角三角形,且︒=∠90ACB ,AC =2,D 是AA 1的中点.(1)求异面直线AB 和C 1D 所成的角;(2)设E 是AB 上一点,试确定E 的位置,使得A 1E ⊥C 1D .(3)(只理科做)在(2)的条件下,求点D到平面B 1C 1E 1的距离.21.(本小题满分12分)如图(甲)所示为一几何体的展开图.(1)沿图中虚线将它们折叠起来,是哪一种几何体?试用文字描述并画图;(2)需要多少个这样的几何体才能拼成一个棱长为6cm的正方体?请你在图(乙)中棱长为6cm的正方体ABCD—A1B1C1D1中指出这几个几何体的名称.(3)如图(丙)所示,设棱长为6cm的正方体ABCD—A1B1C1D1的棱CC1的中点为E,试求:①(文)异面直线EB与AB1所成角的大小;②(理)平面AB1E与平面ABC所成二面角(锐角)的大小.22.(本小题满分12分)已知:如图,一个等腰直角三角形的硬纸片ABC 中,︒=∠90ACB ,AC =4cm ,CD 是斜边上的高,沿CD 把△ABC 折成直二面角.(1)如果你手中只有一把能度量长度的直尺,应该如何确定A ,B 的位置,使二面角A —CD —B 是直二面角?证明你的结论;(2)试在三棱锥的面ABC 上确定一点P ,使DP 与平面ABC 内任意一条直线都垂直,试证明你的结论.(3)如果在折成的三棱锥内有一个小球,求出小球半径的最大值.参考答案1.(理)B )(32213221OM OM ++-+=+=+= .313161)](2121[3221•++=-++-+= (文)D ∵AC AB AC AQ AB AC AR AP 2141])(21[21)(21+=++=+= .21418781•+=⇒+ ∴.7472b •a += 2.C 对于①“如果向量a ,b 与任何向量不能构成空间向量的一组基底,那么,a ,b 的关系一定共线”,所以①错误;对于②,由于)O ,A ,B ,C 为空间四点,且向量••O B •••,,不构成空间的一个基底,故向量••O B •••,,共面,点O ,A ,B ,C 一定共面;对于③,∵向量a ,b ,c 是空间的一个基底,故向量a ,b ,c 不共面,从而可以判断向量a +b ,a -b ,c 也不共面,∴向量a+b ,a-b ,c 是空间的一个基底.3.A 作PQ ⊥AD ,连结D 1Q ,则∠PD 1Q 就是D 1P 与平面ADD 1A 1所成的角,在Rt △PD 1Q 中,,310,321•Q •D PQ == .510tan 11•Q D PQ Q PD •==4.(理)A 如图,设正四面体O —ABC中的棱长为1,=a ,=b ,=c ,则21=∙=∙=∙a c c b b a , 21=(a +b ),21=c -b , 21=∙(a +b )·(21c -b )=∙21(21a ·c +21b ·c -a ·b -|b |2) =21(1214141--+)=21- ∴cos 〈••,〉32232321||||-=∙-=∙BF OE 故OE 与BF 所成角的余弦值为.32• (文)C 设点P 的坐标为(x ,y ),则有⎩⎨⎧-=+=θy θx sin 2cos 1,可得点P 的轨迹方程为圆,1)2()1(:22•y x C =-+- 问题表达的意思是圆上的点到原点距离的最大值,显然结果为.51||•rOC +=+ 5.D ①当侧面SBC ⊥底面ABC 时,过点P 作PH ⊥BC 于H ,点P 到底面ABC的距离即PH ,则|PH |=|PS |,在同一平面内一动点到一定点距离等于它到一定直线距离的轨迹为抛物线,故P 点轨迹为抛物线在△SBC 内的一部分.②当侧面SBC 不垂直于底面ABC 时,设H 为点P 在底面ABC 内射影,过点P 作PG ⊥BC 于G ,设二面角为θ,连结PH 、HG 、PG ,则∠PGH =θ为定值,在Rt △PHG中,|PG |>|PH |,依题意知|PH |=|PS |. 且|PG |=|PH |/sin θ(定值)∴|PG |>|PS |即.)||||(1||||•PG PS •PG PS 为定值< ∴在平面内,一动点到一定点的距离与它到一定直线距离的比为一定值e ,且0<e <1的轨迹为椭圆,故点P 的轨迹为椭圆在△SBC 内的一部分.6.B 如图,设AC AN ••AB AM 51,52==,则+=. 由平行四边形法则知NP ∥AB ,所以•S S ABC ABP 51=∆∆,同理可得41=∆∆ABC ABQ S S . 故ABQ ABP S S ∆∆,即选B.第6题解题图第7题解题图7.A G点一定在面A1DB与面A1ACC1的交线A1O上,而△AGO~△A1GC1,21111==GAGOCAAO,∴G为△A1BD的重心.8.C 连结BC1,则AD1∥BC1,异面直线BP与AD1所成角即∠C1BP,当P运动到C1时,∠C1BP=0(不能取到),当P运动到A1时,∠C1BP=3π,∴0<∠C1BP.3••π≤9.A 设P A=a,PB=b,PC=c,则a2+b2+c2=(2R)2=4,侧面积为)(21acbcabS++=.2)(2122221222222222•cbacacbba=++=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫⎝⎛++⎪⎪⎭⎫⎝⎛++⎪⎪⎭⎫⎝⎛+≤10.B 点A、B1已经在平面ABB1A1内,关键找C、C1的射影位置,取C、C1的射影分别在AB、A1B1的中点即可.11.D 每个面都有4条棱与其垂直,6×4=24,每个对角面都可组成两个“正交线面对”,则6×2=12,∴共有24+12=36.12.D 在正方体ABCD—A1B1C1D1中,设AB=a,CC1=b,则b与a异面,b与a所成的角为定值θ=90°b与a的距离d为定值,那么,在平面CDD1C1中,与b平行的直线也满足全部条件. 故这样的直线有无数条.13.120°∵)2,3,1(,)3,1,2(--=--=••••••••••,∴cos〈••,〉=•211471414)2(33)1()1()2(-=-=∙-⨯+⨯-+-⨯-,∴θ=〈••,〉=120°.14.576 如图所示,AB=16,SC=18,其余各棱长均为17. 取AB的中点M,则SM⊥AB,MC⊥AB,∴面SMC⊥面ABC,过点S作SH⊥底面ABC,在△SMC中SM=MC=15过M作MN⊥SC,N为SC的中点,∴在Rt△SMN中SM=15,SN=9. ∴MN=12.又SH ·MC =SC ·MN ,∴SH =572151218=⨯, ∴.57657215162131—•V ABC S =⨯⨯⨯⨯= 15.2或2 如图,因为︒=∠90ACD , 所以0=∙. 同理,==0. 因为折叠后AB 与CD 成60°角,所以〈••,〉=60°或120°. 因为++=,所以222222222+=∙+∙+∙+++=cos 112322⨯⨯⨯+=∙+〈••,〉⎪⎩⎪⎨⎧︒>=<︒>=<=)120,(2)60,(4••••••,所以|BD |=2或2,即B 、D 间的距离为2或2.16.(理)②③ 容易得知命题①是错的,命题②③都是对的,对于命题④,我们考查如图所示的正方体,设正方体的棱长为d ,显然D C B A ''与为平面D BC A ''内两条距离为d 的平行直线,它们在底面ABCD 内的射影AB 、CD 仍为两条距离为d 的平行直线;但两平面D BC A ''与平面ABCD 却是相交的.(文)①②④ ③中a 有可能在α内.17.取BC 的中点O ,由侧面PBC ⊥底面ABCD ,△PBC 是等边三角形,得PO ⊥底面ABCD . 以BC 中点O 为原点,以BC 所在直线为x 轴,过点O 与AB 平行的直线为y 轴,建立如图所示的空间直角坐标系O —xyz ,设CD =1,则在直角梯形中,AB=BC =2,在等边三角形PBC 中,3=PO ,∴)3,0,0(,)0,1,1(,),0,0,1(,)0,2,1(••••P ••••••D ••••••B •••A ---,.)3,2,1(,)0,1,2(••••••PA ••••••BD --=--=(1)P A 与BD 相互垂直,证明如下: ∵0)3(0)2()1(1)2(=-⨯+-⨯-+⨯-=∙,∴.BD •PA ⊥ (2)连结AO ,设AO 与BD 相交于点E ,连结PE , 由000)1()2()2(1=⨯+-⨯-+-⨯=∙,得BD AO ⊥,又∵AO 为P A 在平面ABCD 的射影.∴PEO •BD •PE ∠⊥,为二面角P —BD —C 的平面角.在Rt △BEO 中,OE=OB ·sin OBE =.55• 在Rt △BEO 中,15tan ==OE PO PEO . ∴二面角P —BD —C 的大小为.15arctan •(3)取P A 的中点M ,连结DM ,则M 的坐标为••••••.23,1,21⎪⎪⎭⎫ ⎝⎛-又⎪⎪⎭⎫ ⎝⎛=23,0,23••••,)3,2,1(,)3,0,1(--=-=••••••••••, ∴.0•=∙0=∙,∴⊥,⊥,即•PB ••D M PA ••D M ,,⊥⊥ ∴⊥DM 平面P AB . ∴平面P AD ⊥平面P AB .考点备忘 本题主要考查线垂直、面面垂直、二面角的大小的有关知识及思维能力与空间想象能力,立体几何的证明通过向量工具的计算来解决,显得尤为的简易.18.(1)以O 为原点,O O ••••',,分别为x ,y ,z 轴建立直角坐标系,由条件知:EC=BC =2,FB =1,OA =1,OB =3,从而坐标E (0,1,2),F (3,0,1). (1)连结AE 与O O '交于M ,连结MF , 可得121==EC MO ,M (0,0,1), =(3,0,0).则MF ⊥平面yOz ,即MF ⊥平面C AC A '',所以平面AEF ⊥平面C AC A ''.(2)取EC 中点G ,得平面MFG ∥底面ABCD ,所以只要求面AEF 与面MFG 所成的二面角即可.•••••••••••••••••••••••G 0,0,)0,1,0(,)1,1,0(,)1,1,0(=∙=∙==, 即MG MF ••ME MF ⊥⊥,,可见EMG ∠是面AEF 与面MFG 所成二面角的平面角.在Rt △MGE 中,EG =1,MG =1,ME =2,显然4π=∠EMG ,所求二面角为4π. 考点备忘 用空间向量解决立体几何问题,通常先建立空间直角坐标系,而证明面面垂直、二面角都是通过法向量完成的,即面面垂直只需要平面的法向量垂直;求二面角则根据实际情况选择法向量的夹角.19.以DA ,DC ,DP 所在直线为x 轴,y 轴,z 轴建立空间直角坐标系,如图,设AD =a ,则)0,0,(,)0,0,0(•••a ••A •••••D ,),0,0(,)2,2,2(,)0,2,(,)0,,0(,)0,,(a ••••P •a ••a ••a •F •••a •a ••E •••a •••C ••a •a •B(1)••••a ••••a ••••a ,0)0,,0(,2,0,2=⎪⎭⎫ ⎝⎛-=∙ ∴.DC •EF ⊥ (2)设),0,(•z••x •G ,则G ∈平面P AD . ⎪⎭⎫ ⎝⎛---=2,2,2a •z •a ••a x , =∙CB FG ⎪⎭⎫ ⎝⎛---2,2,2a •z •a ••a x 02)0,0,(=⎪⎭⎫ ⎝⎛-=∙a x a •••a •,则2a x =; 0)2(2),,0(2,2,22=-+=-∙⎪⎭⎫ ⎝⎛---=∙a z a a •a a •••a •z •a ••a x ,则z =0. ∴G 是坐标为(2a ,0,0),即G 为AD 的中点. (3)(只理科做)设平面DEF 的法向量为.)(•n z y •,x •,= 由⎪⎩⎪⎨⎧=∙=∙.,•n •n 00DE 得⎪⎪⎩⎪⎪⎨⎧=∙=⎪⎭⎫ ⎝⎛∙.••,a •a •,z y •,x •,,a ••,a ••,a z y •,x •,•0)02()(•0222)(即⎪⎪⎩⎪⎪⎨⎧=+=++.•y a ax z y x a 020•,)(2取x =1,则y =-2,z =1,∴ n =(1,-2,1).cos 〈•n ,•BD 〉,•6362=∙=a a ∴DB 与平面DEF 所成角大小为63arccos 2-π (即arcsin 63). 考点备忘 本题主要考查线线垂直,线面垂直,线面角. 第(2)问是找出G 的位置,通过方程的思想来解决G 点的位置,线面角的问题是高考的热点考题,解答此题需要一定的空间想象和运算等方面的能力.20.(1)如图,取CC 1的中点F ,连结AF ,则AF ∥C 1D ,故∠BAF (工其补角)为异面直线AB 与C 1D 所成的角.在△ABF 中,AB =22,AF=BF =5,则cos BAF =.•BAF •.•AF AB 510arccos 5105221=∠== (2)过C 1作C 1G ⊥A 1B 1,垂足为G ,则G 为A 1B 1的中点,且C 1G ⊥AA 1B 1B ,故GD 为C 1D 在平面AA 1B 1B 上的射影. 由A 1E ⊥C 1D ,可知A 1E ⊥DG .在矩形AA 1B 1B 中,AB =22,AA 1=2,D 为AA 1的中点,G 为A 1B 1的中点,在Rt △DA 1G 中,DH =3321=DG D A ,又sin EA 1A =E A AE D A DH 11=,∴AE =AB 212=, ∴E 为AB 的中点.(3)(只理科做)设点D 到平面B 1C 1E 的距离为h .易知点C 1到平面B 1ED 的距离为2,2232111=∙=∆DE E B S ED B , 则.•V ED B —C 111=在E C B 11∆中,B 1C 1=2,则B 1E =C 1E =6,则.•S E C B 511=∆由ED B —C E C B —D V V 1111=,得1531=⨯⨯h ,解得553=h . 考点备忘 在求解角的问题时,注意紧扣定义,寻求角的位置,将空间胸转化为平面角来处理;计算空间距离特别是点到平面的距离转化为用等体积法来计算,使问题更加简捷.21.(1)有一条侧棱垂直于底面且底面为正方形的四棱锥,如图甲所示.甲 乙(2)需要3个这样的几何体,如图乙所示,分别为四棱锥A 1—CDD 1C 1,A 1—ABCD ,A 1—BCC 1B 1.(3)①(文)取DD 1中点F ,连结AF ,则AF ∥BE .∴∠F AB 1为异面直线EB 与AB 1的成的角.易计算得B 1F =9cm ,AF =53cm ,AB 1=26cm. ∴1010265328172452cos 1212121=⨯⨯-+=∙-+=AB AF FB AB AF FAB cm. ∴异面直线EB 与AB 1所成角为arccos 1010. ②(理)设B 1E ,BC 的延长线交于点G ,连结GA ,则GA 为平面AB 1E 与平面ABC 所成二面角的棱,在底面ABC 内作BH ⊥AG ,垂足为H ,连结HB 1,由三垂线定理知:B 1H ⊥AG .∴∠B 1HB 为平面AB 1E 与平面ABC 所成二面角的平面角.在Rt △ABC 中,BH =51214436126=+⨯cm , ∴5183651442121=+=+=BB BH HB cm, ∴ cos 3211==HB HB HB B , ∴ 平面AB 1E 与平面ABC 所成二面角为arccos 32. 考点备忘 本题考查折叠后与图形的对照来研究图形的特征,培养了学生的空间想象能力和逻辑思想能力,然后在图形中考查异面直线所成角和二面角的问题.22.(1)用直尺度量折后的AB 长,若AB =4cm ,则二面角A —CD —B 为直二面角.∵△ABC 是等腰直角三角形,∴AD=DB=CD =22cm.. 又∵AD ⊥DC ,BD ⊥DC , ∴∠ADB 是二面角A —CD —B 的平面角.∵AD=DB =22cm ,当AB =4cm 时,有AD 2+DB 2=AB 2,∴∠ADB =90°,(2)取△ABC 的中心P ,连结DP ,则DP 满足条件.∵△ABC 为正三角形,且AD=DB=DC ,∴三棱锥D —ABC 是正三棱锥.由P 为△ABC 的中心,则DP ⊥平面ABC .∴DP 与平面ABC 内任意一条直线都垂直.(3)当小球半径最大时,此小球与三棱锥的四个面都相切. 设小球球心为O ,半径为r ,连结OA ,OB ,OC ,OD ,则三棱锥被分为四个小棱锥,则有•V V V V V ABC —O ABD —O BCD —O ADC —O BCD —A +++=, 即⎥⎦⎤⎢⎣⎡∙∙+∙∙∙2242321)2(232131r 即3)2(261r )388(361=∙+∙ ,•22)2(221312∙∙∙= ∴•.•r 36233322-=+=故小球半径最大值为.•3623- 考点备忘 本题通过折叠来构造的立体图形,而且要求动手去解决问题,培养了空间想象能力和逻辑思维能力,第(3)问通过体积法来解决小球的半径的最大值,具有一定的综合性,也正是高考命题的热点方向之一.。
(完整word版)空间向量与立体几何测试题及答案
高中 数学选修(2-1)空间向量与立体几何测试题一、选择题1 •若把空间平行于同一平面且长度相等的所有非零向量的始点放置在同一点,则这些向量 的终点构成的图形是()A. —个圆 E. —个点 C.半圆 D.平行四边形答案:A2 .在长方体 ABCD -ABQD i 中,下列关于 AG 的表达中错误的一个是( )答案:E3.若a , b, c 为任意向量, A. (a 亠b ) c =a - (b c )B. (a 亠b )・c =a ・c b-cC.m(a 亠 b ) =m a 亠 m bD. (a ・b )・c=a ・( b-c ) 答案:D1A. 1B. -1C.丄D -22答案:BA.B. AB DD^ De lC. AD CC 1 DC 1D.1(AB i CD i ) - AC im R ,下列等式不一定成立的是(4.若三点A B , e 共线,P 为空间任意一点, 且 PA 叱iPB = 1 PC ,^y - 的值为5. 设 a =(x,4,3), b= (3,2, z),且 a II b , A. -4 B. 9 C. -9答案:B6 . 已知非零向量 e b e 2不共线, 如果A B, C , D ( )A. 一定共圆则四点亠A DB.恰是空间四边形的四个顶点心C. 一定共面D. 肯定不共面答案:C则xz 等于(AB = e AC =2 e 2 8 e AD =3 e -3 e 2,答案:B则x, y , z 的值分别为( )9 .若向量a =(1, ,2)与b= (2, -1,2)的夹角的余弦值为答案:c答案:D12.给出下列命题:① 已知 a _b ,则 a-(b c ) c-(b a ) =b c ;② A, B, M , N 为空间四点,若BA,B M ,BN 不构成空间的一个基底, 那么A , B, M , N 共面; ③ 已知a_b ,则a , b 与任何向量都不构成空间的一个基底; ④ 若a, b 共线,则a, 正确的结论的个数为(A. 1B. 2 答案:C 二、填空题13.已知 a =(3,15), b = (1,2,3),向量 c 与 z 轴垂直,且满足 c-a = 9, c-b - -4,则 c =7.如图1空间四边形 ABCD 的四条边及对 角线长都是a ,点E , F , G 分别是AB, AD , CD 的中点,贝U a 2等于() B. 2AD-BD C. 2FG-CAD. 8 .右 a = e e 2 - e 3, b =e ^ - e 2 ■ e 3, c =e<i • e 2 — e 3,d =e 2 e 2 3 e ,且 d = x a y b z c ,1.1,2 5 厶D1 - 1「25 /1 - 1「2 5 ~1 - 2-A. 2B. -2C.-2或—55D. 2 或-5510 •已知ABCD 为平行四边形,且A(413),A. -,4,12答案:DB. (2,4,1) 11 .在正万体 ABCD - A| B 1C 1D 1 中,A. 60°B. 90°B(2,— 5,1), C(3,7, -5),则顶点D 的坐标为(C. (24,1)D. (513, -3)O 为AC , BD 的交点,则 C品C. arccos ——3GO 与AD 所成角的(D. arccos ——6b 所在直线或者平行或者重合.)D. 4A. 2EF-CB答案:22, -21 , 0 5 514.已知A B, C 三点不共线,O 为平面ABC 外一点,若由向量 ■ OC 确5 3 定的点P 与A, B, C 共面,那么,二 ____________ . 答案:-1515.已知线段 AB_面〉,BC 二卅,CD _BC , DF _ 面〉于点 F , / DCF =30°,且 D , A 在平面:-的同侧,若 AB =BC 二CD =2,则AD 的长为 ____________________ . 答案:2 216.在长方体ABCD —ABQ i D i 中,BQ 和CQ 与底面所成的角分别为 60°和45°,则异面直 线BC 和CQ 所成角的余弦值为 _____________________ . 答案:—4 三、解答题17 .设 a t =2i - j +K 逊=i +3 j -2 k 爲=-2 i + j 弋 k a =3 i +2 j +5 k,试问是否存在实 数-,7,使a 4 a 「;[_a 2 •a 3成立?如果存在,求出 \ ;如果不存在,请写出证明.答案:解:假设a 4 = ■ a^ ''a 2亠、.①成立. •- a 1 =(2, -1,1), a 2 =(13, -2), a 3 =(-21,3), a^(3,2,5), ••• (2 •-2、,-,3二朕:,• -2」- 3、)=(3,2,5).◎人+4-2v=3, j\ = -2, •. -2,解得」=1,■ -2」-3.. =5,- -3.所以存在,=-2, " =1 , v = -3 使得 a 4 = -2a 1 a 2 -3a 3. 理由即为解答过程.18 .如图2,正三棱柱AB^ -A 1B 1C 1的底面边长为a ,侧棱长为 所成的角.解:建立如图所示的空间直角坐标系,则 A(0,0, 0, B(0 , a , 0, A (0,0, V2a) , C 「一亟 a, - , ,7a2 2 由于n = ( -1,0, 0)是面ABB 1A ]的法向量,1*122a ,求AC 1与侧面ABB 1A\故AC i与侧面ABB i A所成的角为30°.19 •如图3,直三棱柱ABC- ABC中,底面是等腰直角三角形, .ACB 二90°,侧棱AA i =2, D, E分别是CC i与AB的中点,点E在平面ABD上的射影是求点A i到平面AED的距离. △ ABD的重心G ,解:建立如图所示的空间直角坐标系,设CA=2a ,则A(2a,0,0, B(0,2a,0, D(0,0,1), A(2a,0,2) E(a, a,),-(0 , -2a,1).由GE_BD=GE・BD=0,得a=1,则A i(2,0,2) A(2,0,0) E(1,1,1).自A1作AH —面AED于M,并延长交xOy面于H,设H (x, y,0), —I则AH =(x —2, y, -2).又AD =(-2,0,1) , AE =(—1,1,1).丄AH _AD, —2(x—2)—2=0, x =1, ZR由1得H (1,1,0)."H _ AE -(x -2) y -2 =0 y =1,又AM =A1A90s A1AAM = AA^cos A1AAH =2 —=20.已知正方体ABCD -ABGD1的棱长为2, P, Q分别是BC, CD上的动点,且PQ = . 2 ,确定P, Q的位置,使QB1 _PD . 解:建立如图所示的空间直角坐标系,设BP =t ,得CQ = 2 -(2 -t)2, DQ =2 - 2 -(2 -t)2.那么B(2,0, 2) D1(0,2,2, P(2 , , 0) Q(2 - 2-(2-t)2,2,0),从而QB =( 2 -(2 -t)2, -2 ,2) , PD1 =(22 -t,2),T —+由QB _ PD = QB^PD t =0 ,即-2 2 -(2 -t)2 -2(2 -t) 4 =0二t =1 .故P, Q分别为BC, CD的中点时,QB i _PD i .21.如图4,在底面是直角梯形的四棱锥S—ABCD中,.ABC=90°,SA_面ABCD ,1SA二AB二BC =1, AD ,求面SCD与面SBA所成二面角的正切2值.解:建立如图所示的空间直角坐标系,(1\则A(0,0,0, B(—1,0,0, C(—1,1,0) D .0, 2 0 , S(0,0,1).延长CD交x轴于点F ,易得F(1,0, 0),作AE _SF于点E ,连结DE ,则ZDEA即为面SCD与面SBA所成二面角的平面角.又由于SA二AF且SA_AF,得E -€5那么从而乩一1,°,」,ED…丄,1,V 2 2 丿V 2 2cos EA, EDEA-ED因此tan EAF , ED 二彳.故面SCD与面SBA所成二面角的正切值为22.平行六面体ABCD -A1B1C1D1的底面ABCD是菱形,且.GCB =. GCD = BCD ,试问:CD的值为多少时,AQ _面GBD ?请予以证明.当CG解:欲使AQ _面GBD ,只须AC _GD ,且AC _GB .欲证AC丄GD ,只须证CA・CD =0 ,t —t T 即(CA AA)・(CD -CG) =0 ,也就是(CD CB CC)(CD _CCJ =0,|C^2 -|C CJ2+|CB|C D|COS^BCD由于• GCB =/BCD , 显然,当CD |CC1时,上式成立;cos _GCB = 0 .同理可得,当时,AC —GB .CD因此,当时, AC _面G BD ..选择题:(10小题共40分)定共面的是2.直三棱柱 ABC — A B i G 中,若 CA = a, CB = b, CC r = C,则 A )B =3.若向量m 垂直向量a 和b ,向量n = ■ a h :b(',」:=只且■、,北0)则A. m 〃 nB. m _ nC. mi 不平行于n,m 也不垂直于nD.以上三种情况都可台匕 冃匕4.以下四个命题中,正确的是C. (a b)c5.对空间任意两个向量 a,b(b o),a//b 的充要条件是6.已知向量a =(0,2,1),b =(-1,1,-2),则a 与b 的夹角为A B i = a, A i D i = b, A A = c ,则下列向量中与B 1M 相等的是1.已知A B C 三点不共线,对平面ABC 外的任一点O,下列条件中能确定点 M 与点A. OM = OA 亠 OB 亠 OCB . OM = 2OA _ OB _ OCC . OM =OA !OB !OC2 3D.OM =1OA 」0B -OC3 3 3A. a b —cB. a — b eC. 一 a b cD. - a b - cA.若00=丄0入+丄0目 则P 、 2 3 'A 、E 三点共线 B.设向量{a,b,c }是空间一个基底,c + a }构成空间的另一个基底D. △ ABC 是直角三角形的充要条件是 AB AC =0A. a 二 bB. a - -bC. b - ■ aA.0 °B.45C.90o.D.180 °7.在平行六面体 ABCD - A 1B 1C 1D 1中,M 为AC 与 BD 的A. -lalb lc B. la 」b 」c C. 2 2 2 28.已知 a =(• 1,0,2 Jb =(6,2」 -1,2),若a 〃b,则•与•啲值分别为9.已知a =3i 2j - k,b = i - j 2k,则5a 与3b 勺数量积等于10.在棱长为1的正方体ABC —A i B i CD 中,M 和N 分别为AB 和BB 的中点,那么直线CN所成角的余弦值是二.填空题:(4 小题共16分)11.若 A(m+1,n-1,3),B(2m,n,m-2n),c(m+3,n-3,9) 12.已知 A(0, 2, 3), B(-2 , 1, 6), C( 1, -1 , 5),若|a |二.3,且a _ AB,a _ AC,则向量 a的坐标为13.已知a,b 是空间二向量,若心|=3,闪|=2扁4卜.7,则a 与b 的夹角为 14.已知点 G 是厶ABC 的重心,O 是空间任一点,若 OA • OB • OC 」OG,贝,的值三.解答题:(10+8+12+14=44 分)15. 如图:ABCD 为矩形,PAL 平面 ABCD PA=AD M N 分别是PC AB 中点,16. 一条线段夹在一个直二面角的两个面内, 它和两个面所成的角都是300,求这条线段与这个二面角的棱所成的角的大小B.5, 2D.-5 , -2-b c 2A.-15B.-5C.-3D.-1AM 与2 B.-5C.35 D 」10三点共线,则 m+n= (1)求证:MN L 平面PCD (2)求NM 与平面 ABCD 所成的角的大小•17. 正四棱锥S—ABCD中,所有棱长都是2, P为SA的中点,如图(1) 求二面角B—SC- D的大小;(2)求DP与SC所成的角的大小18. 如图,直三棱柱ABC-A1B1C1,底面△ ABC中,CA=CB=1 / BCA=90,棱AA=2, M N分别是A1B1, AA的中点;(1)求BN的长;⑵求cos ::: BA1,CB1的值;⑶求证:AB _CM•(4)求CB与平面AABB所成的角的余弦值高中数学选修2-1测试题(10)—空间向量⑴参考答案DDBB DCDA AB 11.0 12.(1 ,1 , 1) 13.60 0 14.315.(1) 略⑵45 016.45 0 17.(1) 1 3⑵18.(1) 3 (2) ■ 30(3) 略(4) 3 1010 1018.如图,建立空间直角坐标系O—xyz. (1 )依题意得B ( 0, 1, 0)、N( 1, 0, 1) •••I BN |= .(1 一0)2(0 一1)2 (1 - 0)2「3.(2) 依题意得A1 (1, 0, 2)、B ( 0, 1 , 0)、C (0, 0, 0)、B…BA ={ —1, —1, 2}, CB1 ={0, 1, 2, }, BA| • CB1 =3,BA. CB 11CB 1 |= J5 ••• cos< BA 1 , CB 1 >=(3)证明:依题意,得 G (0, 0, 2)、M( 1,1,2), A 1B ={ - 1 , 1 , 2} , CM,2 2 1 2 2评述:本题主要考查空间向量的概念及运算的基本知识 .考查空间两向量垂直的充要条件——-1 . 30. |BAJ|CB i |102‘20}. • A , B • C 1M =-1 12+ 2+0=0,AB 丄 C 1M ,• AB 丄CM.。
2023年人教版高考数学总复习第一部分考点指导第八章立体几何第五节空间向量的运算及其坐标表示
3.空间向量有关运算
(1)坐标运算:设a=x1,y1,z1 ,b=x2,y2,z2 , 则a+b= (x1 x2,y1 y2,z1 z2 ) ; a-b= (x1 x2,y1 y2,z1 z2 ) ; λa= (x1, y1,z1) .
(2)数量积运算:a·b= x1x2+y1y2+z1z2 = |a||b|cos〈a,b〉.
B.共面 C.共线 D.不共线
②对空间中四点 A,B,C,P,若A→P =81 A→B +18 A→C ,则 P,A,B,C 四点( )
A.不共面
B.共面 C.共线 D.不共线
பைடு நூலகம்
③对空间中四点 A,B,C,P,若空间任意一点 O 都有O→P =43 O→A +81 O→B +
1 8
O→ C
,则 P,A,B,C 四点(
(2)已知a=(2,-1,3),b=(-1,4,-2),c=(7,5,λ),若a,b,c三向量共
面,则实数λ等于(
A.672
B.673
) C.674
D.675
【解析】选D.由a,b,c三向量共面,设a=mb+nc,
则(2,-1,3)=m(-1,4,-2)+n(7,5,λ),
2=-m+7n
即 -1=4m+5n ,解得λ=675 . 3=-2m+nλ
=12
O→ A
+23
1 (2
O→ B
+12
O→ C
-21
O→ A
)=61
O→ A
+13
O→ B
+13
O→ C
,
所以x=16 ,y=13 ,z=13 .
答案:16 ,31 ,13
2.如图,在长方体ABCD-A1B1C1D1中,O为AC的中点. ①化简 A1O -12 A→B -21 A→D =________. ②用A→B ,A→D , AA1 表示 OC1 ,则 OC1 =________.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题能力训练13空间向量与立体几何
(时间:60分钟满分:100分)
一、选择题(本大题共8小题,每小题5分,共40分)
1.直三棱柱ABC-A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1,AA1=,M是CC1的中点,则异面直线AB1与A1M所成的角为()
A.60°
B.45°
C.30°
D.90°
2.已知平面α内有一点M(1,-1,2),平面α的一个法向量为n=(6,-3,6),则下列点P中,在平面α内的是()
A.P(2,3,3)
B.P(-2,0,1)
C.P(-4,4,0)
D.P(3,-3,4)
3.在正方体ABCD-A1B1C1D1中,E为BB1的中点,则平面A1ED与平面ABCD所成的锐二面角的余弦值为()
A B C D
4.(2017浙江金华联盟联考)已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则直线BD1与平面ABCD所成的角的正切值为()
A B C D
5.在棱长为1的正方体ABCD-A1B1C1D1中,M是BC的中点,P,Q是正方体内部或面上的两个动点,则的最大值是()
A B.1 C D
6.在直三棱柱A1B1C1-ABC中,∠BAC=,AB=AC=AA1=1,已知G和E分别为A1B1和CC1的中点,D与F分别为线段AC和AB上的动点(不包括端点),若GD⊥EF,则线段DF的长度的取值范围为()
A B
C D
7.
如图,在四棱锥P-ABCD中,侧面PAD为正三角形,底面ABCD为正方形,侧面PAD⊥底面ABCD,M
为底面ABCD内的一个动点,且满足MP=MC,则点M在正方形ABCD内的轨迹为()
8.如图,在棱长为1的正方体ABCD-A1B1C1D1中,P,Q分别是线段CC1,BD上的点,R是直线AD上的点,满足PQ∥平面ABC1D1,PQ⊥RQ,且P,Q不是正方体的顶点,则|PR|的最小值是()
A B C D
二、填空题(本大题共6小题,每小题5分,共30分)
9.如图所示,在正方体ABCD-A1B1C1D1中,棱长为a,M,N分别为A1B和AC上的点,A1M=AN=,则MN 与平面BB1C1C的位置关系是.
10.(2017浙江杭州模拟)在长方体ABCD-A1B1C1D1中,AB=2,BC=AA1=1,则D1C1与平面A1BC1所成角的正弦值为.
11.过正方形ABCD的顶点A作线段PA⊥平面ABCD,若AB=PA,则平面ABP与平面CDP所成的二面角为.
12.
如图,正方体ABCD-A1B1C1D1的棱长为3,在面对角线A1D上取点M,在面对角线CD1上取点N,使得MN∥平面AA1C1C,当线段MN长度取到最小值时,三棱锥A1-MND1的体积为.。
