高考数学中档大题规范练(4)——立体几何
2018版考前三个月高考数学理科总复习中档大题规范练3:立体几何(含解析)

3.立体几何1.(2017·全国Ⅲ)如图,四面体ABCD 中,△ABC 是正三角形,△ACD 是直角三角形,∠ABD=∠CBD ,AB =BD. (1)证明:平面ACD ⊥平面ABC ;(2)过AC 的平面交BD 于点E ,若平面AEC 把四面体ABCD 分成体积相等的两部分,求二面角D -AE -C 的余弦值.(1)证明由题设可得△ABD ≌△CBD.从而AD =CD ,又△ACD 为直角三角形,所以∠ADC =90°,取AC 的中点O ,连接DO ,BO ,则DO ⊥AC ,DO =AO ,又因为△ABC 是正三角形,故BO ⊥AC ,所以∠DOB 为二面角D -AC -B 的平面角,在Rt △AOB 中,BO 2+OA 2=AB 2,又AB =BD ,所以BO 2+DO 2=BO 2+AO 2=AB 2=BD 2,故∠DOB =90°,所以平面ADC ⊥平面ABC.(2)解由题设及(1)知,OA ,OB ,OD 两两垂直,以O 为坐标原点,OA →为x 轴正方向,OB →为y 轴正方向,OD →为z 轴正方向,|OA →|为单位长度,建立如图所示的空间直角坐标系Oxyz ,则O(0,0,0),A ()1,0,0,D ()0,0,1,B ()0,3,0,C(-1,0,0),由题意知,四面体ABCE 的体积为四面体ABCD 的体积的12,从而E 到平面ABC 的距离为D 到平面ABC 的距离的12,即E 为DB 的中点,得E 0,32,12,故AE →=-1,32,12,AD →=()-1,0,1,OA →=()1,0,0.设平面AED 的法向量为n 1=(x 1,y 1,z 1),平面AEC 的法向量为n 2=(x 2,y 2,z 2),则AE →·n 1=0,AD →·n 1=0,解得n 1=1,33,1,AE →·n 2=0,OA →·n 2=0,解得n 2=(0,-1,3),设二面角D -AE -C 为θ,易知θ为锐角,则cos θ=|n 1·n 2||n 1||n 2|=77.2.(2017·河南百校联盟模拟)在如图所示的直三棱柱ABC -A 1B 1C 1中,D ,E 分别是BC ,A 1B 1的中点.(1)求证:DE ∥平面ACC 1A 1;(2)若AB ⊥BC ,AB =BC ,∠ACB 1=60°,求直线BC 与平面AB 1C 所成角的正切值.(1)证明取AB 中点F ,连接DF ,EF.在△ABC 中,因为D ,F 分别为BC ,AB 的中点,所以DF ∥AC ,又DF ?平面ACC 1A 1,AC?平面ACC 1A 1,所以DF ∥平面ACC 1A 1.在矩形ABB 1A 1中,因为E ,F 分别为A 1B 1,AB 的中点,所以EF ∥AA 1,又EF ?平面ACC 1A 1,AA 1?平面ACC 1A 1,所以EF ∥平面ACC 1A 1.因为DF ∩EF =F ,所以平面DEF ∥平面ACC 1A 1.因为DE?平面DEF ,故DE ∥平面ACC 1A 1.(2)解因为三棱柱ABC -A 1B 1C 1为直三棱柱,所以BC ⊥BB 1,又AB ⊥BC ,AB ∩BB 1=B ,所以BC ⊥平面ABB 1A 1.因为AB =BC ,BB 1=BB 1,所以△ABB 1≌△CBB 1,AB 1=CB 1,又∠ACB 1=60°,所以△AB 1C 为正三角形,所以AB 1=AB 2+BB 21=AC =2AB ,所以BB 1=AB.取AB 1的中点O ,连接BO ,CO ,所以AB 1⊥BO ,AB 1⊥CO ,所以AB 1⊥平面BCO ,所以平面AB 1C ⊥平面BCO ,点B 在平面AB 1C 上的射影在CO 上,所以∠BCO 即为直线BC 与平面AB 1C 所成的角.在Rt △BCO 中,BO =22AB =22BC ,所以tan ∠BCO =BO BC =22. 3.(2017·中原名校豫南九校模拟)如图,在矩形ABCD 中,AB =1,AD =a ,PA ⊥平面ABCD ,且P A =1,E ,F 分别为AD ,P A 的中点,在BC 上有且只有一个点Q ,使得PQ ⊥QD. (1)求证:平面BEF ∥平面PDQ ;(2)求二面角E -BF -Q 的余弦值.(1)证明方法一(向量法)以A 点为原点,分别以AB →,AD →,AP →的方向为x 轴,y 轴,z 轴的正方向,建立空间直角坐标系Axyz ,则A(0,0,0),B(1,0,0),D(0,a ,0),P(0,0,1),设Q(1,x ,0),则PQ →=(1,x ,-1),QD →=(-1,a -x ,0),若PQ ⊥QD ,则PQ →·QD →=-1+x(a -x)=0,即x 2-ax +1=0,Δ=a 2-4=0,∴a =2,x =1.∴Q ()1,1,0,QD →=()-1,1,0,又E 是AD 的中点,∴E ()0,1,0,BE →=()-1,1,0,∴QD →=BE →,∴BE ∥DQ ,又BE?平面PDQ ,DQ?平面PDQ ,∴BE ∥平面PDQ ,又F 是P A 的中点,∴EF ∥PD ,∵EF ?平面PDQ ,PD ?平面PDQ ,∴EF ∥平面PDQ ,∵BE ∩EF =E ,BE ,EF?平面BEF ,∴平面BEF ∥平面PDQ.方法二(几何法)题意转化为矩形ABCD 中AQ 垂直于QD 的点Q 只有一个,则以AD 为直径的圆与线段BC 相切,易得BC =2,Q 是线段BC 的中点,由BE ∥QD ,EF ∥DP ,易得两平面平行.(2)解设平面BFQ 的一个法向量m =()x ,y ,z ,则m ·BF →=m ·BQ →=0,由(1)知,BF →=-1,0,12,BQ →=()0,1,0,∴-x +12z =y =0,取z =2,得m =()1,0,2,同样求得平面BEF 的一个法向量n =()1,1,2,cos 〈m ,n 〉=m ·n ||m ||n =306,∵二面角E -BF -Q 为锐角,∴二面角E -BF -Q 的余弦值为306. 4.(2017·云南大理统测)在四棱锥P -ABCD 中,底面ABCD 是正方形,侧面P AD ⊥底面ABCD ,且P A =PD =22AD ,E ,F 分别为PC ,BD 的中点. (1)求证:EF ∥平面PAD ;(2)在线段AB 上是否存在点G ,使得二面角C -PD -G 的余弦值为33,若存在,请求出点G 的位置;若不存在,请说明理由.(1)证明连接AC ,由正方形性质可知,AC 与BD 相交于点F ,所以在△P AC 中,EF ∥P A ,又P A?平面PAD ,EF ?平面PAD ,所以EF ∥平面P AD.(2)解取AD 的中点O ,连接OP ,OF ,因为P A =PD ,所以PO ⊥AD ,又因为侧面P AD ⊥底面ABCD ,交线为AD ,所以PO ⊥平面ABCD ,以O 为原点,分别以射线OA ,OF 和OP 为x 轴,y 轴和z 轴建立空间直角坐标系Oxyz ,不妨设AD =2,则P ()0,0,1,D ()-1,0,0,C ()-1,2,0,假设在AB 上存在点G ()1,a ,0,0<a <2,则PC →=()-1,2,-1,PD →=()-1,0,-1,DG →=()2,a ,0.因为侧面P AD ⊥底面ABCD ,交线为AD ,且底面是正方形,所以CD ⊥平面P AD ,则CD ⊥PA ,由P A 2+PD 2=AD 2,得PD ⊥PA ,又PD ∩CD =D ,PD ,CD?平面PDC ,所以P A ⊥平面PDC ,即平面PDC 的一个法向量为PA →=(1,0,-1).设平面PDG 的法向量为n =(x ,y ,z),由PD →·n =0,DG →·n =0,即-x -z =0,2x +ay =0,亦即z =-x ,y =-2xa ,可取n =(a ,-2,-a).所以|cos 〈PA →,n 〉|=|PA →·n ||PA →||n |=2a 2×4+2a 2=33,解得a =1或a =-1(舍去).所以线段AB 上存在点G ,且G 为AB 的中点,使得二面角C -PD -G 的余弦值为33. 5.(2017·吉林长春检测)已知三棱锥A -BCD 中,△ABC 是等腰直角三角形,且AC ⊥BC ,BC =2,AD ⊥平面BCD ,AD =1.(1)求证:平面ABC ⊥平面ACD ;(2)若E 为AB 的中点,求二面角A -CE -D 的余弦值.(1)证明因为AD ⊥平面BCD ,BC?平面BCD ,所以AD ⊥BC ,又因为AC ⊥BC ,AC ∩AD =A ,AD ,AC?平面ACD ,所以BC ⊥平面ACD ,又BC?平面ABC ,所以平面ABC ⊥平面ACD.(2)解由已知可得CD =3,如图所示建立空间直角坐标系,由已知C(0,0,0),B(0,2,0),A(3,0,1),D(3,0,0),E 32,1,12,则CE →=32,1,12,CA →=(3,0,1),CD →=(3,0,0),设平面ACE 的法向量n =(x 1,y 1,z 1),则n ·CA →=0,n ·CE →=0,3x 1+z 1=0,32x 1+y 1+12z 1=0,令x 1=1,得n =(1,0,-3),设平面CED 的法向量m =(x 2,y 2,z 2),则m ·CD →=0,m ·CE →=0,3x 2=0,32x 2+y 2+12z 2=0,令y 2=1,得m =(0,1,-2),二面角A -CE -D 的余弦值cos 〈m ,n 〉=|n ·m ||n ||m |=2325=155.6.(2017·福建厦门模拟)如图,在梯形ABCD 中,AB ∥CD ,AD =DC =CB =1,∠ABC =60°,四边形ACFE 为矩形,平面ACFE ⊥平面ABCD ,CF =1.(1)求证:BC ⊥平面ACFE ;(2)点M 在线段EF 上运动,设平面MAB 与平面FCB 所成二面角为θ()θ≤90°,试求cos θ的取值范围.(1)证明在梯形ABCD 中,因为AB ∥CD ,AD =DC =CB =1,∠ABC =60°,所以AB =2,所以AC 2=AB 2+BC 2-2AB ·BC ·cos 60°=3,所以AB 2=AC 2+BC 2,所以BC ⊥AC.因为平面ACFE ⊥平面ABCD ,平面ACFE ∩平面ABCD =AC ,BC?平面ABCD ,所以BC ⊥平面ACFE.(2)解建立以直线CA ,CB ,CF 为x 轴,y 轴,z 轴的空间直角坐标系如图所示,令FM =λ(0≤λ≤3),则C(0,0,0),A(3,0,0),B(0,1,0),M(λ,0,1),所以AB →=(-3,1,0),BM →=(λ,-1,1),设n 1=(x ,y ,z)为平面MAB 的一个法向量,由n 1·AB →=0,n 1·BM →=0,得-3x +y =0,λx-y +z =0,取x =1,所以n 1=(1,3,3-λ),因为n 2=(1,0,0)是平面FCB 的一个法向量.所以cos θ=|n 1·n 2||n 1||n 2|=11+3+3-λ2×1=1λ-32+4.因为0≤λ≤3,所以当λ=0时,cos θ有最小值77,当λ=3时,cos θ有最大值12.所以cos θ∈77,12.。
全国卷新课标高考中档大题专项训练立体几何与空间向量

高考中档大题专项训练-立体几何与空间向量1.如图,菱形ABCD的对角线AC与BD交于点O,AB=5,AC=6,点E,F分别在AD,CD上,AE=CF =错误!,EF交BD于点H.将△DEF沿EF折到△D′EF的位置,OD′=错误!.1证明:D′H⊥平面ABCD;2求二面角B-D′A-C的正弦值.1证明由已知得AC⊥BD,AD=CD.又由AE=CF得错误!=错误!,故AC∥EF.因此EF⊥HD,从而EF⊥D′H.由AB=5,AC=6得DO=BO=错误!=4.由EF∥AC得错误!=错误!=错误!.所以OH=1,D′H=DH=3.于是D′H2+OH2=32+12=10=D′O2,故D′H⊥OH.又D′H⊥EF,而OH∩EF=H,所以D′H⊥平面ABCD.2解如图,以H为坐标原点,错误!的方向为x轴正方向,错误!的方向为y轴正方向,错误!的方向为z轴正方向,建立空间直角坐标系,则H0,0,0,A-3,-1,0,B0,-5,0,C3,-1,0,D′0,0,3,错误!=3,-4,0,错误!=6,0,0,错误!=3,1,3.设m=x1,y1,z1是平面ABD′的法向量,则错误!即错误!所以可取m=4,3,-5.设n=x2,y2,z2是平面ACD′的法向量,则错误!即错误!所以可取n=0,-3,1.于是cos〈m,n〉=错误!=错误!=-错误!. sin〈m,n〉=错误!.因此二面角B-D′A-C的正弦值是错误!.2.在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O′的直径,FB是圆台的一条母线.1已知G,H分别为EC,FB的中点,求证:GH∥平面ABC;2已知EF=FB=错误!AC=2错误!,AB=BC,求二面角F-BC-A的余弦值.1证明设FC中点为I,连接GI,HI.在△CEF中,因为点G,I分别是CE,CF的中点,所以GI∥EF.又EF∥OB,所以GI∥OB.在△CFB中,因为H是FB的中点,所以HI∥BC.又HI∩GI=I,BC∩OB=B,所以平面GHI∥平面ABC.因为GH平面GHI,所以GH∥平面ABC.2解连接OO′,则OO′⊥平面ABC.又AB=BC,且AC是圆O的直径,所以BO⊥AC.以O为坐标原点,建立如图所示的空间直角坐标系.由题意得B0,2错误!,0,C-2错误!,0,0.过点F作FM⊥OB于点M,所以FM=错误!=3,可得F0,错误!,3.故错误!=-2错误!,-2错误!,0,错误!=0,-错误!,3.设m=x,y,z是平面BCF的法向量.由错误!可得错误!可得平面BCF的一个法向量m=错误!,因为平面ABC的一个法向量n=0,0,1,所以cos〈m,n〉=错误!=错误!.所以二面角F-BC-A的余弦值为错误!.3.将边长为1的正方形AA1O1O 及其内部绕OO1旋转一周形成圆柱,如图,AC 长为错误!π,11A B 长为错误!,其中B1与C 在平面AA1O1O 的同侧.1求三棱锥C —O1A1B1的体积;2求异面直线B1C 与AA1所成的角的大小.解 1连接O 1B 1,则11A B =∠A 1O 1B 1=错误!,∴△O 1A 1B 1为正三角形,∴111O A B S =错误!,∴111—C O A B V=错误!OO 1·111O A B S =错误!.2设点B 1在下底面圆周的射影为B ,连接BB 1,则BB 1∥AA 1,∴∠BB 1C 为直线B 1C 与AA 1所成角或补角,BB 1=AA 1=1.连接BC ,BO ,OC ,AB =11A B =错误!,AC =错误!,∴BC =错误!,∴∠BOC =错误!,∴△BOC 为正三角形,∴BC =BO =1,∴tan∠BB 1C =错误!=1,∴∠BB 1C =45°,∴直线B 1C 与AA 1所成的角的大小为45°.4.如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=错误!为棱AD的中点,异面直线PA与CD所成的角为90°.1在平面PAB内找一点M,使得直线CM∥平面PBE,并说明理由;2若二面角P-CD-A的大小为45°,求直线PA与平面PCE所成角的正弦值.解1在梯形ABCD中,AB与CD不平行.延长AB,DC,相交于点MM∈平面PAB,点M即为所求的一个点.理由如下:由已知,BC∥ED,且BC=ED.所以四边形BCDE是平行四边形.从而CM∥EB.又EB平面PBE,CM平面PBE.所以CM∥平面PBE.说明:延长AP至点N,使得AP=PN,则所找的点可以是直线MN上任意一点2方法一由已知,CD⊥PA,CD⊥AD,PA∩AD=A,所以CD⊥平面PAD.从而CD⊥PD.所以∠PDA是二面角P-CD-A的平面角.所以∠PDA=45°.设BC=1,则在Rt△PAD中,PA=AD=2.过点A作AH⊥CE,交CE的延长线于点H,连接PH.易知PA⊥平面ABCD,从而PA⊥CE.且PA∩AH=A,于是CE⊥平面PAH.又CE平面PCE,所以平面PCE⊥平面PAH.过A作AQ⊥PH于Q,则AQ⊥平面PCE.所以∠APH是PA与平面PCE所成的角.在Rt△AEH中,∠AEH=45°,AE=1,所以AH=错误!.在Rt△PAH中,PH=错误!=错误!.所以sin∠APH=错误!=错误!.方法二由已知,CD⊥PA,CD⊥AD,PA∩AD=A,所以CD⊥平面PAD.于是CD⊥PD.从而∠PDA是二面角P-CD-A的平面角.所以∠PDA=45°.由∠PAB=90°,且PA与CD所成的角为90°,可得PA⊥平面ABCD.设BC=1,则在Rt△PAD中,PA=AD=2.作Ay⊥AD,以A为原点,以错误!,错误!的方向分别为x轴,z轴的正方向,建立如图所示的空间直角坐标系,则A0,0,0,P0,0,2,C2,1,0,E1,0,0.所以错误!=1,0,-2,错误!=1,1,0,错误!=0,0,2.设平面PCE的法向量为n=x,y,z.由错误!得错误!设x=2,解得n=2,-2,1.设直线PA与平面PCE所成的角为α,则sin α=错误!=错误!=错误!.所以直线PA与平面PCE所成角的正弦值为错误!.5.如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC =CD=错误!.1求证:PD⊥平面PAB;2求直线PB与平面PCD所成角的正弦值;3在棱PA上是否存在点M,使得BM∥平面PCD若存在,求错误!的值;若不存在,说明理由.1证明∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,又AB⊥AD,AB平面ABCD,∴AB⊥平面PAD.∵PD平面PAD,∴AB⊥PD,又PA⊥PD,PA∩AB=A,∴PD⊥平面PAB.2解取AD中点O,连接CO,PO.∵PA=PD,∴PO⊥AD.又∵PO平面PAD,平面PAD⊥平面ABCD,∴PO⊥平面ABCD,∵CO平面ABCD,∴PO⊥CO,∵AC=CD,∴CO⊥AD.以O为原点建立如图所示空间直角坐标系.易知P0,0,1,B1,1,0,D0,-1,0,C2,0,0.则错误!=1,1,-1,错误!=0,-1,-1,错误!=2,0,-1.设n=x0,y0,1为平面PDC的一个法向量.由错误!得错误!解得错误!即n=错误!.设PB与平面PCD的夹角为θ.则sin θ=|cos〈n,错误!〉|=错误!=错误!=错误!.3解设在棱PA上存在点M,使得BM∥平面PCD,则存在λ∈0,1使得错误!=λ错误!,因此点M0,1-λ,λ,错误!=-1,-λ,λ.∵BM平面PCD,∴BM∥平面PCD,当且仅当错误!·n=0,即-1,-λ,λ·错误!=0,解得λ=错误!,∴在棱PA上存在点M使得BM∥平面PCD,此时错误!=错误!.。
高考数学中档大题规范练中档大题3.docx

扩大我国中等收入阶层比重的对策研究作者:牟粼琳王刚来源:《群文天地》2011年第02期扩大中等收入阶层比重是我国现代化发展的必然趋势,其研究对加快我国现代化进程具有深刻意义。
本文对我国收入分配的现状进行分析,找出现阶段贫富差距扩大的根本原因,针对多元原因,提出培养和扩大中等收入阶层比重的对策,以期为我国解决贫富差距的问题,实现共同富裕做出贡献。
一、我国中等收入阶层现状分析目前中国经济社会发展的总体水平不是很高,导致中等收入者的比重相对过低。
根据中科院的测算标准,家庭财产在15万元至30万元之间可以算作是“中产”。
目前中国城市居民中有49%的家庭符合这一标准,但考虑到中国农村大多数家庭收入偏低的现实,最终可以推测出,目前我国的中等收入阶层人数只占全国人口的19%左右,这个比例很低。
而我国2002年全年城镇居民人均可支配收入为7500元,农民人均纯收入仅为2470元,我们的中收系数较高是建立在总体收入水平不高和高收入人群过于集中的基础之上的,这导致拥有有效需求能力和稳定心态的中等收入者的比重在这一经济发展阶段相对较低。
从纵向比较来看,中等收入者比重的增幅小于高收入者,1986至1999年,10%的最高收入户的收入就增长了8倍,远远高于中低收入层的增长,而且这种趋势还没有明显缓和的迹象,这使中等收入者比重趋于降低。
二、扩大中等收入阶层比重的积极作用1、扩大中等收入者比重有助于刺激消费,拉动经济增长。
我国现阶段消费差距很大:低收入人群收入太低,消费不足;而高收入阶层虽然拥有巨额财富,应有尽有,但他们要么不消费,导致资金闲置,要么过度消费,导致浪费资源,这种消费很不持续。
而我国中等收入阶层,他们消费意识和消费能力很强,为了过上更好的生活,他们积极工作,努力拼搏。
如果我国中等阶层人数占绝大多数,这意味将有一个庞大的消费市场,这有利于缓解和消除“需求不足”的市场经济问题;同时,中等收入阶层可以理性消费,可持续消费,对其它阶层有很好的示范作用,可以促进整个国家的经济持续、有序的发展。
高考数学 中档大题分类练4-立体几何

精品基础教育教学资料,仅供参考,需要可下载使用!中档大题分类练(四) 立体几何(建议用时:60分钟)1.如图57,已知多面体PE ABCD 的底面ABCD 是边长为2的菱形,且PA ⊥平面ABCD ,ED ∥PA ,且PA =2ED =2.图57(1)证明:平面PAC ⊥平面PCE ;(2)若∠ABC =60°,求点P 到平面ACE 的距离.[解] (1)证明:连接BD ,交AC 于点O ,设PC 中点为F , 连接OF ,EF .因为O ,F 分别为AC ,PC 的中点,所以OF ∥PA ,且OF =12PA ,因为DE ∥PA ,且DE =12PA ,所以OF ∥DE ,且OF =DE .所以四边形OFED 为平行四边形,所以OD ∥EF ,即BD ∥EF . 因为PA ⊥平面ABCD ,BD ⊂平面ABCD ,所以PA ⊥BD . 因为ABCD 是菱形,所以BD ⊥AC .因为PA ∩AC =A ,所以BD ⊥平面PAC, 因为BD ∥EF ,所以EF ⊥平面PAC ,因为EF ⊂平面PCE ,所以平面PAC ⊥平面PCE .(2)因为∠ABC =60°,所以△ABC 是等边三角形,所以AC =2. 又因为PA ⊥平面ABCD ,AC ⊂平面ABCD , ∴PA ⊥AC ,∴S △PAC =12×PA ×AC =2,因为EF ⊥面PAC ,所以EF 是三棱锥E PAC 的高,EF =DO =BO =3,∴V P ACE =V E PAC =13S △PAC ×EF =13×2×3=233,∵DE ∥PA ,PA ⊥平面ABCD ,∴DE ⊥平面ABCD ,∴DE ⊥AD ,DE ⊥CD , ∵DE =1,∴AE =CE =5,∴S △ACE =2×2×12=2,所以点P 到平面ACE 的距离h =V P ACE13S △ACE=23323=3.2.如图58,在四棱锥P ABCD 中,四边形ABCD 是菱形,△PAD ≌△BAD ,平面PAD ⊥平面ABCD ,AB =4,PA =PD ,M 在棱PD 上运动.图58(1)当M 在何处时,PB ∥平面MAC ;(2)已知O 为AD 的中点,AC 与OB 交于点E ,当PB ∥平面MAC 时,求三棱锥E BCM的体积.[解] (1)如图,设AC 与BD 相交于点N ,当M 为PD 的中点时,PB ∥平面MAC ,证明:∵四边形ABCD 是菱形,可得:DN =NB ,又∵M 为PD 的中点,可得:DM =MP ,∴NM 为△BDP 的中位线,可得NM ∥PB ,又∵NM ⊂平面MAC ,PB ⊄平面MAC ,∴PB ∥平面MAC .(2)∵O 为AD 的中点,PA =PD ,则OP ⊥AD ,又△PAD ≌△BAD , ∴OB ⊥AD ,且OB =23,又∵△AEO ∽△CEB ,∴OE BE=OA BC=12. ∴BE =23OB =433.∴S △EBC =12×4×433=833.又∵OP =4×32=23,点M 为PD 的中点,∴M 到平面EBC 的距离为3. ∴V E BCM =V M EBC =13×833×3=83.3.在三棱柱ABC A 1B 1C 1中,AB =BC =CA =AA 1=2,侧棱AA 1⊥平面ABC ,且D ,E 分别是棱A 1B 1,AA 1的中点,点F 在棱AB 上,且AF =14AB .图59(1)求证:EF ∥平面BDC 1; (2)求三棱锥D BEC 1的体积. [解] (1)取AB 的中点O ,连接A 1O ,∵AF =14AB ,∴F 为AO 的中点,又E 为AA 1的中点,∴EF ∥A 1O ,∵A 1D =12A 1B 1,BO =12AB ,AB 綊A 1B 1,∴A 1D 綊BO ,∴四边形A 1DBO 为平行四边形,∴A 1O ∥BD , ∴EF ∥BD ,又EF ⊄平面BDC 1,BD ⊂平面BDC 1, ∴EF ∥平面BDC 1.(2)∵AA 1⊥平面A 1B 1C 1,C 1D ⊂平面A 1B 1C 1, ∴AA 1⊥C 1D ,∵A 1C 1=B 1C 1=A 1B 1=2,D 为A 1B 1的中点, ∴C 1D ⊥A 1B 1,C 1D =3,又AA 1⊂平面AA 1B 1B ,A 1B 1⊂平面AA 1B 1B ,AA 1∩A 1B 1=A 1, ∴C 1D ⊥平面AA 1B 1B ,∵AB =AA 1=2,D ,E 分别为A 1B 1,AA 1的中点, ∴S △BDE =22-12×1×2-12×1×2-12×1×1=32.∴VD BEC 1=VC 1BDE =13S △BDE ·C 1D =13×32×3=32. 4.如图60所示,在四棱锥P ABCD 中,△BCD ,△PAD 都是等边三角形,平面PAD ⊥平面ABCD ,且AD =2AB =4,CD =23.图60(1)求证:平面PCD ⊥平面PAD ;(2)E 是AP 上一点,当BE ∥平面PCD 时,求三棱锥C PDE 的体积. [解] (1)因为AD =4,AB =2,BD =23,所以AD 2=AB 2+BD 2,所以AB ⊥BD ,∠ADB =30°,又因为△BCD 是等边三角形,所以∠ADC =90°,所以DC ⊥AD ,因为平面PAD ⊥平面ABCD , 平面PAD ∩平面ABCD =AD ,所以CD ⊥平面PAD ,因为CD ⊂平面PCD ,所以平面PCD ⊥平面PAD . (2)过点B 作BG ∥CD 交AD 于G ,过点G 作EG ∥PD 交于AP 于点E , 因为BG ∥CD ,BG ⊄平面PCD ,CD ⊂平面PCD ,所以BG ∥平面PCD , 同理可得EG ∥平面PCD ,所以平面BEG ∥平面PCD , 因为BE ⊂平面BEG ,所以BE ∥平面PCD . 因为EG ∥PD ,所以PE PA =DGDA,在直角三角形BGD 中,BD =23,∠BDG =30°,所以DG=23cos 30°=3,所以PEPA=DGDA=34,在平面PAD内过E作EH⊥PD于H,因为CD⊥平面PAD,EH⊂平面PAD,所以CD⊥EH,因为PD∩CD=D,所以EH⊥平面PCD,所以EH是点E到平面PCD的距离,过点A作AM⊥PD于M,则AM=32×4=23,由AM∥EH,得EHAM=PEPA=34,所以EH=323.因为S△PCD=12×4×23=43,所以V CPDE=13×43×323=6.(教师备选)1.如图,已知三棱柱ABCA1B1C1的侧棱长和底面边长均为2,A1在底面ABC内的射影O为底面△ABC的中心,如图所示.(1)求异面直线AA1与BC1所成角的大小;(2)求三棱锥C1BCA1的体积.[解] (1)连接AO ,并延长与BC 交于点D , 则D 是BC 边上的中点.因为点O 是正△ABC 的中心,且A 1O ⊥平面ABC , 所以BC ⊥AD ,BC ⊥A 1O . 因为AD ∩A 1O =O , 所以BC ⊥平面ADA 1. 所以BC ⊥AA 1.又AA 1∥CC 1,所以BC ⊥CC 1,所以异面直线AA 1与BC 1所成的角为∠BC 1C . 因为BC =CC 1=2,所以异面直线AA 1与BC 1所成角的大小为π4.(2)因为三棱柱的所有棱长都为2, 所以可求得AD =3,AO =23AD =233 ,A 1O =AA 21-AO 2=263.因为S △ABC =12×2×3=3,所以VABC A 1B 1C 1=S △ABC ·A 1O =22,VA 1BCC 1B 1=VABC A 1B 1C 1-VA 1ABC =423.所以VC 1BCA 1=VA 1BCC 1=12VA 1BCC 1B 1=223.2.如图①,在直角梯形ABCD 中,AD ∥BC ,∠BAD =90°,AB =BC =12AD =a ,E 是AD 的中点,O 是AC 与BE 的交点.将△ABE 沿BE 折起到图②中△A 1BE 的位置,得到四棱锥A 1BCDE .图① 图②(1)证明:CD ⊥平面A 1OC ;(2)当平面A 1BE ⊥平面BCDE 时,四棱锥A 1BCDE 的体积为362,求a 的值.[解] (1)证明:在图题①中,连接EC (图略), 因为AB =BC =12AD =a ,∠BAD =90°,AD ∥BC ,E 是AD 的中点,所以四边形ABCE 为正方形,所以BE ⊥AC ,即在图题②中,BE ⊥A 1O ,BE ⊥OC . 又A 1O ∩OC =O ,从而BE ⊥平面A 1OC , 又CD ∥BE ,所以CD ⊥平面A 1OC . (2)由已知,平面A 1BE ⊥平面BCDE , 且平面A 1BE ∩平面BCDE =BE ,又由(1)可知A 1O ⊥BE ,所以A 1O ⊥平面BCDE , 即A 1O 是四棱锥A 1BCDE 的高, 由图1知,A 1O =22AB =22a ,平行四边形BCDE 的面积S =BC ·AB =a 2, 从而四棱锥A 1BCDE 的体积V =13×S ×A 1O =13×a 2×22a =26a 3,由26a 3=362,解得a =6.。
新高考2023版高考数学一轮总复习练案45高考大题规范解答系列四__立体几何

高考大题规范解答系列(四)——立体几何1.(2022·安徽黄山质检)如图,直三棱柱ABC-A1B1C1中,D是BC的中点,且AD⊥BC,四边形ABB1A1为正方形.(1)求证:A1C∥平面AB1D;(2)若∠BAC=60°,BC=4,求点A1到平面AB1D的距离.[解析] (1)连接BA1,交AB1于点E,再连接DE,由已知得,四边形ABB1A1为正方形,E为A1B的中点,∵D是BC的中点,∴DE∥A1C,又DE⊂平面AB1D,A1C⊄平面AB1D,∴A1C∥平面AB1D.(2)∵在直三棱柱ABC-A1B1C1中,平面BCC1B1⊥平面ABC,且BC为它们的交线,又AD⊥BC,∴AD⊥平面BCC1B1,又∵B1D⊂平面BCC1B1,∴AD⊥B1D,且AD=2,B1D=2.同理可得,过D作DG⊥AB,则DG⊥面ABB1A1,且DG=.设A1到平面AB1D的距离为h,由等体积法可得:VA1-AB1D=VD-AA1B1,即··AD·DB1·h=··AA1·A1B1·DG,即2×2·h=4×4×,∴h=.即点A1到平面AB1D的距离为.(注:本题也可建立空间直角坐标系用向量法求解.)2.(2022·陕西汉中质检)如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点.(1)求证:平面PDE⊥平面APC;(2)求直线PC与平面PDE所成的角的正弦值.[解析] 如图所示,以点C为坐标原点,直线CD,CB,CP分别为x,y,z轴,建立空间直角坐标系C-xyz,则相关点的坐标为C(0,0,0),A(2,1,0),B(0,3,0),P(0,0,2),D(2,0,0),E(1,2,0).(1)由于DE=(-1,2,0),CA=(2,1,0),CP=(0,0,2),所以DE·CA=(-1,2,0)·(2,1,0)=0,DE·CP=(-1,2,0)·(0,0,2)=0,所以DE⊥CA,DE⊥CP,而CP∩CA=C,所以DE⊥平面PAC,∵DE⊂平面PDE,∴平面PDE⊥平面PAC.(2)设n=(x,y,z)是平面PDE的一个法向量,则n·DE=n·PE=0,由于DE=(-1,2,0),PE=(1,2,-2),所以有,令x=2,则y=1,z=2,即n=(2,1,2),再设直线PC与平面PDE所成的角为α,而PC=(0,0,-2),所以sin α=|cos〈n,PC〉|===,∴直线PC与平面PDE所成角的正弦值为.3.(2022·湖北百师联盟质检)斜三棱柱ABC-HDE中,平面ABC⊥平面BCD,△ABC为边长为1的等边三角形,DC⊥BC,且DC长为,设DC中点为M,F、G分别为CE、AD的中点.(1)证明:FG∥平面ABC;(2)求二面角B-AC-E的余弦值.[解析] (1)解法一:取BD中点N,连结GN,NF,易知N、M、F三点共线,由GN∥AB,且GN⊄平面ABC,AB⊂平面ABC,故GN∥平面ABC,同理可得NF∥平面ABC,因为GN∩NF=N,故平面GNF∥平面ABC.由FG⊂平面FGN,故FG∥平面ABC.解法二:取AB中点N,连结GN,NC,易知GN是△ABD的中位线,故GN∥BD,GN=BD,因为CE綊BD,F为CE的中点.所以CF綊GN.四边形FGNC是平行四边形,故FG∥CN,因为CN⊂平面ABC,FG⊄平面ABC,故FG∥平面ABC.(2)以BC中点O为坐标原点,以OC、ON、OA分别为x、y、z轴,建立空间直角坐标系O-xyz,由已知可得A,C,E,故CE=(1,,0),AC=,设m=(x,y,z)为平面ACE的法向量,则,解得m=(,-1,1),由于ON⊥平面ABC,不妨取平面ABC的法向量为n=(0,1,0).所以cos〈m,n〉==-.由图可知所求二面角为钝角,故二面角B-AC-E的余弦值为-.4.(2021·全国新高考)在四棱锥Q-ABCD中,底面ABCD是正方形,若AD=2,QD=QA=,QC=3.(1)证明:平面QAD⊥平面ABCD;(2)求二面角B-QD-A的平面角的余弦值.[解析] (1)取AD的中点为O,连接QO,CO.因为QA=QD,OA=OD,则QO⊥AD,而AD=2,QA=,故QO==2.在正方形ABCD中,因为AD=2,故DO=1,故CO=,因为QC=3,故QC2=QO2+OC2,故△QOC为直角三角形且QO⊥OC,因为OC∩AD=O,故QO⊥平面ABCD,因为QO⊂平面QAD,故平面QAD⊥平面ABCD.(2)在平面ABCD内,过O作OT∥CD,交BC于T,则OT⊥AD,结合(1)中的QO⊥平面ABCD,故可建如图所示的空间坐标系.则D(0,1,0),Q(0,0,2),B(2,-1,0),故BQ=(-2,1,2),BD=(-2,2,0).设平面QBD的法向量n=(x,y,z),则即,取x=1,则y=1,z=,故n=.而平面QAD的法向量为m=(1,0,0),故cos〈m,n〉==.二面角B-QD-A的平面角为锐角,故其余弦值为.5.(2021·安徽省淮北市一模)在直角梯形ABCD(如图1)中,∠ABC=90°,BC∥AD,AD=8,AB=BC=4,M为线段AD中点.将△ABC沿AC折起,使平面ABC⊥平面ACD,得到几何体B-ACD(如图2).(1)求证:CD⊥平面ABC;(2)求AB与平面BCM所成角θ的正弦值.[解析] (1)由题设可知AC=4,CD=4,AD=8,∴AD2=CD2+AC2,∴CD⊥AC,又∵平面ABC⊥平面ACD,平面ABC∩平面ACD=AC,∴CD⊥平面ABC.(2)解法一:等体积法取AC的中点O连接OB,由题设可知△ABC为等腰直角三角形,所以OB⊥面ACM,∵V B-ACM=V A-BCM且V B-ACM=S △ACM·BO=,而SΔBCM=4,∴A到面BCM的距离h=,所以sin θ==.解法二:向量法,取AC的中点O,连接OB,由题设可知△ABC为等腰直角三角形,所以OB⊥面ACM,连接OM,因为M、O分别为AD和AC的中点,所以OM∥CD,由(1)可知OM⊥AC,故以OM、OC、OB所在直线为x轴、y轴、z轴建立空间直角坐标系,如图所示.则A(0,-2,0),B(0,0,2),C(0,2,0),M(2,0,0),∴CB=(0,-2,2),CM=(2,-2,0),BA=(0,-2,-2),设平面BCM法向量n=(x,y,z)由得令y=1得n=(1,1,1)∴平面BCM的一个法向量n=(1,1,1),∴sin θ==.6.(2021·山东聊城三模)如图,在平面四边形ABCD中,BC=CD,BC⊥CD,AD⊥BD,以BD为折痕把△ABD折起,使点A到达点P的位置,且PC⊥BC.(1)证明:PD⊥CD;(2)若M为PB的中点,二面角P-BC-D的大小为60°,求直线PC与平面MCD所成角的正弦值.[解析] (1)证明:因为BC⊥CD,BC⊥PC,PC∩CD=C,所以BC⊥平面PCD,又因为PD⊂平面PCD,所以BC⊥PD,又因为PD⊥BD,BD∩BC=B,所以PD⊥平面BCD,又因为CD⊂平面BCD,所以PD⊥CD.(2)因为PC⊥BC,CD⊥BC,所以∠PCD是二面角P-BC-D的平面角,即∠PCD=60°,在Rt△PCD中,PD=CD tan 60°=CD,取BD的中点O,连接OM,OC,因为BC=CD,BC⊥CD,所以OC⊥BD,由(1)知,PD⊥平面BCD,OM为△PBD的中位线,所以OM⊥BD,OM⊥OC,即OM,OC,BD两两垂直,以O为原点,建立如图所示的空间直角坐标系O-xyz,设OB=1,则P(0,1,),C(1,0,0),D(0,1,0),M,CP=(-1,1,),CD=(-1,1,0),CM=,设平面MCD的一个法向量为n=(x,y,z),则由得令z=,得n=(,,),所以cos〈n,CP〉===,所以直线PC与平面MCD所成角的正弦值为.7.(开放题)(2022·云南昆明模拟)如图,在三棱锥A-BCD中,△BCD是边长为2的等边三角形,AB=AC,O是BC的中点,OA⊥CD.(1)证明:平面ABC⊥平面BCD;(2)若E是棱AC上的一点,从①CE=2EA;②二面角E-BD-C大小为60°;③A-BCD的体积为这三个论断中选取两个作为条件,证明另外一个成立.[证明] (1)因为AB=AC,O是BC的中点,所以OA⊥BC,又因为OA⊥CD,所以OA⊥平面BCD,因为OA⊂平面ABC,所以平面ABC⊥平面BCD.(2)连接OD,又因为△BCD是边长为2的等边三角形,所以DO⊥BC,由(1)知OA⊥平面BCD,所以AO,BC,DO两两互相垂直.以O为坐标原点,OA,OB,OD所在直线分别为x轴,y轴,z轴建立如图所示空间直角坐标系.设|OA|=m,则O(0,0,0),A(0,0,m),B(1,0,0),C(-1,0,0),D(0,,0),若选①②作为条件,证明③成立.因为CE=2EA,所以E,易知平面BCD的法向量为n=(0,0,1),BE=,BD=(-1,,0),设m=(x,y,z)是平面BDE的法向量,则,所以,可取m=,由二面角E-BD-C大小为60°可得cos θ===,解得m=3,所以A-BCD的体积为×2×××3=.若选①③作为条件,证明②成立.因为A-BCD的体积为,所以×2×××|OA|=,解得|OA|=3,又因为CE=2EA,所以E,易知平面BCD的法向量为n=(0,0,1),BE=,BD=,设m=(x,y,z)是平面BDE的法向量,则所以,可取m=,所以cos θ===,即二面角E-BD-C大小为60°.若选②③作为条件,证明①成立.因为A-BCD的体积为,所以×2×××|OA|=,解得|OA|=3,即A(0,0,3),AC=(-1,0,-3),不妨设AE=λAC(0≤λ≤1),所以E(-λ,0,-3λ+3),易知平面BCD的法向量为n=(0,0,1),BE=(-λ-1,0,-3λ+3),BD=(-1,,0),设m=(x,y,z)是平面BDE的法向量,取m=(3(1-λ),(1-λ),λ+1)cos θ===,解得λ=3(舍),λ=,所以CE=2EA.8.(2022·河北石家庄质检)如图,四棱锥P-ABCD中,底面ABCD为正方形,△PAB 为等边三角形,平面PAB⊥底面ABCD,E为AD的中点.(1)求证:CE⊥PD;(2)在线段BD(不包括端点)上是否存在点F,使直线AP与平面PEF所成角的正弦值为,若存在,确定点F的位置;若不存在,请说明理由.[解析] (1)证明:取AB的中点O,连结PO,OD,因为PA=PB,所以PO⊥AB,又因为平面PAB⊥平面ABCD,所以PO⊥底面ABCD,取CD的中点G,连结OG,则OB,OP,OG两两垂直,分别以OB,OG,OP所在直线为x轴,y轴,z轴建立空间直角坐标系(如图所示),设AB=2,则C(1,2,0),P(0,0,),E(-1,1,0),D(-1,2,0),所以CE=(-2,-1,0),PD=(-1,2,-),则CE·PD=2-2=0,故CE⊥PD,所以CE⊥PD.(2)由(1)可知,A(-1,0,0),B(1,0,0),所以PE=(-1,1,-),AP=(1,0,),BD=(-2,2,0),BE=(-2,1,0),设BF=λBD(0<λ<1),则BF=(-2λ,2λ,0),所以EF=BF-BE=(-2λ+2,2λ-1,0),设平面PEF的法向量为n=(x,y,z),令y=1,则x=,z=,故n=,所以|cos〈AP,n〉|===,整理可得9λ2-6λ+1=0,解得λ=,所以在BD上存在点F,使得直线AP与平面PEF所成角的正弦值为,此时点F为靠近点B的三等分点,即BF=BD.。
高考数学 考前三个月 中档大题规范练 立体几何与空间

中档大题规范练——立体几何与空间向量1. 有一个倒圆锥形容器,它的轴截面是一个正三角形,在容器内放一个半径为r 的铁球,并注入水,使水面与球正好相切,然后将球取出,求这时容器中水的深度. 解 由题意知,圆锥的轴截面为正三角形,如图所示为圆锥的轴截面. 根据切线性质知,当球在容器内时,水深为3r ,水面的半径为3r ,则容器内水的体积为V =V 圆锥-V 球=13π·(3r )2·3r -43πr 3=53πr 3,而将球取出后,设容器内水的深度为h ,则水面圆的半径为33h , 从而容器内水的体积是V ′=13π·(33h )2·h =19πh 3,由V =V ′,得h =315r .即容器中水的深度为315r .2. 如图1所示,正三角形ABC 的边长为2a ,CD 是AB 边上的高,E ,F 分别是AC ,BC 的中点.现将△ABC 沿CD 翻折,翻折后平面ACD ⊥平面BCD (如图2).求三棱锥C —DEF 的体积.图1 图2解 过点E 作EM ⊥DC 于点M ,因为平面ACD ⊥平面BCD ,平面ACD ∩平面BCD =CD , 而EM ⊂平面ACD , 所以EM ⊥平面BCD .即EM 是三棱锥E —CDF 的高. 又CD ⊥BD ,AD ⊥CD ,F 为BC 的中点,所以S △CDF =12S △BCD =12×12CD ×BD=14×2a2-a 2×a =34a 2, 因为E 为AC 的中点,EM ⊥CD ,所以EM =12AD =12a .所以三棱锥C —DEF 的体积为V C —DEF =V E —CDF =13S △CDF ×EM =13×34a 2×12a =324a 3.3. 如图,在多面体ABCDEF 中,四边形ABCD 是正方形,EF ∥AB ,EF ⊥FB ,AB =2EF ,∠BFC=90°,BF =FC ,H 为BC 的中点.(1)求证:FH ∥平面EDB ; (2)求证:AC ⊥平面EDB .证明 (1)设AC 与BD 交于点G ,则G 为AC 的中点.如图,连接EG 、GH ,又H 为BC 的中点,∴GH 綊12AB .又EF 綊12AB ,∴EF 綊GH .∴四边形EFHG 为平行四边形.∴EG ∥FH . 又∵EG ⊂平面EDB ,FH ⊄平面EDB , ∴FH ∥平面EDB .(2)由四边形ABCD 为正方形,得AB ⊥BC . 又EF ∥AB ,∴EF ⊥BC . 又∵EF ⊥FB ,BC ∩FB =B ,∴EF ⊥平面BFC .∴EF ⊥FH .∴AB ⊥FH . 又BF =FC ,H 为BC 的中点,∴FH ⊥BC . ∴FH ⊥平面ABCD .∴FH ⊥AC .又FH ∥EG ,∴AC ⊥EG .又AC ⊥BD ,EG ∩BD =G , ∴AC ⊥平面EDB .4. 如图所示,已知三棱锥A -BPC 中,AP ⊥PC ,AC ⊥BC ,M 为AB 的中点,D 为PB 的中点,且△PMB 为正三角形.(1)求证:DM ∥平面APC ; (2)求证:平面ABC ⊥平面APC ;(3)若BC =4,AB =20,求三棱锥D -BCM 的体积. (1)证明 由已知,得MD 是△ABP 的中位线,所以MD ∥AP . 又MD ⊄平面APC ,AP ⊂平面APC , 故MD ∥平面APC .(2)证明 因为△PMB 为正三角形,D 为PB 的中点, 所以MD ⊥PB .所以AP ⊥PB .又AP ⊥PC ,PB ∩PC =P ,所以AP ⊥平面PBC .因为BC ⊂平面PBC ,所以AP ⊥BC .又BC ⊥AC ,AC ∩AP =A ,所以BC ⊥平面APC . 因为BC ⊂平面ABC ,所以平面ABC ⊥平面APC . (3)解 由题意,可知MD ⊥平面PBC , 所以MD 是三棱锥D -BCM 的一条高,所以V D -BCM =V M -DBC =13×S △BCD ×MD=13×221×53=107. 5. 如图,在底面是矩形的四棱锥P —ABCD 中,PA ⊥底面ABCD ,E ,F 分别是PC ,PD 的中点,PA =AB =1,BC =2.(1)求证:EF ∥平面PAB ; (2)求证:平面PAD ⊥平面PDC .证明 (1)以A 为原点,AB 所在直线为x 轴,AD 所在直 线为y 轴,AP 所在直线为z 轴,建立如图所示的空间直 角坐标系,则A (0,0,0),B (1,0,0),C (1,2,0),D (0,2,0),P (0,0,1),∵E ,F 分别是PC ,PD 的中点,∴E ⎝ ⎛⎭⎪⎫12,1,12,F ⎝ ⎛⎭⎪⎫0,1,12,EF →=⎝ ⎛⎭⎪⎫-12,0,0,PB →=(1,0,-1),PD →=(0,2,-1),AP →=(0,0,1),AD →=(0,2,0),DC→=(1,0,0),AB →=(1,0,0).∵EF →=-12AB →,∴EF →∥AB →,即EF ∥AB ,又AB ⊂平面PAB ,EF ⊄平面PAB , ∴EF ∥平面PAB .(2)∵AP →·DC →=(0,0,1)·(1,0,0)=0, AD →·DC →=(0,2,0)·(1,0,0)=0, ∴AP →⊥DC →,AD →⊥DC →,即AP ⊥DC ,AD ⊥DC . 又AP ∩AD =A ,∴DC ⊥平面PAD . ∵DC ⊂平面PDC ,∴平面PAD ⊥平面PDC .6. 如图,在四棱锥P -ABCD 中,PC ⊥底面ABCD ,ABCD 是直角梯形,AB ⊥AD ,AB ∥CD ,AB=2AD =2CD =2.E 是PB 的中点.(1)求证:平面EAC ⊥平面PBC ; (2)若二面角P -AC -E 的余弦值为63,求直线PA 与平面EAC 所成角的正弦值. (1)证明 ∵PC ⊥平面ABCD ,AC ⊂平面ABCD , ∴AC ⊥PC ,∵AB =2,AD =CD =1,∴AC =BC =2, ∴AC 2+BC 2=AB 2,∴AC ⊥BC , 又BC ∩PC =C , ∴AC ⊥平面PBC , ∵AC ⊂平面EAC , ∴平面EAC ⊥平面PBC .(2)解 如图,以C 为原点,DA →、CD →、CP →分别为x 轴、y 轴、z 轴正向,建立空间直角坐标系,则C (0,0,0), A (1,1,0),B (1,-1,0).设P (0,0,a )(a >0),则E 12,-12,a 2,CA →=(1,1,0),CP →=(0,0,a ),CE →=12,-12,a 2,设m =(b ,p ,m )为面PAC 的法向量,则m ·CA →=m ·CP →=0, 即⎩⎪⎨⎪⎧b +p =0am =0,取m =(1,-1,0), 设n =(x ,y ,z )为面EAC 的法向量,则n ·CA →=n ·CE →=0, 即⎩⎪⎨⎪⎧x +y =0,x -y +az =0,取x =a ,y =-a ,z =-2, 则n =(a ,-a ,-2),依题意,|cos 〈m ,n 〉|=|m ·n ||m ||n |=a a 2+2=63,则a =2.于是n =(2,-2,-2),PA →=(1,1,-2). 设直线PA 与平面EAC 所成角为θ,则sin θ=|cos 〈PA →,n 〉|=|PA →·n ||PA →||n |=23,即直线PA 与平面EAC 所成角的正弦值为23.。
2024届新高考数学大题精选30题--立体几何含答案
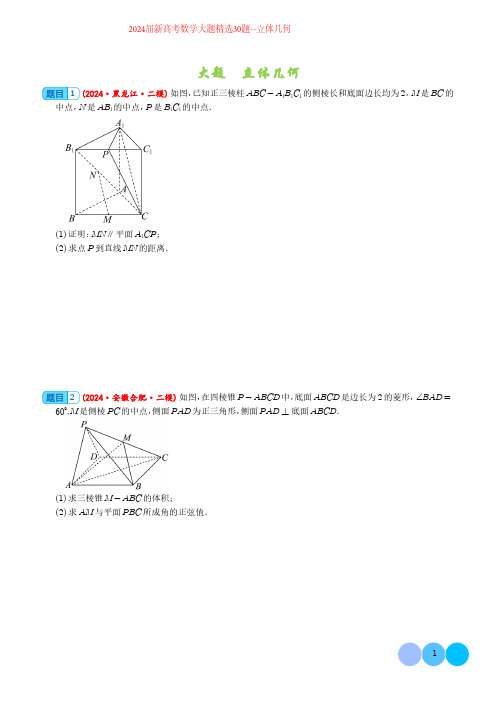
大题立体几何1(2024·黑龙江·二模)如图,已知正三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,M是BC的中点,N是AB1的中点,P是B1C1的中点.(1)证明:MN⎳平面A1CP;(2)求点P到直线MN 的距离.2(2024·安徽合肥·二模)如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,M是侧棱PC的中点,侧面PAD为正三角形,侧面PAD⊥底面ABCD.(1)求三棱锥M-ABC的体积;(2)求AM与平面PBC所成角的正弦值.2024届新高考数学大题精选30题--立体几何3(2023·福建福州·模拟预测)如图,在三棱柱ABC-A1B1C1中,平面AA1C1C⊥平面ABC,AB= AC=BC=AA1=2,A1B=6.(1)设D为AC中点,证明:AC⊥平面A1DB;(2)求平面A1AB1与平面ACC1A1夹角的余弦值.4(2024·山西晋中·三模)如图,在六面体ABCDE中,BC=BD=6,EC⊥ED,且EC=ED= 2,AB平行于平面CDE,AE平行于平面BCD,AE⊥CD.(1)证明:平面ABE⊥平面CDE;(2)若点A到直线CD的距离为22,F为棱AE的中点,求平面BDF与平面BCD夹角的余弦值.5(2024·辽宁·二模)棱长均为2的斜三棱柱ABC-A1B1C1中,A1在平面ABC内的射影O在棱AC的中点处,P为棱A1B1(包含端点)上的动点.(1)求点P到平面ABC1的距离;(2)若AP⊥平面α,求直线BC1与平面α所成角的正弦值的取值范围.6(2024·重庆·模拟预测)在如图所示的四棱锥P-ABCD中,已知AB∥CD,∠BAD=90°,CD= 2AB,△PAB是正三角形,点M在侧棱PB上且使得PD⎳平面AMC.(1)证明:PM=2BM;(2)若侧面PAB⊥底面ABCD,CM与底面ABCD所成角的正切值为311,求二面角P-AC-B的余弦值.7(2024·安徽·模拟预测)2023年12月19日至20日,中央农村工作会议在北京召开,习近平主席对“三农”工作作出指示.某地区为响应习近平主席的号召,积极发展特色农业,建设蔬菜大棚.如图所示的七面体ABG-CDEHF是一个放置在地面上的蔬菜大棚钢架,四边形ABCD是矩形,AB=8m,AD=4m,ED=CF=1m,且ED,CF都垂直于平面ABCD,GA=GB=5m,HE=HF,平面ABG⊥平面ABCD.(1)求点H到平面ABCD的距离;(2)求平面BFHG与平面AGHE所成锐二面角的余弦值.8(2024·重庆·模拟预测)如图,ACDE为菱形,AC=BC=2,∠ACB=120°,平面ACDE⊥平面ABC,点F在AB上,且AF=2FB,M,N分别在直线CD,AB上.(1)求证:CF⊥平面ACDE;(2)把与两条异面直线都垂直且相交的直线叫做这两条异面直线的公垂线,若∠EAC=60°,MN为直线CD,AB的公垂线,求ANAF的值;(3)记直线BE与平面ABC所成角为α,若tanα>217,求平面BCD与平面CFD所成角余弦值的范围.9(2024·安徽·二模)将正方形ABCD 绕直线AB 逆时针旋转90°,使得CD 到EF 的位置,得到如图所示的几何体.(1)求证:平面ACF ⊥平面BDE ;(2)点M 为DF 上一点,若二面角C -AM -E 的余弦值为13,求∠MAD .10(2024·安徽黄山·二模)如图,已知AB 为圆台下底面圆O 1的直径,C 是圆O 1上异于A ,B 的点,D 是圆台上底面圆O 2上的点,且平面DAC ⊥平面ABC ,DA =DC =AC =2,BC =4,E 是CD 的中点,BF =2FD .(1)证明:DO 2⎳BC ;(2)求直线DB 与平面AEF 所成角的正弦值.11(2024·黑龙江哈尔滨·一模)正四棱台ABCD -A 1B 1C 1D 1的下底面边长为22,A 1B 1=12AB ,M 为BC 中点,已知点P 满足AP =1-λ AB +12λ⋅AD +λAA 1 ,其中λ∈0,1 .(1)求证D 1P ⊥AC ;(2)已知平面AMC 1与平面ABCD 所成角的余弦值为37,当λ=23时,求直线DP 与平面AMC 1所成角的正弦值.12(2024·辽宁·三模)如图,在三棱柱ABC -A 1B 1C 1中,侧面ACC 1A 1⊥底面ABC ,AC =AA 1=2,AB =1,BC =3,点E 为线段AC 的中点.(1)求证:AB 1∥平面BEC 1;(2)若∠A 1AC =π3,求二面角A -BE -C 1的余弦值.13(2024·广东广州·一模)如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,△DCP是等边三角形,∠DCB=∠PCB=π4,点M,N分别为DP和AB的中点.(1)求证:MN⎳平面PBC;(2)求证:平面PBC⊥平面ABCD;(3)求CM与平面PAD所成角的正弦值.14(2024·广东梅州·二模)如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD 为直角梯形,△PAD为等边三角形,AD⎳BC,AD⊥AB,AD=AB=2BC=2.(1)求证:AD⊥PC;(2)点N在棱PC上运动,求△ADN面积的最小值;(3)点M为PB的中点,在棱PC上找一点Q,使得AM⎳平面BDQ,求PQQC的值.15(2024·广东广州·模拟预测)如图所示,圆台O1O2的轴截面A1ACC1为等腰梯形,AC=2AA1= 2A1C1=4,B为底面圆周上异于A,C的点,且AB=BC,P是线段BC的中点.(1)求证:C1P⎳平面A1AB.(2)求平面A1AB与平面C1CB夹角的余弦值.16(2024·广东深圳·二模)如图,三棱柱ABC-A1B1C1中,侧面BB1C1C⊥底面ABC,且AB= AC,A1B=A1C.(1)证明:AA1⊥平面ABC;(2)若AA1=BC=2,∠BAC=90°,求平面A1BC与平面A1BC1夹角的余弦值.17(2024·河北保定·二模)如图,在四棱锥P -ABCD 中,平面PCD 内存在一条直线EF 与AB 平行,PA ⊥平面ABCD ,直线PC 与平面ABCD 所成的角的正切值为32,PA =BC =23,CD =2AB =4.(1)证明:四边形ABCD 是直角梯形.(2)若点E 满足PE =2ED ,求二面角P -EF -B 的正弦值.18(2024·湖南衡阳·模拟预测)如图,在圆锥PO 中,P 是圆锥的顶点,O 是圆锥底面圆的圆心,AC 是圆锥底面圆的直径,等边三角形ABD 是圆锥底面圆O 的内接三角形,E 是圆锥母线PC 的中点,PO =6,AC =4.(1)求证:平面BED ⊥平面ABD ;(2)设点M 在线段PO 上,且OM =2,求直线DM 与平面ABE 所成角的正弦值.19(2024·湖南岳阳·三模)已知四棱锥P -ABCD 的底面ABCD 是边长为4的菱形,∠DAB =60°,PA =PC ,PB =PD =210,M 是线段PC 上的点,且PC =4MC .(1)证明:PC ⊥平面BDM ;(2)点E 在直线DM 上,求BE 与平面ABCD 所成角的最大值.20(2024·湖南·二模)如图,直四棱柱ABCD -A 1B 1C 1D 1的底面是边长为2的菱形,∠ABC =60°,BD 1⊥平面A 1C 1D .(1)求四棱柱ABCD -A 1B 1C 1D 1的体积;(2)设点D 1关于平面A 1C 1D 的对称点为E ,点E 和点C 1关于平面α对称(E 和α未在图中标出),求平面A 1C 1D 与平面α所成锐二面角的大小.21(2024·山东济南·二模)如图,在四棱锥P-ABCD中,四边形ABCD为直角梯形,AB∥CD,∠DAB=∠PCB=60°,CD=1,AB=3,PC=23,平面PCB⊥平面ABCD,F为线段BC的中点,E为线段PF上一点.(1)证明:PF⊥AD;(2)当EF为何值时,直线BE与平面PAD夹角的正弦值为74.22(2024·山东潍坊·二模)如图1,在平行四边形ABCD中,AB=2BC=4,∠ABC=60°,E为CD 的中点,将△ADE沿AE折起,连结BD,CD,且BD=4,如图2.(1)求证:图2中的平面ADE⊥平面ABCE;(2)在图2中,若点F在棱BD上,直线AF与平面ABCE所成的角的正弦值为3010,求点F到平面DEC 的距离.23(2024·福建·模拟预测)如图,在三棱锥P-ABC中,PA⊥PB,AB⊥BC,AB=3,BC=6,已知二面角P-AB-C的大小为θ,∠PAB=θ.(1)求点P到平面ABC的距离;(2)当三棱锥P-ABC的体积取得最大值时,求:(Ⅰ)二面角P-AB-C的余弦值;(Ⅱ)直线PC与平面PAB所成角.24(2024·浙江杭州·二模)如图,在多面体ABCDPQ中,底面ABCD是平行四边形,∠DAB=60°, BC=2PQ=4AB=4,M为BC的中点,PQ∥BC,PD⊥DC,QB⊥MD.(1)证明:∠ABQ=90°;(2)若多面体ABCDPQ的体积为152,求平面PCD与平面QAB夹角的余弦值.25(2024·浙江嘉兴·二模)在如图所示的几何体中,四边形ABCD为平行四边形,PA⊥平面ABCD,PA∥QD,BC=2AB=2PA=2,∠ABC=60°.(1)证明:平面PCD⊥平面PAC;(2)若PQ=22,求平面PCQ与平面DCQ夹角的余弦值.26(2024·浙江绍兴·二模)如图,在三棱锥P-ABC中,AB=4,AC=2,∠CAB=60°,BC⊥AP.(1)证明:平面ACP⊥平面ABC;(2)若PA=2,PB=4,求二面角P-AB-C的平面角的正切值.27(2024·河北沧州·一模)如图,在正三棱锥A -BCD 中,BC =CD =BD =4,点P 满足AP=λAC ,λ∈(0,1),过点P 作平面α分别与棱AB ,BD ,CD 交于Q ,S ,T 三点,且AD ⎳α,BC ⎳α.(1)证明:∀λ∈(0,1),四边形PQST 总是矩形;(2)若AC =4,求四棱锥C -PQST 体积的最大值.28(2024·湖北·二模)如图1.在菱形ABCD 中,∠ABC =120°,AB =4,AE =λAD ,AF =λAB(0<λ<1),沿EF 将△AEF 向上折起得到棱锥P -BCDEP .如图2所示,设二面角P -EF -B 的平面角为θ.(1)当λ为何值时,三棱锥P -BCD 和四棱锥P -BDEF 的体积之比为95(2)当θ为何值时,∀λ∈0,1 ,平面PEF 与平面PFB 的夹角φ的余弦值为5529(2024·湖北·模拟预测)空间中有一个平面α和两条直线m ,n ,其中m ,n 与α的交点分别为A ,B ,AB =1,设直线m 与n 之间的夹角为π3,(1)如图1,若直线m ,n 交于点C ,求点C 到平面α距离的最大值;(2)如图2,若直线m ,n 互为异面直线,直线m 上一点P 和直线n 上一点Q 满足PQ ⎳α,PQ ⊥n 且PQ ⊥m ,(i )求直线m ,n 与平面α的夹角之和;(ii )设PQ =d 0<d <1 ,求点P 到平面α距离的最大值关于d 的函数f d .30(2024·浙江绍兴·模拟预测)如图所示,四棱台ABCD -A 1B 1C 1D 1,底面ABCD 为一个菱形,且∠BAD =120°. 底面与顶面的对角线交点分别为O ,O 1. AB =2A 1B 1=2,BB 1=DD 1=392,AA 1与底面夹角余弦值为3737.(1)证明:OO 1⊥平面ABCD ;(2)现将顶面绕OO 1旋转θ角,旋转方向为自上而下看的逆时针方向. 此时使得底面与DC 1的夹角正弦值为64343,此时求θ的值(θ<90°);(3)求旋转后AA 1与BB 1的夹角余弦值.大题 立体几何1(2024·黑龙江·二模)如图,已知正三棱柱ABC -A 1B 1C 1的侧棱长和底面边长均为2,M 是BC 的中点,N 是AB 1的中点,P 是B 1C 1的中点.(1)证明:MN ⎳平面A 1CP ;(2)求点P 到直线MN 的距离.【答案】(1)证明见解析(2)3【分析】(1)建立如图空间直角坐标系A -xyz ,设平面A 1CP 的一个法向量为n=(x ,y ,z ),利用空间向量法证明MN ⋅n=0即可;(2)利用空间向量法即可求解点线距.【详解】(1)由题意知,AA 1⊥平面ABC ,∠BAC =60°,而AB ⊂平面ABC ,所以AA 1⊥AB ,在平面ABC 内过点A 作y 轴,使得AB ⊥y 轴,建立如图空间直角坐标系A -xyz ,则A (0,0,0),B (2,0,0),C (1,3,0),A 1(0,0,2),B 1(2,0,2),得M 32,32,0,N (1,0,1),P 32,32,2,所以A 1C =(1,3,-2),A 1P =32,32,0 ,MN =-12,-32,1 ,设平面A1CP 的一个法向量为n=(x ,y ,z ),则n ⋅A 1C=x +3y -2z =0n ⋅A 1P =32x +32y =0,令x =1,得y =-3,z =-1,所以n=(1,-3,-1),所以MN ⋅n =-12×1+-32×(-3)+1×(-1)=0,又MN 不在平面A 1CP 内即MN ⎳平面A 1CP ;(2)如图,连接PM ,由(1)得PM =(0,0,-2),则MN ⋅PM =-2,MN =2,PM =2,所以点P 到直线MN 的距离为d =PM 2-MN ⋅PMPM2= 3.2(2024·安徽合肥·二模)如图,在四棱锥P -ABCD 中,底面ABCD 是边长为2的菱形,∠BAD =60°,M 是侧棱PC 的中点,侧面PAD 为正三角形,侧面PAD ⊥底面ABCD .(1)求三棱锥M -ABC 的体积;(2)求AM 与平面PBC 所成角的正弦值.【答案】(1)12(2)3311.【分析】(1)作出辅助线,得到线线垂直,进而得到线面垂直,由中位线得到M 到平面ABCD 的距离为32,进而由锥体体积公式求出答案;(2)证明出BO ⊥AD ,建立空间直角坐标系,求出平面的法向量,进而由法向量的夹角余弦值的绝对值求出线面角的正弦值.【详解】(1)如图所示,取AD 的中点O ,连接PO .因为△PAD 是正三角形,所以PO ⊥AD .又因为平面PAD ⊥底面ABCD ,PO ⊂平面PAD ,平面PAD ∩平面ABCD =AD ,所以PO ⊥平面ABCD ,且PO =3.又因为M 是PC 的中点,M 到平面ABCD 的距离为32,S △ABC =12×2×2×sin 2π3=3,所以三棱锥M -ABC 的体积为13×3×32=12.(2)连接BO ,BD ,因为∠BAD =π3,所以△ABD 为等边三角形,所以BO ⊥AD ,以O 为原点,OA ,OB ,OP 所在直线分别为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系,则P 0,0,3 ,A 1,0,0 ,B 0,3,0 ,C -2,3,0 ,所以M -1,32,32 ,AM =-2,32,32,PB =0,3,-3 ,BC =-2,0,0 .设平面PBC 的法向量为n=x ,y ,z ,则PB ⋅n =0BC ⋅n =0,即3y -3z =0-2x =0 ,解得x =0,取z =1,则y =1,所以n=0,1,1 .设AM 与平面PBC 所成角为θ,则sin θ=cos AM ,n =AM ⋅nAM ⋅n=-2,32,32 ⋅0,1,14+34+34×1+1=3311.即AM 与平面PBC 所成角的正弦值为3311.3(2023·福建福州·模拟预测)如图,在三棱柱ABC -A 1B 1C 1中,平面AA 1C 1C ⊥平面ABC ,AB =AC =BC =AA 1=2,A 1B =6.(1)设D 为AC 中点,证明:AC ⊥平面A 1DB ;(2)求平面A 1AB 1与平面ACC 1A 1夹角的余弦值.【答案】(1)证明见解析;(2)55【分析】(1)根据等边三角形的性质得出BD ⊥AC ,根据平面ACC 1A 1⊥平面ABC 得出BD ⊥平面ACC 1A 1,BD ⊥A 1D ,利用勾股定理得出AC ⊥A 1D ,从而证明AC ⊥平面A 1DB ;(2)建立空间直角坐标系,利用坐标表示向量,求出平面A 1AB 1的法向量和平面ACC 1A 1的一个法向量,利用向量求平面A 1AB 1与平面ACC 1A 1的夹角余弦值.【详解】(1)证明:因为D 为AC 中点,且AB =AC =BC =2,所以在△ABC 中,有BD ⊥AC ,且BD =3,又平面ACC 1A 1⊥平面ABC ,且平面ACC 1A 1∩平面ABC =AC ,BD ⊂平面ABC ,所以BD ⊥平面ACC 1A 1,又A 1D ⊂平面ACC 1A 1,则BD ⊥A 1D ,由A 1B =6,BD =3,得A 1D =3,因为AD =1,AA 1=2,A 1D =3,所以由勾股定理,得AC ⊥A 1D ,又AC ⊥BD ,A 1D ∩BD =D ,A 1D ,BD ⊂平面A 1DB ,所以AC ⊥平面A 1DB ;(2)如图所示,以D 为原点,建立空间直角坐标系D -xyz ,可得A (1,0,0),A 1(0,0,3),B (0,3,0),则AA 1 =-1,0,3 ,AB=-1,3,0 ,设平面A 1AB 1的法向量为n=(x ,y ,z ),由n ⋅AA 1=-x +3z =0n ⋅AB=-x +3y =0,令x =3,得y =1,z =1,所以n=3,1,1 ,由(1)知,BD ⊥平面ACC 1A 1,所以平面ACC 1A 1的一个法向量为BD=(0,-3,0),记平面A 1AB 1与平面ACC 1A 1的夹角为α,则cos α=|n ⋅BD ||n ||BD |=35×3=55,所以平面A 1AB 1与平面ACC 1A 1夹角的余弦值为55.4(2024·山西晋中·三模)如图,在六面体ABCDE 中,BC =BD =6,EC ⊥ED ,且EC =ED =2,AB 平行于平面CDE ,AE 平行于平面BCD ,AE ⊥CD .(1)证明:平面ABE ⊥平面CDE ;(2)若点A 到直线CD 的距离为22,F 为棱AE 的中点,求平面BDF 与平面BCD 夹角的余弦值.【答案】(1)证明见解析(2)10535【分析】(1)设平面ABE 与直线CD 交于点M ,使用线面平行的性质,然后用面面垂直的判定定理即可;(2)证明BE ⊥平面CDE ,然后构造空间直角坐标系,直接用空间向量方法即可得出结果.【详解】(1)设平面ABE 与直线CD 交于点M ,连接ME ,MB ,则平面ABE 与平面CDE 的交线为ME ,平面ABE 与平面BCD 的交线为MB ,因为AB 平行于平面CDE ,AB ⊂平面ABE ,平面ABE 和平面CDE 的交线为ME ,所以AB ∥ME .同理AE ∥MB ,所以四边形ABME 是平行四边形,故AE ∥MB ,AB ∥ME .因为CD ⊥AE ,AE ∥MB ,所以CD ⊥MB ,又BC =BD =6,所以M 为棱CD 的中点在△CDE 中,EC =ED ,MC =MD ,所以CD ⊥ME ,由于AB ∥ME ,故CD ⊥AB .而CD ⊥AE ,AB ∩AE =A ,AB ,AE ⊂平面ABE ,所以CD ⊥平面ABE ,又CD ⊂平面CDE ,所以平面ABE ⊥平面CDE .(2)由(1)可知,CD ⊥平面ABME ,又AM ⊂平面ABME ,所以CD ⊥AM .而点A 到直线CD 的距离为22,故AM =2 2.在等腰直角三角形CDE 中,由EC =ED =2,得CD =2,MC =MD =ME =1.在等腰三角形BCD 中,由MC =MD =1,BC =BD =6,得BM = 5.在平行四边形ABME 中,AE =BM =5,AB =EM =1,AM =22,由余弦定理得cos ∠MEA =EM 2+AE 2-AM 22EM ·AE=-55,所以cos ∠BME =55,所以BE =BM 2+EM 2-2BM ·EM cos ∠BME =2.因为BE 2+ME 2=22+12=5 2=BM 2,所以BE ⊥ME .因为平面ABME ⊥平面CDE ,平面ABME 和平面CDE 的交线为ME ,BE 在平面ABME 内.所以BE ⊥平面CDE .如图,以E 为坐标原点,EC ,ED ,EB 分别为x ,y ,z 轴正方向,建立空间直角坐标系.则E 0,0,0 ,C 2,0,0 ,D 0,2,0 ,B 0,0,2 ,A -22,-22,2 ,F -24,-24,1.所以CD =-2,2,0 ,DB =0,-2,2 ,FB =24,24,1 .设平面BCD 的法向量为m=x 1,y 1,z 1 ,则m ⋅CD=0m ⋅DB =0,即-2x 1+2y 1=0-2y 1+2z 1=0 .则可取x 1=2,得m=2,2,2 .设平面BDF 的法向量为n =x 2,y 2,z 2 ,则n ⋅FB =0n ⋅DB=0,即24x 2+24y 2+z 2=0-2y 2+2z 2=0.取z 2=1,则n=-32,2,1 .设平面BDF 与平面BCD 的夹角为θ,则cos θ=m ⋅n m ⋅n =-3210×21=10535.所以平面BDF 与平面BCD 夹角的余弦值为10535.5(2024·辽宁·二模)棱长均为2的斜三棱柱ABC -A 1B 1C 1中,A 1在平面ABC 内的射影O 在棱AC 的中点处,P 为棱A 1B 1(包含端点)上的动点.(1)求点P 到平面ABC 1的距离;(2)若AP ⊥平面α,求直线BC 1与平面α所成角的正弦值的取值范围.【答案】(1)23913;(2)25,104.【分析】(1)以O 为原点建立空间直角坐标系,求出平面ABC 1的法向量,再利用点到平面距离的向量求法求解即得.(2)由向量共线求出向量AP的坐标,再利用线面角的向量求法列出函数关系,并求出函数的值域即可.【详解】(1)依题意,A 1O ⊥平面ABC ,OB ⊥AC (底面为正三角形),且A 1O =OB =3,以O 为原点,OB ,OC ,OA 1的方向分别为x ,y ,z 轴的正方向,建立空间直角坐标系,如图,则O (0,0,0),A (0,-1,0),B (3,0,0),C (0,1,0),A 1(0,0,3),C 1(0,2,3),AC 1 =(0,3,3),BC 1 =(-3,2,3),AA 1 =(0,1,3),由A 1B 1⎳AB ,A 1B 1⊄平面ABC 1,AB ⊂平面ABC 1,则A 1B 1⎳平面ABC 1,即点P 到平面ABC 1的距离等于点A 1到平面ABC 1的距离,设n =(x ,y ,z )为平面ABC 1的一个法向量,由n ⋅AC 1=3y +3z =0n ⋅BC 1=-3x +2y +3z =0,取z =3,得n=(1,-3,3),因此点A 1到平面ABC 1的距离d =|AA 1 ⋅n||n |=2313=23913,所以点P 到平面ABC 1的距离为23913.(2)设A 1P =λA 1B 1 ,λ∈[0,1],则AP =AA 1 +A 1P =AA 1 +λAB=(0,1,3)+λ(3,1,0)=(3λ,1+λ,3),由AP ⊥α,得AP为平面α的一个法向量,设直线BC 1与平面α所成角为θ,则sin θ=|cos ‹BC 1 ,AP ›|=|BC 1 ⋅AP||BC 1 ||AP |=|5-λ|10⋅3λ2+(1+λ)2+3=5-λ25⋅2λ2+λ+2,令t =5-λ,则λ=5-t ,t ∈[4,5],则sin θ=t 25⋅2(5-t )2+(5-t )+2=t25⋅2t 2-21t +57=125⋅2-21t+57t 2=125571t-7382+576,由t ∈[4,5],得1t ∈15,14 ,于是571t -738 2+576∈225,516,25⋅571t -738 2+576∈2105,52 ,则sin θ∈25,104,所以直线BC 1与平面α所成角的正弦值的取值范围是25,104.6(2024·重庆·模拟预测)在如图所示的四棱锥P -ABCD 中,已知AB ∥CD ,∠BAD =90°,CD =2AB ,△PAB 是正三角形,点M 在侧棱PB 上且使得PD ⎳平面AMC .(1)证明:PM =2BM ;(2)若侧面PAB ⊥底面ABCD ,CM 与底面ABCD 所成角的正切值为311,求二面角P -AC -B 的余弦值.【答案】(1)证明见解析;(2)1010.【分析】(1)连接BD 与AC 交于点E ,连接EM ,由已知得AB CD=EBED ,由线面平行的性质得PD ∥EM ,根据三角形相似可得EB ED =BM PM=12,即PM =2BM(2)设AB 的中点O ,首先由已知得PO ⊥底面ABCD ,在△PAB 中过点M 作MF ∥PO 交AB 于点F ,得MF ⊥底面ABCD ,则∠MCF 为CM 与底面ABCD 所成角,在底面ABCD 上过点O 作OG ⊥AC 于点G ,则∠PGO 是二面角P -AC -B 的平面角,根据条件求解即可【详解】(1)证明:连接BD 与AC 交于点E ,连接EM ,在△EAB 与△ECD 中,∵AB ∥CD ,∴AB CD=EBED ,由CD =2AB ,得ED =2EB ,又∵PD ⎳平面AMC ,而平面PBD ∩平面AMC =ME ,PD ⊂平面PBD ,∴PD ∥EM ,∴在△PBD 中,EB ED =BM PM=12,∴PM =2BM ;(2)设AB 的中点O ,在正△PAB 中,PO ⊥AB ,而侧面PAB ⊥底面ABCD ,侧面PAB ∩底面ABCD =AB ,且PO ⊂平面PAB ,∴PO ⊥底面ABCD ,在△PAB 中过点M 作MF ⎳PO 交AB 于点F ,∴MF ⊥底面ABCD ,∴∠MCF 为CM 与底面ABCD 所成角,∴MF CF=311,设AB =6a ,则MF=3a,∴CF=11a,BF=MF3=a,则在直角梯形ABCD中,AF=5a,而CD=12a,则AD=11a2-12a-5a2=62a,在底面ABCD上过点O作OG⊥AC于点G,则∠PGO是二面角P-AC-B的平面角,易得OA=3a,AC=66a,在梯形ABCD中,由OAOG=ACAD⇒3aOG=66a62a,得OG=3a,在Rt△POG中,PG=30a,∴cos∠PGO=OGPG=1010.7(2024·安徽·模拟预测)2023年12月19日至20日,中央农村工作会议在北京召开,习近平主席对“三农”工作作出指示.某地区为响应习近平主席的号召,积极发展特色农业,建设蔬菜大棚.如图所示的七面体ABG-CDEHF是一个放置在地面上的蔬菜大棚钢架,四边形ABCD是矩形,AB=8m,AD=4m,ED=CF=1m,且ED,CF都垂直于平面ABCD,GA=GB=5m,HE=HF,平面ABG⊥平面ABCD.(1)求点H到平面ABCD的距离;(2)求平面BFHG与平面AGHE所成锐二面角的余弦值.【答案】(1)4(2)413【分析】(1)取AB,CD的中点M,N,证得平面ADE⎳平面MNHG,得到AE⎳GH,再由平面ABG⎳平面CDEHG,证得AG⎳EH,得到平行四边形AGHE,得到GH=AE,求得HN=4,结合HN⊥平面ABCD,即可求解;(2)以点N为原点,建立空间直角坐标系,分别求得平面BFHG和平面AGHE的法向量n =(1,3,4)和m =(1,-3,4),结合向量的夹角公式,即可求解.【详解】(1)如图所示,取AB,CD的中点M,N,连接GM,MN,HN,因为GA=GB,可得GM⊥AB,又因为平面ABG⊥平面ABCD,且平面ABG∩平面ABCD=AB,GM⊂平面ABG,所以GM⊥平面ABCD,同理可得:HN⊥平面ABCD,因为ED⊥平面ABCD,所以ED⎳HN,又因为ED⊄平面MNHG,HN⊂平面MNHG,所以ED⎳平面MNHG,因为MN⎳AD,且AD⊄平面MNHG,MN⊂平面MNHG,所以AD⎳平面MNHG,又因为AD∩DE=D,且AD,DE⊂平面ADE,所以平面ADE⎳平面MNHG,因为平面AEHG与平面ADE和平面MNHG于AE,GH,可得AE⎳GH,又由GM⎳HN,AB⎳CD,且AB∩GM=M和CD∩HN=N,所以平面ABG⎳平面CDEHG,因为平面AEHG与平面ABG和平面CDEHF于AG,EH,所以AG⎳EH,可得四边形AGHE 为平行四边形,所以GH =AE ,因为AE =AD 2+DE 2=42+12=17,所以GH =17,在直角△AMG ,可得GM =GB 2-AB 22=52-42=3,在直角梯形GMNH 中,可得HN =3+17-42=4,因为HN ⊥平面ABCD ,所以点H 到平面ABCD 的距离为4.(2)解:以点N 为原点,以NM ,NC ,NH 所在的直线分别为x ,y ,z 轴,建立空间直角坐标系,如图所示,则E (0,-4,1),F (0,4,1),G (4,0,3),H (0,0,4),可得HE =(0,-4,-3),HF =(0,4,-3),HG=(4,0,-1),设平面BFHG 的法向量为n=(x ,y ,z ),则n ⋅HG=4x -z =0n ⋅HF=4y -3z =0,取z =4,可得x =1,y =3,所以n=(1,3,4),设平面AGHE 的法向量为m=(a ,b ,c ),则m ⋅HG=4a -c =0m ⋅HE=-4b -3c =0,取c =4,可得a =1,b =-3,所以m=(1,-3,4),则cos m ,n =m ⋅n m n=1-9+161+9+16⋅1+9+16=413,即平面BFHG 与平面AGHE 所成锐二面角的余弦值413.8(2024·重庆·模拟预测)如图,ACDE 为菱形,AC =BC =2,∠ACB =120°,平面ACDE ⊥平面ABC ,点F 在AB 上,且AF =2FB ,M ,N 分别在直线CD ,AB 上.(1)求证:CF ⊥平面ACDE ;(2)把与两条异面直线都垂直且相交的直线叫做这两条异面直线的公垂线,若∠EAC =60°,MN 为直线CD ,AB 的公垂线,求ANAF的值;(3)记直线BE 与平面ABC 所成角为α,若tan α>217,求平面BCD 与平面CFD 所成角余弦值的范围.【答案】(1)证明见解析(2)AN AF=913(3)528,255 【分析】(1)先通过余弦定理及勾股定理得到CF ⊥AC ,再根据面面垂直的性质证明;(2)以C 为原点,CA 的方向为x 轴正方向,建立如图所示空间直角坐标系C -xyz ,利用向量的坐标运算根据MN ⋅CD =0MN ⋅AF =0,列方程求解即可;(3)利用向量法求面面角,然后根据tan α>217列不等式求解.【详解】(1)AB 2=AC 2+BC 2-2AC ⋅BC ⋅cos ∠ACB =12,AB =23,AF =2FB ,所以AF =433,CF=13CA +23CB ,CF 2=19CA 2+49CB 2+49CA ⋅CB =43,AC 2+CF 2=4+43=163=AF 2,则CF ⊥AC ,又因为平面ACDE ⊥平面ABC ,平面ACDE ∩平面ABC =AC ,CF ⊂面ABC ,故CF ⊥平面ACDE ;(2)以C 为原点,CA 的方向为x 轴正方向,建立如图所示空间直角坐标系C -xyz ,由∠EAC =60°,可得∠DCA =120°,DC =2,所以C 0,0,0 ,D -1,0,3 ,A 2,0,0 ,F 0,233,0 所以AF =-2,233,0 ,CD =-1,0,3 ,设AN =λAF =-2λ,233λ,0 ,则N 2-2λ,233λ,0 ,设CM =μCD ,则M -μ,0,3μ ,MN =2-2λ+μ,233λ,-3μ ,由题知,MN ⋅CD=0MN ⋅AF =0 ⇒2λ-2-μ-3μ=04λ-4-2μ+43λ=0 ,解得λ=913,μ=-213,故AN AF=913;(3)B -1,3,0 ,设∠EAC =θ,则E 2-2cos θ,0,2sin θ ,BE=3-2cos θ,-3,2sin θ ,可取平面ABC 的法向量n=0,0,1 ,则sin α=cos n ,BE=n ⋅BEn ⋅BE =2sin θ 3-2cos θ 2+3+4sin 2θ=sin θ4-3cos θ,cos α=4-3cos θ-sin 2θ4-3cos θ,则tan α=sin θ4-3cos θ-sin 2θ>217,整理得10cos 2θ-9cos θ+2<0,故cos θ∈25,12,CF =0,23,0,CD =-2cos θ,0,2sin θ ,CB =-1,3,0 ,记平面CDF 的法向量为n 1 =x ,y ,z ,则有n 1 ⋅CD =0n 1 ⋅CF =0 ⇒-2x cos θ+2z sin θ=023y =0,可得n 1=sin θ,0,cos θ ,记平面CBD 的法向量为n 2 =a ,b ,c ,则有n 2 ⋅CD=0n 2 ⋅CB =0 ⇒-2a cos θ+2c sin θ=0-a +3b =0,可得n 2=3sin θ,sin θ,3cos θ ,记平面BCD 与平面CFD 所成角为γ,则cos γ=cos n 1 ,n 2 =33+sin 2θ,cos θ∈25,12 ,所以sin 2θ∈34,2125 ,3+sin 2θ∈152,465 ,故cos γ=33+sin 2θ∈528,255 .9(2024·安徽·二模)将正方形ABCD 绕直线AB 逆时针旋转90°,使得CD 到EF 的位置,得到如图所示的几何体.(1)求证:平面ACF ⊥平面BDE ;(2)点M 为DF上一点,若二面角C -AM -E 的余弦值为13,求∠MAD .【答案】(1)证明见解析(2)∠MAD =45°【分析】(1)根据面面与线面垂直的性质可得BD ⊥AF ,结合线面、面面垂直的判定定理即可证明;(2)建立如图空间直角坐标系,设∠MAD =α,AB =1,利用空间向量法求出二面角C -AM -E 的余弦值,建立方程1-sin αcos α1+sin 2α1+cos 2α=13,结合三角恒等变换求出α即可.【详解】(1)由已知得平面ABCD ⊥平面ABEF ,AF ⊥AB ,平面ABCD ∩平面ABEF =AB ,AF ⊂平面ABEF ,所以AF ⊥平面ABCD ,又BD ⊂平面ABCD ,故BD ⊥AF ,因为ABCD 是正方形,所以BD ⊥AC ,AC ,AF ⊂平面ACF ,AC ∩AF =A ,所以BD ⊥平面ACF ,又BD ⊂平面BDE ,所以平面ACF ⊥平面BDE .(2)由(1)知AD ,AF ,AB 两两垂直,以AD ,AF ,AB 所在直线分别为x ,y ,z 轴,建立空间直角坐标系,如图.设∠MAD =α,AB =1,则A 0,0,0 ,M cos α,sin α,0 ,C 1,0,1 ,E 0,1,1 ,故AM =cos α,sin α,0 ,AC =1,0,1 ,AE =0,1,1设平面AMC 的法向量为m =x 1,y 1,z 1 ,则m ⋅AC =0,m ⋅AM=0故x 1+z 1=0x 1cos α+y 1sin α=0,取x 1=sin α,则y 1=-cos α,z 1=-sin α所以m=sin α,-cos α,-sin α设平面AME 的法向量为n =x 2,y 2,z 2 ,n ⋅AE =0,n ⋅AM=0故y 2+z 2=0x 2cos α+y 2sin α=0,取x 2=sin α,则y 2=-cos α,z 2=cos α所以n=sin α,-cos α,cos α ,所以cos m ,n =1-sin αcos α1+sin 2α1+cos 2α,由已知得1-sin αcos α1+sin 2α1+cos 2α=13,化简得:2sin 22α-9sin2α+7=0,解得sin2α=1或sin2α=72(舍去)故α=45°,即∠MAD =45°.10(2024·安徽黄山·二模)如图,已知AB 为圆台下底面圆O 1的直径,C 是圆O 1上异于A ,B 的点,D 是圆台上底面圆O 2上的点,且平面DAC ⊥平面ABC ,DA =DC =AC =2,BC =4,E 是CD 的中点,BF =2FD .(1)证明:DO 2⎳BC ;(2)求直线DB 与平面AEF 所成角的正弦值.【答案】(1)证明见解析(2)68585【分析】(1)取AC 的中点O ,根据面面垂直的性质定理,可得DO ⊥平面ABC ,即可求证DO 2⎳OO 1,进而可证矩形,即可根据线线平行以及平行的传递性求解.(2)建系,利用向量法,求解法向量n =1,-12,3 与方向向量DB =(-1,4,-3)的夹角,即可求解.【详解】(1)证明:取AC 的中点为O ,连接DO ,OO 1,O 1O 2,∵DA =DC ,O 为AC 中点,∴DO ⊥AC ,又平面DAC ⊥平面ABC ,且平面DAC ∩平面ABC =AC ,DO ⊂平面DAC ,∴DO ⊥平面ABC ,∴DO ⎳O 1O 2,DO =O 1O 2,故四边形DOO 1O 2为矩形,∴DO 2⎳OO 1,又O ,O 1分别是AC ,AB 的中点,∴OO 1⎳BC ,∴DO 2⎳BC ;(2)∵C 是圆O 1上异于A ,B 的点,且AB 为圆O 1的直径,∴BC ⊥AC ,∴OO 1⊥AC ,∴如图以O 为原点建立空间直角坐标系,由条件知DO =3,∴A (1,0,0),B (-1,4,0),C (-1,0,0),D (0,0,3),∴E -12,0,32 ,设F (x ,y ,z ),∴BF =(x +1,y -4,z ),FD=(-x ,-y ,3-z ),由BF =2FD ,得F -13,43,233 ,∴AF =-43,43,233 ,∴DB =(-1,4,-3),AE =-32,0,32 ,设平面AEF 法向量为n=(x 1,y 1,z 1),则n ⋅AE=-32x 1+32z 1=0n ⋅AF =-43x 1+43y 1+233z 1=0,取n =1,-12,3 ,设直线BD 与平面AEF 所成角为θ,则sin θ=|cos <n ,DB>|=625⋅172=68585∴直线BD 与平面AEF 所成角的正弦值为68585.11(2024·黑龙江哈尔滨·一模)正四棱台ABCD -A 1B 1C 1D 1的下底面边长为22,A 1B 1=12AB ,M 为BC 中点,已知点P 满足AP =1-λ AB +12λ⋅AD +λAA 1,其中λ∈0,1 .(1)求证D 1P ⊥AC ;(2)已知平面AMC 1与平面ABCD 所成角的余弦值为37,当λ=23时,求直线DP 与平面AMC 1所成角的正弦值.【答案】(1)证明见解析(2)241391【分析】(1)方法一运用空间向量的线性运算,进行空间位置关系的向量证明即可.方法二:建立空间直角坐标系,进行空间位置关系的向量证明即可.(2)建立空间直角坐标系,利用线面角的向量求法求解即可.【详解】(1)方法一:∵A 1B 1=12AB ,∴AA 1 ⋅AB =AA 1 ⋅AD =22×22=2.∵D 1A =-12AD-AA 1∴D 1P =D 1A +AP =1-λ AB +12λ-12AD+λ-1 AA 1∴D 1P ⋅AC =1-λ AB +12λ-12AD +λ-1 AA 1 ⋅AB +AD =1-λ AB 2+12λ-12 AD2+λ-1 AB ⋅AA 1 +λ-1 AD ⋅AA 1=81-λ +812λ-12+4λ-1 =0.∴D 1P ⊥AC ,即D 1P ⊥AC .方法二:以底面ABCD 的中心O 为原点,以OM 方向为y 轴,过O 点平行于AD 向前方向为x 轴,以过点O 垂直平面ABCD 向上方向为z 轴,建立如图所示空间直角坐标系,设正四棱台的高度为h ,则有 A 2,-2,0 ,B 2,2,0 ,C -2,2,0 ,D -2,-2,0 ,A 122,-22,h ,C 1-22,22,h ,D 1-22,-22,h ,M 0,2,0 ,AC =-22,22,0AP =1-λ 0,22,0 +12λ-22,0,0 +λ-22,22,0 =-322λ,22-322λ,λhD 1A =322,-22,-h ,D 1P =D 1A +AP =-322λ+322,-322λ+322,λh -h .故AC ⋅D 1P=0,所以D 1P ⊥AC .(2)设平面ABCD 的法向量为n=0,0,1 ,设平面AMC 1的法向量为m =x ,y ,z ,AM =-2,22,0 ,AC 1 =-322,322,h ,则有AM ⋅m=0AC 1 ⋅m=0 ,即-2x +22y =0-322x +322y +hz =0,令x =22h ,则m=22h ,2h ,3 .又题意可得cos m ,n =38h 2+2h 2+9=37,可得h =2.因为λ=23,经过计算可得P 0,0,43 ,D 1-22,-22,2 ,D 1P =2,2,43.将h =2代入,可得平面AMC 1的法向量m=42,22,3 .设直线DP 与平面AMC 1所成角的为θsin θ=cos DP ,m =8+4+42+2+16932+8+9=241391.12(2024·辽宁·三模)如图,在三棱柱ABC -A 1B 1C 1中,侧面ACC 1A 1⊥底面ABC ,AC =AA 1=2,AB =1,BC =3,点E 为线段AC 的中点.(1)求证:AB 1∥平面BEC 1;(2)若∠A 1AC =π3,求二面角A -BE -C 1的余弦值.【答案】(1)证明见详解(2)-22【分析】(1)连接BC 1,交B 1C 于点N ,连接NE ,利用线面平行的判定定理证明;(2)由已知可知,△AA 1C 为等边三角形,故A 1E ⊥AC ,利用面面垂直的性质定理可证得A 1E ⊥底面ABC ,进而建立空间直角坐标系,利用向量法即可求二面角余弦值.【详解】(1)连接BC 1,交B 1C 于点N ,连接NE ,因为侧面BCC 1B 1是平行四边形,所以N 为B 1C 的中点,又因为点E 为线段AC 的中点,所以NE ⎳AB 1,因为AB 1⊄面BEC 1,NE ⊂面BEC 1,所以AB 1⎳面BEC 1.(2)连接A 1C ,A 1E ,因为∠A 1AC =π3,AC =AA 1=2,所以△AA 1C 为等边三角形,A 1C =2,因为点E 为线段AC 的中点,所以A 1E ⊥AC ,因为侧面ACC 1A 1⊥底面ABC ,平面ACC 1A 1∩平面ABC =AC ,A 1E ⊂平面ACC 1A 1,所以A 1E ⊥底面ABC ,过点E 在底面ABC 内作EF ⊥AC ,如图以E 为坐标原点,分布以EF ,EC ,EA 1 的方向为x ,y ,z 轴正方向建立空间直角坐标系,则E 0,0,0 ,B 32,-12,0 ,C 10,2,3 ,所以EB =32,-12,0 ,EC 1 =0,2,3 ,设平面BEC 1的法向量为m=x ,y ,z ,则m ⋅EB =32x -12y =0m ⋅EC 1=2y +3z =0,令x =1,则y =3,z =-2,所以平面BEC 1的法向量为m=1,3,-2 ,又因为平面ABE 的法向量为n=0,0,1 ,则cos m ,n =-21+3+4=-22,经观察,二面角A -BE -C 1的平面角为钝角,所以二面角A -BE -C 1的余弦值为-22.13(2024·广东广州·一模)如图,在四棱锥P -ABCD 中,底面ABCD 是边长为2的菱形,△DCP 是等边三角形,∠DCB =∠PCB =π4,点M ,N 分别为DP 和AB 的中点.(1)求证:MN ⎳平面PBC ;(2)求证:平面PBC ⊥平面ABCD ;(3)求CM 与平面PAD 所成角的正弦值.【答案】(1)证明见解析;(2)证明见解析;(3)33.【分析】(1)取PC 中点E ,由已知条件,结合线面平行的判断推理即得.(2)过P 作PQ ⊥BC 于点Q ,借助三角形全等,及线面垂直的判定、面面垂直的判定推理即得.(3)建立空间直角坐标系,利用线面角的向量求法求解即得.【详解】(1)取PC 中点E ,连接ME ,BE ,由M 为DP 中点,N 为AB 中点,得ME ⎳DC ,ME =12DC ,又BN ⎳CD ,BN =12CD ,则ME ⎳BN ,ME =BN ,因此四边形BEMN 为平行四边形,于是MN ⎳BE ,而MN ⊄平面PBC ,BE ⊂平面PBC ,所以MN ⎳平面PBC .(2)过P 作PQ ⊥BC 于点Q ,连接DQ ,由∠DCB =∠PCB =π4,CD =PC ,QC =QC ,得△QCD ≌△QCP ,则∠DQC =∠PQC =π2,即DQ ⊥BC ,而PQ =DQ =2,PQ 2+DQ 2=4=PD 2,因此PQ ⊥DQ ,又DQ ∩BC =Q ,DQ ,BC ⊂平面ABCD ,则PQ ⊥平面ABCD ,PQ ⊂平面PBC ,所以平面PBC ⊥平面ABCD .(3)由(2)知,直线QC ,QD ,QP 两两垂直,以点Q 为原点,直线QC ,QD ,QP 分别为x ,y ,z 轴建立空间直角坐标系,则C (2,0,0),P (0,0,2),D (0,2,0),M 0,22,22,A (-2,2,0),CM =-2,22,22,AD =(2,0,0),DP =(0,-2,2),设平面PAD 的一个法向量n =(x ,y ,z ),则n ⋅AD=2x =0n ⋅DP=-2y +2z =0,令y =1,得n=(0,1,1),设CM 与平面PAD 所成角为θ,sin θ=|cos ‹CM ,n ›|=|CM ⋅n||CM ||n |=23⋅2=33,所以CM 与平面PAD 所成角的正弦值是33.14(2024·广东梅州·二模)如图,在四棱锥P -ABCD 中,平面PAD ⊥平面ABCD ,底面ABCD 为直角梯形,△PAD 为等边三角形,AD ⎳BC ,AD ⊥AB ,AD =AB =2BC =2.(1)求证:AD ⊥PC ;(2)点N 在棱PC 上运动,求△ADN 面积的最小值;(3)点M 为PB 的中点,在棱PC 上找一点Q ,使得AM ⎳平面BDQ ,求PQQC的值.【答案】(1)证明见解析(2)2217(3)4【分析】(1)取AD 的中点H ,连接PH ,CH ,依题意可得四边形ABCH 为矩形,即可证明CH ⊥AD ,再由PH ⊥AD ,即可证明AD ⊥平面PHC ,从而得证;(2)连接AC 交BD 于点G ,连接MC 交BQ 于点F ,连接FG ,即可得到CG AG=12,再根据线面平行的性质得到CF FM =12,在△PBC 中,过点M 作MK ⎳PC ,即可得到MKCQ=2,最后由PQ =2MK 即可得解.【详解】(1)取AD 的中点H ,连接PH ,CH ,则AH ⎳BC 且AH =BC ,又AD ⊥AB ,所以四边形ABCH 为矩形,所以CH ⊥AD ,又△PAD 为等边三角形,所以PH ⊥AD ,PH ∩CH =H ,PH ,CH ⊂平面PHC ,所以AD ⊥平面PHC ,又PC ⊂平面PHC ,所以AD ⊥PC .(2)连接HN ,由AD ⊥平面PHC ,又HN ⊂平面PHC ,所以AD ⊥HN ,所以S △ADH =12AD ⋅HN =HN ,要使△ADN 的面积最小,即要使HN 最小,当且仅当HN ⊥PC 时HN 取最小值,因为平面PAD ⊥平面ABCD ,平面PAD ∩平面ABCD =AD ,PH ⊂平面PAD ,所以PH ⊥平面ABCD ,又HC ⊂平面ABCD ,所以PH ⊥HC ,在Rt △HPC 中,CH =2,PH =3,所以PC =CH 2+PH 2=7,当HN ⊥PC 时HN =PH ⋅CH PC =237=2217,所以△ADN 面积的最小值为2217.(3)连接AC 交BD 于点G ,连接MC 交BQ 于点F ,连接FG ,因为AD ⎳BC 且AD =2BC =2,所以△CGB ∽△AGD ,所以CG AG =BC AD=12,因为AM ⎳平面BDQ ,又AM ⊂平面ACM ,平面BDQ ∩平面ACM =GF ,所以GF ⎳AM ,所以CF FM =CG AG=12,在△PBC 中,过点M 作MK ⎳PC ,则有MK CQ =MF CF=2,所以PQ =2MK ,所以PQ =2MK =4CQ ,即PQQC=415(2024·广东广州·模拟预测)如图所示,圆台O 1O 2的轴截面A 1ACC 1为等腰梯形,AC =2AA 1=2A 1C 1=4,B 为底面圆周上异于A ,C 的点,且AB =BC ,P 是线段BC 的中点.(1)求证:C 1P ⎳平面A 1AB .(2)求平面A 1AB 与平面C 1CB 夹角的余弦值.【答案】(1)证明见解析(2)17【分析】(1)取AB 的中点H ,连接A 1H ,PH ,证明四边形A 1C 1PH 为平行四边形,进而得C 1P ⎳A 1H ,即可证明;(2)建立空间直角坐标系,求两平面的法向量,利用平面夹角公式求解.【详解】(1)取AB 的中点H ,连接A1H ,PH ,如图所示,因为P 为BC 的中点,所以PH ⎳AC ,PH =12AC .在等腰梯形A 1ACC 1中,A 1C 1⎳AC ,A 1C 1=12AC ,所以HP ⎳A 1C 1,HP =A 1C 1,所以四边形A 1C 1PH 为平行四边形,所以C 1P ⎳A 1H ,又A 1H ⊂平面A 1AB ,C 1P ⊄平面A 1AB ,所以C 1P ⎳平面A 1AB .(2)因为AB =BC ,故O 2B ⊥AC ,以直线O 2A ,O 2B ,O 2O 1分别为x ,y ,z 轴,建立空间直角坐标系,如图所示,在等腰梯形A 1ACC 1中,AC =2AA 1=2A 1C 1=4,此梯形的高为h =AA 21-AC -A 1C 122= 3.因为A 1C 1=12AC ,A 1C 1⎳AC ,。
近年年高考数学一轮复习高考大题专项练4高考中的立体几何(2021学年)

2019年高考数学一轮复习高考大题专项练4高考中的立体几何编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2019年高考数学一轮复习高考大题专项练4高考中的立体几何)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2019年高考数学一轮复习高考大题专项练4 高考中的立体几何的全部内容。
高考大题专项练四高考中的立体几何1。
如图,四棱锥P—ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点。
(1)证明:PB∥平面AEC;(2)设AP=1,AD=,三棱锥P—ABD的体积V=,求点A到平面PBC的距离.2.如图,四棱锥P—ABCD,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.(1)求证:PC⊥AD;(2)证明在PB上存在一点Q,使得A,Q,M,D四点共面;(3)求点D到平面PAM的距离。
3.如图所示,△ABC为正三角形,CE⊥平面ABC,BD∥CE,CE=CA=2BD,M是EA的中点。
求证:(1)DE=DA。
(2)平面BDM⊥平面ECA.4。
如图,在底面是菱形的四棱柱ABCD—A1B1C1D1中,∠ABC=60°,AA1=AC=2,A1B=A1D=2,点E在A1D上.(1)证明:AA1⊥平面ABCD;(2)当为何值时,A1B∥平面EAC,并求出此时三棱锥D-AEC的体积.5。
(2017山东,文18)由四棱柱ABCD—A1B1C1D1截去三棱锥C1—B1CD1后得到的几何体如图所示.四边形ABCD为正方形,O为AC与BD的交点,E为AD的中点,A1E⊥平面ABCD。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题分层训练(三十一) 中档大题规范练(4)——立体几何1.如图,四边形ABCD为正方形,PD⊥平面ABCD,∠DPC=30°,AF⊥PC于点F,FE∥CD,交PD于点E.(1)证明:CF⊥平面ADF;(2)求二面角D-AF-E的余弦值.解(1)证明:由题意可知DA⊥DC,DA⊥DP,DC⊥DP,故可以D为原点,DP所在直线为x轴,DC所在直线为y轴,DA所在直线为z轴建立空间直角坐标系.设正方形ABCD 的边长为a , 则C (0,a,0),A (0,0,a ),由平面几何知识可求得F ⎝⎛⎭⎪⎪⎫34a ,34a ,0, 所以CF →=⎝⎛⎭⎪⎪⎫34a ,-14a ,0, DF →=⎝⎛⎭⎪⎪⎫34a ,34a ,0, DA →=(0,0,a ),CF →·DF →=34a ×34a +⎝ ⎛⎭⎪⎫-14a ×34a +0=0,CF →·DA →=⎝⎛⎭⎪⎪⎫34a ,-14a ,0·(0,0,a )=0, 故CF ⊥DF ,CF ⊥DA .又DF ∩DA =D ,所以CF ⊥平面ADF .(2)可求得E ⎝ ⎛⎭⎪⎪⎫34a ,0,0,则AE →=⎝⎛⎭⎪⎪⎫34a ,0,-a , 又AF →=⎝⎛⎭⎪⎪⎫34a ,34a ,-a , 设平面AEF 的法向量为n =(x ,y ,z ),则n ·AE →=(x ,y ,z )·⎝ ⎛⎭⎪⎪⎫34a ,0,-a =34ax -az =0,n ·AF →=(x ,y ,z )·⎝ ⎛⎭⎪⎪⎫34a ,34a ,-a =34ax +34ay -az =0,取x =1,得平面AEF 的一个法向量n =⎝⎛⎭⎪⎪⎫1,0,34.又由(1)知平面ADF 的一个法向量为CF →=⎝⎛⎭⎪⎪⎫34a ,-14a ,0, 故cos 〈n ,CF →〉=⎝ ⎛⎭⎪⎪⎫1,0,34·⎝ ⎛⎭⎪⎪⎫34a ,-14a ,0194×12a =25719,由图可知二面角D -AF -E 为锐二面角,所以其余弦值为25719.2.如图,四棱锥P -ABCD 中,底面是以O 为中心的菱形,PO ⊥底面ABCD ,AB =2,∠BAD =π3,M 为BC 上一点,且BM =12,MP ⊥AP .(1)求PO 的长;(2)求二面角A -PM -C 的正弦值. 解 (1)如图,连接AC ,BD ,OM ,因ABCD 为菱形,则AC ∩BD =O ,且AC ⊥BD .以O 为坐标原点,OA →,OB →,OP →的方向分别为x 轴、y 轴、z 轴的正方向,建立空间直角坐标系O -xyz .因∠BAD =π3,故OA =AB ·cos π6=3,OB =AB ·sin π6=1,所以O (0,0,0),A (3,0,0),B (0,1,0),C (-3,0,0), OB →=(0,1,0),BC →=(-3,-1,0). 由BM =12,BC =2知,BM →=14BC →=⎝⎛⎭⎪⎪⎫-34,-14,0, 从而OM →=OB →+BM →=⎝⎛⎭⎪⎪⎫-34,34,0, 即M ⎝⎛⎭⎪⎪⎫-34,34,0. 设P (0,0,a ),a >0,则AP →=(-3,0,a ),MP →=⎝⎛⎭⎪⎪⎫34,-34,a . 因为MP ⊥AP ,故MP →·AP →=0,即-34+a 2=0,所以a =32,a =-32(舍去),即PO =32.(2)由(1)知,AP →=⎝⎛⎭⎪⎪⎫-3,0,32, MP →=⎝ ⎛⎭⎪⎪⎫34,-34,32,CP →=⎝⎛⎭⎪⎪⎫3,0,32. 设平面APM 的法向量为n 1=(x 1,y 1,z 1),平面PMC 的法向量为n 2=(x 2,y 2,z 2).由n 1·AP →=0,n 1·MP →=0,得⎩⎪⎨⎪⎧ -3x 1+32z 1=0,34x 1-34y 1+32z 1=0,故可取n 1=⎝ ⎛⎭⎪⎪⎫1,533,2. 由n 2·MP →=0,n 2·CP →=0,得⎩⎪⎨⎪⎧34x 2-34y 2+32z 2=0,3x 2+32z 2=0,故可取n 2=(1,-3,-2). 从而法向量n 1,n 2的夹角的余弦值为cos 〈n 1,n 2〉=n 1·n 2|n 1||n 2|=-155,故所求二面角A -PM -C 的正弦值为105. 3.如图,在三棱柱ABC -A 1B 1C 1中,AA 1C 1C 是边长为4的正方形.平面ABC ⊥平面AA 1C 1C ,AB =3,BC =5.(1)求证:AA 1⊥平面ABC ;(2)求二面角A 1-BC 1-B 1的余弦值;(3)证明:在线段BC 1上存在点D ,使得AD ⊥A 1B ,并求BDBC 1的值.解(1)证明:在正方形AA 1C 1C 中,A 1A ⊥AC .又平面ABC ⊥平面AA 1C 1C ,且平面ABC ∩平面AA 1C 1C =AC ,∴AA 1⊥平面ABC .(2)在△ABC 中,AC =4,AB =3,BC =5, ∴BC 2=AC 2+AB 2,AB ⊥AC ,∴以A 为坐标原点,建立如图所示空间直角坐标系A -xyz .A 1(0,0,4),B (0,3,0),C 1(4,0,4),B 1(0,3,4),A 1C 1→=(4,0,0),A 1B →=(0,3,-4),B 1C 1→=(4,-3,0),BB 1→=(0,0,4).设平面A 1BC 1的法向量n 1=(x 1,y 1,z 1), 平面B 1BC 1的法向量n 2=(x 2,y 2,z 2).∴⎩⎨⎧A 1C 1→·n 1=0,A 1B →·n 1=0⇒⎩⎪⎨⎪⎧4x 1=0,3y 1-4z 1=0.∴取向量n 1=(0,4,3).由⎩⎨⎧B 1C 1→·n 2=0,BB 1→·n 2=0⇒⎩⎪⎨⎪⎧4x 2-3y 2=0,4z 2=0.取向量n 2=(3,4,0).∴cos 〈n 1·n 2〉=n 1·n 2|n 1|·|n 2|=165×5=1625.∴所求二面角A 1-BC -B 1的余弦值为1625.(3)证明:设D (x ,y ,z )是直线BC 1上一点,且BD →=λBC 1→.∴(x ,y -3,z )=λ(4,-3,4),解得x =4λ,y =3-3λ,z =4λ, ∴AD →=(4λ,3-3λ,4λ).又AD ⊥A 1B ,∴0+3(3-3λ)-16λ=0, 则λ=925,因此BD BC 1=925.4.如图,在四棱锥P -ABCD 中,平面PAC ⊥平面ABCD ,且PA ⊥AC ,PA =AD =2.四边形ABCD 满足BC ∥AD ,AB ⊥AD ,AB =BC =1.点E ,F 分别为侧棱PB ,PC 上的点,且PE PB =PFPC=λ.(1)求证:EF ∥平面PAD ;(2)当λ=12时,求异面直线BF 与CD 所成角的余弦值;(3)是否存在实数λ,使得平面AFD ⊥平面PCD ?若存在,试求出λ的值;若不存在,请说明理由.解 (1)证明:由已知PE PB =PFPC=λ,∴EF ∥BC , 又BC ∥AD ,∴EF ∥AD , 而EF ⊄平面PAD ,AD ⊂平面PAD , ∴EF ∥平面PAD .(2)∵平面ABCD ⊥平面PAC ,平面ABCD ∩平面PAC =AC ,且PA ⊥AC , ∴PA ⊥平面ABCD . ∴PA ⊥AB ,PA ⊥AD . 又∵AB ⊥AD ,∴PA ,AB ,AD 两两垂直.如图所示,建立空间直角坐标系. ∵AB =BC =1,PA =AD =2,∴A (0,0,0),B (1,0,0,),C (1,1,0),D (0,2,0),P (0,0,2), 当λ=12时,F 为PC 中点,∴F ⎝ ⎛⎭⎪⎫12,12,1, ∴BF →=⎝ ⎛⎭⎪⎫-12,12,1,CD →=(-1,1,0),设异面直线BF 与CD 所成的角为θ, ∴cos θ=|cos 〈BF →,CD →〉|=12+1262×2=33. 故异面直线BF 与CD 所成角的余弦值为33.(3)设F (x 0,y 0,z 0),则PF →=(x 0,y 0,z 0-2),PC →=(1,1,-2),又PF →=λPC →,∴⎩⎪⎨⎪⎧x 0=λ,y 0=λ,z 0=2-2λ,∴AF →=(λ,λ,2-2λ),设平面AFD 的一个法向量为m =(x 1,y 1,z 1),则⎩⎨⎧m ·AF →=0,m ·AD →=0,即⎩⎪⎨⎪⎧λx 1+λy 1+(2-2λ)z 1=0,2y 1=0,令z 1=λ,得m =(2λ-2,0,λ).设平面PCD 的一个法向量为n =(x 2,y 2,z 2).则⎩⎨⎧n ·PD →=0,n ·CD →=0,即⎩⎪⎨⎪⎧2y 2-2z 2=0,-x 2+y 2=0,取y 2=1,则x 2=1,z 2=1, ∴n =(1,1,1),由m ⊥n ,得m ·n =(2λ-2,0,λ)·(1,1,1)=2λ-2+λ=0, 解得λ=23.∴当λ=23时,使得平面AFD ⊥平面PCD .5.如图,在四棱锥S -ABCD 中,底面ABCD 是直角梯形,侧棱SA ⊥底面ABCD ,AB 垂直于AD 和BC ,SA =AB =BC =2,AD =1.M 是棱SB 的中点.(1)求证:AM ∥平面SCD ;(2)求平面SCD 与平面SAB 所成二面角的余弦值;(3)设点N 是直线CD 上的动点,MN 与平面SAB 所成的角为θ,求sinθ的最大值.解(1)证明:以点A 为原点建立如图所示的空间直角坐标系,则A (0,0,0),B (0,2,0),C (2,2,0),D (1,0,0),S (0,0,2),M (0,1,1).则AM →=(0,1,1),SD →=(1,0,-2),CD →=(-1,-2,0).设平面SCD 的法向量为n =(x ,y ,z ),则⎩⎨⎧ SD →·n =0,CD →·n =0,即⎩⎪⎨⎪⎧ x -2z =0,-x -2y =0. 令z =1,得n =(2,-1,1).∵AM →·n =0,∴AM →⊥n . ∴AM ∥平面SCD .(2)易知平面SAB 的一个法向量为n 1=(1,0,0).设平面SCD 与平面SAB 所成的二面角为φ,易知0<φ<π2, 则|cos φ|=⎪⎪⎪⎪⎪⎪n 1·n |n 1|·|n |=21·6=63,即cos φ=63.∴平面SCD 与平面SAB 所成二面角的余弦值为63. (3)设N (x,2x -2,0),则MN →=(x,2x -3,-1).∵平面SAB 的一个法向量为n 1=(1,0,0),∴sin θ=⎪⎪⎪⎪⎪⎪⎪⎪x 5x 2-12x +10 =110×⎝ ⎛⎭⎪⎫1x 2-12×1x +5=110×⎝ ⎛⎭⎪⎫1x -352+75,当1x =35,即x =53时,(sin θ)max =357.。
