材料力学矩阵位移法作业示例
结构力学 矩阵位移法作业

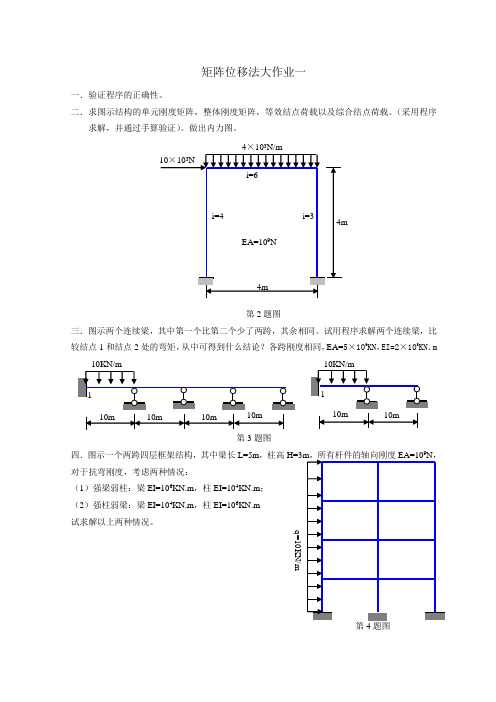
1.作图示刚架的N F 、S F 、M 图,已知各杆截面均为矩形,柱截面宽0.4m,高0.4m, 大跨梁截面宽0.35m,高0.85m ,小跨梁截面宽0.35m,高0.6m ,各杆E=3.0×104 MPa标号及分单元划分计算输出结果************************************************************************* * * wang cheng hao 200901 * * * ************************************************************************The Input DataThe General InformationE NM NJ NS NLC 3.000E+07 10 9 9 1The Information of Membersmember start end A I1 12 1.600000E-01 2.133000E-03 2 2 3 1.600000E-01 2.133000E-03 3 3 6 2.975000E-01 1.790000E-024 25 2.975000E-01 1.790000E-02 5 4 5 1.600000E-01 2.133000E-036 5 6 1.600000E-01 2.133000E-037 58 2.100000E-01 6.300000E-03 8 69 2.100000E-01 6.300000E-03 9 7 8 1.600000E-01 2.133000E-03 10 8 9 1.600000E-01 2.133000E-03The Joint Coordinatesjoint X Y1 .000000 .0000002 .000000 4.5000003 .000000 7.7000004 7.200000 .0000005 7.200000 4.5000006 7.200000 7.7000007 10.000000 .0000008 10.000000 4.5000009 10.000000 7.700000The Information of SupportsIS VS11 .00000012 .00000013 .00000041 .00000042 .00000043 .00000071 .00000072 .00000073 .000000( NA= 180 )( NW= 673 )Loading Case 1The Loadings at JointsNLJ= 1ILJ PX PY PM9 .0000 .0000 -15.00000The Loadings at MembersNLM= 7ILM ITL PV DST1 3 20.0000 4.5000002 3 20.0000 3.2000003 4 -196.0000 7.2000004 4 -36.0000 7.2000007 2 -26.0000 2.7000007 4 -36.0000 3.8000008 4 -196.0000 3.800000The Results of CalculationThe Joint Displacementsjoint u v phi1 3.034552E-21 -7.568894E-20 -7.494658E-212 4.656375E-03 -7.095838E-04 -4.689976E-043 6.414487E-03 -1.138627E-03 -3.252309E-034 4.091261E-21 -1.284215E-19 -9.106066E-215 4.698061E-03 -1.203951E-03 6.981090E-056 6.309349E-03 -1.976041E-03 2.021588E-037 3.774187E-21 -5.368958E-20 -8.623830E-218 4.687578E-03 -5.033399E-04 -9.276283E-059 6.303058E-03 -7.395401E-04 -5.394127E-04The Terminal Forcesmember N(st) Q(st) M(st) N(en) Q(en) M(en)1 756.889 75.346 108.697 -756.889 14.654 27.8582 643.565 -66.328 -84.600 -643.565 130.328 -230.0493 130.328 643.565 230.049 -130.328 767.635 -676.7014 -51.673 113.325 56.742 51.673 145.875 -173.9265 1284.215 40.913 91.061 -1284.215 -40.913 93.0466 1158.135 116.174 146.849 -1158.135 -116.174 224.9087 23.588 -19.795 -65.969 -23.588 182.595 -115.1788 14.154 390.500 451.794 -14.154 354.300 -28.7159 536.896 37.742 86.238 -536.896 -37.742 83.60010 354.300 14.154 31.578 -354.300 -14.154 13.715( NA= 180 )( NW= 701 )2、计算图示桁架各杆的轴力。
矩阵位移法大作业
①
1
2
ql
②
2
3
③
4
q
1① 2 ② 3 ③
4
y M, x
(a)
(b)
第 3 题图
各 杆 EI 、l 相 同,杆长也相同,具体数值可自己给定。
四.采用程序计算图示结构
i
跨长 l(m)
层高 h(m)
集中力(KN)
1
6
7
30
2
10
4
100
3
8
3
50
其他:
柱刚度:EA=105KN,EI=1.5×104KN.m2 梁刚度:EA=106KN,EI=1.0×104KN.m2 支座沉降 C=0.01m
四.采用程序计算图示结构,并作出弯矩图。 已知各杆 E=3.0×106KN/m2,A1=0.16m2,I1=0.012m4,I2=2I1, A2=2A1,I3=3I1,A3=3A1
第 3 题图
20KN
40KN.m
I1,A1 50KN
40KN
15KN/m I3,A3
25KN
I2,A2 40KN.m
4m
4m
3m
3m
五.编写一段程序,实现“将已知支座位移转化为等效节点荷载”。 六.采用程序计算图示结构,并作出最后内力图。已知各杆 E=3.2×106KN/m2,A=0.16m2,I=0.012m4。
36KN
8KN/m
12KN/m
36KN 54KN.m 3m
3m
q=10KN/m
6KN/m
36KN
3m
3m
六.不修改源程序,计算图示结构。
10KN
35KN
6m
15KN
矩阵位移法的计算步骤及示例

单元①②和③:
35
⎡ 500 0 0 − 500 0 0 ⎤
⎢ ⎢
0
12 24
0
− 12
24
⎥ ⎥
(1)
k
=
(2)
k
=
(3)
k
=
10
3
⎢ ⎢⎢−
0 500
24 0
64 0
0 − 24 32 ⎥
500 0
0
⎥ ⎥
⎢ 0 −12 − 24 0 12 − 24⎥
⎢ ⎢⎣ 0
24 32
0
− 24
⎥ 64 ⎥⎦
8-8 矩阵位移法的计算步骤及示例 1
矩阵位移法的计算步骤:(以后处理为例)
(1)对结点和单元进行编号,建立结构(整
体)坐标系和单元(局部)坐标系,并对结
点位移进行编号。
(2)计算各杆的单元刚度矩 k (e)、k (e) 。
(3)形成结构原始刚度矩阵K。
(4)计算固端力
F
(e) F
、等效结点荷载FE及综合
⎢⎣0.0 0.0 6.0 12.0⎥⎦
由于连续梁的单元刚度矩阵为非奇异矩阵, 由此组集而成的结构刚度矩阵K 也是非奇异 的,故无需再进行支座约束条件处理。
(4)计算固端力列阵及等效结点 15 荷载列阵。
②单元的固端力列阵
F (2) F
=
⎧ 300 ⎫ ⎩⎨− 300⎭⎬kN
⋅
m
等效结点荷载列阵:
k(3)
=
⎢ ⎢ ⎢
l(3) 2EI
⎢⎣ l ( 3 )
4
2EI l(3) 4EI l(3)
⎤ ⎥ ⎥ ⎥ ⎥⎦
3 4
(3)集成结构刚度矩阵K
结构力学之矩阵位移法

第十二章 矩阵位移法【例12-1】 图 a 所示 连 续 梁 ,EI=常数,只 考 虑 杆 件 的 弯 曲 变 形 。
分别用位移法和矩阵位移法计算。
图12-1解:(1)位移法解•基本未知量和基本结构的确定用位移法解的基本结构如图c 所示。
这里我们将结点1处的转角也作为基本未知数,这样本题仅一种基本单元,即两端固定梁。
•位移法基本方程的建立⎪⎭⎪⎬⎫=+θ+θ+θ=+θ+θ+θ=+θ+θ+θ000333323213123232221211313212111P P P R K K K R K K K R K K K 将上式写成矩阵形式⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧θθθ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡000321321333231232221131211P P P R R R K K K K K K K K K•系数项和自由项 计算(须绘出单位弯矩图和荷载弯矩图)由图d ,结点力矩平衡条件∑=0M ,得 EI K 411=,l EI K 221=,031=K由图e ,结点力矩平衡条件∑=0M ,得l EI K 212=,l EI l EI l EI K 84422=+=,l EI K 232=由图f ,结点力矩平衡条件∑=0M ,得 013=K ,l EI K 223=,l EI EI EI K 84433=+=由图g ,结点力矩平衡条件∑=0M ,得81Pl R p -=,2Pl R P -=,03=P R将系数项和自由项代入位移法基本方程,得⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧--+⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧θθθ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡0000118820282024321Pl l EI •解方程,得⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧-=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧θθθ14114162321EI Pl •由叠加法绘弯矩图,如图h 所示。
(2)矩阵位移法解•对单元和结点编号(图a ) 本题只考虑弯曲变形的影响,故连续梁每个结点只有一个角位移未知数。
结构力学应用-矩阵位移法

3、集成总刚
(6)定位向量法:对号入座,同号相加 定位向量法:对号入座,
4.综合结点荷载
综合结点荷载 {F}={FD}+{FE} }――直接结点荷载 ①{FD}――直接结点荷载 }――等效结点荷载 ②{FE}――等效结点荷载 (7-1)局部坐标系单元固端力 (7-2)整体坐标系单元固端力 (7-3)单元等效结点荷载。 单元等效结点荷载。
等效原则: 等效原则: ——两种荷载对基本体系产生相同的结点位移。 两种荷载对基本体系产生相同的结点位移 ——两种荷载对基本体系产生相同的结点位移。
矩阵位移法的计算步骤及示例
矩阵位移法计算平面刚架 计算机计算――程序化) 程序化) (计算机计算 程序化
1. 编码、整理原始数据 编码、
(1)整体与局部坐标系 ) (2)结点位移编码 ) 单元编码 (3)原始数据: )原始数据: E 、A i、I i、l i 定位向量{λ} 定位向量 e, αi([ T ]) ])
几点补充说明
1、结点位移分量编号,定位向量 、结点位移分量编号,
——引入支承条件:已知位移约束的方向,编码为零。 引入支承条件:已知位移约束的方向,编码为零。 引入支承条件
2、铰结点处理: 铰结点处理: 铰结点处理
铰结的各杆杆端的转角均为基本未知量 ——分别编码(统一单元,程序简单) 分别编码(统一单元,程序简单) 分别编码
矩阵位移法
矩阵位移法——基本原理与位移法相同 基本原理与位移法相同 矩阵位移法 *数学工具 —— 矩阵运算
1、矩阵知识 矩阵: (1)矩阵:A 方阵: 方阵: 阶方阵A相应的行列式 (2)行列式:n阶方阵 相应的行列式 )行列式: 阶方阵 相应的行列式D 若D=0,A为奇异矩阵 (3)矩阵运算 相等:加减:数乘: 相等:加减:数乘: l aik 乘法: 乘法:Cmn=Aml*Bln,则 cij =
习题课1 矩阵位移法(含答案作业)_518706462

4
5
6
7
8
k
i = 2,3 (1) 54
+ k
i = 2,3 (1) 55
(2) (3) (3) (3) k16 k15 k16 k14 0 (2) (3) (3) (3) k26 k25 k26 k24 0 (2) (3) (3) (3) k36 k34 k35 k36 0
+ k
+
(i ) 33
k
3EIa 2 a 3 + b3
A
3EIab a 3 + b3
B A
3EIab a 3 + b3
3EIb 2 a 3 + b3
B
3EIa a 3 + b3
e θA =1
−3EIa a 3 + b3
3EIb a 3 + b3
e θB =1
−3EIb a 3 + b3
[k ]
e
=
a2 ab
ab b2
e
3EI a 3 + b3
{F }
u2
v2 θ 2 θ 3 ]
−M 0 ]
[0 M 0
0 0 2M 0
T
4
3
3
4
5
0
0
6
2 2 2 2 2 2 k12 k13 k14 k15 k16 k11
2 2 2 2 2 2 k22 k24 k25 k21 k23 k26 2 2 2 2 2 2 k32 k34 k35 k31 k33 k36 2 2 2 2 2 2 k42 k45 k44 k41 k46 k43
y
x
解: T 用位移法求解,未知量为 {∆} = [θ 2 v3 ] 。 1) 杆端弯矩表达式
结构力学基础矩阵位移法基本概念、计算程序和例题讲解

序和例题讲解
§9-1 矩阵位移法基本概念 §9-2 单元劲度矩阵 §9-3 可动结点劲度矩阵 §9-4 可动结点等效荷载列阵 §9-5 单元杆端力和支座反力 §9-6 例题 §9-7 平面刚架计算程序
§9—1 矩阵位移法的基本概念
一、坐标系和符号规定 图示连续梁:
4.求 K
(1)计算机各单元的方向余弦和杆长:
(2)求 kmi
(3)求ki
单元(1):Cx=0 Cy=1
杆长:l 同理:
(4)求 按照“对号入座“原则,由ki形成k哪
例如: 同理:
5.求: 对于桁架,一般只有结点荷
载,于是
得 6.求结点位移
7.求杆端力Fmi
8.求支座反力
例 设 EI=常数,EA=常数, EI=20EA,试用矩阵位移法分析
5
6
1 2
88.889 0.0
0.0 5.268
0.0 11.852
-88.889 0.0
0.0 -5.268
0.0 11.852
1 2
k②
EA l1
3 4
0.0 88.889
5 0.0
11.852 0.0
5.268
35.556 0.0
11.852
0.0 88.889
0.0
11.852 0.0
返回
§9—3 可动结点劲度矩阵
一、形成可动结点劲度矩阵的步骤
步骤: 1.对结构进行结点编号、单元标号、自由度编号: 2.确定单元杆端自由度序号(考虑约束条件); 3.计算单元在局部坐标系中的劲度矩阵kmi 4.计算单元转换矩阵Ti 5.形成单元在整体坐标系中的劲度矩阵ki TiTkmiTi
矩阵位移法例题

3→4 0° 1
1
4×105
0.12×105
§10-7 矩阵位移法的计算步骤和示例
(3) 列出单元刚度矩阵 整体坐标表示的单元刚度矩阵公式
BC
2 x
12i l2
C
2 y
K (e)
B
12i l2
C
xC
y
BC
2 y
12i l2
Cx2
对称
6i l Cy 6i l Cx
4i
BC
2 x
12i l2
1 EA
49.64
0 49.64
kN
0
结果的正确性很容易从结 点2的平衡条件判断出来。
§10-7 矩阵位移法的计算步骤和示例
例 2: 平面刚架如图所示,各杆截面相同。A=0.24 m2,
E=1×107 kN/m2, I=0.0072 m4,试求各杆端力,并画出内
力图。
11
20kN/m
3 34
Δ 0 0 85.98 309 0 0T 1
EA (5) 求杆端力
F (e) K (e)T (e) Δ(e)
1 30℃
2
F2 F1
2
§10-7 矩阵位移法的计算步骤和示例
单元①的单元结点位移向量为
Δ(1) 0 0 85.98 309T 1
EA
单元①的杆端力为 F (1) K δ (1) (1) K T Δ (1) (1) (1)
3
1 30℃
2
F2 F1
2
原始总刚度矩阵为:
1
[K
]
K K
(1) ii
(1) ji
0
2
3
K (1) ij
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
MEMBER END FORCE(杆端力数值) AXIAL FORCE(轴力) SHEARING FORCE(剪力) BENDING MOMEMT(弯矩) NE= 1 FMJ= FMK= NE= 2 FMJ= FMK= NE= 3 FMJ= FMK= NE= 4 FMJ= FMK= 4.6825 -4.6825 3.0076 -3.0076 0.5473 -0.5473 -1.1508 1.1508 -0.5473 0.5473 1.6981 -1.6981 4.6825 -4.6825 7.6901 112.3099 6.7642 -4.5750 9.2435 -16.0357 4.5750 -23.3049 39.3406 169.8990
!支座信息,共三个固定支座。 3 0 0 0 4 0 0 0 5 0 0 0
!结点坐标,取 A 点即 4 号点坐标为(0.0,4.0) 。 0.0,4.0,4.0,4.0,8.0,4.0,0.0,0.0,4.0,0.0 !受结点荷载的结点数,这里为零,为了防止运算出错,取为 1,将荷载设为 0,可以减少运算错误。 1 1 0.0,0.0,0.0
第 1 页 共 3 页
整理:以吻封缄 ZSY.
VAIUE OF FIXING FORCE ELEMEMT I-NX 4 0.0000 I-QZ I-MM J-NX 0.0000 J-QZ 60.0000 J=MM 40.0000
60.0000 -40.0000
NODAL EQUIVALENT LOAD 0.000 0.000 0.000 0.000 -60.000 40.000
I bh 3 h2 , A 12bh 12
在采用合理截面时,C 一般介于 0.01-0.1,此时的结构内力分布比较均匀,符合实际工程需要。 在考虑结构相对刚度对内力的影响时,可通过改变截面形状(比如采用蜂窝梁,箱式梁)调节 系数 C 值,尽量使结构内力分布均匀,避免内力值峰值过大,从而间接的节省材料,使结构设 计合理、经济。
第 3 页 共 3 页
!受荷载的单元号,4 号单元受负 z 向的均布荷载。6 个固端约束反力求解见附图。 1 运算结果见下 N0. OF SET MODULUS OF ELASTICITY 1 2 2000000.00000 2000000.00000 DATA OF ELEMENT (杆件数据) 4 5 1 2 1 2 2 3 1 1 2 2 CROSS-AREA 0.05000 0.05000 MOMEMT OF INERTIA(材料特性) 1.00000 2.00000 DATA OF SUPPORT(支座数据) 3 4 5 0 0 0 0 0 0 0 0 0 4 0.0,60.0,-40.0,0.0,60.0,40.0
F N 图(kN)
-3.0076
F Q 图(kN)
比较 I=CA 的系数 C 变化对内力的影响 制作表格比较 C 的变化对内力的影响,这里取 C 的值分别为 1,10,20,50,100,1000,10000(模拟抗弯刚度无穷大)
第 2 页 共 3 页
整理:以吻封缄 ZSY.
结论:在系数比 C 值是 1 的时候,内力分布是比较均匀的,即各个杆件上均有较大内力,这可 以理解为:杆件位移的协调性使结构整体承担荷载作用,避免受荷载杆内力过大引起破坏。 当系数值逐渐变大时,即受荷载杆的抗弯刚度逐渐加大,会使该杆左端变形逐渐变小,荷 载作用不能传递到左端结构, 此时的内力分布趋近与悬臂梁内力分布,超静定结构的优点不再 存在。 当系数值逐渐变小时,即各杆的轴向变形逐渐变小,可以认为受荷载杆的左端水平向和竖 直向位移几乎为零, 此时的受荷载杆内力分布趋近于简支梁,同样的超静定结构的优点也不再 存在,多余的约束条件并没有使内力分布均匀,对工程结构也是不利的。 另一方面,从数值上看。当杆件为矩形截面(底宽为 b,高为 h)时得 C
NODAL DISPLACEMENT(结点位移与转角) ELEMENT 1 2 3 4 5 XX -0.000024 -0.000046 0.000000 0.000000 0.000000 ZZ -0.000187 -0.000120 0.000000 0.000000 0.000000 ANGLE -0.000011 -0.000025 0.000000 0.000000 0.000000
169.8990 1.1508 E C D -0.5473 E C -0.5473 1.6981 A 6.6742 B 9.2435 A -4.6825 B A B -112.3099
4.5750
4.5750 C
D 16.0357 23.3049 39.3406
4.6825 D
7.6901 E
M 图(kN·m)
SUPPOT REACTION(约束反力) NUMBER OF NODE 3 4 5 X-FORCE 1.1508 0.5473 -1.6981 Z-FORCE 112.3099 4.6825 3.0076 BENDING MOMEMT 169.8990 6.7642 9.2435
******************************************* END 根据结果作内力图如下图
EI
2
D
④
3
E
M ED =40kN ·m
X
4
A
B
5
F QDE =60kN
F QED =60kN
4m
4m
输入数据 !NE 单元总数 NP 结点总数 NR 支座结点数 MT 材料类型数组 4,5,3,2,1 !材料共两种,考虑到 I=20A,且内力仅与相对刚度有关 取 E=2.0×106 kN·m2,A=0.05m2 ,I=1.00m4 (后续在讨论 I=CA 中系数 C 的变化对内力的影响时,固定 E 和 A 不变,仅改变 I 值) 。 2000000.0,0.05,1.00 !单元编号信息,四杆共两种材料特性。 4 1 1 5 2 1 1 2 2 2 3 2 2000000.0,0.05,2.00 MX 工况数
整理:以吻封缄 ZSY.
计算力学基础作业题
Ⅰ-3 试用平面刚架程序计算图示结构内力,并作出内力图。EI=常数,EA=常数。 (1)I=20A; (2)变化 I=CA 中的 C 值,比较内力的变化。
30kN/m
1
C
① EI
Z
2
2EI ③
3
D
2EI ④
Z
E
Y
M DE =40kN ·m
ห้องสมุดไป่ตู้
30kN/m
4m
②
Y X
