立体几何中轨迹问题
立体几何中的轨迹问题求解策略

立体几何中的轨迹问题求解策略
轨迹问题是一种有趣而又棘手的立体几何问题,它涉及寻找一条从一个点到另一个点的最短路径。
解决轨迹问题的一种策略是使用贪心算法。
贪心算法是一种迭代的搜索算法,它假定每次都可以选择最优的路径,从而最终达到最优解。
贪心算法的基本步骤是:
1. 首先,找出所有可能的路径,并计算每条路径的代价;
2. 然后,选择代价最小的路径;
3. 接下来,重复步骤2,直到达到目标点为止。
另一种策略是使用动态规划来求解轨迹问题。
动态规划是一种分析问题的技术,它通过拆分大问题,将其转换为许多小问题,从而得到最优解。
动态规划的基本步骤是:
1. 首先,对于每个状态,确定可能的动作;
2. 然后,计算每个动作的代价;
3. 接下来,选择代价最小的动作;
4. 最后,重复步骤2和3,直到达到目标点为止。
谈立体几何中动点轨迹问题的解题策略

立体几何中的动点轨迹问题是一个常见的问题类型,它涉及到空间几何中的点、线、面等元素的运动和变化。
解决这类问题的关键在于理解运动和变化的过程,并能够通过数学模型进行描述。
解题策略主要包括以下几个方面:
1. **建立空间坐标系**:为了更好地描述空间几何元素的位置和运动,需要建立一个适当的空间坐标系。
坐标系的建立应依据问题的具体情境和需求,通常选择一个固定点作为原点,并确定三个互相垂直的轴。
2. **确定动点的坐标**:在确定了坐标系之后,需要确定动点的坐标。
这可以通过设定动点的坐标变量来实现,例如设动点的坐标为$(x, y, z)$。
3. **分析运动过程**:在确定了动点的坐标后,需要分析动点的运动过程。
这包括了解动点的运动方向、速度、加速度等参数,以及这些参数与坐标变量的关系。
4. **建立数学模型**:通过分析运动过程,可以建立描述动点运动的数学模型。
这通常涉及到物理、几何、代数等多个方面的知识,需要根据具体问题进行选择和应用。
5. **求解数学模型**:建立了数学模型后,需要求解该模型以得到动点的轨迹方程。
这可能涉及到微积分、线性代数、解析几何等多个数学领域的知识,需要根据问题的复杂程度和要求进行选择和应用。
6. **验证答案**:最后,需要对得到的答案进行验证,以确保其正确性和有效性。
这可以通过将答案代入原问题中进行检验,或者通过与其他已知的答案进行比较来进行验证。
综上所述,解决立体几何中的动点轨迹问题需要综合运用空间几何、物理、数学等多个领域的知识,并能够根据具体问题进行选择和应用。
同时,还需要有一定的逻辑思维和分析能力,以更好地理解和解决这类问题。
例谈立体几何中轨迹问题

3根据截面图形求轨迹 . 例 3 正方体AB D— l E、 C A BCD ,
盼 别是A 、C的 中点 ,是 C 。 的 A, C P C上 动点 ( 括端点 )过E、 P 包 , D、 作正 方体
的截面 , 若截面 为四边形 , 点P 则 的轨
迹为( ) .
A直线 .
算题 , ) 略
2 3 5, × = . + = 2 3 6
解. 近年来 高考 中常见的题 型有 以下几类.
1利 用 圆锥 曲线 定 义 求轨 迹 . 点评 : 圆锥 曲 线 的 统 一 定 义 为 : 定 点 的距 离与 到 到
学思 想 与方法 , 综合性 强 , 能力 要求高 , 教师可集 中讲 定直线的距 离比为常数 的点的轨迹 , 该常数 叫做 圆锥 曲 线的 离心 率 , 表 示. < < 时 , 用e 当0 e l 为椭 圆; = 时, 当e l 为
点 评 : 面 图形确 定后 , 点 的轨 迹 也 是 确 定 的 , 截 动 此 4 立 函 数模 型 求 函数 解 析式 建
的轨迹是以c点 为焦点 , C 以B 为准线 的抛 物线 ( 在侧 面 线 与D 平 行 , E 由此 得 , 与c 当P 重合时 , 面过B 。 中 截 B的 点评 : 点在平 面 内运动的轨迹有 直线、 圆和 圆锥 曲 而 当截面过c时 , 。 截面也是四边形. 故选C .
抛 物 线 ; > 时 . 双 曲 线. 当e l 为
例 1 如 图 ,在 正 方 体A C B D— ABCD 中 , 侧 面 BB C 内一 动 1 P是 1C 点 ,若P 到直线B 与直线 CD的距离 C 。 相等 ,则动点J p 的轨迹所在 的曲线是
( ) . d
2025年新人教版高考数学一轮复习讲义 第七章 §7.10 立体几何中的动态、轨迹问题

所以 V=2ab≤a2+b2=1,当且仅当 a=b= 22时,等号成立.
如图,设AC,BD相交于点O,
因为BO⊥AC,BO⊥AA1,AC∩AA1=A,AC,AA1⊂平面A1ACC1, 所以 BO⊥平面 A1ACC1,因为直线 BP 与平面 A1ACC1
2π 则在此过程中动点M形成的轨迹长度为___8___.
如 图 , 设 AC 的 中 点 为 M0 , △ADE 沿 DE 翻 折 90°,此时平面A′DE⊥平面ABCD,取CD中 点P,CE中点Q,PQ中点N, 连接PQ,MP,MQ,MN,M0P,M0Q,M0N. MP=M0P=12AD=12,MQ=M0Q=12AE=12,PQ=12DE= 22,△MPQ 和△M0PQ 是等腰直角三角形,
1 2 3 4 5 6 7 8 9 10
知BP⊥平面ACN,CN⊂平面ACN,所以BP⊥CN, 所以动点Q的轨迹为线段CN, 在Rt△ABN,Rt△RAB中,∠BAN=∠ARB, 所以Rt△ABN∽Rt△RAB,
则BANB=ARBA,得 BN=12, 易得 CN= BN2+BC2=
212+12=
5 2.
题型一 平行、垂直中的动态轨迹问题
例1 如图,在棱长为a的正方体ABCD-A1B1C1D1 中,E,F,G,H,N分别是CC1,C1D1,DD1,CD, BC的中点,M在四边形EFGH边上及其内部运动,
若MN∥平面A1BD,则点M轨迹的长度是
A. 3a
B. 2a
3a C. 2
√D.
2a 2
连接HN,GN(图略), ∵在棱长为a的正方体ABCD-A1B1C1D1中,E,F,G,H,N分别是 CC1,C1D1,DD1,CD,BC的中点,则GH∥BA1,HN∥BD, 又GH⊄平面A1BD,BA1⊂平面A1BD, ∴GH∥平面A1BD, 同理可证得NH∥平面A1BD, 又GH∩HN=H,GH,HN⊂平面GHN,
立体几何中地轨迹问题

例析空间中点的轨迹问题的转化求空间图形中点的轨迹既是中学数学学习中的一个难点,又是近几年高考的一个热点,这是一类立体几何与解析几何的交汇题,既考查空间想象能力,同时又考查如何将空间几何的轨迹问题转化为平面的轨迹问题来处理的基本思想。
一.轨迹为点例1已知平面βα||,直线α⊂l ,点P l ∈,平面βα,之间的距离为8,则在β内到P 点的距离为10且到直线l 的距离为9的点的轨迹是 ( )A .一个圆 B.两条直线 C.两个点 D.四个点解析:设Q 为β内一动点,点P 在β内射影为O ,过O, l 的平面与β的交线为l ', PQ=10,∴OQ==-228106点Q 在以O 为圆心6为半径圆上,过Q 作QM l '⊥于M ,又 点Q 到直线l 的距离为9∴QM=178922=-则点Q 在以l '平行距离为17的两条平行线上 两条平行线与圆有四个交点∴这样的点Q 有四个,故答案选D 。
点评:本题以空间图形为背景,把立体几何问题转化到平面上,再用平面几何知识解决,要熟记一些平面几何点的轨迹。
二. 轨迹为线段例2. 如图,正方体1111ABCD A BC D -中,点P 在侧面11BCC B及其边界上运动,并且总保持1AP BD ⊥,则动点P 的轨迹是( )。
βαlMOQPA. 线段1B CB.线段1BCC. 1BB 中点与1CC 中点连成的线段D. BC 中点与11B C 中点连成的线段解:连结11,,AB AC B C ,易知111BD A AB ⊥所以11111,,AB BD AC BD B C BD ⊥⊥⊥,所以1BD ⊥面1ABC ,若P ∈1B C ,则AP ⊂平面1ABC ,于是1BD AP ⊥,因此动点P 的轨迹是线段1B C 。
评注:本题是由线面垂直的性质从而求出点P 的轨迹。
例3 已知圆锥的轴截面SAB 是边长为2的等边三角形,O 为底面中心,M 为SO 的中点,动点P 在圆锥底面内(包括圆周),若MP AM ⊥,则点P 的轨迹是________。
立体几何中的轨迹问题(总结+讲义+练习)
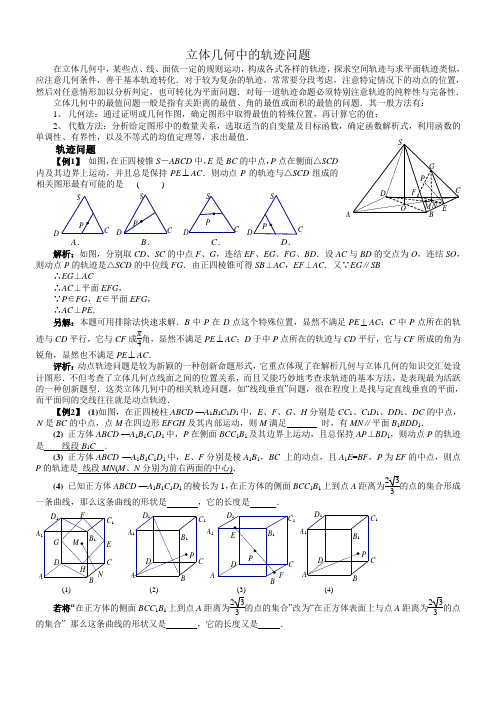
立体几何中的轨迹问题在立体几何中,某些点、线、面依一定的规则运动,构成各式各样的轨迹,探求空间轨迹与求平面轨迹类似,应注意几何条件,善于基本轨迹转化.对于较为复杂的轨迹,常常要分段考虑,注意特定情况下的动点的位置,然后对任意情形加以分析判定,也可转化为平面问题.对每一道轨迹命题必须特别注意轨迹的纯粹性与完备性.立体几何中的最值问题一般是指有关距离的最值、角的最值或面积的最值的问题.其一般方法有: 1、 几何法:通过证明或几何作图,确定图形中取得最值的特殊位置,再计算它的值;2、 代数方法:分析给定图形中的数量关系,选取适当的自变量及目标函数,确定函数解析式,利用函数的单调性、有界性,以及不等式的均值定理等,求出最值.轨迹问题【例1】 如图,在正四棱锥S -ABCD 中,E 是BC 的中点,P 点在侧面△SCD 内及其边界上运动,并且总是保持PE ⊥AC .则动点P 的轨迹与△SCD 组成的相关图形最有可能的是 ( )解析:如图,分别取CD 、SC 的中点F 、G ,连结EF 、EG 、FG 、BD .设AC 与BD 的交点为O ,连结SO ,则动点P 的轨迹是△SCD 的中位线FG .由正四棱锥可得SB ⊥AC ,EF ⊥AC .又∵EG ∥SB∴EG ⊥AC∴AC ⊥平面EFG ,∵P ∈FG ,E ∈平面EFG , ∴AC ⊥PE .另解:本题可用排除法快速求解.B 中P 在D 点这个特殊位置,显然不满足PE ⊥AC ;C 中P 点所在的轨迹与CD 平行,它与CF 成π4角,显然不满足PE ⊥AC ;D 于中P 点所在的轨迹与CD 平行,它与CF 所成的角为锐角,显然也不满足PE ⊥AC .评析:动点轨迹问题是较为新颖的一种创新命题形式,它重点体现了在解析几何与立体几何的知识交汇处设计图形.不但考查了立体几何点线面之间的位置关系,而且又能巧妙地考查求轨迹的基本方法,是表现最为活跃的一种创新题型.这类立体几何中的相关轨迹问题,如“线线垂直”问题,很在程度上是找与定直线垂直的平面,而平面间的交线往往就是动点轨迹.【例2】 (1)如图,在正四棱柱ABCD —A 1B 1C 1D 1中,E 、F 、G 、H 分别是CC 1、C 1D 1、DD 1、DC 的中点,N 是BC 的中点,点M 在四边形EFGH 及其内部运动,则M 满足 时,有MN ∥平面B 1BDD 1.(2) 正方体ABCD —A 1B 1C 1D 1中,P 在侧面BCC 1B 1及其边界上运动,且总保持AP ⊥BD 1,则动点P 的轨迹是 线段B 1C .(3) 正方体ABCD —A 1B 1C 1D 1中,E 、F 分别是棱A 1B 1,BC 上的动点,且A 1E =BF ,P 为EF 的中点,则点P 的轨迹是 线段MN (M 、N 分别为前右两面的中心).(4) 已知正方体ABCD —A 1B 1C 1D 1的棱长为1,在正方体的侧面BCC 1B 1上到点A 距离为233的点的集合形成一条曲线,那么这条曲线的形状是 ,它的长度是 .若将“在正方体的侧面BCC 1B 1上到点A 距离为23 3 的点的集合”改为“在正方体表面上与点A 距离为233的点的集合” 那么这条曲线的形状又是 ,它的长度又是 .1AC C 1AEC C 1A AB1A 1(1)(2)(3)(4)DDA .B .C .D . A【例3】 (1)(04北京)在正方体ABCD -A 1B 1C 1D 1中,P 是侧面BB 1C 1C 内一动点,若P 到直线BC 与直线C 1D 1的距离相等,则动点P 的轨迹所在的曲线是 ( D )A . A 直线B .圆C .双曲线D .抛物线 变式:若将“P 到直线BC 与直线C 1D 1的距离相等”改为“P 到直线BC 与直线C 1D 1的距离之比为1:2(或2:1)”, 则动点P 的轨迹所在的曲线是 椭圆 (双曲线). (2)(06北京)平面α的斜线AB 交α于点B ,过定点A 的动直线l 与AB 垂直,且交α于点C ,则动点C 的轨迹是 (A )A .一条直线B .一个圆C .一个椭圆D .双曲线的一支解:设l 与l 是其中的两条任意的直线,则这两条直线确定一个平面,且斜线AB 垂直这个平面,由过平面外一点有且只有一个平面与已知直线垂直可知过定点A 与AB 垂直所有直线都在这个平面内,故动点C 都在这个平面与平面α的交线上,故选A . (3)已知正方体ABCD —A 1B 1C 1D 1的棱长为1,M 在棱AB 上,且AM =13,点P 到直线A 1D 1的距离与点P 到点M 的距离的平方差为1,则点P 的轨迹为 抛物线 .(4)已知正方体ABCD —A 1B 1C 1D 1的棱长为3,长为2的线段MN 点一个端点M 在DD 1上运动,另一个端点N 在底面ABCD 上运动,则MN 的中点P 的轨迹与正方体的面所围成的几何体的体积为 π6. 【例4】 (04重庆)若三棱锥A -BCD 的侧面ABC 内一动点P 到底面BCD 的距离与到棱AB 的距离相等,则动点P 的轨迹与△ABC 组成图形可能是:( D )【例5】 四棱锥P -ABCD ,AD ⊥面P AB ,BC ⊥面P AB ,底面ABCD 为梯形,AD =4,BC =8,AB =6,∠APD =∠CPB ,满足上述条件的四棱锥的顶点P 的轨迹是( )A .圆B .不完整的圆C .抛物线D .抛物线的一部分 分析:∵AD ⊥面P AB ,BC ⊥平面P AB ∴AD ∥BC 且AD ⊥P A ,CB ⊥PB ∵∠APD =∠CPB ∴tanAPD =tanCPB∴AD P A =CB PB ∴PB =2P A在平面APB 内,以AB 的中点为原点,AB 所在直线为x 轴建立平面直角坐标系,则A (-3,0)、B (3,0),设P (x ,y )(y ≠0),则(x -3)2+y 2=4[(x +3)2+y 2](y ≠0)即(x +5)2+y 2=16(y ≠0) ∴P 的轨迹是(B )BABCDA3P A BC D立体几何中的轨迹问题(教师版)1.在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 与到直线B 1C 1的距离相等,则动点P 所在曲线的形状为(D ).A .线段B .一段椭圆弧C .双曲线的一部分D .抛物线的一部分 简析 本题主要考查点到直线距离的概念,线面垂直及抛物线的定义.因为B 1C 1⊥面AB 1,所以PB 1就是P 到直线B 1C 1的距离,故由抛物线的定义知:动点的轨迹为抛物线的一段,从而选D .2.在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 的距离与到直线B 1C 1的距离之比为2:1,则动点P 所在曲线的形状为(B ).A .线段B .一段椭圆弧C .双曲线的一部分D .抛物线的一部分3.在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 的距离与到直线B 1C 1的距离之比为1:2,则动点P 所在曲线的形状为(C ).A .线段B .一段椭圆弧C .双曲线的一部分D .抛物线的一部分4.在正方体ABCD-A 1B 1C 1D 1中,E 为AA 1的中点,点P 在其对角面BB 1D 1D 内运动,若EP 总与直线AC 成等角,则点P 的轨迹有可能是(A ).A .圆或圆的一部分B .抛物线或其一部分C .双曲线或其一部分D .椭圆或其一部分 简析 由条件易知:AC 是平面BB 1D 1D 的法向量,所以EP 与直线AC 成等角,得到EP 与平面BB 1D 1D 所成的角都相等,故点P 的轨迹有可能是圆或圆的一部分.5.已知正方体ABCD A B C D -1111的棱长为a ,定点M 在棱AB 上(但不在端点A ,B 上),点P 是平面ABCD 内的动点,且点P 到直线A D 11的距离与点P 到点M 的距离的平方差为a 2,则点P 的轨迹所在曲线为(A ). A .抛物线B .双曲线C .直线D .圆简析在正方体ABCD A B C D -1111中,过P 作PF ⊥AD ,过F 作FE ⊥A 1D 1,垂足分别为F 、E ,连结PE .则PE 2=a 2+PF 2,又PE 2-PM 2=a 2,所以PM 2=PF 2,从而PM =PF ,故点P 到直线AD 与到点M 的距离相等,故点P 的轨迹是以M 为焦点,AD 为准线的抛物线.6.在正方体ABCD A B C D -1111中,点P 在侧面BCC 1B 1及其边界上运动,总有AP ⊥BD 1,则动点P 的轨迹为__________. 简析 在解题中,我们要找到运动变化中的不变因素,通常将动点聚焦到某一个平面.易证BD 1⊥面ACB 1,所以满足BD 1⊥AP 的所有点P 都在一个平面ACB 1上.而已知条件中的点P 是在侧面BCC 1B 1及其边界上运动,因此,符合条件的点P 在平面ACB 1与平面BCC 1B 1交线上,故所求的轨迹为线段B 1C .本题的解题基本思路是:利用升维,化“动”为“静”,即先找出所有点的轨迹,然后缩小到符合条件的点的轨迹.7.在正四棱锥S-ABCD 中,E 是BC 的中点,点P 在侧面∆SCD 内及其边界上运动,总有PE ⊥AC ,则动点P 的轨迹为_______________.答案 线段MN (M 、N 分别为SC 、CD 的中点)8.若A 、B 为平面α的两个定点,点P 在α外,PB ⊥α,动点C (不同于A 、B )在α内,且PC ⊥AC ,则动点C 在平面内的轨迹是________.(除去两点的圆) 9.若三棱锥A —BCD 的侧面ABC 内一动点P 到底面BCD 的距离与到棱AB 的距离相等,则动点P 的轨迹与∆ABC 组成的图形可能是:(D )A A AP PP PB C B C B C B C A B C D简析 动点P 在侧面ABC 内,若点P 到AB 的距离等于到棱BC 的距离,则点P 在∠ABC 的内角平分线上.现在P 到平面BCD 的距离等于到棱AB 的距离,而P 到棱BC 的距离大于P 到底面BCD 的距离,于是,P 到棱AB 的距离小于P 到棱BC 的距离,故动点P 只能在∠ABC 的内角平分线与AB 之间的区域内.只能选D . 10.已知P 是正四面体S-ABC 的面SBC 上一点,P 到面ABC 的距离与到点S 的距离相等,则动点P 的轨迹所在的曲线是(B ). A .圆 B .椭圆 C .双曲线 D .抛物线解题的要领就是化空间问题为平面问题,把一些重要元素集中在某一个平面内,利 用相关的知识去解答,象平面几何知识、解析几何知识等.11.已知正方体ABCD A B C D -1111的棱长为1,在正方体的侧面BCC B 11上到点A 距离为233的点的轨迹形成一条曲线,那么这条曲线的形状是_________,它的长度为__________. 简析以B 为圆心,半径为33且圆心角为π2的圆弧,长度为36π. 12.已知长方体ABCD A B C D -1111中,AB BC ==63,,在线段BD 、A C 11上各有一点P 、Q ,PQ 上有一点M ,且PM MQ =2,则M 点轨迹图形的面积是 . 提示轨迹的图形是一个平行四边形.13.已知棱长为3的正方体ABCD A B C D -1111中,长为2的线段MN 的一个端点在DD 1上运动,另一个端点N 在底面ABCD 上运动,求MN 中点P 的轨迹与正方体的面所围成的几何体的体积.简析 由于M 、N 都是运动的,所以求的轨迹必须化“动”为“静”,结合动点P 的几何性质,连结DP ,因为MN=2,所以PD=1,因此点P 的轨迹是一个以D 为球心,1为半径的球面在正方体内的部分,所以点P 的轨迹与正方体的表面所围成的几何体的体积为球的体积的18,即1843163⨯⨯=ππ. 14.已知平面//α平面β,直线l α⊂,点l P ∈,平面α、β间的距离为4,则在β内到点P 的距离为5且到直线l 的距离为29的点的轨迹是( ) 简析:如图,设点P 在平面β内的射影是O ,则OP 是α、β的公垂线,OP=4.在β内到点P 的距离等于5的点到O 的距离等于3,可知所求点的轨迹是β内在以O 为圆心,3为半径的圆上.又在β内到直线l 的距离等于29的点的集合是两条平行直线m 、n ,它们到点O 的距离都等于32174)29(22<=-,所以直线m 、n 与这个圆均相交,共有四个交点.因此所求点的轨迹是四个点,故选C .16.在四棱锥ABCD P -中,⊥AD 面PAB ,⊥BC 面PAB ,底面ABCD 为梯形,AD=4,BC=8,AB=6,CPB APD ∠=∠,满足上述条件的四棱锥的顶点P 的轨迹是( )A .圆B .不完整的圆C .抛物线D .抛物线的一部分简析:因为⊥AD 面PAB ,⊥BC 面PAB ,所以AD//BC ,且︒=∠=∠90CBP DAP . 又8BC ,4AD ,CPB APD ==∠=∠,可得CPB tan PB CB PA AD APD tan ∠===∠,即得2ADCBPA PB == 在平面PAB 内,以AB 所在直线为x 轴,AB 中点O 为坐标原点,建立平面直角坐标系,则A (-3,0)、B(3,0).设点P (x ,y ),则有2y )3x (y )3x (|PA ||PB |2222=+++-=,整理得09x 10y x 22=+++由于点P 不在直线AB 上,故此轨迹为一个不完整的圆,选B .17.如图,定点A 和B 都在平面α内,定点P ,PB ,α⊥α∉C 是α内异于A 和B 的动点.且AC PC ⊥,那么动点C 在平面α内的轨迹是( )A .一条线段,但要去掉两个点B .一个圆,但要去掉两个点C .一个椭圆,但要去掉两个点D .半圆,但要去掉两个点简析:因为PC AC ⊥,且PC 在α内的射影为BC ,所以BC AC ⊥,即︒=∠90ACB .所以点C 的轨迹是以AB 为直径的圆且去掉A 、B 两点,故选B .18.如图,在正方体1111D C B A ABCD -中,P 是侧面1BC 内一动点,若P 到直线BC 与直线11D C 的距离相等,则动点P 的轨迹所在的曲线是( )A .直线B .圆C .双曲线D .抛物线简析:因为P 到11D C 的距离即为P 到1C 的距离,所以在面1BC 内,P 到定点1C 的距离与P 到定直线BC 的距离相等.由圆锥曲线的定义知动点P 的轨迹为抛物线,故选D .19.已知正方体1111D C B A ABCD -的棱长为1,点P 是平面AC 内的动点,若点P 到直线11D A 的距离等于点P 到直线CD 的距离,则动点P 的轨迹所在的曲线是( )A .抛物线B .双曲线C .椭圆D .直线简析:如图4,以A 为原点,AB 为x 轴、AD 为y 轴,建立平面直角坐标系.设P (x ,y ),作AD PE ⊥于E 、11D A PF ⊥于F ,连结EF ,易知1x |EF ||PE ||PF |2222+=+=又作CD PN ⊥于N ,则|1y ||PN |-=.依题意|PN ||PF |=, 即|1y |1x 2-=+,化简得0y 2y x 22=+- 故动点P 的轨迹为双曲线,选B .20.如图,AB是平面a的斜线段,A为斜足,若点P在平面a内运动,使得△ABP的面积为定值,则动点P的轨迹是()(A)圆(B)椭圆(C)一条直线(D)两条平行直线分析:由于线段AB是定长线段,而△ABP的面积为定值,所以动点P到线段AB 的距离也是定值.由此可知空间点P在以AB为轴的圆柱侧面上.又P在平面内运动,所以这个问题相当于一个平面去斜切一个圆柱(AB是平面的斜线段),得到的切痕是椭圆.P的轨迹就是圆柱侧面与平面a的交线.21.如图,动点P在正方体1111ABCD A B C D-的对角线1BD上.过点P作垂直于平面11BB D D的直线,与正方体表面相交于M N,.设BP x=,MN y=,则函数()y f x=的图象大致是()分析:将线段MN投影到平面ABCD内,易得y为x一次函数.22.已知异面直线a,b成︒60角,公垂线段MN的长等于2,线段AB两个端点A、B分别在a,b上移动,且线段AB长等于4,求线段AB中点的轨迹方程.图5简析:如图5,易知线段AB的中点P在公垂线段MN的中垂面α上,直线'a、'b为平面α内过MN的中点O分别平行于a、b的直线,'a'AA⊥于'A,'b'BB⊥于'B,则P'B'AAB=⋂,且P也为'B'A的中点.由已知MN=2,AB=4,易知,2AP,1'AA==得32'B'A=.则问题转化为求长等于32的线段'B'A的两个端点'A、'B分别在'a、'b上移动时其中点P的轨迹.现以'OB'A∠的角平分线为x轴,O为原点建立如图6所示的平面直角坐标系.A BCDMNPA1 B1C1D1yxOyxOyxOyxO图6设)y ,x (P ,n |'OB |,m |'OA |==, 则)n 21,n 23('B ),m 21,m 23('A - )n m (41y ),n m (43x -=+=222)32()n m (41)n m (43=++- 消去m 、n ,得线段AB 的中点P 的轨迹为椭圆,其方程为1y 9x 22=+.点评:例5和例6分别将立体几何与解析几何中的双曲线与椭圆巧妙地整合在一起,相互交汇和渗透,有利于培养运用多学科知识解决问题的能力.立体几何中的轨迹问题1.在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 与到直线B 1C 1的距离相等,则动点P 所在曲线的形状为 ( ) A .线段 B .一段椭圆弧 C .双曲线的一部分 D .抛物线的一部分2.在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 的距离与到直线B 1C 1的距离之比为2:1,则动点P 所在曲线的形状为 ( ) A .线段 B .一段椭圆弧 C .双曲线的一部分 D .抛物线的一部分3.在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 的距离与到直线B 1C 1的距离之比为1:2,则动点P 所在曲线的形状为 ( ) A .线段 B .一段椭圆弧 C .双曲线的一部分 D .抛物线的一部分4.在正方体ABCD-A 1B 1C 1D 1中,E 为AA 1的中点,点P 在其对角面BB 1D 1D 内运动,若EP 总与直线AC 成等角,则点P 的轨迹有可能是 ( ) A .圆或圆的一部分 B .抛物线或其一部分 C .双曲线或其一部分 D .椭圆或其一部分 5.已知正方体ABCD A B C D -1111的棱长为a ,定点M 在棱AB 上(但不在端点A ,B 上),点P 是平面ABCD 内的动点,且点P 到直线A D 11的距离与点P 到点M 的距离的平方差为a 2,则点P 的轨迹所在曲线为( ) A .抛物线B .双曲线C .直线D .圆6.若三棱锥A —BCD 的侧面ABC 内一动点P 到底面BCD 的距离与到棱AB 的距离相等,则动点P 的轨迹与∆ABC 组成的图形可能是 ( ) A A AP PP PB C B C B C B CA B C DA B C D 7.已知P 是正四面体S-ABC 的面SBC 上一点,P 到面ABC 的距离与到点S 的距离相等,则动点P 的轨迹所在的曲线是 ( )A .圆B .椭圆C .双曲线D .抛物线8.已知平面//α平面β,直线l α⊂,点l P ∈,平面α、β间的距离为4,则在β内到点P 的距离为5且到直线l 的距离为29的点的轨迹是( )A .一个圆B .两条平行直线C .四个点D .两个点9.在四棱锥ABCD P -中,⊥AD 面PAB ,⊥BC 面PAB ,底面ABCD 为梯形,AD=4,BC=8,AB=6,CPB APD ∠=∠,满足上述条件的四棱锥的顶点P 的轨迹是( ) A .圆 B .不完整的圆 C .抛物线 D .抛物线的一部分 10.如图,定点A 和B 都在平面α内,定点P ,PB ,α⊥α∉C 是α内异于A 和B 的动点.且AC PC ⊥,那么动点C 在平面α内的轨迹是( )A .一条线段,但要去掉两个点B .一个圆,但要去掉两个点C .一个椭圆,但要去掉两个点D .半圆,但要去掉两个点11.已知正方体1111D C B A ABCD -的棱长为1,点P 是平面AC 内的动点,若点P 到直线11D A 的距离等于点P 到直线CD 的距离,则动点P 的轨迹所在的曲线是( )A .抛物线B .双曲线C .椭圆D .直线12.如图,AB 是平面a 的斜线段,A 为斜足,若点P 在平面a 内运动,使得△ABP 的面积为定值,则动点P 的轨迹是( )A .圆B .椭圆C .一条直线D .两条平行直线 13.如图,动点P 在正方体1111ABCD A B C D -的对角线1BD 上.过点P 作垂直于平面11BB D D 的直线,与正方体表面相交于M N ,.设BP x =,MN y =,则函数()y f x =的图象大致是( )14.在正方体ABCD A B C D -1111中,点P 在侧面BCC 1B 1及其边界上运动,总有AP ⊥BD 1,则动点P 的轨迹为________.15.在正四棱锥S-ABCD 中,E 是BC 的中点,点P 在侧面∆SCD 内及其边界上运动,总有PE ⊥AC ,则动点P 的轨迹为_______________.16.若A 、B 为平面α的两个定点,点P 在α外,PB ⊥α,动点C (不同于A 、B )在α内,且PC ⊥AC ,则动点C 在平面内的轨迹是________.17.已知正方体ABCD A B C D -1111的棱长为1,在正方体的侧面BCC B 11上到点A 距离为233的点的轨迹形成一条曲线,那么这条曲线的形状是_________,它的长度为__________.18.已知长方体ABCD A B C D -1111中,AB BC ==63,,在线段BD 、A C 11上各有一点P 、Q ,PQ 上有一点M ,且PM MQ =2,则M 点轨迹图形的面积是 .19.已知棱长为3的正方体ABCD A B C D -1111中,长为2的线段MN 的一个端点在DD 1上运动,另一个端点N 在底面ABCD 上运动,则MN 中点P 的轨迹与正方体的面所围成的几何体的体积是 .20.已知异面直线a ,b 成︒60角,公垂线段MN 的长等于2,线段AB 两个端点A 、B 分别在a ,b 上移动,且线段AB 长等于4,求线段AB 中点的轨迹方程.ABC D MNP A 1B 1C 1D 1 yxOyxOyxOyx O。
立体几何中轨迹问题的处理技巧与方法

ʏ陈 婷立体几何中的轨迹问题,是立体几何与解析几何的知识交汇点㊂这类问题,立意新颖,重视不同知识的交叉与渗透,重视对数学知识与数学能力的考查与应用,是培养同学们数学核心素养的好素材㊂一㊁直接法直接法就是直接利用立体几何的相关知识,合理分析和研究问题中各个元素之间的关系,或者直接利用轨迹定义进行求解的方法㊂例1 如图1,在正方体A B C D -A 1B 1C 1D 1中,P 是侧面B C C 1B 1上的一个动点,若点P 到直线B C 与直线C 1D 1的距离相等,则动点P 的轨迹是下列哪种线的一部分( )㊂图1A.直线 B .圆C .双曲线 D .抛物线分析:根据题设条件,利用空间点线面的位置关系,直接得到动点P 到直线B C 与到点C 1的距离相等,再结合解析几何中抛物线的定义,可得对应的答案㊂解:根据正方体的性质,可知C 1D 1ʅ平面B C C 1B 1,所以动点P 到直线C 1D 1的距离与到点C 1的距离相等㊂又动点P 到直线B C 与到直线C 1D 1的距离相等,所以动点P 到直线B C 与到点C 1的距离相等㊂根据抛物线的定义,可得动点P 的轨迹是一条抛物线的一部分㊂应选D ㊂二㊁转化法转化法就是将立体几何问题转化为平面几何问题,进行合理 降维 处理,进而应用平面几何㊁解析几何等相关知识来分析与求解的方法㊂例2 (2022年高考北京卷)已知正三棱锥P -A B C 的六条棱长均为6,S 是әA B C 及其内部的点构成的集合㊂设集合T ={Q ɪS |P Q ɤ5},则T 表示的区域的面积为( )㊂A .3π4B .πC .2πD .3π分析:根据题设条件,结合正三棱锥的性质,合理构建点P 在底面әA B C 内的射影点O ,结合集合的创新设置进行合理转化,将空间中的距离问题转化为平面上的距离问题加以分析与求解㊂解:设点P 在底面әA B C 内的射影为点O ㊂依题意知әA B C 是边长为6的正三角形,所以A O =B O =C O =23㊂因为P A =P B =P C =6,所以P O =62-(23)2=26㊂若P Q =5,则O Q =P Q 2-P O 2=1,可知动点Q 的轨迹是在底面әA B C 内,以O 为圆心,半径为r =1的圆及其内部,其对应的面积为πr 2=π㊂应选B ㊂三㊁解析法解析法就是利用解析几何在研究轨迹方面的一整套比较完整的理论体系,通过坐标法进行代数运算与逻辑推理的一种求轨迹的方法㊂解析法是解决立体几何图形的二维轨迹问题的常用方法之一㊂例3 (多选题)如图2所示,在正方体A B C D -A 1B 1C 1D 1中,E 是C C 1的中点,点P 在底面A B C D 内运动,若P D 1,P E 与底面A B C D 所成的角相等,则动点P 的轨迹是( )㊂71知识结构与拓展高一数学 2023年4月Copyright ©博看网. All Rights Reserved.图2A.圆的一部分B.椭圆的一部分C.经过线段B C靠近B的三等分点D.经过线段C D靠近C的三等分点分析:根据题意得D P=2P C,以点D为坐标原点,建立平面直角坐标系,通过坐标法进行讨论求解㊂解:由正方体的性质得D D1ʅ平面A B C D,E Cʅ平面A B C D,所以øD P D1,øC P E分别为P D1,P E与底面A B C D所成的角,所以øD P D1=øC P E㊂因为t a nøD P D1=D D1D P,t a nøC P E= C EP C,又D D1=2C E,所以D P=2P C㊂在平面A B C D中,以D为坐标原点,建立平面直角坐标系,如图3所示㊂图3设正方体的边长为a,点P(x,y),xȡ0,yȡ0,则点D(0,0),C(a,0),所以D P2= x2+y2,P C2=(x-a)2+y2,所以x2+y2= 4(x-a)2+4y2,整理得3x2+3y2-8a x+ 4a2=0,显然3x2+3y2-8a x+4a2=0表示圆的方程,所以动点P的轨迹是圆的一部分,A正确,B错误㊂线段B C靠近B的三等分点的坐标为a,23a,线段C D靠近C的三等分点的坐标为23a,0,分别代入方程3x2+3y2-8a x+4a2=0,可得3a2+3ˑ23a2-8a2+4a2=13a2ʂ0,3ˑ23a2+ 3ˑ02-8aˑ23a+4a2=0,所以23a,0在圆3x2+3y2-8a x+4a2=0上,a,23a不在圆3x2+3y2-8a x+4a2=0上,C错误,D 正确㊂应选A D㊂四㊁性质法性质法就是利用轨迹的相关知识来解决立体几何中轨迹问题的一种基本方法㊂有些空间图形的轨迹不一定是二维的,转化为平面问题比较困难,这时可借助性质法来处理㊂例4已知棱长为3的正方体A B C D-A1B1C1D1中,长为2的线段M N的一个端点M在D D1上运动,另一个端点N在底面A B-C D上运动,则线段M N的中点P的轨迹与正方体的面所围成的几何体的体积为㊂分析:不论әMD N如何变化,点P到点D的距离始终等于1㊂从而点P的轨迹是一个以点D为球心,半径为1的球的18,由此可求出体积㊂解:如图4所示,端点N在正方形A B C D内运动㊂图4因为әMD N为直角三角形,P为斜边MN的中点,所以不论әMD N如何变化,点P到点D的距离始终等于1㊂利用立体几何的性质,可知动点P的轨迹是一个以点D为球心,半径为1的球的18,所以所求体积V= 18ˑ43ˑπˑ13=π6㊂作者单位:江苏省海安高级中学(责任编辑郭正华)8 1知识结构与拓展高一数学2023年4月Copyright©博看网. All Rights Reserved.。
最新立体几何中的轨迹问题(总结+讲义+练习)

立体几何中的轨迹问题在立体几何中,某些点、线、面依一定的规则运动,构成各式各样的轨迹,探求空间轨迹与求平面轨迹类似,应注意几何条件,善于基本轨迹转化.对于较为复杂的轨迹,常常要分段考虑,注意特定情况下的动点的位置,然后对任意情形加以分析判定,也可转化为平面问题.对每一道轨迹命题必须特别注意轨迹的纯粹性与完备性.立体几何中的最值问题一般是指有关距离的最值、角的最值或面积的最值的问题.其一般方法有: 1、 几何法:通过证明或几何作图,确定图形中取得最值的特殊位置,再计算它的值;2、 代数方法:分析给定图形中的数量关系,选取适当的自变量及目标函数,确定函数解析式,利用函数的单调性、有界性,以及不等式的均值定理等,求出最值.轨迹问题【例1】 如图,在正四棱锥S -ABCD 中,E 是BC 的中点,P 点在侧面△SCD 内及其边界上运动,并且总是保持PE ⊥AC .则动点P 的轨迹与△SCD 组成的相关图形最有可能的是 ( )解析:如图,分别取CD 、SC 的中点F 、G ,连结EF 、EG 、FG 、BD .设AC 与BD 的交点为O ,连结SO ,则动点P 的轨迹是△SCD 的中位线FG .由正四棱锥可得SB ⊥AC ,EF ⊥AC .又∵EG ∥SB∴EG ⊥AC∴AC ⊥平面EFG ,∵P ∈FG ,E ∈平面EFG , ∴AC ⊥PE .另解:本题可用排除法快速求解.B 中P 在D 点这个特殊位置,显然不满足PE ⊥AC ;C 中P 点所在的轨迹与CD 平行,它与CF 成π4角,显然不满足PE ⊥AC ;D 于中P 点所在的轨迹与CD 平行,它与CF 所成的角为锐角,显然也不满足PE ⊥AC .评析:动点轨迹问题是较为新颖的一种创新命题形式,它重点体现了在解析几何与立体几何的知识交汇处设计图形.不但考查了立体几何点线面之间的位置关系,而且又能巧妙地考查求轨迹的基本方法,是表现最为活跃的一种创新题型.这类立体几何中的相关轨迹问题,如“线线垂直”问题,很在程度上是找与定直线垂直的平面,而平面间的交线往往就是动点轨迹.【例2】 (1)如图,在正四棱柱ABCD —A 1B 1C 1D 1中,E 、F 、G 、H 分别是CC 1、C 1D 1、DD 1、DC 的中点,N 是BC 的中点,点M 在四边形EFGH 及其内部运动,则M 满足 时,有MN ∥平面B 1BDD 1.(2) 正方体ABCD —A 1B 1C 1D 1中,P 在侧面BCC 1B 1及其边界上运动,且总保持AP ⊥BD 1,则动点P 的轨迹是 线段B 1C .(3) 正方体ABCD —A 1B 1C 1D 1中,E 、F 分别是棱A 1B 1,BC 上的动点,且A 1E =BF ,P 为EF 的中点,则点P 的轨迹是 线段MN (M 、N 分别为前右两面的中心).(4) 已知正方体ABCD —A 1B 1C 1D 1的棱长为1,在正方体的侧面BCC 1B 1上到点A 距离为233的点的集合形成一条曲线,那么这条曲线的形状是 ,它的长度是 .若将“在正方体的侧面BCC 1B 1上到点A 距离为23 3 的点的集合”改为“在正方体表面上与点A 距离为233的点的集合” 那么这条曲线的形状又是 ,它的长度又是 .1AC C 1AEC C 1A AB1A 1(1)(2)(3)(4)DDA .B .C .D . A【例3】 (1)(04北京)在正方体ABCD -A 1B 1C 1D 1中,P 是侧面BB 1C 1C 内一动点,若P 到直线BC 与直线C 1D 1的距离相等,则动点P 的轨迹所在的曲线是 ( D )A . A 直线B .圆C .双曲线D .抛物线 变式:若将“P 到直线BC 与直线C 1D 1的距离相等”改为“P 到直线BC 与直线C 1D 1的距离之比为1:2(或2:1)”, 则动点P 的轨迹所在的曲线是 椭圆 (双曲线). (2)(06北京)平面α的斜线AB 交α于点B ,过定点A 的动直线l 与AB 垂直,且交α于点C ,则动点C 的轨迹是 (A )A .一条直线B .一个圆C .一个椭圆D .双曲线的一支解:设l 与l 是其中的两条任意的直线,则这两条直线确定一个平面,且斜线AB 垂直这个平面,由过平面外一点有且只有一个平面与已知直线垂直可知过定点A 与AB 垂直所有直线都在这个平面内,故动点C 都在这个平面与平面α的交线上,故选A . (3)已知正方体ABCD —A 1B 1C 1D 1的棱长为1,M 在棱AB 上,且AM =13,点P 到直线A 1D 1的距离与点P 到点M 的距离的平方差为1,则点P 的轨迹为 抛物线 .(4)已知正方体ABCD —A 1B 1C 1D 1的棱长为3,长为2的线段MN 点一个端点M 在DD 1上运动,另一个端点N 在底面ABCD 上运动,则MN 的中点P 的轨迹与正方体的面所围成的几何体的体积为 π6. 【例4】 (04重庆)若三棱锥A -BCD 的侧面ABC 内一动点P 到底面BCD 的距离与到棱AB 的距离相等,则动点P 的轨迹与△ABC 组成图形可能是:( D )【例5】 四棱锥P -ABCD ,AD ⊥面P AB ,BC ⊥面P AB ,底面ABCD 为梯形,AD =4,BC =8,AB =6,∠APD =∠CPB ,满足上述条件的四棱锥的顶点P 的轨迹是( )A .圆B .不完整的圆C .抛物线D .抛物线的一部分 分析:∵AD ⊥面P AB ,BC ⊥平面P AB ∴AD ∥BC 且AD ⊥P A ,CB ⊥PB ∵∠APD =∠CPB ∴tanAPD =tanCPB∴AD P A =CB PB ∴PB =2P A在平面APB 内,以AB 的中点为原点,AB 所在直线为x 轴建立平面直角坐标系,则A (-3,0)、B (3,0),设P (x ,y )(y ≠0),则(x -3)2+y 2=4[(x +3)2+y 2](y ≠0)即(x +5)2+y 2=16(y ≠0) ∴P 的轨迹是(B )BABCDAB1A lAB Cα A B CD D 1 C 1B 1A 1 M PABCDD 1 C 1 B 1 A 1 M N3 323P A BC D立体几何中的轨迹问题(教师版)1.在正方体ABCD-A1B1C1D1的侧面AB1内有一点P到直线AB与到直线B1C1的距离相等,则动点P所在曲线的形状为(D).2.在正方体ABCD-A1B1C1D1的侧面AB1内有一点P到直线AB的距离与到直线B1C1的距离之比为2:1,则动点P所在曲线的形状为(B).A.线段B.一段椭圆弧C.双曲线的一部分D.抛物线的一部分3.在正方体ABCD-A1B1C1D1的侧面AB1内有一点P到直线AB的距离与到直线B1C1的距离之比为1:2,则动点P所在曲线的形状为(C).A.线段B.一段椭圆弧C.双曲线的一部分D.抛物线的一部分4.在正方体ABCD-A1B1C1D1中,E为AA1的中点,点P在其对角面BB1D1D内运动,若EP总与直线AC成等角,则点P的轨迹有可能是(A).A.圆或圆的一部分B.抛物线或其一部分C.双曲线或其一部分D.椭圆或其一部分简析由条件易知:AC是平面BB1D1D的法向量,所以EP与直线AC成等角,得到EP与平面BB1D1D 所成的角都相等,故点P的轨迹有可能是圆或圆的一部分.5a,定点M在棱AB上(但不在端点A,B上),点P是平面ABCD内的动点,且点P P到点M的距离的平方差为a2,则点P的轨迹所在曲线为(A).A.抛物线B.双曲线C.直线D.圆连结PE.则PE2=a2+PF2,又PE2-PM2=a2,所以PM2=PF2,从而PM=PF,故点P到直线AD与到点M的距离相等,故点P的轨迹是以M为焦点,AD为准线的抛物线.6P在侧面BCC1B1及其边界上运动,总有1,则动点P的轨迹为的轨迹为_______________.答案线段MN(M、N分别为SC、CD8.若A、B P C(不同于A、B,则动点C在平面内的轨迹是________.(除去两点的圆)A—BCD的侧面ABC内一动点P到底面BCD的距离与到棱AB的距离相等,则动点P的轨迹与组成的图形可能是:(D)A A AP PP PB C B C B C B C A B C D简析 动点P 在侧面ABC 内,若点P 到AB 的距离等于到棱BC 的距离,则点P 在∠ABC 的内角平分线上.现在P 到平面BCD 的距离等于到棱AB 的距离,而P 到棱BC 的距离大于P 到底面BCD 的距离,于是,P 到棱AB 的距离小于P 到棱BC 的距离,故动点P 只能在∠ABC 的内角平分线与AB 之间的区域内.只能选D . 10.已知P 是正四面体S-ABC 的面SBC 上一点,P 到面ABC 的距离与到点S 的距离相等,则动点P 的轨迹所在的曲线是(B ). A .圆 B .椭圆 C .双曲线 D .抛物线解题的要领就是化空间问题为平面问题,把一些重要元素集中在某一个平面内,利 用相关的知识去解答,象平面几何知识、解析几何知识等.11.已知正方体ABCD A B C D -1111的棱长为1,在正方体的侧面BCC B 11上到点A 距离为233的点的轨迹形成一条曲线,那么这条曲线的形状是_________,它的长度为__________. 简析以B 为圆心,半径为33且圆心角为π2的圆弧,长度为36π. 12.已知长方体ABCD A B C D -1111中,AB BC ==63,,在线段BD 、A C 11上各有一点P 、Q ,PQ 上有一点M ,且PM MQ =2,则M 点轨迹图形的面积是 . 提示轨迹的图形是一个平行四边形.13.已知棱长为3的正方体ABCD A B C D -1111中,长为2的线段MN 的一个端点在DD 1上运动,另一个端点N 在底面ABCD 上运动,求MN 中点P 的轨迹与正方体的面所围成的几何体的体积.简析 由于M 、N 都是运动的,所以求的轨迹必须化“动”为“静”,结合动点P 的几何性质,连结DP ,因为MN=2,所以PD=1,因此点P 的轨迹是一个以D 为球心,1为半径的球面在正方体内的部分,所以点P 的轨迹与正方体的表面所围成的几何体的体积为球的体积的18,即1843163⨯⨯=ππ.14.已知平面//α平面β,直线l α⊂,点l P ∈,平面α、β间的距离为4,则在β内到点P 的距离为5且到直线l 的距离为29的点的轨迹是( ) 简析:如图,设点P 在平面β内的射影是O ,则OP 是α、β的公垂线,OP=4.在β内到点P 的距离等于5的点到O 的距离等于3,可知所求点的轨迹是β内在以O 为圆心,3为半径的圆上.又在β内到直线l 的距离等于29的点的集合是两条平行直线m 、n ,它们到点O 的距离都等于32174)29(22<=-,所以直线m 、n 与这个圆均相交,共有四个交点.因此所求点的轨迹是四个点,故选C .16.在四棱锥ABCD P -中,⊥AD 面PAB ,⊥BC 面PAB ,底面ABCD 为梯形,AD=4,BC=8,AB=6,CPB APD ∠=∠,满足上述条件的四棱锥的顶点P 的轨迹是( )A .圆B .不完整的圆C .抛物线D .抛物线的一部分简析:因为⊥AD 面PAB ,⊥BC 面PAB ,所以AD//BC ,且︒=∠=∠90CBP DAP . 又8BC ,4AD ,CPB APD ==∠=∠,可得CPB tan PB CB PA AD APD tan ∠===∠,即得2ADCBPA PB == 在平面PAB 内,以AB 所在直线为x 轴,AB 中点O 为坐标原点,建立平面直角坐标系,则A (-3,0)、B(3,0).设点P (x ,y ),则有2y )3x (y )3x (|PA ||PB |2222=+++-=,整理得09x 10y x 22=+++由于点P 不在直线AB 上,故此轨迹为一个不完整的圆,选B .17.如图,定点A 和B 都在平面α内,定点P ,PB ,α⊥α∉C 是α内异于A 和B 的动点.且AC PC ⊥,那么动点C 在平面α内的轨迹是( )A .一条线段,但要去掉两个点B .一个圆,但要去掉两个点C .一个椭圆,但要去掉两个点D .半圆,但要去掉两个点简析:因为PC AC ⊥,且PC 在α内的射影为BC ,所以BC AC ⊥,即︒=∠90ACB .所以点C 的轨迹是以AB 为直径的圆且去掉A 、B 两点,故选B .18.如图,在正方体1111D C B A ABCD -中,P 是侧面1BC 内一动点,若P 到直线BC 与直线11D C 的距离相等,则动点P 的轨迹所在的曲线是( )A .直线B .圆C .双曲线D .抛物线简析:因为P 到11D C 的距离即为P 到1C 的距离,所以在面1BC 内,P 到定点1C 的距离与P 到定直线BC 的距离相等.由圆锥曲线的定义知动点P 的轨迹为抛物线,故选D .19.已知正方体1111D C B A ABCD -的棱长为1,点P 是平面AC 内的动点,若点P 到直线11D A 的距离等于点P 到直线CD 的距离,则动点P 的轨迹所在的曲线是( )A .抛物线B .双曲线C .椭圆D .直线简析:如图4,以A 为原点,AB 为x 轴、AD 为y 轴,建立平面直角坐标系.设P (x ,y ),作AD PE ⊥于E 、11D A PF ⊥于F ,连结EF ,易知1x |EF ||PE ||PF |2222+=+=又作CD PN ⊥于N ,则|1y ||PN |-=.依题意|PN ||PF |=,即|1y|1x2-=+,化简得0y2yx22=+-故动点P的轨迹为双曲线,选B.20.如图,AB是平面a的斜线段,A为斜足,若点P在平面a内运动,使得△ABP的面积为定值,则动点P的轨迹是()(A)圆(B)椭圆(C)一条直线(D)两条平行直线分析:由于线段AB是定长线段,而△ABP的面积为定值,所以动点P到线段AB的距离也是定值.由此可知空间点P在以AB为轴的圆柱侧面上.又P在平面内运动,所以这个问题相当于一个平面去斜切一个圆柱(AB是平面的斜线段),得到的切痕是椭圆.P的轨迹就是圆柱侧面与平面a的交线.21.如图,动点P在正方体1111ABCD A B C D-的对角线1BD上.过点P作垂直于平面11BB D D的直线,与正方体表面相交于M N,.设BP x=,MN y=,则函数()y f x=的图象大致是()分析:将线段MN投影到平面ABCD内,易得y为x一次函数.22.已知异面直线a,b成︒60角,公垂线段MN的长等于2,线段AB两个端点A、B分别在a,b上移动,且线段AB长等于4,求线段AB中点的轨迹方程.图5简析:如图5,易知线段AB的中点P在公垂线段MN的中垂面α上,直线'a、'b为平面α内过MN的中点O分别平行于a、b的直线,'a'AA⊥于'A,'b'BB⊥于'B,则P'B'AAB=⋂,且P也为'B'A的中点.由已知MN=2,AB=4,易知,2AP,1'AA==得32'B'A=.则问题转化为求长等于32的线段'B'A的两个端点'A、'B分别在'a、'b上移动时其中点P的轨迹.现以'OB'A∠的角平分线为x轴,O为原点建立如图6所示的平面直角坐标系.A BCDMNPA1 B1C1D1yxOyxOyxOyxO图6设)y ,x (P ,n |'OB |,m |'OA |==, 则)n 21,n 23('B ),m 21,m 23('A - )n m (41y ),n m (43x -=+=222)32()n m (41)n m (43=++- 消去m 、n ,得线段AB 的中点P 的轨迹为椭圆,其方程为1y 9x 22=+.点评:例5和例6分别将立体几何与解析几何中的双曲线与椭圆巧妙地整合在一起,相互交汇和渗透,有利于培养运用多学科知识解决问题的能力.立体几何中的轨迹问题1.在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 与到直线B 1C 1的距离相等,则动点P 所在曲线的形状为 ( ) A .线段 B .一段椭圆弧 C .双曲线的一部分 D .抛物线的一部分2.在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 的距离与到直线B 1C 1的距离之比为2:1,则动点P 所在曲线的形状为 ( ) A .线段 B .一段椭圆弧 C .双曲线的一部分 D .抛物线的一部分3.在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 的距离与到直线B 1C 1的距离之比为1:2,则动点P 所在曲线的形状为 ( ) A .线段 B .一段椭圆弧 C .双曲线的一部分 D .抛物线的一部分4.在正方体ABCD-A 1B 1C 1D 1中,E 为AA 1的中点,点P 在其对角面BB 1D 1D 内运动,若EP 总与直线AC 成等角,则点P 的轨迹有可能是 ( ) A .圆或圆的一部分 B .抛物线或其一部分 C .双曲线或其一部分 D .椭圆或其一部分5a ,定点M 在棱AB 上(但不在端点A ,B 上),点P 是平面ABCD内的动点,且点P P 到点M 的距离的平方差为a 2,则点P 的轨迹所在曲线为( ) A .抛物线 B .双曲线 C .直线 D .圆A —BCD 的侧面ABC 内一动点P 到底面BCD 的距离与到棱AB 的距离相等,则动点P 的轨迹与组成的图形可能是( )A A AB C B C B C B CA B C DA B C D 7.已知P 是正四面体S-ABC 的面SBC 上一点,P 到面ABC 的距离与到点S 的距离相等,则动点P 的轨迹所在的曲线是 ( )A .圆B .椭圆C .双曲线D .抛物线8.已知平面//α平面β,直线l α⊂,点l P ∈,平面α、β间的距离为4,则在β内到点P 的距离为5且到直线l 的距离为29的点的轨迹是( )A .一个圆B .两条平行直线C .四个点D .两个点9.在四棱锥ABCD P -中,⊥AD 面PAB ,⊥BC 面PAB ,底面ABCD 为梯形,AD=4,BC=8,AB=6,CPB APD ∠=∠,满足上述条件的四棱锥的顶点P 的轨迹是( ) A .圆 B .不完整的圆 C .抛物线 D .抛物线的一部分10.如图,定点A 和B 都在平面α内,定点P ,PB ,α⊥α∉C 是α内异于A 和B 的动点.且AC PC ⊥,那么动点C 在平面α内的轨迹是( )A .一条线段,但要去掉两个点B .一个圆,但要去掉两个点C .一个椭圆,但要去掉两个点D .半圆,但要去掉两个点11.已知正方体1111D C B A ABCD -的棱长为1,点P 是平面AC 内的动点,若点P 到直线11D A 的距离等于点P 到直线CD 的距离,则动点P 的轨迹所在的曲线是( )A .抛物线B .双曲线C .椭圆D .直线12.如图,AB 是平面a 的斜线段,A 为斜足,若点P 在平面a 内运动,使得△ABP 的面积为定值,则动点P 的轨迹是( )A .圆B .椭圆C .一条直线D .两条平行直线 13.如图,动点P 在正方体1111ABCD A B C D -的对角线1BD 上.过点P 作垂直于平面11BB D D 的直线,与正方体表面相交于M N ,.设BP x =,MN y =,则函数()y f x =的图象大致是( )14.在正方体ABCD A B C D -1111中,点P 在侧面BCC 1B 1及其边界上运动,总有AP ⊥BD 1,则动点P 的轨迹为________.15.在正四棱锥S-ABCD 中,E 是BC 的中点,点P 在侧面∆SCD 内及其边界上运动,总有PE ⊥AC ,则动点P 的轨迹为_______________.16.若A 、B 为平面α的两个定点,点P 在α外,PB ⊥α,动点C (不同于A 、B )在α内,且PC ⊥AC ,则动点C 在平面内的轨迹是________.17.已知正方体ABCD A B C D -1111的棱长为1,在正方体的侧面BCC B 11上到点A 距离为233的点的轨迹形成一条曲线,那么这条曲线的形状是_________,它的长度为__________.18.已知长方体ABCD A B C D -1111中,AB BC ==63,,在线段BD 、A C 11上各有一点P 、Q ,PQ 上有一点M ,且PM MQ =2,则M 点轨迹图形的面积是 .A BC D MNP A 1B 1C 1D 1 yxOyOxOyx O19.已知棱长为3的正方体ABCD A B C D -1111中,长为2的线段MN 的一个端点在DD 1上运动,另一个端点N 在底面ABCD 上运动,则MN 中点P 的轨迹与正方体的面所围成的几何体的体积是 .20.已知异面直线a ,b 成︒60角,公垂线段MN 的长等于2,线段AB 两个端点A 、B 分别在a ,b 上移动,且线段AB 长等于4,求线段AB 中点的轨迹方程.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立体几何中的轨迹问题
立体几何是考查学生空间想象能力和转化能力,在立体几何中出现了一些轨迹问题,本人将这些问题作了如下归类,以供参考。
一、轨迹是抛物线
例1.2004年高考北京卷(文),如图,在正方体abcd-a1b1c1d1中,p是侧面bb1c1c内一动点,若点p到直线bc与直线c1d1的距离相等,则动点p的轨迹所在的曲线是()
a.直线
b.圆
c.双曲线
d.抛物线
解:连接pc1,∵d1c1⊥面bb1c1c,又pc?奂面bb1c1c,∴d1c1⊥pc1,即可得线段pc1长为点p到c1d1的距离,原题意可转化为:在平面bb1c1c中,动点p到定点c1的距离与点p到定直线bc(点c1不在直线bc上)的距离相等.由抛物线定义可知:点p的轨迹所在的曲线是抛物线.
例2.2004年高考北京卷(理),正方体abcd-a1b1c1d1的棱长为1,点m在棱ab上,且am=,点p是平面abcd上的动点,且点p到直线a1d1的距离与到点m的距离的平方差为1,则点p的轨迹是()
a.抛物线
b.双曲线
c.直线
d.以上都不对
解:在正方形add1a1中过点e作ef⊥a1d1交ad于f,连接
pf,pe,pm. ∵pe为点p到a1d1的距离∴pe⊥a1d1∴a1d1⊥efp面,又ad∥a1d1∴pf⊥ad即pf为点p到直线ad的距离.由条件和所作
不难知ef⊥fp.pe2-pm2=ef2+pf2-pm2=1+pf2-pm2=1即:pf=pm,同样由抛物线定义可知:点p的轨迹所在的曲线是抛物线.
二、轨迹是椭圆
例3.由2004年高考北京卷,(文4)得变题1,在正方体
abcd-a1b1c1d1中,p是侧面bb1c1c内一动点,若点p到直线bc的距离是点p到直线c1d1的距离2倍,则动点p的轨迹是()
a.线段
b.椭圆的一部分
c.双曲线的一部分
d.抛物线的一部分
解:变为在平面bb1c1c中,动点p到定点c1的距离与点p到定直线bc(点c1不在直线bc上)的距离之比为1∶2.由椭圆第二定义可知:点p的轨迹所在的曲线是椭圆(在正方形bb1c1c内),且离心率为.故本题选b.
三、轨迹是双曲线
例4.变题2,在正方体abcd-a1b1c1d1中,p是侧面bb1c1c内一动点,若点p到直线bc的距离是点p到直线c1d1的距离一半,则动点p的轨迹是双曲线的一部分,且离心率为2.
四、轨迹是线段
例5.变题3,如图,在正方体abcd-a1b1c1d1中,p是侧面bb1c1c 内一动点,且始终满足ap⊥d1b,则动点p的轨迹所在的曲线是() a.线段 b.椭圆的一部分
c.双曲线的一部分
d.抛物线的一部分
解:连接ac,ab1,b1c,易证bd1⊥面ab1c,∴点p在线段b1c动,
才能满足ap⊥d1b.故本题选a.
例6.(2005年5月苏州市高三教学调研测试)如图,△adp为正三角形,四边形abcd为正方形,平面pad⊥平面abcd.m为平面abcd内的一动点,且满足mp=mc.点m在正方形abcd内的轨迹为(o为正方形abcd的中心)()
解:空间中到p、c两点距离相等的点应在过线段pc中点且垂直于此线段pc的平面α上。
而m点又在面abcd上,所以m在平面α与面abcd的交线上,故答案可能是a或b。
当点m在b处时
pm=pb==ab=mc,所以选a.
五、轨迹是圆
例7.四棱锥p-abcd中,ad⊥面pab,bc⊥面pab,底面abcd是梯形,ad=4,bc=8,ab=6,∠apd=∠cpb,满足上述条件的四棱锥的顶点p 的轨迹是()
a.圆的一部分
b.椭圆的一部分
c.双曲线的一部分
d.抛物线的一部分
解:∵ad⊥面pab,bc⊥面pab,∠apd=∠cpb,∴△pbc∽△pad,∴pa∶pb=ab∶bc=1∶2,又可证得面pab⊥面abcd。
即在平面pab中,动点p到两定点a、b的距离之比是定值。
在平面pab中以ab所在直线为x轴,以ab中点为原点建立如图直角坐标系,则
a(-3,0),b(3,0),设动点p(x,y),则有:=,即,化简得:由于点p在面
abcd的一侧,所以本题选a.
这些问题的处理办法还是将空间立体几何转化为平面问题,再通过定义法、轨迹法等,像对待解析几何问题一样求出曲线方程或得到轨迹形状。
作者单位:江苏省连云港海州高级中学。
