立体几何-利用空间向量求二面角的平面角
利用空间向量知识求空间中的二面角

所以 cos〈n1,n2〉=
所以n1=(1,1,1).同理可求得平面BMN的一个法向量n2=(1,-1,-1).
令x=1,解得y=1,z=1,
方法二:设平面AMN的法向量n1=(x,y,z).
故所求两平面所成角的余弦值为
练习:如图所示,四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别为PC,PD,BC的中点.
易知 =(0,0,1), =(1,0,0), =(-2,1,-1),
01
设平面DFG的法向量m=(x1,y1,z1),
02
则 解得 令x1=1,得m=(1,2,0)是平面DFG的一个法向量.
03
01
设平面EFG的法向量n=(x2,y2,z2),
05
所以cos θ=
03
因为cos〈m,n〉=
01
知识点:二面角
01
用向量方法求二面角 平面α与β相交于直线l,平面α的法向量为n1,平面β的法向量为n2,<n1,n2>=θ,则二面角α-l-β为θ或π-θ.设二面角大小为φ,则|cosφ|=__________=__________.
|cosθ|
01
02
利用向量法求二面角的两种方法
例题讲解:正方体ABEF-DCE′F′中, M,N分别为AC,BF的中点(如图),求平面MNA与平面MNB所成角的余弦值.
【解析】方法一:设正方体棱长为1.以B为坐标原点,BA,BE,BC所在直线分别为x轴,y轴,z轴建立空间直角坐标系B-xyz,则A(1,0,0),B(0,0,0).取MN的中点G,连接BG,AG,则 因为△AMN,△BMN为等腰三角形, 所以AG⊥MN,BG⊥MN.所以∠AGB为 二面角的平面角或其补角. 因为 所以
用法向量求二面角的大小及其角度关系的确定

用法向量求二面角的大小及其角度关系的确定我们都知道,向量知识在数学学科里有其非常广泛的应用,尤其是在立体几何求角和距离时,若利用向量知识求解会得到事半功倍的效果,也正体现了向量知识的工具性和灵活性。
而在应用向量知识求解二面角的大小时,不是所有的二面角的两个半平面的法向量的夹角都和二面角相等,有时是互补,那么,什么时候相等,什么时候互补,如何确定其“角度之间的大小关系”一直以来是困扰很多教师和学生的一个难题。
向量有其自身的独特性质—自由性,当一个向量在空间的某一位置时,可以自由移动,只要满足其方向不变,其无论移动到任何位置,向量都是相等的。
根据这一性质,当我们把二面角的某个半平面的法向量求出后,把它的起点放到坐标原点,然后确定其向量的方向的指向,从而确定其法向量的夹角和二面角的大小的关系,在确定了法向量的夹角与二面角的关系后,再利用向量的数量积求出二面角的大小,下面就来具体阐述一下这一做法。
一.规定法向量的指向方向1.当法向量的方向指向二面角的内部时称之为向里指,如:图1中的向量。
1n 2.当法向量的方向指向二面角的外部时称之为向外指,如:图1中的向量。
2n 二.法向量的夹角和二面角大小的关系1.设 分别为平面的法向量,二面角的大小为,向量21,n n βα,βα--l θ的夹角为,当两个法向量的方向都向里或都向外指时,则有21,n n ϕ(图2);πϕθ=+2.当两个法向量的方向一个向里指一个向外指时(图3)ϕθ=图2图3三、在坐标系中做出法向量,从而确定法向量的方向指向1.已知二面角,若平面的法向量,由向量的相等条βα--l α)3,4,4(=n 件知,坐标是(4,4,3)的向量有无数多个,根据向量的自由性,我们只需n 做出由原点出发的一个向量便可,如图4所示,从而,我们很容易的判断出平面法向量的方向的指向,是指向二面角的里面。
α2.若平面法向量,同理可做出从原点出发的法向量,如图5α)1,3,4(--=n 所示,显然,方向是指向二面角的外面。
立体几何向量法求二面角

立体几何向量法求二面角一、引言在几何学中,二面角是指两个平面或者一个平面和一个直线之间的夹角。
它是描述多面体中相邻两个面之间的夹角的重要参数。
在工程学、物理学和化学等领域,求解二面角是非常常见的问题。
本文将介绍立体几何向量法求解二面角的方法。
二、立体几何向量法立体几何向量法是一种非常有效的求解二面角的方法。
它基于向量叉积和点积的运算,通过将多面体分解成若干个三角形来计算二面角。
1. 向量叉积向量叉积是两个向量所构成的新向量,其大小等于两个向量所构成平行四边形的面积,方向垂直于这两个向量所构成平行四边形所在平面。
设有两个三维向量a = (a1, a2, a3)和b = (b1, b2, b3),则它们的叉积c = a × b定义为:c = (a2b3 - a3b2, a3b1 - a1b3, a1b2 - a2b1)其中c表示a和b所构成平行四边形所在平面上一条垂直这个平行四边形的向量。
2. 向量点积向量点积是两个向量所构成的标量,其大小等于两个向量夹角的余弦值乘以两个向量的模长之积。
设有两个三维向量a = (a1, a2, a3)和b = (b1, b2, b3),则它们的点积c = a · b定义为:c = a1b1 + a2b2 + a3b3其中c表示a和b之间夹角的余弦值乘以它们的模长之积。
3. 二面角计算公式二面角可以通过计算相邻两个面法线向量之间夹角的余弦值来求解。
具体地,设有一个多面体,其中相邻两个面A和B所对应的法线分别为nA和nB,则它们之间的二面角θAB可以通过以下公式计算:cosθAB = -nA·nB / |nA||nB|其中“·”表示向量点积,“| |”表示向量模长。
4. 多面体分解在实际问题中,通常需要将多面体分解成若干个三角形来计算二面角。
具体地,考虑一个四面体(如图1),其中相邻两个三角形ABC和ABD所对应的法线分别为nABC和nABD,则它们之间的二面角θABC-D可以通过以下公式计算:cosθABC-D = -nABC·nABD / |nABC||nABD|其中“·”表示向量点积,“| |”表示向量模长。
空间向量与立体几何向量法求二面角(二

D
AB CD
面面角:
②法向量法n1,n2源自 n1,n2n2
n1,n2
n2
n1,n2
n1
n1
l
l
cos cos n1, n2 cos cos n1, n2
注意法向量的方向:一进一出,二面角等于法向量夹角; 同进同出,二面角等于法向量夹角的补角
(2)求证:PB⊥平面EFD
(2)证明:依题意得B(1,1,0),PB (1,1,1)
又DE (0, 1 , 1),故PB DE 0 1 1 0
22
所以PB DE
2 2Z
由已知EF PB,
P
且EF DE E,
所以PB 平面EFD
E F
D
C Y
A B
X
BC SO,BC AO,SO AO O BC 平面SOA, BC SA
(2)求直线SD与平面SAB所成角的正弦值。 z
解:由(1)知SO,OA,BC两两垂直。
S
故以OA、OB、OS为正交基底建立
空间直角坐标系如图。则 S(0,0,1),D( 2,- 2 2,0),
C O By
四边形,侧面SBC 底面ABCD。已知 ABC 450
AB=2,BC= 2 2 ,SA=SB= 3 .
(1)求证 SA BC.
(2)求直线SD与平面SAB所成角的正弦值。
S
C
OB
D
A
证明:(1)取BC中点O,连接OA、OS。 S
则由BC 2 2得OB 2,
又AB 2,ABC 450, 得OA 2
依题意得A(1, 0, 0), P(0, 0,1), P
高中数学第二章空间向量与立体几何夹角的计算空间向量求二面角的方法素材

空间向量求二面角的方法方法一:先作出二面角的平面角,再利用向量的内积公式求解:设∠AOB 是二面角l αβ--的一个平面角,则向量OA 与OB 所成的角就是所求的二面角的大小.例1 正四面体ABCD 中,求相邻两个面所成的二面角.解析:如图1,取BC 边的中点E,连结AE 、DE ,则AE⊥BC,DE⊥BC,所以∠AED 就是正四面体的两个相邻面ABC 与DBC 所成二面角的平面角,且BC⊥平面ADE ,∴BC⊥AD,∴0EC DA =.设正四面体棱长为1.∵()()ED EA EC CD EC CD DA =+++ =222EC EC CD EC DA CD DA CD ++++ 11121cos120011cos1201424=+⨯⨯⨯++⨯⨯+=. 又在△ABC 与△BCD 中,可求得32ED EA ==, ∴cos ED EAED EA ED EA =,11433322==⨯. 故正四面体的两个相邻面所成的二面角大小为1arccos3.方法二:利用法向量求解:设1n 是平面α的法向量,2n 是平面β的法向量.①若两个平面的二面角如图2所示的示意图,则1n 与2n 之间的夹角θ就是欲求的二面角;②若两个平面的二面角如图3所示的示意图,设1n 与2n 之间的夹角为θ.则两个平面的二面角为πθ-. 例2 如图4,△ABC 是以∠B 为直角的直角三角形,SA⊥平面ABC ,SA=BC=2,AB=4,D 、N 分别是BC 、AB 的中点.求二面角S —ND-A 的余弦值.解析:平面ABC 的法向量是AS ,设平面SND 的法向量为BC AB AS λμ=++n .∵SA⊥平面ABC ,∴SA⊥BC,SA⊥AB,∴0AS BD =,0AS BN =,0AS BC =,0AS AB = 又AB⊥BC,∴0BC BN =,0AB BD =,0BC NA =. 由()()ND BC AB AS BD BN λμ=++-n 280BC BD AB BN λμλμ=-=+=。
二面角的求法和利用空间向量解决立体几何问题
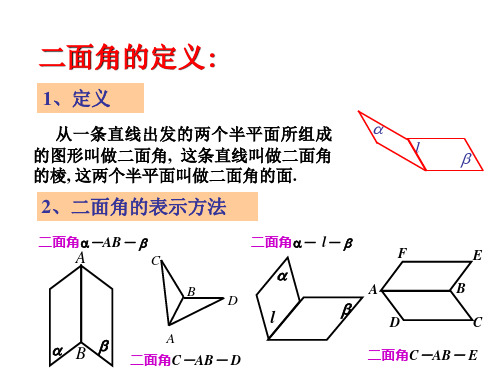
二面角的定义:
1、定义
从一条直线出发的两个半平面所组成
的图形叫做二面角, 这条直线叫做二面角
l
的棱, 这两个半平面叫做二面角的面.
2、二面角的表示方法
二面角-AB-
A
C
B
二面角- l-
D
l
B
A
二面角C-AB- D
F
E
A
B
D
C
二面角C-AB- E
二面角的平面角:
以二面角的棱上任意一点为端
点, 在两个面内分别作垂直于棱的 两条射线, 这两条射线所成的角叫 做二面角的平面角。
面面平行
∥ n1 ∥ n2 n1 kn2
二、垂直关系:
设直线 l, m 的方向向量分别为 AB,CD ,
平面 , 的法向量分别为 n1 , n2 , 线线垂直:
l ⊥ m AB ⊥ CD AB • CD 0 ;
Bl
A
平面 内的两个相交向量垂直
(4)解方程组,令其中一个量的值求另外两个, 即得法向量。
一、平行关系:
设直线 l, m 的方向向量分别为 AB,CD ,
lm
BD
平面 , 的法向量分别为
线线平行:
n1
, n2
,
l ∥ m AB ∥ CD AB kCD
;
x1 y1
=
A
x2 y2
=
C
x3 y3
线面平行
AB
l ∥ AB n1 AB n1 0 ;
分别作垂直于a 的两条射线OA,OB,则∠AOB就 是此二面角的平面角。
2、垂线法: 在一个平面 内选一点A向另一平面 作 垂线AB,
垂足为B,再过点B向棱a作垂线BO,垂足 为O, 连结AO,则∠AOB就是二面角的平面角。
立体几何中二面角的求法

立体几何中二面角的求法立体几何中二面角的求法知识综合性强,方法灵活性大,需要学生将二面角问题转化为其平面角问题,在培养其空间想象能力和分析、解决问题能力的前提下,求解过程中又要利用平面几何、立体几何、三角函数等重要知识。
因此,二面角的求法是一个重点及难点内容,以下便谈谈解决该问题的方法:一、传统方法解决二面角问题传统方法求解二面角,关键在于准确作出二面角的平面角,从而化归为求三角形内角大小。
主要有以下几种作法:1.定义法二面角的定义——以二面角的棱上任意一点(点O)为端点,在两个面内分别作垂直于棱的两条射线OA、OB,则∠AOB叫作二面角的平面角。
例1:如图,平行六面体ABCD-A1B1C1D1底面ABCD是菱形,且∠C1CB=∠C1CD=∠BCD=60°,CD=2,CC1=,求二面角C1-BD-C的余弦值。
解析:由∠C1CB=∠C1CD及底面ABCD是菱形可得△C1CB≌△C1CD,则C1B=C1D,即△C1BD与△CBD是两个同底的等腰三角形;取BD中点O,得到C1O⊥BD、CO⊥BD,则∠C1OC为二面角C1-BD-C的平面角。
2.三垂线法三垂线定理——平面内的一条直线,如果与这个平面的一条斜线在这个平面上的射影垂直,那么它也和这条斜线垂直。
三垂线逆定理——平面内的一条直线,如果它和这个平面的一条斜线垂直,那么它也和这条斜线在平面内的射影垂直。
例2:如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点。
求二面角A-PD-C的余弦值。
解析:易证AE⊥平面PCD,过点A作AM⊥PD,垂足为M,连结EM,AM在平面PCD内的射影是EM,则EM⊥PD(三垂线逆定理),因此∠AME是二面角A-PD-C的平面角。
3.垂面法根据二面角平面角的定义知两个半平面α、β的公垂面γ与棱垂直,则公垂面γ与两个半平面交线所成的角∠AOB,就是二面角的平面角。
立体几何中的向量方法及二面角的平面角求法总结

讲义:立体几何中的向量方法及二面角的平面角求法总结一、几种角的范围1、 _________________________________ 二面角平面角的范围:2、 _________________________________ 线面角的范围:3、 _________________________________ 直线倾斜角范围:4、异面直线夹角范围:_______________5、向量夹角范围:_________________二、立体几何中的向量方法1.三个重要向量(1)直线的方向向量:直线的方向向量是指和这条直线平行(或重合)的向量,一条直线的方向向量有 ______ .(2)平面的法向量:直线I丄平面a取直线I的方向向量,则这个向量叫做平面a的法向量.显然一个平面的法向量有 ____ ,它们是共线向量.(3)直线的正法向量:直线L:Ax+By+C=O的正法向量为n=(A,B).2.直线的方向向量与平面的法向量在确定直线和平面位置关系中的应用(1)直线l i的方向向量为u 1= (a i, b i, c i),直线l2的方向向量为比=(a2, b2, C2).女口果丨1 //丨2,那么U1 // U2? 5=右2? _____________________________ ;女口果丨1丄l2, 那么U1丄U2? U1 U2= 0? ________________⑵直线I的方向向量为u= (a1, b1, C1),平面a的法向量为n= (a2, b2, C2).若I // a 贝U u 丄n? u n = 0? _________________若I 丄a 贝U u // n? u = k n? _____________________(3)平面a的法向量为U1 = (a1, b1, C1),平面B的法向量为u2= (a2, b2, C2).若all B U1 / U2? U1 = k u2? (a1, b1, G)=_________ ;若a丄B 贝y U1 丄U2? U1 U2= 0? ____________________3.利用空间向量求空间角(1)求两条异面直线所成的角:设a, b分别是两异面直线I1, I2的方向向量,则(2) 求直线与平面所成的角:设直线I 的方向向量为a ,平面a 的法向量为n ,直线I 与平面a 所成的角为 0,则 si nA |cos 〈 a , n > |=(3) 求二面角的大小:(I )若 AB , CD 分别是二面角a — I — B 的两个半平面内与棱I 垂直的异面直线,则二面角的大 小就是向量AB , CD 的夹角(如图①所示).(H )设n i , n 2分别是二面角a — I — B 的两个半平面a, B 的法向量,贝U 向量n i 与n 2的夹角(或其补角)的大小就是二面角的大小(如图②③).4. 求点面距:平面a 外一点P 到平面a 的距离为:其中n 为平面a 的法向量,PQ 为平面a 的斜线,Q 为斜足 5. 平面法向量的求法设出平面的一个法向量n = (x , y , z),利用其与该平面内的两个不共线向量垂直,即数量积为 0, 列出方程组,两个方程,三个未知数,此时给其中一个变量恰当赋值,求出该方程组的一个非零 解,即得到这个法向量的坐标.注意,赋值不同得到法向量的坐标也不同, 法向量的坐标不唯一. 6. 射影面积公式:二面角的平面角为 a ,则cos a=7. 利用空间向量求角要注意的问题(1)异面直线所成的角、直线和平面所成的角、二面角都可以转化成空间向量的夹角来求.⑵空间向量的夹角与所求角的范围不一定相同,如两向量的夹角范围是[0, n,两异面直线所成的角的范围是o , n . (3)用平面的法向量求二面角时,二面角的大小与两平面法向量的夹角有相等和互补两种情况 .三、二面角的平面角的求法1、定义法: 从一条直线出发的两个半平面所组成的图形叫做二面角 ,这条直线叫做二面角的棱,这两个半平面叫做二面角的面,在棱上取点,分别在两面内引两条射线与棱垂直,这两条垂线d=② ③所成的角的大小就是二面角的平面角。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1A 利用空间向量求二面角的平面角1.二面角的概念:二面角的定义.从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,每个半平面叫做二面角的面若棱为l ,两个面分别为,αβ的二面角记为l αβ--.2.二面角的平面角:(1)过二面角的棱上的一点O 分别在两个半平面内作棱的两条垂线,OA OB ,则AOB ∠叫做二面角l αβ--的平面角(2)一个平面垂直于二面角l αβ--的棱l ,且与两半平面交线分别为,,OA OB O 为垂足,则AOB ∠也是l αβ--的平面角说明:(1)二面角的平面角范围是[0,180]o o;(2)二面角的平面角为直角时,则称为直二面角,组成直二面角的两个平面互相垂直引导:请学生归纳已学过的求二面角的大小的方法,教师作必要的补充与引导.明确本节课的课题. 二.求二面角的平面角:【回顾复习定义法求二面角的平面角】例1:在棱长为1的正方体1AC 中,求平面1C BD 与底面ABCD 所成二面角1C BD C --的平面角正弦值大小. 解:过1C 作1C O BD ⊥于点O , ∵正方体1AC ,∴1CC ⊥平面ABCD ,∴1COC ∠为平面1C BD 与平面ABCD 所成二面角1C BD C --的平面角,可以求得:36sin 1=∠COC ,所以,平面1C BD 与底面ABCD 所成 二面角1C BD C --的平面角的正弦值大小为36 【回顾复习用三垂线法求二面角的平面角】例2.如图,AB ⊥平面BCD ,BD CD ⊥,若2AB BC BD ==,求二面角B AC D --的正弦值分析:要求二面角的正弦值,首先要找到二面角的平面角解:过D 作BC DF ⊥于F ,过D 作AC DE ⊥于E ,连结EF ,则AC 垂直于平面DEF , FED ∠为二面角B AC D --的平面角, 又AB ⊥平面BCD ,∴AB DF ⊥,AB CD ⊥,∴DF ⊥平面ABC , ∴DF EF ⊥又∵AB CD ⊥,BD CD ⊥,∴CD ⊥平面ABD ,∴CD AD ⊥,设BD a =,则2AB BC a ==,在Rt BCD ∆中,1122BCD S BC DF BD CD ∆=⋅=⋅,∴DF = AB C DEF同理,Rt ACD ∆中,1522DE a =, ∴3102sin 51522aDF FED DE a ∠===, 所以,二面角B AC D --的正弦值为105. 通过观察探究利用法向量解决: 例1:解:建立空间直角坐标系得:)1,1,0(1=DC ,)0,1,1(=DB ,)0,1,0(=DC设平面1C BD 的法向量),,(1111z y x n =,平面CBD 的法向量),,(2222z y x n =,可得)1,1,1(1-=n ,)1,0,0(2=n ,33,cos 21=n n ,即二面角的平面角36sin =θ 例2:解:建立空间直角坐标系得: )2,21,23(),2,0,0(),2,2,0(-==-=AD BA AC 设平面BAC 的法向量),,(1111z y x n =,平面DAC 的法向量),,(2222z y x n =得:)1,0,0(1=n ,)33,33,1(2=n ,515,cos 21=n n 所以,二面角B AC D --的正弦值为10. 三.归纳小结:本节课回忆巩固了求解二面角的一些方法,并且通过类比用空间向量知识求解二面角,我们感受到空间向量的巧妙之处,但要让同学们认识到法向量之间的夹角与二面角的平面角的异同之处。
四.作业求二面角专题l2n u u r 1n u u r βαcos θ=12cos ,<>u r u u rn n2n u u r 1n u u r βαθ=12>u r u r45如何用空间向量求解二面角求解二面角大小的方法很多,诸如定义法、三垂线法、垂面法、射影法、向量法等若干种。
而这些方法中最简单易学的就是向量法,但在实际教学中本人发现学生利用向量法求解二面角还是存在一些问题,究其原因应是对向量法的源头不尽了解。
本文就简要介绍有关这类问题的处理方法,希望对大家有所帮助。
在立体几何中求二面角可归结为求两个向量的夹角问题.对于空间向量→a 、→b ,有cos <→a ,→b >=→→→→⋅⋅||||b a ba .利用这一结论,我们可以较方便地处理立体几何中二面角的问题.例1 在四棱锥V-ABCD 中,底面ABCD 是正方形,侧面VAD 是正三角形,平面VAD ⊥底面ABCD .求面VAD 与面VDB 所成的二面角的余弦值.证明: 建立如图空间直角坐标系,并设正方形边 长为1,依题意得AB −−→= (0,1,0),是面VAD 的法向量,A BC VD xyz设n →= (1,y ,z)是面VDB 的法向量,则0,0.n VB n VB →−−→→−−→⎧⋅=⎪⎨⎪⋅=⎩⇒1,y z =-⎧⎪⎨=⎪⎩⇒n →= (1,-1,-3)。
∴cos <AB −−→,n →>||||AB nAB n −−→→−−→→⋅⋅=-7, 又由题意知,面VAD 与面VDB所成的二面角为锐角,所以其余弦值是7例2如图,直三棱柱ABC —A 1B 1C 1中,∠ACB =90︒,AC=1,CB=2,侧棱AA 1=1,侧面AA 1B 1B 的两条对角线交点为D ,B 1C 1的中点为M .⑴求证CD ⊥平面BDM ;⑵求面B 1BD 与面CBD 所成二面角的余弦值. 解:⑴略⑵如图,以C 为原点建立坐标系.设BD 中点为G ,连结B 1G ,则依14,14),BD −−→= (,12,12),1B G −−→= (-4,-34,14), ∴BD −−→·1B G −−→= 0,∴BD ⊥B 1G .又CD ⊥BD ,∴CD −−→与1B G −−→的夹角θ等于所求二面角的平面角.∴ cos θ=11||||CD B G CD B G −−→−−→−−→−−→⋅⋅=例3如图,在四棱锥P —ABCD 中,底面ABCD 是正方形,侧棱PD ⊥底面ABCD ,PD=DC ,E 是PC 的中点,作EF ⊥PB 交PB 于点F .求二面角C —PB —D 的大小解:如图所示建立空间直角坐标系,D 为坐标原点,设a DC = 设点F 的坐标为000()x y z ,,,PA −−→=PB λ−−→,则000()()x y z a a a a λ-=-,,,,.从而000(1)x a y a z a λλλ===-,,.所以PE −−→=00011(,,)(,(),())2222a a x y z a a a λλλ---=---.BB 1C 1A 1CADM由条件EF ⊥PB 知,PE −−→·PB −−→= 0,即0)21()21(222=---+-a a a λλλ,解得31=λ. ∴点F 的坐标为2()333a a a,,,且()366a a a PE −−→=--,,,2()333a a a FD −−→=---,,, ∴PB −−→·FD −−→22220333a a a =--+=,即FD PB ⊥,故EFD ∠是二面角C —PB —D 的平面角. ∵PE −−→·FD −−→=222291896a a a a =-+=,且||6PE −−→==,||3FD −−→==,∴21cos 2||||a PE FDEFD PE FD −−→−−→−−→−−→⋅∠===,∴3π=∠EFD . 所以,二面角C —PB —D 的大小为3π. 例4 已知三棱柱OAB —1O A 1B 1中,平面11O OBB ⊥平面OAB ,∠AOB =︒90,∠OB O 1=︒60,且OB =1OO = 2,OA =3,求二面角1O —AB —O 的余弦值.解:以O 为原点,分别以OA ,OB 所在的直线为x ,y 轴,过O 点且与平面AOB 垂直的直线为z 轴,建立空间直角坐标系.如图,则O (0,0,0),1O (0,1,3),A(3,0,0),1A (3,1,3),B(0,2,0).∴−→−1AO = (-3,1,3),−→−AB = (-3,2,0).显然−→−OZ 为平面AOB 的法向量,取→1n = (0,0,1),设平面AB O 1的法向量为→2n = (x ,y ,z),则→2n ·−→−1AO = 0,→2n ·−→−AB = 0.即⎪⎩⎪⎨⎧=+-=++-023033y x z y x ,令y =3,x = 2,z = 1,则→2n = (2,3,1). ∴cos <→1n ,→2n >=||||2121→→→→⋅⋅n n n n =221=42, 故二面角1O —AB —O 的余弦值是42。
