细长中心受压直杆临界力欧拉公式30页PPT
临界力及临界应力的计算 PPT

不同支承情况的压杆其边界条件不同,临界力值也不同。
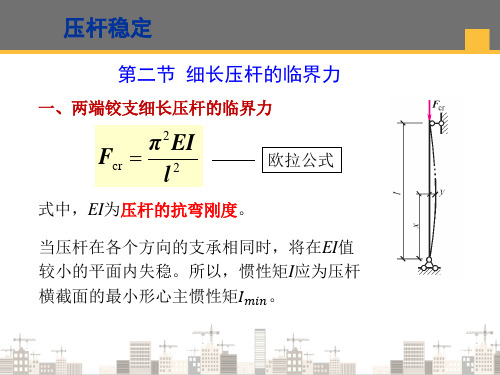
欧拉公式的通式:
Fcr
2EI
(ul)2
式中: E材料的弹性模量;
I压杆横截面对中性轴的最小惯性矩;单位:m4;
μl计算长度;
长度系数,与杆端支承有关。
一端固定,一端自由压杆:μ=2;
两端铰支细长压杆:
μ=1;
一端固定,一端铰支压杆:μ=0.7;
3)临界压力与压杆失稳:
在较小轴向压力F 作用下,
试件可保持稳定平衡;
但 F 增大到某一值 Fcr 时,
试件开始出现不稳定平衡,
试
我们将此 Fcr称为临界压力。
件
压杆由于处于不稳定衡
状态而造成的失效时,
我们称之为“压杆失
稳” 。
三、工程中的压杆稳定性问题 压杆失稳导致钢梁倒塌
顶杆 的
稳定性
吊车塔身的稳定性
64
i I d 7mm; 1;
A4
l
i
11000 7
142.9
p
123;
大柔度杆;
cr
2E 2
2 200000 142 .92
96.7MPa
Fcr cr A 96.7 615 .75 59.6kN NBA;
钢的弹性模量E=200GPa,试验算此杆是否能够承受此压力。
解:查表知A=42cm2,imin=2.31cm,μ=1,则柔度
l
i
1 3000 23.1
129.9
p
123
大柔度杆
由欧拉公式
压杆稳定—细长压杆的临界力(建筑力学)
(μl)
式中,μl为计算长度,μ称为长度系数。
不同支承下的计算长度及长度系数见下表。
压杆稳定
临界力的影响因素
临界力Fcr的大小反映了压杆失稳的难易,而压杆失稳
就是直杆变弯,发生弯曲变形,因此临界力的大小与影响
直杆弯曲变形的因素有关:
杆的长度l
抗弯刚度EI
杆端支承
l越大
EI越大
越牢固
抵抗变形的能力越小
弹性模量E=200GPa。试计算其临界力。
解 查型钢表得Iz=2370cm4,Iy=158cm4,应取小值。
π 2 EI π 2 200 103 158 10 4
Fcr 2
N 346kN
2
l
3 103
压杆稳定
二、其他支承情况下细长压杆的临界力的欧拉公式
π 2 EI
Fcr
a);在最小刚度平面
内弯曲时为两端固定(
图b)。木材的弹性模
量E=10GPa,试求木柱
的临界力。
解 由于最大刚度平面与最小刚度平面内的支承
情况不同,所以需分别计算。
Fcr
(1)计算最大刚度平面内的临界力
截面的惯性矩为
两端铰支,长度系数μ=1
2 EI y 3.14 2 10 109 8 10 5
12
2.88 107 mm 4
2.88 10 m
z
4
y
两端固定,长度系数μ=0.5
EI Z 3.14 10 10 2.88 10
Fcr
N
2
2
( l )
(0.5 8)
2
2
177 103 N 177 kN
细长压杆的临界力公式—欧拉公式.

细长压杆的临界⼒公式—欧拉公式.10.2 细长压杆的临界⼒公式—欧拉公式⼀、两端铰⽀压杆的临界⼒图9—4为两端受压杆件,⼈们经过对不同长度(l ),不同截⾯(I ),不同材料(E )的压杆在内⼒不超过材料的⽐例极限时发⽣失稳的临界⼒P cr 研究得知: 22lPcr EI=π(9—1)式中:π—圆周率;E —材料的弹性摸量;l —杆件长度;I —杆件截⾯对⾏⼼主轴的惯性矩。
图9-4当杆端在各⽅向的约束情况相同时,压杆总是在抗弯刚度最⼩的纵向平⾯内失稳,所以(9-1)式中的惯性矩应取截⾯最⼩的形⼼惯性矩I min 。
瑞⼠科学家欧拉(L.Eular )早在18世纪,就对理想细长压杆在弹性范围的稳定性进⾏了研究。
从理论上证明了上述(9-1)式是正确的,因此(9-1)式⼜称为计算临界⼒的欧拉公式。
⼆、杆端⽀承对临界⼒的影响图9-5(a)(b)(c)(d)⼯程上常见的杆端⽀承形式主要有四种,如图9-5所⽰,欧拉进⼀步研究得出各种⽀承情况下的临界⼒。
如⼀端固定,⼀端⾃由的杆件,这种⽀承形式下压杆的临界⼒,只要在(9-1)式中以2l 代替l 即可。
()222l P cr EI=π(a )同理,可得两端固定⽀承的临界⼒为()225.0l P cr EI=π(b )⼀端固定,⼀端铰⽀压杆的临界⼒为 ()227.0l P cr EIπ(c )式(a ),(b),(c)和(9-1)可归纳为统⼀的表达式()22l P cr µπEI = (9-2)式中l µ称为压杆计算长度,µ称为长度系数,⼏种不同杆端⽀承的各µ值列于表9—1中,µ反映了杆端⽀承情况对临界⼒的影响。
表9-1 各种杆端⽀承压杆的长度系数图例9.1 图⽰轴⼼受压杆,截⾯⾯积为10mm ?20mm 。
已知其为细长杆,弹性模量E=200GPa ,试计算其临界⼒。
2m20图9-6单位:mm解:由杆件的约束形式可知:7.0=µ4333min1067.112102012mm hb I I y ?=?===临界⼒:223320010 1.67101076.2 1.076()(0.7 2.510)cr EI P N kN l ππµ====?? 三、临界应⼒和柔度在临界⼒的作⽤下,细长压杆横截⾯上的平均应⼒叫做压杆的临界应⼒,⽤cr σ表⽰。
材料力学:压杆稳定

坍塌后的奎拜克桥
材料力学教学课件
韩国汉城
1995年6月29日下午,韩国汉城三 丰百货大楼,由于盲目扩建、加层, 致使大楼四五层立柱不堪重负而产 生失稳破坏,大楼倒塌,死502人, 伤930人,失踪113人。
2020年2月3日星期一
10
第九章 压杆稳定
中国南京 2000年10月25日上午10时,南京电视台演播中 心演播大厅的屋顶的施工中,由于脚手架失稳, 造成屋顶模板倒塌,死6人,伤34人。
材料力学教学课件
2020年2月3日星期一
26
第九章 压杆稳定
1)、细长杆的临界应力
cr
2E 2
p
2E p
引入记号 1
2E p
欧拉公式的适用范围
l
i
1
2E p
2)、中长杆的临界应力(经验公式)
cr a b, 2 1
sin
kl
l
coskl
0
2020年2月3日星期一
19
第九章 压杆稳定
由于杆在微弯状态下保持平衡时,
Fy不可能等于零,故由上式得
1 sin kl l coskl 0 k 亦即 tan kl kl
满足此条件的最小非零解为kl=4.49,亦即 Fcr l 4.49 EI
从而得到此压杆求临界力的欧拉公式:
受均匀压力的球形薄壳或薄圆环,当压力超过一定数值时,圆环将 不能保持圆对称的平衡形式,而突然变为非圆对称的平衡形式。
材料力学教学课件
2020年2月3日星期一
9
第九章 压杆稳定
由于构件的失稳往往是突然发生的,因而其危害性也较大。 历史上曾多次发生因构件失稳而引起的重大事故。如1907年 加拿大劳伦斯河上,跨长为548米的奎拜克大桥,因压杆失 稳,导致整座大桥倒塌。近代这类事故仍时有发生。
细长压杆的临界压力欧拉公式

(2)
Fc r正 Fc r圆
π2EI正
( l)2
π2 EI圆
I正 I圆
a4
12 πd 4
( l)2
64
πd 2 4
2
12 πd 4
64
π 3
例2:图示两桁架中各杆的材料和截面均相同,设 F1和F2 分别为这两个
桁架稳定的最大载荷,则
(A) F1 = F2;
π2EI
( l )2
称为长度因数,l 称为相当长度
π2EI (0.5l ) 2
0.5
Fc r
π2EI (0.7l ) 2
0.7
Fc r
~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~~~~~~~~~~
π2EI (2l ) 2
2
Fc r
π2EI l2
1
Fc r
例1:圆截面的细长压杆,材料、杆长和杆端约束保持不变,若将压杆的
直径缩小一半,则其临界力为原压杆的多少倍?若将压杆的横截面改变为面
积相同的正方形截面,则其临界力为原压杆的多少倍?
解:(1)
Fc r
π2EI
(l)2
π2E πd 4 64
第一讲 基本概念与欧拉公式
一:压杆稳定的概念
钢板尺:一端固 定 一端自由
Fcr :临界压力
二:细长压杆的临界压力
一、两端铰支细长压杆的临界压力
M (x) F w
EI w M (x) F w
材料力学压杆稳定第3节 欧拉公式及经验公式

2E 12
2
206109 1602
79.3 MPa
Fcr1 cr1A 79.3106 0.00785N 623 kN
(b)第二根压杆的临界载荷
2
l2
i
21 0.025
80
60 P 100
60 P 100 该杆为中柔度压杆,用直线公式求:
cr S
cr (a b)
cr
2E 2
根据欧拉公式与抛
物线经验公式,得
低合金结构钢等压
杆的 cr 总图。
S
P
2、抛物线型经验公式
在工程实际中,对于中、小柔度压杆的临界应力计 算,也有建议采用抛物线型经验公式的,此公式为
cr a1 b12
式中 a1 、b1 与是与材料
cr?令令aii?aleiaf22crcr?????22222crilelei???????令令il???临界应力形式的欧拉公式22cr???e?式中柔度是一个无量纲的量它综合反映了压杆的长度杆端的约束以及截面尺寸对临界应力的影响
一、临界应力与压杆柔度
压杆处于临界状态时,将压杆的临界载荷除以横
截面面积 A,得到横截面上的应力,称为压杆的临界
式中 为具体压杆的柔度,a﹑b为与材料的力学
性能有关的常数,单位为 MPa。表 7-2 中列出了几
种常用材料的 a、b 值。
表 7-2 几种常用材料的 a、b 的值
材料
(强度极限 b/ MPa ) (屈服点 S /MPa )
a
b
(MPa) (MPa)
P
S
Q235 钢( b 372 , S 235 ) 304 1.12 100
材料力学:第九章 压杆稳定问题
实际临界力
若杆端在不同方向的约束情况不同, I 应取挠 曲时横截面对其中性轴的惯性矩。即,此时要 综合分析杆在各个方向发生失稳时的临界压力, 得到直杆的实际临界力(最小值)。
求解临界压力的方法:
1. 假设直梁在外载荷作用下有一个初始的弯曲变形
2. 通过受力分析得到梁截面处的弯矩,并带入挠曲线 的微分方程
P
采用挠曲线近似微分方程得
B
到的d —P曲线。
Pcr A
B'
可见,采用挠曲线近
似微分方程得到的d —P曲
线在压杆微弯的平衡形态
d
下,呈现随遇平衡的假象。
大挠度理论、小挠度理论、实际压杆
欧拉公式
在两端绞支等截面细长中心受压直杆
的临界压力公式中
2EI
Pcr l 2
形心主惯矩I的选取准则为
若杆端在各个方向的约束情况相同(如球形
P
压杆稳定性的概念
当P较小时,P
Q
P
当P较大时,
P Q
稳定的平衡态
P
撤去横向力Q 稳定的
小
稳
P定
的
P P
临界压力
Pcr
不
稳
撤去横向力Q 不稳定的
定 的
P
大
不稳定的平衡态
压杆稳定性的概念
压杆稳定性的工程实例
细长中心受压直杆临界 力的欧拉公式
细长中心受压直杆临界力的欧拉公式
压杆的线(性)弹性稳定性问题
利用边界条件
得 w D,
xl
Dcos kl 0
若解1
D0
表明压杆未发生失稳
w(x) Asin kx B cos kx D
临界力和欧拉公式定理

第二节临界力和欧拉公式浏览字体设置:- 11pt+ 10pt12pt14pt16pt放入我的网络收藏夹第二节临界力和欧拉公式杆件所受压力逐渐增加到某个限度时,压杆将由稳定状态转化为不稳定状态。
这个压力的限度称为临界力P cr。
它是压杆保持直线稳定形状时所能承受的最小压力。
为了计算压杆的稳定性,就要确定临界力的大小。
通过实验和理论推导,压杆临界力与各个因素有关:(1) 压杆的材料,P cr与材料的弹性模量E成正比,即(2)压杆横截面的形状和尺寸,P cr与压杆横截面的轴惯性矩J成正比,即(3) 压杆的长度,P cr与长度的平方l2成反比,即(4) 压杆两端的支座形式有关,用一个系数表示,称为支座系数,列于表1-10。
表1-10 压杆长度系数杆端约束情况两端固定一端固定一端铰支两端铰支一端固定一端自由长度系数0.5 ≈0.7 1.0 2.0压杆的挠曲线形状为计算方便,写成细长中心受压直杆临界力的欧拉公式对于两端铰支的细长中心受压直杆,当其在临界力cr P,的作用下处于不稳定直线形式的平衡状态,若其材料仍处于理想的线弹性范围内,从力学的观点讲,这类稳定问题称为线弹性稳定问题。
这是压杆稳定问题中最简单的一种。
由临界力的定义可知,中心受压直杆只有在临界力的作用下才有可能在微弯形态下维持平衡(见图7-3)。
现假设压杆轴线在临界力cr P作用下呈图7-3(b)所示的曲线形态。
在图示的坐标系下,压力cr P取正值,位移忙V=f(x)以沿y轴正方向为正,弯矩的正负号规定同2.3节。
压杆任一x 截面上弯矩为将式(7-1a)代入挠曲线的近似微分方程(6-8h)中,并利用压杆支承处的边界条件就可求出压杆的挠曲线的表达式,并进一步导出压杆承受的临界力crP 。
这个临界力实际也就是使压杆维持微弯平衡的..........最小压力....。
将式(7-1a)代入公式(6-8h)可得其中I 为压杆横截面的最小形心主惯性矩。
令公式(7-1b)可改写为如下形式的二阶常系数线性微分方程其通解为式中A 、B 、k 三个待定常数可利用该挠曲线的三个边界条件来确定。
