苏教版高中数学选修(2-2)-1.5用定积分求面积的两个重要公式
高中数学第1章1.5定积分1.5.3微积分基本定理讲义(含解析)苏教版选修2_2

1.5.3 微积分基本定理[对应学生用书P28]已知函数f (x )=2x +1,F (x )=x 2+x . 问题1:f (x ) 和F (x )有何关系? 提示:F ′(x )=f (x ).问题2:利用定积分的几何意义求⎠⎛20(2x +1)d x 的值.提示:⎠⎛20(2x +1)d x =6.问题3:求F (2)-F (0)的值. 提示:F (2)-F (0)=4+2=6. 问题4:你得出什么结论?提示:⎠⎛20f (x )d x =F (2)-F (0),且F ′(x )=f (x ).问题5:已知f (x )=x 3,F (x )=14x 4,试探究⎠⎛10f (x )d x 与F (1)-F (0)的关系. 提示:因⎠⎛10f (x )d x =⎠⎛10x 3d x =14.F (1)-F (0)=14,有⎠⎛10f (x )=F (1)-F (0)且F ′(x )=f (x ).微积分基本定理对于被积函数f (x ),如果F ′(x )=f (x ),那么⎠⎛ba f (x )d x =F (b )-F (a ),即⎠⎛ba F ′(x )d x=F (b )-F (a ).1.微积分基本定理表明,计算定积分⎠⎛a bf (x )d x 的关键是找到满足F ′(x )=f (x )的函数F (x ).通常,我们可以运用基本初等函数的求导公式和导数的四则运算法则从反方向上求出F (x ).2.微积分基本定理揭示了导数与定积分之间的内在联系,最重要的是它也提供了计算定积分的一种有效方法.[对应学生用书P29]求简单函数的定积分[例1] (1)⎠⎛21(x 2+2x +3)d x ;(2)⎠⎛π0(sin x -cos x )d x ;(3)⎠⎛0-π(cos x -e x)d x . [思路点拨] 先求被积函数的原函数,然后利用微积分基本定理求解. [精解详析] (1)取F (x )=x 33+x 2+3x ,则F ′(x )=x 2+2x +3,从而⎠⎛12(x 2+2x +3)d x =⎠⎛12F ′(x )d x =F (2)-F (1)=253. (2)取F (x )=-cos x -sin x , 则F ′(x )=sin x -cos x ,从而⎠⎛0π(sin x -cos x )d x =⎠⎛0πF ′(x )d x =F (π)-F (0)=2.(3)取F (x )=sin x -e x ,则F ′(x )=cos x -e x,从而⎠⎛0-π(cos x -e x)d x =⎠⎛0-πF ′(x )d x =F (0)-F (-π)=1e π-1. [一点通] 求简单的定积分关键注意两点:(1)掌握基本函数的导数以及导数的运算法则,正确求解被积函数的原函数,当原函数不易求时,可将被积函数适当变形后再求解;(2)精确定位积分区间,分清积分下限与积分上限.1.(江西高考改编)若f (x )=x 2+2⎠⎛01f (x )d x ,则⎠⎛01f (x )d x =____________.解析:∵f (x )=x 2+2⎠⎛01f (x )d x ,∴⎠⎛01f (x )d x =⎝ ⎛⎭⎪⎫13x 3+2x ⎠⎛01f (x )d x 10=13+2⎠⎛01f (x )d x . ∴⎠⎛01f (x )d x =-13. 答案:=-132.⎠⎛0π(cos x +1)d x =________. 解析:∵(sin x +x )′=cos x +1,∴⎠⎛π0(cos x +1)d x =(sin x +x )|π0 =(sin π+π)-(sin 0+0)=π. 答案:π3.求下列定积分:(1)∫π20sin 2x 2d x ;(2)⎠⎛23(2-x 2)(3-x )d x .解:(1)sin 2x 2=12-cos x 2,而⎝ ⎛⎭⎪⎫12x -12sin x ′=12-12cos x ,所以∫π20sin 2x 2d x =∫π20⎝ ⎛⎭⎪⎫12-12cos x d x=⎝ ⎛⎭⎪⎫12x -12sin x |π20=π4-12=π-24. (2)原式=⎠⎛32(6-2x -3x 2+x 3)d x=⎝⎛⎭⎪⎫6x -x 2-x 3+14x 4|32=⎝ ⎛⎭⎪⎫6×3-32-33+14×34-⎝ ⎛⎭⎪⎫6×2-22-23+14×24 =-74.求分段函数的定积分 [例2] (1)设f (x )=⎩⎪⎨⎪⎧x 2,x ≤0,cos x -1,x >0.求⎠⎛1-1f (x )d x ; (2)求⎠⎛a-a x 2d x (a >0). [思路点拨] 按照函数f (x )的分段标准,求出每一段上的积分,然后求和. [精解详析] (1)⎠⎛1-1f (x )d x =⎠⎛0-1x 2d x +⎠⎛01(cos x -1)d x =13x 3|0-1+(sin x -x )|10=sin 1-23.(2)由x2=⎩⎪⎨⎪⎧x ,x ≥0,-x ,x <0,得⎠⎛a -a x 2d x =⎠⎛a 0x d x +⎠⎛0-a (-x )d x =12x 2|a0-12x 2|0-a =a 2.[一点通] (1)分段函数在区间[a ,b ]上的积分可分成几段积分的和的形式. (2)分段的标准是使每一段上的函数表达式确定,按照原函数分段的情况分即可,无需分得过细.4.⎠⎛3-4|x +2|d x =________. 解析:∵|x +2|=⎩⎪⎨⎪⎧x +2,(-2<x ≤3)-x -2,(-4≤x ≤-2)∴⎠⎛3-4|x +2|d x =⎠⎛3-2(x +2)d x +⎠⎛-4-2(-x -2)d x =⎝ ⎛⎭⎪⎫12x 2+2x |3-2+⎝ ⎛⎭⎪⎫-12x 2-2x |-2-4=292.答案:2925.设f (x )=⎩⎪⎨⎪⎧lg x , x >0,x +∫a 0 3t 2d t ,x ≤0,若f (f (1))=1,则a =________.解析:显然f (1)=lg 1=0, 故f (0)=0+∫a 0 3t 2d t =t 3|a0=1, 得a =1. 答案:1求图形的面积[例3] 求由曲线x 2x y x [思路点拨]在坐标系中作出图象→求曲线与直线的交点→利用定积分求面积.[精解详析] 画出草图,如图所示.解方程组⎩⎪⎨⎪⎧y =x +3,y =x 2-2x +3,得A (0,3),B (3,6).所以S =⎠⎛30(x +3)d x -⎠⎛30(x 2-2x +3)d x ,取F (x )=12x 2+3x ,则F ′(x )=x +3,取H (x )=13x 3-x 2+3x ,则H ′(x )=x 2-2x +3,从而S =F (3)-F (0)-[H (3)-H (0)]=⎝ ⎛⎭⎪⎫12×32+3×3-0-⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫13×33-32+3×3-0 =92. [一点通] 利用定积分求曲线所围成的平面图形的面积的步骤: (1)根据题意画出图形;(2)找出范围,定出积分上、下限; (3)确定被积函数;(4)写出相应的定积分表达式,即把曲边梯形面积表示成若干个定积分的和或差; (5)用微积分基本定理及其运算性质计算定积分,求出结果.6.曲线y = x ,直线y =x -2及y 轴所围成的图形的面积为________. 解析:所围成的图形如图阴影部分所示,点A (0,-2),由⎩⎨⎧y =x ,y =x -2,得⎩⎪⎨⎪⎧x =4,y =2,所以B (4,2),因此所围成的图形的面积为∫40()x -x +2d x =⎪⎪⎪⎝ ⎛⎭⎪⎫23x 32-12x 2+2x 40=163.答案:1637.设a >0,若曲线y =x 与直线x =a ,y =0所围成封闭图形的面积为a 2,则a =________. 解析:由已知得S =⎠⎛0ax d x =23x 32|a 0=23a 32=a 2,所以a 12=23,所以a =49. 答案:491.求定积分的一些常用技巧(1)对被积函数,要先化简,再求积分.(2)求被积函数是分段函数的定积分,应分段求定积分再求和. (3)对于含有绝对值符号的被积函数,要去掉绝对值符号后才能积分. 2.利用定积分求曲边梯形的面积(1)在利用定积分求平面图形的面积时,一般要先画出它的草图,再借助图形直观地确定出被积函数以及积分的上、下限.(2)要把定积分和用定积分计算平面图形的面积这两个概念区分开,定积分是一种积分和的极限,可为正,也可为负或零;而平面图形的面积在一般意义下总为正,因此当f (x )≤0时要通过绝对值处理为正,一般情况下是借助定积分求出两个曲边梯形的面积,然后相加起来.[对应课时跟踪训练(十一)]一、填空题1.⎠⎛1e1x d x =________.解析:⎠⎛1e1xd x =ln x |e1=ln e -ln 1=1. 答案:12.⎠⎛0π(2sin x -3e x+2)d x =________.解析:⎠⎛0π(2sin x -3e x +2)d x =(-2cos x -3e x +2x )|π0=7+2π-3e π.答案:7+2π-3e π3.(江西高考改编)若S 1=⎠⎛12x 2d x ,S 2=⎠⎛121xd x , S 3=⎠⎛12e x d x ,则S 1,S 2,S 3的大小关系为________.解析:S 1=13x 3⎪⎪⎪21=83-13=73,S 2=ln x ⎪⎪⎪21=ln 2<ln e =1,S 3=e x⎪⎪⎪21=e 2-e ≈2.72-2.7=4.59,所以S 2<S 1<S 3.答案:S 2<S 1<S 34.设f (x )=错误!则错误!f (x )d x =________.解析:⎠⎛02f (x )d x =⎠⎛01x 2d x +⎠⎛12(2-x )d x=13x 3|10+(2x -12x 2)|21=56.答案:565.(福建高考)如图,在边长为e(e 为自然对数的底数)的正方形中随机撒一粒黄豆,则它落到阴影部分的概率为________.解析:因为函数y =e x与函数y =ln x 互为反函数,其图象关于直线y =x 对称,又因为函数y =e x与直线y =e 的交点坐标为(1,e),所以阴影部分的面积为2(e ×1-⎠⎛01e x d x )=2e -2e x |10=2e -(2e -2)=2,由几何概型的概率计算公式, 得所求的概率P =S 阴影S 正方形=2e 2. 答案:2e 2二、解答题6.f (x )是一次函数,且∫ 10f (x )d x =5,∫ 10xf (x )d x =176,求f (x )的解析式.解:设f (x )=ax +b (a ≠0),则⎠⎛01(ax +b )d x =⎝ ⎛⎭⎪⎫12ax 2+bx |10=12a +b =5. ⎠⎛01x (ax +b )d x =⎠⎛01(ax 2+bx )d x =⎝ ⎛⎭⎪⎫13ax 3+12bx 2|10=13a +12b =176,所以由⎩⎪⎨⎪⎧12a +b =5,13a +12b =176,解得a =4,b =3,故f (x )=4x +3.7.求由曲线y =x 2与直线x +y =2围成的面积.解:如图,先求出抛物线与直线的交点,解方程组⎩⎪⎨⎪⎧y =x 2,x +y =2,得⎩⎪⎨⎪⎧x 1=1,y 1=1或⎩⎪⎨⎪⎧x 2=-2,y 2=4,即两个交点为(1,1),(-2,4).直线为y =2-x ,则所求面积S 为: S =⎠⎛1-2[(2-x )-x 2]d x =⎝⎛⎭⎪⎫2x -x 22-x 33|1-2=92.8.设f (x )是二次函数,其图象过点(0,1),且在点(-2,f (-2))处的切线方程为2x +y +3=0.(1)求f (x )的表达式;(2)求f (x )的图象与两坐标轴所围成图形的面积;(3)若直线x =-t (0<t <1)把f (x )的图象与两坐标轴所围成图形的面积二等分,求t 的值.解:(1)设f (x )=ax 2+bx +c , ∵其图象过点(0,1),∴c =1,又∵在点(-2,f (-2))处的切线方程为2x +y +3=0,∴⎩⎪⎨⎪⎧f (-2)=1,f ′(-2)=-2.∵f ′(x )=2ax +b ,∴⎩⎪⎨⎪⎧a ·(-2)2+b ·(-2)+1=1,2a ·(-2)+b =-2.∴a =1,b =2,故f (x )=x 2+2x +1.(2)依题意,f (x )的图象与两坐标轴所围成的图形如图中阴影部分所示,故所求面积S =∫0-1(x 2+2x +1)d x =⎪⎪⎪⎝ ⎛⎭⎪⎫13x 3+x 2+x 0-1=13. (3)依题意,有12S =∫0-t (x 2+2x +1)d x =⎪⎪⎪⎝ ⎛⎭⎪⎫13x 3+x 2+x 0-t =16,即13t3-t2+t=16,∴2t3-6t2+6t-1=0,∴2(t-1)3=-1,∴t=1-132.。
选修2-2 1.5定积分的概念-讲

n
n
n
y
N个小曲边梯形的面 积分别记作:
S1 , S2 , , Sn .
y x2
O
1 n
2 n
k n
n n
x
S Si
i 1
n
(2)用矩形来近似代替
i 1 i ' 在区间 , 上,用小矩形的面积 Si n n 2 i 1 i 1 ' 近似地代替Si 则有Si Si f ( )x x
矩形面积和与曲边梯形面积的关系.
观察下列演示过程,注意当分割加细时,
矩形面积和与曲边梯形面积的关系.
观察下列演示过程,注意当分割加细时,
矩形面积和与曲边梯形面积的关系.
观察下列演示过程,注意当分割加细时,
矩形面积和与曲边梯形面积的关系.
观察下列演示过程,注意当分割加细时,
矩形面积和与曲边梯形面积的关系.
a a
三:
定积分的基本性质
性质3.
定积分关于积分区间具有可加性
b
a
f ( x )dx f ( x )dx f ( x )dx
a c
c
b
y
yf ( x)
O
a
c1 c2 a c1
C
b x
b c2
b
a
f ( x )dx f ( x )dx f ( x )dx f ( x )dx
性质 3 不论a,b,c的相对位置如何都有
a f (x)dx a f (x)dx c
y
b
c
用定积分求面积的两个重要公式
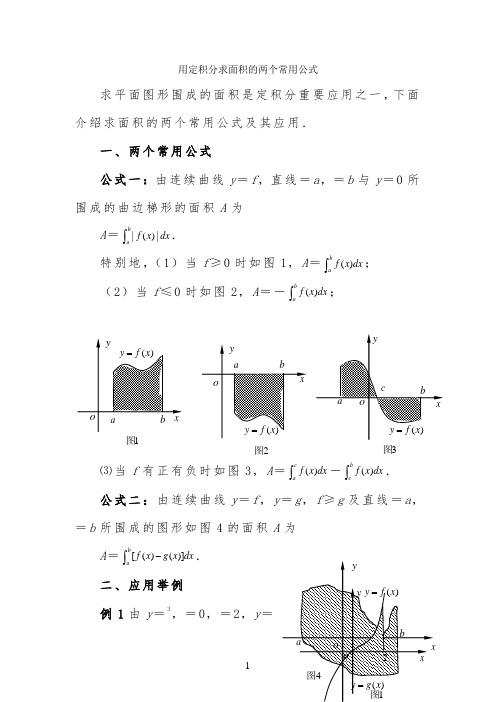
用定积分求面积的两个常用公式求平面图形围成的面积是定积分重要应用之一,下面介绍求面积的两个常用公式及其应用.一、两个常用公式公式一:由连续曲线y =f ,直线=a ,=b 与y =0所围成的曲边梯形的面积A 为A =|()|ba f x dx ⎰.特别地,(1)当f ≥0时如图1,A =()ba f x dx ⎰;(2)当f ≤0时如图2,A =-()baf x dx ⎰;⑶当f 有正有负时如图3,A =()caf x dx ⎰-()bcf x dx ⎰.公式二:由连续曲线y =f ,y =g ,f ≥g 及直线=a ,=b 所围成的图形如图4的面积A 为A =[()()]ba f x g x dx -⎰.二、应用举例例1由y =3,=0,=2,y =1图2图3图0围成的图形面积.分析:先画出图象,利用公式1转化为定积分问题即可解决.解:(1)如图1,由公式1,得S =230x dx ⎰=42440111|204444x =⨯-⨯=.评注:注意定积分与利用定积分计算曲线围成图形的面积区别.定积分是一种积分和的极限,可为正,也可为负或零,而平面图形的面积在一般意义上总为正.一般情况下,借助定积分分别求出每一部分曲边梯形的面积,然后将它们加在一起.例2(1)由曲线y =2,y 2=所围成图形的面积. (2)由y =142-1,y =12,y =34x 在第一象限所围成图形的面积.分析:先画图象找出范围,利用公式2,用积分表示,再求积分.解:(1)如图2,所求面积为阴影部分. 解方程组22y xy x⎧=⎪⎨=⎪⎩,得交点0,0,1,1,由公式2,得S =120)x dx ⎰=331202211()|33333x x -=-=.(2)如图3,解方程组211412y x y x ⎧=-⎪⎪⎨⎪=⎪⎩和211434y x y x ⎧=-⎪⎪⎨⎪=⎪⎩,得=0,=1+的舍去,=4.由公式2,得图形面积S=1031()42x dx -⎰+42111[(1)]42x x dx --⎰216-=.3图。
苏教版数学高二- 选修2-2素材 1.5解读定积分的概念

1.5解读定积分的概念教材上从求曲边梯形的面积和变速运动的路程出发引入了定积分的概念:如果函数()f x 在区间[],a b 上是连续的,用分点011i i n a x x x x x b -=<<<<<<=将区间[],a b 等分成n 个小区间,在每个小区间[]1,i i x x -上任取一点i ξ(1,2,,i n =),作和式()()11n n i i i i b a f x f nξξ==-∆=∑∑,当n →∞时,上述和式无限接近某个常数,这个常数叫做函数()f x 在区间[],a b 上的定积分,记作()ba f x dx ⎰,即()()1lim nb i a n i b a f x dx f nξ→∞=-=∑⎰. 对这个概念我们应从如下几个方面进行理解1.对区间[],a b 分割的绝对任意性:在定义中我们将区间[],a b 进行等分是为了计算上的方便,实际上对区间[],a b 的分割是任意的,这时只要这些区间中长度最大的区间的长度趋向于零即可.2.在每个小区间[]1,i i x x -上取点的绝对任意性:在教材上的两个例题是为了计算的方便将点取小区间[]1,i i x x -的端点,实际上我们可以在区间[]1,i i x x -上任意取点,如取中点等.3.当n →∞时,和式()()11n n ii i i b a f x f nξξ==-∆=∑∑无限接近某个常数的唯一确定性.它不依赖于对区间[],a b 的分割方法,也不依赖于在每个小区间[]1,i i x x -上取点的方式.即()ba f x dx ⎰是一个客观上存在的仅仅依赖于积分上下限和被积函数的唯一确定的常数.同时它也与积分变量无关,即()()b ba a f x dx f t dt =⎰⎰. 4.数学思想上的划时代意义.产生定积分概念的"以直代曲""以匀速代变速"和"无限逼近"的数学思想,使人类在认识数学世界的观念上有了重大突破,在数学的发展史上具有重大意义.我们要仔细理解体会这种思想,可以说这才是我们在高中阶段学习定积分的真正目的.例如在求曲边梯形的面积的课本例1中,我们把区间[]0,1等分成n 个小区间,在每个小区间上"以直代曲"就将曲边问题转化为直边问题,随着n 的增大这些小区间的宽度越来越小,这时在每个小区间上直边形的面积已经和曲边形的面积非常接近,我们就可以以这些小直边形的面积之和近似代替曲边形的面积,而当n →∞时这些小直边形就几乎变成了线段,这时小直边形的面积几乎就等于小曲边形的面积,这无穷个几乎变成了线段的直边形的面积之和就是所求的曲边形的面积了.我们常说"线动成面",对课本例1,我们也可以这样形象的理解:就将小直边形的宽度变成零,使其成为线段,这时小直边形和小曲边形的就完全重合了,而将这些线段从0到1运动就形成了()2f x x =,1x =, x 轴所围成的曲边形,将这些线段的"面积"积累起来就是所求的曲边形的面积.。
苏教版数学选修22讲义:第1章1.5.1+1.5.2定积分

1
图 1-5-1 2.求曲边梯形的面积的步骤 求曲边梯形面积的过程可以用流程图表示为: 分割→以直代曲→作和→逼近
由直线 x=1,y=0,x= 0 和曲线 y=x3 所围成的曲边梯形,将区间 4 等分, 则曲边梯形面积的近似值 (取每个区间的右端点 )是 ________.
1 11 13 【解析】 将区间 [0,1] 四等分,得到 4 个小区间: 0,4 , 4,2 , 2,4 , 3 4, 1 ,
间 [a,b]上的定积分.记为 S=_ bf(x) dx.
a
其中, f(x)称为被积函数, [a,b]称为积分区间, a 称为积分下限, b 称为积
分上限.
2(x+ 1)dx 的值与直线 x=1,x=2,y=0,f(x)=x+1 围成的梯形的面积有
1
2
以每个小区间右端点的函数值为高, 4 个小矩形的面积和为曲边梯形面积的
近似值
S=
1 4
3×14+
1 2
3×
1 4+
3 4
3×14+
13×
1 4=64.
【答案】
25 64
教材整理 2 定积分
阅读教材 P47“例 1”以上部分,完成下列问题.
一般地,设函数 f(x)在区间 [a,b]上有定义, 将区间 [ a,b] 等分成 n 个小区间,
每个小区间长度为
Δx
Δx=
b- n
a
,在每个小区间上取一点,依次为
x1 , x2,…,
xi,…, xn.作和 Sn= f(x1) Δx+ f(x2) Δx+…+ f(xi) Δx+…+ f(xn) Δx. 如果当 Δx→0(亦即 n→+∞ )时,Sn→S(常数 ),那么称常数 S 为函数 f(x)在区
苏教版数学高二-苏教版数学选修2-2 1.5.2 定积分

1.5.2 定积分课时目标 1.了解定积分的概念.2.了解定积分的几何意义和性质.3.会用定义求定积分.1.定积分的概念:一般地,设函数f (x )在区间[a ,b ]上有意义,将区间[a ,b ]等分成n个小区间,每个小区间长度为Δx (Δx =b -a n),在每个小区间上取一点,依次为x 1,x 2,…,x n ,作和.S n =f (x 1)Δx +f (x 2)Δx +…+f (x i )Δx +…+f (x n )Δx .如果当Δx →0(亦即n →+∞)时,S n →S (常数),那么称常数S 为函数f (x )在区间[a ,b ]上的定积分,记为:S =ʃb a f (x )d x ,其中,f (x )称为__________,[a ,b ]称为__________,a 称为____________,b 称为____________.2.定积分的几何意义:一般地,定积分()ba f x dx ⎰的几何意义是,在区间[a ,b ]上________与________所围图形面积的________.(即x 轴上方的面积减去x 轴下方的面积)一、填空题1.定积分ʃ213d x =________.2.由直线x =1,x =2和y =x +1围成的图形的面积为________.3.若20cos xdx π⎰=1,则由x =0,x =π,f (x )=sin x 及x 轴围成的图形的面积为________. 4.求由曲线y =e x ,直线x =2,y =1围成的曲边梯形的面积时,若选择x 为积分变量,则积分上限和积分下限分别为________.5.ʃ2-2(-4-x 2)d x =________. 6.ʃ4-416-x 2d x =________. 7.设变速直线运动物体的速度为v (t ),则在t 1到t 2这一时间段内,该物体经过的位移S =________.8.如图,阴影部分的面积分别以A 1,A 2,A 3表示,则定积分ʃb a f (x )d x =________.二、解答题9.用定义计算:ʃ21(x +1)d x .10.利用定积分的几何意义求下列定积分.(1)ʃ101-x 2d x ; (2)ʃ2π0cos x d x .能力提升11.用定积分的定义证明:ʃb a k d x =k (b -a ).12.利用定积分的几何意义求2222()sin cos f x dx x xdx ππ--+•⎰⎰, 其中f (x )=⎩⎪⎨⎪⎧2x -1 (x ≥0)3x -1 (x <0).1.利用定积分的定义求定积分,分四步:分割、以直代曲、作和、逼近.2.利用几何意义求定积分,关键是准确确定被积函数的图象,以及积分区间,正确利用相关的几何知识求面积,不规则的图形常用分割法求面积,注意分割点的准确确定.答 案知识梳理1.被积函数 积分区间 积分下限 积分上限2.曲线 x 轴 代数和作业设计1.3 2.523.2解析 根据定积分的几何意义和函数图象的对称性.4.2,0解析 解⎩⎪⎨⎪⎧ y =e x y =1,得⎩⎪⎨⎪⎧ x =0y =1. 解⎩⎪⎨⎪⎧ y =e x x =2,得⎩⎪⎨⎪⎧x =2y =e 2. ∴积分上限为2,积分下限为0.5.-2π解析 ʃ2-2(-4-x 2)d x 表示半圆x 2+y 2=4 (y ≤0)的面积的相反数. 6.8π7.21()t t v t dt ⎰ 8.A 1+A 3-A 2解析 利用定积分的几何意义,在区间[a ,b ]上,用x 轴上方f (x )所围面积减去x 轴下方f (x )所围面积.9.解 f (x )=x +1在区间[1,2]上连续,将区间[1,2]等分成n 个小区间,每个区间的长度为Δx =1n, 在[x i -1,x i ]=⎣⎢⎡⎦⎥⎤1+i -1n ,1+i n 上取ξi =x i -1=1+i -1n (i =1,2,…,n ), ∴f (ξi )=f (x i -1)=1+1+i -1n =2+i -1n, ∴∑n i=1f (ξi )·Δx =∑n i =1 ⎝ ⎛⎭⎪⎫2+i -1n ·1n=∑ni=1⎝ ⎛⎭⎪⎫2n +i -1n 2 =2n ·n +1n 2[0+1+2+…+(n -1)] =2+n -12n =2+12-12n =52-12n, ∴n →∞时,52-12n →52, ∴ʃ21(1+x )d x =52. 10.解 (1)由y =1-x 2得x 2+y 2=1(y ≥0),其图象是以原点为圆心,半径为1的圆的14部分. ∴ʃ101-x 2d x =14π·12=14π. (2)由函数y =cos x ,x ∈[0,2π]的图象的对称性(如图)知,ʃ2π0cos x d x =0.11.证明 令f (x )=k ,用分点a =x 0<x 1<…<x i -1<x i <…<x n =b .将区间[a ,b ]等分成n 个小区间[xi -1,x i ] (i =1,2,…,n ),在每个小区间上任取一点ξi (i =1,2,…,n ),作和式∑n i=1f (ξi )Δx =∑ni=1k ·b -a n =k (b -a ), ∴当n →∞时,ʃb a k d x =k (b -a ).12.解 ʃ2-2f (x )d x +22sin cos x xdx ππ-⎰=ʃ0-2(3x -1)d x +ʃ20(2x -1)d x +22sin cos x xdx ππ-⎰, ∵y =sin x cos x 为奇函数,∴22sin cos x xdx ππ-⎰=0. 利用定积分的几何意义,如图,∴ʃ0-2(3x -1)d x =-7+12×2=-8. ʃ20(2x -1)d x =3+12×1=2. ∴ʃ2-2f (x )d x +22sin cos x xdx ππ-⎰ =2-8+0=-6.。
(好题)高中数学高中数学选修2-2第四章《定积分》测试题(答案解析)

一、选择题1.4片叶子由曲线2||y x =与曲线2||y x =围成,则每片叶子的面积为() A .16B .36C .13D .232.如图,由曲线21y x =-直线0,2x x ==和x 轴围成的封闭图形的面积是( )A .1B .23C .43D .23.若曲线ln y kx x =+在点()1,k 处的切线平行于x 轴,则k =( ) A .2- B .1- C .0 D .14.已知二次函数()y f x =的图象如图所示,则它与x 轴所围图形的面积为:A .2π5B .32C .43D .π25.如图,矩形ABCD 的四个顶点()(0,1),(,1),(,1),0,1A B C D ππ--,正弦曲线f xsinx 和余弦曲线()g x cosx =在矩形ABCD 内交于点F ,向矩形ABCD 区域内随机投掷一点,则该点落在阴影区域内的概率是( )A .B .C .D .6.设若20lg ,0()3,0ax x f x x t dt x >⎧⎪=⎨+≤⎪⎩⎰,((1))1f f =,则a 的值是( ) A .-1 B .2 C .1 D .-27.定积分220[4(2)]x x dx ---⎰的值为( )A .24π- B .2π- C .22π- D .48π-8.曲线22,y x y x ==所围成图形的面积是( ) A .1B .13C .12D .239.已知幂函数a y x =图像的一部分如下图,且过点(2,4)P ,则图中阴影部分的面积等于( )A .163B .83C .43D .2310.曲线()sin 0πy x x =≤≤与直线12y =围成的封闭图形的面积是 A .3B .23-C .π23-D .π33-11.等比数列{}n a 中,39a =前三项和为32303S x dx =⎰,则公比的值是( )A .1B .12-C .1或12- D .-1或12-12.曲线2y x 与直线y x =所围成的封闭图形的面积为( )A .16 B .13C .12D .56二、填空题13.如图所示,直线y kx =分抛物线2y x x 与x 轴所围图形为面积相等的两部分,则k的值为__________.14.若2211S x dx =⎰,2211S dx x=⎰,231x S e dx =⎰,则1S ,2S ,3S 的大小关系为___.15.直线x =0、直线y =e +1与曲线y =e x +1围成的图形的面积为_____. 16.由曲线2y x=,直线y =2x ,x =2所围成的封闭的图形面积为______. 17.()12012x x dx -+=⎰__________.18.由直线2y x =+与曲线2y x 围成的封闭图形的面积是__________.19.曲线()sin 0πy x x =≤≤与x 轴围成的封闭区域的面积为__________. 20.曲线2y x =与直线230x y --=所围成的平面图形的面积为________.三、解答题21.求曲线y x =,2y x =-,13y x =-所围成图形的面积.22.已知函数()221y f x x x ==-++和()1y g x x ==-,求:由()y f x =和()y g x =围成区域的面积.23.现有一个以OA 、OB 为半径的扇形池塘,在OA 、OB 上分别取点C 、D ,作DE OA 、CF OB 分别交弧AB 于点E 、F ,且BD AC =,现用渔网沿着DE 、EO 、OF 、FC 将池塘分成如图所示的养殖区域.已知1km OA =,2AOB π∠=,EOF θ∠=(02πθ<<).(1)若区域Ⅱ的总面积为21km 4,求θ的值; (2)若养殖区域Ⅰ、Ⅱ、Ⅲ的每平方千米的年收入分别是30万元、40万元、20万元,试问:当θ为多少时,年总收入最大?24.如图:已知2y ax bx =+通过点(1,2),与22y x x =-+有一个交点横坐标为1x ,且0,1a a <≠-.(1)求2y ax bx =+与22y x x =-+所围的面积S 与a 的函数关系; (2)当,a b 为何值时,S 取得最小值.25.求曲线6y x =-和8y x =y =0围成图形的面积. 26.已知()ln f x x x mx =+,2()3g x x ax =-+-(1)若函数()f x 在(1,)+∞上为单调函数,求实数m 的取值范围;(2)若当0m =时,对任意(0,),2()()x f x g x ∈+∞≥恒成立,求实数a 的取值范围.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】先计算图像交点,再利用定积分计算面积. 【详解】如图所示:由2y x y x ⎧=⎪⎨=⎪⎩0,0,x y =⎧⎨=⎩11x y =⎧⎨=⎩, 根据图形的对称性,可得每片叶子的面积为)13023210211d 333x x x x x ⎛⎫⎰=-= ⎪⎝⎭.故答案选C 【点睛】本题考查定积分的应用,考查运算求解能力2.D解析:D 【解析】由曲线21y x =-直线0,2x x ==和x 轴围成的封闭图形的面积是122201(1)(1)S x dx x dx =---⎰⎰31320111281()|()|2133333x x x x -+-=+--+ 3.B解析:B【解析】因为1y k x'=+,所以10,1k k +==- ,选B. 点睛:(1)求曲线的切线要注意“过点P 的切线”与“在点P 处的切线”的差异,过点P 的切线中,点P 不一定是切点,点P 也不一定在已知曲线上,而在点P 处的切线,必以点P 为切点.(2)利用导数的几何意义解题,主要是利用导数、切点坐标、切线斜率之间的关系来进行转化.以平行、垂直直线斜率间的关系为载体求参数的值,则要求掌握平行、垂直与斜率之间的关系,进而和导数联系起来求解.4.C解析:C 【解析】试题分析:由图像可知函数解析式为()21f x x =-+∴由定积分的几何意义可知面积()12311111141|113333Sx dx x x --⎛⎫⎛⎫⎛⎫=-+=-+=---=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎰ 考点:定积分及其几何意义5.B解析:B 【解析】试题分析:阴影部分的面积()044sin cos (cos sin )|12S x x dx x x ππππ=-=--=+⎰ 由几何概型可知:向矩形ABCD 区域内随机投掷一点,则该点落在阴影区域内的概率是01+2=ABCDS P S =矩形 ,故选B . 考点:几何概型.6.C解析:C 【详解】233003|aat dt t a ==⎰,33(1)lg10,(0),1, 1.f f a a a ===∴==故选:C7.B解析:B 【解析】试题分析:由定积分的几何意义有2204(2)x dx --⎰表示的是以(2,0)为圆心,半径为2的圆的14部分,而20xdx ⎰表示的是直线y x =,0,2,x x x ==轴所围成的面积,故220[4(2)]x x dx ---⎰表示的图形如下图的阴影部分,面积为221122242ππ⨯-⨯=-.故选B.考点:1.定积分的几何意义;2.方程的化简.8.B解析:B 【分析】由题意,可作出两个函数y x =与2yx 的图象,先求出两函数图象交点A 的坐标,根据图象确定出被积函数2 x x -与积分区间[0,1],计算出定积分的值即可. 【详解】 作出如图的图象联立22 y x y x ⎧=⎨=⎩解得0 0x y =⎧⎨=⎩或1 1x y =⎧⎨=⎩,即点()11A ,, 所求面积为)132312002121133333S x x dx x x ⎛⎫==-=-= ⎪⎝⎭⎰,故选B. 【点睛】本题考点是定积分在求面积中的应用,考查了作图的能力及利用积分求面积,解题的关键是确定出被积函数与积分区间,熟练掌握积分的运算.9.B解析:B 【解析】试题分析:由题意得,因为幂函数a y x =图像过点(2,4)P ,所以42α=,解得2α=,所以幂函数2yx ,则阴影部分的面积为22320018|33S x dx x ===⎰,故选B.考点:幂函数的解析式;定积分的应用.10.D解析:D 【解析】曲线()sin 0πy x x =≤≤与直线12y =的两个交点坐标分别为(π6,12),(5π6,12),则封闭图形的面积为5π5π66ππ6611πsin cos |223x dx x x ⎛⎫⎛⎫-=--= ⎪ ⎪⎝⎭⎝⎭⎰本题选择D 选项.点睛:(1)用微积分基本定理求定积分,关键是求出被积函数的原函数.此外,如果被积函数是绝对值函数或分段函数,那么可以利用定积分对积分区间的可加性,将积分区间分解,代入相应的解析式,分别求出积分值相加. (2)根据定积分的几何意义可利用面积求定积分. (3)若y =f (x )为奇函数,则()()0aaf x dx a ->⎰ =0.11.C解析:C 【解析】由题意得3330|27S x ==. ①当q ≠1时,则有313231(1)2719a q S q a a q ⎧-==⎪-⎨⎪==⎩,解得12q =-或1q =(舍去).②当q =1时,a 3=a 2=a 1=9,故S 3=27,符合题意. 综上12q =-或1q =.选C . 点睛:在运用等比数列的前n 项和公式时,必须注意对1q =与1q ≠分类讨论,防止因忽略1q = 这一特殊情况而导致解题失误.12.A解析:A 【解析】曲线2y x =与直线y x =的交点坐标为()()0,0,1,1 ,由定积分的几何意义可得曲线2y x =与直线y x =所围成的封闭图形的面积为()122310111|236x x dx x x ⎛⎫-=-= ⎪⎝⎭⎰ ,故选A. 二、填空题13.【分析】根据题意求出直线与抛物线的交点横坐标再根据定积分求两部分的面积列出等式求解即可【详解】联立或由图易得由题设得即即化简得解得故答案为:【点睛】本题主要考查了定积分的运用需要根据题意求到交界处的解析:3412-【分析】根据题意求出直线与抛物线的交点横坐标,再根据定积分求两部分的面积,列出等式求解即可. 【详解】联立2y x x y kx⎧=-⇒⎨=⎩ 0x =或1x k =-.由图易得1,11x k k由题设得()()1122012kx x kx dx x x dx ---=-⎰⎰, 即232123100111111||232223k x x kx x x -⎛⎫⎛⎫--=- ⎪ ⎪⎝⎭⎝⎭. 即()()()232111111123212k k k k -----= 化简得()3112k -=. 解得3412k =-. 故答案为:341【点睛】本题主要考查了定积分的运用,需要根据题意求到交界处的点横坐标,再根据定积分的几何意义列式求解即可.属于中档题.14.【分析】先利用积分基本定理计算三个定积分再比较它们的大小即可【详解】故答案为:【点睛】本小题主要考查定积分的计算不等式的大小比较等基础知识考查运算求解能力属于中档题 解析:213S S S <<【分析】先利用积分基本定理计算三个定积分,再比较它们的大小即可. 【详解】22321111733S x dx x ===⎰2221112S dx lnx ln x===⎰222311|x x S e dx e e e ===-⎰ 2723ln e e <<- 213S S S ∴<<故答案为:213S S S << 【点睛】本小题主要考查定积分的计算、不等式的大小比较等基础知识,考查运算求解能力,属于中档题.15.1【分析】如图所示:计算交点为计算积分得到面积【详解】依题意令e+1=ex+1得x =1所以直线x =0y =e+1与曲线y =ex+1围成的区域的面积为S 故答案为:1【点睛】本题考查了利用积分求面积意在考解析:1 【分析】如图所示:计算交点为()1,1e +计算积分()()111xe e dx ⎡⎤+-+⎣⎦⎰得到面积.【详解】依题意,令e +1=e x +1,得x =1,所以直线x =0,y =e +1与曲线y =e x +1围成的区域的面积为S ()()()1111110xx x e e dx e e dx ex e ⎡⎤=⎰+-+=⎰-=-=⎣⎦ 故答案为:1【点睛】本题考查了利用积分求面积,意在考查学生的计算能力.16.3-2ln2【分析】求出曲线直线y=2x 的交点坐标根据定积分的几何意义列式即可求解【详解】依题意联立方程组解得所以封闭的图形面积为=(x2-2lnx )=3-2ln2故答案为:3-2n2【点睛】本题考解析:3-2ln2【分析】求出曲线2 yx=,直线y=2x的交点坐标,根据定积分的几何意义列式,即可求解.【详解】依题意,联立方程组22yxy x⎧=⎪⎨⎪=⎩,解得12xy=⎧⎨=⎩,所以封闭的图形面积为212(2)x dxx-⎰=(x2-2lnx)21=3-2ln2.故答案为:3-2n2.【点睛】本题考查了定积分的几何意义,定积分的求法,其中解答中确定定积分式,准确运算是解答的关键,着重考查数形结合思想,以及计算能力,属于基础题.17.【解析】【分析】根据定积分的运算将函数分为两个部分分别用定积分的几何意义和微积分基本定理两个内容求解再合并起来即可【详解】由定积分的几何意义可知表示的为单位圆在第一象限内的面积即由微积分基本定理可知解析:14π+【解析】【分析】根据定积分的运算,将函数分为两个部分,分别用定积分的几何意义和微积分基本定理两个内容求解,再合并起来即可。
高二数学选修22~154定积分的应用

M(0,-3)和N(3,0)处的两条切线所围成
的图形的面积。
y
略解: y / 2x 4
则在M、N点、 处的切线方程
分别为
y 4x 3 y 2x 6 o
x
则所求图形的面积为
y=-x2+4x-3
3
S= 2[(4x 3) ( x2 4x 3)]dx 0
3
3 [(2 x
2
6)
(
x
如果 F ( x) 是连续函数 f (x) 在区间[a, b]上的一个原函
b
数,则 a f ( x)dx F (b) F (a) .
即
b a
f
( x)dx
F(x)
b a
F(b)
F (a)
F ( x)ba
2020/6/12
6
微积分基本定理表明:
一个连续函数 f(x)在区间[a, b]上的定积分等于它 的任意一个原函数 F(x)在区间[a, b]上的增量.
一吐为快篇(小结)
本节课主要学习了哪些内容?
注意点:
请想一想?
课题:定积分的应用
我行 我能 我要成功 我能成功
恩格斯说:“在一切理论中,未必再有什 么像17世纪下半叶微积分的发现那样被看作人 类精神的最高胜利了。如果在某个地方我们看 到人类精神的纯粹和唯一的功绩,那就正是在 这里。”
导数非常明显的特征就是和实际问题联系
以及x 轴所围成的曲边梯形的面积:S=ab f ( x)dx
(2)曲线 y f (x)(其中f (x) 0)与直线 x a, x b(a b)
以及x 轴所围成的曲边梯形的面积:S=
y
ya
-
b
f
a
b
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用定积分求面积的两个常用公式
求平面图形围成的面积是定积分重要应用之一,下面介绍求面积的两个常用公式及其应用.
一、两个常用公式
公式一:由连续曲线y =f (x ),直线x =a ,x =b 与y =0所围成的曲边梯形的面积A 为
A =
|()|b
a
f x dx ⎰
.
特别地,(1)当f (x )≥0时(如图1),A =()b
a
f x dx ⎰
;
(2)当f (x )≤0时(如图2),A =-
()b
a
f x dx ⎰
;
(3)当f (x )有正有负时(如图3),A =
()c
a
f x dx ⎰
-
()b
c
f x dx ⎰
.
公式二:由连续曲线y =f (x ),y =g (x ),f (x )≥g (x )及直线x =a ,x =b 所围成的图形(如图4)的面积A 为
A =
[()()]b
a
f x
g x dx -⎰.
二、应用举例
例1 由y =x 3
,x =0,x =2,y =0围成的图形面积.
分析:先画出图象,利用公式1转化为定积分问题即可解决.
解:(1)如图1,由公式1,得
1
图2
图
S =
2
30
x dx ⎰
=
4244
0111|204444
x =⨯-⨯=. 评注:注意定积分与利用定积分计算曲线围成图形的面积区别.定积分是一种积分和的极限,可为正,也可为负或零,而平面图形的面积在一般意义上总为正.一般情况下,借助定积分分别求出每一部分曲边梯形的面积,然后将它们加在一起.
例2 (1)由曲线y =x 2,y 2
=x 所围成图形的面积. (2)由y =14x 2-1,y =12x ,y =3
4
x 在第一象限所围成图形的面积.
分析:先画图象找出范围,利用公式2,用积分表示,再求积分. 解:(1) 如图2,所求面积为阴影部分.
解方程组22
y x
y x
⎧=⎪⎨=⎪⎩,得交点(0,0),(1,1),由公式2,得 S
=1
2
0)x dx ⎰=3312
02211()|33333
x x -=-=.
(2)如图3,解方程组2114
12y x y x ⎧
=-⎪⎪⎨⎪=⎪⎩和
2114
34
y x y x ⎧
=-⎪⎪⎨
⎪=⎪⎩, 得x =0,x =1
+负的舍去),x =4. 由公式2,得图形面积 S
=10
31
()42
x dx -⎰
+4
2111
[(1)]42
x x dx --
⎰
216-=.
3
图。
