第二章 固体的能量状态

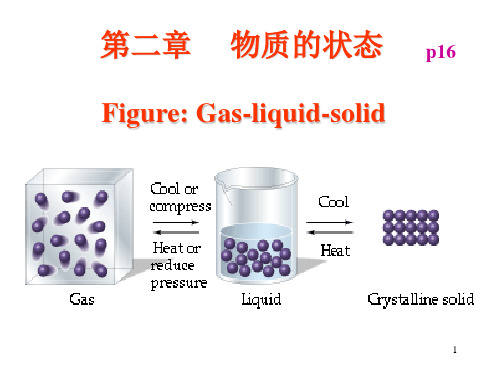
第二章 固体的能量状态
辐射场与原子体系的总哈密顿量
0S R I I H H H H H H =++≡+
零级近似
()00S R H H H E Θ≡+Θ=Θ
体系总的状态 ()
(),n κΘ=
ΞψR r
辐射场的本征状态 用{}n κ标记。

（模标记:,k κκπ）
()()R R H n E n κκΞ=Ξ
(){
}12...,,.........n n n n n n κκκκκκΞ===
()...,,...R E n n κκκ
κ
ω=∑
固体的本征状态
()()
,,S S H E =ψψR r R r
固体是由大量带负电的电子和带正电的核构成的多粒子体系。

这些带电粒子间存在库仑相互作用。

如果忽略磁的，以及其它相对较弱的相互作用，体系（固体）的总能量，或哈密顿量，包括： 所有电子的动能
2
2
ˆ2e
i i
e
T m =-∇
∑，
所有核的动能 2
2ˆ2L
I I
I
T M =-∇∑，
电子间的库仑相互作用
()2
1
4ee i j
j i
e V r r πε<=
-∑
r ，
核之间的库仑相互作用
()
2
14I J LL I J
I
J
Z Z e V R
R πε<=
-∑R ，
以及电子与核间的库仑相互作用
()
2
,0
1,4I eL i I
I
i
Z e V R
r πε=-
-∑R r 。

上面的表示式中i r 为电子位置，下标i 或j 标记不同的电子，e m 为电子质量，I R 为核坐标，下标I 或J 标记不同的核，M 为核的质量，Z 为核电荷数。

原子体系（固体）总的哈密顿量为：
()
()()
2
2
2222
,002
0ˆˆˆˆˆ,ˆˆ,2211
4414S e L e L ee eL LL
e L e
LL
i
I
i
I
e I
I i j i I
j i I i I J I J I J
H T T V T T V V V T T V V m M e Z e r r R r Z Z e R R πεπεπε<<=++≡++++≡+++=-∇-∇
⎛⎫
⎪+- ⎪
--⎝
⎭
+-∑
∑
∑∑
∑R r R r R
描述体系状态的波函数是原子体系中所有粒子的位置
的函数，我们用()
,ψR r 来表示，其中简略地用R 和r 分别代表体系中所有核和电子的位置。

体系的定态波函数满足定态薛定谔方程，或哈密顿方程：
()()
ˆ,,S S
H E =ψψR r R r （2.1-2）
其中本征值S E 为相应本征态或定态的能量。

一个由存在相互作用的微观粒子组成的系统，体系中每个粒子的运动都与其它粒子的运动密切相关，无法确切地给出每个粒子的状态，只能确定整个体系的状态。

体系状态的描述非常复杂。

10量级，显然，对这样考虑到构成固体的粒子数多达23
的多粒子体系，上面的方程是无法严格求解的。

必须作近似，使问题简化
为便于对固体能量状态的描述和讨论，人们引进了一些有效的近似。

一个经常采用的近似：
上述问题中，很多电子是牢固地束缚在某个核的周围，它们与核一起组成所谓的原子实：
原子核 + 相应原子的内层电子（构成满壳层）
在光跃迁过程中，原子实内部运动状态很少受影响，因而这些结合紧密的粒子集合—原子实，在所考虑的问题中可以近似地看成是一个粒子，于是整个固体就变成由大量的原子实和外层（价）电子组成，体系的粒子数大大减少。

问题没有实质性的改变。