数学建模作业2汽车的刹车距离模型及黄灯持续时间分析模型
汽车刹车距离---数学建模

汽车刹车距离---数学建模桓台一中2010级31班曲庆渝辅导老师:崔禹摘要:由于本县近段时间某些司机因判断刹车距离失误而酿成交通悲剧,为使这一现象得到缓解,使交通出行更加安全,本文就通常所说的“2秒准则”展开讨论,建立数学模型,通过理论来估计实际问题。
(由于“2秒法则”最初由北美流行而来,故以下部分数据采用美制即英制单位)关键词:2秒准则;刹车距离;反应距离;制动距离一、问题提出:背景:汽车驾驶员培训过程中的“2秒准则”是否有道理——给出合理性解释:正常驾驶条件下:车速(在原车速基础上)每增加16千米/小时,则后车与前车之间的距离就应增加一个车身长度:车身作用:后车刹车的距离与后车的车速有关,车速快,车子动能大,增加与前车的距离可以保证后车刹车的安全,不致于同前车相撞(尾追)。
具体操作办法:——“2秒准则”增加一个车长的简便办法即“2秒准则”——即,当前车经过某一标志时,后车司机开始计算2秒钟后也到达同一标志,不管车速如何,即可保证后车刹车时不致于撞上前车,即不至于发生“尾追”现象。
(此“2秒准则”不管车速如何都可这样操作)2.问题:“2秒准则”的合理性的质疑:(1)“2秒准则”是否合理性假如汽车速度16千米/小时,计算2秒钟所行走的距离16千米/时≈4.44米/秒,故“2秒”走过的路程为:S=4.44米/秒*2秒=8.88米而车身的平均长度为: 4.6米显然:2秒准则走过路程8.88米>4.6米≈2个车身长度。
所以“2秒准则”的合理性受到质疑, 为此要寻求更合理的刹车距离方案: (2)设计出合理的刹车距离方案二、建模机理分析与符号说明刹车机理分析:分析:刹车距离“d ”与时间“t ”的关系:刹车距离 = 反应距离 + 制动距离符号说明:反应距离1d = 司机决定刹车起到制动器开始起作用,这段时间汽车的行驶的距离 制动距离2d = 以制动器开始起作用到汽车完全停止时刻,这段时间内汽车所行驶的距离。
刹车距离 数学建模

刹车距离数学建模刹车距离是指车辆从发现需要停车的信号或情况到完全停下来所需的距离。
在驾驶中,我们常常需要根据道路情况和车速合理判断刹车距离,以确保安全停车。
本文将从数学建模的角度出发,探讨影响刹车距离的因素,并介绍一种常用的数学模型来计算刹车距离。
刹车距离受到车速的影响,一般来说,车速越高,刹车距离就会越长。
这是因为车辆在高速行驶时具有更大的动能,需要更长的距离来消耗这部分能量,才能停下来。
因此,在高速行驶时,我们需要提前做好刹车准备,以避免刹车距离过长导致事故发生。
刹车距离还受到刹车系统的性能和状态的影响。
刹车系统包括刹车片、刹车盘、刹车液等部件,它们的磨损程度和工作状态会直接影响刹车的效果。
如果刹车片磨损严重或刹车盘存在问题,会导致刹车距离增加。
因此,定期检查和维护刹车系统是确保刹车距离符合要求的重要措施之一。
刹车距离还与路面情况和天气条件有关。
在湿滑或结冰的路面上刹车,由于附着力减小,刹车距离会明显增加。
此时,驾驶员需要根据实际情况调整刹车力度,以减少刹车距离。
针对刹车距离的计算,数学建模提供了一种有效的方法。
常用的刹车距离计算模型是基于物理学中的运动学原理建立的。
根据运动学原理,刹车距离与车速的平方成正比,与刹车加速度的倒数成正比。
具体来说,刹车距离可以表示为刹车时间乘以车速的一半,即:刹车距离 = 时间× 速度 / 2。
在实际应用中,为了更加准确地计算刹车距离,需要考虑到刹车系统的响应时间。
刹车系统的响应时间是指从踩下刹车踏板到刹车系统开始工作的时间间隔。
在这段时间内,车辆仍然以原有的速度行驶,因此需要额外的距离来消耗动能。
因此,最终的刹车距离计算公式应为:刹车距离 = 响应时间× 速度 + 时间× 速度 / 2。
需要注意的是,刹车距离的计算模型只是一个理论模型,实际情况可能会受到多种因素的影响。
在实际驾驶中,驾驶员应根据实际情况综合考虑车辆性能、道路条件和天气因素,合理判断刹车距离,并采取相应的措施确保安全驾驶。
交通灯控制系统中黄灯时间的确定

( 重庆工学院 ,重庆 400050)
Ξ
摘要 : 介绍了电灯的由来 ,探讨了黄灯时间的长短对交通安全正负两方面的影 , 在应用力学和运 动学原理的基础上 ,提出了一种计算黄灯时间的模型 . 分析了模型建立的全部过程 , 最后列出了 黄灯时间的求解公式 . 关 键 词 :黄灯时间 ; 交通控制系统 ; 运动学 中图分类号 :U121 文献标识码 :A 文章编号 :1671 - 0924 (2008) 04 - 0154 - 03
离为 x .
2) 十字路口处同一条路上 2 条停车线之间的
距离为 H.
3) 典型的车辆车身长为 L , 车辆总质量 ( 包括
车身和载重) 为 W .
4) 在刹车时 , 车辆与地面的摩擦系数为 f . 5) 每次黄灯亮的时间为 T. 3. 2 模型假设
通过前面的分析和对问题所涉及的主要量的 确定 , 给出黄灯时间求解模型假设 [ 1 ] :
[3 ] 郑积仕 ,汤志康 . 一种基于模糊神经网络的城市道路
有 代入式 ( 4) , 得 :
t 1 = v0 / ( f g ) v0 x ( t1) = D a = 2f g
交叉口可变相序控制 [J ] . 重庆工学院学报 ,2006 ,20
(5) :143 - 147.
( 9)
将式 ( 2) 和式 ( 9) 代入式 ( 1) , 得黄灯亮的时间
- fW = W d2 x ・ 2 g dt = v0 ( 4)
4 结束语
美国公路安全保险公司的发言人理克德・ 雷 廷表示 ,部分司机在钻黄灯和红灯之间的空子 , 因 此确立黄灯亮的时间实际上是在维护红灯的尊 严 . 同时他又认为 ,增加亮黄灯的时间虽然有一些 好处 ,但他的研究小组发现 , 缩短黄灯时间对习惯 闯红灯的人其实是一个威慑 . 其实 , 保证交通安全 的关键还是所有驾驶员都按正规的操作规范和交 通信号指示来驾驶车辆 [2 - 3 ] .
数学建模-黄灯亮多久
t2
所以只有 是需要进一步求得的。
t1
v0
解题过程
第三步 : 下面先计算刹车距离. 设车辆的重量为 W ,车 辆刹车时,水平方向只受到摩擦力fW 作用,其方向 与运动方向相反。设刹车后,汽车走过的位移x (t ), 根据牛顿第二定律有如下的微分方程:
W d x 2 , fW g dt dx v0 , dt t0 x (0) 0.
0
进一步的问题
即使给了充分的停车时间,仍有许多驾驶员企 图加速想抢在红灯亮之前冲过交叉路口。但驾驶员 们并不知道什么时候红绿灯转为红灯。有一种“倒 数”型的红绿灯可以部分地解决这个问题,在黄灯 亮的最后几秒钟内,黄灯上显示出一窜倒着数的数 字,它们准确地警告驾驶员红绿灯何时将变为红色。 这种系统在我国的部分城市正使用着,它成功地降 低了事故发生率。
40 30
20
10
v (m/s) 0
5 10 15 20 25 30
数学实验
当 v 0 30 、45、60、75(km/h ),也即约8.3, T 12.5, 16.7,20.8(m/s )时, 的值如下表所 示:
v0 (km/h)
T (s)
经验法(s) 2
30
4.92.03
3
4 5
数学实验
表中的“经验法”是按如下“经验”得到:对法 定的迫近速度的每个15 km/h亮黄灯1秒。我们注意 到,经验法的结果一律比我们预测的黄灯状态短些。 这使人想起,许多交叉路口的设计很可能使车辆在 绿灯转为红灯时正处在交叉路口上。
顺便地,我们还可以求得使 T 取最小值时的法 定速度 v 7.67(m/s)=27.6(km/h),此时T *= 4.91s。
数学建模-黄灯亮多久
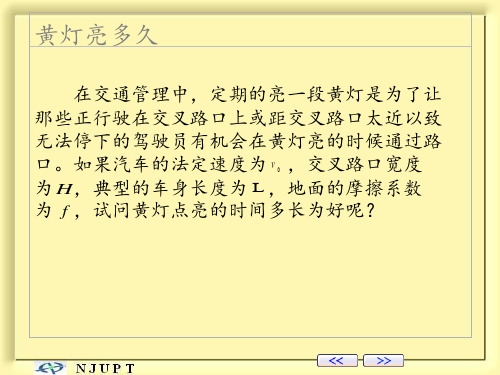
在 x(0) 0的条件下,对(2)式再积分得到
x(t)12fg2tv0t
(3)
从而刹车距离
x(t ') D v02 .
(4)
2 fg
解题过程
第五步 : 由(4)式得
所以
t1
D v0
v0 2 fg
,
T2vf0gLv0Ht0 .
对 T关于 v 0 求导数,令 T 0 0 得到驻 点 v0 2fg(LH) ,所以当 v0 2fg(LH)时, T有 极小值
顺便地,我们还可以求得使 T取最小值时的法 定速度v0 7.67(m/s)=27.6(km/h),此时T *= 4.91s。
进一步的问题
即使给了充分的停车时间,仍有许多驾驶员企 图加速想抢在红灯亮之前冲过交叉路口。但驾驶员 们并不知道什么时候红绿灯转为红灯。有一种“倒 数”型的红绿灯可以部分地解决这个问题,在黄灯 亮的最后几秒钟内,黄灯上显示出一窜倒着数的数 字,它们准确地警告驾驶员红绿灯何时将变为红色。 这种系统在我国的部分城市正使用着,它成功地降 低了事故发生率。
fW
W g
d d
2x t2
,
dx dt
t 0
v0,
x(0) 0.
(1)
解题过程
其中 g为重力加速度,负号是因为速度与摩擦力方
向相反,从而
dv d2x dt dt2 0
.
解题过程
第四步 : 对(1)式积分得
由于车停下后速v度为ddxt零,f所gt以v0在(2)式中(令2)v 0 得到汽车自刹车至停下所用的时间 t ' v 0 。
设驾驶员作出决定的反应时间为 t 0 ,通过刹车 距离的时间为 t1 ,通过路口和一个车身距离的时间 为 t 2 ,黄灯点亮的时间为 T 。
数学建模作业2汽车的刹车距离模型及黄灯持续时间分析模型
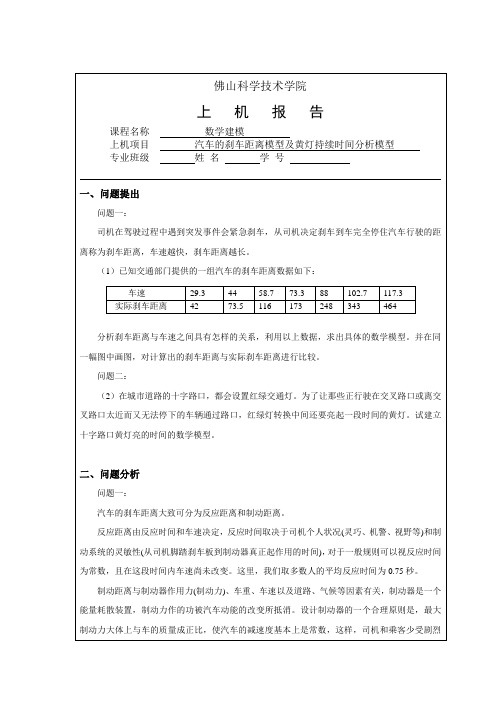
佛山科学技术学院上机报告课程名称数学建模上机项目汽车的刹车距离模型及黄灯持续时间分析模型专业班级姓名学号一、问题提出问题一:司机在驾驶过程中遇到突发事件会紧急刹车,从司机决定刹车到车完全停住汽车行驶的距离称为刹车距离,车速越快,刹车距离越长。
(1)已知交通部门提供的一组汽车的刹车距离数据如下:车速29.3 44 58.7 73.3 88 102.7 117.3 实际刹车距离42 73.5 116 173 248 343 464分析刹车距离与车速之间具有怎样的关系,利用以上数据,求出具体的数学模型。
并在同一幅图中画图,对计算出的刹车距离与实际刹车距离进行比较。
问题二:(2)在城市道路的十字路口,都会设置红绿交通灯。
为了让那些正行驶在交叉路口或离交叉路口太近而又无法停下的车辆通过路口,红绿灯转换中间还要亮起一段时间的黄灯。
试建立十字路口黄灯亮的时间的数学模型。
二、问题分析问题一:汽车的刹车距离大致可分为反应距离和制动距离。
反应距离由反应时间和车速决定,反应时间取决于司机个人状况(灵巧、机警、视野等)和制动系统的灵敏性(从司机脚踏刹车板到制动器真正起作用的时间),对于一般规则可以视反应时间为常数,且在这段时间内车速尚未改变。
这里,我们取多数人的平均反应时间为0.75秒。
制动距离与制动器作用力(制动力)、车重、车速以及道路、气候等因素有关,制动器是一个能量耗散装置,制动力作的功被汽车动能的改变所抵消。
设计制动器的一个合理原则是,最大制动力大体上与车的质量成正比,使汽车的减速度基本上是常数,这样,司机和乘客少受剧烈的冲击。
至于道路、气候等因素,对于一般规则又可以看作是固定的。
问题二:设汽车行驶速度为法定速度0v ,一定的刹车距离为1S ,通过十字路口的距离为2S ,车身的长度为L ,则黄灯的时间应t 使距停车线1S 之内的汽车能通过路口,即021/)(v L S S t ++≈,如果考虑到司机有一定的反应时间,则黄灯持续的状态就也包括驾驶员的反应时间。
数学建模汽车刹车距离

数学建模汽车刹车距离1. 前言汽车刹车距离在车辆的安全行驶和驾驶过程中起着至关重要的作用。
单独考虑车辆的马力、制动能力和路面情况都是不够的,需要将这些因素综合考虑,以保证行驶的安全性。
本文通过建立模型,探究车辆刹车距离的影响因素,以及如何优化车辆的行驶效率。
2. 模型的建立在考虑汽车刹车距离时,需要综合考虑车辆的制动性能、车速、路面状态等多个因素。
为了更好地探究这些因素之间的关系,我们建立了如下的数学模型。
设汽车在行驶过程中的车速为v,制动的加速度为a,路面的摩擦系数为μ,刹车距离为d。
根据牛顿第二定律可得:$$F=ma$$其中F为刹车制动力,m为车辆质量,a为制动加速度。
由于制动力与车速、制动器摩擦系数均有关系,因此可以通过以上参数进行表达。
可得到如下公式:$$F=C_{f}+C_{r}mg(v)$$式中,Cf和Cr分别为车轮前后制动器产生的制动力,g(v)为与车速有关的函数,m为车辆质量。
在刹车的过程中,系统对车辆施加一定的制动力,车速逐渐降低,直到最终停止。
设t为刹车的时间,可得如下公式:$$d=\frac{1}{2}at^{2}+\frac{1}{2}vt$$式中,第一项为制动过程加速度造成的路程,第二项为刹车前车辆的行驶路程。
将制动加速度a代入上述公式,可以得到:代入刚才的F公式,可以得到:这便是本文研究的汽车刹车距离的数学模型。
从中可以看出,刹车距离与车速、制动力、摩擦系数等参数均有关系,需要综合考虑。
3. 模型的应用和分析在上一章节中,我们得到了汽车刹车距离的数学模型。
下面将具体分析模型中的各个参数。
3.1 制动加速度制动加速度是指行驶中车辆的减速度,即刹车踏板产生的力作用在车辆质量上所产生的减速度。
制动加速度越大,车速下降的速率就越快,刹车距离也就相应越短。
反之,制动加速度越小,刹车距离就越长。
3.2 车速3.3 摩擦系数摩擦系数是路面与轮胎之间的摩擦力系数。
摩擦系数越大,所产生的摩擦力也就越大,车辆制动效果就越好,刹车距离就相应更短。
数学建模-黄灯亮多久ppt课件

在交通管理中,定期的亮一段黄灯是为了让那 些正行驶在交叉路口上或距交叉路口太近以致无 法停下的驾驶员有机会在黄灯亮的时候通过路口。 如果汽车的法定速度为 ,交v0叉路口宽度为 ,典 型的H 车身长度为 ,地面的L摩擦系数为 ,试问黄 灯点f 亮的时间多长为好呢?
应用背景
相关知识点
1.函数最大(小)值的求法 2.高阶可降阶微分方程的解法 3.微分方程的几何应用和简单物理应用
fg
在 x(0的) 条0件下,对(2)式再积分得到
x(t)
1 2
f gt2
v0t
(3)
从而刹车距离
x(t ') D v02 .
(4)
2 fg
解题过程
第五步 : 由(4)式得
所以
t1
D v0
v,0
2 fg
T
v0 2 fg
L
v0
H.
t
0
对 关T于 求v导0 数,令
得T0到 0驻点
以当v0 2 fg(L 时H), 有极小值v0 2 fg(L H)
假设汽车以法定速度 通过路口。由于 为常数,
而
v0
t0
LH , 所以只有 是需要进t一2 步求v0得的。
t1
解题过程
第三步 : 下面先计算刹车距离. 设车辆的重量为 ,W车辆
刹车时,水平方向只受到摩擦力 作fW用,其方向与 运动方向相反。设刹车后,汽车走过的位移 ,x(根t) 据牛顿第二定律有如下的微分方程:
设驾驶员作出决定的反应时间为 ,t0 通过刹车距 离的时间为 ,t1通过路口和一个车身距离的时间为 , 黄灯t2 点亮的时间为 。 T
解题过程
第二步 :
因此,如果取
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
佛山科学技术学院
上机报告
课程名称数学建模
上机项目汽车的刹车距离模型及黄灯持续时间分析模型
专业班级姓名学号
一、问题提出
问题一:
司机在驾驶过程中遇到突发事件会紧急刹车,从司机决定刹车到车完全停住汽车行驶的距离称为刹车距离,车速越快,刹车距离越长。
(1)已知交通部门提供的一组汽车的刹车距离数据如下:
车速29.3 44 58.7 73.3 88 102.7 117.3 实际刹车距离42 73.5 116 173 248 343 464
分析刹车距离与车速之间具有怎样的关系,利用以上数据,求出具体的数学模型。
并在同一幅图中画图,对计算出的刹车距离与实际刹车距离进行比较。
问题二:
(2)在城市道路的十字路口,都会设置红绿交通灯。
为了让那些正行驶在交叉路口或离交叉路口太近而又无法停下的车辆通过路口,红绿灯转换中间还要亮起一段时间的黄灯。
试建立十字路口黄灯亮的时间的数学模型。
二、问题分析
问题一:
汽车的刹车距离大致可分为反应距离和制动距离。
反应距离由反应时间和车速决定,反应时间取决于司机个人状况(灵巧、机警、视野等)和制动系统的灵敏性(从司机脚踏刹车板到制动器真正起作用的时间),对于一般规则可以视反应时间为常数,且在这段时间内车速尚未改变。
这里,我们取多数人的平均反应时间为0.75秒。
制动距离与制动器作用力(制动力)、车重、车速以及道路、气候等因素有关,制动器是一个能量耗散装置,制动力作的功被汽车动能的改变所抵消。
设计制动器的一个合理原则是,最大制动力大体上与车的质量成正比,使汽车的减速度基本上是常数,这样,司机和乘客少受剧烈
的冲击。
至于道路、气候等因素,对于一般规则又可以看作是固定的。
问题二:
设汽车行驶速度为法定速度0v ,一定的刹车距离为1S ,通过十字路口的距离为2S ,车身的长度为L ,则黄灯的时间应t 使距停车线1S 之内的汽车能通过路口,即021/)(v L S S t ++≈,如果考虑到司机有一定的反应时间,则黄灯持续的状态就也包括驾驶员的反应时间。
根据分析,下面建立十字路口黄灯亮的时间的数学模型。
三、模型假设
(一)为了解决汽车刹车距离问题,作出以下几点假设:
(1) 道路、气候、驾驶员等条件相同,汽车没有超载,也没有出现故障;
(2) 汽车在平直道路上行驶,驾驶员紧急刹车,一脚把刹车脚踏踩到底,汽车在刹车过程没
有转方向;
(3) 驾驶员的反应时间为常数1t ,汽车在反应时间做匀速直线运动;
(4) 汽车在制动过程做匀速直线运动,减速度a 是常数,制动力所做的功等于汽车功能的损
失。
引入以下符号:
v ~车速(m/s );d ~刹车距离(m );1d ~反应距离(m );2d ~制动距离(m ); 1t ~反应时间(s )。
(二)为了计算十字路口黄灯亮的时间,作出以下几点假设: (1)驾驶员在通过交叉路口时,匀速驾驶车辆;
(2)汽车在平直道路上行驶,驾驶员紧急刹车,一脚把刹车脚踏踩到底; (3)仅仅考虑汽车直行的情况,不考虑转弯或掉头的情况; (4)不考虑人行道中路人对来往车辆的影响。
符合说明:
四、模型建立
(显示模型函数的构造过程)
(一) 汽车刹车距离模型: 由分析得
d =1d +2d
由假设(3)得
1d =1t v
又由假设(4)得
m a 2d =
1
2
m (v ^2) 解得2d =(v ^2)/2a 则汽车距离与速度的模型为
d =1t v +k (v ^2)
其中1t 根据经验取0.75秒,则只要确定k 。
(二)黄灯持续时间的数学模型
五、模型求解
(显示模型的求解方法、步骤及运算程序、结果)
v=[29.3 44 58.7 73.3 88 102.7 117.3]; d=[42 73.5 116 173 248 343 464]; fun=inline('0.75*v+k*v.^2','k','v') k=lsqcurvefit(fun,0,v,d)
fprintf('0.75*v+k*v.^2µÄ²ÎÊýk=%.4f\n',k)
y=0.75*v+_0.0255*v.^2 hold on plot(v,d) plot(v,y 'r+')
求得
k=0.0255
拟合后的曲线中各点的数据是
y =
43.8665 82.3680 131.8901 191.9837 263.4720 345.9809 438.8369 可得,汽车刹车实际距离与计算距离相当。
