重庆大学 数学模型 数学实验作业一
数学实验_重庆大学中国大学mooc课后章节答案期末考试题库2023年

数学实验_重庆大学中国大学mooc课后章节答案期末考试题库2023年1.无向图中边的端点地位是平等的、边是无序点对。
而有向图中边的端点的地位不平等,边是有序点对,不可以交换。
参考答案:正确2.人口数量与下列因素都有关,人口基数、出生率、死亡率、年龄结构、性别比例、医疗水平、工农业生产水平、环境、生育政策等等。
参考答案:正确3.一元5次代数方程在复数范围内有多少个根?参考答案:54.任何贪心算法都能求出最优解。
参考答案:错误5.二维插值函数z=interp2(x0,y0,z0,x,y,’method’)中,method的缺省值是()参考答案:linear6.在当前文件夹和搜索路径中都有文件ex1.m,在命令行窗口输入ex1时,则执行的文件是当前文件夹中的ex1.m参考答案:正确7.下列关于Dijkstra算法的哪些说法正确参考答案:Dijkstra算法是求加权图G中从某固定起点到其余各点最短路径的有效算法;_Dijkstra算法的时间复杂度为O(n2),其中n为顶点数;_Dijkstra算法可用于求解无向图、有向图和混合图的最短路径问题;8.如果x=1: 2 : 10,则x(1)和x(5)分别是( )参考答案:1,99.人口是按指数规律无限增长的。
参考答案:错误10.在包汤圆问题的整个建模过程,包括了如下几个步骤(1)找出问题涉及的主要因素(变量),重新梳理问题使之更明确(2)作出简化、合理的假设(3)用数学的语言来描述问题(4)用几何的知识解决问题(5)模型应用参考答案:正确11.下面程序所解的微分方程组,对应的方程和初始条件为:(1)函数M文件weif.m:function xdot=weif(t, x)xdot=[3*x(1)+x(3);2*x(1)+6;-3*x(2)^2+2*x(3)];(2)脚本M文件main.m:x0=[1,2,3] ;[t,x]=ode23(‘weif’,[0,1],x0),plot(t,x’),figure(2),plot3(x( :,1),x( :,2),x( :,3)参考答案:___12.某公司投资2000万元建成一条生产线。
重庆大学 数学模型 数学实验作业1

开课学院、实验室:数统学院实验时间:2015年11月18日
在窗口二(figure(2))中画图:
分段线性插值本吻合性最差的,但当取点足够密集时,它能很好的与原函数吻合。
三次样条插值吻合性最好。
而拉格朗日多项式插值在本题中随着n的增大越来越逼近原函数。
应用实验(或综合实验)
一、问题重述
2.火车行驶的路程、速度数据如表7.2,计算从静止开始20 分钟内走过的路程。
可将此图近似的看做一个底为20,高为32/60的三角形,故算得路程大概为5.3km,与结果相符。
3.得到结果y =25.0000。
4.得到下图:
教师签名
年月。
数学模型与实验报告习题

数学模型与实验报告姓名:王珂班级:121111学号:442指导老师:沈远彤数学模型与实验一、数学规划模型某企业将铝加工成A,B两种铝型材,每5吨铝原料就能在甲设备上用12小时加工成3 吨A 型材,每吨A 获利2400 元,或者在乙设备上用8 小时加工成4 吨B 型材,每吨B 获利1600 元。
现在加工厂每天最多能得到250 吨铝原料,每天工人的总工作时间不能超过为480 小时,并且甲种设备每天至多能加工100 吨A,乙设备的加工能力没有限制。
(1 )请为该企业制定一个生产计划,使每天获利最大。
(2)若用1000 元可买到1 吨铝原料,是否应该做这项投资若投资,每天最多购买多少吨铝原料(3)如果可以聘用临时工人以增加劳动时间,付给工人的工资最多是每小时几元(4)如果每吨A 型材的获利增加到3000 元,应否改变生产计划题目分析:每5 吨原料可以有如下两种选择:在甲机器上用12 小时加工成3 吨A 每吨盈利2400 元在乙机器上用8 小时加工成4 吨B 每吨盈利1600 元限制条件:原料最多不可超过250 吨,产品A 不可超过100 吨。
工作时间不可超过480 小时线性规划模型:设在甲设备上加工的材料为x1 吨,在乙设备上加工的原材料为x2 吨,获利为z,由题意易得约束条件有:Max z = 7200x1/5 +6400x2/5x1 + x2 三25012x1/5 + 8x2/5 三4800 三3x1/5 三100, x2 三0用LINGO 求解得:VARIABLE VALUE REDUCED COSTX1X2ROW SLACK OR SURPLUS DUAI PRICE1234做敏感性分析为:VARIABLE CURRENT ALLOWABLE ALLOWABLECOFF INCREASE DECREASEX1X2ROW CURRENT ALLOWABLE ALLOWABLERHS INCREASE DECREASE234INFINITY可见最优解为x1= 100, x2=150, MAXz=33600Q因此最优解为在甲设备上用100吨原料生产A产品,在乙设备上用150吨原料生产B产品。
数学建模 -实验报告1

������������⁄������������ = ������������(1 − (������ + ������)) − ������1������∗������,
(4 − 3)
������������∗⁄������������ = −������1������∗������ + ������2������
二、 问题分析
建立肿瘤细胞增长模型时,我们可以从自由增长模型开始分析,引进 Logistic 阻滞增长模型,构成肿瘤细胞增长初步框架。再者肿瘤细胞不同于普 通细胞,其生长受到人体自身免疫系统的制约。于是综合考虑正常细胞转化,癌 细胞增殖,癌细胞死亡,癌细胞被效应细胞消除等情况,建立动力学方程。并对 模型进行适当简化求解。在放射治疗方案的设计中,我们可以引入放射生物学中 广泛接受的 LQ 模型对问题进行分析,由于放疗对人体伤害相当大,因此我们采 取分次逐次放疗的方式进行治疗。我们具体分两种情形进行讨论,一是在总剂量 一定的条件下,不同的分次剂量组合对生物效应的影响;二是在产生相同生物效 应的情况下,分析最优的分次剂量组合。
易算出癌细胞转入活动期已有 300 多天,故如何在早期发现癌症是攻克癌症的关键之一 (2)手术治疗常不能割去所有癌细胞,故有时需进行放射疗法。射线强度太小无法杀
死癌细胞,太强病人身体又吃不消且会使病人免疫功能下降。一次照射不可能杀死全部癌细 胞,请设计一个可行的治疗方案(医生认为当体内癌细胞数小于 100000 个时即可凭借体内 免疫系统杀灭)。
进一步简化,根据(4-4),(4-5)式可知,效应细胞������∗和复合物������有出有进.假 设出入保持平衡,则有
������ + ������∗ = C (C 为常数)
数学模型大作业
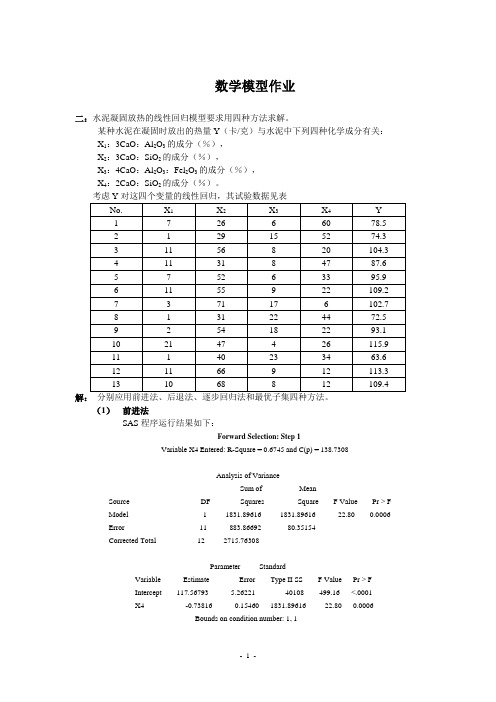
数学模型作业二:水泥凝固放热的线性回归模型要求用四种方法求解。
某种水泥在凝固时放出的热量Y(卡/克)与水泥中下列四种化学成分有关:X1:3CaO:Al2O3的成分(%),X2:3CaO:SiO2的成分(%),X3:4CaO:Al2O3:Fel2O3的成分(%),X4:2CaO:SiO2的成分(%)。
解:分别应用前进法、后退法、逐步回归法和最优子集四种方法。
(1)前进法SAS程序运行结果如下:Forward Selection: Step 1Variable X4 Entered: R-Square = 0.6745 and C(p) = 138.7308Analysis of VarianceSum of MeanSource DF Squares Square F Value Pr > FModel 1 1831.89616 1831.89616 22.80 0.0006Error 11 883.86692 80.35154Corrected Total 12 2715.76308Parameter StandardVariable Estimate Error Type II SS F Value Pr > FIntercept 117.56793 5.26221 40108 499.16 <.0001X4 -0.73816 0.15460 1831.89616 22.80 0.0006Bounds on condition number: 1, 1Forward Selection: Step 2Variable X1 Entered: R-Square = 0.9725 and C(p) = 5.4959Analysis of VarianceSum of MeanSource DF Squares Square F Value Pr > F Model 2 2641.00096 1320.50048 176.63 <.0001 Error 10 74.76211 7.47621Corrected Total 12 2715.76308Parameter StandardVariable Estimate Error Type II SS F Value Pr > FIntercept 103.09738 2.12398 17615 2356.10 <.0001X1 1.43996 0.13842 809.10480 108.22 <.0001X4 -0.61395 0.04864 1190.92464 159.30 <.0001Bounds on condition number: 1.0641, 4.2564Forward Selection: Step 3Variable X2 Entered: R-Square = 0.9823 and C(p) = 3.0182Analysis of VarianceSum of MeanSource DF Squares Square F Value Pr > F Model 3 2667.79035 889.26345 166.83 <.0001 Error 9 47.97273 5.33030Corrected Total 12 2715.76308Parameter StandardVariable Estimate Error Type II SS F Value Pr > FIntercept 71.64831 14.14239 136.81003 25.67 0.0007X1 1.45194 0.11700 820.90740 154.01 <.0001X2 0.41611 0.18561 26.78938 5.03 0.0517X4 -0.23654 0.17329 9.93175 1.86 0.2054Bounds on condition number: 18.94, 116.36No other variable met the 0.5000 significance level for entry into the model.Summary of Forward SelectionVariable Number Partial ModelStep Entered Vars In R-Square R-Square C(p) F Value Pr > F1 X4 1 0.6745 0.6745 138.731 22.80 0.00062 X1 2 0.2979 0.9725 5.4959 108.22 <.00013 X2 3 0.0099 0.9823 3.0182 5.03 0.0517在前进法中,模型中变量从无到有依次选一变量进入模型,并根据该变量在模型中的Ⅱ型离差平和(SS2)计算F统计量及P值。
重庆大学数学实验一 matlab的基本应用 参考答案

《数学实验》第一次上机实验1. 设有分块矩阵⎥⎦⎤⎢⎣⎡=⨯⨯⨯⨯22322333S O R E A ,其中E,R,O,S 分别为单位阵、随机阵、零阵和对角阵,试通过数值计算验证⎥⎦⎤⎢⎣⎡+=22S 0RS R E A 。
程序及结果:E=eye(3); %创建单位矩阵E% R=rand(3,2); %创建随机矩阵R% O=zeros(2,3); %创建0矩阵% S=diag(1:2); %创建对角矩阵% A=[E,R;O,S]; %创建A 矩阵%B=[E,(R+R*S);zeros(2,3),S^2] %计算等号右边的值%A^2 %计算等号左边的值%运行结果:B =1.00 0 0 1.632.74 0 1.00 0 1.81 1.90 0 0 1.00 0.25 0.29 0 0 0 1.00 0 0 0 0 0 4.00 ans =1.00 0 0 1.632.740 1.00 0 1.81 1.90 0 0 1.00 0.25 0.29 0 0 0 1.00 0 0 0 0 0 4.002.某零售店有9种商品的单件进价(元)、售价(元)及一周的销量如表1.1,问哪种商品的利润最大,哪种商品的利润最小;按收入由小到大,列出所有商品及其收入;求这一周该10种商品的总收入和总利润。
表1.11)程序:a=[7.15 8.25 3.20 10.30 6.68 12.03 16.85 17.51 9.30]; b=[11.10 15.00 6.00 16.25 9.90 18.25 20.80 24.15 15.50]; c=[568 1205 753 580 395 2104 1538 810 694];s=sum((b-a).*c)i=b.*cmax((b-a).*c)min((b-a).*c)[m,n]=sort(b.*c)2)运行结果:s =4.6052e+004i =1.0e+004 *0.6305 1.8075 0.4518 0.9425 0.3911 3.8398 3.1990 1.95621.0757ans =1.3087e+004ans =1.2719e+003m =1.0e+004 *0.3911 0.4518 0.6305 0.9425 1.0757 1.8075 1.9562 3.1990 3.8398n =5 3 1 4 9 2 8 7 63. 近景图将x的取值范围局限于较小的区间内可以画出函数的近景图,用于显示函数的局部特性。
数学建模第一次实验报告

数学建模第一次实验报告问题描述:2.某动物从食物中每天得到2500卡(1卡=4.18焦)的热量,其中1200卡用于基本的新陈代谢,每天每kg的体重要再消耗16卡,假如它每增加1kg体重需要10000卡的热量,问该动物体重将怎样变化?解:设动物体重为m。
令动物每日消耗热量等于获取的热量,可求得最大体重。
此时,2500=1200+16mm=81.25kg根据生物学知识可知,没有动物的出生时的体重会大于成年后的体重,即m≤81.25kg。
又设每天体重的变化量为dm,2500=1200+16m+10000dm/dtt=625In(16m-1300)m=1/16*(e^(t/625)+1300)3.37支球队进行冠军争夺赛,每轮比赛中出场的两只球队中的胜者及轮空着进入下一轮,直至比赛结束,问共需进行多少场比赛?解:各球队的胜负对比赛场次无影响,忽略。
将其拆解为一轮一轮的比赛分析:第一轮:37÷2=18……1——>19第二轮:19÷2=9 ……1——>10第三轮:10÷2=5 ——>5第四轮: 5÷2=2 ……1——>3第五轮: 3÷2=1 ……1——>2第六轮: 2÷2=1 ——>1所以,一共进行六轮比赛,其场数为:18+9+5+2+1+1=36(场)答:一共36场比赛。
4.1条河宽1km,两岸各有一个城镇A与B,A与B的直线距离为4km。
今需铺设一条电缆连接A与B,已知地下电缆的修建费是2万元/km,水下电缆的修建费是4万元/km,假设两岸为平行的直线,问应该如何架设电缆方可以使总建设费用最少?AB D C如图,设C 点。
易知A-D-B 为铺设路线,设AD 长为a ,BD 长为b ,总花费为m 。
其中1<a<4,0<b<15所以,m=4a+2b (1)(15-b )2+12=a 2 (2)所以, m=4215216b b +-+2b 求得m 最小值即可。
重庆大学--数学模型--数学实验作业七
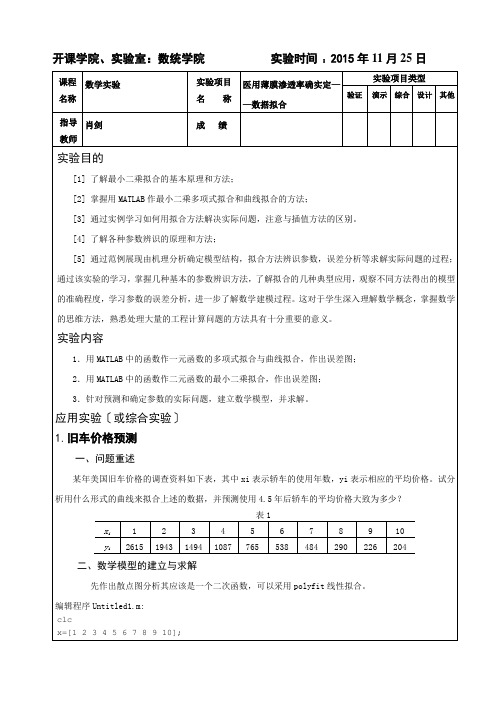
开课学院、实验室:数统学院实验时间:2015年11月25日y=[2615 1943 1494 1087 765 538 484 290 226 204];plot(x,y,'+')hold ona=polyfit(x,y,2)y1=polyval(a,x);plot(x,y1,'r')t=4.5;cost=polyval(a,t)三、实验结果及分析a =1.0e+03*。
一.问题重述机器人在不同层次上应用于工业生产、水下探测、核点开发、军事研究等领域和部门。
当一个机器人工作时,经常需要识别那些从外形上看来是圆形或椭圆形的仪器或工具柄等基本设备,以便执行进一步的操作。
通常在所需操纵的工具柄上放置适当数量的传感器,这些传感器不断向四周发射电信号,机器人身上安置有接收电信号的硬件装置,根据这些信号,机器人将估算出各个传感器当时所在的位置,然后,再利用这些数据获得工具柄的位置。
由于硬件设备的限制和测量的随机偏差,所获得的传感器位置数据是有误差的。
因此,为了增强识别的准确性和可靠性,工具柄上放置的传感器应多于确定该定形曲线所需的最少点数。
〔能否获得比较准确的工具柄位置,对机器人能否有效抓握、操作该工具柄起着关键的作用。
〕现有一个圆形工具柄,其边缘上放置了6个传感器,一机器人在某一个时刻测得这些传感器的位置坐标为:(1,7),(2,6),(5,8),(7,7),(9,5),(3,7),如何确定该圆形工具柄的圆心坐标和半径。
二.问题分析此题很难写出显式表达式,故可用regress回归分析求解函数表达式。
三.数学模型的建立与求解圆的函数表达式都具有x²+y²+Ax+By+C=0的形式,即Ax+By+C=-x²-y².则圆心为O〔-A/2,-B/2〕,半径的平方为R²=〔A²/4+B²/4-C〕故编辑程序Untitled2.m:clcx1=[1;2;5;7;9;3];y1=[7;6;8;7;5;7];y=-x1.^2-y1.^2;D=ones(6,1);x=[x1,y1,D];b=[];b=regress(y,x)ezplot('x^2+y^2-9.4847*x-7.6702*y+20.3160',[-4,14,-1,9])hold onplot(x1,y1,'.')disp('圆心O 半径R')O=[9.4847/2,7.6702/2]R=((9.4847/2)^2+(7.6702/2)^2-20.3160)^(1/2)四、实验结果及分析得到圆心O=〔,〕,半径R=.3.经济增长模型一.问题重述。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
求在图上加各种标注,观察到什么现象?发现有什么规律?同时用 subplot 分别在不同的坐标系下作出这
四条曲线,为每幅图形加上标题。
6.作出下列曲面的 3 维图形,
z sin( x2 y2 ) ;
7. 作出函数 y=x4-4x3+3x+5 (x[0,6])的图形,标出其在[0,6]之间的最小值点,并在最小值点附
2.某零售店有 9 种商品的单件进价(元)、售价(元)及一周的销量如表 1.1,问哪种商品的利
润最大,哪种商品的利润最小;按收入由小到大,列出所有商品及其收入;求这一周该 10 种商品的总收
入和总利润。
表 1.1
货号
12
3
4
5
6
7
8
9
单件进价
7.15 8.25 3.20 10.30 6.68 12.03 16.85 17.51 9.30
0 1.0000
0 2.5294 1.6406
0
0 1.0000 0.3902 2.8725
0
0
0 9.0000
0
0
0
0
0 4.0000
2. 编程3;04
V= 6
u= 1.2719e+03
v= 5
f= 1.0e+04 * 0.1272 0.2108 0.2244 0.3451 0.4303
实验项目类型
验证 演示 综合 设计 其他
[1] 熟悉 MATLAB 软件的用户环境;
[2] 了解 MATLAB 软件的一般目的命令;
[3] 掌握 MATLAB 数组操作与运算函数;
[4] 掌握 MATLAB 软件的基本绘图命令;
[5] 掌握 MATLAB 语言的几种循环、条件和开关选择结构。
通过该实验的学习,使学生能灵活应用 MATLAB 软件解决一些简单问题,能借助 MATLAB 软件的绘图功能,
对函数的特性进行探讨,广泛联想,大胆猜想,发现进而证实其中的规律。
实验内容
1.MATLAB 软件的数组操作及运算练习;
2.直接使用 MATLAB 软件进行作图练习;
3.用 MATLAB 语言编写命令 M-文件和函数 M-文件。
基础实验
一、问题重述
1.设有分块矩阵 ,其中 E,R,O,S 分别为单位阵、随机阵、零阵和对角阵,试通过数值计算验证 。
3. Untitled3: for i=100:1:999
a=fix(i/100); b=fix((i-100*a)/10); c=fix(i-100*a-10*b); if i==a^3+b^3+c^3
i end end
4. sq.m. function a=sq(x) n=1; a(1)=1; a(2)=2; while abs(a(n+1)-a(n))>=0.00001
1.3087 S= 4.6052e+04 3.编程 Untitled3,运行结果:i = 153 i= 370 i= 371 i= 407 4. 编辑函数式 M 文件 sq.m。 5. 编程 Untitled5,运行后标注得 1.fig 和 2.fig。 6.编程 Untitled6,运行后得 3.fig. 7. 编程 Untitled7,运行后标注得 4.fig.
近标出该最小值点的坐标值;
二、实验过程
1. 编程 Untitled1,运行结果为 B =
1.0000
0
0 3.6535 0.8355
0 1.0000
0 2.5294 1.6406
0
0 1.0000 0.3902 2.8725
0
0
0 9.0000
0
0
0
0
0 4.0000
C=
1.0000
0
0 3.6535 0.8355
单件售价
11.10 15.00 6.00 16.25 9.90 18.25 20.80 24.15 15.50
销量
568 1205 753 580 395 2104 1538 810 694
3.建立一个命令 M-文件:求所有的“水仙花数”,所谓“水仙花数”是指一个三位数,其各位数字
的立方和等于该数本身。例如,153 是一个水仙花数,因为 153=13+53+33。
n=n+1; a(n+1)=(a(n)+x./a(n))./2; end a=a(n+1); end
5. Untitled5: x=-2:0.01:2; y1=exp(x); y2=1+x; y3=1+x+(1/2).*x.^2; y4=1+x+(1/2).*x.^2+(1/6).*x.^3; plot(x,y1,'k',x,y2,'b',x,y3,'g',x,y4,'m') figure(2) subplot(2,2,1) plot(x,y1) title('y1=e^x')
五、附录(程序等)
1. Untitled1: E=eye(3,3);R=rand(3,2);O=zeros(2,3);S=[3 0;0 2]; A=[E R;O S]; B=A*A D=zeros(2,3); H=R*S+R;G=S*S;
0.5378
0.6075
0.8134
C=[E H;D G]
2. Untitled2: a=[7.15 8.25 3.20 10.30 6.68 12.03 16.85 17.51 9.30]; b=[11.10 15.00 6.00 16.25 9.90 18.25 20.80 24.15 15.50]; c=b-a; d=[568 1205 753 580 395 2104 1538 810 694]; e=c.*d; [U V]=max(e) [u v]=min(e) f=sort(e) S=sum(e)
4.编写函数 M-文件 sq.m:用迭代法求 x a 的值。求平方根的迭代公式为
z sin( x2 y2 )
迭代的终止条件为前后两次求出的 x 的差的绝对值小于 105。
5 在同一个坐标下作出 y1=ex,y2=1+x,y3=1+x+(1/2)x2,y4= 1+x+(1/2)x2+(1/6)x3 这四条曲线的图形,要
重庆大学 学生实验报告
实验课程名称
数学实验
开课实验室
DS1408
学
院 年级 专业班
学生姓名
学号
开 课 时 间 学年第 1 学期
总成绩 教师签名
数学与统计学院制
开课学院、实验室:数统学院
实验时间 :
课程 数学实验 名称 指导 肖剑 教师
实验目的
实验项目 MATLAB 软件入门 名称
成绩
2015 年 9 月 30 日
