结构力学第七章

合集下载

结构力学第七章力法

§7-3 力法的基本概念
1 0
力1.确法定步基骤本:体系111X111
1P
11
0
力法方程
2.写出位移条件,力11法 X方1程 1P 0
34..作求单出位系弯数1 矩和图自11 由,荷l项载3 /弯3E矩I 图;1P ql 4 / 8EI
5.解力法方程X1 3ql / 8() M M1 X1 M P
11
1 2EI
l2 2
2l 3
1 EI
l3
7 6
l3 EI
EI
l
2 X1
12
1 EI
l2 2
l
1 2
l3 EI
l 荷载作用下超静定结构内1力1 分布与刚度的12
21
1 EI
l2 2
l
1 2
l3 EI
绝对值无关只与各杆X刚2=1
l度内Mq1的力21 分比XX1=布1值1 与有关.l
22
M2 X 2
X5
X4
X9
X6
X 10
638 10
§7-4 力法的典型方程
1.力法的典型方程
q 2EI EI l
q
1 X2
变形条件:
2EI
l
EI
2 X1 l
12
0 0
l
1.力法的典型方程
q
2EI
EI
l
q 2
1 X2
X1
变形条件:
12
0 0
1 11 X1 12 X2 1P 0
2 21 X1 22 X2 2P 0
M3 31X1 32 X 2 33 X3 3P 0
MP
X1
X2
X3

结构力学第七章计算超静定梁结构力学

(b) A
q X 1
C
"基本体系 "
法中把原超静定结构称为原 (c) A
结构，去掉多余联系后的静
11
B X 1
C
定结构称为基本结构。所去
q
(d)
掉的多余联系，则以相应的
A
B
C
ip
多余未知力X1来代替。
图7-4
这样，基本结构就同时承受着荷载和多余未知力X1的作用，基本结构在原有荷载和多余未知力X1共同作用下的体系称为力法的基本体系。现在分析一下如何计算X1 。对原结构讲它代表B支座反力，是一个被动力，而对基本结构来讲它是一个主
1P
M1MP ds EI
1[1l(2lFllPl)]
EI 6 2
2 22
5Fl3 48EI
(5) 解力法方程。
X1
1P
11
5F 16
所得正号说明X1的实际方向与假设方向相同。
结构力学第七章计算超静定梁结构力学
2．求解超静定结构要考虑的条件
求解任何超静定结构，都要考虑三个方面的条件：（1）平衡条件；（2）几何条件（变形条件或位移条件）；（3）物理条件。
力法和位移法是超静定结构计算的两种基本方法。力法是以多余联系的约束力——多余未知力作未知量,位移法则是以结点的某些位移作为基本未知量。计算超静定结构除上述两种方法外,常用的还有力矩分配法、有限单元法等。
力法的基本特点可归纳如下： 1.以多余未知力(被撤消多余联系处的约束力)为基本未知量。 2.根据所去掉的多余联系处的变形协调条件建立力法方程，从而求出多余未知力。 3.根据平衡条件求出全部反力及内力。 4.一切计算均在基本结构上进行。
例7-1 用力法计算图7-5(a)所 (a) A

结构力学第七章位移法

几何不变体系
10
§7-3 位移法基本结构与未知量数目
二位移法基本结构 1 附加刚臂控制结点转动 2 附加链杆控制结点线位移
ΔC C θC
ΔD θD
D
基本结构
将原结构结点位移锁住，所得单跨梁的组合体
11
三位移法基本结构与未知量数目
ΔC
ΔD
Z1
θD
C θC
D
Z2 Z3
基本结构
结点角位移的数目=刚结点的数目=附加刚臂的数目独立结点线位移的数目=附加链杆的数目
B
15i 16
6
0(2)
位移法方程实质上平衡方程 33
2i
3i/2Z2=1
A
D
2i
k 21
FQ BA
FQ CD
3i 2
B
C k22
FQBA
FQCD
3i
i2
3i/2
k 22
i
3i 4

3i 16
15i 16
B i
0
FQ BA
3i 4
C FQCD i
3i 2
M1
3i 4
A
FQ CD
3i 16
3i/2
D 3i/4 26
4
B
C F2P
3kN/m 3kN/m
16
皮肌炎图片——皮肌炎的症状表现
▪ 皮肌炎是一种引起皮肤、肌肉、心、肺、肾等多脏器严重损害的，全身性疾病，而且不少患者同时伴有恶性肿瘤。它的1症状表现如下：
▪ 1、早期皮肌炎患者，还往往伴有全身不适症状，如-全身肌肉酸痛，软弱无力，上楼梯时感觉两腿费力；举手梳理头发时，举高手臂很吃力；抬头转头缓慢而费力。

结构力学：第七章力法

A
B
两铰拱，一次超静定结构。
A
B
一次超静定桁架
A
B
曲梁，静定结构。
A
B
静定桁架
§7-2 超静定次数的确定
去掉几个约束后成为静定结构,则为几次超静定
X1 X2 X3 X1 X2 X3
X1 X2 X3
去掉一个链杆或切断一个链杆相当于去掉一个约束
§7-2 超静定次数的确定
（2）去掉一个铰支座或一个单铰，等于拆掉两个约束。
以位移作为基本未知量，在自动满足变形协调条件的基础上来分析，当然这时主要需解决平衡问题，这种分析方法称为位移法（displacement method）。
3. 混合法----以结点位移和多余约束力作为基本未知量
如果一个问题中既有力的未知量，也有位移的未知量，力的部分考虑位移协调，位移的部分考虑力的平衡，这样一种分析方案称为混合法（mixture method）。
思考：多余约束是多余的吗？
从几何角度与结构的受力特性和使用要求两方面讨论。
q
q
A
B
A
B
C
l
A
B
q l2 8
超静定结构的优点为:
0.5l
A
ql 2 64
0.5l
q l2
32
B
C ql 2
64
1. 内力分布均匀 2. 抵抗破坏的能力强
§7-1 超静定结构概述
二、超静定结构的类型
超静定梁超静定刚架超静定拱
A
C
D
B
A
CD
B
F E
以五个支座链杆为多余约束
其它形式的静定刚架：
AA
CC KK DD

结构力学第七章力矩分配法

§7-1 引言
➢ 力矩分配法是基于位移法的逐步逼近精确解的近似方法。
➢ 力矩分配法可以避免解联立方程组，其计算精度可按要求来控制。在工程中曾经广泛应用。
➢ 从数学上说，是一种异步迭代法。
➢ 单独使用时只能用于无侧移（线位移）的结构。
➢ 力矩分配法的理论基础是位移法，力矩分配法中对杆端转角、杆端弯矩、固端弯矩的正负号规定，与位移法相同（顺时针旋转为正号）。
1
远端铰支时: 3i A i B
C=0
1
远端定向时: i A i B
C=-1
与远端支承情况有关
§7-2 力矩分配法的基本原理
例7-1 结构的A端、B端，C端的支撑及各杆刚度如图
所示，求SBA、SBC、SBD及CBA、CBC、CBD。
(a)
B
C
A EI
EI
EI l
D
l
l
(b) A
B EI
EI
θB C
结点B作用的力偶，按各杆的分配系数分配给各杆的近端；
可见：各杆B 端的弯矩与各杆B 端的转动刚度成正比。例7-1 结构的A端、B端，C端的支撑及各杆刚度如图所示，求SBA、SBC、SBD及CBA、CBC、CBD。
近端弯矩MBA、MBC为
§7-2 力矩分配法的基本原理
利用结点B的力矩平衡条件∑MB=0，得
A
B
k=EI/l 3 l
A
θ =1
B
Δ =θ l
FyB=k
SAB
A
B
FyB EI/l
解:当A 端转动θ=1时，因AB杆是刚性转动，所以B 产
生向下的竖向位移Δ=l×θ=l ，弹簧反力FyB=kΔ=EI/l2 。则

结构力学课件7静定结构总论

E
B
xx
X
7
小结：1）虚功原理（这里是用虚位移原理）的特点是用几何方法解决平衡问题。
2）求解问题直接，不涉及约束力。
二、应用虚功原理求解静定结构的约束力
P
p
A
C
B
a X
b P
A
C
B
x
X
a
b
将求约束力的问题转化为求平衡力的问题
2020/2/10
8
用虚位移原理求内力的问题
1）求截面C的弯矩
m
c
a
X bP a
6
例：求机构相应的平衡力X=？
[解]：（1）建立虚功方程
X X PP 0
pp
P
F
（2）几何关系以d作为位移参数
b 2a cos c a sin
D
3c c
当有虚位移 d 时，b和c的变化
db 2asin d dc a cosd
PB
A
N AB
N AB
P
P
2020/2/10
2
2
4
（4）构造作等效变换的影响
P
A N
A
2020/2/10
B
N
B
5
§7-2 刚体体系的虚功原理（具有理想约束）
计算静定结构内力的另一个普遍方法—虚功原理，它等价于平衡方程。
一、虚功原理
设体系上作用任意的平衡力系，又设体系发生符合约束的无限小刚体体系位移，则主动力在位移上所作的虚功总和恒等于零。
第七章
2020/2/10
1
§7-1 静定结构的一般性质
静定结构的几何特性: 无多余约束的几何不变体系; 静定结构的静力特性: 全部反力和内力均可由静力平衡条件求得，解答是唯一的。

结构力学第7章

EI l
称杆件的线刚度。
M
F AB
,M
为由荷载和温度变化引起的杆端弯矩，称为固端弯矩。
同理，另两类杆的转角位移方程为
A端固定B端铰支
M
AB
3 i
A

3i l
AB M
F AB
A端固定B端定向
M M
AB
i A M
F AB F BA
BA
i A M
§7-3
无侧移刚架的计算
附加刚臂
P A
C
θA
A
θA
C
附加刚臂限制结点
位移，荷载作用下
B 附加刚臂上产生附加力矩
施加力偶使结点产生的 B角位移，以实现结点位移状态的一致性。
P
θA
A
θA
C
实现位移状态可分两步完成： 1）在可动结点上附加约束，限制其位移，在荷载作用下，附加约束上产生附加约束力；
B
分析：
2）在附加约束上施加外力，使结构发生与原结构一致的结点位移。
BA
1
同理可得
B
1 6i
M
AB

1 3i
M
BA
MAB
A
A
1 3i
1
M
AB

1 6i
1
M
BA
E I l
B
B
M
6i
AB
M
3i
BA
MBA
（2）由于相对线位移引起的A和B
A B
l
MAB
A
B
以上两过程的叠加
MBA
A
1 3i

结构力学第七章结构位移计算

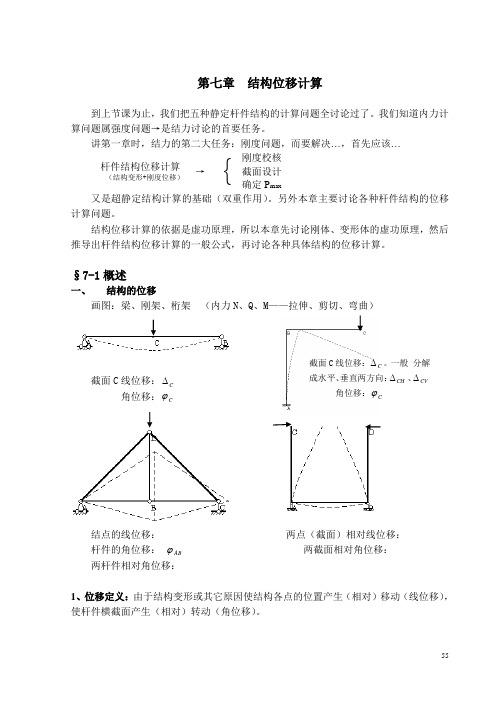
第七章结构位移计算到上节课为止，我们把五种静定杆件结构的计算问题全讨论过了。

我们知道内力计算问题属强度问题→是结力讨论的首要任务。

讲第一章时，结力的第二大任务：刚度问题，而要解决…，首先应该…杆件结构位移计算（结构变形+刚度位移）→{刚度校核截面设计确定P max又是超静定结构计算的基础（双重作用）。

另外本章主要讨论各种杆件结构的位移计算问题。

结构位移计算的依据是虚功原理，所以本章先讨论刚体、变形体的虚功原理，然后推导出杆件结构位移计算的一般公式，再讨论各种具体结构的位移计算。

§7-1概述一、结构的位移画图：梁、刚架、桁架（内力N 、Q 、M ——拉伸、剪切、弯曲）截面C 线位移：C ∆ 角位移：C ϕ结点的线位移：两点（截面）相对线位移：杆件的角位移： AB ϕ 两截面相对角位移：两杆件相对角位移：1、位移定义：由于结构变形或其它原因使结构各点的位置产生（相对）移动（线位移），使杆件横截面产生（相对）转动（角位移）。

截面C 线位移：C ∆。

一般分解成水平、垂直两方向：CH ∆、CV ∆ 角位移：C ϕ2、位移的分类：6种绝对位移：点（截面）线位移——分解成水平、垂直两方向截面角位移：杆件角位移：相对位移：两点（截面）相对线位移——沿连线方向两截面相对角位移：两杆件相对角位移：统称为：广义位移：角、线位移；相对、绝对位移Δki：k：产生位移的方向；i：引起位移原因。

如ΔA P、Δat、ΔA C广义力：集中力、力偶、分布荷载，也可以是上述各种力的综合二、引起位移的原因1、荷载作用：（荷载→内力→变形→位移）2、温度改变：静定结构，温度改变，→0应力非0应变→结构变形（材料胀缩引起的位移性质同）3、支座移动；(无应力，无应变，但几何位置发生变化){刚体位移（制造误差同）变形位移三、计算位移的目的1）刚度验算：最大挠度的限制（框架结构弹性层间位移限值1/450）2）为超静定结构的弹性分析打下基础3）预先知道变形后的位置，以便作出一定的施工措施：（起重机吊梁、板）（屋架安装）（建筑起拱）（屋窗、门、过梁）（结构要求高，精密）四、计算位移的有关假定（简化计算）1）弹性假设2）小变形假设建立平衡、应变与位移、位移与荷载成线性关系3）理想约束（联结，不考虑阻力摩擦）变形体系{ 线性变形体系（线弹性体系）荷载和位移呈线性关系，且荷载全撤除后位移将全部消失，无残余变形，（可用位移叠加原理）非线形变形体系（分段线形叠加）4）位移叠加原理（类似内力、反力叠加）§7-2 变形体系的虚功原理一、位移实位移：外因作用下结构实际位移虚位移：根据解题需要，虚设位移状态（满足变形协调＋边界条件）统称为：广义位移二、功：力所做的功：该力大小乘以力方向上的相应位移常力的功： T ＝P ×Δ＝P ×D ×cos a （大小、方向、作用点不变）变力的功：Ｔ＝⎰s dT ＝⎰s P ×cos （P ，d s ）×d s力偶所做的功：功两要素：力与位移P ：广义力（力、力偶、相对力、相对力偶）Δ：和广义力相对应的广义位移（线、角、相对线、相对角）注意：在定义功T 时，没有说位移Δ是由力P 引起的，可能由P 或其它原因，但P 力照样作功。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2、结构抗力 —— 结构或构件承受作用效应的能力，如构件的承载力、刚度、抗裂度等，用R表示。结构抗力是结构内部固有的，其大小主要取决于材料性能、构件几何参数及计算模式的精确性等。
3、结构的功能函数
Z g (S , R) R S
(7.2)
实际工程中，可能出现以下三种情况
二、结构的可靠性和可靠度的概念 1、结构的可靠度结构可靠性——结构的安全性、适用性和耐久性的总称。结构可靠度——结构在规定时间内，在规定条件下，完成预定功能的概率。规定时间指设计使用年限；规定条件指正常设计、正常施工、正常使用和正常维护，不包括错误设计、错误施工和违反原来规定的使用情况。
（2）可变荷载可变荷载也称为活荷载，是指在结构使用期间，其值随时间变化，且其变化值与平均值相比不可忽略的荷载。（3）偶然荷载在结构使用期间不一定出现，而一旦出现，其量值很大且持续时间很短的荷载称为偶然荷载。
2、荷载代表值定义：结构设计时，对于不同的荷载和不同的设计情况，应赋予荷载不同的量值，该量值即荷载代表值。（1）荷载标准值定义：荷载标准值就是结构在设计基准期内具有一定概率的最大荷载值,它是荷载的基本代表值。设计基准期——为确定可变荷载代表值而选定的时间参数，一般取为50年。
极限状态
承载力极限状态正常使用极限状态
2、分类承载能力极限状态 —— 这种极限状态对应于结构或结
构构件达到最大承载能力或不适于继续承载的变形。承载能力极限状态主要考虑关于结构安全性的功能。当结构或结构构件出现下列状态之一时，即认为超过了承载能力极限状态： ●结构构件或连接因材料强度不够而破坏； ●整个结构或结构的一部分作为刚体失去平衡（如倾覆等）； ●结构转变为机动体系； ●结构或结构构件丧失稳定（如柱子被压曲等）。
正常使用极限状态 —— 正常使用极限状态对应于结构或结构构件达到正常使用或耐久性能的某项规定限值。这一状态对应于适用性或耐久性的功能。
当结构或结构构件出现下列状态之一时，即认为超过了正常使用极限状态：
●影响正常使用或外观的变形； ●影响正常使用或耐久性能的局部损坏（包括裂缝）； ●影响正常使用的振动； ●影响正常使用的其他特定状态等。
一级
很严重
重要的房屋
二级
严重
一般的房屋
三级
不严重
次要的房屋
2、结构的设计使用年限定义：房屋建筑在正常设计、正常施工、正常使用
和维护下所应达到的持久年限。结构的设计使用年限应按下表采用。
类别
设计使用年限（年）
1
5
2
25
3
50
4
100
示例临时性结构易于替换的结构构件普通房屋和构筑物纪念性建筑和特别重要的建筑结构
3、结构的功能要求安全性——结构在正常施工和正常使用的条件下，能承受可能出现的各种作用；在设计规定的偶然事件（如强烈地震、爆炸、车辆撞击等）发生时和发生后，仍能保持必需的整体稳定性，即结构仅产生局部的损坏而不致发生连续倒塌。适用性——结构在正常使用时具有良好的工作性能。例如，不会出现影响正常使用的过大变形或振动；不会产生使使用者感到不安的裂缝宽度等。
§7.2 建筑结构极限状态设计法一、结构上的作用和作用效应
1、作用效应和结构抗力的概念
作用效应—— 结构上的各种作用，在结构内产生的内力（轴力、弯矩、剪力、扭矩等）和变形（如挠度、转角、裂缝等）的总称，用S 表示。由直接作用产生的效应，通常称为荷载效应。
S=CQ Q—某种荷载作用
C—荷载效应系数
2、结构构件的可靠指标 β—结构的可靠指标
z z
1 1 pf
[β]值见课本பைடு நூலகம்7.1
三、荷载代表值和材料性能的标准值 1、荷载分类按随时间的变异，结构上的荷载可分为以下三类：
（1）永久荷载永久荷载亦称恒荷载，是指在结构使用期间，其值不
随时间变化，或者其变化与平均值相比可忽略不计的荷载。如结构自重、土压力、预应力等。
结构的可靠度是结构可靠性的概率度量，即对结构可靠性的定量描述。注意1：结构可靠度与结构使用年限长短有关。《统一标准》以结构的设计使用年限为计算结构可靠度的时间基准。注意2：结构的设计使用年限虽与结构使用寿命有联系，但不等同。当结构的使用年限超过设计使用年限后，并不意味着结构就要报废，但其可靠度将逐渐降低。
耐久性——结构在正常维护条件下具有足够的耐久性能，
即在正常维护条件下结构能够正常使用到规定的设计使用
年限。例如，结构材料不致出现影响功能的损坏，钢筋混
凝土构件的钢筋不致因保护层过薄或裂缝过宽而锈蚀等。
二、结构功能的极限状态 1、定义整个结构或结构的一部份，超过某一特定状态就不能满足设计规定的某一功能（安全性、适用性、耐久性）要求，该特定状态称为该功能的极限状态。
§7.1 结构的功能要求和极限状态
一、结构的功能要求 1、结构的安全等级
建筑结构设计时，应根据结构破坏可能产生的后果（危及人的生命、造成经济损失、产生社会影响等）的严重性，采用不同的安全等级。
根据破坏后果的严重程度，建筑结构划分为三个安全等级。
表建筑结构的安全等级
安全等级
破坏后果
建筑物类型
可变荷载准永久值
定义：在设计基准期内经常达到或超过的那部份荷载值（总的持续时间不低于25年），称为可变荷载准永久值。
可变荷载准永久值可表示为ψqＱk ，其中Ｑk为可变荷载标准值，ψq为可变荷载准永久值系数。
可变荷载组合值
定义：两种或两种以上可变荷载同时作用于结构上时，除主导荷载（产生最大效应的荷载）仍可以其标准值为代表值外，其他伴随荷载均应以小于标准值的荷载值为代表值，此即可变荷载组合值。
永久荷载标准值永久荷载主要是结构自重及粉刷、装修，固定设备的重量。一般可按结构构件的设计尺寸和材料或结构构件单位体积（或面积）的自重标准值确定。对于自重变异性较大的材料，在设计中应根据其对结构有利或不利的情况，分别取其自重的下限值或上限值。 [例] 取钢筋混凝土单位体积自重标准值为25 kN/m3，则截面尺寸为200×500mm的钢筋混凝土矩形截面梁的自重标准值为0.2×0.5×25=2.5kN/m。