计算传热学第7节-第4章 求解代数方程组
合集下载
传热学第四章

2 m2x2 2 1 3
2 m2x2 3 2 4
2 m2x2 4 23
得
Ac
1 x
2
d 2
4
1 2 x
如采用粗网格 , x 15 则类似可以得 :
2 m2x2 2 1 3 2 m2x2 3 22
三种情况的计算结果如下 温度分布
X
0
10 15
20
30
175 139.5 127.9 119.7 113.4
m, n 1
tm1,n
tm,n
t x
m,n
x
21!
2t x2
m,n
x2
1 3!
3t x3
m,n
x3
0(x 4 )
tm1,n
tm,n
t x
m,n
x
1 2!
2t x2
m,n
x2
31!
3t x3
m,n
x3
0(x4 )
两式相加得:
tm1,n
tm1,n
2tm,n
(
2t x 2
)
m,n
x
2
0(x4 )
第四章 导热问题的数值解法
Numerical Methods of Heat Conduction
§ 4-1 导热问题数值求解的基本思想
及内节点离散方程的建立
导热问题一般为:
c t (t)
0 t f (x, y.z)
边界条件
上述问题的解法有以下两种:
1. 理论解(analytical method): 通过对上述方程积分求得(有限 情况)。
建立节点物理量的代数方程 设立迭代初场
求解代数方程组
空间坐标 x 1N x 空间步长
《传热学》教学课件—第4章 导热问题数值解法基础

基本泰勒 展开式
一阶导数
t i 1,
j
ti,
j
t x
i,
j
x
2t x 2
i, j
x 2
2!
3t x 3
i, j
x 3
3!
t i 1,
j
ti,
j
t x
i,
j
x
2t x 2
i, j
x 2
2!
3t x 3
i,
j
x 3
3!
二阶导数中心差分
向前 差分
向后 差分
中心 差分
t x
i, j
F
o
a
x2
稳定性条件 14Fo0
11
隐式格式
tin1,j tin,j y tin1,j tin,j y tin,j1 tin,j x tin,j1 tin,j x
x
x
y
y
c x y tin,j tin,j1
或 xy 时:
14Fotin,j Fo tin1,j tin1,j tin,j1tin,j1 tin,j1
ti1, j ti, j
x
Ox
2t x 2
i, j
ti1, j
ti1, j
x 2
2ti, j
O
x 2
t x
i, j
ti, j
ti1, j
x
Ox
同理,y方向二阶导数中心差分
t x
i, j
ti1, j ti1, j
2x
O
x 2
2t y 2
i, j
ti, j1 ti, j1
tin,j1 Fo 2tin1,j tin,j1tin,j12Bit f 14Fo2BiFotin,j
传热学:第四章 导热问题数值解法

t m,n
1 t m 1,n t m 1,n t m ,n 1 t m ,n 1 4
•二维导热问题;网格线;
沿x、y方向的间距为x、 y;网格单元。
每个节点温度就代表了它 所在网格单元的温度。 p(m,n)
•此方法求得的温度场
在空间上不连续。
•网格越细密、节点越多,结果越接近分析解 •网格越细密,计算所花时间越长
2) 数值计算法,把原来在时间和空间连续的物理量的
场,用有限个离散点上的值的集合来代替,通过求解
按一定方法建立起来的关于这些值的代数方程,从而
获得离散点上被求物理量的值;并称之为数值解;
3) 实验法 就是在传热学基本理论的指导下,采用实
验对所研究对象的传热过程进行测量的方法。 3 三种方法的特点 1) 分析法 a 能获得所研究问题的精确解,可以为实验和数值 计算提供比较依据;
t m,n 1 2t m,n t m,n 1 2t 同理: 2 y y 2 m,n
将以上两式代入导热微分方程得到节点(m,n)的温 度离散方程: t tm,n1 2tm,n tm,n1 m 1, n 2t m , n t m 1, n 0 2 2 x y
x y 上式可简化
第三类边界条件: y x
qw h(t f tm,n )
2hx 2hx x 2 tm1,n tm,n1 2 tf 0 tm,n 2
(3) 内部角点
y t m 1,n t m ,n y y qw 2 x x 2 t m ,n 1 t m ,n x x t m ,n 1 t m ,n x qw 2 y 2 y 3xy 0 4
传热学-第四章.

m ,n
m ,n
m ,n
m ,n
若取上面式右边的前三项,并将两式相加,移项整理 即得二阶导数的中心差分:
2t x
2 m ,n
t m 1,n 2t m ,n t m 1,n x 2
截断误差 未明确 o ( x 2 ) 写出的级数余项中 的 Δ x 的最低阶数 为2
同样可以写出:
2t y 2
m ,n
2t y
2
t m,n 1 2t m,n t m,n 1 y 2
0 无内热源 2t x
2
o (y 2 )
2t y
2
根据
2t x2Fra bibliotek
v
0 有内热源
t m1,n 2t m,n t m1,n x
2
t m,n 1 2t m,n t m,n 1 y
2
, v m ,n
0
如果x=y ,则
t m ,n 1 v ,m , n 2 t m1,n t m1,n t m,n 1 t m,n 1 x 4
对于无内热源,且x=y
t m,n 1 tm1,n tm1,n tm,n1 tm,n1 4
根据泰勒级数可知一阶导数的近似公式
t n 1 t n x 2 t ( x) t ( x) x 2
tn2 tn1 tn1 tn tn2 2tn1 tn x x t ( x) x x 2
改进初场
是否收敛 是 解的分析
否
(1) 建立控制方程及定解条件 二维矩形域内稳态无内 热源,常物性的导热问题。 控制方程: 2t
m ,n
m ,n
m ,n
若取上面式右边的前三项,并将两式相加,移项整理 即得二阶导数的中心差分:
2t x
2 m ,n
t m 1,n 2t m ,n t m 1,n x 2
截断误差 未明确 o ( x 2 ) 写出的级数余项中 的 Δ x 的最低阶数 为2
同样可以写出:
2t y 2
m ,n
2t y
2
t m,n 1 2t m,n t m,n 1 y 2
0 无内热源 2t x
2
o (y 2 )
2t y
2
根据
2t x2Fra bibliotek
v
0 有内热源
t m1,n 2t m,n t m1,n x
2
t m,n 1 2t m,n t m,n 1 y
2
, v m ,n
0
如果x=y ,则
t m ,n 1 v ,m , n 2 t m1,n t m1,n t m,n 1 t m,n 1 x 4
对于无内热源,且x=y
t m,n 1 tm1,n tm1,n tm,n1 tm,n1 4
根据泰勒级数可知一阶导数的近似公式
t n 1 t n x 2 t ( x) t ( x) x 2
tn2 tn1 tn1 tn tn2 2tn1 tn x x t ( x) x x 2
改进初场
是否收敛 是 解的分析
否
(1) 建立控制方程及定解条件 二维矩形域内稳态无内 热源,常物性的导热问题。 控制方程: 2t
传热学—第4章 热传导问题的数值解法

(k ) t max
⎧a11t1 + a12 t2 + a13t3 = b1 ⎪ ⎨a21t1 + a22 t2 + a23t3 = b2 ⎪a t + a t + a t = b 33 3 3 ⎩ 31 1 32 2
假定初场
⎧ (1) ⎪t1 = ⎪ ⎪ Jacobi ⎨t(1) = 2 ⎪ ⎪ (1) ⎪t3 = ⎩
4.1.1 4 1 1 基本思想 把原来在时间、空间坐标系中连续的物理量的场, 用有限个离散点上的值的集合来代替,通过求解按 定方 建 起来 关 值 代数方程 来获 一定方法建立起来的关于这些值的代数方程,来获 得离散点上被求物理量的值。 这些离散点上被求物理量值的集合称为该物理量 的数值解。
4.1.1 基本思想
λ Δy
Δx = Δy 时: tm −1,n
+ tm+1,n + tm,n+1 + tm,n−1 − 4tm,n = 0
tm ,n
1 = ( tm−1,n + tm+1,n + tm,n+1 + tm ,n−1 ) 4
与Taylor级数法相比,热平衡法物理意义明显。
4.3.1 边界节点离散方程的建立
4-2 内部节点离散方程的建立
4.2.1 4 2 1 Taylor级数展开法
4-2 内部节点离散方程的建立 内部节点离散方程的建
∂ 2t ∂x 2
=
m ,n
tm+1 n − 2tm ,n + tm −1 n 1, 1, Δx 2
控制方程
∂ 2t ∂ 2t + =0 ∂x 2 ∂y 2
∂ 2t ∂y 2
⎧a11t1 + a12 t2 + a13t3 = b1 ⎪ ⎨a21t1 + a22 t2 + a23t3 = b2 ⎪a t + a t + a t = b 33 3 3 ⎩ 31 1 32 2
假定初场
⎧ (1) ⎪t1 = ⎪ ⎪ Jacobi ⎨t(1) = 2 ⎪ ⎪ (1) ⎪t3 = ⎩
4.1.1 4 1 1 基本思想 把原来在时间、空间坐标系中连续的物理量的场, 用有限个离散点上的值的集合来代替,通过求解按 定方 建 起来 关 值 代数方程 来获 一定方法建立起来的关于这些值的代数方程,来获 得离散点上被求物理量的值。 这些离散点上被求物理量值的集合称为该物理量 的数值解。
4.1.1 基本思想
λ Δy
Δx = Δy 时: tm −1,n
+ tm+1,n + tm,n+1 + tm,n−1 − 4tm,n = 0
tm ,n
1 = ( tm−1,n + tm+1,n + tm,n+1 + tm ,n−1 ) 4
与Taylor级数法相比,热平衡法物理意义明显。
4.3.1 边界节点离散方程的建立
4-2 内部节点离散方程的建立
4.2.1 4 2 1 Taylor级数展开法
4-2 内部节点离散方程的建立 内部节点离散方程的建
∂ 2t ∂x 2
=
m ,n
tm+1 n − 2tm ,n + tm −1 n 1, 1, Δx 2
控制方程
∂ 2t ∂ 2t + =0 ∂x 2 ∂y 2
∂ 2t ∂y 2
计算传热学第11节-第4章 求解代数方程组2
x
柱坐标网格
Sun Jining 2008 @ BUAA
6
4 求解代数方程组
网格分类
结构化网格
贴体坐标网格 曲线坐标网格
Sun Jining 2008 @ BUAA
7
4 求解代数方程组
网格分类
非结构化网格
非结构化网格的根本特征:网格之间的相邻关系没有清晰的规律
Sun Jining 2008 @ BUAA
Sun Jining 2008 @ BUAA
11
4 求解代数方程组
网格分类
分块结构化网格
网格编号形式: (B,i,j) 每个块有一个数字编号B; 记录每个块的块的imax,jmax; 记录块边界网格的相邻网格编号
查找相邻网格过程 块内网格(i,j)相邻网格为(i+1,j) (i-1,j) (i,j+1) (i,j-1) A块边界网格(imax,j),则到记录列表中查找 其相邻网格
网格分类
Sun Jining 2008 @ BUAA
25
计算传热学
求解代数方程组 结束
Solving Algebraic Equations
孙纪宁
Sun Jining 2008 @ BUAA
26
网格分类
笛卡尔自适应网格
笛卡尔自适应网格的根本特征:整个区域的网格线均平行于直角坐 标轴,在物面、物理属性大梯度变化区域进行网格细化(1分2/4), 出现1个大网格对应2个小网格的特殊对应关系
Sun Jining 2008 @ BUAA
16
4 求解代数方程组
网格分类
嵌套网格
嵌套网格的根本特征:同一物理空间存在2套或2套以上的网格,各 个网格之间通过守恒或非守恒方式插值以交换计算数据
哈尔滨工业大学计算传热学第四章扩散方程的数值解法及其应用资料重点

1
y
xw
TP
aETE
aNTN
aSTS
1
y
xw
Tf
Scxy
kB
kB
所以对第三类边界条件不仅有附加常数源项,而且还有 附加源项的斜率项
aPTP aETE aNTN aSTS (Sc•ad Sc )xy
aP aE 0 aN aS (Sp•ad Sp )xy
Sp•ad
y xy
a)算术平均线性分布
ke
kp
xe+ xe
kE
xe xe
e
••
•
W
Pxe xe E
xe
b)调和平均
qe
TE TP
xe
ke
TE Te
xe
kE
Te Tp
xe
kp
TE
xe
kE
TP
xe
kP
ke
kP kExe xek p xekE
当 xe xe
kP kE
算术平均
ke
kP
kE 2
kP 2
第四章 扩散方程的数值解法及其应用
§4.1 一维稳态导热
1 • d [kF(x) dT ] S 0
F (x) dx
dx
F(x):与坐标系和截面形状有关的计算因子
S:内热源。
w
e
△x
e d
dT
[kF (x) ]dx
w dx
dx
e
F (x) • Sdx 0
w
•
W
xw
•
P
xe
•
E
keFe
W PE
ap
Fe k e
xe
第五版传热学第四章

3.C++ —— C plus plus,C语言的增强版,目前最常用的应用程序设计 语言,数值计算软件主要使用的语言。
二、常用计算软件
1.MATLAB——矩阵计算软件
matlab软件主界面
2.FLUENT——流体流动通用数值计算软件
3. FLUENT AIRPAK ——人工环境系统分析软件,暖通空调专业和传热学领域必备软件
第四章 导热数值解法基础
本章研究的目的 ——利用计算机求解难以用 分析解求解的导热问题 基本思想 ——把原来在时间、空间坐 标系中连续的物理量的场, 用有限个离散点的值的集合 来代替,通过求解按一定方 法建立起来的关于这些值的 代数方程,来获得离散点 上被求物理量的值。 研究手段——有限差分法
物理问题的数值求解过程
优点——无条件稳定 缺点——不可根据kΔ τ 时刻温度分布直接计算 (k+1)Δ τ 时刻温度分布
ቤተ መጻሕፍቲ ባይዱ
第四节 常用算法语言和计算软件简介
一、常用算法语言
1.FORTRAN语言 ——Formula Translation,数值计算领域所使用的主要语言。
2.C语言 ——将高级语言的基本结构和语句与低级语言的对地址操作结合 起来的应用程序设计语言。
k k k k ti Fo ti 1 ti 1 1 2 Foti
优点——可根据kΔ τ 时刻温度分布直接计算(k+1)Δ τ 时刻温度分布 缺点——选择Δ x和 Δ τ 时必须满足稳定性条件 a a 1 或 1 2 0 2 2 x x 2
第三节 非稳态导热的数值计算
研究对象——一维非稳态导热问题 一、显式差分格式
t 2t a x 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 0
u jn 1
0 0 lij
lnj
0 1 u12 0 1 0 0 0 0 lnn 0 0
A LU
AX LUX b
u1 j u1n 令 u2 n Y UX u jn 则 LY b 1
克服发散算法通常增加计算时间,但不必然增加计算时间
Sun Jining 2008 @ BUAA
26
4 求解代数方程组
迭代求解方法
SIP迭代(强隐过程迭代)
Sun Jining 2008 @ BUAA
27
lim[T ]n [T ] *
n
Sun Jining 2008 @ BUAA
17
4 求解代数方程组
迭代求解方法
点迭代
Jacobi点迭代格式 aPTPk+1=aETEk +aWTWk +aNTNk +aSTSk + b Gauss-Seidel点迭代格式 aPTPk+1=aETEk +aWTWk+1 +aNTNk +aSTSk+1 + b n=1
Sun Jining 2008 @ BUAA
22
例:设有一正方形区域,其边界温度如图。物体 内无热源,物性为常数。试分别用Jacobi点迭代、 G-S点迭代及线迭代求解稳态导热问题(1、2、3、 4点的温度)
Jacobi点迭代
G-S点迭代
线迭代
4 求解代数方程组
迭代求解方法
加速收敛
当然,迭代函数
x
*
xk
( x)
Sun Jining 2008 @ BUAA 16
的构造方法是多种多样的。
上若干节回顾
f ( x) 0 x ( x)
xk 1 ( xk )
lim xn x *
n
[ A][T ] [b]
[T ] [ A*][T ] [b*]
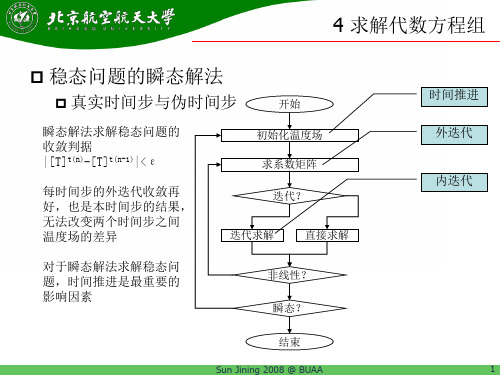
开始 初始化温度场 求系数矩阵
时间推进 外迭代
内迭代
迭代?
迭代求解
直接求解
非线性? 瞬态? 结束
Sun Jining 2008 @ BUAA 7
4 求解代数方程组
代数方程组分类
线性代数方程组(内迭代) 求解线化了的代数方程组
[A][T]=[b] 非线性代数方程组(外迭代) 代数方程组系数的更新 [A([T])][T]=[b([T])]
[T ]k 1 [ A*][T ]k [b*]
lim[T ]n [T ] *
n
[ A([T ])][ T ] [b([T ])]
[T ] [ A * ([T ])][T ] [b * ([T ])]
[T ]k 1 [ A * ([T ]k )][T ]k [b * ([T ]k )]
a11 a 21j 2 ai1 an1 a12
22 i2 n2
a1n a2 j 2 a 2 n n aij ain anj jn ann a1 j
11
12
1j
1n
21
22
2j
2n
l l l 0 ij i1 i 2 0 0 l l l l nj nn 0 0 n1 n 2A LU
* x 即如果数
x1 ( x 0 )
再将 x1 代入式 x ( x) 的右端, 得到 x2 依此类推, 得到一个数列 x3 ( x2 ) …, 其一般表示
xk 1 ( xk ) (k 0,1,2,)
( x1 ) ,
(2.4)
15
式(2.4)称为求解非线性方程的简单迭代法。
Sun Jining 2008 @ BUAA
8
4 求解代数方程组
线性代数方程组(内迭代)
直接求解方法
高斯消元法 LU分解法 TDMA方法
迭代求解方法
Jacobi点迭代 Gauss-Seidel迭代 亚松弛与超松弛 线迭代 ADI迭代 显式迭代与隐式迭代 SIP迭代
Sun Jining 2008 @ BUAA
如果由迭代格式 xk 1 ( xk ) 产生的序列 xn 收敛, 即 lim x n x *
n
则称迭代法收敛。
实际计算中当然不可能也没必要无穷多步地做 下去, 对预先给定的精度要求ε,只要某个k满足
xk xk 1
即可结束计算并取
可以直接求解的线性代数方程组 需要迭代求解的线性代数方程组 需要迭代求解的非线性方程组 需要时间推进的非线性方程组
Sun Jining 2008 @ BUAA
5
4 求解代数方程组
最复杂的求解过程
Sun Jining 2008 @ BUAA
6
4 求解代数方程组
最复杂的导热求解过程
11 12 1j 1n 21 22 2j 2n
ai1 an1
ai 2 an 2
aij anj
ain ann
u a u 4 求解代数方程组 a 1 a u 0 0 0 1 u l u u l l 0 0 0 1 u u 1 0
n=0
Sun Jining 2008 @ BUAA
20
4 求解代数方程组
迭代求解方法
ADI迭代
Jacobi ADI迭代格式 aPTPk+1/2=aETEk+1/2 +aWTWk+1/2 +aNTNk +aSTSk + b aPTPk+1=aETEk+1/2 +aWTWk+1/2 +aNTNk+1 +aSTSk+1 + b Gauss-Seidel ADI迭代格式 aPTPk+1/2=aETEk+1/2 +aWTWk+1/2 +aNTNk +aSTSk+1/2 + b aPTPk+1=aETEk+1 +aWTWk+1/2 +aNTNk+1 +aSTSk+1 + b n=2 n=3
n=0 n=1
Sun Jining 2008 @ BUAA
21
4 求解代数方程组
迭代求解方法
显式迭代与隐式迭代
显式迭代:新一轮计算完全用上一轮迭代值计算 Jacobi点迭代格式 aPTPk+1=aETEk +aWTWk +aNTNk +aSTSk + b 隐式迭代:新一轮计算完全用本轮迭代值 计算 直接求解 aPTPk+1=aETEk+1 +aWTWk+1 +aNTNk+1 +aSTSk+1 + b 部分隐式迭代:新一轮计算部分用上一轮迭代 值计算,部分用本轮迭代值计算 Gauss-Seidel点迭代格式、线迭代、ADI迭代 n=0 n=1 n=2 n=3
4 求解代数方程组
物理问题分类
二维稳态物理属性为常数的导热问题
——对角占优的常系数矩阵线性代数方程组 二维瞬态物理属性为温度函数的导热问题 ——按时间步推进,每时间步为系数矩阵为求解变量 函数的非线性代数方程组
Sun Jining 2008 @ BUAA
4
4 求解代数方程组
求解方程分类
计算传热学
第4章 求解代数方程组
Solving Algebraic Equations
Sun Jining 2008 @ BUAA
1
4 求解代数方程组
物理问题分类
一维稳态物理属性为常数的导热问题
——三对角常系数矩阵线性代数方程组 一维稳态物理属性为温度函数的导热问题 ——三对角系数矩阵为求解变量函数的非线性代数方程 组
n=0
Sun Jining 2008 @ BUAA
18
4 求解代数方程组
迭代求解方法
亚松弛与超松弛
aPTP*=aETEk +aWTWk +aNTNk +aSTSk + b TPk+1 =fTP* +(1-f)TPk 0<f<1时为亚松弛,亚松弛可以减小每步变化量,避免发散 1<f时为超松弛,超松弛可以放大每步变化量,加速收敛 超松弛Tk+1
收敛速度是指达到一定的残差需要用多少轮迭代
对线性代数方程组,加速收敛有两类主要思路 一类是通过超松弛,放大每步变化的量,使之加速逼近真值 一类是通过增加迭代公式中隐式迭代的比例,使每一步内各节点相互 影响更充分,影响因素更快向各个方向扩展 加速收敛算法不一定减少计算时间 计算时间不但取决于迭代步数,还取决于每迭代步的计算量 隐式比例越重,每迭代步计算量越大
Sun Jining 2008 @ BUAA
2
一维瞬态物理属性为常数的导热问题,时间显式格式 ——按时间步推进,每时间步做代数计算,不需要求解代数方程组 一维瞬态物理属性为常数的导热问题,时间隐式格式 ——按时间步推进,每时间步为三对角常系数矩阵线性代数方程组 一维瞬态物理属性为温度函数的导热问题,时间显式格式 ——按时间步推进,时间步做代数计算,不需要求解代数方程组 一维瞬态物理属性为温度函数的导热问题,时间隐式格式 ——按时间步推进,每时间步为三对角系数矩阵为求解变量函数 的非线性代数方程组
