ADAMS数学函数
ADAMS常用函数的说明
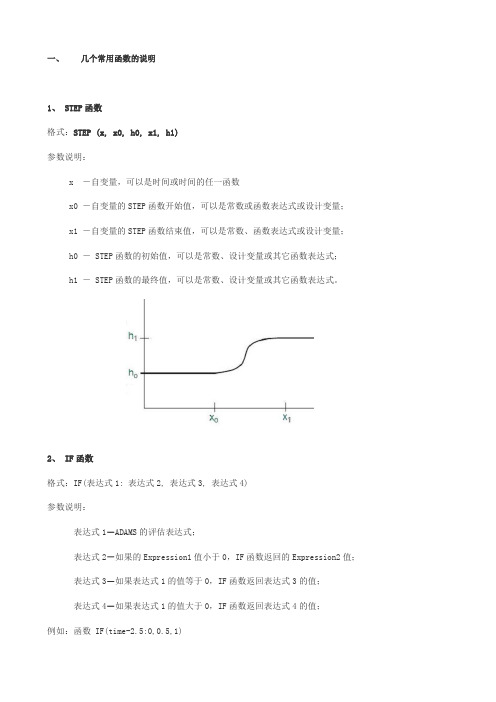
一、几个常用函数的说明1、 STEP函数格式:STEP (x, x0, h0, x1, h1)参数说明:x ―自变量,可以是时间或时间的任一函数x0 ―自变量的STEP函数开始值,可以是常数或函数表达式或设计变量;x1 ―自变量的STEP函数结束值,可以是常数、函数表达式或设计变量;h0 ― STEP函数的初始值,可以是常数、设计变量或其它函数表达式;h1 ― STEP函数的最终值,可以是常数、设计变量或其它函数表达式。
2、 IF函数格式:IF(表达式1: 表达式2, 表达式3, 表达式4)参数说明:表达式1-ADAMS的评估表达式;表达式2-如果的Expression1值小于0,IF函数返回的Expression2值;表达式3-如果表达式1的值等于0,IF函数返回表达式3的值;表达式4-如果表达式1的值大于0,IF函数返回表达式4的值;例如:函数IF(time-2.5:0,0.5,1)结果:0.0 if time < 2.50.5 if time = 2.51.0 if time >2.53、AKISPL函数格式:AKISPL (First Independent Variable, Second Independent Variable,Spline Name, Derivati ve Order)参数说明:First Independent Variable ——spline中的第一个自变量Second Independent Variable(可选) ——spline中的第二自变量Spline Name ——数据单元spline的名称Derivative Order(可选) ——插值点的微分阶数,一般用0就可以了例如:function = AKISPL(DX(marker_1, marker_2), 0, spline_1)spline_1用下表中的离散数据定义:AKISPL的拟合曲线如下:二、实例说明1、分段函数的表示在ADMA中如何输入力或位移、速度、加速度等的分段曲线,这一直是一个值得注意的问题。
adams函数学习总结

矩阵/数组函数
• • • • 矩阵/数组的基本操作函数 ALIGN 将数组转换到从特定值开始 ALLM 返回矩阵元素的逻辑值 ANGLES 将方向余弦矩阵转换为指定旋转顺序下的 角度矩阵 ANYM 返回矩阵元素的逻辑和 APPEND 将一个矩阵中的行添加到另一矩阵 CENTER 返回数列最大、最小值的中间值 CLIP 返回矩阵的一个子阵 COLS 返回矩阵列数 COMPRESS 压缩数组、删除其中的空值元素(零,空字符及空格) CONVERT ANGLES 将313旋转顺序转化为用户自定义的旋转顺序 CROSS 返回两矩阵的向量积 DET 返回方阵M的行列式值
位置/方向函数
一、位置函数
LOC_ALONG_LINE LOC_CYLINDRICAL LOC_FRAME_MIRROR LOC_GLOBAL LOC_INLINE 下的坐标值并归一化 LOC_LOC 下的坐标值 LOC_LOCAL LOC_MIRROR LOC_ON_AXIS LOC_ON_LINE LOC_PERPENDICULAR LOC_PLANE_MIRROR LOC_RELATIVE_TO LOC_SPHERICAL LOC_X_AXIS LOC_Y_AXIS LOC_Z_AXIS 返回两点连线上与第一点距离为指定值的点 将圆柱坐标系下坐标值转化为笛卡儿坐标系下坐标值 返回指定点关于指定坐标系下平面的对称点 返回参考坐标系下的点在全局坐标系下的坐标值 将一个参考坐标系下的坐标值转化为另一参考坐标系
样条插值 AKIMA_SOLINE 使用Akima迭代插值法生成内插样条曲线 CSPLINE 生成3次内插样条曲线 CUBIC_SPLINE 生成3阶内插多项式曲线 DETREND 返回最小二乘拟合曲线与输入数据的差值 HERMITE_SPLINE 使用荷尔米特插值法生成内插样条曲线 LINEAR_SPLINE 线性插值生成内插样条曲线 NOTAKNOT_SPLINE 生成3次光顺连续插值样条曲线 SPLINE 生成插值样条曲线 频域分析 FFTMAG 返回快速傅立叶变换后的幅值 FFTPHASE 返回快速傅立叶变换后的相位 FILTER 返回按指定格式滤波处理后的数据 FREQUENCY 返回快速傅立叶变换频率数 HAMMING 采用HAMMING窗处理数据 HANNING 采用HANNING窗处理数据 WELCH 采用WELCH窗处理数据 PSD 计算功率谱密度
adams函数使用方法介绍

LOC_LOCAL LOC_MIRROR LOC_ON_AXIS LOC_ON_LINE LOC_PERPENDICULAR LOC_PLANE_MIRROR LOC_RELATIVE_TO LOC_SPHERICAL LOC_X_AXIS LOC_Y_AXIS LOC_Z_AXIS
step(time,0,0,1,-30*time)+step(time,1,0,3,-30+58*(time-1))+step(time,3,0,4,8664.5*(time-3))+step(time,4,0,5,21.5-21.5*(time-4))
If函数
• 在ADMA中如何输入力或位移、速度、加速度等的分段曲 线,这一直是一个值得注意的问题。
数字表达式x取整 数字表达式x向绝对值小的方向取整 数字表达式x向绝对值大的方向取整 数字表达式x向正无穷的方向取整 数字表达式x向负无穷的方向取整 最接近数字表达式x的整数值 返回数字表达式x的整数部分
位置/方向函数
一、位置函数
LOC_ALONG_LINE LOC_CYLINDRICAL LOC_FRAME_MIRROR LOC_GLOBAL LOC_INLINE 下的坐标值并归一化
在使用后者的过程中很多人会误表示为: step(time,0,0d,3,0d)+ step(time,3,0d,5,5d)+ step(time,5,5d,8,5d)+ step(time,8,5d,10,0d)+ step(time,10,0d,12,0d) 还有一种是错误的: step(time,3,0d,5,5d)+ step(time,8,5d,10,0d) 这两种都是错误的表示的方法,不信你自己可以试试的
ADAMS常用函数的说明

一、几个常用函数的说明1、 STEP函数格式:STEP (x, x0, h0, x1, h1)参数说明:x ―自变量,可以是时间或时间的任一函数x0 ―自变量的STEP函数开始值,可以是常数或函数表达式或设计变量;x1 ―自变量的STEP函数结束值,可以是常数、函数表达式或设计变量;h0 ― STEP函数的初始值,可以是常数、设计变量或其它函数表达式;h1 ― STEP函数的最终值,可以是常数、设计变量或其它函数表达式。
2、 IF函数格式:IF(表达式1: 表达式2, 表达式3, 表达式4)参数说明:表达式1-ADAMS的评估表达式;表达式2-如果的Expression1值小于0,IF函数返回的Expression2值;表达式3-如果表达式1的值等于0,IF函数返回表达式3的值;表达式4-如果表达式1的值大于0,IF函数返回表达式4的值;例如:函数IF(time-2.5:0,0.5,1)结果:0.0 if time < 2.50.5 if time = 2.51.0 if time >2.53、AKISPL函数格式:AKISPL (First Independent Variable, Second Independent Variable,Spline Name, Derivati ve Order)参数说明:First Independent Variable ——spline中的第一个自变量Second Independent Variable(可选) ——spline中的第二自变量Spline Name ——数据单元spline的名称Derivative Order(可选) ——插值点的微分阶数,一般用0就可以了例如:function = AKISPL(DX(marker_1, marker_2), 0, spline_1)spline_1用下表中的离散数据定义:AKISPL的拟合曲线如下:二、实例说明1、分段函数的表示在ADMA中如何输入力或位移、速度、加速度等的分段曲线,这一直是一个值得注意的问题。
ADAMS函数简介

ADAMS/View函数及ADAMS/Solver函数的类型及建立ADAMS/View函数包括设计函数Design-Time Functions与运行函数Run-Time Functions两种类型,函数的建立对应有表达式模式和运行模式两种。
表达式模式下在设计过程中对设计函数求值,而运行模式下会在仿真过程中对运行函数进行计算更新。
ADAMS/Solver函数支持ADAMS/View运行模式下的函数,在仿真过程中采用ADAMS/Solver 解算时对这些函数进行计算更新。
建立表达式模式下的函数在进行建立表达式、产生和修改需要计算的测量及建立设计函数等操作时,会采用表达式模式。
在建立表达式时,首先在接受表达式的文本框处右击,然后选择“Parameterize”再选择“Expression Euilder”,进入建立设计函数表达式对话框。
在该对话框中输入表达式,然后单击“OK”完成操作。
在产生和修改需要计算的测量时,首先在“Build”菜单中选择“Measure”,然后指向“Computed”,再选择“New”或“Modified”确定是新建还是修改,进入产生和修改需要计算的测量对话框。
在该对话框中输入表达式,然后单击“OK”完成操作。
在建立设计函数时,首先在“Build”菜单中选择“Function”,然后选择“New”或“Modified”确定是新建还是修改,进入产生和修改设计函数对话框。
在该对话框中输入表达式,然后单击“OK”完成操作。
建立运行模式下的函数在进行建立运行函数、产生和修改函数型的测量等操作时,会采用运行模式。
在建立运行函数时,首先在接受表达式的文本框处右击,然后选择“Function Euilder”,进入建立运行函数表达式对话框。
在该对话框中输入表达式,然后单击“OK”完成操作。
在产生和修改函数型的测量时,首先在“Build”菜单中选择“Measure”,然后指向“Function”,再选择“New”或“Modified”确定是新建还是修改,进入产生和修改函数型的度量对话框。
adams幂函数表达

adams幂函数表达
(原创版)
目录
1.介绍 Adams 幂函数
2.Adams 幂函数的表达式
3.Adams 幂函数的性质和应用
正文
Adams 幂函数是一种以数学家 Adams 命名的函数,它是幂函数的一种。
幂函数是指形如 y=x^n 的函数,其中 n 是实数,而 Adams 幂函数则是幂函数的一种广义形式。
Adams 幂函数的表达式为 y=x^(1/n),其中 x 是自变量,n 是正实数。
这个函数的图像在 x=0 处无定义,而在 x>0 时是增函数,x<0 时是减函数。
Adams 幂函数在 x=1 处取得最大值,即 y=1,而在 x=-1 处取得最小值,即 y=-1。
Adams 幂函数具有很多重要的性质。
例如,它是偶函数,即满足
y(x)=y(-x) 的函数。
这意味着它的图像关于 y 轴对称。
此外,Adams 幂函数的导数是 y"=n*x^(1/n-1),这个导数在 x=0 处无定义,但在 x>0 时是增函数,x<0 时是减函数。
Adams 幂函数在很多领域都有应用。
例如,在计算机科学中,它常用于插值和逼近问题。
在物理学中,它也常用于描述物体的运动。
在经济学中,它则可以用于描述价格和需求的关系。
第1页共1页。
ADAMS常用函数
在使用adams的过程中,由于函数比较多,大概有11种之多,如1、Displacement Function 2、Velocity Functions 3、Acceleration Functions 4、Contact Functions 5、Spline Functions 6、Force in Object Functions 7、Resultant Force Functions 8、Math Functions 9、Data Element Access 10、User-Written Subroutine Invocation 11、Constants & Variables。
在adams中也有帮助文档,但是对于初学者来说还是有一定的难度的,基于这种情况我总结了一下几种常用的函数,希望能够起到抛砖引玉的作用!1、STEP函数格式:STEP (x, x0, h0, x1, h1)参数说明:x―自变量,可以是时间或时间的任一函数x0 ―自变量的STEP函数开始值,可以是常数或函数表达式或设计变量;x1 ―自变量的STEP函数结束值,可以是常数、函数表达式或设计变量h0 ―STEP函数的初始值,可以是常数、设计变量或其它函数表达式h1 ―STEP函数的最终值,可以是常数、设计变量或其它函数表达式2、IF函数格式:IF(表达式1: 表达式2, 表达式3, 表达式4)参数说明:表达式1-ADAMS的评估表达式;表达式2-如果的Expression1值小于0,IF函数返回的Expression2值;表达式3-如果表达式1的值等于0,IF函数返回表达式3的值;表达式4-如果表达式1的值大于0,IF函数返回表达式4的值;例如:函数IF(time-2.5:0,0.5,1)结果:0.0 if time < 2.50.5 if time = 2.51.0 if time >2.53、AKISPL函数格式:AKISPL (First Independent Variable, Second Independent Variable,Spline Name, Derivative Order)参数说明:First Independent Variable——spline中的第一个自变量Second Independent Variable (可选) ——spline中的第二自变量Spline Name——数据单元spline的名称Derivative Order (可选) ——插值点的微分阶数,一般用0就可以function = AKISPL(DX(marker_1, marker_2, marker_2), 0, spline_1)spline_1用下表中的离散数据定义自变量x 函数值y-4.0 -3.6-3.0 -2.5-2.0 -1.2-1.0 -0.40.0 0.01 0.42 1.23 2.54 3.64、碰撞函数impact其实质是:用只抗压缩的非线性的弹簧阻尼方法近似计算出单边碰撞力。
【2017年整理】ADAMS常用函数的说明
一、几个常用函数的说明1、 STEP函数格式:STEP (x, x0, h0, x1, h1)参数说明:x ―自变量,可以是时间或时间的任一函数x0 ―自变量的STEP函数开始值,可以是常数或函数表达式或设计变量;x1 ―自变量的STEP函数结束值,可以是常数、函数表达式或设计变量;h0 ― STEP函数的初始值,可以是常数、设计变量或其它函数表达式;h1 ― STEP函数的最终值,可以是常数、设计变量或其它函数表达式。
2、 IF函数格式:IF(表达式1: 表达式2, 表达式3, 表达式4)参数说明:表达式1-ADAMS的评估表达式;表达式2-如果的Expression1值小于0,IF函数返回的Expression2值;表达式3-如果表达式1的值等于0,IF函数返回表达式3的值;表达式4-如果表达式1的值大于0,IF函数返回表达式4的值;例如:函数IF(time-2.5:0,0.5,1)结果:0.0 if time < 2.50.5 if time = 2.51.0 if time >2.53、AKISPL函数格式:AKISPL (First Independent Variable, Second Independent Variable,Spline Name, Derivati ve Order)参数说明:First Independent Variable ——spline中的第一个自变量Second Independent Variable(可选) ——spline中的第二自变量Spline Name ——数据单元spline的名称Derivative Order(可选) ——插值点的微分阶数,一般用0就可以了例如:function = AKISPL(DX(marker_1, marker_2), 0, spline_1)spline_1用下表中的离散数据定义:AKISPL的拟合曲线如下:二、实例说明1、分段函数的表示在ADMA中如何输入力或位移、速度、加速度等的分段曲线,这一直是一个值得注意的问题。
ADAMS常用函数文本说明
ADAMS常用函数文本说明ADAMS常用函数文本说明在使用adams的过程中,由于函数比较多,大概有11种之多,如1、Displacement Function2、Velocity Functions3、 Acceleration Functions4、 Contact Functions5、 Spline Functions6、 Force in Object Functions7、Resultant Force Functions8、 Math Functions9、 Data Element Access10、User-Written Subroutine Invocation11、Constants & Variables。
……在adams中也有帮助文档,但是对于初学者来说还是有一定的难度的,基于这种情况我总结了一下几种常用的函数,希望能够起到抛砖引玉的作用!1、 STEP函数格式:STEP (x, x0, h0, x1, h1)参数说明:x ―自变量,可以是时间或时间的任一函数x0 ―自变量的STEP函数开始值,可以是常数或函数表达式或设计变量;x1 ―自变量的STEP函数结束值,可以是常数、函数表达式或设计变量h0 ― STEP函数的初始值,可以是常数、设计变量或其它函数表达式h1 ― STEP函数的最终值,可以是常数、设计变量或其它函数表达式2、 IF函数格式:IF(表达式1: 表达式2, 表达式3, 表达式4)参数说明:表达式1-ADAMS的评估表达式;表达式2-如果的Expression1值小于0,IF函数返回的Expression2值;表达式3-如果表达式1的值等于0,IF函数返回表达式3的值;表达式4-如果表达式1的值大于0,IF函数返回表达式4的值;例如:函数 IF(time-2.5:0,0.5,1)结果: 0.0 if time < 2.50.5 if time = 2.51.0 if time >2.53、AKISPL函数格式:AKISPL (First Independent Variable, Second Independent Variable,Spline Name, Derivative Order) 参数说明:First Independent Variable ——spline中的第一个自变量Second Independent Variable (可选) ——spline中的第二自变量Spline Name ——数据单元spline的名称Derivative Order (可选) ——插值点的微分阶数,一般用0就可以function = AKISPL(DX(marker_1, marker_2, marker_2), 0, spline_1)spline_1用下表中的离散数据定义自变量x 函数值y-4.0 -3.6-3.0 -2.5-2.0 -1.2-1.0 -0.40.0 0.01 0.42 1.23 2.54 3.64、碰撞函数impact其实质是:用只抗压缩的非线性的弹簧阻尼方法近似计算出单边碰撞力。
adams函数使用方法介绍
在使用后者的过程中很多人会误表示为: step(time,0,0d,3,0d)+ step(time,3,0d,5,5d)+ step(time,5,5d,8,5d)+ step(time,8,5d,10,0d)+ step(time,10,0d,12,0d) 还有一种是错误的: step(time,3,0d,5,5d)+ step(time,8,5d,10,0d) 这两种都是错误的表示的方法,不信你自己可以试试的
二、方向函数
ORI_ALIGN_AXIS 的角度
将坐标系按指定方式旋转至与指定方向对齐所需旋转
ORI_ALONG_AXIS_EUL 对齐所需旋转的角度
将坐标系按指定方式旋转至与全局坐标系一个轴方向
ORI_ALL_AXES
将坐标系旋转至由平面上的点定义的特定方向(第一
轴与指定平面上两点连线平行,第二轴与指定平面平行)时所需旋转的角度
总结:从上面的例子中大家可以清楚的看出,增量式明显比嵌 入式要简洁的多,但是嵌入式却比增量式思路要清晰、严谨的 多,他们各有自己的优点,所以大家可以针对性的使用他们, 习惯用什么方式就用什么方式,当然他们还有其他的不同点我 还没想到的,也欢迎你多多提出意见。
IF与step
• IF(x1: x2, x3, x4) 如果x1<0,返回x2;
ORI_ALONG_AXIS 的角度
将坐标系旋转至其一轴线沿指定轴线方向时所需旋转
ORI_FRAME_MIRROR ORI_GLOBAL ORI_IN_PLANE 指定平面平行时所需旋转的角度
返回坐标系旋转镜像到指定坐标系下所需旋转的角度 返回参考坐标系在全局坐标系下的角度值 将坐标系旋转至特定方向(与指定两点连线平行、与
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
LOC_ON_AXIS(Fra me,Distance,Axi s) LOC_ON_LINE(Loc ation1,location 2,Distance) LOC_PERPENDICUL AR(Location1,Lo cation2,Locatio n3) LOC_PLANE_MIRRO R(Location,Loca tion1,Location2 ,Location3) LOC_RELATIVE_TO (Location,Frame ) LOC_SPHERICAL(R ho,Theta,Phi) LOC_X_AXIS(Fram e) LOC_Y_AXIS(Fram e) LOC_Z_AXIS(Fram e)
将一个坐标系 Frame 某个轴与另一个坐标系 Frame 的某个轴 重合时,需要转过的角度,Axis Spec 可以是 xx,xy,xz, ORI_ALIGN_AXIS( yx,yy,yz,zx,zy,zz,x+x,x+y,x+z,y+x,y+y,y+z,z+x, Frame,Axis Spec) z+y,z+z,x-x,x-y,x-z,y-x,y-y,y-z,z-x,z-y 和 z-z,+表示 正的方向,-表示反方向,例如 ORI_ALIGN_AXIS(marker_1, “z-z”),返回值与当前的旋转序列有关 Location1-Location3 确定一个坐标系,Axes 确定坐标系的 轴,Axes 的取值为 xy,yx,xz,zx,yz 和 zy,Axes 确定的 ORI_ALL_AXES(Lo 第一个轴与 Location1 和 Location2 确定的直线平行,Axes cation1,Locatio 确定的第二个轴在 Location1,Location2,Location3 平面 n2,Location3,Ax 内, ORI_ALL_AXES 返回坐标系的按照 313 旋转序列的欧拉角, es) 例如 ORI_ALL_AXES({{14,18,0},{10,14,0},{16,14,0}}, “xz”) 将一个坐标系的某个轴转到与一条直线平行时,需要旋转的 ORI_ALONG_AXIS( 角度,其中 From Frame 确定直线的起始点,To Frame 确定 From Frame,To 直线的终止点, Axis 的取值为 x, y 或 z, 例如 ORI_ALONG_AXIS Frame,Axis) (marker_1,marker_2,“y”) ORI_ALIGN_AXIS_ 将一个坐标系的一个轴与另一个坐标系的一个轴旋转到平
பைடு நூலகம்
AZ(Object, Frame) PSI(Object, Frame) THETA(Object, Frame) PHI(Object, Frame) YAW(Object, Frame) PICH(Object, Frame) ROLL(Object, Frame)
返回坐标系 Object 相对于参考坐标系 Frame 的 Z 轴旋转的 角度 返回坐标系 Object 相对于参考坐标系 Frame 按照 313 旋转 序列的第一个转角,即欧拉角中的章动角 返回坐标系 Object 相对于参考坐标系 Frame 按照 313 旋转 序列的第二个转角,即欧拉角中的拉动角 返回坐标系 Object 相对于参考坐标系 Frame 按照 313 旋转 序列的第三个转角,即欧拉角中的自转角 返回坐标系 Object 相对于参考坐标系 Frame 按照 321 旋转 序列的第一个转角 返回坐标系 Object 相对于参考坐标系 Frame 按照 321 旋转 序列的第二个转角 返回坐标系 Object 相对于参考坐标系 Frame 按照 321 旋转 序列的第三个转角
返回沿某坐标系的某个坐标轴距原点为 Distance 的点坐标 值,例如 LOC_ON_AXIS)(marker_2,5,“x”) 点 Location1 和点 Location2 决定一条直线,沿该直线点 Location1 距离为 Distance 得到的点的坐标,例如 LOC_ON_LINE({{7,5,0},{15,11,0}},7) 由 Location1,Location2,Location3 得到一个平面,在过 Location1 与该平面垂直的直线上确定一点,且该点与 Location 的距离为 1, 例如 LOC_PERPENDICULAR ({{10,12,0}, {14,12,0},{12,10,0}})将得到 10,12,1 由 Location1,Location2,Location3 确定一个平面,将 Location 沿该平面进行镜像而得到一个点,例如 LOC_PLANE_MIRROR({2,4,0},{{10,12,0},{14,12,0},{12,1 0,0}}) 将坐标系 Frame 中表示的点 Location 转换到全局坐标系中, 例如 LOC_RELATIVE_TO({16,8,0},marker_2) 将球坐标系表示的点(Rho,Theta,Phi)转换成直角坐标 系中表示的点(x,y,z) 返回坐标系 Frame 的 X 轴在总体坐标系中的分量 返回坐标系 Frame 的 Y 轴在总体坐标系中的分量 返回坐标系 Frame 的 Z 轴在总体坐标系中的分量
IF
MODE
表 2 建模函数(Modeling Functions)
函数及格式 DX(Object1, Object2,Frame) DY(Object1, Object2,Frame) DZ(Object1, Object2,Frame) DM(Object1, Object2) AX(Object, Frame) AY(Object, Frame) 函数功能 返回坐标系 Object1 相对于 Object2 在参考坐标系 Frame 的 X 轴方向的位移 返回坐标系 Object1 相对于 Object2 在参考坐标系 Frame 的 Y 轴方向的位移 返回坐标系 Object1 相对于 Object2 在参考坐标系 Frame 的 Z 轴方向的位移 返回坐标系 Object1 相对于 Object2 的位移 返回坐标系 Object 相对于参考坐标系 Frame 的 X 轴旋转的 角度 返回坐标系 Object 相对于参考坐标系 Frame 的 Y 轴旋转的 角度
表 3 数学函数(Math Functions)
函数及格式 ABS(x) ACOS(x) AINT(x) ANINT(x) ASIN(x) ATAN(x) 函数功能 返回参数 x 的绝对值 返回参数 x 的反余弦值 返回参数 x 向零取整的整数,例如 AINT(-6.5)=-6,AINT(4.6)=4 返回参数 x 背离零取整的整数,例如 ANINT(-4.6)=-5,ANINT(4.6)=5 返回参数 x 的反正弦值 返回参数 x 的反正切值 返回参数 x1/x2 的反正切值,且满足 ATAN2(x1,x2)>0,如 果 x1>0;ATAN2 (x1,x2) =0, 如果 x1=0, x2>0;ATAN2(x1,x2)=
将一个点相对于一个平面进行镜像,得到另外一个对称点, Location 指点的坐标值,Frame 指坐标系,Plane 指坐标系 的 xy,yx,xz,zx,yz 和 zy 面,例如 LOC_FRAME_MIRROR ({5,6,30},marker_2,“zy”) 将一个在局部坐标系 Frame 表示的一个坐标值 Location, 转 LOC_GLOBAL(Loca 换到全局坐标系中的坐标值, 例如 LOC_GLOBAL ({-5, -8,0}, tion,Frame) marker_1) LOC_INLINE(Loca 将一个在某坐标系中表示的坐标值转换到另一个坐标系表 tion,In Frame,To 示的坐标值,并将新的坐标值用本身的模型进行归一化,例 Frame) 如 LOC_INLINE({-18,-2,30},marker_1,marker_2) LOC_LOC(Locatio 将一个在某坐标系中表示的坐标值转换到另一个坐标系表 n,In Frame,To 示的坐标值 Frame) LOC_LOCAL(Locat 将一个在全局坐标系中表示的坐标值转换到另一个局部坐 ion,Frame) 标系中表示的坐标值 LOC_MIRROR(Loca 将一个点相对于一个平面进行镜像,得到另外一个对称点, tion,Frame,Plan Location 指点的坐标值,Frame 指坐标系,Plane 指坐标系 e) 的 xy,yx,xz,zx,yz 和 zy 面
表 1 常值函数(Constants)
函数 PI TWO_PI HALF_PI THREE_HALVES_PI RTOD 指圆周率 表示 2 表示 /2 表示 3 /2 将一个弧度值转换成度数值时的乘积系数,它等于 180 / , 例如 *RTOD 表示 180 DTOR SIN45 SQRT2 TIME 将一个度数值转换成弧度值时的乘积系数,它等于 / 180 , 例如 180*DTOR 表示 表示 sin(45 ) ,即 2 / 2 表示 2 TIME 是一个状态变量,它含有多个时间值,记录了仿真过程 中每帧的时间,并返回当前的仿真时间 IF 函数是一个判断函数,其格式为 IF (表达式 1:表达式 2, 表达式 3, 表达式 4) , 如果表达式 1<0, 返回表达式 2 的值, 如果表达式 1=0,返回表达式 3 的值,如果表达式 1>0,返 回表达式 4 的值。 MODE 是一个变量, 返回当前的仿真类型, 1 表示 Kinematics, 2 表示 Reserved,3 表示 Initialconditions,4 表示 Dynamics,5 表示 Statics,6 表示 Quasi-statics,7 表示 Linearanalysis,MODE 常用语脚本仿真控制中 函数功能
ATAN2(x1,x2)
CEIL(x) COS(x) COSH(x) DIM(x1,x2) EXP(x) FLOOR(x) INT(x)
