综合与实践一次函数模型的应用
沪科版数学八年级上册12.4综合与实践——一次函数模型的应用课件(共21张PPT)

(2)设获得的利润为y元,由题意,得y=50[4x+2(150-x)] +80[2x+6(150-x)],即 y= -220x+87 000.因为-220<0,所以y随x的增大而减小,所以 x=50时,y取得最大值,最大值为 -220×50+87000 = 76 000.答:该工艺厂购买A,B两类原木分别为50根和100根时获得利润最大,最大利润是76000元.
同学们再见!
授课老师:
时间:2024年9月1日
(2)当0<x≤1时,令22x>16x+3,解得 ;令22x=16x+3,解得 ; 令22x<16x+3,解得 .当x>1时,令15x+7>16x+3,解得x<4;令15x+7=16x+3,解得x=4; 令15x+7<16x+3,解得x>4.综上所述,当快递物品的重量少于 千克或者多于4千克时,选择甲公司更省钱;当快递物品的重量等于 千克或者4千克时,选择甲,乙两家公司费用一样;当快递物品的重量多于 千克且少于4千克时,选择乙公司更省钱.
2.50
(1)在图2中描出表中的数据,观察判断x,y的函数关系,并求秤杆上秤砣到秤纽的水平距离为16厘米时,秤钩上所挂物的质量是多少?(2)已知秤砣到秤纽的最大水平距离为50厘米,这杆秤的可称物重范围是多少?
解:(1)描点如图所示,这些点在一条直线上,故y与x满足一次函数关系.
一次函数(综合与实践)

210
200
x/ 年
0(1980) 1(1984) 2(1988) 3(1992) 4(1996) 5(2000) 6(2004)7(2008) 8(2012)
·
(2观察描出的点的整体分布,他们基本在一条直线附 近波动,y不x之间的函数 关系可以用一次函数去模拟。 即:y=kx+b
确定一次函数关系式,关键是选出两个点的坐标,选 哪两个点呢? y/s
思考
请找出一个能建立数学模型解决实际问题的例子, 然后仿照前面例题去解出来
240
230
·
·
220
210
·
·
·
·
·
·
200
x/ 年
0(1980) 1(1984) 2(1988) 3(1992) 4(1996) 5(2000) 6(2004)7(2008) 8(2012)
这里我们选取从原点向右的第三个点(3, 225)及第6个点(6,223.1)的坐标代入 y=kx+b中,得
12.4
综合与实践:一次函数的模型的应用
(提出问题) 奥运会每4年举办一次,奥运会的 游泳成绩在丌断的刷新,如男子400m自由泳项目, 1996年奥运冠军的成绩比1990年的约提高了30s,下 面是该项目冠军的一些数据:
年份 冠军成绩/s 年份 2000 2004 2008 2012 冠军成绩/s 220.59 223.10 221.86 ?
3k+b=225 6k+b=223.1 解方程组可得:k=-0.7, b=227 所以,一次函数的解析式为:y=-0.7x+227
3. 当把1980年的x值作为0,以后每增加4年得x的 一个值,这样2012年时的x值为8,把x=8代入上式, 得y=-8+227=219(s)
12.4综合与实践一次函数模型的应用-沪科版八年级数学上册教案

12.4 综合与实践一次函数模型的应用-沪科版八年级数学上册教案一、教学目标1.理解一次函数模型的概念和基本特征;2.掌握利用一次函数模型解决实际问题的方法;3.培养学生综合运用数学知识解决实际问题的能力。
二、教学重点1.理解一次函数模型的概念和基本特征;2.掌握利用一次函数模型解决实际问题的方法。
三、教学难点1.培养解决实际问题的能力;2.能够运用数学知识解决跨学科问题。
四、教学内容及安排1. 一次函数模型的概念和基本特征1.通过教学PPT介绍一次函数的概念和定义;2.讲解一次函数的基本特征,如自变量、因变量、斜率、截距等。
2. 一次函数模型解决实际问题的方法Step1: 明确问题解题思路1.分析问题条件;2.明确问题所求。
Step2: 求解过程1.确定自变量和因变量;2.列出函数模型;3.解方程,求出变量值;4.求解问题。
3. 练习与拓展1.在课堂上进行部分例题的讲解;2.布置习题课后练习;3.扩展问题的解决。
五、教学方法1.教师讲授与学生练习相结合;2.合作学习、讨论、呈现等多种方式;3.引导学生思考,培养学生解决问题的能力。
六、教学过程与时间安排1. 教师引入(5分钟)介绍本节课的教学目标和安排,并激发学生学习的兴趣和热情。
2. 阐述一次函数的概念和基本特征(15分钟)1.通过PPT进行讲解;2.询问学生,让学生拓展思路,增加理解。
3. 讲解一次函数模型解决实际问题的方法(25分钟)1.通过教学PPT,讲解解决问题的方法,引导学生理解方法;2.对选择的实际问题进行解题演示;3.鼓励学生自己动手解题。
4. 练习及拓展(20分钟)1.转化思路,增加难度,进行课堂练习;2.接着进行拓展,探究更多实际问题。
5. 课堂总结(5分钟)回顾本节课教学目标,并询问学生遇到的问题和思路拓展。
七、课堂设计说明本节课的教学重点在于提高学生的综合运用数学知识解决实际问题的能力。
在教学过程中,既要让学生掌握一次函数模型的基本概念和特征,又要引导学生把数学知识应用到实际问题中去,帮助学生培养跨学科问题解决的能力。
沪科版数学八年级上册《12.4 综合与实践 一次函数模型的应用》教学设计

沪科版数学八年级上册《12.4 综合与实践一次函数模型的应用》教学设计一. 教材分析《12.4 综合与实践一次函数模型的应用》是沪科版数学八年级上册的教学内容。
本节课的主要内容是一次函数在实际问题中的应用,通过解决实际问题,让学生理解一次函数的意义,提高解决实际问题的能力。
教材中给出了两个实际问题,分别是“工资问题”和“商品打折问题”,旨在让学生通过解决这两个问题,掌握一次函数模型的应用。
二. 学情分析学生在学习本节课之前,已经学习了一次函数的定义、性质和图像。
他们对于一次函数的概念和性质有一定的了解,能够画出一次函数的图像,但对于一次函数在实际问题中的应用还不够熟练。
因此,在教学过程中,教师需要引导学生将所学的一次函数知识与实际问题相结合,提高他们的应用能力。
三. 教学目标1.理解一次函数在实际问题中的意义和作用。
2.学会用一次函数模型解决实际问题。
3.提高学生的数学应用能力和解决问题的能力。
四. 教学重难点1.一次函数模型在实际问题中的应用。
2.如何将实际问题转化为一次函数模型。
五. 教学方法1.案例教学法:通过分析教材中的实际问题,让学生理解一次函数模型的应用。
2.问题驱动法:引导学生主动思考,将实际问题转化为一次函数模型。
3.小组合作法:让学生在小组内讨论、交流,共同解决问题,提高他们的合作能力。
六. 教学准备1.教材《沪科版数学八年级上册》。
2.课件或黑板。
3.实际问题素材。
4.计时器。
七. 教学过程1.导入(5分钟)教师通过引入“工资问题”和“商品打折问题”,激发学生的兴趣,引导学生思考一次函数在实际问题中的应用。
2.呈现(10分钟)教师展示教材中的两个实际问题,让学生明确本节课的学习目标。
3.操练(10分钟)教师引导学生用一次函数模型解决“工资问题”,学生独立思考,小组内交流讨论,共同解决问题。
教师巡回指导,帮助学生克服困难。
4.巩固(10分钟)教师引导学生用一次函数模型解决“商品打折问题”,学生独立思考,小组内交流讨论,共同解决问题。
初中数学八年级上册 综合与实践 一次函数模型的应用-“百校联赛”一等奖

中考专题复习——方案设计型问题教学目标:通过建立方程(组)、不等式(组)、一次函数等数学模型来解决有关的实际问题。
教学重点:选择适当的数学模型来解决有关的实际问题。
教学难点:用分类讨论的思想方法解决有关实际问题。
教学过程:一、创设情景:方案设计型问题,通常是指根据题目提供的信息,综合运用已有的知识,构造解决问题的可行方案,或者针对给出的若干种解决方法,通过计算、证明或动手操作,比较其优劣得失,确定最佳方案的一类问题。
由于它具有联系实际,取材广泛,表述冗杂,解法法灵活等显著特点,因而被作为考查学生分析问题、解决问题能力重要题型。
频繁出现在全国各地的中考数学试卷中。
问题1:淮北市春华家具厂厂长小张去木材厂购买板材,现有A、B、C三种规格板材,价格分别是15元/张、21元/张、25元/张,若将9000元全部用于购买其中两种板材共500张,则有几种购买方案可供选择引入课题:方案设计问题的解法探究二、自主探究:问题2:厂里现有A板材292张、B板材198张,要加工成课桌、餐桌共80张,已知制作一张课桌用A板材2张、B板材3张,已知制作一张餐桌用A板材5张、B板材2张。
1、有哪几种制作方案?2、售出后,课桌、餐桌每张可以分别获利45元、50元,问哪种加工方案获利最大?三、迁移拓展:问题2:经过市场调查发现,该厂决定每套课桌上调a(a≥0)元(不影响其销售量,为回报社会,该厂决定将次销售获利全部捐款给希望工程,试问:选择哪种加工方案将捐款最多?四、课堂小结:这节课你有什么收获请你用自己的话谈谈你的体会。
五、作业:1、必做题:小王的家具长生意兴隆,决定扩大规模,与某木材加工厂联营,联营后共有职工100人,分别从事木材加工、家具制作、销售等三项业务(每人只能从事一项工作)。
已知每人每天可加工板材600张或制造家具15套,每套用板材4张,且木材加工员,家具制造人员、销售人员日工资分别为40元、50元、30元,若企业每天支付工人工资总额4600元,且销售员不少于14人,请你帮忙设计人事分工方案。
新泸教版数学八年级上册课件:12.4 综合与实践 一次函数模型的应用

( 1 )以海拔高度为x轴,根据上表提供的数据在如图的平面直角坐标系中描点并连线. ( 2 )观察( 1 )中所画出的图象,猜想y与x之间的函数关系,求出所猜想的函数表达式,并根据表 中提供的数据验证你的猜想.
8.某水果批发市场香蕉的价格如下表:
购买香蕉数 ( 千克 )
不超过 20 千克
20 千克以上 但不超过 40
千克
40
千克以上
每千克价格 6 元 5 元
4元
若小丽购买香蕉x千克( x大于40 )付了y元,则y关于x的函数关系式为 y=4x+60 .
9.一次越野跑中,当小明跑了1600米时,小刚跑了1400米,小明、小刚在此后所跑的路程y( 米 ) 与时间t( 秒 )之间的函数关系如图,则这次越野跑的全程为 2200 米.
12.4 综合与实践 一次函数模型的应用
知识点1 构建一次函数模型求表达式
1.某超市进了一些食品,出售时要在进价的基础上加一定的利润,其数量x( 千克 )与售价y( 元 ) 的关系如下表:
数量 x( 千克 ) 1 2
3
4
5
…
售价 y( 元 ) 6+0.5 12+1.0 18+1.5 24+2.0 30+2.5 …
所以需要携带外套上山.
12.在北方冬季,对某校一间坐满学生、门窗关闭的教室中二氧化碳的总量进行检测,部分数据 如下:
教室连续使用时间 x( 分 )5 10 15 20 二氧化碳总量 y( m3 ) 0.6 1.1 1.6 2.1
经研究发现,该教室空气中二氧化碳总量y( m3 )是教室连续使用时间x( 分 )的一次函数. ( 1 )求y与x的函数表达式.( 不要求写出自变量x的取值范围 ) ( 2 )根据有关资料推算,当该教室空气中二氧化碳总量达到6.7 m3时,学生将会稍感不适,请通 过计算说明,该教室连续使用多长时间学生将会开始稍感不适? ( 3 )如果该教室在连续使用45分钟时开门通风,在学生全部离开教室的情况下,5分钟可将教室 空气中二氧化碳的总量减少到0.1 m3,求开门通风时教室空气中二氧化碳平均每分钟减少多少 m3?
一次函数模型的应用
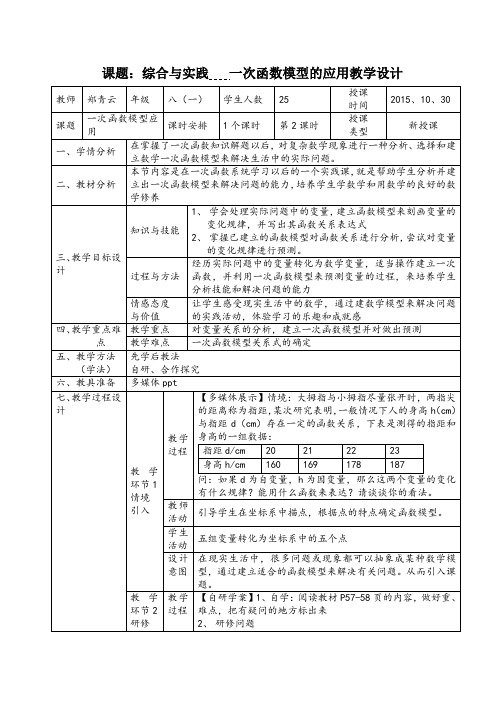
2、观察点的特征,确定选用的函数形式,并根据已知的数据求出函数表达式
3、进行检验
4、应用这个函数模型解决问题
九、作业设计
课内;教材P65第3题
课外:完成教材P59的问题3
十、教学反思
另附文
(3)观察描出的点的分布情况,猜测两个变量x、y之间是何种函数关系?
(4)用待定系数法求出函数的解析式。思考:选择哪两点来写这个函数的解析式?
(5)根据所得的函数预测2012年伦敦奥运会时该项目的冠军成绩。思考:能否用此数学模型预测2016年奥运会的该项目冠军的成绩呢?
3、通过学习,你能总结出建立两个变量之间的函数模型,需要哪几个步骤?
情感态度
与价值
让学生感受现实生活中的数学,通过建数学模型来解决问题的实践活动,体验学习的乐趣和成就感
四、教学重点难点
教学重点
对变量关系的分析,建立一次函数模型并对做出预测
教学难点
一次函数模型关系式的确定
五、教学方法
(学法)
先学后教法
自研、合作探究
六、教具准备
多媒体ppt
七、教学过程设计
教学环节1
情境
引入
教学过程
【多媒体展示】情境:大拇指与小拇指尽量张开时,两指尖的距离称为指距,某次研究表明,一般情况下人的身高h(cm)与指距d(cm)存在一定的函数关系,下表是测得的指距和身高的一组数据:
指距d/cm
20
21
22
23
身高h/cm
160
169
178
187
问:如果d为自变量,h为因变量,那么这两个变量的变化有什么规律?能用什么函数来表达?请变量?自变量和因变量是什么?它们之间是什么函数关系?
安徽省八年级数学上册第12章一次函数:综合与实践一次函数模型的应用pptx课件新版沪科版

匀速驶向索道口.两辆大巴车行驶的路程 s (km)随行驶的
时间 t (h)变化的图象如图所示.
(2)求甲大巴车比乙大巴车提前多少
小时到达索道口.
1
2
3
4
5
6
7
解:(2)令70 t -40=100,解得 t =2.设乙大巴车 s 与 t 的
函数表达式为 s = mt ,把(1.5,65)代入,得1.5 m =
得0< x <
> ,
15.因为 x , y 都是整数,所以 x 为3的倍数,所以 y =
- x +10(0< x <15,且 x 为3的倍数).
1
2
3
4
5
6
7
6. [2023·合肥月考]某水果种植基地计划租几辆货车装运苹果
和橘子共60 t(两种水果都装)去外地销售,要求每辆货车
只能装一种水果,且必须装满.设装运苹果的货车有 x
65,解得 m =
,所以 s =
t ,令
t =100,解
Hale Waihona Puke
得 t = . -2= (h),所以甲大巴车比乙大巴车提前 h
到达索道口.
1
2
3
4
5
6
7
最值及择优方案问题
5. [2024·南京月考]某电脑公司经营 A , B 两种台式电脑,分
析过去的销售记录可以知道:每台 A 型电脑可盈利200
辆,装运橘子的货车有 y 辆,销售获得的总利润为 W 元.
根据表格中提供的信息,解答问题.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)写出y与x之间的函数表达式;
(2)旅客最多可免费携带多少千克的行李?
解(1)设此一次函数表达式为:y=kx+b(k≠0,k,b为常数)
12.4综合与实践 一次函数模型的应用
数学组:张家硕
2018年10月12日
学习目标
知识目标: 1、进一步理解一次函数与二元一次方程的
关系; 2、掌握运用二元一次方程和一次函数解决
实际问题的方法。 能力目标:
1、培养同学们分析问题、运用所学的知识 解决实际问题的能力;
2、体会对应关系和数形结合思想。 情感目标:
60
s甲 20t
40
可以分别作出两人 20 s 与t 之间的关系图象, 找出交点的横坐标就行了! (A0)
11 22 33 4 t
小明的方法求出的 结果准确吗?
用方程 解 行程问题
A、B 两地相距150千米,
1小时后乙距A
甲、乙两人骑自行车分别从A、
地120千米, 即乙的
B 两地同时相向而行。假设他 小彬 速度是 30千米/时,
11 2 3 4 x
2、在弹性限度内,弹随簧堂练的习 y
长度y(厘米)是所挂物体质量
17 16
x(千克)的一次函数。当所挂 15
14
物体的质量为1千克时,弹簧长 13
15厘米;当所挂物体的质量为3 12
l1
11
千克时,弹簧长16厘米。写出 10
y 与 x 之间的关系式,并求出
9 8
所挂物体的质量为4千克时弹簧 7
s 20t s 150 30t
消去 s
t3
在以上的解题过程中你受到什么启发?
用一元一次方程的 方法可以解决问题
用图象法可以 解决问题
小彬
小明
用作图象的方法可以
直观地获得问题的结果, 但有时却难以准确,为了 获得准确的结果,我们一 般用代数方法。
小颖
用方程组的方法可 以解决问题
例2、某长途汽车客运站规定,乘客可以免费携
答下列问题:
s
(1)途中乙发生了什么事,
(2)他们是相遇还是追击;
P
(3)他们几时相遇。
D
12
E
10
AB
8
0
0.5 1 1.2
t
y/元
6000
5000
l11 l22
4000
3000
2000
1000
O 1 23 4 5 6
x/ 吨
例:
海B
A
公
下图中 l1 ,l2 分别表示A,B离岸 岸
起两船相对于海岸的距离s与追赶时
海
间t之间的关系。
根据图象回答下列问题:
当时间t等于多少分钟时,我边防快艇B能够追赶上A。
s /海里
8 6 4 2
议一议:
A、B 两地相距150千米,甲、乙两人骑
自行车分别从A、B 两地相向而行。假设他 们都保持匀速行驶,则他们各自到A地的距
离 s(千米)都是骑车时间 t (时)的一次函
数. 1小时后乙距A地120千米, 2小时后甲距A地 40千米.
问:经过多长时间两人相遇 ?
议一议: A、B 两地相距150千米,甲、乙两人骑自行车分别从
A、B 两 两地 140
图象表示
相向而行。假设他们都保持匀速行 驶,则他们各自到A地的距离s(千米)
120
s乙 150 30t
都是骑车时间t(时)的一次函数.
100
1 时后乙距A地120千米,
2 时后甲距A地 40千米.
80
l2
l1
问 经过多长时间两人相遇 ?
是骑车时间 t (时) 的一次函数.
当t=1时,s=120。将它们分
1 时后乙距A地120千米,
别代入s=kt+b中,可以求出k
2 时后甲距A地 40千米.
、b的值,也即可以求出乙 s
问 经过多长时间两人相遇 ?
与t 之间的函数表达式。
同样可求出甲s与t之间的函
数表达式。
再联立这两个表达式,求解
方程组就行了。
们都保持匀速行驶,则他们各
自到A地的距离s(千米)都是骑 车时间t(时)的一次函数.
1 时后乙距A地120千米, 2 时后甲距A地 40千米.
2 时后甲距A 地 40千米, 故甲的速度是 20千米/时,
由此可求出甲、乙两人的 速度。
问 经过多长时间两人相遇 ?
你明白他的想法吗?
设同时出发后t 时相遇, 则 20 t 30 t 150
l22A l11 B
O
2 4 6 8 10
t /分
思考题:
ax 3y 5
2、已知方程组 2x by 1
,
所对应的一次函数的图象表示如
图,试求出a-b的值。
Y
0 1/2
-1
X
1、右图中的两直线l1 、l2 的交点坐标可以看作
y 2x 1
方程组
y
x
4
的解
y 44
l1
33
2
l2 1
-1 0 -1
A、B 两地相向而行。假设他们都保持匀速行驶,则他们
各自到A地的距离 s(千米)都是骑车时间 t (时)的一次
函数. 1小时后乙距A地120千米, 2小时后甲距A地 40千米.
问:经过多长时间两人相遇 ?
直线型图表示
2时,40千米
甲 A
120千米
B 1时 乙
s甲 20t
s乙 150 30t
用图象法 解 行程问题
根据题意,可得方程组:
5 60k b 10 90k b
k 1/ 6 解得: b 5
(2)当x=30时,y=0。
∴y=1/6x—5
所以旅客最多可免费携带30千克的行李。
引例. 如图,l11反映了某公司产品的销售收入与销售量的 关系,l22反映了该公司产品的销售成本与销售量的关 系,根据图意填空: 当销售量为4000元时,销售收入等于销售成本。
用他的方法做一做,看 看和你的结果一致吗?
t=3
求出s与t之间的关系式,联立解方程组
A、B 两地相距150千米,甲、
对于乙,s 是t
乙两人骑自行车分别从A、B 两地相
的一次函数,
向而行。假设他们都保持匀速行驶, 则他们各自到A 地的距离s (千米) 都
小颖
可设 s=kt+b。 当t=0时,s=150;
的长度。
6 5
4
3
y = 0.5x + 14.5
2
1
当 x = 4 时, y = 16.5。
00
11 2 33 44 5 x
课外思考
1、用作图象法解方程组
23x 17y 63 17x 23y 57
课外思考
2、如图,L1和L2分别表示甲走路和乙骑自
行车(在同一条路上)行走的路程s(千米)
与时间t(小时)之间的关系,观察图象,回
体会数学知识间的联系与转化,培养探究 创新精神。
复习提问:
一:二元一次方程的解与相应的一次函数图象上点 对应。
以方程 x+y=3 的解为坐标的所有点组成的图形
就是 一次函数 y=3_-x 的图象.
三、用图象法解二元一次方程组的一般步骤: 1.把两个方程都化成函数表达式的形式。 2.画出两个函数的图象。 3.找出交点坐标,交点坐标即为方程组的解。
